Abstract
The “polar data gap” is a region around the North Pole where satellite orbit inclination and instrument swath for SMMR and SSM/I-SSMIS satellites preclude retrieval of sea ice concentrations. Data providers make the irregularly shaped data gap round by centering a circular “pole hole mask” over the North Pole. The area within the pole hole mask has conventionally been assumed to be ice-covered for the purpose of sea ice extent calculations, but recent conditions around the perimeter of the mask indicate that this assumption may already be invalid. Here we propose an objective, partial differential equation based model for estimating sea ice concentrations within the area of the pole hole mask. In particular, the sea ice concentration field is assumed to satisfy Laplace’s equation with boundary conditions determined by observed sea ice concentrations on the perimeter of the gap region. This type of idealization in the concentration field has already proved to be quite useful in establishing an objective method for measuring the “width” of the marginal ice zone—a highly irregular, annular-shaped region of the ice pack that interacts with the ocean, and typically surrounds the inner core of most densely packed sea ice. Realistic spatial heterogeneity in the idealized concentration field is achieved by adding a spatially autocorrelated stochastic field with temporally varying standard deviation derived from the variability of observations around the mask. To test the model, we examined composite annual cycles of observation-model agreement for three circular regions adjacent to the pole hole mask. The composite annual cycle of observation-model correlation ranged from approximately 0.6 to 0.7, and sea ice concentration mean absolute deviations were of order or smaller. The model thus provides a computationally simple approach to solving the increasingly important problem of how to fill the polar data gap. Moreover, this approach based on solving an elliptic partial differential equation with given boundary conditions has sufficient generality to also provide more sophisticated models which could potentially be more accurate than the Laplace equation version. Such generalizations and potential validation opportunities are discussed.
1. Introduction
Declines in Arctic sea ice provide some of the most compelling evidence of climate change, and quantitative assessment of sea ice trends from 1979 to the present relies heavily on satellite-based passive microwave retrievals of sea ice concentrations [1,2]. The satellite platforms used to observe these long-term concentration trends are the Special Sensor Microwave Imager/Sounder (SSMIS) and its two predecessors: the Special Sensor Microwave/Imager (SSM/I), and the Scanning Multichannel Microwave Radiometer (SMMR). Data from these platforms suffer from a “polar data gap”, which is an irregularly-shaped region around the pole that is never measured due to orbit inclination and instrument swath. As described in the data documentation [3,4], the data gap is made round by applying a circular “pole hole mask”. The radius of the mask is platform-dependent, and was decreased from 611 km to 311 km in July 1987, and then decreased again to 94 km in January 2008 (Table 1; blue circles, Figure 1). Researchers often resort to some assumptions or interpolation method to account for the missing values within the polar data gap. For example, the area of the pole hole mask is often assumed to be “ice-filled” for sea ice extent calculations (extent is the total ice-filled area, meaning at least 15% concentration). Recent conditions around the perimeter of the pole hole mask suggest that the ice-filled assumption may no longer be valid (e.g., Figure 1).

Table 1.
For the circular “pole hole mask” covering the polar data gap: the satellite platform, the hole radius, the latitude of the hole’s outer edge, and the applicable time periods.
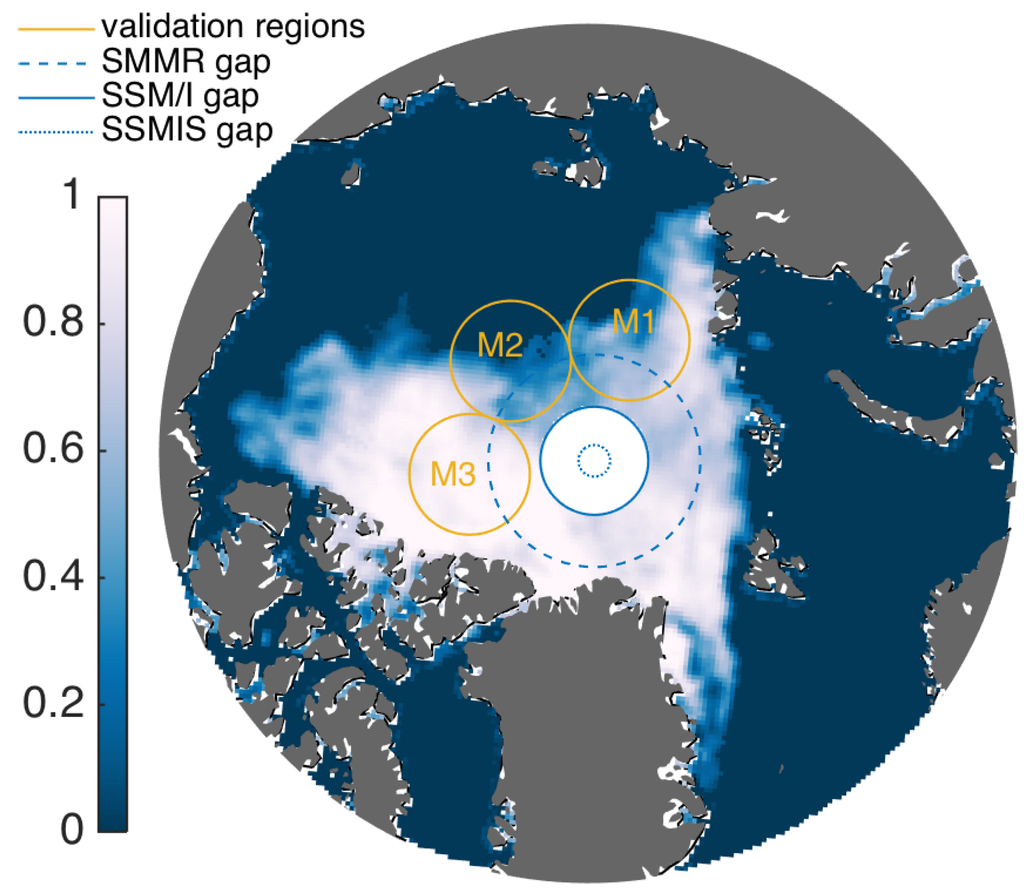
Figure 1.
Yellow outlines indicate the three circular regions used to estimate the parameters of the stochastic term. These three circular regions were also used to validate and assess performance of the solution to Laplace’s equation. Blue circles show polar data gap extent for the three sensors indicated in the legend (see also Table 1). Shading indicates sea ice concentrations for 3 September 2007.
Here we propose an objective and automated method for estimating sea ice concentrations within the area of the pole hole mask using a partial differential equation with boundary conditions taken from the circular perimeter around the mask. Realistic spatial heterogeneity in the concentration field is obtained by adding a spatially autocorrelated stochastic field with temporally varying standard deviation derived from the variability of observations around the mask. The method is presented in Section 3, results are shown in Section 4, discussion is provided in Section 5, and conclusions are in Section 6.
2. Data
We explored filling the polar data gap in three principal passive microwave sea ice concentration data sets from the National Snow and Ice Data Center (NSIDC): concentrations based on the Bootstrap algorithm [5], concentrations based on the National Aeronautics and Space Administration (NASA) Team algorithm [6], and concentrations from the Climate Data Record of Passive Microwave Sea Ice Concentration (CDR) which is a blending of different algorithms intended to produce a consistent record over time [4]. The presented analyses use the NASA Team algorithm, which tends to produce lower concentrations [7], and hence more challenging cases for filling the polar data gap (i.e., boundary concentrations uniformly close to 1.0 can be realistically treated with more trivial interpolation). Using the other two data sets (bootstrap and CDR), the proposed model performed comparably (not shown) to the NASA Team algorithm data results presented in Section 4.
3. Method
3.1. Formulation of Data Fill Model
In prior publications (e.g., [8]), we filled the polar data gap (region here denoted G) using methods based on “thin plate splines” or other radial basis functions [9]. In exploring alternative methods for the present study, we also experimented with techniques similar to a modified spherical Shepard’s interpolant [10] and various planar multiquadric methods [11]. These families of interpolation techniques can produce seemingly realistic fills at modest computational expense, but we are here interested in presenting and exploring advantages of fills based on solutions to partial differential equations. Specifically, we investigate ideas emerging from “inpainting” or “disocclusion” techniques [12], meaning that a partial differential equation (PDE) is solved in a domain to replace missing data within its perimeter, given known boundary conditions on the perimeter. Here, we propose to model the sea ice concentration field (f) in a region G on Earth’s surface, the pole hole mask, as the sum of two functions
where λ is longitude and is latitude, or where . The scalar field ψ is assumed to be a solution of Laplace’s equation
in spherical coordinates, and Ω is a stochastic term that provides realistic spatial heterogeneity associated with deviations of the concentration field from ψ. We show below that Ω estimated from observations exhibits a characteristic spatial autocorrelation, and we incorporate this into its formulation (Section 3.2).
Dirichlet boundary conditions for ψ are obtained from ice concentration data on the pole hole mask boundary . Then a unique harmonic function ψ, satisfying Equation (2), exists if is sufficiently smooth and the ice concentration is a continuous function along . Using m to denote the number of grid points within the mask, we have m unknown sea ice concentrations for each day. Expressing the Laplacian as a second-order finite difference operator gives m linear equations in m unknowns with boundary conditions specified by the concentrations on . The unknown concentrations are then obtained using computationally efficient methods for solving sparse linear systems [13]. For convenience, we hereafter work with the Cartesian coordinates of the polar stereographic projection used by NSIDC. This projection is a conformal mapping, so also solves Laplace’s equation when projected back onto the sphere as .
3.2. Stochastic Term Ω
Satellite-retrieved sea ice concentration fields contain noise or uncertainty associated with the passive microwave retrieval algorithms, and also heterogeneity due to physical processes such as melt pond formation and the various thermodynamic and dynamic controls on concentration [14]. Here, we model Ω as spatially correlated, zero-mean additive Gaussian noise with two parameters: σ, the standard deviation of the surface amplitude, and η, the spatial autocorrelation length scale. They are both estimated using data from regions near the pole hole mask (yellow circles M1–M3, Figure 1). These circles were chosen to be the size of the SSM/I pole hole mask used for the majority of the record (Table 1), they were positioned close to the pole hole mask but away from regions where open ocean is common, and they were arranged so as to be non-overlapping. The parameter σ has a strong annual cycle as shown below, but is assumed spatially uniform on any given day of year.
For each day of the year, we collected three samples of the stochastic function Ω by first solving Laplace’s equation to obtain ψ within each of the circular regions M1–M3 in Figure 1. Given the solution ψ, we then solved Equation (1) to obtain a sample stochastic field via
where is the observed sea ice field from region , j = 1,2,3. The spatial standard deviation of for all the M regions displayed together (Figure 2) motivates a model of σ with higher values in the melt season. Specifying that t denotes decimal day of the year, the model
accounts for 52% of the variation in σ with , , , and .
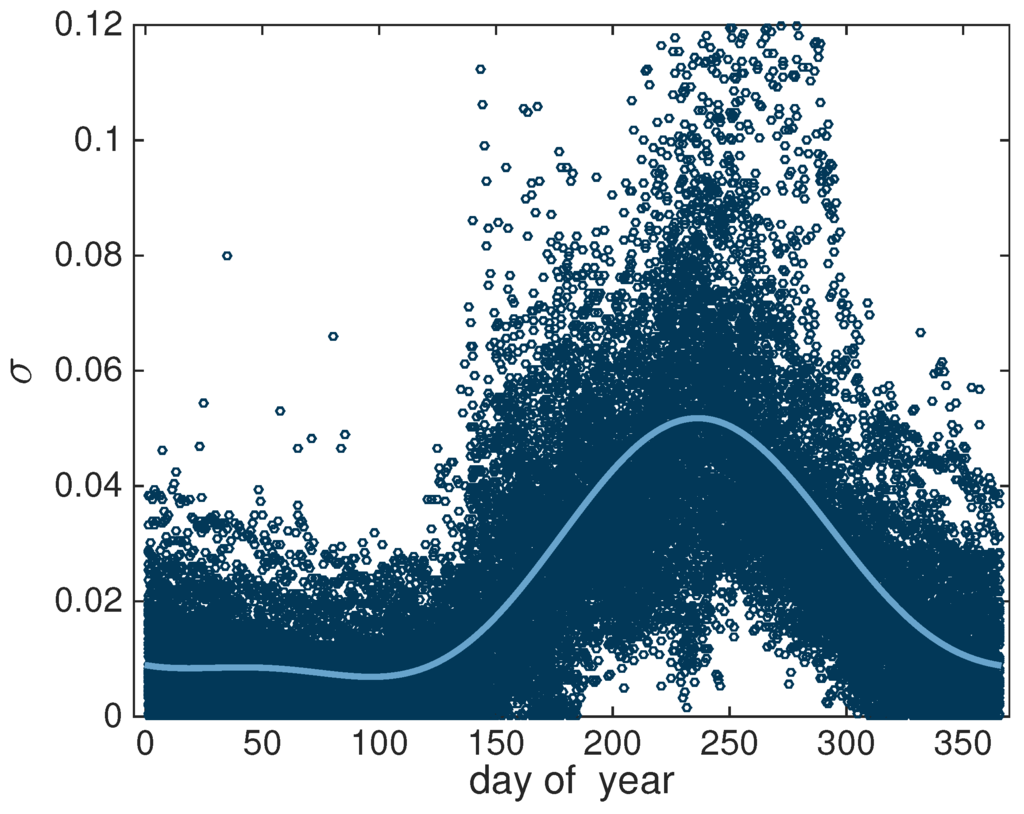
Figure 2.
Circles indicate empirical estimates of the standard deviation σ of the stochastic term Ω, as a function of day of the year for 1988–2013, where 1988 is selected because it is the first full year after adoption of the moderately-sized pole hole mask (radius 311 km, Table 1). The curve is a fit of Equation (4) with . Values exceeding 0.12 (less than 1% of the data) are not shown, but were included in the curve fit.
We defined η as the spatial autocorrelation e-folding distance, and we calculated it for each row and column of grid points in the smallest square capturing M1, M2, or M3 for each day of the year for 1988–2013. The parameter η had neither a strong annual cycle nor a strong anisotropy (e.g., averaged 60 km versus 62 km in two orthogonal directions), and we prescribed η to be 61 km.
To generate a realization of Ω, we produced a field of spatially uncorrelated Gaussian noise with standard deviation σ. We then introduced the desired spatial autocorrelation by convolution of Γ with the Gaussian function
which yields η as the autocorrelation e-folding length scale (e.g., [15]). The full field Ω is defined by
where the convolution is achieved via Fourier transform for computational efficiency, the symbol · denotes point-wise multiplication, h is the grid spacing, and the coefficient is included to approximately recover σ as the root mean square amplitude of Ω. Having calculated a solution ψ and a stochastic realization Ω, we restricted concentration to the range by imposing
4. Results
4.1. Illustrative Examples
The sea ice concentration field f is demonstrated for the 6 January 1985 polar data gap (Figure 3a–c) and for the 30 August 2007 polar data gap (Figure 3d–f). In the first example, the boundary conditions show lower concentrations toward the lower right of the gap (Figure 3a), and the model fills the circle with a modest concentration gradient (Figure 3b,c). On the other hand, the observations in Figure 3d have a large concentration range along the perimeter of the pole hole mask (), which is visualized in three dimensions with the shaded surface in Figure 4a. The term in Figure 4b captures the large-scale concentration gradient, but is very smooth and highly idealized because Laplace’s equation precludes local extrema. Addition of the stochastic term within the fill helps it to blend realistically with the “texture” and small-scale heterogeneity evident in surrounding observations (Figure 3e,f and Figure 4d,e).
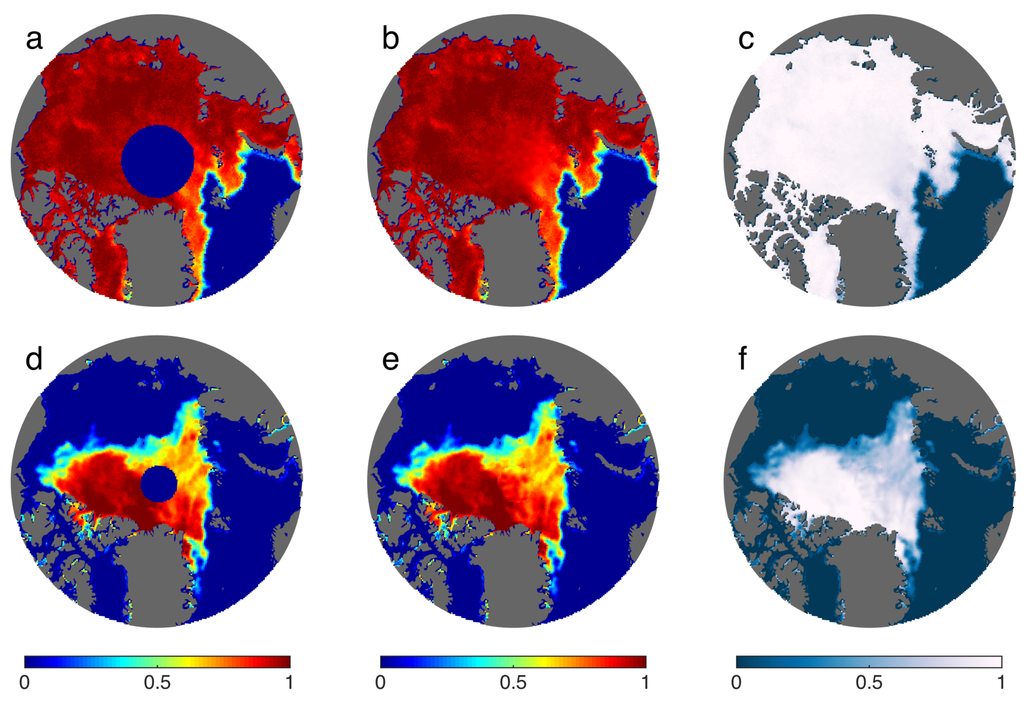
Figure 3.
Examples of filling the polar data gap. For 6 January 1985: (a) sea ice concentration; (b) sea ice concentration with polar data gap filled using f (solution to Laplace’s equation plus a stochastic field Ω); and (c) same as (b) but color scheme follows nsidc.org; (d–f) Same as (a–c), but for 30 August 2007.
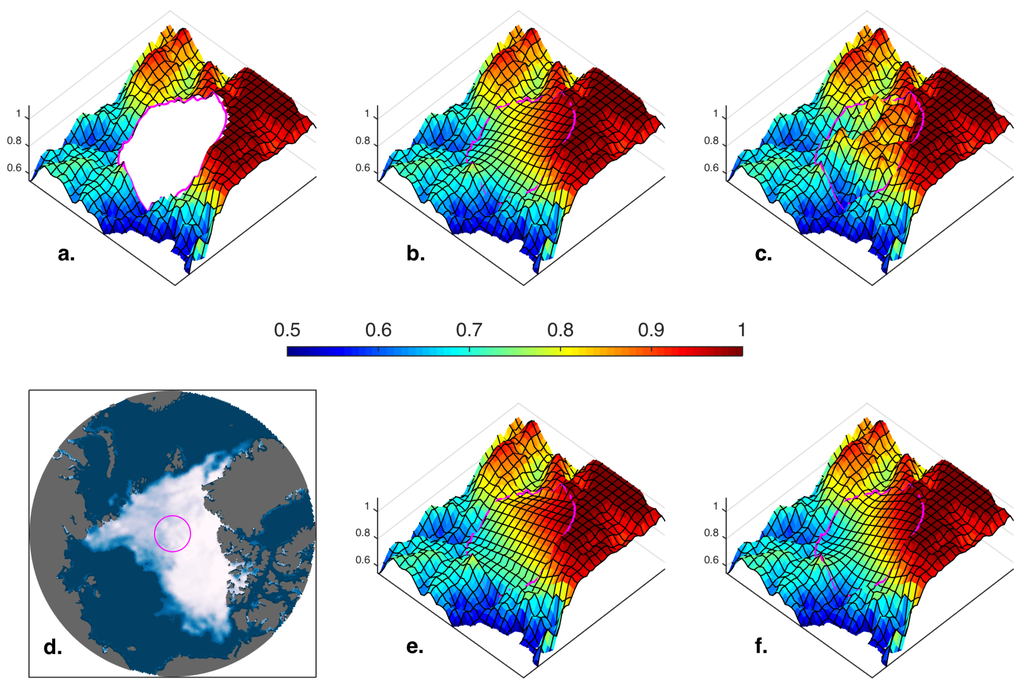
Figure 4.
A three-dimensional view of the 30 August 2007 example from Figure 3d–f. Shading and surface elevation indicate concentration, and black curves are provided to help visualize the three dimensionality of the surface. (a) Observed sea ice concentrations around the polar data gap; (b) polar data gap replaced by solution to Laplace’s equation ; (c) polar data gap replaced by ψ plus the stochastic term Ω; (d) same as Figure 3f but rotated to illustrate the geographic orientation of the other panels; (e) polar data gap replaced by bilinear interpolation; and (f) polar data gap replaced by thin plate spline.
For comparison with the solution to Laplace’s equation in Figure 4b, we show two interpolation methods – bilinear in Figure 4e and thin plate spline in Figure 4f. The bilinear interpolation captures the large-scale concentration gradient, but its formulation yields an overall lack of realistic curvature. The thin plate spline interpolation appears more realistic than the bilinear interpolation and resembles the solution to Laplace’s equation (compare Figure 4b,f), and could thus be a satisfactory replacement for ψ in the formulation of the model Equation (1). The solution ψ is preferred, however, in part because it yields slightly better correlations and mean absolute deviations under observational validation as presented in Section 4.2. Moreover, ψ is a solution to a partial differential equation, thus rooting the model in a mathematical framework whose generalization may ultimately yield insight into physical processes governing sea ice concentration variability within the data gap (Section 5).
4.2. Validation and Performance Assessment
To validate the data fill model and assess performance, we generated ψ for the three regions M1–M3 (Figure 1) for each day of the year from 1988–2013. Because Ω in Equation (1) is stochastic, it has zero correlation with observations, so the performance analysis is on ψ rather than the full f. Our validation method assumes that the three selected regions near the polar data gap are representative of concentration conditions within the gap itself. Validation results are presented for each region as composite annual cycles (Figure 5), meaning values were averaged across years to produce one value for each day of the year.
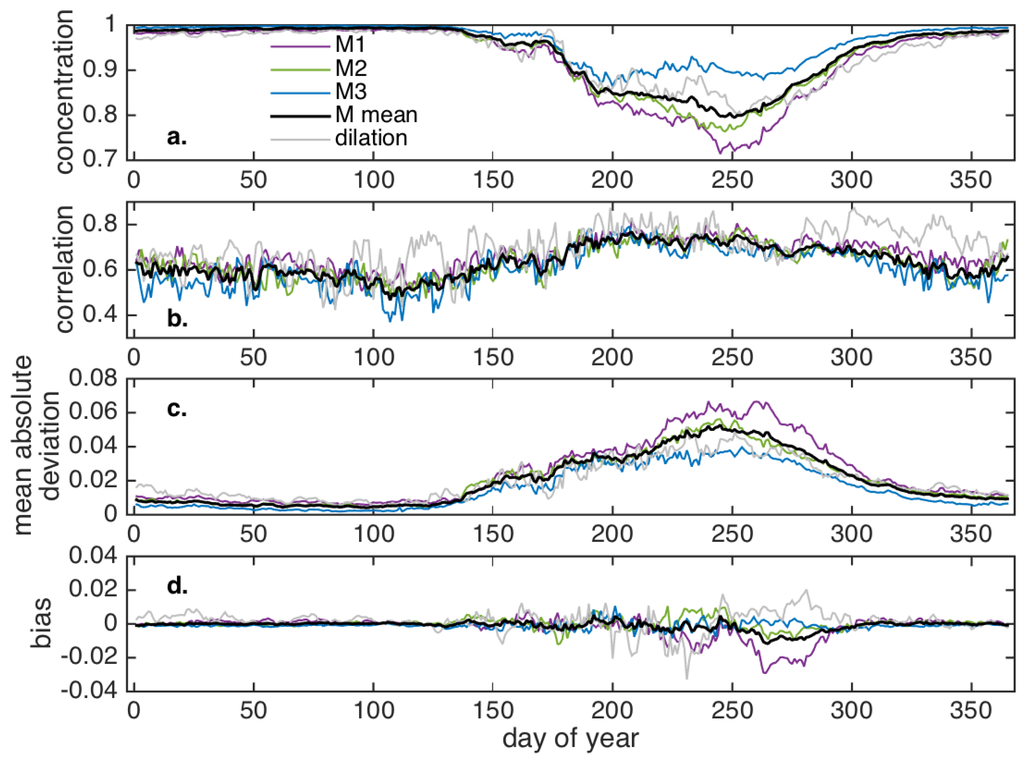
Figure 5.
For each of the regions M1–M3 in Figure 1, color curves indicate values averaged by day of the year: (a) mean observed sea ice concentration; (b) spatial correlation between observed sea ice concentration and the solution to Laplace’s equation ψ; (c) the mean absolute deviation between observed sea ice concentration and ψ; and (d) the spatially averaged bias between observed sea ice concentration and ψ. In each panel, the black curve is the average across the three M regions and the gray curve corresponds to validation via dilation of the polar data gap as described in Section 4.2.
All three regions had concentrations close to 1.0 for days of year 1–130 (Figure 5a), and we refer to this as the “high-concentration period”. There was little observed variance for ψ to account for during this period, with the observed daily concentration range within the M regions averaging only 0.04 to 0.07 (not shown). Correlation between ψ and observed concentration was 0.63 averaged across the three regions during the high-concentration period (Figure 5b), meaning that ψ accounted for approximately 40% of the observed variance. Composite mean absolute deviations were very small during the high-concentration period, averaging around 0.01 (Figure 5c), with composite bias averaging (Figure 5d).
As melt began after day of year 130, concentrations decreased in all three M regions, with declines in M1 and M2 being approximately twice as large as those in M3 (Figure 5a). Correlation between ψ and observed concentration increased to values above 0.7 by day 200, meaning that ψ accounted for more than half of the observed variance (Figure 5b). Composite mean absolute deviations increased with melting, but remained of order (Figure 5c). Composite bias also increased in magnitude during lower concentrations (Figure 5d), reaching close to −0.03 in the M1 region on day of year 264 because local maxima of concentration formed on the interior of this region during several of the analyzed years (recall that the solution to Laplace’s equation precludes local extrema). Averaged across the three M regions, the composite bias remained smaller than in magnitude and averaged overall (black curve, Figure 5d).
As an additional validation, we also dilated the SSMIS 94-km radius gap to the 311-km radius of its SSMI/I predecessor, and compared modeled and observed concentrations within the 311-km radius region (the 94-km and 311-km radius gaps are indicated by dotted and solid blue circles, respectively, Figure 1). This dilation-based validation has more sampling variability than the M-region analysis because the 94-km radius is available for only 2008–2015, but the results are similar for the two validations (gray curves, Figure 5).
As noted in Section 4.1, a thin plate spline could provide a reasonable substitute for ψ in the model formulation (compare Figure 4b,f). We repeated the above-described observational validation procedure for the M regions, but now replacing ψ with a thin plate spline, and found a slight degradation in overall performance. Specifically, correlation averaged for the thin plate spline versus for ψ, and the overall mean absolute deviation was approximately 8% larger for the thin plate spline (not shown).
5. Discussion
The model proposed here is toward the simpler end of the spectrum of possible methods. An even simpler fill method could replace the solution to Laplace’s equation (ψ in Equation (1)) with a linear function of the form
where the γ parameters minimize, for example, the sum of squared deviations from observations along the gap’s perimeter. The simplest possible model would be the special case of Equation (8) where , meaning the gap is filled by a constant. Using a PDE such as Laplace’s equation enables the solution to agree with observations on the boundary , which is clearly desirable. We could instead specify the normal derivative of concentration on the boundary rather than the concentration itself (i.e., impose Neumann boundary conditions), but then existence imposes restrictions on the derivative and we have uniqueness only up to a constant.
If we progress in complexity beyond the model proposed here, we could consider generalizations of Laplace’s equation such as Poisson’s equation or time-dependent formulations. The incorporation of a local conductivity or diffusivity field , written
would enable the PDE portion of the model (ψ) to accommodate a much broader class of concentration features including local extrema precluded by Laplace’s equation. At maximal conceptual complexity, and perhaps also maximal computational expense, we have dynamic-thermodynamic sea ice models that simulate evolution of fractional ice coverage across multiple thickness classes, and it would be possible to fill the polar data gap using this class of models along with suitable initial and boundary conditions.
We also sought relative simplicity in our treatment of the stochastic term . Its amplitude clearly motivated a time-dependent standard deviation, but we assumed this parameter was homogeneous in space for any given day of the year. Observations moreover supported a relatively simple isotropic autocorrelation e-folding length scale η for the stochastic term. The preceding produces realistic results suitable for displaying single maps or initializing a simulation. Other applications may motivate a more sophisticated treatment where the stochastic term is an evolving space-time field with temporal as well as spatial autocorrelation, and this model could be estimated as, for example, a vector autoregressive process. Finally, our formulation of the stochastic term uses parameters (η and σ) that are empirically estimated from observations, and further advances in realism may be possible by adjusting parameters of the stochastic realization to reflect, for example, surrounding variance and anisotropy in the observed ice field.
The availability of concentration data within the pole hole mask now or in the future presents an opportunity to enhance the proposed model. Examples of data available now include values within the irregular edge of the polar data gap that are currently covered by the circular pole hole mask, but their inclusion may invalidate the assumption that the perimeter is sufficiently smooth. Considering hypothetical data sets, a single measurement at the pole could provide an additional Dirichlet boundary condition for solving Laplace’s equation. If the new data are distributed sparsely across the gap, they could pair with the boundary conditions around the perimeter to inform a least-squares solution to Laplace’s equation or, perhaps more effectively, to inform the stochastic heterogeneity field that is added to the solution to Laplace’s equation.
6. Conclusions
A conceptually and computationally simple model was proposed for objective, automated filling of the polar data gap in passive microwave sea ice concentration data. The formulation of the model is largely a solution to a PDE (here we used Laplace’s equation) with boundary conditions taken from the circular perimeter of the pole hole mask. The solution of the PDE was added to a spatially autocorrelated, additive Gaussian white noise that mimics the spatial heterogeneity evident in surrounding observations of sea ice concentration. The standard deviation of the stochastic term fit to observations had a prominent annual cycle, with maxima during low sea ice concentrations. The stochastic term has cosmetic utility, helping the fill data to blend naturally with surrounding observations, and it also provides a realistic spatial heterogeneity enabling observations to be used as initial conditions for simulation.
The fill also enables objective treatment of the missing data for the purpose of calculating extent and area trends. The polar data gap has conventionally been assumed to be ice-covered for the purpose of extent calculations, but recent conditions around the perimeter of the gap indicate that this assumption may already be invalid. Fortunately, the trend toward lower concentrations near the pole has been accompanied by two substantial reductions in the radius of the pole hole mask, mitigating uncertainty associated with the assumptions made in treating the missing data. Based on validation and skill assessment in circular regions around the pole hole mask, the PDE portion of the fill maintains composite mean absolute deviations of order or smaller, and accounts for 40%–50% of the variance in observed concentrations depending on region.
Acknowledgments
The authors gratefully acknowledge support from the Division of Mathematical Sciences at the U.S. National Science Foundation (NSF) through Grants DMS-1413454 and DMS-0940249. We also thank the NSF Math Climate Research Network for their support of this work. Three anonymous reviewers provided comments that helped to improve an earlier version of the manuscript.
Author Contributions
Courtenay Strong and Kenneth Golden conceived the research project and contributed to writing the manuscript. Courtenay Strong performed the coding and data analysis.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cavalieri, D.J.; Parkinson, C.L. Arctic sea ice variability and trends, 1979–2010. Cryosphere 2012, 6, 881–889. [Google Scholar] [CrossRef]
- Simmonds, I. Comparing and contrasting the behavior of Arctic and Antarctic sea ice over the 35 year period 1979–2013. Ann. Glaciol. 2015, 56, 18–28. [Google Scholar] [CrossRef]
- Cavalieri, D.; Parkinson, C.; Gloersen, P.; Zwally, H.J. Sea Ice Concentrations from Nimbus-7 SMMR and DMSP SSM/I Passive Microwave Data; National Snow and Ice Data Center: Boulder, CO, USA, 1996. [Google Scholar]
- Meier, W.; Fetterer, F.; Savoie, M.; Mallory, S.; Duerr, R.; Stroeve, J. NOAA/NSIDC Climate Data Record of Passive Microwave Sea Ice Concentration; National Snow and Ice Data Center: Boulder, CO, USA, 2011. [Google Scholar]
- Comiso, J.C. Characteristics of arctic winter sea ice from satellite multispectral microwave observations. J. Geophys. Res. 1986, 91, 975–994. [Google Scholar] [CrossRef]
- Cavalieri, D.J.; Gloersen, P.; Campbell, W.J. Determination of sea ice parameters with the NIMBUS 7 SMMR. J. Geophys. Res. 1984, 89, 5355–5369. [Google Scholar] [CrossRef]
- Notz, D. Sea-ice extent and its trend provide limited metrics of model performance. Cryosphere 2014, 8, 229–243. [Google Scholar] [CrossRef]
- Strong, C.; Rigor, I.G. Arctic marginal ice zone trending wider in summer and narrower in winter. Geophys. Res. Lett. 2013, 40, 4864–4868. [Google Scholar] [CrossRef]
- Duchon, J. Splines minimizing rotation-invariant semi-norms in Sobolev spaces. In Constructive Theory of Functions of Several Variables; Springer: Berlin, Germany; Heidelberg, Germany, 1977; Volume 571, pp. 85–100. [Google Scholar]
- Cavoretto, R.; De Rossi, A. Fast and accurate interpolation of large scattered data sets on the sphere. J. Comput. Appl. Math. 2010, 234, 1505–1521. [Google Scholar] [CrossRef]
- Pottmann, H.; Eck, M. Modified multiquadric methods for scattered data interpolation over a sphere. Computer Aided Geometr. Des. 1990, 7, 313–321. [Google Scholar] [CrossRef]
- Arias, P.; Facciolo, G.; Caselles, V.; Sapiro, G. A Variational Framework for Exemplar-Based Image Inpainting. Int. J. Computer Vis. 2011, 93, 319–347. [Google Scholar] [CrossRef]
- Gilbert, J.R.; Moler, C.; Schreiber, R. Sparse Matrices in MATLAB: Design and Implementation. SIAM J. Matrix Anal. Appl. 1992, 13, 333–356. [Google Scholar] [CrossRef]
- Carsey, F.D. Microwave Remote Sensing of Sea Ice; American Geophysical Union: Washington, DC, USA, 1992; p. 462. [Google Scholar]
- Garcia, N.; Stoll, E. Monte Carlo Calculation for Electromagnetic-Wave Scattering from Random Rough Surfaces. Phys. Rev. Lett. 1984, 52, 1798–1801. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).