A Comparative Study of Cross-Product NDVI Dynamics in the Kilimanjaro Region—A Matter of Sensor, Degradation Calibration, and Significance
Abstract
:1. Introduction
2. Experimental Section
2.1. Study Area
2.2. Satellite Data
2.2.1. MODIS NDVI
2.2.2. AVHRR GIMMS NDVI3g
2.3. Summary of Applied Methods
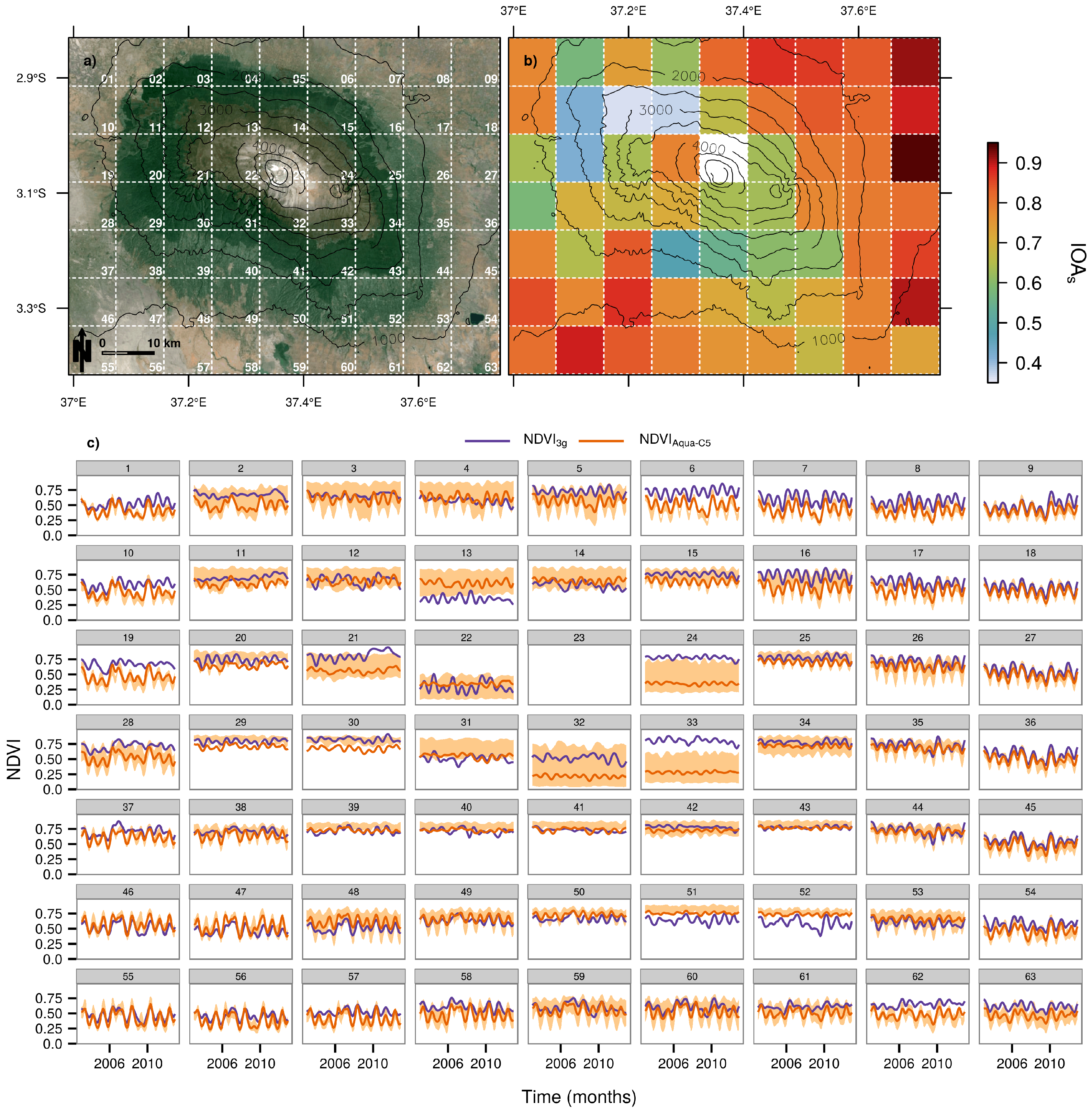
2.3.1. Index of Association
2.3.2. Mann–Kendall Trend Test
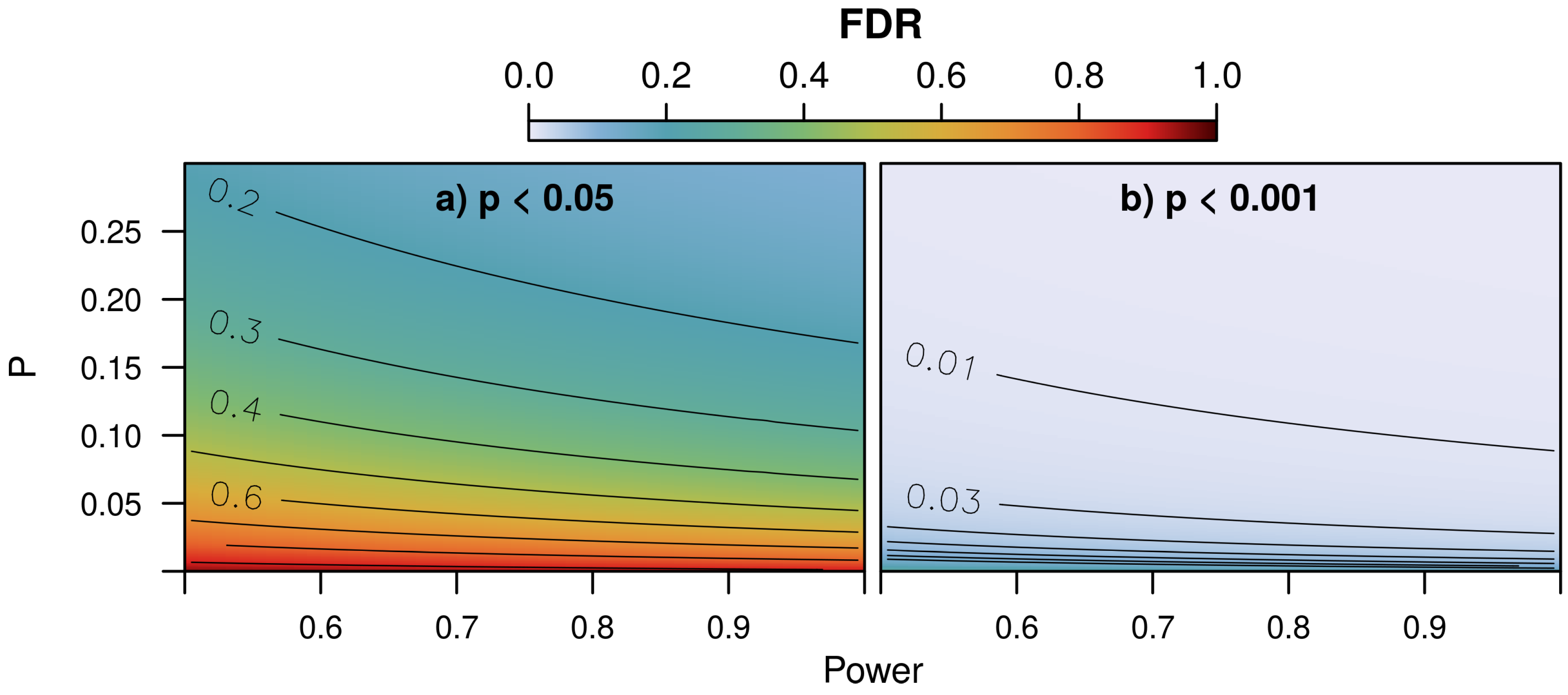
2.3.3. False Discovery Rate
3. Results
3.1. Seasonality
3.2. Long-Term Monotonic Trends
3.2.1. “Significant” Trends
3.2.2. “Conclusive” Trends
3.2.3. Implications of the Significance Level on FDR
4. Discussion
4.1. Seasonality
4.2. Long-Term Monotonic Trends
“If you want to avoid making a fool of yourself very often, do not regard anything greater than as a demonstration that you have discovered something. Or, slightly less stringently, use a three-sigma rule.”
5. Conclusions
- In terms of seasonality, the respective MODIS sensors agreed best across collections indicating that the seasonal signal largely remained unaffected by the recent product update. Across sensors, the IOAs slightly decreased which was attributed to the different timing of Terra and Aqua overpasses.
- When MODIS was combined with GIMMS, a spatial gradient became apparent ranging from high IOAs in savanna to low IOAs when approaching the mountain. This was possibly owing to (a) the loss of a clear phenological cycle when moving towards the mountain; and (b) an increasing level of sub-pixel heterogeneities that could not be adequately captured by the 8-km GIMMS grid.
- As concerns long-term monotonic trends, we found that the coarse resolution of GIMMS tended to dilute small-scale signals that were adequately captured by MODIS. Moreover, no GIMMS trends remained when considering “conclusive” trends (), suggesting that the bulk of identified “significant” trends () was introduced by random chance rather than reflecting real trends.
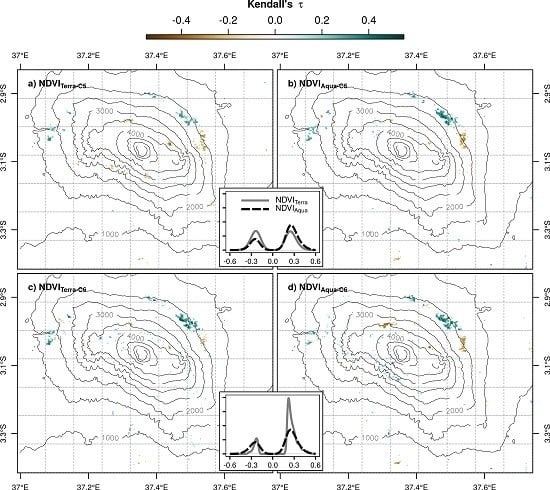
- NDVITerra-C5 revealed distinctly more browning (and also less intense greening) than the other MODIS products as a consequence of sensor degradation. Such effects were found to vanish for NDVITerra-C6 suggesting that the new calibration approach accounts for band ageing. However, the finding that a distinctly higher portion of greening becomes apparent from NDVITerra-C6 when directly compared with NDVIAqua-C6 requires further investigation of a possible overcompensation of Terra-MODIS band ageing in Collection 6.
- As seen from the FDR, the relative amount of false alarms in the trend fraction heavily depended upon the applied p-value. For instance, if we estimated the power of the Mann–Kendall test to be and real trends to make up of the study area, then of all “significant” trends and only of all “conclusive” trends were assumed to originate from random chance.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Alcaraz-Segura, D.; Chuvieco, E.; Epstein, H.E.; Kasischke, E.S.; Trishchenko, A. Debating the greening vs. browning of the North American boreal forest: Differences between satellite datasets. Glob. Chang. Biol. 2010, 16, 760–770. [Google Scholar] [CrossRef]
- Tucker, C.; Pinzon, J.; Brown, M.; Slayback, D.; Pak, E.; Mahoney, R.; Vermote, E.; El Saleous, N. An extended AVHRR 8-km NDVI dataset compatible with MODIS and SPOT vegetation NDVI data. Int. J. Remote Sens. 2005, 26, 4485–4498. [Google Scholar] [CrossRef]
- Latifovic, R.; Trishchenko, A.; Chen, J.; Park, W.B.; Khlopenkov, K.V.; Fernandes, R.; Pouliot, D.; Ungureanu, C.; Luo, Y.; Wang, S.; et al. Generating historical AVHRR 1 km baseline satellite data records over Canada suitable for climate change studies. Can. J. Remote Sens. 2005, 31, 324–346. [Google Scholar] [CrossRef]
- Helsel, D.R.; Hirsch, R.M. Statistical Methods in Water Resources (Techniques of Water-Resources Investigation, Book 4, Chapter A3); Elsevier: Amsterdam, The Netherlands, 2002; pp. 338–340. [Google Scholar]
- Fensholt, R.; Proud, S.R. Evaluation of Earth Observation based global long term vegetation trends—Comparing GIMMS and MODIS global NDVI time series. Remote Sens. Environ. 2012, 119, 131–147. [Google Scholar] [CrossRef]
- Guay, K.C.; Beck, P.S.; Berner, L.T.; Goetz, S.J.; Baccini, A.; Buermann, W. Vegetation productivity patterns at high northern latitudes: A multi-sensor satellite data assessment. Glob. Chang. Biol. 2014, 20, 3147–3158. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Morton, D.; Masek, J.; Wu, A.; Nagol, J.; Xiong, X.; Levy, R.; Vermote, E.; Wolfe, R. Impact of sensor degradation on the MODIS NDVI time series. Remote Sens. Environ. 2012, 119, 55–61. [Google Scholar] [CrossRef]
- Lyapustin, A.; Wang, Y.; Xiong, X.; Meister, G.; Platnick, S.; Levy, R.; Franz, B.; Korkin, S.; Hilker, T.; Tucker, J.; et al. Scientific impact of MODIS C5 calibration degradation and C6+ improvements. Atmos. Meas. Tech. 2014, 7, 4353–4365. [Google Scholar] [CrossRef]
- Didan, K.; Munoz, A.B.; Solano, R.; Huete, A. MODIS Vegetation Index User’s Guide (MOD13 Series); Version 3.0.0 (Collection 6); Vegetation Index and Phenology Lab, The University of Arizona: Tucson, AZ, USA, 2015. [Google Scholar]
- Detsch, F.; Otte, I.; Appelhans, T.; Nauss, T. Seasonal and long-term vegetation dynamics from NDVI time series at Mt. Kilimanjaro, Tanzania. Remote Sens. Environ. 2016. under review. [Google Scholar]
- Pinzon, J.E.; Tucker, C.J. A non-stationary 1981-2012 AVHRR NDVI3g time series. Remote Sens. 2014, 6, 6929–6960. [Google Scholar] [CrossRef]
- Appelhans, T.; Mwangomo, E.; Otte, I.; Detsch, F.; Nauss, T.; Hemp, A. Eco-Meteorological Characteristics of the Southern Slopes of Mt. Kilimanjaro, Tanzania. Int. J. Climatol. 2015. in Press. Available online: http://onlinelibrary.wiley.com/doi/10.1002/joc.4552/full (accessed on 20 January 2016). [Google Scholar]
- Buytaert, W.; Cuesta-Camacho, F.; Tobón, C. Potential impacts of climate change on the environmental services of humid tropical alpine regions. Glob. Ecol. Biogeogr. 2011, 20, 19–33. [Google Scholar] [CrossRef]
- Hemp, A. Climate change-driven forest fires marginalize the impact of ice cap wasting on Kilimanjaro. Glob. Chang. Biol. 2005, 11, 1013–1023. [Google Scholar] [CrossRef]
- Otte, I.; Detsch, F.; Mwangomo, E.; Nauss, T.; Appelhans, T. Decadal trends and interannual variability of atmospheric parameters as observed from local and remote sensing time series at Mt. Kilimanjaro, Tanzania. Clim. Dyn. 2016. under review. [Google Scholar]
- Oettli, P.; Camberlin, P. Influence of topography on monthly rainfall distribution over East Africa. Clim. Res. 2005, 28, 199–212. [Google Scholar] [CrossRef]
- Hemp, A. Vegetation of Kilimanjaro: Hidden endemics and missing bamboo. Afr. J. Ecol. 2006, 44, 305–328. [Google Scholar] [CrossRef]
- Maeda, E.E.; Hurskainen, P. Spatiotemporal characterization of land surface temperature in Mount Kilimanjaro using satellite data. Theor. Appl. Climatol. 2014, 118, 497–509. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Solano, R.; Didan, K.; Jacobson, A.; Huete, A. MODIS Vegetation Index User’s Guide (MOD13 Series); Version 2.00, May 2010 (Collection 5); Vegetation Index and Phenology Lab, The University of Arizona: Tucson, AZ, USA, 2010. [Google Scholar]
- LPDAAC. NASA Land Data Products and Services. Available online: https://lpdaac.usgs.gov/ (accessed on 20 January 2016).
- MODIS Land Team: MODIS Grids. Available online: http://modis-land.gsfc.nasa.gov/MODLAND_grid.html (accessed on 20 January 2016).
- MODIS Land Team: MODIS News. Available online: http://modis-land.gsfc.nasa.gov/news.html (accessed on 20 January 2016).
- Hyndman, R.J. Forecast: Forecasting Functions for Time Series and Linear Models. Available online: http://rpackages.ianhowson.com/cran/forecast/ (accessed on 7 December 2015).
- Atzberger, C.; Eilers, P.H. A time series for monitoring vegetation activity and phenology at 10-daily time steps covering large parts of South America. Int. J. Digit. Earth 2011, 4, 365–386. [Google Scholar] [CrossRef]
- Wittich, K.P.; Hansing, O. Area-averaged vegetative cover fraction estimated from satellite data. Int. J. Biometeorol. 1995, 38, 209–215. [Google Scholar] [CrossRef]
- Brown, M.E.; Pinzon, J.E.; Didan, K.; Morisette, J.T.; Tucker, C.J. Evaluation of the Consistency of Long-Term NDVI Time Series Derived From AVHRR, SPOT-Vegetation, SeaWIFS, MODIS, and Landsat ETM+ Sensors. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1787–1793. [Google Scholar] [CrossRef]
- ECOCAST. Data Directory. Available online: http://ecocast.arc.nasa.gov/data/pub/gimms/3g.v0/ (accessed on 20 January 2016).
- Zhu, L.; Meng, J. Determining the relative importance of climatic drivers on spring phenology in grassland ecosystems of semi-arid areas. Int. J. Biometeorol. 2015, 59, 237–248. [Google Scholar] [CrossRef] [PubMed]
- Detsch, F. Gimms: Download and Process GIMMS NDVI3g Data. Available online: http://CRAN.R-project.org/package=gimms (accessed on 20 January 2016).
- Matloff, N. The Art of R Programming; No Starch Press: San Francisco, CA, USA, 2011; pp. 49–51. [Google Scholar]
- Appelhans, T.; Detsch, F.; Nauss, T. remote: Empirical Orthogonal Teleconnections in R. J. Stat. Softw. 2015, 65, 1–19. [Google Scholar] [CrossRef]
- de Jong, R.; de Bruin, S.; de Wit, A.; Schaepman, M.E.; Dent, D.L. Analysis of monotonic greening and browning trends from global NDVI time-series. Remote Sens. Environ. 2011, 115, 692–702. [Google Scholar] [CrossRef]
- Yue, S.; Pilon, P.; Phinney, B.; Cavadias, G. The influence of autocorrelation on the ability to detect trend in hydrological series. Hydrol. Process. 2002, 16, 1807–1829. [Google Scholar] [CrossRef]
- Neeti, N.; Eastman, J.R. A Contextual Mann–Kendall Approach for the Assessment of Trend Significance in Image Time Series. Trans. GIS 2011, 15, 599–611. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Bronaugh, D.; Werner, A. Zyp: Zhang + Yue-Pilon Trends Package. Available online: http://CRAN.R-project.org/package=zyp (accessed on 20 January 2016).
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. A new measure of rank correlation. Biometrika 1938, 30, 81–93. [Google Scholar] [CrossRef]
- Meals, D.W.; Spooner, J.; Dressing, S.A.; Harcum, J.B. Statistical Analysis for Monotonic Trends; Tech Notes 6; National Nonpoint Source Monitoring Program: Fairfax, VA, USA, 2011; pp. 1–23. [Google Scholar]
- McLeod, A.I. Kendall: Kendall Rank Correlation and Mann–Kendall Trend Test. Available online: http://CRAN.R-project.org/package=Kendall (accessed on 20 January 2016).
- Önöz, B.; Bayazit, M. The Power of Statistical Tests for Trend Detection. Turk. J. Eng. Environ. Sci. 2003, 27, 247–251. [Google Scholar]
- Colquhoun, D. An investigation of the false discovery rate and the misinterpretation of p-values. R. Soc. Open Sci. 2014, 1. [Google Scholar] [CrossRef] [PubMed]
- Benjamini, Y.; Hochberg, Y. Controlling the False Discovery Rate: A Practical and Powerful Approach to Multiple Testing. J. R. Stat. Soc. Ser. B 1995, 57, 289–300. [Google Scholar]
- Miller, D.A. “Significant” and “Highly Significant”. Nature 1966, 210, 1190. [Google Scholar] [CrossRef] [PubMed]
- Map Data: Google, TerraMetrics. Available online: http://maps.googleapis.com/maps/api/staticmap?center=-3.123553240247,37.366348380164&zoom=10&size=640x497&maptype=satellite&format=gif&sensor=false&scale=2 (accessed on 20 January 2016).
- Ong’injo, J.; (Deputy registrar, Kisumu); Lambrechts, C.; (United Nations Environment Programme); Hemp, A.; (Plant physiology, University of Bayreuth). Personal communication, 2015.
- OpenStreetMap. Copyright and License. Available online: http://www.openstreetmap.org/copyright (accessed on 20 January 2016).
- Duane, W.J.; Pepin, N.C.; Losleben, M.L.; Hardy, D.R. General Characteristics of Temperature and Humidity Variability on Kilimanjaro, Tanzania. Arct. Antarct. Alp. Res. 2008, 40, 323–334. [Google Scholar] [CrossRef]
- Ivory, S.J.; Russell, J.; Cohen, A.S. In the hot seat: Insolation, ENSO, and vegetation in the African Tropics. J. Geophys. Res. Biogeosci. 2013, 118, 1347–1358. [Google Scholar] [CrossRef]
- Huete, A.R.; Saleska, S.R. Remote Sensing of Tropical Forest Phenology: Issues and Controversies. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2010, 38, 539–541. [Google Scholar]
- Rutten, G.; Ensslin, A.; Hemp, A.; Fischer, M. Vertical and Horizontal Vegetation Structure across Natural and Modified Habitat Types at Mount Kilimanjaro. PLoS ONE 2015, 10, e0138822. [Google Scholar] [CrossRef] [PubMed]
- Yin, H.; Udelhoven, T.; Fensholt, R.; Pflugmacher, D.; Hostert, P. How Normalized Difference Vegetation Index (NDVI) Trends from Advance Very High Resolution Radiometer (AVHRR) and Système Probatoire d’Observation de la Terre VEGETATION (SPOT VGT) Time Series Differ in Agricultural Areas: An Inner Mongolian Case Study. Remote Sens. 2012, 4, 3364–3389. [Google Scholar] [CrossRef]
- Kidwell, K.B. NOAA POLAR ORBITER DATA USER’S GUIDE (TIROS-N, NOAA-6, NOAA-7, NOAA-8, NOAA-9, NOAA-10, NOAA-11, NOAA-12, NOAA-13 AND NOAA-14). Available online: https://www.ncdc.noaa.gov/oa/pod-guide/ncdc/docs/podug/index.htm (accessed on 20 January 2016).
- Tian, F.; Fensholt, R.; Verbesselt, J.; Grogan, K.; Horion, S.; Wang, Y. Evaluating temporal consistency of long-term global NDVI datasets for trend analysis. Remote Sens. Environ. 2015, 163, 326–340. [Google Scholar] [CrossRef]
- Barreto-Munoz, A. Multi-Sensor Vegetation Index and Land Surface Phenology Earth Science Data Records in Support of Global Change Studies: Data Quality Challenges and Data Explorer System. Ph.D. Thesis, Department of Agricultural and Biosystems Engineering, The University of Arizona, Tucson, AZ, USA, 2013. [Google Scholar]
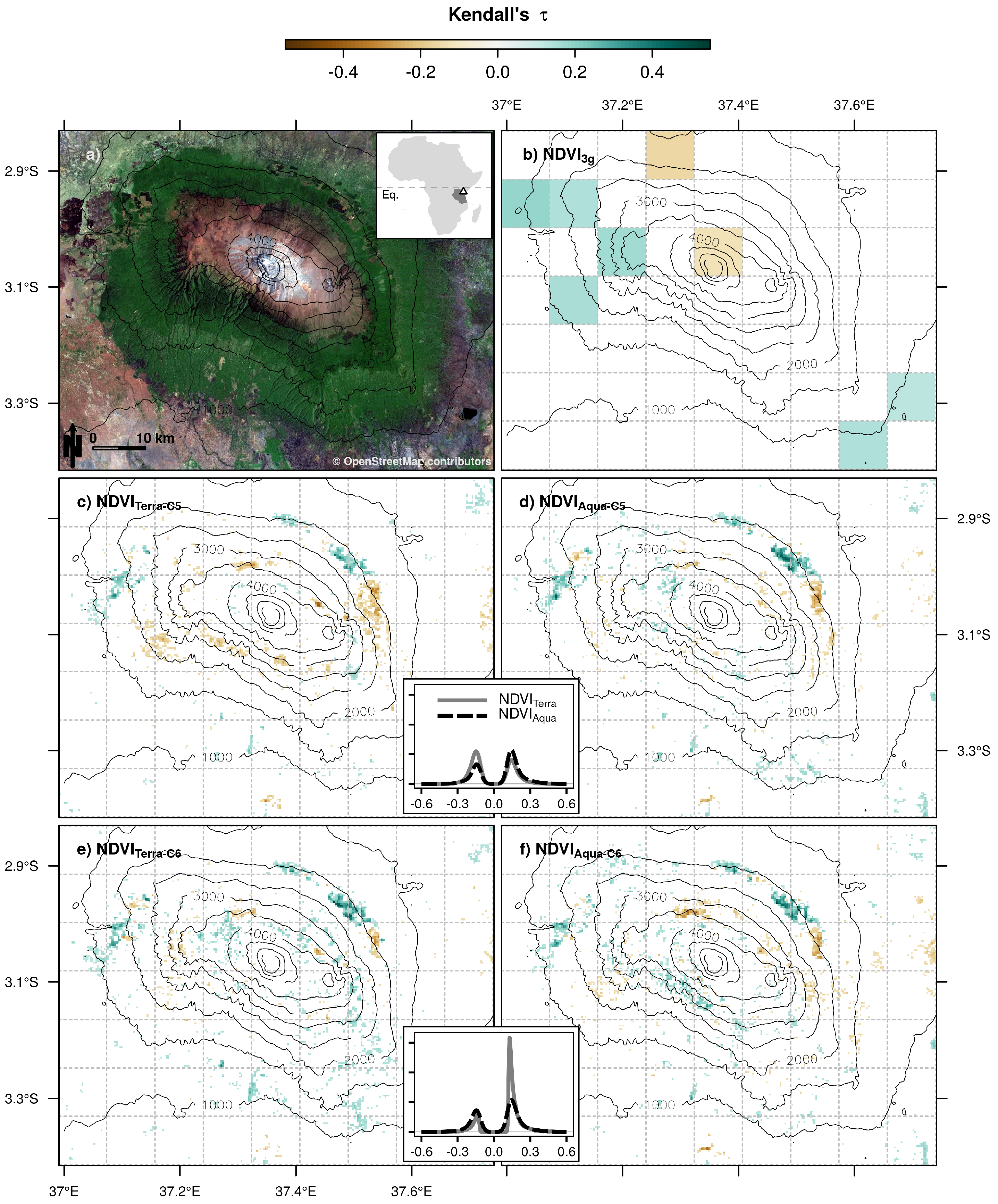



| NDVI3g | NDVITerra-C5 | NDVIAqua-C5 | NDVITerra-C6 | NDVIAqua-C6 | |
|---|---|---|---|---|---|
| NDVI3g | 1 | ||||
| NDVITerra-C5 | 0.750 | 1 | |||
| NDVIAqua-C5 | 0.776 | 0.811 | 1 | ||
| NDVITerra-C6 | 0.745 | 0.861 | 0.807 | 1 | |
| NDVIAqua-C6 | 0.736 | 0.801 | 0.853 | 0.804 | 1 |
| Trend Pixels | Trends (%) | Greening (%) | Browning (%) | |
|---|---|---|---|---|
| NDVI3g | 8 | 0.127 | 0.750 | 0.250 |
| NDVITerra-C5 | 4124 | 0.044 | 0.435 | 0.565 |
| NDVIAqua-C5 | 3817 | 0.040 | 0.654 | 0.346 |
| NDVITerra-C6 | 4631 | 0.049 | 0.817 | 0.183 |
| NDVIAqua-C6 | 4765 | 0.050 | 0.615 | 0.385 |
| Trend Pixels | Trends (%) | Greening (%) | Browning (%) | |
|---|---|---|---|---|
| NDVI3g | 0 | 0 | − | − |
| NDVITerra-C5 | 607 | 0.006 | 0.511 | 0.489 |
| NDVIAqua-C5 | 712 | 0.008 | 0.729 | 0.271 |
| NDVITerra-C6 | 736 | 0.008 | 0.833 | 0.167 |
| NDVIAqua-C6 | 892 | 0.009 | 0.693 | 0.307 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Detsch, F.; Otte, I.; Appelhans, T.; Nauss, T. A Comparative Study of Cross-Product NDVI Dynamics in the Kilimanjaro Region—A Matter of Sensor, Degradation Calibration, and Significance. Remote Sens. 2016, 8, 159. https://doi.org/10.3390/rs8020159
Detsch F, Otte I, Appelhans T, Nauss T. A Comparative Study of Cross-Product NDVI Dynamics in the Kilimanjaro Region—A Matter of Sensor, Degradation Calibration, and Significance. Remote Sensing. 2016; 8(2):159. https://doi.org/10.3390/rs8020159
Chicago/Turabian StyleDetsch, Florian, Insa Otte, Tim Appelhans, and Thomas Nauss. 2016. "A Comparative Study of Cross-Product NDVI Dynamics in the Kilimanjaro Region—A Matter of Sensor, Degradation Calibration, and Significance" Remote Sensing 8, no. 2: 159. https://doi.org/10.3390/rs8020159
APA StyleDetsch, F., Otte, I., Appelhans, T., & Nauss, T. (2016). A Comparative Study of Cross-Product NDVI Dynamics in the Kilimanjaro Region—A Matter of Sensor, Degradation Calibration, and Significance. Remote Sensing, 8(2), 159. https://doi.org/10.3390/rs8020159