Application of Physically-Based Slope Correction for Maximum Forest Canopy Height Estimation Using Waveform Lidar across Different Footprint Sizes and Locations: Tests on LVIS and GLAS
Abstract
:1. Introduction
2. Materials Section
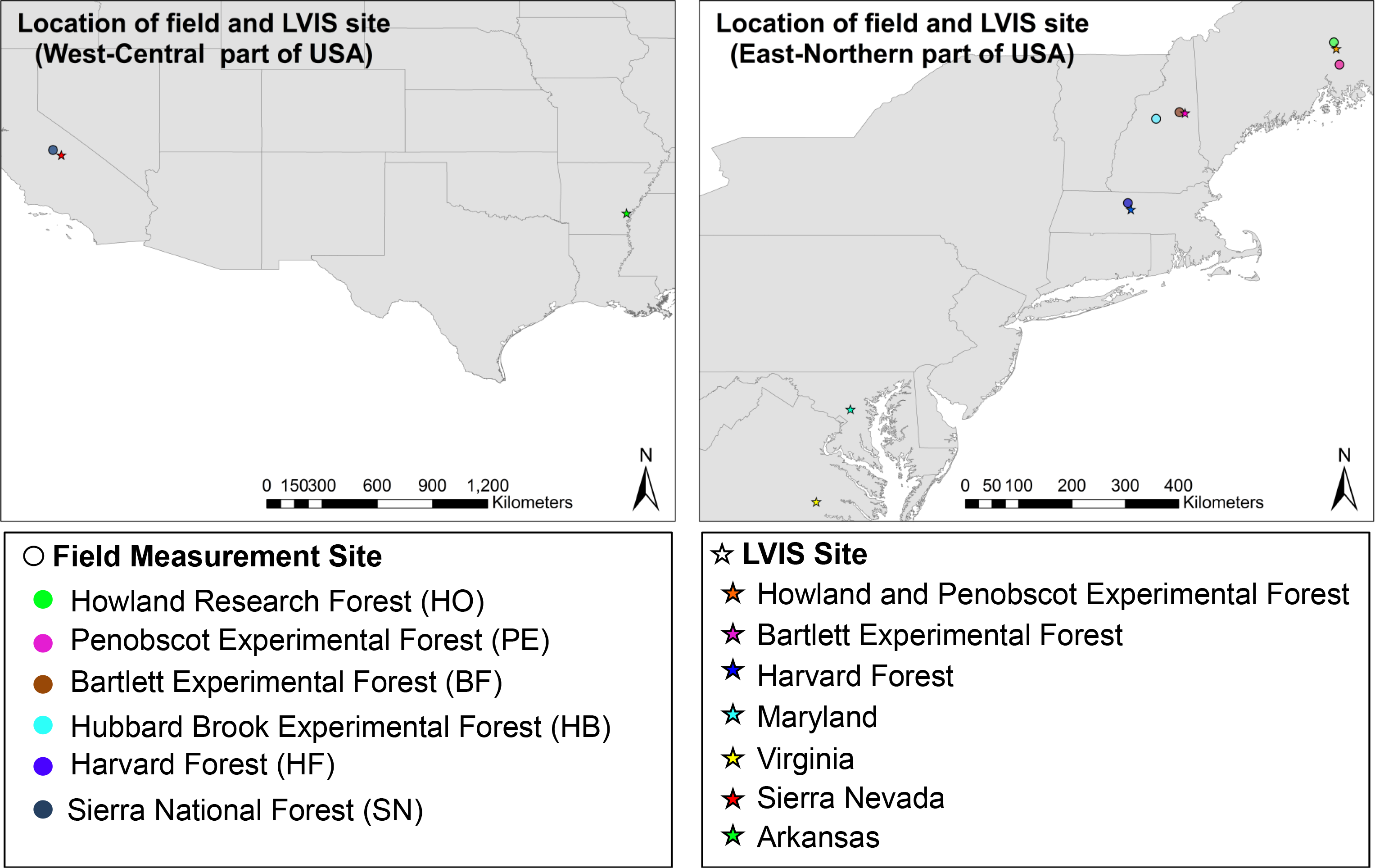
2.1. Field Measurements
2.2. LVIS
2.3. GLAS
2.4. Ancillary Datasets
3. Methods
3.1. GLAS Preprocessing
3.2. Maximum Forest Canopy Height Retrieval from LVIS and GLAS
3.3. Comparison of LVIS Metrics to Field Measurements
3.4. GLAS Maximum Height Estimation and Evaluation
4. Results and Discussion
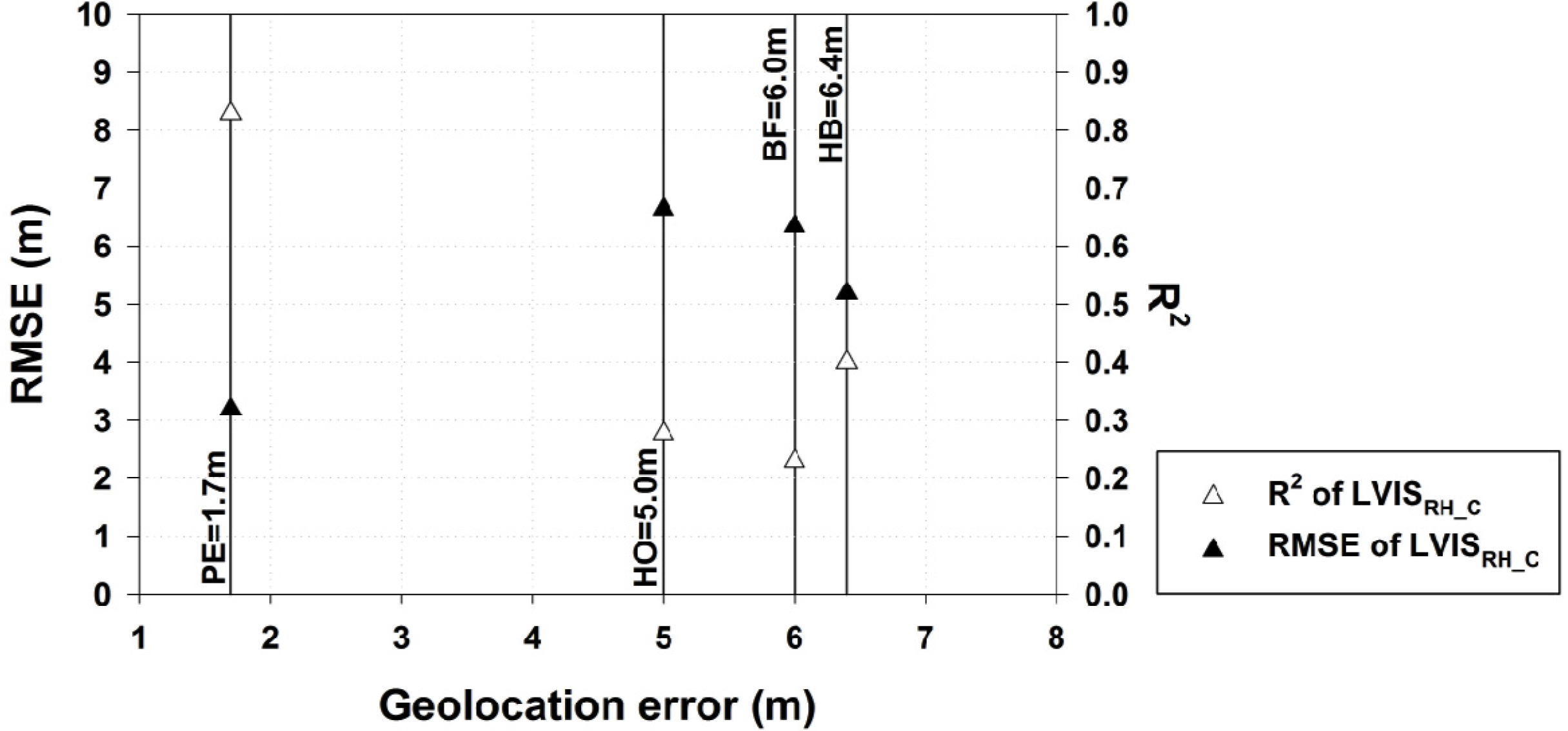
4.1. Comparison between LVIS and Field Measurements
4.2. Comparison between GLAS and LVIS
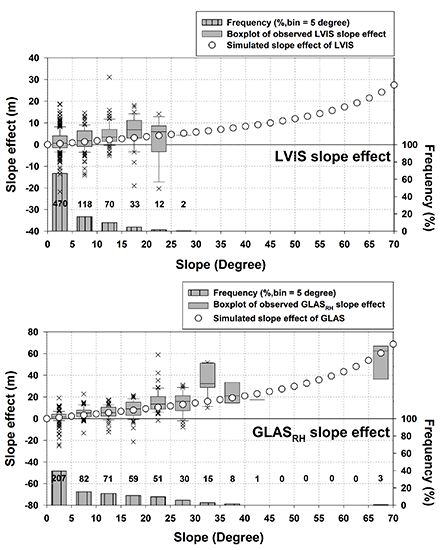
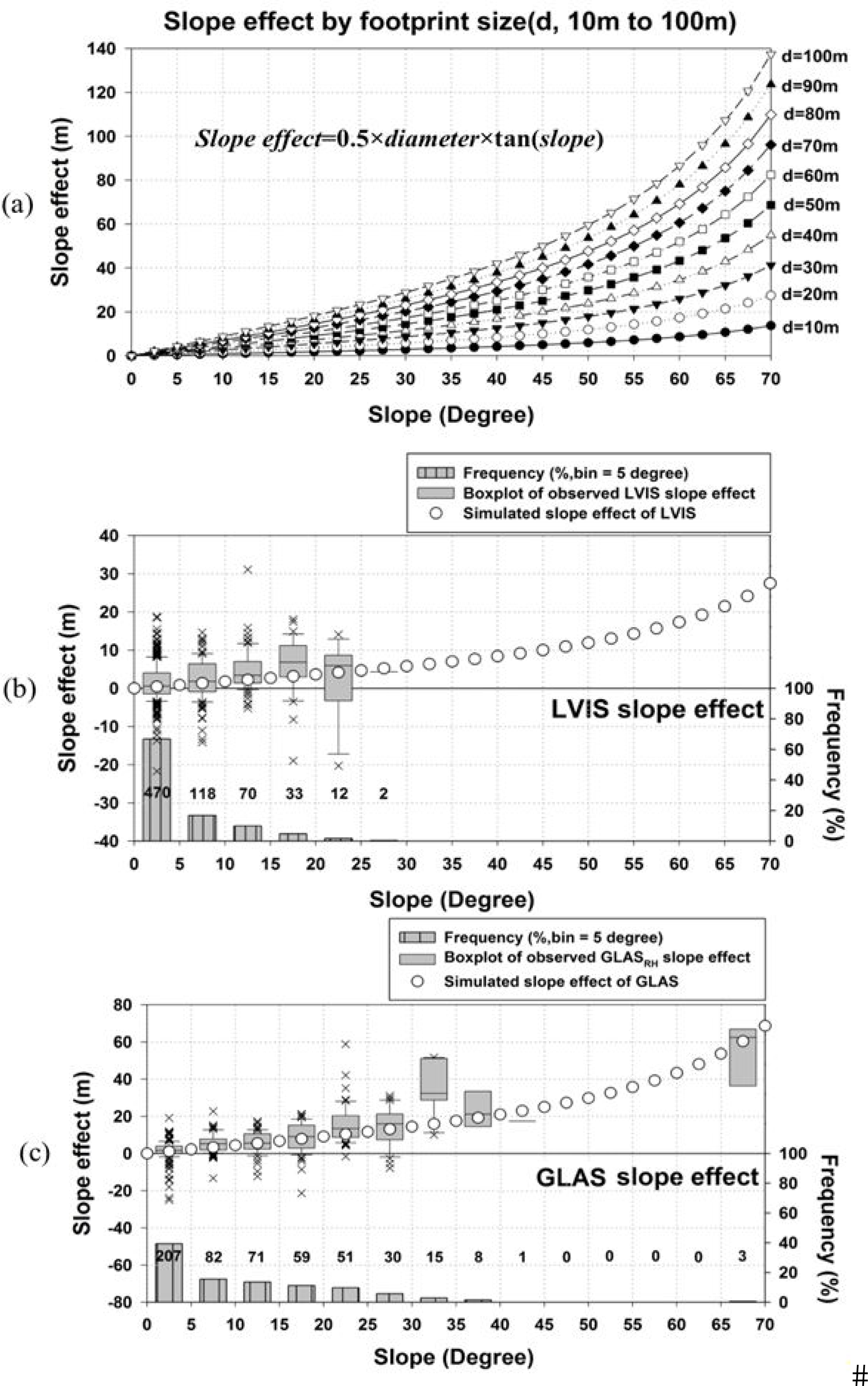
4.3. Physical Slope Correction and Lidar Footprint Size
4.4. Limitations and Further Plans
5. Conclusions
Acknowledgments
Author Contributions
Conflict of Interest
References
- Rosenqvist, Å.; Milne, A.; Lucas, R.; Imhoff, M.; Dobson, C. A review of remote sensing technology in support of the Kyoto Protocol. Environ. Sci. Policy 2003, 6, 441–455. [Google Scholar]
- Chen, J.; Saunders, S.C.; Crow, T.R.; Naiman, R.J.; Brosofske, K.D.; Mroz, G.D.; Brookshire, B.L.; Franklin, J.F. Microclimate in forest ecosystem and landscape ecology. BioScience 1999, 49, 288–297. [Google Scholar]
- Parker, G.G.; Harmon, M.E.; Lefsky, M.A.; Chen, J.; van Pelt, R.; Weis, S.B.; Thomas, S.C.; Winner, W.E.; Shaw, D.C.; Frankling, J.F. Three-dimensional structure of an old-growth Pseudotsuga-Tsuga canopy and its implications for radiation balance, microclimate, and gas exchange. Ecosystems 2004, 7, 440–453. [Google Scholar]
- Turner, W.; Spector, S.; Gardiner, N.; Fladeland, M.; Sterling, E.; Steininger, M. Remote sensing for biodiversity science and conservation. Trends Ecol. Evol 2003, 18, 306–314. [Google Scholar]
- Lefsky, M.A.; Cohen, W.B.; Parker, G.G.; Harding, D.J. Lidar remote sensing for ecosystem studies: Lidar, an emerging remote sensing technology that directly measures the three-dimensional distribution of plant canopies, can accurately estimate vegetation structural attributes and should be of particular interest to forest, landscape, and global ecologists. BioScience 2002, 52, 19–30. [Google Scholar]
- Wulder, M.A.; Hall, R.J.; Coops, N.C.; Franklin, S.E. High spatial resolution remotely sensed data for ecosystem characterization. BioScience 2004, 54, 511–521. [Google Scholar]
- Myneni, R.; Hoffman, S.; Knyazikhin, Y.; Privette, J.; Glassy, J.; Tian, Y.; Wang, Y.; Song, X.; Zhang, Y.; Smith, G. Global products of vegetation leaf area and fraction absorbed PAR from year one of MODIS data. Remote Sens. Environ 2002, 83, 214–231. [Google Scholar]
- Myneni, R.; Dong, J.; Tucker, C.; Kaufmann, R.; Kauppi, P.; Liski, J.; Zhou, L.; Alexeyev, V.; Hughes, M. A large carbon sink in the woody biomass of northern forests. Proc. Natl. Acad. Sci. USA 2001, 98, 14784–14789. [Google Scholar]
- Running, S.W.; Nemani, R.R.; Heinsch, F.A.; Zhao, M.; Reeves, M.; Hashimoto, H. A continuous satellite-derived measure of global terrestrial primary production. Bioscience 2004, 54, 547–560. [Google Scholar]
- Zhao, M.; Heinsch, F.A.; Nemani, R.R.; Running, S.W. Improvements of the MODIS terrestrial gross and net primary production global data set. Remote Sens. Environ 2005, 95, 164–176. [Google Scholar]
- Kasischke, E.S.; Melack, J.M.; Craig Dobson, M. The use of imaging radars for ecological applications—A review. Remote Sens. Environ 1997, 59, 141–156. [Google Scholar]
- Nelson, R.; Krabill, W.; MacLean, G. Determining forest canopy characteristics using airborne laser data. Remote Sens. Environ 1984, 15, 201–212. [Google Scholar]
- Jones, H.G.; Vaughan, R.A. Remote Sensing of Vegetation: Principles, Techniques, and Applications; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Carlson, T.N.; Ripley, D.A. On the relation between NDVI, fractional vegetation cover, and leaf area index. Remote Sens. Environ 1997, 62, 241–252. [Google Scholar]
- Turner, D.P.; Cohen, W.B.; Kennedy, R.E.; Fassnacht, K.S.; Briggs, J.M. Relationships between leaf area index and Landsat TM spectral vegetation indices across three temperate zone sites. Remote Sens. Environ 1999, 70, 52–68. [Google Scholar]
- Wulder, M.A.; White, J.C.; Nelson, R.F.; Næsset, E.; Ørka, H.O.; Coops, N.C.; Hilker, T.; Bater, C.W.; Gobakken, T. Lidar sampling for large-area forest characterization: A review. Remote Sens. Environ 2012, 121, 196–209. [Google Scholar]
- Patenaude, G.; Hill, R.; Milne, R.; Gaveau, D.L.; Briggs, B.; Dawson, T. Quantifying forest above ground carbon content using LiDAR remote sensing. Remote Sens. Environ 2004, 93, 368–380. [Google Scholar]
- Jung, S.E.; Kwak, D.A.; Park, T.; Lee, W.K.; Yoo, S. Estimating crown variables of individual trees using airborne and terrestrial laser scanners. Remote Sens 2011, 3, 2346–2363. [Google Scholar]
- Dubayah, R.O.; Drake, J.B. Lidar remote sensing for forestry. J. For 2000, 98, 44–46. [Google Scholar]
- Lefsky, M.A.; Harding, D.J.; Keller, M.; Cohen, W.B.; Carabajal, C.C.; Espirito-Santo, F.D.; Hunter, M.O.; de Oliveira, R. Estimates of forest canopy height and aboveground biomass using ICESat. Geophys. Res. Lett 2005, 32. [Google Scholar] [CrossRef]
- Drake, J.B.; Dubayah, R.O.; Clark, D.B.; Knox, R.G.; Blair, J.B.; Hofton, M.A.; Chazdon, R.L.; Weishampel, J.F.; Prince, S. Estimation of tropical forest structural characteristics using large-footprint lidar. Remote Sens. Environ 2002, 79, 305–319. [Google Scholar]
- Drake, J.B.; Dubayah, R.O.; Knox, R.G.; Clark, D.B.; Blair, J.B. Sensitivity of large-footprint lidar to canopy structure and biomass in a neotropical rainforest. Remote Sens. Environ 2002, 81, 378–392. [Google Scholar]
- Lefsky, M.A. A global forest canopy height map from the Moderate Resolution Imaging Spectroradiometer and the Geoscience Laser Altimeter System. Geophys. Res. Lett 2010, 37. [Google Scholar] [CrossRef]
- Simard, M.; Pinto, N.; Fisher, J.B.; Baccini, A. Mapping forest canopy height globally with spaceborne lidar. J. Geophys. Res.-Biogeosci 2011, 116. [Google Scholar] [CrossRef]
- Saatchi, S.S.; Harris, N.L.; Brown, S.; Lefsky, M.; Mitchard, E.T.; Salas, W.; Zutta, B.R.; Buermann, W.; Lewis, S.L.; Hagen, S. Benchmark map of forest carbon stocks in tropical regions across three continents. Proc. Natl. Acad. Sci. USA 2011, 108, 9899–9904. [Google Scholar]
- Harding, D.J.; Carabajal, C.C. ICESat waveform measurements of within-footprint topographic relief and vegetation vertical structure. Geophys. Res. Lett 2005, 32. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Keller, M.; Pang, Y.; De Camargo, P.B.; Hunter, M.O. Revised method for forest canopy height estimation from Geoscience Laser Altimeter System waveforms. J. Appl. Remote Sens 2007, 1. [Google Scholar] [CrossRef]
- Chen, Q. Retrieving vegetation height of forests and woodlands over mountainous areas in the Pacific Coast region using satellite laser altimetry. Remote Sens. Environ 2010, 114, 1610–1627. [Google Scholar]
- Lee, S.; Ni-Meister, W.; Yang, W.Z.; Chen, Q. Physically based vertical vegetation structure retrieval from ICESat data: Validation using LVIS in White Mountain National Forest, New Hampshire, USA. Remote Sens. Environ 2011, 115, 2776–2785. [Google Scholar]
- Hilbert, C.; Schmullius, C. Influence of surface topography on ICESat/GLAS forest height estimation and waveform shape. Remote Sens 2012, 4, 2210–2235. [Google Scholar]
- Rosette, J.A.B.; North, P.R.J.; Suarez, J.C.; Los, S.O. Uncertainty within satellite LiDAR estimations of vegetation and topography. Int. J. Remote Sens 2010, 31, 1325–1342. [Google Scholar]
- Yang, W.; Ni-Meister, W.; Lee, S. Assessment of the impacts of surface topography, off-nadir pointing and vegetation structure on vegetation lidar waveforms using an extended geometric optical and radiative transfer model. Remote Sens. Environ 2011, 115, 2810–2822. [Google Scholar]
- Pang, Y.; Lefsky, M.; Sun, G.Q.; Ranson, J. Impact of footprint diameter and off-nadir pointing on the precision of canopy height estimates from spaceborne lidar. Remote Sens. Environ 2011, 115, 2798–2809. [Google Scholar]
- Neuenschwander, A.L.; Urban, T.J.; Gutierrez, R.; Schutz, B.E. Characterization of ICESat/GLAS waveforms over terrestrial ecosystems: Implications for vegetation mapping. J. Geophys. Res.-Biogeosci 2008, 113. [Google Scholar] [CrossRef]
- Sun, G.; Ranson, K.J.; Kimes, D.S.; Blair, J.B.; Kovacs, K. Forest vertical structure from GLAS: An evaluation using LVIS and SRTM data. Remote Sens. Environ 2008, 112, 107–117. [Google Scholar]
- Wofsy, S.; Harriss, R. The North American Carbon Program (NACP); US Global Change Research Program: Washington, DC, USA, 2002; p. 59. [Google Scholar]
- Cook, B.; Dubayah, R.; Hall, F.; Nelson, R.; Ranson, J.; Strahler, A.; Siqueira, P.; Simard, M.; Griffith, P. NACP New England and Sierra National Forests Biophysical Measurements: 2008–2010; Oak Ridge National Laboratory Distributed Active Archive Center: Oak Ridge, TN, USA, 2011; Available online: http://dx.doi.org/10.3334/ORNLDAAC/1046 (accessed on 15 March 2013).
- Blair, J.; Hofton, M.; Rabine, D. NASA LVIS Elevation and Canopy (LGE, LCE, and LGW) Data Products, Version 1.02. Available online: http://lvis.gsfc.nasa.gov (accessed on 27 March 2013).
- Zwally, H.J.; Schutz, B.; Abdalati, W.; Abshire, J.; Bentley, C.; Brenner, A.; Bufton, J.; Dezio, J.; Hancock, D.; Harding, D.; et al. ICESat’s laser measurements of polar ice, atmosphere, ocean, and land. J. Geodyn 2002, 34, 405–445. [Google Scholar]
- Choi, S.; Ni, X.; Shi, Y.; Ganguly, S.; Zhang, G.; Duong, H.V.; Lefsky, M.A.; Simard, M.; Saatchi, S.S.; Lee, S. Allometric scaling and resource limitations model of tree heights: Part 2. Site based testing of the model. Remote Sens 2013, 5, 202–223. [Google Scholar]
- Bae, S.; Urban, T. Summary of Laser Profile Array (LPA) Parameter Estimation, Version 2.0. Available online: http://nsidc.org/data/icesat/pdf/CSR_Summary_of_LPA_param_est_v2.pdf (accessed on 2 May 2013).
- Gesch, D.B. The national elevation dataset. In Digital Elevation Model Technologies and Applications: The DEM Users Manual, 2nd ed.; Maune, D., Ed.; American Society for Photogrammetry and Remote Sensing: Bethesda, MD, USA, 2007; pp. 99–118. [Google Scholar]
- Holmes, K.; Chadwick, O.; Kyriakidis, P.C. Error in a USGS 30-meter digital elevation model and its impact on terrain modeling. J. Hydrol 2000, 233, 154–173. [Google Scholar]
- Fry, J.; Xian, G.; Jin, S.; Dewitz, J.; Homer, C.; Yang, L.; Barnes, C.; Herold, N.; Wickham, J. Completion of the 2006 National Land Cover Database for the conterminous United States. Photogramm. Eng. Remote Sens 2011, 77, 858–864. [Google Scholar]
- Brenner, A.C.; Zwally, H.J.; Bentley, C.R.; Csatho, B.M.; Harding, D.J.; Hofton, M.A.; Minster, J.-B.; Roberts, L.; Saba, J.L.; Thomas, R.H. Derivation of Range and Range Distributions from Laser Pulse Waveform Analysis for Surface Elevations, Roughness, Slope, and Vegetation Heights. Available online: http://www.csr.utexas.edu/glas/atbd.html (accessed on 27 March 2013).
- Quinn, G.P.; Keough, M.J. Experimental Design and Data Analysis for Biologists; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Blair, J.B.; Hofton, M.A. Modeling laser altimeter return waveforms over complex vegetation using high resolution elevation data. Geophys. Res. Lett 1999, 26, 2509–2512. [Google Scholar]
- Hyde, P.; Dubayah, R.; Peterson, B.; Blair, J.; Hofton, M.; Hunsaker, C.; Knox, R.; Walker, W. Mapping forest structure for wildlife habitat analysis using waveform lidar: Validation of montane ecosystems. Remote Sens. Environ 2005, 96, 427–437. [Google Scholar]
- Kellndorfer, J.; Walker, W.; Pierce, L.; Dobson, C.; Fites, J.A.; Hunsaker, C.; Vona, J.; Clutter, M. Vegetation height estimation from shuttle radar topography mission and national elevation datasets. Remote Sens. Environ 2004, 93, 339–358. [Google Scholar]
- Kenyi, L.; Dubayah, R.; Hofton, M.; Schardt, M. Comparative analysis of SRTM–NED vegetation canopy height to LIDAR derived vegetation canopy metrics. Int. J. Remote Sens 2009, 30, 2797–2811. [Google Scholar]
- Nelson, R.; Ranson, K.; Sun, G.; Kimes, D.; Kharuk, V.; Montesano, P. Estimating Siberian timber volume using MODIS and ICESat/GLAS. Remote Sens. Environ 2009, 113, 691–701. [Google Scholar]




| a Name of Sites | Subplot Size (m × m) | Field Data Acquisition Year | LVIS Data Acquisition Year |
|---|---|---|---|
| BF | 25 × 25 | 2009 | 2009 |
| HB | 25 × 25 | 2009 | 2009 |
| HF | 25 × 25 | 2009 | 2009 |
| PE | 25 × 25 | 2009 | 2009 |
| HO | 25 × 25 | 2009 | 2009 |
| SN | 33.3 × 33.3 | 2008 | 2008 |
| LVIS Data Locations by States | LVIS Acquisition Year | GLAS Acquisition Year |
|---|---|---|
| Bartlett Experimental Forest, NH | 2003 | 2005–2006 |
| Howland and Penobscot Experimental Forest, ME | 2003 | 2005–2006 |
| Harvard Forest, MA | 2003 | 2005–2006 |
| Patapsco Forest, MD | 2003 | 2005–2006 |
| Virginia, VA | 2003 | 2005–2006 |
| Sierra Nevada, CA | 2008 | 2005–2006 |
| White River Wildlife Refuge, AR | 2006 | 2005–2006 |
| a Site | No. of Valid Subplots | b Min. (m) | c Max. (m) | d Ave. (m) | e Std. (m) |
|---|---|---|---|---|---|
| BF | 128 | 13.27 | 40.97 | 26.75 | 5.96 |
| HB | 161 | 11.29 | 39.50 | 25.07 | 5.16 |
| HF | 4 | 18.50 | 28.04 | 24.59 | 4.52 |
| PE | 183 | 6.40 | 36.70 | 20.51 | 6.57 |
| HO | 169 | 3.65 | 39.20 | 14.94 | 5.59 |
| SN | 60 | 12.73 | 83.04 | 46.37 | 14.46 |
| Total | 705 * | 3.65 | 83.04 | 26.37 | 7.04 |
| a Site | LVISRH_UC | LVISRH_C | ||||||
|---|---|---|---|---|---|---|---|---|
| Bias | b MAE | c RMSE | d R2 | Bias | MAE | RMSE | R2 | |
| BF | 2.397 | 4.884 | 6.743 | 0.203 | 1.200 | 4.458 | 6.350 | 0.230 |
| HB | 3.986 | 4.849 | 6.299 | 0.370 | 2.247 | 3.781 | 5.187 | 0.400 |
| HF | 2.906 | 3.026 | 4.032 | 0.616 | 2.623 | 2.885 | 3.832 | 0.595 |
| PE | −1.233 | 2.219 | 2.961 | 0.833 | −1.659 | 2.456 | 3.191 | 0.829 |
| HO | 3.655 | 5.425 | 6.824 | 0.276 | 3.363 | 5.250 | 6.642 | 0.277 |
| SN | 2.805 | 4.070 | 5.451 | 0.900 | 1.432 | 3.494 | 4.745 | 0.903 |
| Total | 2.419 | 4.079 | 5.385 | 0.778 | 1.534 | 3.721 | 4.991 | 0.782 |
| Statistics | GLASRH_UC | GLASRH_C | |
|---|---|---|---|
| With outliers | Bias (m) | 7.221 | 1.980 |
| b MAE (m) | 8.398 | 5.133 | |
| c RMSE (m) | 12.741 | 7.829 | |
| d R2 | 0.538 | 0.629 | |
| a Without outliers | Bias (m) | 5.699 | 1.668 |
| MAE (m) | 6.501 | 3.966 | |
| RMSE (m) | 8.737 | 5.323 | |
| R2 | 0.769 | 0.798 | |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Park, T.; Kennedy, R.E.; Choi, S.; Wu, J.; Lefsky, M.A.; Bi, J.; Mantooth, J.A.; Myneni, R.B.; Knyazikhin, Y. Application of Physically-Based Slope Correction for Maximum Forest Canopy Height Estimation Using Waveform Lidar across Different Footprint Sizes and Locations: Tests on LVIS and GLAS. Remote Sens. 2014, 6, 6566-6586. https://doi.org/10.3390/rs6076566
Park T, Kennedy RE, Choi S, Wu J, Lefsky MA, Bi J, Mantooth JA, Myneni RB, Knyazikhin Y. Application of Physically-Based Slope Correction for Maximum Forest Canopy Height Estimation Using Waveform Lidar across Different Footprint Sizes and Locations: Tests on LVIS and GLAS. Remote Sensing. 2014; 6(7):6566-6586. https://doi.org/10.3390/rs6076566
Chicago/Turabian StylePark, Taejin, Robert E. Kennedy, Sungho Choi, Jianwei Wu, Michael A. Lefsky, Jian Bi, Joshua A. Mantooth, Ranga B. Myneni, and Yuri Knyazikhin. 2014. "Application of Physically-Based Slope Correction for Maximum Forest Canopy Height Estimation Using Waveform Lidar across Different Footprint Sizes and Locations: Tests on LVIS and GLAS" Remote Sensing 6, no. 7: 6566-6586. https://doi.org/10.3390/rs6076566