Estimation of the Image Interpretability of ZY-3 Sensor Corrected Panchromatic Nadir Data
Abstract
: Image quality is important for taking full advantage of satellite data. As a common indicator, the National Imagery Interpretability Scale (NIIRS) is widely used for image quality assessment and provides a comprehensive representation of image quality from the perspective of interpretability. The ZY-3 (Ziyuan-3) satellite is the first civil high resolution mapping satellite in China, which was established in 2012. So far, there has been no reports on adopting NIIRS as the common indicator for the quality assessment of that satellite image data. This lack of a common quality indicator results in a gap between satellite data users around the world and those in China regarding the understanding of the quality and usability of ZY-3 data. To overcome the gap, using the general image-quality equation (GIQE), this study evaluates the ZY-3 sensor-corrected (SC) panchromatic nadir (NAD) data in terms of the NIIRS. In order to solve the uncertainty resulting from the exceeding of the ground sample distance (GSD) of ZY-3 data (2.1 m) in GIQE (less than 2.03 m), eight images are used to establish the relationship between the manually obtained NIIRS and the GIQE predicted NIIRS. An adjusted GIQE is based on the relationship and verified by another five images. Our study demonstrates that the method of using adjusted GIQE for calculating NIIRS can be used for the quality assessment of ZY-3 satellite images and reveals that the NIIRS value of ZY-3 SC NAD data is about 2.79.1. Introduction
The ZY-3 (Ziyuan-3) satellite, launched and operated by the Satellite Surveying and Mapping Application Center (SASMAC), National Administration of Surveying, Mapping and Geo-information (NASG), China, is the first of a new type of civil high resolution satellite in China. With a high spatial resolution camera (2.1-m ground sample distance (GSD) TDI-CCD panchromatic (PAN) camera and 5.8 m GSD multispectral (MUX) camera), image products are designed to meet the requirements of the following fields: surveying and mapping, monitoring land resources, land use and planning, agriculture, environmental monitoring and protection, traffic and other important areas. The satellite was launched on 19 January 2012, and to date, there have been 525,824 images, which correspond to approximately 352 TB in the archives, seamlessly covering areas within 84 degrees of north and south latitudes. With a revisit cycle of five days, the mission duration of ZY-3 is five years [1].
The ZY-3 satellite’s 2.1-m panchromatic nadir data can be used in generating orthorectified images, fusing images, updating maps and performing interpretation tasks. The panchromatic band pass of ZY-3 ranges from 450 nm to 800 nm; details of the specifications of ZY-3 can be seen in Table 1. The digital number (DN) dynamic range is 10-bit quantization. The swath width of its panchromatic camera is 50 km at nadir. A technical description of the ZY-3 satellite can be found on the official website of SASMAC [1]. There are five levels of ZY-3 nadir (NAD) products provided by the NASG: sensor-corrected (SC) product, geocoded ellipsoid-corrected (GEC) product, enhanced geocoded ellipsoid-corrected (EGEC) product, geocoded terrain-corrected (GTC) product and digital orthorectification map (DOM) product. The SC product is processed with radiometric calibration and sensor calibration; it is the standard original product and has the widest usage among all of the ZY-3 products.
The image quality of satellite data is of vital importance in various applications, and it can also provide prior knowledge for decision-making and subsequent satellite design [2]. For the panchromatic data of ZY-3, its image quality directly affects the benefit of its usage.
The image quality of the satellite images can be expressed by many technical parameters, such as the GSD, the modulation transfer function (MTF) and the signal-to-noise ratio (SNR) [3–5]. However, these parameters cannot completely describe the quality of the image [6], and they are used primarily in technical fields and by technical people, such as satellite designers, satellite manufacturers, optical engineers or electric engineers; as a result, the parameters provide quality information and feedback for these technical workers. However, these parameters are unfamiliar and complicated to satellite image product users, which, according to a survey of the U.S. Geological Survey (USGS), may come from different fields, such as agriculture, environmental sciences and management, land use/land cover surveying and even education [7]. In this case, an indicator that can present a comprehensive evaluation of the overall image quality can assist image users to understand the usability of the image according to different tasks [8]. For this reason, image interpretability based on the National Imagery Interpretability Scale (NIIRS) has been proposed as a measure of image quality [9].
Developed by the Imagery Resolution Assessments and Reporting Standards (IRARS) Committee, USA, the NIIRS is the subjective assessment standard of image quality connecting with task requirements [10]. From the perspective of the users, the NIIRS is probably the best measure of assessing the quality of panchromatic images in terms of interpretability [11]. Higher interpretability indicates that more ground objects can be detected or identified, and interpretability in an intuitive and quantitative sense determines which task can be performed with the imagery [12].
Although the NIIRS rating can be estimated by human operators, developers require a tool that will estimate or predict NIIRS performance prior to actually building and testing a new sensor system [9]. The general image-quality equation (GIQE) was developed to provide such predictions. The GIQE was developed under the auspices of the IRARS Committee. The GIQE estimates the NIIRS as a function of a predicted images scale, sharpness, resolution and the signal-to-noise ratio [9,13].
Currently, the research on calculating image interpretability using the GIQE is concentrated on satellite data with very high resolution (VHR), such as QuickBird, IKONOS and Komspat-2 [6,14–16]. Ryan et al. [14] discussed the relationship between the NIIRS value and the other parameters of IKONOS imagery. Kim et al. [6] predicted the NIIRS value of IKONOS and QuickBird satellite imagery. For QuickBird images, predicted NIIRS values are provided within the metadata. In addition, the IKONOS NIIRS values are also published for the users. The NIIRS provides a reference of the quality and usability of remote sensing images for researchers and users around the world.
In China, only recently have high resolution (HR) satellites been used. The satellite imagery users outside of China are not yet familiar with these HR satellite products and have rarely used them, not to mention the products of the ZY-3 satellite, which was launched in 2012. There have been studies regarding the statistical characteristics, SNR and MTF of ZY-3 data [17,18]; however, no research is available on using GIQE for evaluating the NIIRS of ZY-3 data, which would be useful for users to assess image quality. For this reason, the NIIRS can be used as a common indicator of image quality for users around the world to determine the quality of ZY-3 data.
There is one question remaining in the study of the NIIRS estimation of ZY-3 imagery using the GIQE. According to the study of Leachtenauer et al. [12], the revised GIQE is validated over the conditioned range listed in Table 2. The accuracy and validity of the GIQE outside of these bounds is unknown. The range of the GSD is from 0.0762 m (3 inches) to 2.032 m (80 inches); however, the published GSD of the ZY-3 SC NAD data is 2.1 m [1], i.e., slightly higher than 2.032 m. Therefore, whether the interpretability of ZY-3 images can still be estimated with the GIQE should be investigated.
With the NIIRS criteria published by IRARS, the NIIRS can be estimated by human operators. The results of operators on one image are so close, with a standard deviation of 0.3 NIIRS [12], that this observed NIIRS (ONIIRS) value can be considered as the approximate value of the true NIIRS value for ZY-3 image interpretability. Meanwhile, the GIQE can be used to calculate the predicted/estimated NIIRS (PNIIRS) value for the same image. The relationship can be found by a regression analysis using the ONIIRS and the PNIIRS as variables. If there is an acceptable correlation between the ONIIRS and PNIIRS, it would be possible to use this regression expression to estimate the true NIIRS for a ZY-3 image, i.e., the adjusted GIQE can be still used for the estimation of the interpretability of the ZY-3 images, even if its GSD is out of the range designated by IRARS [12].
Hence, as mentioned above, the estimation of the NIIRS for the ZY-3 SC NAD data is necessary and feasible. The purpose of this study is to develop a method to estimate the NIIRS of the ZY-3 images, thereby allowing image interpretability assessment of ZY-3 SC NAD data.
This paper is structured as follows. Section 2 presents the data and method of this study. In Section 3, the result of the ONIIRS and PNIIRS assessments will be presented. Next, a regression function between the ONIIRS and PNIIRS is built with the data of nine images, and subsequently, an adjusted GIQE is proposed based on the regression function, followed by verification of the adjusted GIQE using another four images. Finally, conclusions from this study are drawn in Section 4.
2. Data and Method
2.1. Data
ZY-3 SC NAD data provided by SASMAC were used in this study for estimating the ONIIRS and the PNIIRS. The SC data is the raw product that has only been radiometrically calibrated and sensor-response calibrated. There were 13 different SC-level NAD data acquired in different areas (Figure 1) or at different times; some of the metadata are listed below in Table 3. These data were acquired by the ZY-3 panchromatic camera from February 2012 to August 2013, with no clouds or a low percentage of clouds, covering the area of Wuhan of Hubei province (HB), Hangzhou of Zhejiang province (ZJ), Beihai and Baise of Guangxi province (GX), Sanya of Hainan province (HN), Baotou of Inner Mongolia province (IM), Wuhu of Anhui province (AH) and Shanghai. These data were received from the station of Miyun (MYN) in Beijing, the station of Sanya (SAY) in Hainan province and the station of Kashgar (KAS) in Xinjiang province, respectively. In addition, QuickBird panchromatic level 2A imagery, which provided the NIIRS value in its metadata, was used in the study in order to recognize the possible bias of human-obtained NIIRS and the true NIIRS.
All of the image data contained different types of areas, such as urban areas, suburban areas and mountainous areas, where abundant ground objects are found in the image, e.g., buildings, fields, water bodies, grass, forest, ground vehicles and some other geographic or artificial features, all of which were related to interpreting features or elements in the National Imagery Interpretability Scale (NIIRS) criteria and were useful in predicting the NIIRS by human operators or using the GIQE.
2.2. Method Description
There were several steps for estimating the NIIRS of the ZY-3 SC NAD data. First, the ONIIRS is evaluated by human operators. Second, the PNIIRS is calculated through the required parameters using the GIQE. Third, a regression analysis is performed for attaining the expression of the ONIIRS and PNIIRS. Then, we validate the regression expression using correlation coefficients to determine whether this regression expression could be used for estimating the NIIRS of ZY-3 SC NAD data.
2.2.1. Observed NIIRS Assessment
In the experiment, every individual image of these 13 ZY-3 NAD images and one QuickBird image from different areas or different time periods was divided into 4 sub-images. Six participants who were experienced in image processing and analysis interpreted the sub-images according to the Additional NIIRS Criteria [9], in which a number of additional criteria (agricultural, cultural and natural) appeared [19]. In the experiment, the sub-images of ZY-3 and QuickBird were mixed together for a blind test. After the participants interpreted the image by checking the corresponding or similar feature described in the Additional NIIRS Criteria; they provided a decimal score for every sub-image for higher precision, and the final NIIRS level for one image was determined by taking an average of the ONIIRS values estimated for the 4 sub-images from the 6 participants. To achieve an objective result, the test was performed with a sufficient amount of time, with the participants taking 4 working days to complete this interpretation task.
To recognize the possible bias, from the result of QuickBird image, we calculate the error between the ONIIRS and the NIIRS provided in the metadata of the QB image. For the purpose of decreasing the subjective error, the average error is considered as the bias between the ONIIRS and the true NIIRS in our experiment. With the help of this bias, we can revise the ONIIRS for ZY-3 imagery, through which the subsequent analysis is carried out. The revised ONIIRS was regarded as the true NIIRS value for the image in this study.
2.2.2. NIIRS Estimation Using the GIQE
We used the GIQE to predict the NIIRS level of the image as the PNIIRS. The early published GIQE 3.0 version used GSD, RER and SNR to calculate the NIIRS for an optical system. Subsequently, validation and modification was performed on the GIQE 3.0 version to obtain the GIQE version 4.0. GIQE version 4.0 is described by Equation (1):
In the above equation, GSD is the ground sample distance, in units of inches; RER denotes relative edge response; H is the overshoot; G is the noise gain calculated from an optional sharpening kernel; and a and b are parameters. If RER is greater than 0.9, then a is equal to 3.32 and b is equal to 1.559; otherwise, a equals 3.16 and b equals 2.817. This method makes it possible to predict the NIIRS values based on the imaging parameters [12].
The GSD was calculated as the geometric mean of the ground sampled distance based on a projection of the pixel pitch distance to the ground [12,20]. The GSD was computed in inches in both the X and Y dimensions (the along-scan and cross-scan directions, respectively), and we calculated their geometric mean. The GSD is given by Equation (2).
In Equation (2), PP is the pixel pitch, FL is the focal length, SL is the slant range and LA is the look angle; the details can found be in [12].
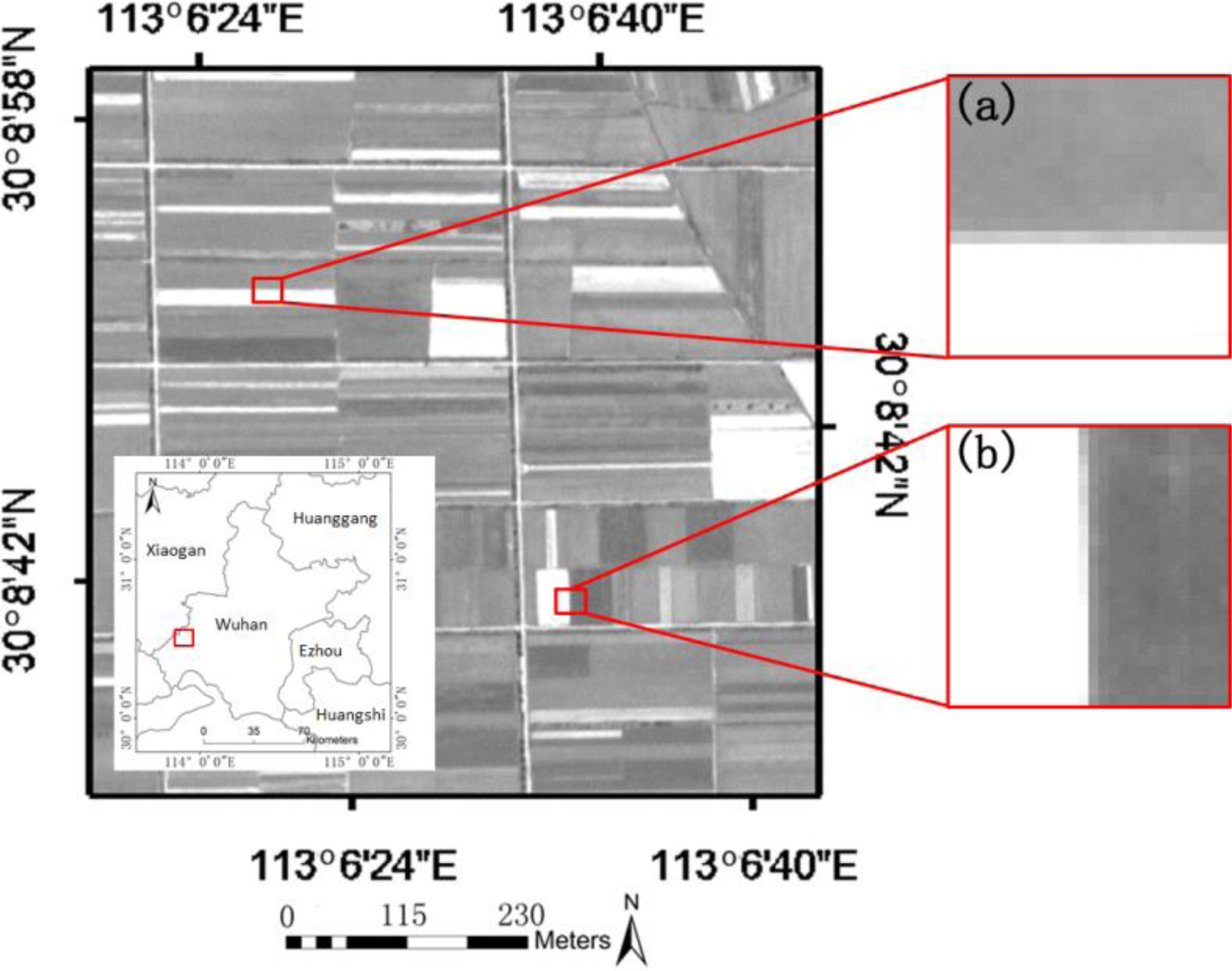
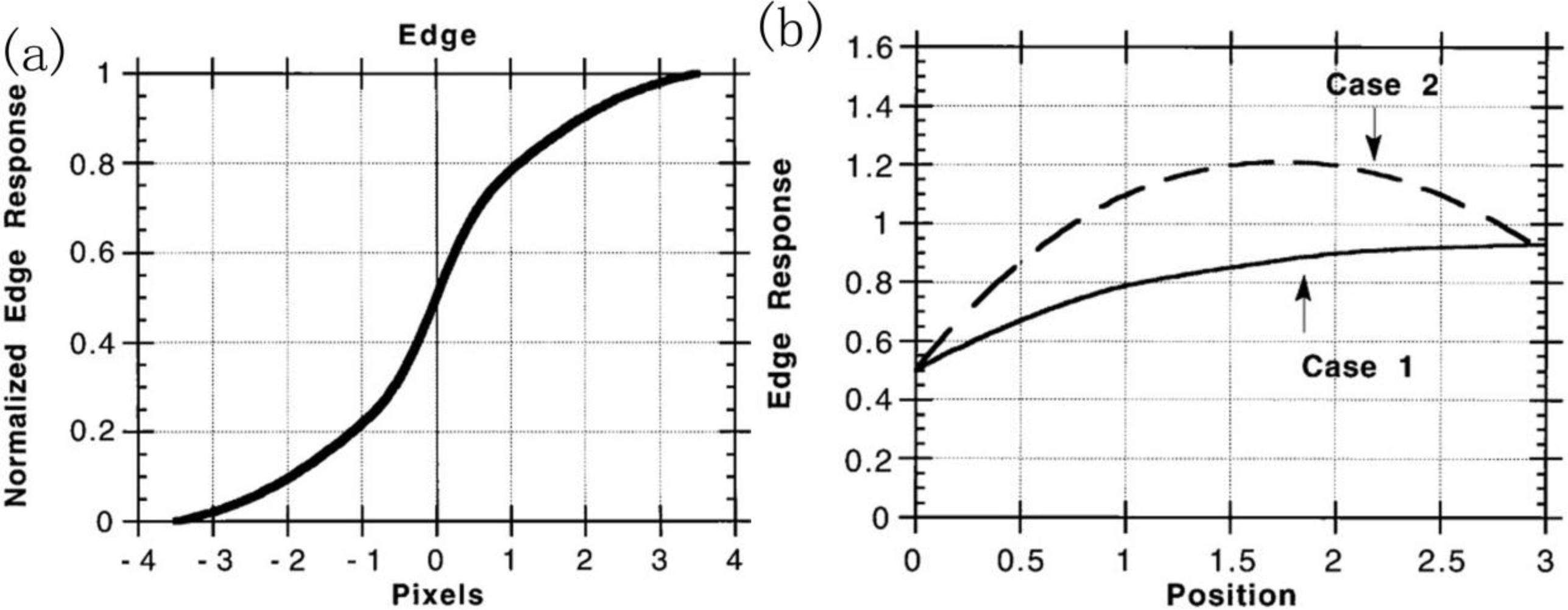
The RER of the image can be measured by analyzing the slopes of the edge profiles within the image, and this value represents the MTF characteristics of the image. To calculate the RER of the image, we first selected the edge manually, where the intensities of the DN value of both sides of the edge were changing rapidly. Figure 2 shows the example of the edge determined manually for edge response (ER) generation; Figure 2a is an edge from the horizontal direction, and Figure 1b presents an edge in the vertical direction. Next, the values of the pixels along the perpendicular lines are interpolated with cubic splines, the edge profile of the row or column perpendicular to the edge provided was calculated. This procedure was repeated for each perpendicular line. Finally, all of the estimated edge profiles were used to obtain one averaged function that could represent the empirical edge spread function (ESF) (Figure 3a) [12]. From this average ESF of the edge, the differential of the normalized ER in +0.5 and −0.5 was calculated in the vertical and horizontal direction, respectively, as the ERx and ERy. The RER is calculated as a geometric mean of ERx and ERy [21].
The GSD and RER are the dominant terms in the equation of GIQE, while the overshoot term, H, the G term and the SNR have a much smaller impact [12]. The overshoot-height term, H, models the RER overshoot that is due to the modular transfer function compensation (MTFC). The overshoot height is measured over the range of 1.0 to 3.0 pixels from the edge in 0.25-pixel increments. If the edge is monotonically increasing, it is defined as the value at 1.25 pixels from the edge. Otherwise, it is the maximum value in the pixel range of +1 to +3, as shown in Figure 3b [12]. As for the GSD and the RER, H is calculated on both the X and Y directions.
G is the noise gain resulting from the edge sharpening and is the geometric mean of the coefficients. Because the ZY-3 SC NAD data are not processed by MTFC, the value of G is 1. The SNR has the least effect on the NIIRS value (GSD 72%, RER 20% and SNR less than 1%) [22]; in this case, although there are methods of analyzing the SNR from the image, we use the laboratory method for its simplicity and convenience. In this method, the ratio of the mean and the standard deviation was calculated from a homogeneous area in the image, and this ratio was used as the approximate value of the SNR [23]. The calculation of the SNR is given by Equations (3)–(5):
Using the values of GSD, RER, H, G and SNR, the PNIIRS can be estimated with GIQE, and its result could be used in the experiment to analyze the relationship between the PNIIRS and the ONIIRS, with the latter value considered as the true value of the NIIRS of the image.
2.2.3. Linear Regression Analysis
Linear regression analysis was further used to investigate the relationships between ONIIRS and PNIIRS values. The PNIIRS values were calculated using the GIQE from eight of the study images and then were related to the ONIIRS values using a linear regression analysis. In the regression analysis, the Shapiro-Wilk test was used to examine the normal distribution of the ONIIRS and the PNIIRS, which were the two variables in the analysis. R and R-squared were used to investigate the correlation between the ONIIRS and PNIIRS. The F-test was used to estimate the significance of the relationship between the ONIIRS and PNIIRS. The analysis involved determining whether the relationship between the ONIIRS and PNIIRS was significant at the 0.05 level. We then validated the PNIIRS and ONIIRS of another five images, examining their NIIRS predicted from the adjusted GIQE with the ONIIRS. If a high correlation and similarity still existed in the result, the adjusted GIQE equation was further proven to be applicable for the estimation of the NIIRS of ZY-3 SC NAD data.
All of the statistical analyses were performed using Microsoft® Excel® 2010 and IBM® SPSS® Statistics 20. A significance level of 0.05 was established in the analysis. If the result fulfills the requirements, then we can use regression expression as the prediction expression for estimating the NIIRS of the ZY-3 SC NAD data.
3. Results and Discussion
3.1. Results of Observed NIIRS Assessment
Subjectivity is the main source of error in image interpretation by human operators, because different individuals may differ in their interpretation of an area of the image, such as different familiarity and experience for the scenes or geographical features. In addition, fatigue may affect the accuracy of the interpretation. In this case, the result that is represented by the NIIRS value may be different. To avoid subjective error, we provided a fixed and stable working environment for the participants. For example, the brightness of the environment was stable, and we set up the same contrast and brightness of the display used by the participants and maintained them for the entire experiment period. There are 56 sub-images in total for the operators to interpret during the experiment; to avoid fatiguing the operators in this exhausting work and to ensure the accuracy of the interpreted result, a period of four working days was provided to the operators as a sufficient amount of time for completing the assessment.
The ONIIRS assessment results are presented in Table 4. In this article, the NIIRS values are set to two decimal places, and the other values without specific states are set to three decimal places to enable higher accuracy and better comparison. As shown in Table 4, the mean value of the ONIIRS was 2.94. Except for the image of Hangzhou, which had a 0.325 standard deviation of the ONIIRS value, all other images had a standard deviation lower than 0.3, and the mean value of their standard deviation was 0.255, which represents an acceptable accuracy for the assessment. The reason why the image in Hangzhou had such a high standard deviation is that the acquisition date of the image was 30 December2012 (winter), when it had just snowed, so some of the ground areas were covered by snow; in addition, although the cloud percentage of the image was only 3%, the clouds were all aggregated on the left bottom of the image. As a result, the difference of the ONIIRS value between the sub-images of the left bottom and other sub-images of the Hangzhou image is significant, which results in a higher standard deviation.
We compared the ONIIRS result of the QuickBird image (4.567 NIIRS on average, for estimating the bias; we set this value three decimal places) with the NIIRS provided in its metadata (4.400 NIIRS), and the bias of ONIIRS and the true NIIRS was attained as 0.167. Therefore, the ONIIRS of the ZY-3 NAD data was revised by the bias, and the final results of the revised ONIIRS are listed in Table 4. The mean of the revised ONIIRS was 2.77, a bit lower than the original ONIIRS value of 2.94. In the subsequent study, we used the revised ONIIRS as the final ONIIRS for analysis.
3.2. Results of NIIRS Predicted Using the GIQE
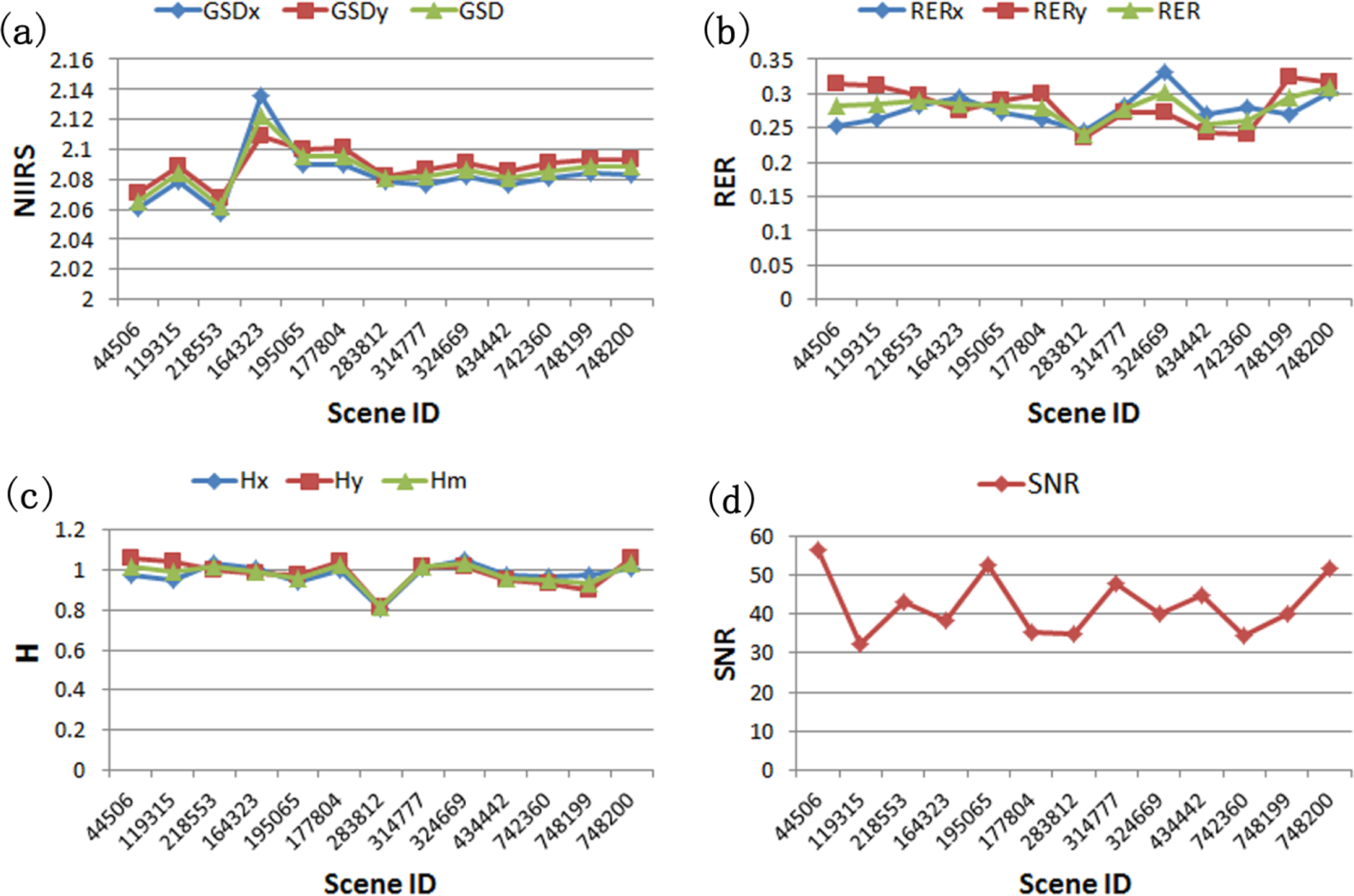
In the experiment, we calculated the GSD, RER, H, G and SNR for every image, with the results listed in Table 5. The GSD in the X dimension had an average value of 2.083, while the average value of the GSD in the Y dimension was 2.089. It was found that the GSD in the Y dimension (GSDy) was 0.3% greater than that in the X dimension (GSDx). The geometric mean of GSDx and GSDy was 2.086 on average. The GSD had a maximum value of 2.062 and a minimum value of 2.122. The results of GSD are shown in Figure 4a. With a standard deviation of 0.013, this GSD value is acceptable. Compared with the GSD required by the original design objective of the ZY-3 satellite (2.1 m), the GSD of the image data in practice (2.086 m) is better than expected.
The results of the calculation of the RER indicate that (Figure 4b) the average value of the ERx and the ERy are 0.277 and 0.284, respectively, with the latter value being 2.52% greater than the former value. The higher ERy value means better sharpness of the edge in the along-scan direction. The average value of the RER is 0.280, with a standard deviation of 0.019. Therefore, according to GIQE 4.0, the RER value is less than 0.9, so a is set as 3.16 and b is set as 2.817 (Equation (1)). In the experiment, we found that the edge used to calculate the ER for the ESF can be found from the triangular roof of the building, a high reflective building and its shadow, the border of a road or runway, the common border of the two different fields (Figure 2) and the edge between the port and water surface.
From the ESF calculated for the ER, we estimated the H value of the image according to the monotonicity of the ESF in the range of +1 to +3 pixels. In the experiment, we found that for the ZY-3 image, the curves of the ESF in both the X dimension and the Y dimension were not monotonically increasing, so the maximum value in the range of +1 to +3 was considered as the Hx or Hy value. H is also the geometric mean of Hx and Hy. The values of Hx and Hy in the images were all very close, as shown in Figure 4c. The mean of the H calculated from the images is 0.982.
Because the ZY-3 SC NAD data are processed without MTFC, the value of G is one. Using the laboratory method to estimate the SNR, we obtained a value of approximately 42 on average. This result is only a probable estimation, because different choices of the homogeneous areas in the same image may result in some different value, and the calculation result of the laboratory method itself has been shown to be slightly greater than the true value [23]. However, the SNR only had a slight effect on the NIIRS (less than 1%), so we used this method for the study. The result is shown in Figure 4d.
With the aid of these parameters, the PNIIRS was calculated for these images; the results are listed in Table 5. A mean value of 1.99 for the PNIIRS was obtained, with a standard deviation of 0.058. The lowest PNIIRS is 1.90 in the Hangzhou area; in contrast, the highest PNIIRS is 2.08 in the middle area of Wuhan. We can compare these two images. The GSD of the image in the middle of Wuhan (Scene ID 748199) has lower resolution (higher GSD), which is 2.088 m in GSD and is 0.3% higher than that of the image of Hangzhou (2.081 m). However, the former image has the RER with a value of 0.295; conversely the RER value of the image of Hangzhou is just 0.256, which is 15% lower. As a result, the image of Wuhan has a 9% higher PNIIRS than that of Hangzhou. Because GSD and RER take up more than 90% of the effect of NIIRS calculation, the values of H, SNR and G are not discussed in this comparison. Therefore, we can find in the comparison that higher GSD cannot guarantee a higher NIIRS of the image, because the sharpness of the edge is also important for image interpretability.
3.3. Linear Regression Analysis
After we estimated the ONIIRS and PNIIRS of the images, we found that there is a significant difference between the PNIIRS and ONIIRS. The value of the PNIIRS calculated using the GIQE is obviously lower than that of the ONIIRS, as found in Table 6. The reason for this difference may be that the GSD of the ZY-3 data exceeds the range of the GSD in the GIQE study.
A linear regression analysis was used to examine the relationship between the ONIIRS and PNIIRS. The results of the ONIIRS and PNIIRS in the Shapiro–Wilk test are 0.489 and 0.536, respectively, which are all greater than 0.05, so a normal distribution can be assumed in both of these two variables. A regression analysis indicates that the value of the ONIIRS and the value of the PNIIRS can effectively predict one another, as shown in Figure 5. The regression expression is given by:
In the expression, y refers to the ONIIRS (which is considered as the true value of the NIIRS), and x refers to the PNIIRS. We discovered that the relationship has a high correlation coefficient, with a value of R-squared of 0.641, i.e., much greater than 0.5. This value of R-squared means that 64.1% of the variation of ONIIRS values can be reflected by the PNIIRS. The adjusted R-squared is 0.582, and we found a significant correlation between these two variables, as the p-value is 0.017, which is less than the significance level of 0.05.
The linear regression analysis results indicate that a highly significant relationship exists between the ONIIRS and the PNIIRS. In addition, with the help of the regression expression, in spite of the fact that the GSD is outside the proper range, the GIQE can still be adjusted to estimate the true NIIRS value of the ZY-3 data using Equation (7):
NIIRSZY3 is the adjusted NIIRS value that is suitable for ZY-3 SC NAD data, and the NIIRS is calculated using GIQE 4.0.
The validation of the equation was performed using five other images, with the results presented in Table 7; the values of the ONIIRS and NIIRSZY3 calculated using the Equation (7) are very close: the mean of the error is 0.054 with a standard deviation of 0.069, which represents the very high similarity of the results.
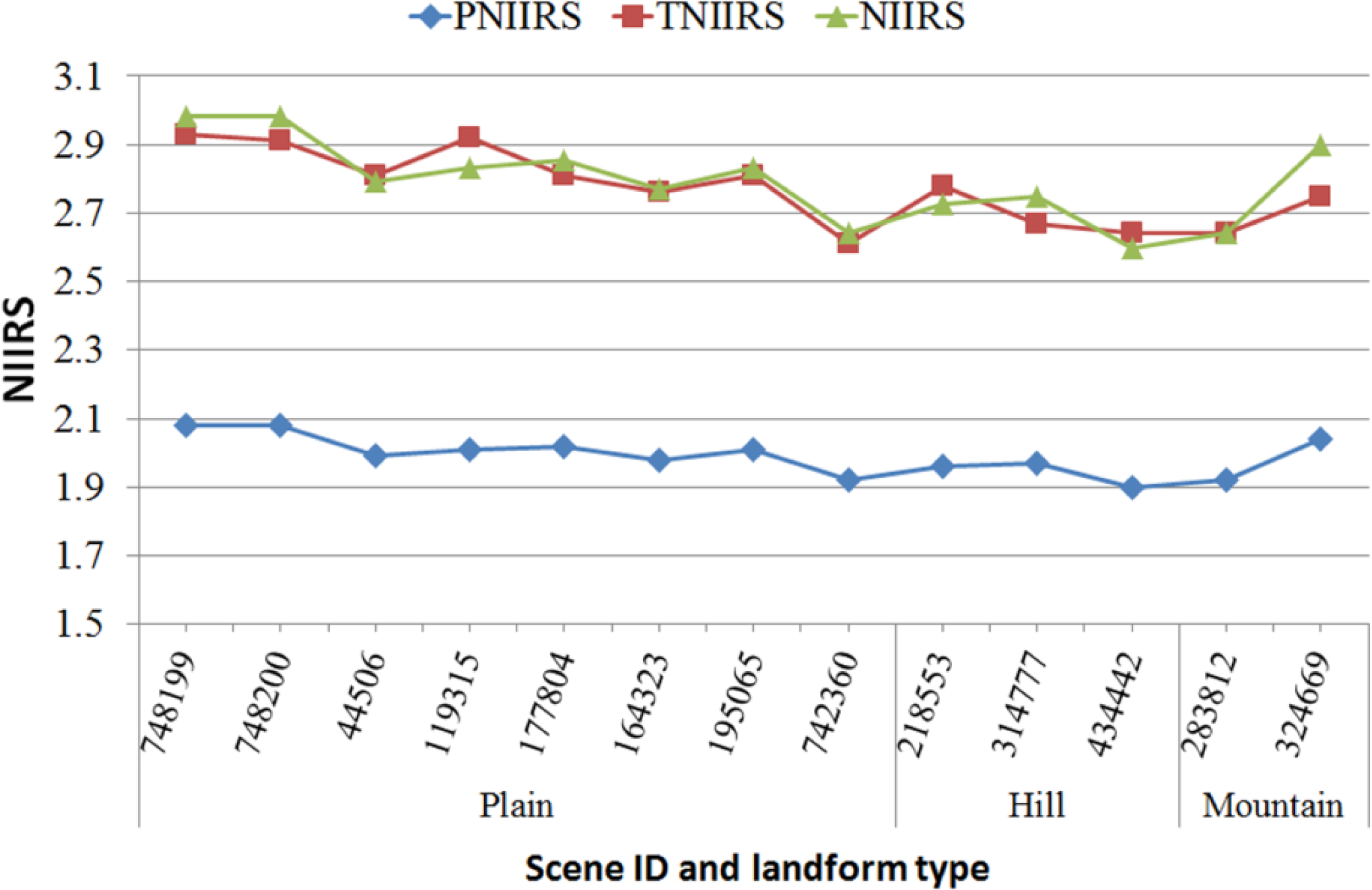
The values of the ONIIRS, PNIIRS and NIIRSZY3 of all thirteen ZY-3 SC-level NAD data are shown in Table 8 and Figure 6. From the results of the estimation, we find that the NIIRSZY3 values calculated using the adjusted GIQE of the study images are nearly equal and are related with the corresponding values of the ONIIRS. The average value of NIIRSZY3 is 2.79, which, to some extent, is nearly the same as that of the ONIIRS (2.77). The standard deviation of NIIRSZY3 is 0.12, i.e., lower than the value of 0.3 in the GIQE. As a result, the approximate NIIRS of the ZY-3 SC NAD data is 2.79.
Considering that the landform type may affect the interpretability of the image, we grouped these 13 images into three types: the plain area, the hill area and the mountain area. Eight images are from the plain area; three images are from the hill area, and only two images are from the mountain area. The average NIIRS of ZY-3 SC NAD data in the plain area is 2.84, which is the highest in all landform types. The mountain area has an average NIIRS of 2.77, and that of the hill area is 2.69, which is the lowest. The reason for this result may be that the image of the plain area has the least distortion and the most abundant ground objects with obvious spatial structures or characteristics (i.e., buildings, roads and fields), which help the image to attain the best interpretability. Compared with the hill area, the greater portion of the vegetation in the mountain area is like a background for other objects, which increases the sharpness of the edge of the object. Therefore, though there is comparatively more distortion in the image of the mountain area, it still has a higher NIIRS than the hill area. The results are in Figure 6.
3.4. NIIRS Level of the ZY-3 Data
The NIIRS is a 10-level scale defined by interpretation tasks or criteria [9]. Once the NIIRS of the image is known, the available interpretation tasks or related applications can be estimated according to the NIIRS Criteria. Conversely, the tasks or applications are assigned by determining which type of image can fulfill the requirements of the users. In addition to the original NIIRS, which is mainly focused on military targets, IRARS has developed and published several other scales and products of potential interest to the civil remote-sensing community [9,24,25]. In this study, we used the adjusted GIQE (based on GIQE 4.0 [26]) to estimate the NIIRS of ZY-3 SC NAD data, with a result of 2.79. According to the Additional NIIRS Criteria in the Civil NIIRS Reference Guide [9], some of the tasks for which ZY-3 SC NAD data can be applied are listed below (Table 9). The images in Figure 7 show some other criteria that can be applied to ZY-3 SC NAD data. These tasks mainly are concentrated in NIIRS Level 1 and Level 2, such as “Distinguish between runways and taxiways at a large airfield (NIIRS 1)” and “Detect large buildings (e.g., station, hospitals, factories) (NIIRS 2)” (Figure 7a) in the Civil NIIRS Criteria; “Identify long-lot land ownership patterns along major waterways (NIIRS 1.7)” and “Detect windbreaks (i.e., rows of trees) between fields (NIIRS 2.6)” (Figure 7c) in the Agricultural Criteria; “Detect multi-lane divided highways (e.g., greater than four lanes (NIIRS 1.9)” and “Identify large buildings as multi-wing (NIIRS 2.7)” in the Cultural Criteria; “Detect large coastal sand beaches (NIIRS 1.8)” and “Detect utility towers in forested regions on the basis of a sequence of circular clearings (NIIRS 2.7)” (Figure 7b) in the Natural Criteria. Briefly, ZY-3 SC NAD data are useful for most of the common interpretation tasks for civil, agricultural and natural applications, among others.
According to the result, we compare the NIIRS of ZY-3 SC NAD data with some other satellite data. QuickBird and IKONOS are famous sub-meter VHR satellites in the world, with a GSD of 0.61 m and 0.82 m, respectively [27,28]. SPOT-5 is also a well-known satellite worldwide, with its 2.5-m GSD [29], and it has been considered as the representative of HR satellites for quite a long time. From the official product guide of QuickBird, we can find that its potential NIIRS is 4.9 [27]. The NIIRS of IKONOS is estimated to be 4.5, which can be found in the literature of Ryan [14]. SPOT-5 has the same problem as ZY-3 in calculating NIIRS using GIQE, in that their GSD (2.5 m) exceed the scope of that in GIQE 4.0 (2.03 m). Therefore, we use the adjusted GIQE in the study for achieving a rough estimation of NIIRS of SPOT-5, and the result is 2.43. As is stated in the manuscript, the NIIRS of ZY-3 is 2.79.
A comparison can be seen in Figure 8. The VHR satellite not only has higher resolution in its imagery, but also a higher NIIRS than the HR satellite. However, considering the wider swath width and lower cost, HR satellites, like ZY-3 and SPOT-5, are still a better choice for some certain tasks or applications.
3.5. Uncertainties, Errors and Accuracies
In the study, we had thirteen ZY-3 SC NAD data available for the estimation of its NIIRS, so errors may exist in the regression analysis. The accuracy of the equation of adjusted GIQE should be further discussed when there are more data. Additionally, in the experiment of ONIIRS, strictly speaking, six participants are not enough for achieving a very high accuracy, because subjective error may occur among the six participants during the experiment. We used the laboratory method in calculating the SNR, because the SNR has the least effect on predicted NIIRS, and this method is comparatively simple and convenient. The SNR derived from this method is proven to be a little greater than the true value [23]. Therefore, the result is only a rough approximation for the SNR.
4. Conclusions
This study estimated the NIIRS of ZY-3 SC NAD data using an adjusted GIQE equation derived from the analysis of the ONIIRS and the PNIIRS. In this study, we not only presented the results of the ONIIRS, but also described the characteristics of the parameters of the ZY-3 data used in the GIQE (GSD, RER, H, G and SNR) and discussed the results of the values of the PNIIRS. A linear regression analysis of the ONIIRS and PNIIRS revealed a significant relationship between these scales. As a result, with the help of the regression expression, the NIIRS of ZY-3 NAD data can be estimated using the adjusted GIQE, in spite of its exceeding the range of the GSD.
The result of the study demonstrates that, as the first civil high resolution satellite for use in China, ZY-3 has a moderate GSD of approximately 2.086 m, i.e., slightly better than its design objective of 2.1 m. Although the ZY-3 SC NAD data are the original product, these data still have good quality regarding sharpness, and the NIIRS value of 2.79 for its interpretability makes it able to completely fulfill the requirements of the tasks of NIIRS 2.7 and lower levels.
The main contributions of this study are as follows:
- (1)
The study is the first to use the GIQE for assessing the interpretability of the image quality of ZY-3 data. We proposed the method of estimating the adjusted NIIRS of ZY-3 SC NAD data. The study provides worldwide users with the results of the interpretability of Chinese ZY-3 SC NAD data based on the NIIRS, which is a common indicator for assessing the image quality of remote sensing data. The method and results are also helpful for expanding the method of assessing the image quality of Chinese remote sensing satellite data.
- (2)
We discussed the availability of using the GIQE to estimate the NIIRS of satellite image data whose GSD is greater than 2.03 m and explored the use of an adjusted GIQE in estimating the NIIRS of such data. The method and the results of this study can be used as a reference for studying the interpretability of other similar satellite remote sensing data (with a GSD greater than 2.03 m) using the GIQE.
In future work, we will perform more experiments to study the relationship between the GIQE and the NIIRS for ZY-3 SC NAD data. Additionally, the parameters of the ZY-3 SC NAD data used in the GIQE will be further examined. For example, other methods will be used to improve the estimation result of the SNR. More ZY-3 SC NAD data will be used to improve the accuracy of analyzing the relationship between the ONIIRS and the PNIIRS using a regression analysis. Then, we can examine the expression used to predict the NIIRS of ZY-3 SC NAD data using the GIQE and appropriately modify it. Moreover, if possible, in addition to ZY-3 data, the data of other satellites with a GSD greater than 2.03 m (80 inches) can be used for studying the uncertainty of the GIQE, such as SPOT-5 (2.5 m), ALOS (2.5 m) and ZY-1-02C (2.36 m in the HR camera and 5 m in the panchromatic camera). Finally, we can achieve a common estimation of the NIIRS using the GIQE for most of the VHR and HR optical satellite data.
Acknowledgments
This research has been funded by the National Science and Technology Support Program of China (2012BAB16B01), the National Natural Science Foundation of China (41271458). We also acknowledge the help of the Satellite Surveying and Mapping Application Center, National Administration of Surveying, Mapping and Geo-information (NASG), China, for providing the ZY-3 SC NAD data.
Author Contributions
This research was mainly performed and prepared by Lin Li and Heng Luo. Lin Li supervised the study and his comments were considered throughout the paper. Heng Luo contributed with ideas, conceived and designed the study, and wrote the paper. Haihong Zhu reviewed and edited the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References and Notes
- Satellite Surveying and Mapping Application Center, NASG. Available online: http://sjfw.sasmac.cn/en/ZY-3.html (accessed on 4 March 2014).
- Kim, H.; Kim, D.; Kim, S.; Kim, T. Analysis of the Effects of Image Quality on Digital Map Generation from Satellite Images. Proceeidngs of the 2012 International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Melbourne, VIC, Australia, 25 August–1 September 2012; pp. 127–130.
- Fiete, R.D.; Tantalo, T. Image quality of increased along-scan sampling for remote sensing systems. Opt. Eng 1999, 38, 815–820. [Google Scholar]
- Leachtenauer, J.C.; Driggers, R.G. Surveillance and Reconnaissance Imaging Systems; Artech House: Boston, MA, USA, 2001. [Google Scholar]
- Javan, F.D.; Samadzadegan, F.; Reinartz, P. Spatial quality assessment of pan-sharpened high resolution satellite imagery based on an automatically estimated edge eased metric. Remote Sens 2013, 5, 6539–6559. [Google Scholar]
- Kim, T.; Kim, H.; Kim, H. Image-Based Estimation and Validation of NIIRS for High-Resolution Satellite Images. Proceeidngs of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Beijing, China, 3–11 July 2008; pp. 1–4.
- Miller, H.M.; Sexton, N.R.; Koontz, L.; Loomis, J.; Koontz, S.R.; Hermans, C. The Users, Uses, and Value of Landsat and Other Moderate-Resolution Satellite Imagery in the United States—Executive Report; U.S. Geological Survey: Reston, VA, USA, 2011. [Google Scholar]
- Maver, L.A.; Erdman, C.D.; Riehl, K. Imagery Interpretability Rating Scales. In Digest of Technical Papers: International Symposium of the Society for Information Display; Society for Information Display: Santa Ana, CA, USA, 1995; Volume 26, pp. 117–120. [Google Scholar]
- Imagery Resolution Assessments and Reporting Standards (IRARS) Committee, Civil NIIRS Reference Guide. Available online: http://www.fas.org/irp/imint/niirs_c/index.html (accessed on 4 March 2014).
- Irvine, J.M. National Imagery Interpretability Rating Scales (NIIRS): Overview and Methodology. In Optical Science, Engineering and Instrumentation’97; International Society for Optics and Photonics: San Diego, CA, USA, 1997; pp. 93–103. [Google Scholar]
- Zhou, W.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. Image Process 2004, 13, 600–612. (In Chinese). [Google Scholar]
- Leachtenauer, C.J.; Malila, W.; Irvine, J.; Colburn, L.; Salvaggio, N. General image-quality equation: GIQE. Appl. Opt 1997, 36, 8322–8328. [Google Scholar]
- Schowengerdt, R.A. Data Models. In Remote Sensing: Models and Methods for Image Processing, 3rd ed; Elsevier: Burlington, MA, USA, 2007; pp. 149–152. [Google Scholar]
- Ryan, R.; Baldridge, B.; Schowengerdt, R.A.; Choi, T. IKONOS spatial resolution and image interpretability characterization. Remote Sens. Environ 2003, 88, 37–52. [Google Scholar]
- Kim, T.; Kim, J.; Kim, D.; Kim, J. Automated Image Interpretability Assessment by Edge Profile Analysis of Natural Targets. Proceedings of the ASPRS 2010 Annual Conference, San Diego, CA, USA, 26–30 April 2010.
- Edward, C.J. Image Quality Evaluation of QuickBird Super Resolution and Revisit of IKONOS. Proceedings of High Spatial Resolution Commercial Imagery Workshop, Reston, VA, USA, 8 November 2004.
- Li, L.; Luo, H.; Zhu, H.H.; Li, Z.; Tang, X. User-Oriented Image Quality Assessment of ZY-3 Product in Agriculture Area. Proceedings of the 2nd International Conference on Agro-Geoinformatics: Information for Sustainable Agriculture, Fairfax, VA, USA, 12–16 August 2013; pp. 22–27.
- Xu, W.; Ge, S.L.; Long, X.X.; Wang, X.; Li, J. Radiometric image quality assessment of ZY-3 TLC camera. Space Recover. Remote Sens 2012, 33, 65–74. [Google Scholar]
- Leachtenauer, J.C. National imagery interpretability rating scales: Overview and product description. Remote Sens. Photo-Gramm 1996, 1, 262–272. [Google Scholar]
- Pagnutti, M.; Blonski, S.; Cramer, M.; Helder, D.; Holekamp, K.; Honkavaara, E.; Ryan, R. Targets, methods, and sites for assessing the in-flight spatial resolution of electro-optical data products. Can. J. Remote Sens 2010, 36, 583–601. [Google Scholar]
- Mattia, C.; Laura, D.V. A procedure for high resolution satellite imagery quality assessment. Sensors 2009, 9, 3289–3313. [Google Scholar]
- Bai, H.G. Research on Image Quality Estimation and Evaluation Methods of Remote sensing Based on NIIRS. Master’s Thesis, Xidian University, Xian, Shaanxi, China. 2010. (In Chinese). [Google Scholar]
- Curran, P.J.; Dungan, J.L. Estimation of SNR: A new procedure applied to AVIRIS data. IEEE Trans. Geosci. Remote Sens 1989, 27, 620–628. [Google Scholar]
- Hothem, D.; Irvine, J.M.; Mohr, E.; Buckley, K.B. Quantifying Image Interpretability for Civil Users. Proceedings of the American Society of Photogrammetry and Remote Sensing Annual Meetings, Bethesda, MD, USA, 1–5 April 1996.
- Greer, J.D.; Caylor, J. Development of an environmental image interpretability rating scale. Airborne Reconnaiss 1992, 1763, 151–157. [Google Scholar]
- National Imagery and Mapping Agency, General Image Quality Equation User’s Guide, Version 4.0.; Data and System Division: Springfield, VA, USA, 1996.
- Digital Globe Core Imagery Products Guide. Available online: http://www.digitalglobe.com/sites/default/files/DigitalGlobe_Core_Imagery_Products_Guide_0.pdf (accessed on 15 April 2014).
- GeoEye. IKONOS Imagery Products Guide. Available online: http://glcf.umd.edu/library/guide/IKONOS_Product_Guide_jan06.pdf (accessed on 15 April 2014).
- Spot-1 to Spot-5 Satellite Images. Available online: http://www.astrium-geo.com/en/4388-spot-1-to-spot-5-satellite-images (accessed on 15 April 2014).



| Specification | Value |
|---|---|
| Orbit height | 505.983 km |
| Orbit inclination | 97.421° |
| Descending node time | 10:30 AM |
| Revisit cycle | 5 days |
| Mission duration | 5 years |
| Field of regard | Up to 32° off-nadir |
| Swath width | 50 km at nadir |
| Radiometric resolution | 10 bit |
| Panchromatic GSD | 2.1 m at nadir |
| Panchromatic band | 450 nm to 800 nm |
| Parameter | Minimum | Maximum |
|---|---|---|
| GSD | 0.076 m | 2.032 m |
| RER | 0.2 | 1.3 |
| Overshoot | 0.9 | 1.9 |
| Noise Gain | 1 | 19 |
| SNR | 2 | 130 |
| Location | Scene ID | Date | Track Number | Longitude/Latitude(°) | Sensor | Level | Receiving Station | Cloud Percentage |
|---|---|---|---|---|---|---|---|---|
| Wuhu, AH | 44506 | 02/19/2012 | 624 | 118.6/31.5 | PAN | SC | MYN | 5 |
| Wuhan, HB | 119315 | 04/22/2012 | 1582 | 114.4/30.7 | PAN | SC | MYN | 9 |
| Beihai, GX | 218553 | 05/16/2012 | 1947 | 109.3/21.5 | PAN | SC | SAY | 5 |
| Shanghai | 164323 | 05/28/2012 | 2137 | 121.4/31.4 | PAN | SC | MYN | 10 |
| Wuhan, HB | 195065 | 06/20/2012 | 2479 | 114.2/30.7 | PAN | SC | MYN | 10 |
| Beihai, GX | 177804 | 07/09/2012 | 2775 | 109.3/21.1 | PAN | SC | MYN | 3 |
| Baotou, IM | 283812 | 09/15/2012 | 3809 | 109.8/40.6 | PAN | SC | MYN | 7 |
| Sanya, HN | 314777 | 09/21/2012 | 3902 | 109.7/18.4 | PAN | SC | KAS | 38 |
| Baise, GX | 324669 | 09/30/2012 | 4037 | 106.7/23.9 | PAN | SC | MYN | 0 |
| Hangzhou, ZJ | 434442 | 12/30/2012 | 5413 | 120.1/30.3 | PAN | SC | SAY | 3 |
| Wuhan, HB | 742360 | 08/07/2013 | 8767 | 113.9/30.7 | PAN | SC | KAS | 0 |
| Wuhan, HB | 748199 | 08/12/2013 | 8843 | 114.4/30.7 | PAN | SC | KAS | 1 |
| Wuhan, HB | 748200 | 08/12/2013 | 8843 | 114.3/30.3 | PAN | SC | KAS | 3 |
| Date | Location | Scene ID | ONIIRS (SD) | Revised ONIIRS |
|---|---|---|---|---|
| 02/19/2012 | Wuhu, AH | 44506 | 2.98 (0.284) | 2.81 |
| 04/22/2012 | Wuhan, HB | 119315 | 3.09 (0.237) | 2.92 |
| 05/16/2012 | Beihai, GX | 177804 | 2.98 (0.267) | 2.81 |
| 05/28/2012 | Shanghai | 164323 | 2.93 (0.245) | 2.76 |
| 06/20/2012 | Wuhan, HB | 195065 | 2.98 (0.285) | 2.81 |
| 07/09/2012 | Beihai, GX | 218553 | 2.95 (0.257) | 2.78 |
| 09/15/2012 | Baotou, IM | 283812 | 2.81 (0.292) | 2.64 |
| 09/21/2012 | Sanya, HN | 314777 | 2.84 (0.272) | 2.67 |
| 09/30/2012 | Baise, GX | 324669 | 2.92 (0.174) | 2.75 |
| 12/30/2012 | Hangzhou, ZJ | 434442 | 2.81 (0.325) | 2.64 |
| 08/07/2013 | Wuhan, HB | 742360 | 2.78 (0.215) | 2.61 |
| 08/12/2013 | Wuhan, HB | 748199 | 3.10 (0.247) | 2.93 |
| 08/12/2013 | Wuhan, HB | 748200 | 3.08 (0.212) | 2.91 |
| Mean | 2.94 (0.255) | 2.77 | ||
| SD | 0.111 | 0.109 | ||
| Date | Location | Scene ID | GSD (m) | RER | H | SNR * | PNIIRS |
|---|---|---|---|---|---|---|---|
| 02/19/2012 | Wuhu, AH | 44506 | 2.066 | 0.282 | 1.018 | 56 | 1.99 |
| 04/22/2012 | Wuhan, HB | 119315 | 2.084 | 0.286 | 0.997 | 32 | 2.01 |
| 05/16/2012 | Beihai, GX | 177804 | 2.062 | 0.289 | 1.015 | 43 | 2.02 |
| 05/28/2012 | Shanghai | 164323 | 2.122 | 0.285 | 0.997 | 38 | 1.98 |
| 06/20/2012 | Wuhan, HB | 195065 | 2.095 | 0.281 | 0.959 | 52 | 2.01 |
| 07/09/2012 | Beihai, GX | 218553 | 2.096 | 0.281 | 1.024 | 35 | 1.96 |
| 09/15/2012 | Baotou, IM | 283812 | 2.080 | 0.240 | 0.814 | 35 | 1.92 |
| 09/21/2012 | Sanya, HN | 314777 | 2.081 | 0.278 | 1.014 | 48 | 1.97 |
| 09/30/2012 | Baise, GX | 324669 | 2.086 | 0.301 | 1.037 | 40 | 2.04 |
| 12/30/2012 | Hangzhou, ZJ | 434442 | 2.081 | 0.256 | 0.962 | 45 | 1.90 |
| 08/07/2013 | Wuhan, HB | 742360 | 2.086 | 0.260 | 0.951 | 35 | 1.92 |
| 08/12/2013 | Wuhan, HB | 748199 | 2.088 | 0.295 | 0.938 | 40 | 2.08 |
| 08/12/2013 | Wuhan, HB | 748200 | 2.088 | 0.309 | 1.036 | 52 | 2.08 |
| Min | 2.062 | 0.240 | 0.814 | 32 | 1.90 | ||
| Max | 2.122 | 0.309 | 1.037 | 56 | 2.08 | ||
| Mean | 2.086 | 0.280 | 0.982 | 42 | 1.99 | ||
| SD | 0.015 | 0.019 | 0.060 | 7.698 | 0.058 | ||
*The value of SNR is in the form of integer.
| Date | Location | Scene ID | PNIIRS | ONIIRS |
|---|---|---|---|---|
| 02/19/2012 | Wuhu, AH | 44506 | 1.99 | 2.81 |
| 04/22/2012 | Wuhan, HB | 119315 | 2.01 | 2.92 |
| 05/16/2012 | Beihai, GX | 177804 | 2.02 | 2.81 |
| 05/28/2012 | Shanghai | 164323 | 1.98 | 2.76 |
| 06/20/2012 | Wuhan, HB | 195065 | 2.01 | 2.81 |
| 07/09/2012 | Beihai, GX | 218553 | 1.96 | 2.78 |
| 09/15/2012 | Baotou, IM | 283812 | 1.92 | 2.64 |
| 09/21/2012 | Sanya, HN | 314777 | 1.97 | 2.67 |
| Date | Location | Scene ID | ONIIRS | NIIRSZY3 | ERROR |
|---|---|---|---|---|---|
| 2012/9/30 | Baise, GX | 324669 | 2.75 | 2.90 | 0.149 |
| 2012/12/30 | Hangzhou, ZJ | 434442 | 2.64 | 2.60 | −0.042 |
| 2013/8/7 | Wuhan, HB | 742360 | 2.61 | 2.64 | 0.031 |
| 2013/8/12 | Wuhan, HB | 748199 | 2.93 | 2.98 | 0.055 |
| 2013/8/12 | Wuhan, HB | 748200 | 2.91 | 2.98 | 0.075 |
| Mean | 2.82 | 2.77 | 0.054 | ||
| SD | 0.188 | 0.148 | 0.069 | ||
| Date | Location | Scene ID | PNIIRS | ONIIRS | NIIRSZY3 |
|---|---|---|---|---|---|
| 2012/2/19 | Wuhu, AH | 44506 | 1.99 | 2.81 | 2.79 |
| 2012/4/22 | Wuhan, HB | 119315 | 2.01 | 2.92 | 2.83 |
| 2012/5/16 | Beihai, GX | 177804 | 2.02 | 2.81 | 2.86 |
| 2012/5/28 | Shanghai | 164323 | 1.98 | 2.76 | 2.77 |
| 2012/6/20 | Wuhan, HB | 195065 | 2.01 | 2.81 | 2.83 |
| 2012/7/9 | Beihai, GX | 218553 | 1.96 | 2.78 | 2.73 |
| 2012/9/15 | Baotou, IM | 283812 | 1.92 | 2.64 | 2.64 |
| 2012/9/21 | Sanya, HN | 314777 | 1.97 | 2.67 | 2.75 |
| 2012/9/30 | Baise, GX | 324669 | 2.04 | 2.75 | 2.90 |
| 2012/12/30 | Hangzhou, ZJ | 434442 | 1.90 | 2.64 | 2.60 |
| 2013/8/7 | Wuhan, HB | 742360 | 1.92 | 2.61 | 2.64 |
| 2013/8/12 | Wuhan, HB | 748199 | 2.08 | 2.93 | 2.98 |
| 2013/8/12 | Wuhan, HB | 748200 | 2.08 | 2.91 | 2.98 |
| Mean | 1.99 | 2.77 | 2.79 | ||
| SD | 0.06 | 0.11 | 0.12 | ||
| NIIRS | Civil NIIRS Criteria | Agricultural Criteria | Cultural Criteria | Natural Criteria |
|---|---|---|---|---|
| 1 | Distinguish between runways and taxiways at a large airfield. | Detect large (i.e., greater than 100 acres) slash and burn clearings in jungle areas. (NIIRS 1.4) | Detect major highway and rail bridges over water (e.g., Golden Gate, Chesapeake Bay). (NIIRS 1.7) | Detect large areas (e.g., greater than 100 acres) of timber clear cutting. (NIIRS 1.7) |
| Identify large area drainage patterns by type (e.g., dendritic, trellis, radial). | Identify long-lot land ownership patterns along major waterways. (NIIRS 1.7) | Detect multi-lane divided highways (e.g., greater than four lanes. (NIIRS 1.9) | Detect large coastal sand beaches. (NIIRS 1.8) | |
| … | … | … | … | |
| 2 | Identify large (i.e., greater than 160 acres) center-pivot irrigated fields during the growing season. | Detect forest clearings in suspected coca growing areas. (NIIRS 2.4) | Identify large buildings as multi-wing. (NIIRS 2.7) | Distinguish between islands and nests of moored ships. (NIIRS 2.2) |
| Detect large buildings (e.g., hospitals, factories). | Detect windbreaks (i.e., rows of trees) between fields. (NIIRS 2.6) | Detect a dual lane/track bridge over water. (NIIRS 2.7) | Detect utility towers in forested regions on the basis of a sequence of circular clearings. (NIIRS 2.7) | |
| … | … | … | … | |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Li, L.; Luo, H.; Zhu, H. Estimation of the Image Interpretability of ZY-3 Sensor Corrected Panchromatic Nadir Data. Remote Sens. 2014, 6, 4409-4429. https://doi.org/10.3390/rs6054409
Li L, Luo H, Zhu H. Estimation of the Image Interpretability of ZY-3 Sensor Corrected Panchromatic Nadir Data. Remote Sensing. 2014; 6(5):4409-4429. https://doi.org/10.3390/rs6054409
Chicago/Turabian StyleLi, Lin, Heng Luo, and Haihong Zhu. 2014. "Estimation of the Image Interpretability of ZY-3 Sensor Corrected Panchromatic Nadir Data" Remote Sensing 6, no. 5: 4409-4429. https://doi.org/10.3390/rs6054409






