Rain-Use-Efficiency: What it Tells us about the Conflicting Sahel Greening and Sahelian Paradox
Abstract
:1. Introduction
1.1. RUE and the Desertification/“Re-greening” Debate
1.2. The Sahelian Hydrological Paradox
1.3. Limitations Related to Methodological Issues
1.4. Limitations Related to Ecological Interpretation
1.5. Limitations Related to the Data Used
1.6. Mains Objectives of this Study
- (i)
- The first methodological goal will be to evaluate the use of remote sensing NDVI data to estimate indicators of land degradation such as RUE and ANPP residuals. The consistency within these two methods (RUE and residuals) will be examined as well.
- (ii)
- The second objective is to understand whether the re-greening trends observed over the Gourma region can be explained by rainfall.
- (iii)
- Then, this study investigates how re-greening and increased run-off coefficient can be observed in the same region: an explanation of the “second Sahelian paradox” that reconciles increased run-off coefficient and overall re-greening trends will be proposed.
2. Data and Methods
2.1. Field Observations of Vegetation
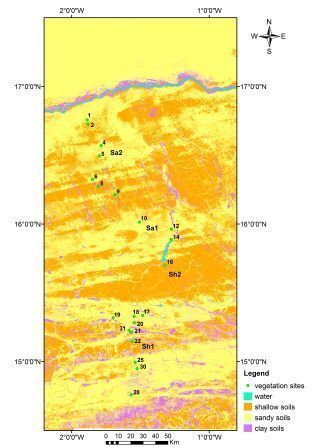
2.1.1. Study Area
2.1.2. Sampling Strategy
2.1.3. ANPP Estimation
2.1.4. Spatial Average
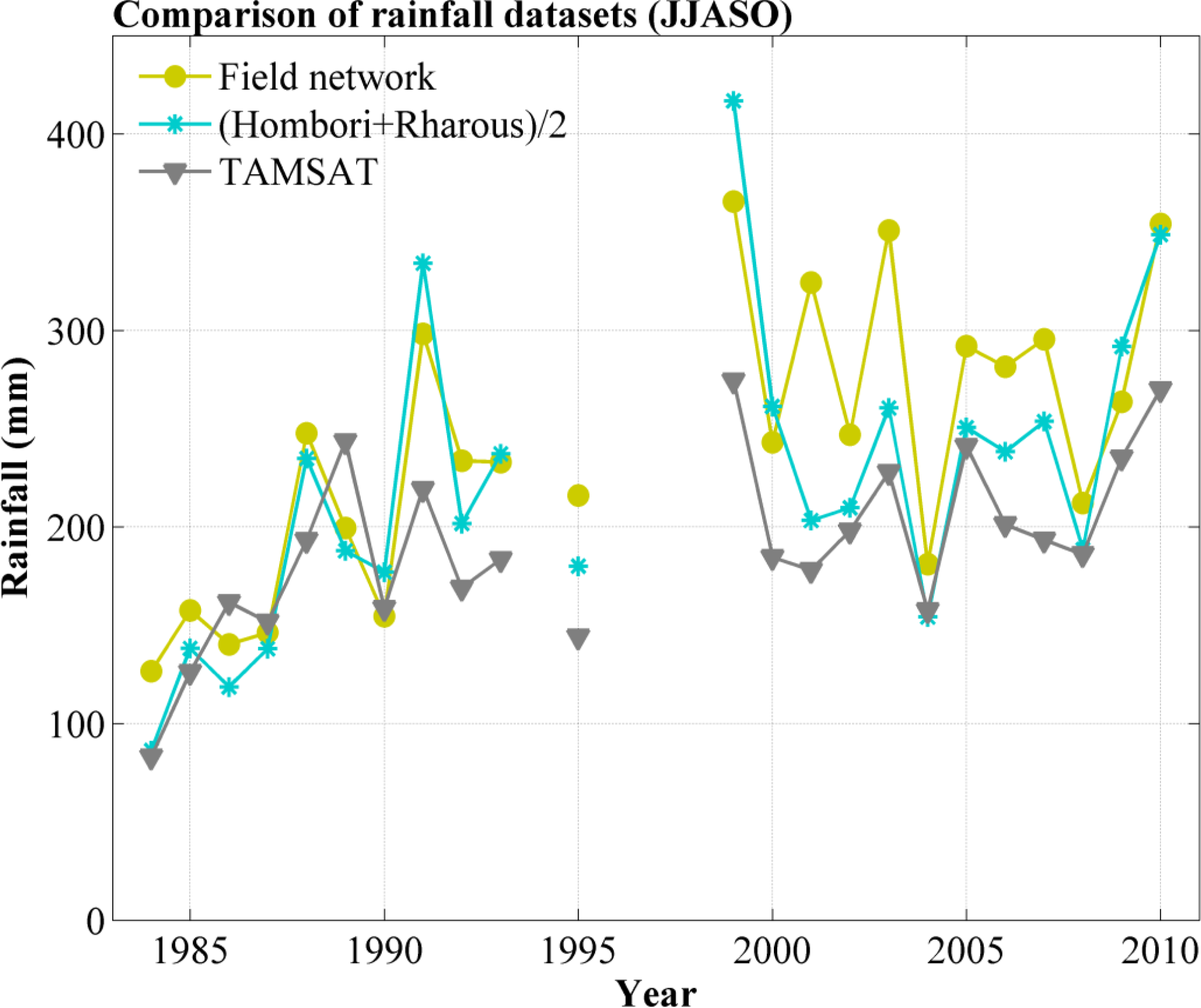
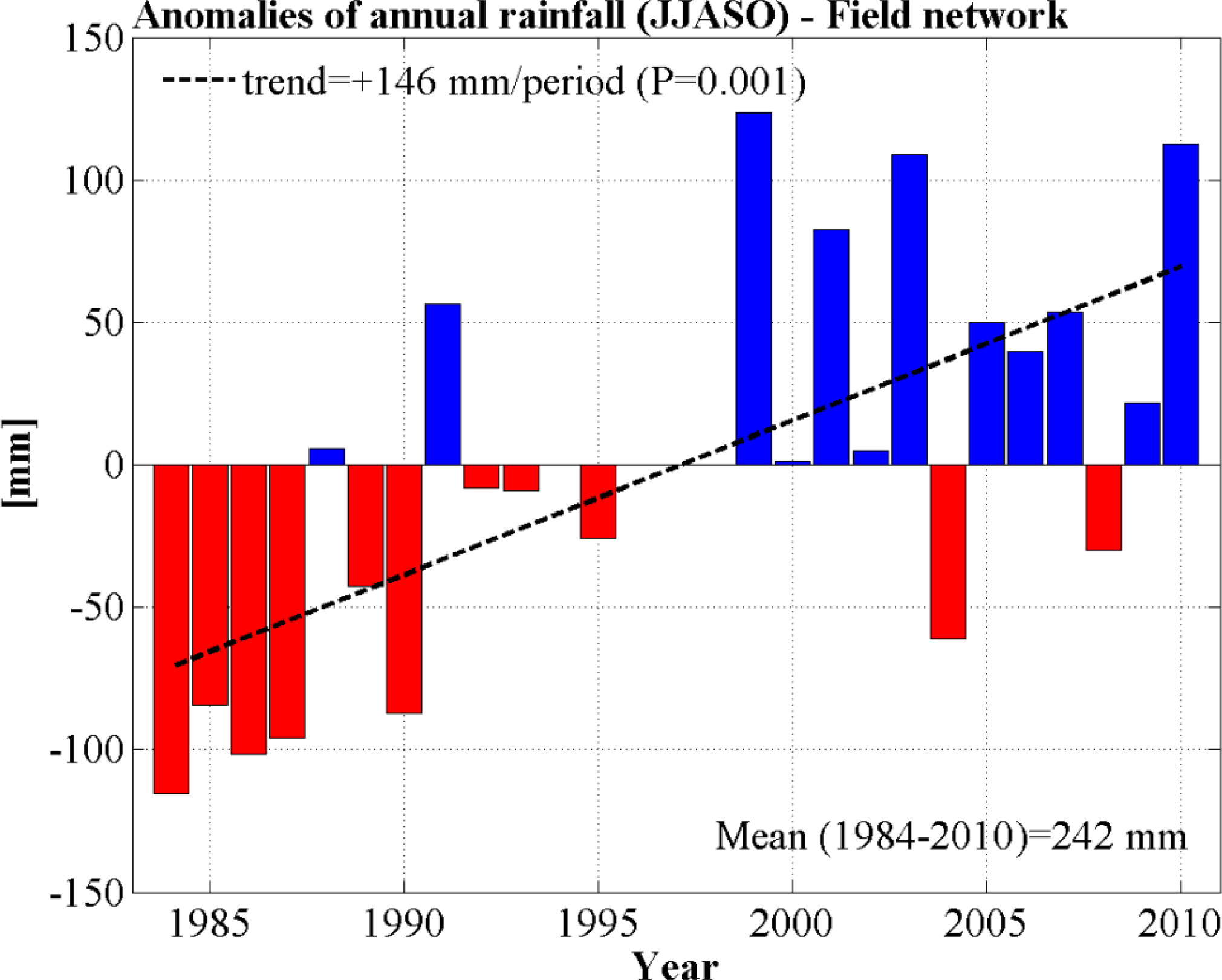
2.2. Rainfall Data
2.3. Normalized Difference Vegetation Index Data
2.3.1. The NDVI GIMMS-3g Dataset
2.3.2. Temporal and Spatial Aggregation
2.4. Estimation of Satellite-Derived ANPP
2.5. Calculation of Rain Use Efficiency and ANPP Residuals
3. Results and Discussion
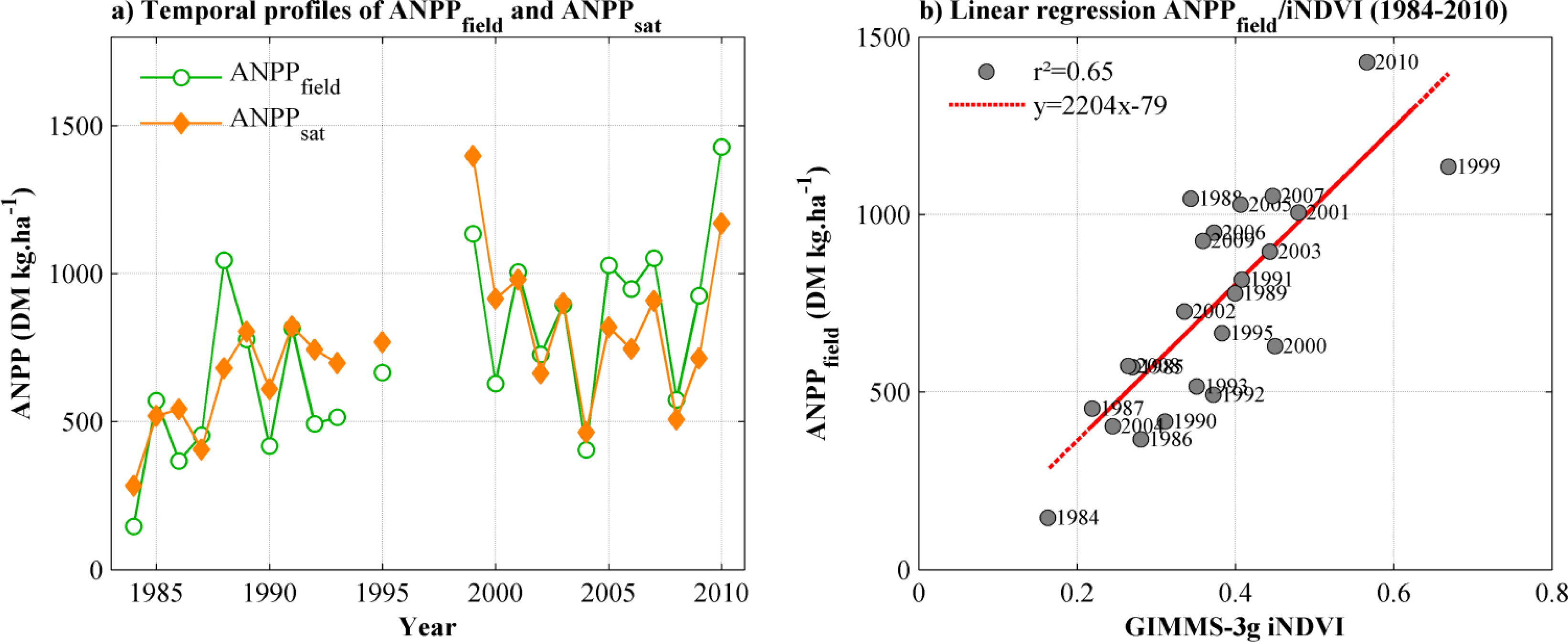
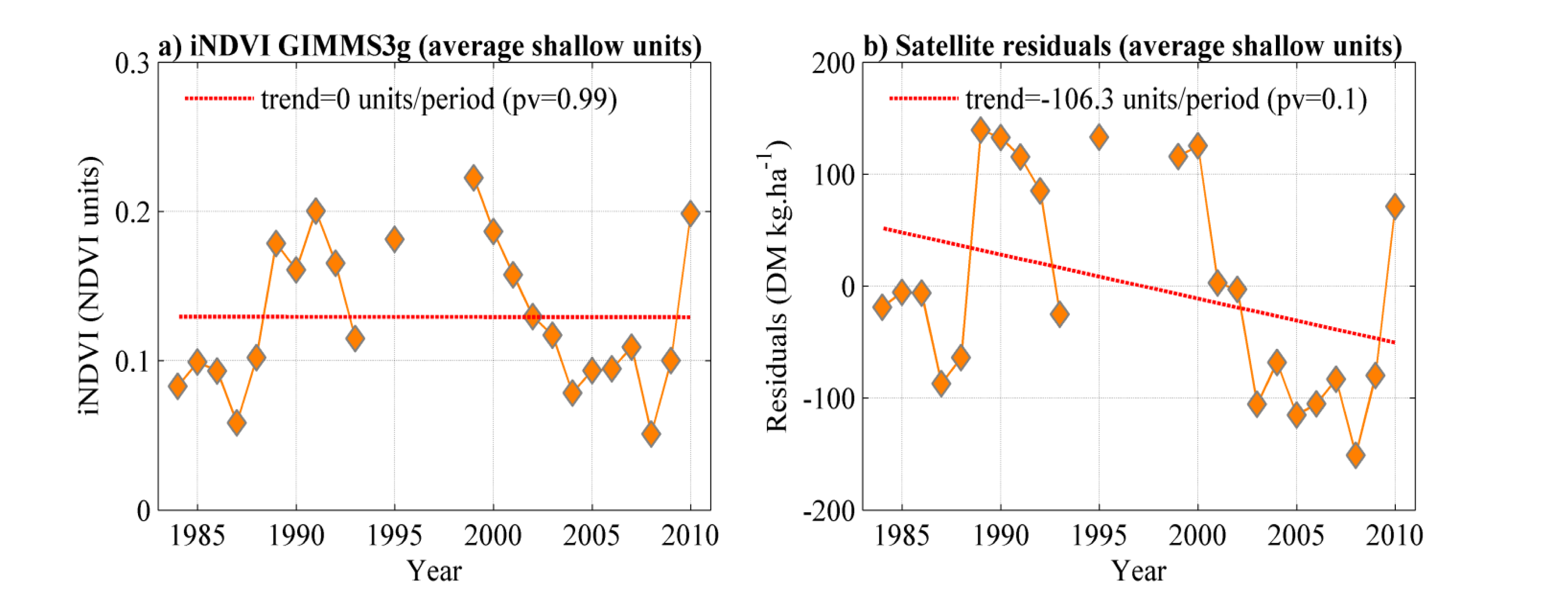
3.1. Limitations Related to ANPP Estimation from iNDVI
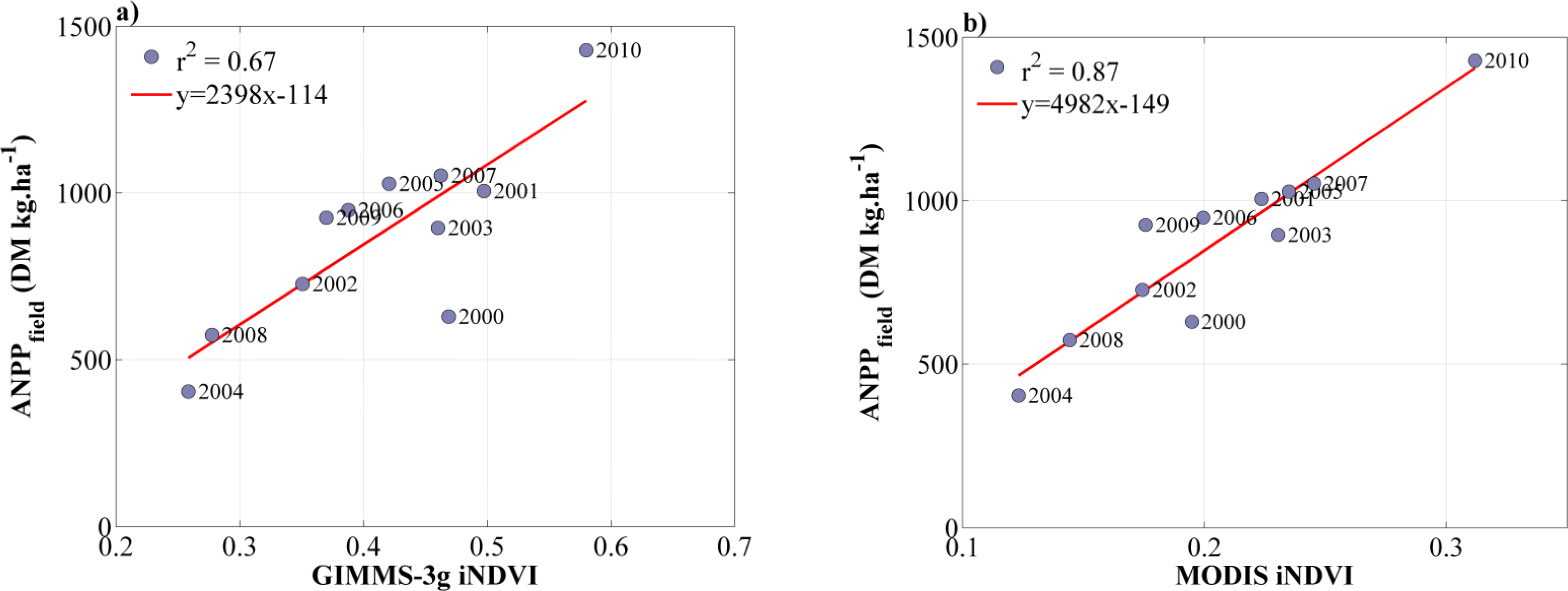
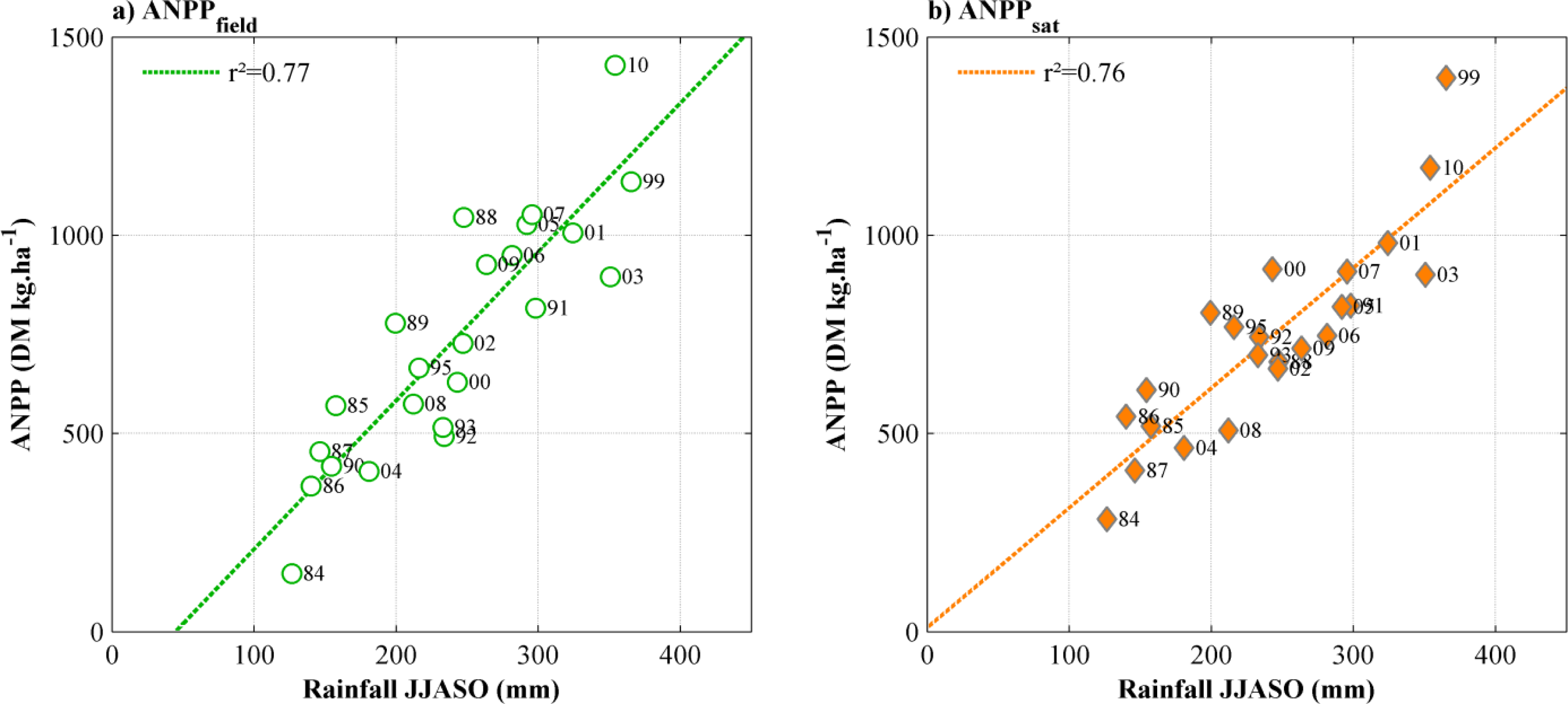
3.2. ANPP and Rainfall
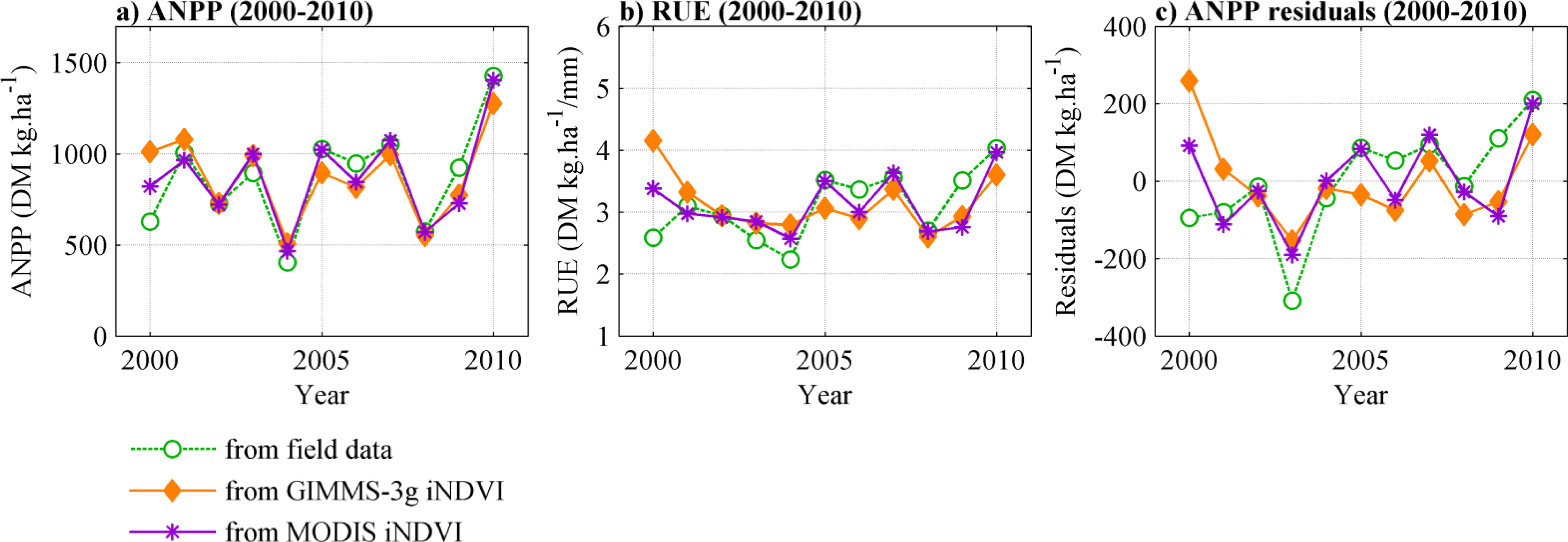
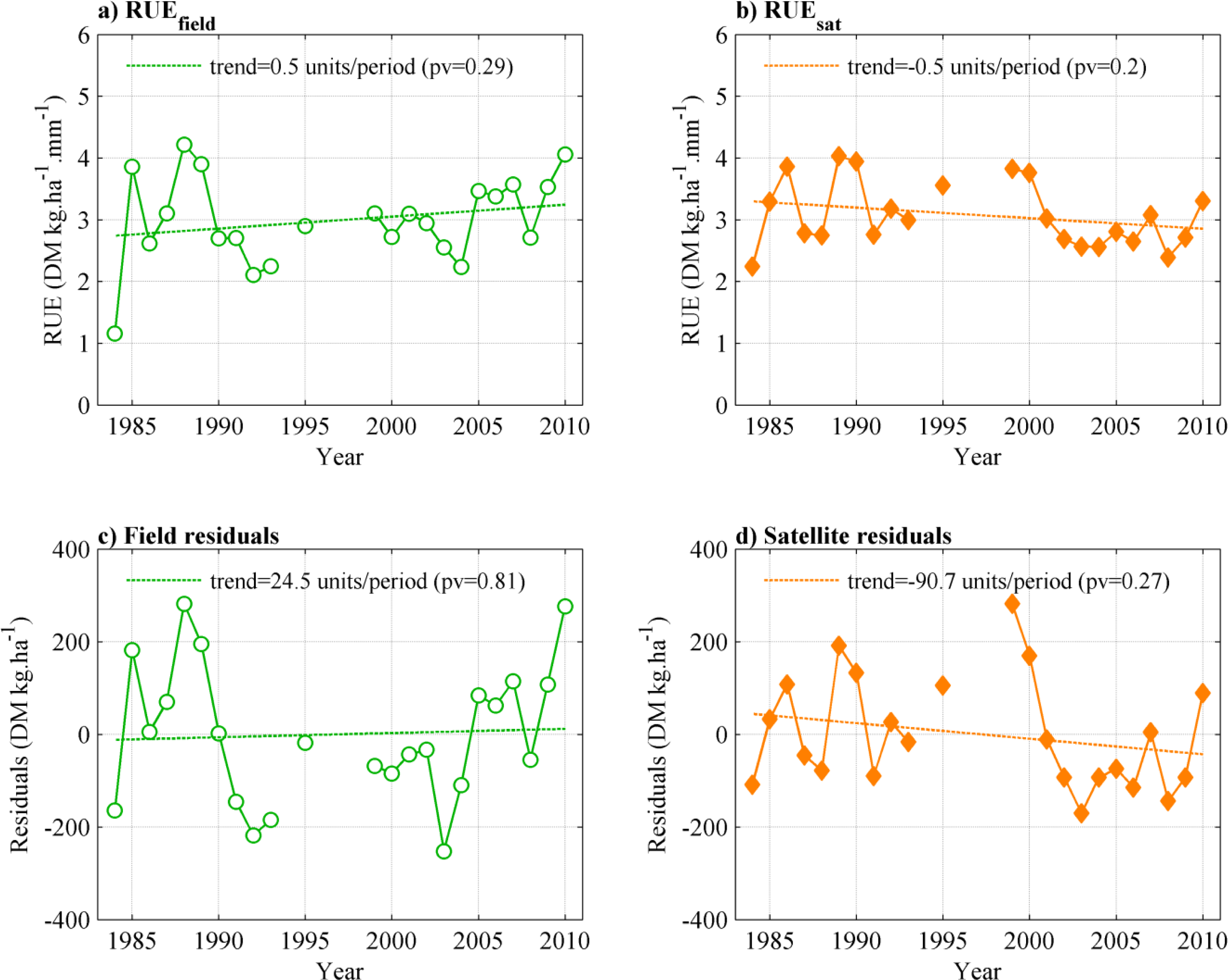
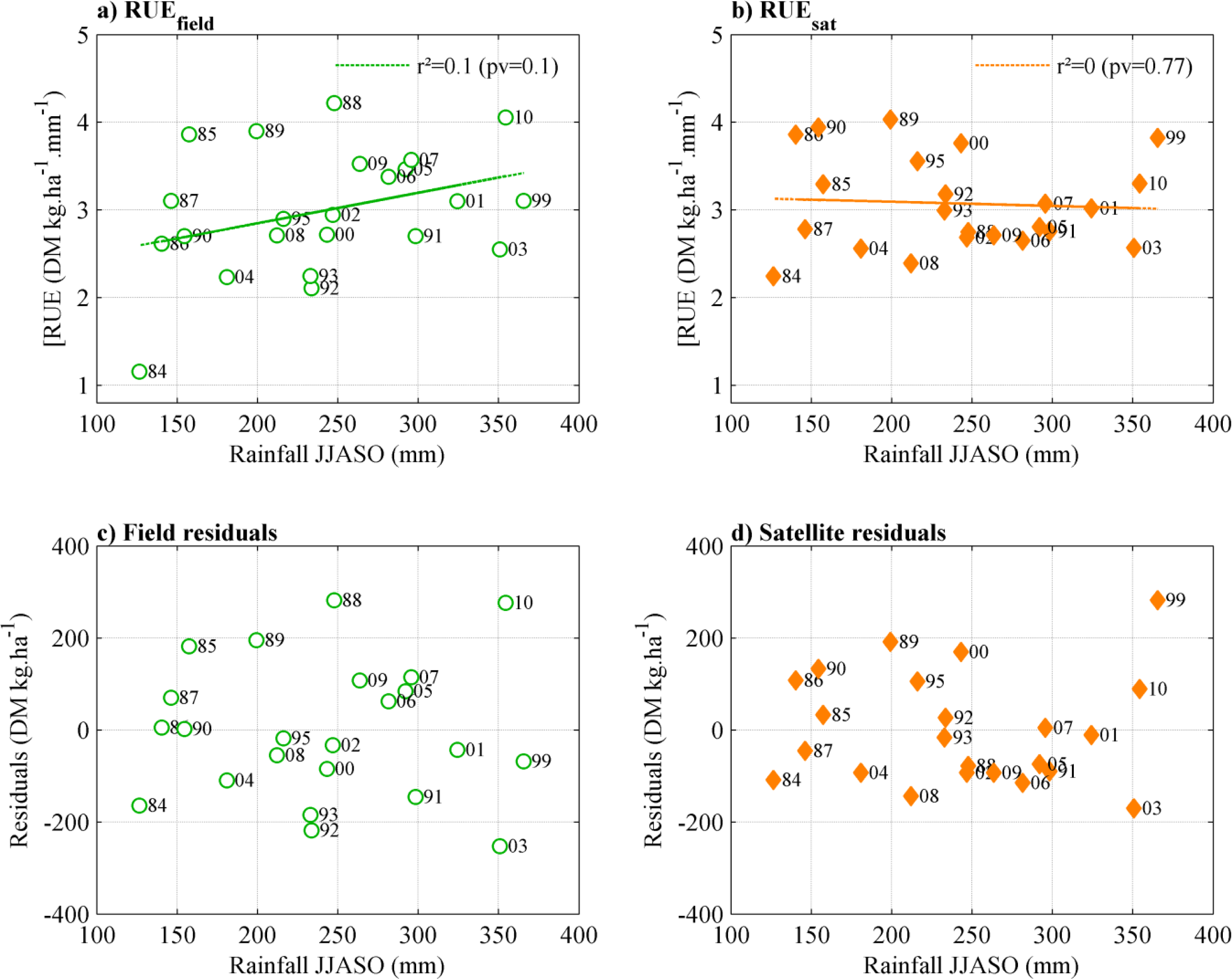
3.3. RUE and Residuals Interannual Variability and Trends
3.4. RUE and ANPP Residuals in Relation to Rainfall Amount
3.5. Ecological Interpretation
3.5.1. Comparison to Literature
3.5.2. Interannual Variability
3.5.3. Ecosystems Resilience
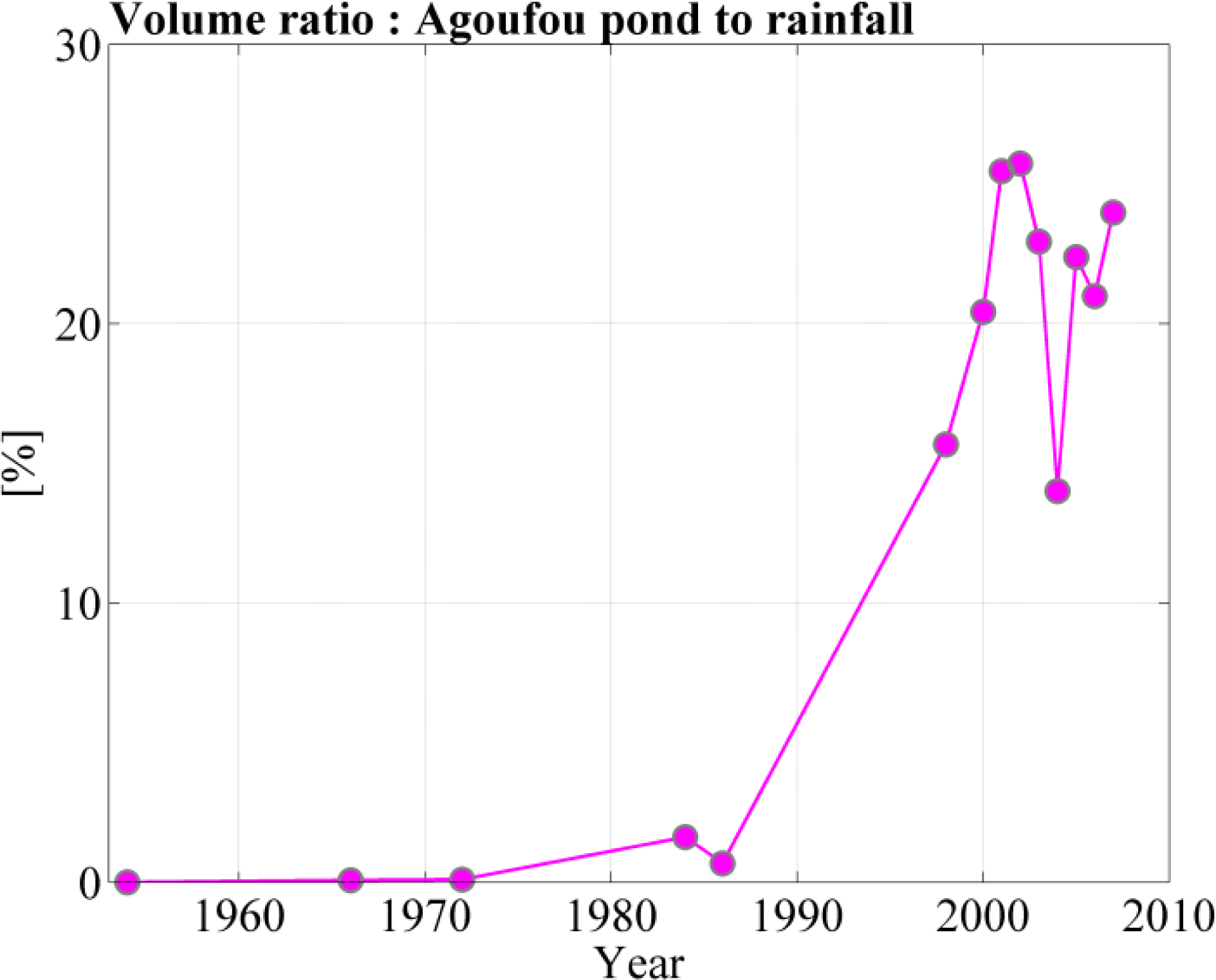
3.6. Reconciling Stable RUE and Increasing Run-off Coefficient
3.6.1. The Hydrological Sahelian Paradox in the Gourma Region
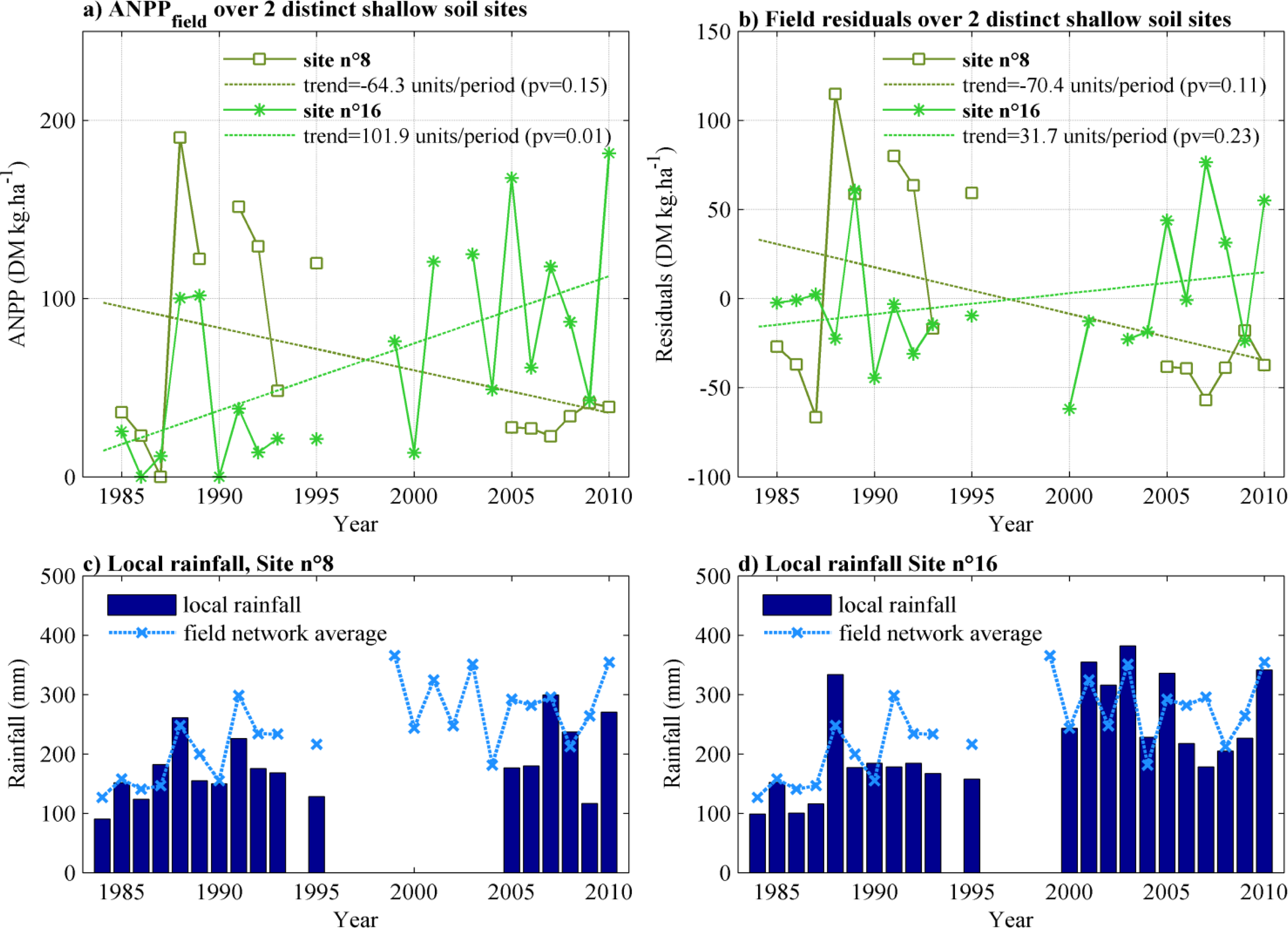
3.6.2. Focus on the Shallow Soils Behavior
3.6.3. Reconciling Re-greening and the Sahelian Hydrological Paradox
4. Conclusions
Acknowledgments
Authors Contributions
Conflicts of Interest
References
- Huxman, T.E.; Smith, M.D.; Fay, P.A.; Knapp, A.K.; Shaw, M.R.; Loik, M.E.; Smith, S.D.; Tissue, D.T.; Zak, J.C.; Weltzin, J.F.; et al. Convergence across biomes to a common rain-use efficiency. Nature 2004, 429, 651–654. [Google Scholar]
- Ruppert, J.C.; Holm, A.; Miehe, S.; Muldavin, E.; Snyman, H.A.; Wesche, K.; Linstadter, A. Meta-analysis of ANPP and rain-use efficiency confirms indicative value for degradation and supports non-linear response along precipitation gradients in drylands. J. Veg. Sci 2012, 23, 1035–1050. [Google Scholar]
- Fensholt, R.; Rasmussen, K.; Nielsen, T.T.; Mbow, C. Evaluation of earth observation based long term vegetation trends—Intercomparing NDVI time series trend analysis consistency of Sahel from AVHRR GIMMS, Terra MODIS and SPOT VGT data. Remote Sens. Environ 2009, 113, 1886–1898. [Google Scholar]
- Veron, S.R.; Paruelo, J.M.; Oesterheld, M. Assessing desertification. J. Arid. Environ 2006, 66, 751–763. [Google Scholar]
- Bai, Y.F.; Wu, J.G.; Xing, Q.; Pan, Q.M.; Huang, J.H.; Yang, D.L.; Han, X.G. Primary production and rain use efficiency across a precipitation gradient on the Mongolia plateau. Ecology 2008, 89, 2140–2153. [Google Scholar]
- Le Houerou, H.N. Rain use efficiency—A unifying concept in arid-land ecology. J. Arid. Environ 1984, 7, 213–247. [Google Scholar]
- Wessels, K.J. Comments on “Proxy global assessment of land degradation” by Bai et al. (2008). Soil Use Manag 2009, 25, 91–92. [Google Scholar]
- Prince, S.D.; de Colstoun, E.B.; Kravitz, L.L. Evidence from rain-use efficiencies does not indicate extensive Sahelian desertification. Glob. Chang. Biol 1998, 4, 359–374. [Google Scholar]
- Hein, L.; de Ridder, N. Desertification in the Sahel: A reinterpretation. Glob. Chang. Biol 2006, 12, 751–758. [Google Scholar]
- Hein, L.; de Ridder, N.; Hiernaux, P.; Leemans, R.; de Wit, A.; Schaepman, M. Desertification in the Sahel: Towards better accounting for ecosystem dynamics in the interpretation of remote sensing images. J. Arid. Environ 2011, 75, 1164–1172. [Google Scholar]
- Miehe, S. Comment on: Hein, L. 2006: The impacts of grazing and rainfall variability on the dynamics of a Sahelian rangeland. J. Arid. Environ 2006, 64, 488–504. [Google Scholar]
- Prince, S.D.; Wessels, K.J.; Tucker, C.J.; Nicholson, S.E. Desertification in the Sahel: A reinterpretation of a reinterpretation. Glob. Chang. Biol 2007, 13, 1308–1313. [Google Scholar]
- Eklundh, L.; Olsson, L. Vegetation index trends for the African Sahel 1982–1999. Geophys. Res. Lett 2003, 30, 1430–1433. [Google Scholar]
- Anyamba, A.; Tucker, C.J. Analysis of Sahelian vegetation dynamics using NOAA-AVHRR NDVI data from 1981–2003. J. Arid. Environ 2005, 63, 596–614. [Google Scholar]
- Herrmann, S.M.; Anyamba, A.; Tucker, C.J. Recent trends in vegetation dynamics in the African Sahel and their relationship to climate. Glob. Environ. Chang.-Hum. Policy Dimens 2005, 15, 394–404. [Google Scholar]
- Fensholt, R.; Proud, S.R. Evaluation of Earth Observation based global long term vegetation trends—Comparing GIMMS and MODIS global NDVI time series. Remote Sens. Environ 2012, 119, 131–147. [Google Scholar]
- Dardel, C.; Kergoat, L.; Hiernaux, P.; Mougin, E.; Grippa, M.; Tucker, C.J. Re-greening Sahel: 30 years of remote sensing data and field observations (Mali, Niger). Remote Sens. Environ 2014, 140, 350–364. [Google Scholar]
- Descroix, L.; Mahe, G.; Lebel, T.; Favreau, G.; Galle, S.; Gautier, E.; Olivry, J.C.; Albergel, J.; Amogu, O.; Cappelaere, B.; et al. Spatio-temporal variability of hydrological regimes around the boundaries between Sahelian and Sudanian areas of West Africa: A synthesis. J. Hydrol 2009, 375, 90–102. [Google Scholar]
- Mahe, G.; Paturel, J.E. Sahelian annual rainfall variability and runoff increase of Sahelian Rivers. Comptes Rendus Geosci 2009, 341. [Google Scholar]
- Leduc, C.; Favreau, G.; Schroeter, P. Long-term rise in a sahelian water-table: The Continental Terminal in South-West Niger. J. Hydrol 2001, 243, 43–54. [Google Scholar]
- Amogu, O.; Descroix, L.; Yero, K.S.; le Breton, E.; Mamadou, I.; Ali, A.; Vischel, T.; Bader, J.C.; Moussa, I.B.; Gautier, E.; et al. Increasing river flows in the Sahel? Water 2010, 2, 170–199. [Google Scholar]
- Descroix, L.; Laurent, J.P.; Vauclin, M.; Amogu, O.; Boubkraoui, S.; Ibrahim, B.; Galle, S.; Cappelaere, B.; Bousquet, S.; Mamadou, I.; et al. Experimental evidence of deep infiltration under sandy flats and gullies in the Sahel. J. Hydrol 2012, 424, 1–15. [Google Scholar]
- Gardelle, J.; Hiernaux, P.; Kergoat, L.; Grippa, M. Less rain, more water in ponds: A remote sensing study of the dynamics of surface waters from 1950 to present in pastoral Sahel (Gourma region, Mali). Hydrol. Earth Syst. Sci 2010, 14, 309–324. [Google Scholar]
- Sighomnou, D.; Descroix, L.; Genthon, P.; Mahé, G.; Bouzou Moussa, I.; Gautier, E.; Mamadou, I.; Vandervaere, J.P.; Bachir, T.; Coulibaly, B.; et al. La crue de 2012 à Niamey: Un paroxysme du paradoxe du Sahel? Sécheresse 2013, 24, 3–13. [Google Scholar]
- Albergel, J. The influence of Climate Change and Climatic Variability on the Hydrologic Regime and Water Resources. In Sécheresse, Désertification et Ressources en Eau de Surface: Application Aux petits Bassins du BURKINA FASO; IAHS Publisher: Vancouver, BC, Canada, 1987; pp. 355–365. [Google Scholar]
- Savenije, H.H.G. The runoff coefficient as the key to moisture recycling. J. Hydrol 1996, 176, 219–225. [Google Scholar]
- Fensholt, R.; Rasmussen, K.; Kaspersen, P.; Huber, S.; Horion, S.; Swinnen, E. Assessing land degradation/recovery in the african sahel from long-term earth observation based primary productivity and precipitation relationships. Remote Sens 2013, 5, 664–686. [Google Scholar]
- Veron, S.R.; Oesterheld, M.; Paruelo, J.M. Production as a function of resource availability: Slopes and efficiencies are different. J. Veg. Sci 2005, 16, 351–354. [Google Scholar]
- Fensholt, R.; Rasmussen, K. Analysis of trends in the Sahelian “rain-use efficiency” using GIMMS NDVI, RFE and GPCP rainfall data. Remote Sens. Environ 2011, 115, 438–451. [Google Scholar]
- Evans, J.; Geerken, R. Discrimination between climate and human-induced dryland degradation. J. Arid. Environ 2004, 57, 535–554. [Google Scholar]
- Begue, A.; Vintrou, E.; Ruelland, D.; Claden, M.; Dessay, N. Can a 25-year trend in Soudano-Sahelian vegetation dynamics be interpreted in terms of land use change? A remote sensing approach. Glob. Environ. Chang 2011, 21, 413–420. [Google Scholar]
- Wessels, K.J.; van den Bergh, F.; Scholes, R.J. Limits to detectability of land degradation by trend analysis of vegetation index data. Remote Sens. Environ 2012, 125, 10–22. [Google Scholar]
- Miehe, S.; Kluge, J.; von Wehrden, H.; Retzer, V. Long-term degradation of Sahelian rangeland detected by 27 years of field study in Senegal. J. Appl. Ecol 2010, 47, 692–700. [Google Scholar]
- Nicholson, S.E.; Tucker, C.J.; Ba, M.B. Desertification, drought, and surface vegetation: An example from the West African Sahel. Bull. Am. Meteorol. Soc 1998, 79, 815–829. [Google Scholar]
- Wessels, K.J.; Prince, S.D.; Malherbe, J.; Small, J.; Frost, P.E.; VanZyl, D. Can human-induced land degradation be distinguished from the effects of rainfall variability? A case study in South Africa. J. Arid. Environ 2007, 68, 271–297. [Google Scholar]
- Diouf, A.; Lambin, E.F. Monitoring land-cover changes in semi-arid regions: Remote sensing data and field observations in the Ferlo, Senegal. J. Arid. Environ 2001, 48, 129–148. [Google Scholar]
- Tucker, C.J.; Vanpraet, C.L.; Sharman, M.J.; Vanittersum, G. Satellite Remote-sensing of total herbaceous biomass production in the senegalese sahel—1980–1984. Remote Sens. Environ 1985, 17, 233–249. [Google Scholar]
- Prince, S.D. Satellite Remote-Sensing of Primary Production—Comparison of Results for Sahelian Grasslands 1981–1988. Int. J. Remote Sens 1991, 12, 1301–1311. [Google Scholar]
- Myneni, R.B.; Williams, D.L. On the Relationship between fAPAR and NDVI. Remote Sens. Environ 1994, 49, 200–211. [Google Scholar]
- Monteith, J.L. Solar-radiation and productivity in tropical ecosystems. J. Appl. Ecol 1972, 9, 747–766. [Google Scholar]
- Tucker, C.J.; Pinzon, J.E.; Brown, M.E.; Slayback, D.A.; Pak, E.W.; Mahoney, R.; Vermote, E.F.; El Saleous, N. An extended AVHRR 8-km NDVI dataset compatible with MODIS and SPOT vegetation NDVI data. Int. J. Remote Sens 2005, 26, 4485–4498. [Google Scholar]
- Frappart, F.; Hiernaux, P.; Guichard, F.; Mougin, E.; Kergoat, L.; Arjounin, M.; Lavenu, F.; Koite, M.; Paturel, J.E.; Lebel, T. Rainfall regime across the Sahel band in the Gourma region, Mali. J. Hydrol 2009, 375, 128–142. [Google Scholar]
- Mougin, E.; Hiernaux, P.; Kergoat, L.; Grippa, M.; de Rosnay, P.; Timouk, F.; le Dantec, V.; Demarez, V.; Lavenu, F.; Arjounin, M.; et al. The AMMA-CATCH Gourma observatory site in Mali: Relating climatic variations to changes in vegetation, surface hydrology, fluxes and natural resources. J. Hydrol 2009, 375, 14–33. [Google Scholar]
- Hiernaux, P.; Mougin, E.; Diarra, L.; Soumaguel, N.; Lavenu, F.; Tracol, Y.; Diawara, M. Sahelian rangeland response to changes in rainfall over two decades in the Gourma region, Mali. J. Hydrol 2009, 375, 114–127. [Google Scholar]
- Sala, O.E.; Austin, A.T. Methods of Estimating Aboveground Net Primary Productivity. In Methods in Ecosystem Science; Sala, O.E., Jackson, R.B., Mooney, H.A., Howarth, R.W., Eds.; Springer: New York, NY, USA, 2000; pp. 31–43. [Google Scholar]
- Maidment, R.; Grimes, D.; Tarnavsky, E.; Allan, R.; Stringer, M.; Hewison, T.; Roebeling, R. Development of the 30-year TAMSAT African Rainfall Time Series and Climatology (TARCAT) dataset part II: Constructing a temporally homogeneous rainfall dataset. 2014; unpublished work. [Google Scholar]
- Pinzon, J.; Tucker, C.J. A non-stationary 1981–2012 AVHRR NDVI3g time series. Remote Sens 2014, in press. [Google Scholar]
- Vermote, E.; Kaufman, Y.J. Absolute calibration of AVHRR visible and near-infrared channels using ocean and cloud views. Int. J. Remote Sens 1995, 16, 2317–2340. [Google Scholar]
- Los, S.O. Estimation of the ratio of sensor degradation between NOAA AVHRR channels 1 and 2 from monthly NDVI composites. IEEE Trans. Geosci. Remote Sens 1998, 36, 206–213. [Google Scholar]
- Pinzon, J.E.; Brown, M.E.; Tucker, C.J. EMD Correction of Orbital Drift Artifacts in Satellite Data Stream. In Hilbert-Huang Transform and Its Applications; Huang, N.E., Shen, S.P.S., Eds.; World Scientific Publishing Co. Pte Ltd.: Singapore, 2005; Volume 5, pp. 167–186. [Google Scholar]
- Mbow, C.; Fensholt, R.; Rasmussen, K.; Diop, D. Can vegetation productivity be derived from greenness in a semi-arid environment? Evidence from ground-based measurements. J. Arid. Environ 2013, 97, 56–65. [Google Scholar]
- Nagol, J.R. Quantification of Error in AVHRR NDVI Data; University of Maryland, College Park: College Park, MD, USA, 2011. [Google Scholar]
- Brett, M.T. When is a correlation between non-independent variables “spurious”? Oikos 2004, 105, 647–656. [Google Scholar]
- Le Houerou, H.N. The Grazing Land Ecosystems of the African Sahel; Springer: Berlin, Germany, 1989; Volume 75, p. 282. [Google Scholar]
- Le Houerou, H.N.; Bingham, R.L.; Skerbek, W. Relationship between the variability of primary production and the variability of annual precipitation in world arid lands. J. Arid. Environ 1988, 15, 1–18. [Google Scholar]
- Muldavin, E.H.; Moore, D.I.; Collins, S.L.; Wetherill, K.R.; Lightfoot, D.C. Aboveground net primary production dynamics in a northern Chihuahuan Desert ecosystem. Oecologia 2008, 155, 123–132. [Google Scholar]
- Sala, O.E.; Parton, W.J.; Joyce, L.A.; Lauenroth, W.K. Primary production of the central grassland region of the United-States. Ecology 1988, 69, 40–45. [Google Scholar]
- Holm, A.M.; Cridland, S.W.; Roderick, M.L. The use of time-integrated NOAA NDVI data and rainfall to assess landscape degradation in the arid shrubland of Western Australia. Remote Sens. Environ 2003, 85, 145–158. [Google Scholar]
- Haas, E.M.; Bartholome, E.; Lambin, E.F.; Vanacker, V. Remotely sensed surface water extent as an indicator of short-term changes in ecohydrological processes in sub-Saharan Western Africa. Remote Sens. Environ 2011, 115, 3436–3445. [Google Scholar]
- Hiernaux, P.; Gerard, B. The influence of vegetation pattern on the productivity, diversity and stability of vegetation: The case of “brousse tigree” in the Sahel. Acta Oecol 1999, 20, 147–158. [Google Scholar]
- Hiernaux, P.; Diarra, L.; Trichon, V.; Mougin, E.; Soumaguel, N.; Baup, F. Woody plant population dynamics in response to climate changes from 1984 to 2006 in Sahel (Gourma, Mali). J. Hydrol 2009, 375, 103–113. [Google Scholar]
- Timouk, F.; Kergoat, L.; Mougin, E.; Lloyd, C.R.; Ceschia, E.; Cohard, J.M.; de Rosnay, P.; Hiernaux, P.; Demarez, V.; Taylor, C.M. Response of surface energy balance to water regime and vegetation development in a Sahelian landscape. J. Hydrol 2009, 375, 178–189. [Google Scholar]
Appendix A


| Correlation Field ANPP/Rainfall | Correlation iNDVI/Rainfall | Correlation between the Rainfall Datasets |
|---|---|---|
| r2 (field ANPP/TAMSAT) = 0.66 | r2 (iNDVI/TAMSAT) = 0.61 | r2 (field network/Homb-Rha) = 0.76 |
| r2 (field ANPP/Homb-Rha) = 0.63 | r2 (iNDVI/Homb-Rha) = 0.75 | r2 (field network/TAMSAT) = 0.62 |
| r2 (field ANPP/field network) = 0.76 | r2 (iNDVI/field network) = 0.76 | r2 (TAMSAT/Homb-Rha) = 0.72 |
Appendix B


© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Dardel, C.; Kergoat, L.; Hiernaux, P.; Grippa, M.; Mougin, E.; Ciais, P.; Nguyen, C.-C. Rain-Use-Efficiency: What it Tells us about the Conflicting Sahel Greening and Sahelian Paradox. Remote Sens. 2014, 6, 3446-3474. https://doi.org/10.3390/rs6043446
Dardel C, Kergoat L, Hiernaux P, Grippa M, Mougin E, Ciais P, Nguyen C-C. Rain-Use-Efficiency: What it Tells us about the Conflicting Sahel Greening and Sahelian Paradox. Remote Sensing. 2014; 6(4):3446-3474. https://doi.org/10.3390/rs6043446
Chicago/Turabian StyleDardel, Cécile, Laurent Kergoat, Pierre Hiernaux, Manuela Grippa, Eric Mougin, Philippe Ciais, and Cam-Chi Nguyen. 2014. "Rain-Use-Efficiency: What it Tells us about the Conflicting Sahel Greening and Sahelian Paradox" Remote Sensing 6, no. 4: 3446-3474. https://doi.org/10.3390/rs6043446
APA StyleDardel, C., Kergoat, L., Hiernaux, P., Grippa, M., Mougin, E., Ciais, P., & Nguyen, C.-C. (2014). Rain-Use-Efficiency: What it Tells us about the Conflicting Sahel Greening and Sahelian Paradox. Remote Sensing, 6(4), 3446-3474. https://doi.org/10.3390/rs6043446