Probability Density Components Analysis: A New Approach to Treatment and Classification of SAR Images
Abstract
:1. Introduction
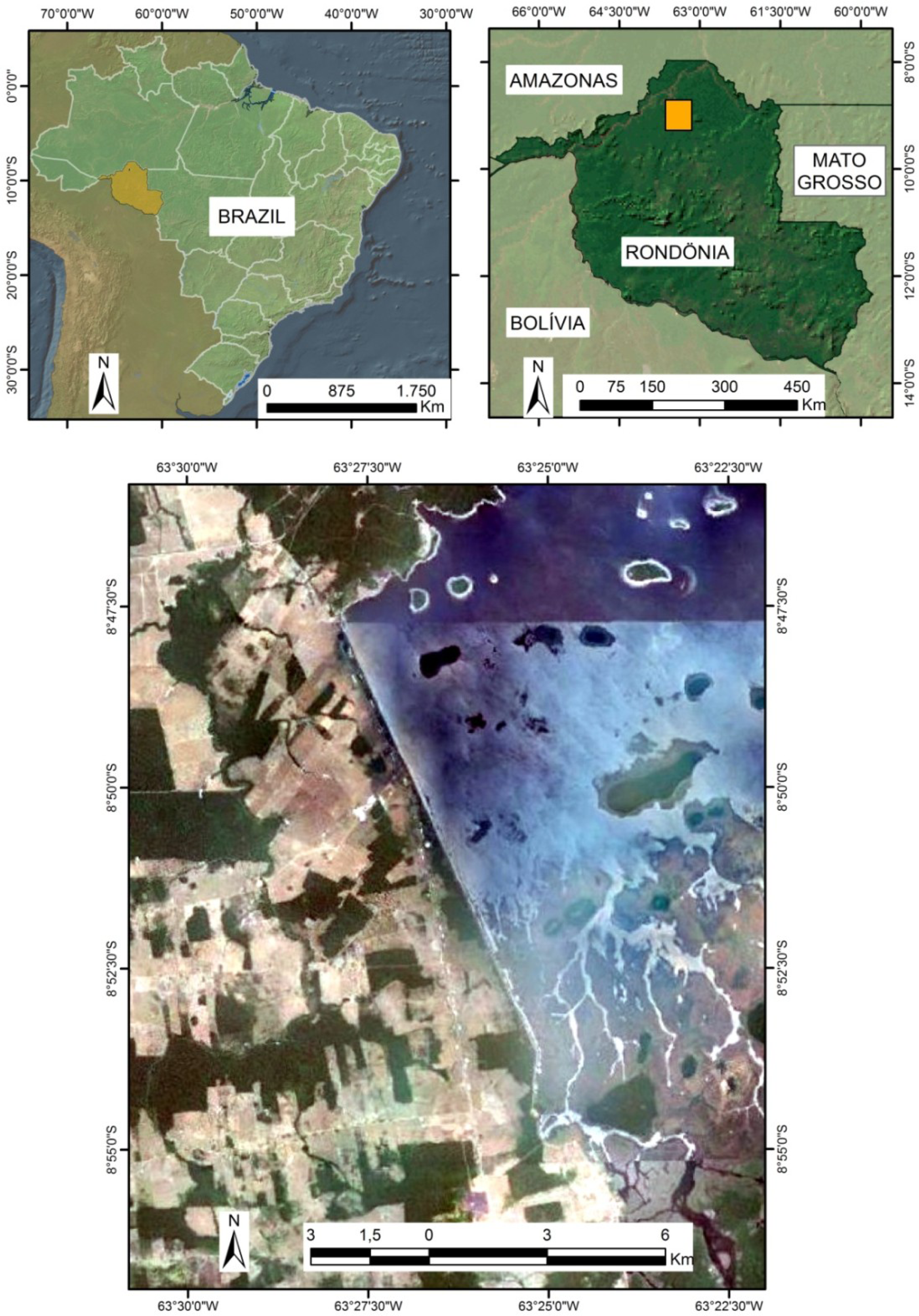
2. Study Area
3. Methodology
3.1. Datasets for Experiments
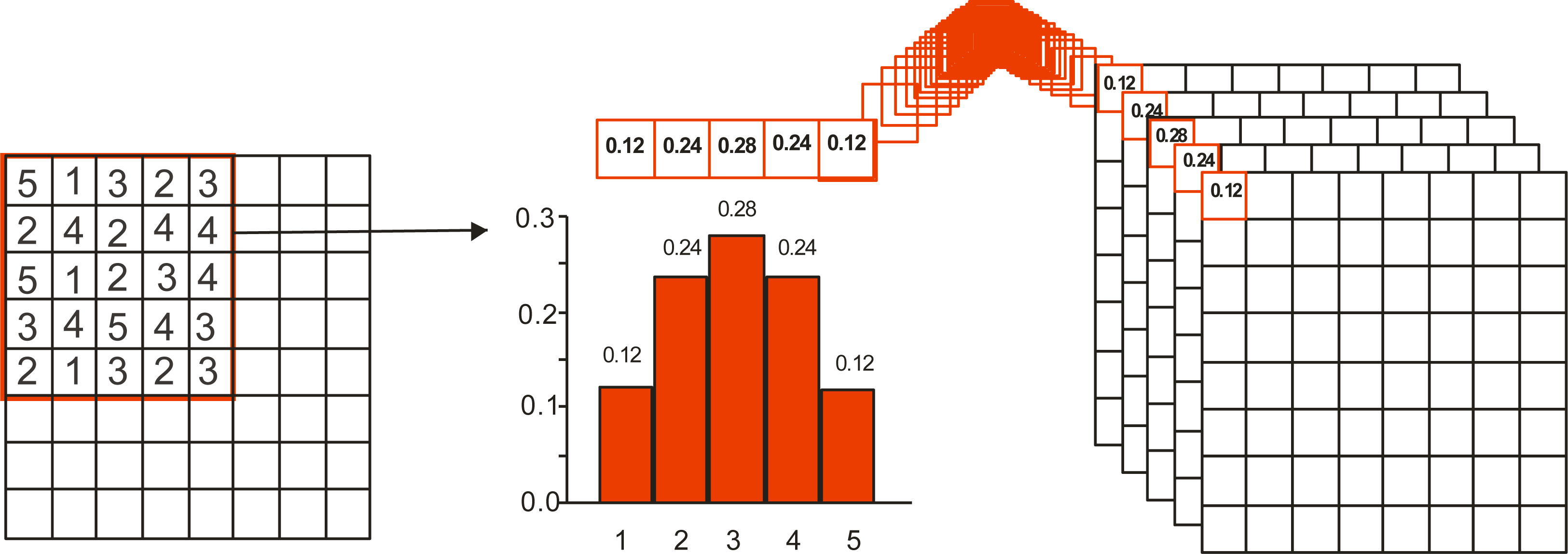
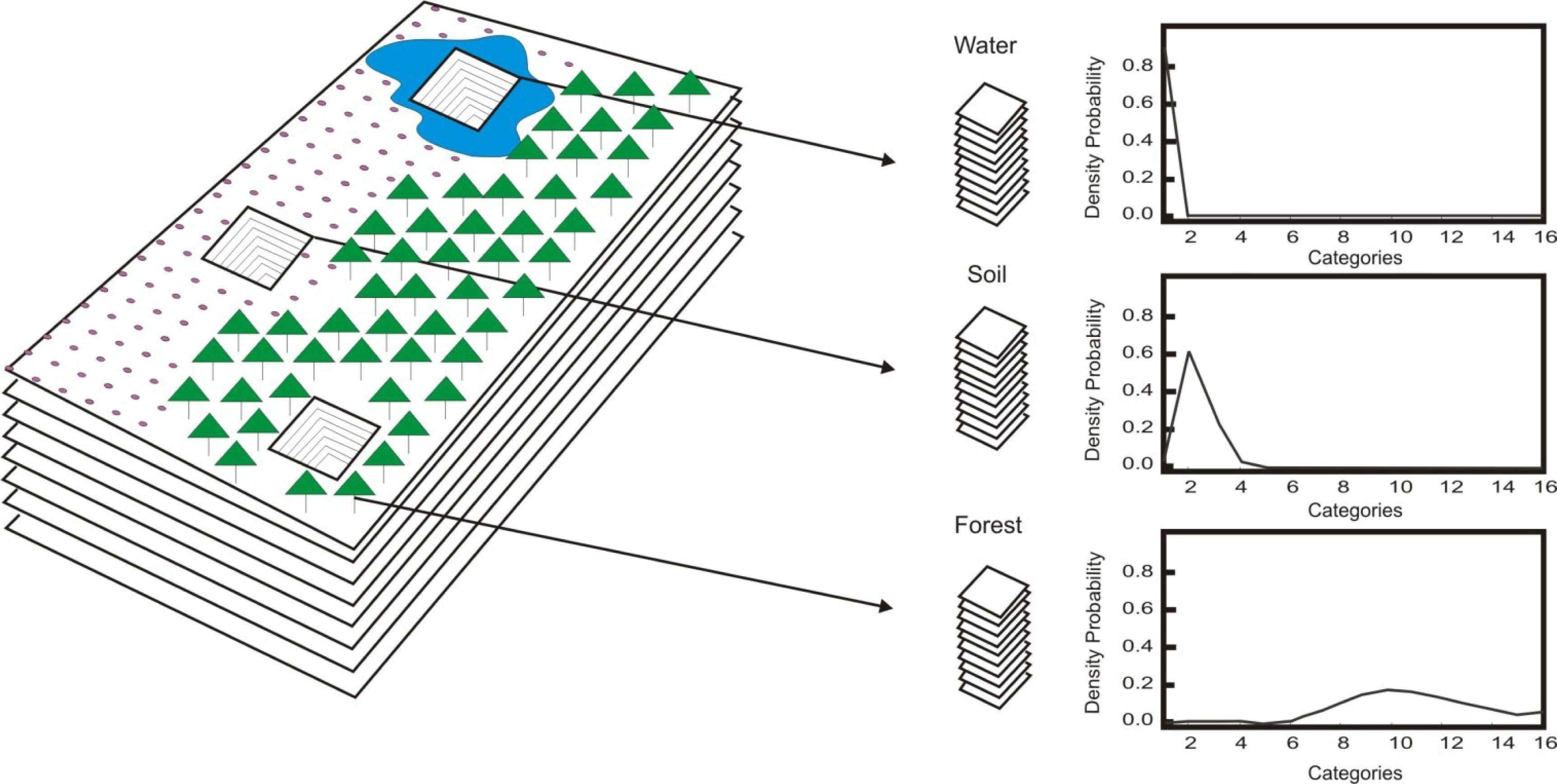
3.2. Probability Density Components Analysis
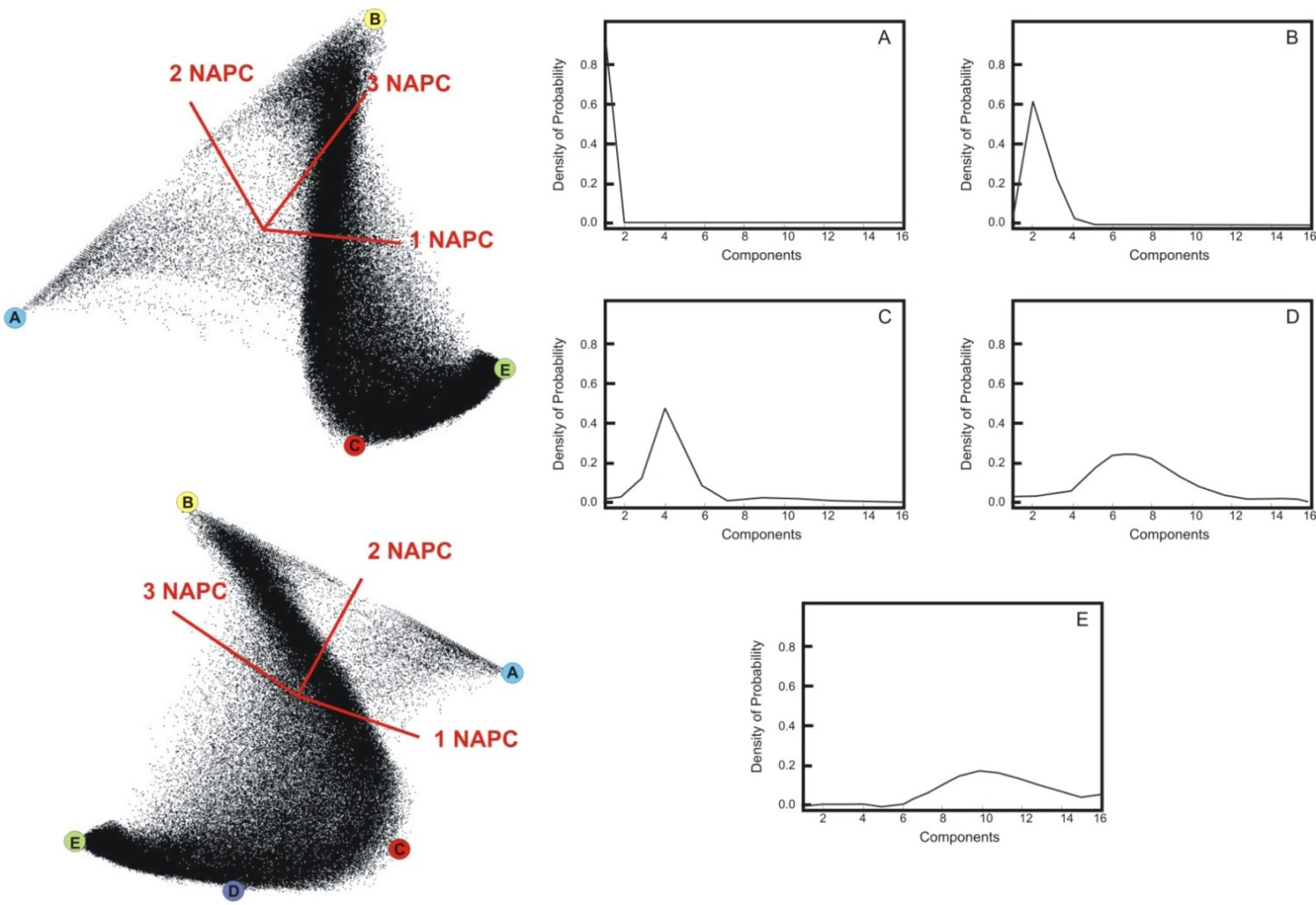
3.3. Endmember Identification
3.4. Spectral Classifier
3.5. Accuracy Analysis
3.6. Comparison with Other Traditional Methods
3.6.1. Gray-Level Co-Occurrence Matrices
3.6.2. Gabor Filters
4. Experimental Results
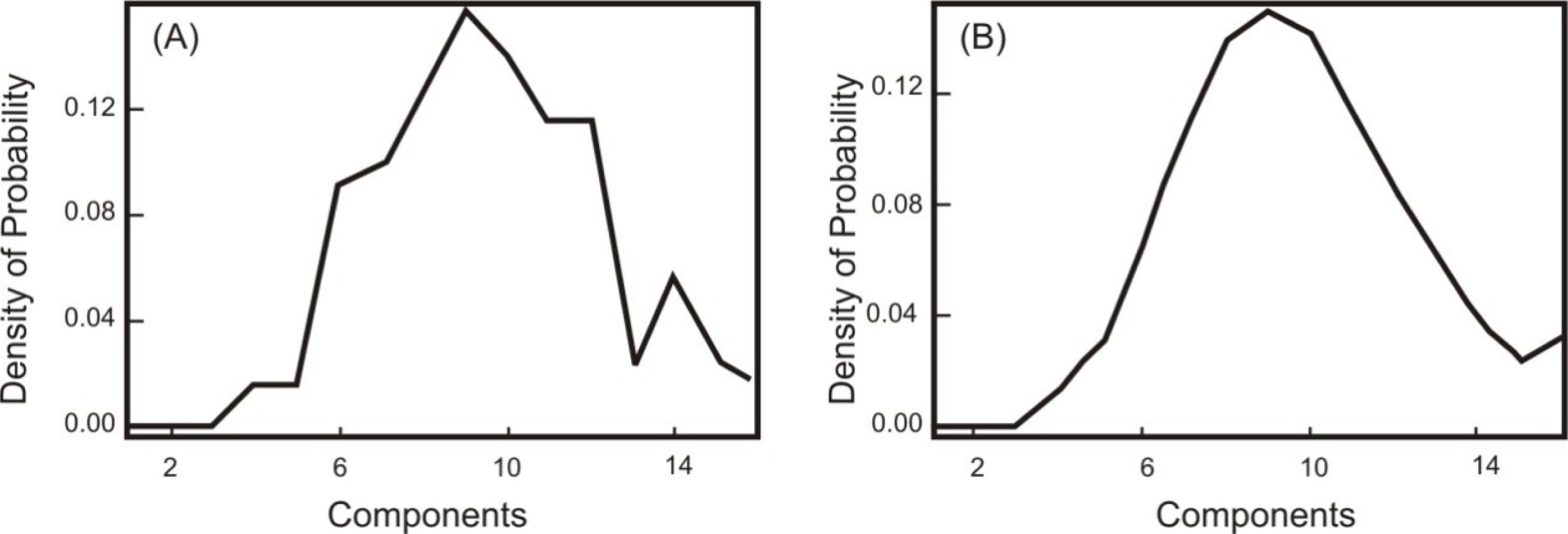
4.1. Probability Density Components
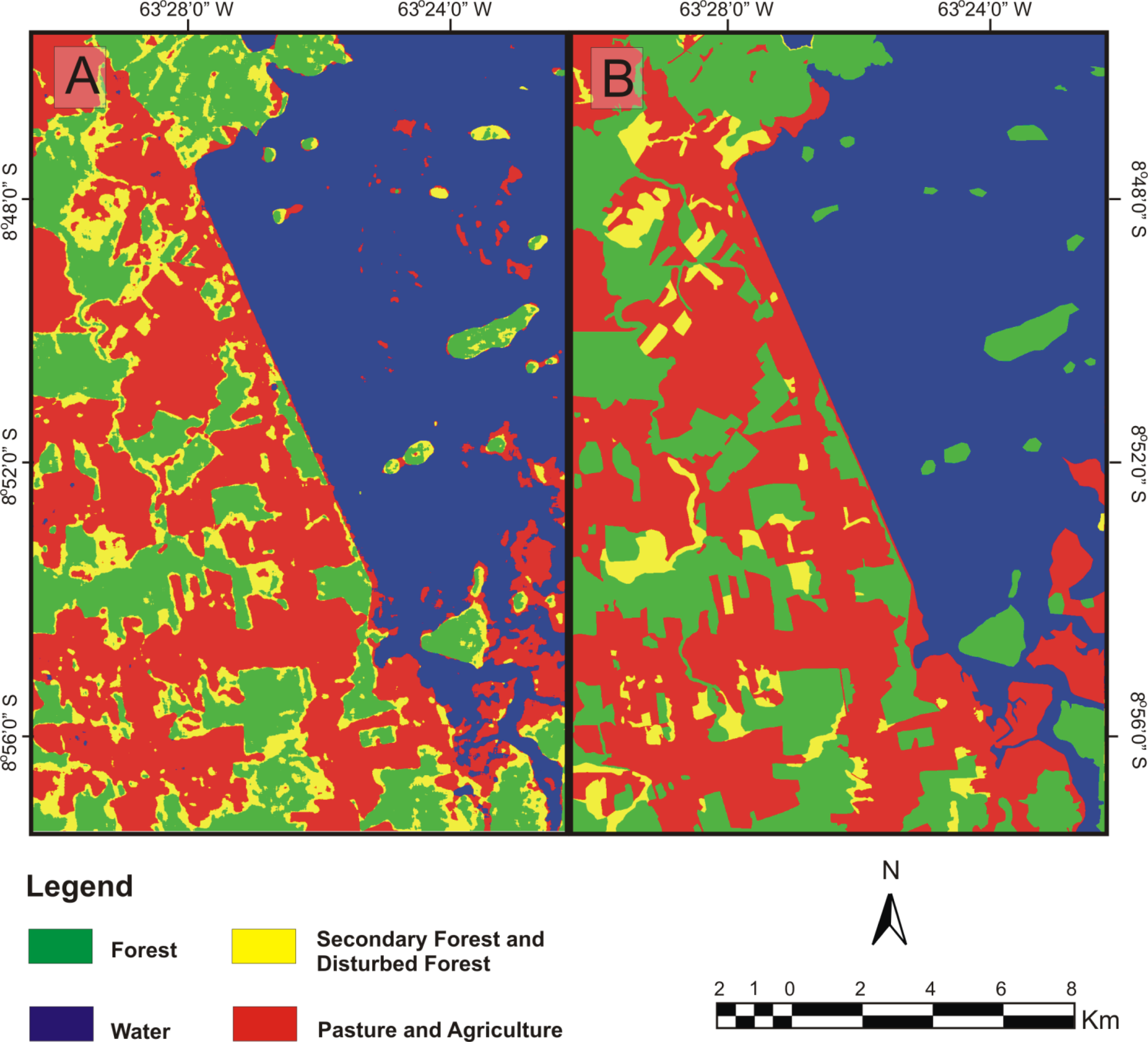
4.2. Classification of the Probability Density Components
4.3. Results of the Comparison with Other Traditional Methods
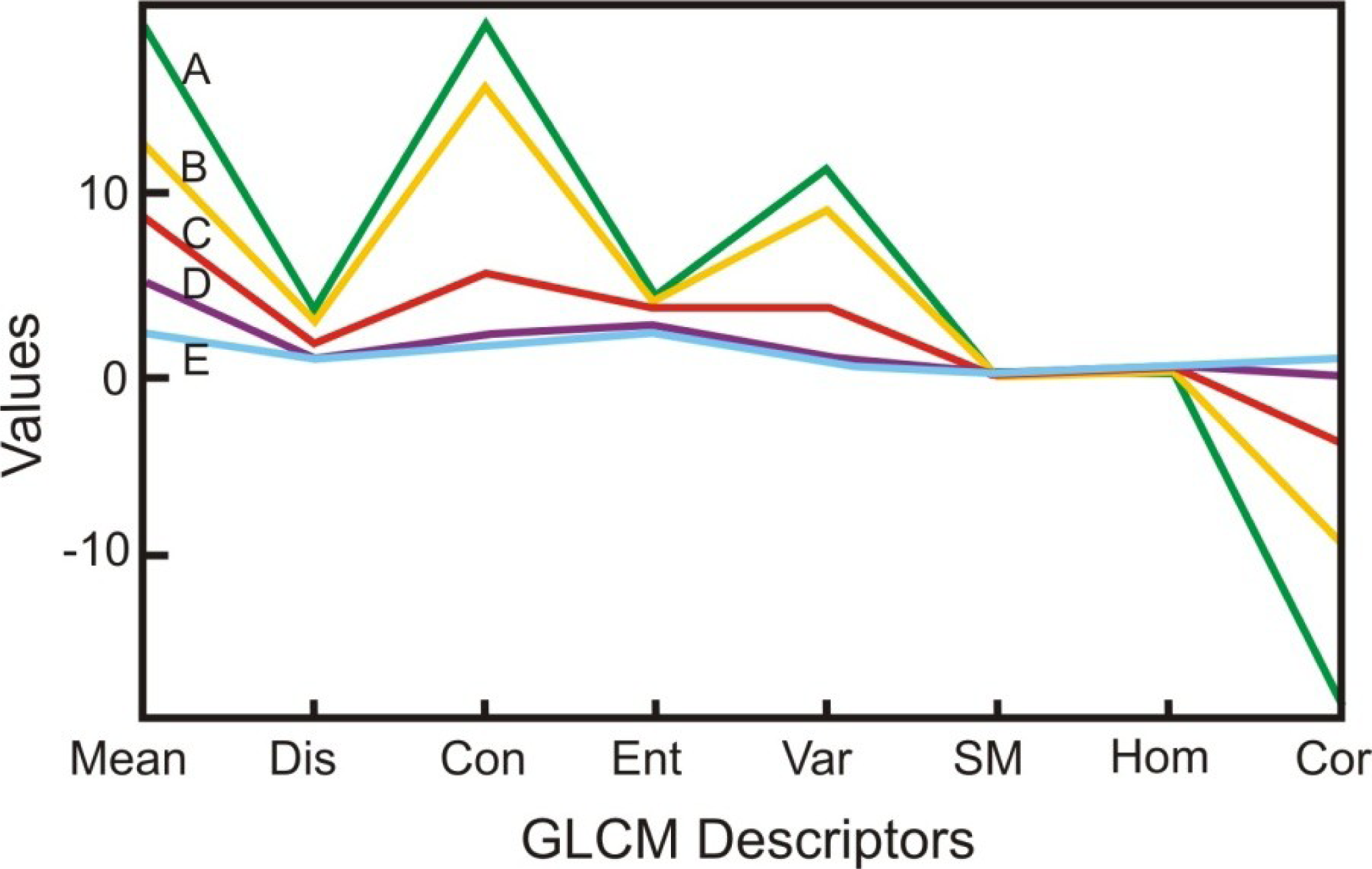
4.3.1. Gray-Level Co-Occurrence Matrices
4.3.2. Gabor Filter
4.4. Program
5. Discussions
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Goodenough, D.G.; Guindon, B.; Teillet, P.M. Correction of Synthetic Aperture Radar and Multispectral Scanner Data Sets. In Proceedings of the Thirteenth International Symposium on Remote Sensing of Environment, Ann Arbor, MI, USA, 23–27 April 1979; Volume 2, pp. 259–270.
- Henninger, D.L.; Carney, J.H. Shuttle Imaging Radar-A (SIR-A) Data as a Complement to Landsat Multispectral Scanner (MSS) Data. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS’83), San Francisco, CA, USA, 31 August–2 September 1983; pp. 7.1–7.7.
- Lee, J.S. Digital image smoothing and the sigma filter. Comput. Vis. Graph. Image Process 1983, 24, 255–269. [Google Scholar]
- Lee, J.S. A simple speckle smoothing algorithm for synthetic aperture radar images. IEEE Trans. Syst. Man Cybern 1983, 13, 85–89. [Google Scholar]
- Lee, J.S.; Wen, J.-H.; Ainsworth, T.L.; Chen, H-S.; Chen, A.J. Improved sigma filter for speckle filtering of SAR imagery. IEEE Trans. Geosci. Remote. Sens 2009, 47, 2002–2013. [Google Scholar]
- Lee, J.S. Digital image enhancement and noise filtering by use of local statistics. IEEE Trans. Pattern Anal. Mach. Intell 1980, 2, 165–168. [Google Scholar]
- Kuan, D.T.; Sawchuk, A.A.; Strand, T.C.; Chavel, P. Adaptive noise filtering for images with signal dependent noise. IEEE Trans. Pattern Anal. Mach. Intell 1985, 7, 165–177. [Google Scholar]
- Gao, G. Statistical modeling of SAR images: A survey. Sensor 2010, 10, 775–795. [Google Scholar]
- Nezry, E.; Lopés, A.; Ducrot-Gambart, D.; Nezry, C.; Lee, J.S. Supervised classification of K-distributed SAR images of natural targets and probability of error estimation. IEEE Trans. Geosci. Remote Sens 1996, 34, 1233–1242. [Google Scholar]
- George, S.F. The Detection of Nonfluctuating Targets in Log-Normal Clutter; NRL Report 6796; Naval Research Laboratory: Washington, DC, USA, 1968. [Google Scholar]
- Ulaby, F.T. Textural information in SAR images. IEEE Trans. Geosci. Remote Sens 1986, 24, 235–245. [Google Scholar]
- Tison, C.; Nicolas, J.M.; Tupin, F. Accuracy of Fisher Distributions and Log-Moment Estimation to Describe Histograms of High-Resolution SAR Images over Urban Areas. In Proceedings of 2003 IEEE International Geoscience and Remote Sensing Symposium, IGARSS’03, Toulouse, France, 21–25 July 2003; pp. 21–25.
- Tison, C.; Nicolas, J.M.; Tupin, F.; Maitre, H. A new statistical model for Markovian classification of urban areas in high-resolution SAR images. IEEE Trans. Geosci. Romote Sens 2004, 42, 2046–2057. [Google Scholar]
- Oliver, C.; Quegan, S. Understanding Synthetic Aperture Radar Images; Artech House: Norwood, MA, USA, 1998. [Google Scholar]
- Duda, R.O.; Hart, P.E.; Stork, D.G. Pattern Classification, 2nd ed.; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Moser, G; Serpico, S.B.; Zerubia, J. Dictionary-based stochastic expectation maximization for SAR amplitude probability density function estimation. IEEE Trans. Geosci. Remote Sens 2006, 44, 188–200. [Google Scholar]
- Parzen, E. On estimation of probability density function and mode. Signal Process 1962, 33, 267–281. [Google Scholar]
- Bruzzone, L.; Marconcini, M.; Wegmuller, U.; Wiesmann, A. An advanced system for the automatic classification of multitemporal SAR images. IEEE Trans. Geosci. Remote Sens 2004, 42, 1321–1334. [Google Scholar]
- Mantero, P.; Moser, G.; Serpico, S.B. Partially supervised classification of remote sensing images through SVM-based probability density estimation. IEEE Trans. Geosci. Remote Sens 2005, 43, 559–570. [Google Scholar]
- Krylov, V.A.; Moser, G.; Serpico, S.B.; Zerubia, J. Enhanced dictionary-based SAR amplitude distribution estimation and its validation with very high-resolution data. IEEE Geosci. Remote Sens. Lett 2011, 8, 148–152. [Google Scholar]
- Kruse, F.A.; Lefkoff, A.B.; Boardman, J.W.; Heiedbrecht, K.B.; Shapiro, A.T.; Barloon, P.J.; Goetz, A.F.H. The Spectral Image Processing System (SIPS)—Interactive visualization and analysis of imaging spectrometer data. Remote Sens. Environ 1993, 44, 145–163. [Google Scholar]
- De Carvalho Júnior, O.A.; Meneses, P.R. Spectral Correlation Mapper (SCM): An Improving Spectral Angle Mapper. In Proceedings of Annual JPL Airborne Earth Science Workshop, Pasadena, CA, USA, 23–25 February 2000; pp. 65–74.
- Azevedo, A.C.R.; Luz, S.L.B.; Vilela, M.L.; Rangel, E.F. Studies on the sandfly fauna of Samuel ecological station Porto Velho municipality, Rondônia State, Brazil. Mem. Inst. Oswaldo Cruz 1993, 88, 509–512. [Google Scholar]
- Luz, S.L.B.; Lourenço-de-Oliveira, R. Forest Culicinae mosquitoes in the environs of Samuel hydroeletric plant, State of Rondônia, Brazil. Mem. Inst. Oswaldo Cruz 1996, 91, 427–432. [Google Scholar]
- Skole, D.; Tucker, C. Evidence for tropical deforestation, fragmented habitat, and adversely affected habitat in the Brazilian Amazon: 1978–1988. Science 1993, 260, 1905–1910. [Google Scholar]
- Laurance, W.F.; Lovejoy, T.E.; Vasconcelos, H.L.; Bruna, E.M.; Didham, R.K.; Stouffer, P.C.; Gascon, C.; Bierregaard, R.O.; Laurance, S.G.; Sampaio, E. Ecosystem decay of Amazonian Forest fragments: A 22-year investigation. Conserv. Biol 2002, 16, 605–618. [Google Scholar]
- Rosenqvist, A.; Shimada, M.; Ito, N.; Watanabe, M. ALOS PALSAR. A pathfinder mission for global-scale monitoring of the environment. IEEE Trans. Geosci. Remote Sens 2007, 45, 3307–3316. [Google Scholar]
- Almeida Filho, R.; Shimabukuro, Y.E.; Rosenqvist, A.; Sanchez, G.A. Using dual polarized ALOS PALSAR data for detecting new fronts of deforestation in the Brazilian Amazônia. Int. J. Remote Sens 2009, 30, 3735–3743. [Google Scholar]
- Walker, W.S.; Stickler, C.M.; Kellndorfer, J.M.; Kirsch, K.M.; Nepstad, D.C. Large-area classification and mapping of forest and land cover in the Brazilian Amazon: A comparative analysis of ALOS/PALSAR and Landsat data sources. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens 2010, 3, 594–604. [Google Scholar]
- Green, R.O.; Eastwood, M.L.; Sarture, C.M.; Chrien, T.G.; Aronson, M.; Chippendale, B.J.; Faust, J.A.; Pavri, B.E.; Chovit, C.J.; Solis, M.; et al. Imaging spectroscopy and the Airborne Visible/Infrared Imaging Spectrometer (AVIRIS). Remote Sens. Environ 1998, 65, 227–248. [Google Scholar]
- Green, A.A.; Berman, M.; Switzer, P.; Craig, M.D. A transformation for ordering multispectral data in terms of images quality with implications for noise removal. IEEE Trans. Geosci. Remote Sens 1988, 6, 65–74. [Google Scholar]
- Lee, J.B.; Woodyatt, A.S.; Berman, M. Enhancement of high spectral resolution remote sensing data by a noise—Adjusted principal components transform. IEEE Trans. Geosci. Remote Sens 1990, 28, 295–304. [Google Scholar]
- Dickson, B.; Taylor, G. Noise reduction of aerial gamma-ray survey. Explor. Geophys 1988, 29, 324–329. [Google Scholar]
- Dickson, B.L.; Taylor, G.F. Maximum noise fraction method reveals detail in aerial gamma-ray surveys. Explor. Geophys 2000, 31, 73–77. [Google Scholar]
- De Carvalho Júnior, O.A.; Hermuche, P.M.; Guimarães, R.F. Identificação regional da floresta decidual na bacia do rio Paranã a partir da análise multitemporal de imagens MODIS. Rev. Bras. Geofís 2006, 24, 319–332. [Google Scholar]
- De Carvalho Júnior, O.A.; Sampaio, C.S.; da Silva, N.C.; Couto Júnior, A.F.; Gomes, R.A.T.; de Carvalho, A.P.F.; Shimabukuro, Y.E. Classificação de padrões de savana usando assinaturas temporais NDVI do sensor MODIS no Parque Nacional Chapada dos Veadeiros. Rev. Bras. Geofís 2008, 26, 1–13. [Google Scholar]
- De Carvalho Junior, O.A.; da Silva, N.C.; de Carvalho, A.P.F.; Couto Júnior, A.F.; Silva, C.R.; Shimabukuro, Y.E.; Guimarães, R.F.; Gomes, R.A.T. Combining noise-adjusted principal components transform and median filter techniques for denoising MODIS temporal signatures. Rev. Bras. Geofís 2012, 30, 147–157. [Google Scholar]
- Switzer, P.; Green, A.A. Min/Max Autocorrelation Factors for Multivariate Spatial Imaging; Technical Report No. 6; Stanford University: Stanford, CA, USA, 1984. [Google Scholar]
- Bateson, C.A.; Curtiss, B. A method for manual endmember selection and spectral unmixing. Remote Sens. Environ 1996, 55, 229–243. [Google Scholar]
- Bateson, C.A.; Asner, G.P.; Wessman, C.A. Endmember bundles: A new approach to incorporating endmember variability into spectral mixture analysis. IEEE Trans. Geosci. Remote Sens 2000, 38, 1083–1094. [Google Scholar]
- Berman, M.; Kiiveri, H.; Ryan, L.; Ernst, A.; Dunne, R.; Huntington, J.F. ICE: A statistical approach to identifying endmembers in hyperspectral images. IEEE Trans. Geosci. Remote Sens 2004, 42, 1–11. [Google Scholar]
- Tompkins, S.; Mustard, J.F.; Pieters, C.M.; Forsyth, D.W. Optimization of endmembers mixture analysis for spectral. Remote Sens. Environ 1997, 59, 472–489. [Google Scholar]
- Winter, M. N-FINDR: An Algorithm for Fast Autonomous Spectral End-Member Determination in Hyperspectral Data. In Proceedings of the SPIE Conference on Imaging Spectrometry V, Denver, CO, USA, 27 October 1999; Volume 3753, pp. 266–275.
- Boardman, J.W.; Kruse, F.A. Automated Spectral Analysis: A Geologic Example Using AVIRIS Data, North Grapevine Mountains, Nevada. In Proceedings of the ERIM–Tenth Thematic Conference on Geologic Remote Sensing, San Antonio, TX, USA, 9–12 May 1994; pp. I-407–I-418.
- ENVI. The Environment for Visualizing Images Users Guide, 4th ed.; Research Systems Inc.: Boulder, CO, USA, 2000; p. 930. [Google Scholar]
- Adams, J.B.; Gillespie, A.R. Remote Sensing of Landscapes with Spectral Images. A Physical Modeling Approach; Cambridge University Press: New York, NY, USA, 2006; p. 362. [Google Scholar]
- Jensen, J.R. Introductory Digital Image Processing; Prentice-Hall: Englewood Cliffs, NJ, USA, 1986. [Google Scholar]
- Congalton, R.; Green, K. Assessing the Accuracy of Remotely Sensed Data: Principles and Practices; CRC/Lewis Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- Campbell, F.W.; Robson, J.G. Application of Fourier analysis to the visibility of gratings. J. Physiol 1968, 197, 551–566. [Google Scholar]
- Jain, A.K.; Farrokhnia, F. Unsupervised texture segmentation using Gabor filters. Pattern Recognit 1991, 24, 1167–1186. [Google Scholar]
- Haralick, R.M.; Shanmugan, K.; Dinstein, I. Textural features for image classification. IEEE Trans. Syst. Man-Cybern 1973, 3, 610–621. [Google Scholar]
- Haralick, R.M. Statistical and structural approaches to texture. Proc. IEEE 1979, 67, 786–804. [Google Scholar]
- Chai, H.Y.; Wee, L.K.; Swee, T.T.; Salleh, S.H.; Ariff, A.K. Gray-level co-occurrence matrix bone fracture detection. Am. J. Appl. Sci 2011, 8, 26–32. [Google Scholar]
- Ou, X.; Pan, W.; Xiao, P. In vivo skin capacitive imaging analysis by using grey level co-occurrence matrix (GLCM). Int. J. Pharm 2014, 460, 28–32. [Google Scholar]
- Rajendra Acharya, U.; Dua, S.; Du, X.; Vinitha Sree, S.; Chua, C.K. Automated diagnosis of glaucoma using texture and higher order spectra features. Trans. Inf. Technol. Biomed 2011, 15, 449–455. [Google Scholar]
- Su, T.L.; Lu, C.F. Automated vision system for recognising Lycra Spandex Defects. Fibres Text. East. Eur 2011, 19, 43–46. [Google Scholar]
- Wang, S.W.; Su, T.L. An identification system for classifying nonwoven quality. Appl. Mech. Mater 2013, 241, 466–469. [Google Scholar]
- Bianconi, F.; Ceccarelli, L.; Fernández, A.; Saetta, S.A. A sequential machine vision procedure for assessing paper impurities. Comput. Ind 2014, 65, 325–332. [Google Scholar]
- Champion, I.; Dubois-Fernandez, P.; Guyon, D.; Cottrel, M. Radar image texture as a function of forest stand age. Int. J. Remote Sens 2008, 29, 1795–1800. [Google Scholar]
- Li, P.; Fang, S. SAR image classification based on its texture features. Geo-Spat. Inf. Sci 2003, 6, 16–19. [Google Scholar]
- Gupta, M.; Bhaskar, D.; Bera, R.; Biswas, S. Target detection of ISAR data by principal component transform on co-occurrence matrix. Pattern Recog. Lett 2012, 33, 1682–1688. [Google Scholar]
- Barber, D.G.; Ledrew, E.F. SAR sea ice discrimination using texture statistics: A multivariate approach. Photogramm. Eng. Remote Sens 1991, 57, 385–395. [Google Scholar]
- Dell’Acqua, F.; Gamba, P. Discriminating urban environments using multiscale texture and multiple SAR images. Int. J. Remote Sens 2006, 27, 3797–3812. [Google Scholar]
- Holmes, Q.A.; Nuesch, D.R.; Shuchman, R.A. Textural analysis and real-time classification of sea-ice types using digital SAR data. IEEE Trans. Geosci. Remote Sens 1984, 22, 113–120. [Google Scholar]
- Shokr, M.E. Evaluation of second-order texture parameters for sea ice classification from radar images. J. Geophys. Res 1991, 96, 10625–10640. [Google Scholar]
- Soh, L.-K.; Tsatsoulis, C. Texture analysis of SAR sea ice imagery using gray level co-occurrence matrices. IEEE Trans. Geosci. Remote Sens 1999, 37, 780–795. [Google Scholar]
- Weszka, J.; Dyer, C.; Rosenfeld, A. A comparative study of texture measures for terrain classification. IEEE Trans. Syst. Man-Cybern 1976, 6, 269–285. [Google Scholar]
- Clausi, D.A. An analysis of co-occurrence texture statistics as a function of grey level quantization. Can. J. Remote Sens 2002, 28, 45–62. [Google Scholar]
- Clausi, D.A.; Yue, B. Comparing cooccurrence probabilities and Markov random fields for texture analysis of SAR sea ice imagery. IEEE Trans. Geosci. Remote Sens 2004, 42, 215–228. [Google Scholar]
- Karathanassi, V.; Iossifidis, C.; Rokos, D. A texture-based classification method for classifying built areas according to their density. Int. J. Remote Sens 2000, 21, 1807–1823. [Google Scholar]
- Zhang, Q.; Wang, J.; Gong, P.; Shi, P. Study of urban spatial patterns from SPOT panchromatic imagery using textural analysis. Int. J. Remote Sens 2003, 24, 4137–4160. [Google Scholar]
- Marceau, D.J.; Gratton, D.J.; Fournier, R.A.; Fortin, J.-P. Remote sensing and the measurement of geographical entities. 2. The optimal spatial resolution. Remote Sens. Environ 1994, 49, 105–117. [Google Scholar]
- Puissant, A.; Hirsch, J.; Weber, C. The utility of texture analysis to improve perpixel classification for high to very high spatial resolution imagery. Int. J. Remote Sens 2005, 26, 733–745. [Google Scholar]
- Franklin, S.E.; Wulder, M.A.; Gerylo, G.R. Texture analysis of IKONOS panchromatic data for Douglas-fire forest age class separability in British Columbia. Int. J. Remote Sens 2001, 22, 2627–2632. [Google Scholar]
- Kiema, J.B.K. Texture analysis and data fusion in the extraction of topographic objects from satellite imagery. Int. J. Remote Sens 2002, 23, 767–776. [Google Scholar]
- Anvs, H.; Bannari, A.; He, D.C.; Morin, D. Texture Analysis for the Mapping of Urban Areas Using Airborne MEIS-ll Images. In Proceedings of the First International Airborne Remote Sensing Conference and Exhibition (ERIM), Strasbourg, France, 11–15 September 1994; Volume 3, pp. 231–245.
- Baraldi, A.; Parmiggiani, F. An investigation of the textural characteristics associated with gray level cooccurrence matrix statistical parameters. IEEE Trans. Geosci. Remote Sens 1995, 33, 293–304. [Google Scholar]
- Clausi, D.A. Comparison and fusion of co-occurrence, Gabor and MRF texture features for classification of SAR sea-ice imagery. Atmosphere-Ocean 2001, 39, 183–194. [Google Scholar]
- Sali, E.; Wolfson, H. Texture classification in aerial photographs and satellite data. Int. J. Remote Sens 1992, 13, 3395–3408. [Google Scholar]
- Clausi, D.A.; Zhao, Y. Rapid extraction of image texture by co-occurrence using a hybrid data structure. Comput. Geosci 2002, 28, 763–774. [Google Scholar]
- Wei, L.; Hu, Z.; Guo, M.; Jiang, M.; Zhang, S. Texture Feature Analysis in Oil Spill Monitoring by SAR Image. In Proceedings of IEEE 20th International Conference on Geoinformatics (GEOINFORMATICS), Hong Kong, China, 15–17 June 2012; pp. 1–6.
- Su, W.; Li, J.; Chen, Y.; Liu, Z.; Zhang, J.; Low, T.M.; Suppiah, I.; Hashim, S.A.M. Textural and local spatial statistics for the object oriented classification of urban areas using high resolution imagery. Int. J. Remote Sens 2008, 29, 3105–3117. [Google Scholar]
- Perez, C.A.; Cament, L.A.; Castillo, L.E. Methodological improvement on local Gabor face recognition based on feature selection and enhanced Borda count. Pattern Recognit 2011, 44, 951–963. [Google Scholar]
- Wang, X.; Ding, X.; Liu, C. Gabor filters-based feature extraction for character recognition. Pattern Recognit 2005, 38, 369–379. [Google Scholar]
- Grigorescu, S.E.; Petkov, N.; Kruizinga, P. Comparison of texture features based on Gabor filters. IEEE Trans. Image Process 2002, 11, 1160–1167. [Google Scholar]
- Petkov, N.; Kruizinga, P. Computational models of visual neurons specialized in the detection of periodic and aperiodic oriented visual stimuli: Bar and grating cells. Biol. Cybern 1997, 76, 83–96. [Google Scholar]
- Petkov, N. Biologically motivated computationally intensive approaches to image pattern recognition. Future Gen. Comput. Syst 1995, 11, 451–465. [Google Scholar]
- De Valois, R.L.; Albrecht, D.G.; Thorell, L.G. Spatial frequency selectivity of cells in macaque visual cortex. Vis. Res 1982, 22, 545–559. [Google Scholar]
- Bianconi, F.; Fernández, A. Evaluation of the effects of Gabor filter parameters on texture classification. Pattern Recognit 2007, 40, 3325–3335. [Google Scholar]
- Kumar, A.; Pang, G.K. Defect detection in textured materials using Gabor filters. IEEE Trans. Ind. Appl 2002, 38, 425–440. [Google Scholar]
- Clausi, D.A.; Deng, H. Design-based texture feature fusion using Gabor filters and co-occurrence probabilities. IEEE Trans. Image Process 2005, 14, 925–936. [Google Scholar]
- Jain, A.K.; Ratha, N.R.; Lakhsmanan, S. Object detection using Gabor filters. Pattern Recognit 1997, 30, 295–309. [Google Scholar]
- Li, S.; Shawe-Taylor, J. Comparison and fusion of multiresolution features for texture classification. Pattern Recognit. Lett 2004, 26, 633–638. [Google Scholar]
- Manjunath, B.S.; Ma, W.Y. Texture features for browsing and retrieval of image data. IEEE Trans. Pattern Anal. Mach. Intell 1996, 18, 837–841. [Google Scholar]
- Turner, M.R. Texture discrimination by Gabor functions. Biol. Cybern 1986, 55, 71–82. [Google Scholar]
- Clausi, D.A.; Jernigan, M.E. Designing Gabor filters for optimal texture separability. Pattern Recognit 2000, 33, 1835–1849. [Google Scholar]
- Spitzer, H.; Hochstein, S. A complex-cell receptive-field model. J. Neurosci 1985, 53, 1266–1286. [Google Scholar]
- Bioucas-Dias, J.M.; Nascimento, J.M. Hyperspectral subspace identification. IEEE Trans. Geosci. Remote Sens 2008, 46, 2435–2445. [Google Scholar]
- Lu, R. Detection of bruises on apples using near-infrared hyperspectral imaging. Trans.-Am. Soc. Agric. Eng 2003, 46, 523–553. [Google Scholar]
- Underwood, E.; Ustin, S.; DiPietro, D. Mapping nonnative plants using hyperspectral imagery. Remote Sens. Environ 2003, 86, 150–161. [Google Scholar]
- Yang, C.; Everitt, J.H.; Fletcher, R.S.; Jensen, R.R.; Mausel, P.W. Evaluating AISA+ hyperspectral imagery for mapping black mangrove along the South Texas Gulf Coast. Photogram. Eng. Remote Sens 2009, 75, 425–435. [Google Scholar]
- Dickson, B.L. Recent advances in aerial gamma-ray surveying. J. Environ. Radioact 2004, 76, 225–236. [Google Scholar]
- Billings, S.D.; Brian, R.M.; Garry, N.N. Deconvolution and spatial resolution of airborne gamma-ray surveys. Geophysics 2003, 68, 1257–1266. [Google Scholar]







| Image Classification | Ground Truth (Percent) | |||
|---|---|---|---|---|
| Pasture and Agriculture | Secondary Forest | Forest | Water | |
| Pasture and agriculture | 87.33 | 19.43 | 4.78 | 3.38 |
| Secondary Forest | 8.61 | 66.78 | 18.54 | 0.45 |
| Forest | 1.27 | 13.38 | 75.62 | 0.14 |
| Water | 2.79 | 0.42 | 1.06 | 96.04 |
| Total | 100.00 | 100.00 | 100.00 | 100.00 |
| Dis | Con | Ent | Var | SM | Hom | Cor | |
|---|---|---|---|---|---|---|---|
| Dis | 1.00 | 0.97 | 0.89 | 0.85 | −0.76 | −0.84 | −0.88 |
| Con | 0.97 | 1.00 | 0.78 | 0.86 | −0.66 | −0.79 | −0.83 |
| Ent | 0.89 | 0.78 | 1.00 | 0.74 | −0.80 | −0.73 | −0.81 |
| Var | 0.85 | 0.86 | 0.74 | 1.00 | −0.63 | −0.71 | −0.64 |
| SM | −0.76 | −0.66 | −0.80 | −0.63 | 1.00 | 0.92 | 0.77 |
| Hom | −0.84 | −0.79 | −0.73 | −0.71 | 0.92 | 1.00 | 0.83 |
| Cor | −0.88 | −0.83 | −0.81 | −0.64 | 0.77 | 0.83 | 1.00 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
De Carvalho Júnior, O.A.; Maciel, L.M.d.M.; De Carvalho, A.P.F.; Guimarães, R.F.; Silva, C.R.; Gomes, R.A.T.; Silva, N.C. Probability Density Components Analysis: A New Approach to Treatment and Classification of SAR Images. Remote Sens. 2014, 6, 2989-3019. https://doi.org/10.3390/rs6042989
De Carvalho Júnior OA, Maciel LMdM, De Carvalho APF, Guimarães RF, Silva CR, Gomes RAT, Silva NC. Probability Density Components Analysis: A New Approach to Treatment and Classification of SAR Images. Remote Sensing. 2014; 6(4):2989-3019. https://doi.org/10.3390/rs6042989
Chicago/Turabian StyleDe Carvalho Júnior, Osmar Abílio, Luz Marilda de Moraes Maciel, Ana Paula Ferreira De Carvalho, Renato Fontes Guimarães, Cristiano Rosa Silva, Roberto Arnaldo Trancoso Gomes, and Nilton Correia Silva. 2014. "Probability Density Components Analysis: A New Approach to Treatment and Classification of SAR Images" Remote Sensing 6, no. 4: 2989-3019. https://doi.org/10.3390/rs6042989
APA StyleDe Carvalho Júnior, O. A., Maciel, L. M. d. M., De Carvalho, A. P. F., Guimarães, R. F., Silva, C. R., Gomes, R. A. T., & Silva, N. C. (2014). Probability Density Components Analysis: A New Approach to Treatment and Classification of SAR Images. Remote Sensing, 6(4), 2989-3019. https://doi.org/10.3390/rs6042989






