Comparison of Eight Techniques for Reconstructing Multi-Satellite Sensor Time-Series NDVI Data Sets in the Heihe River Basin, China
Abstract
:1. Introduction
2. Method
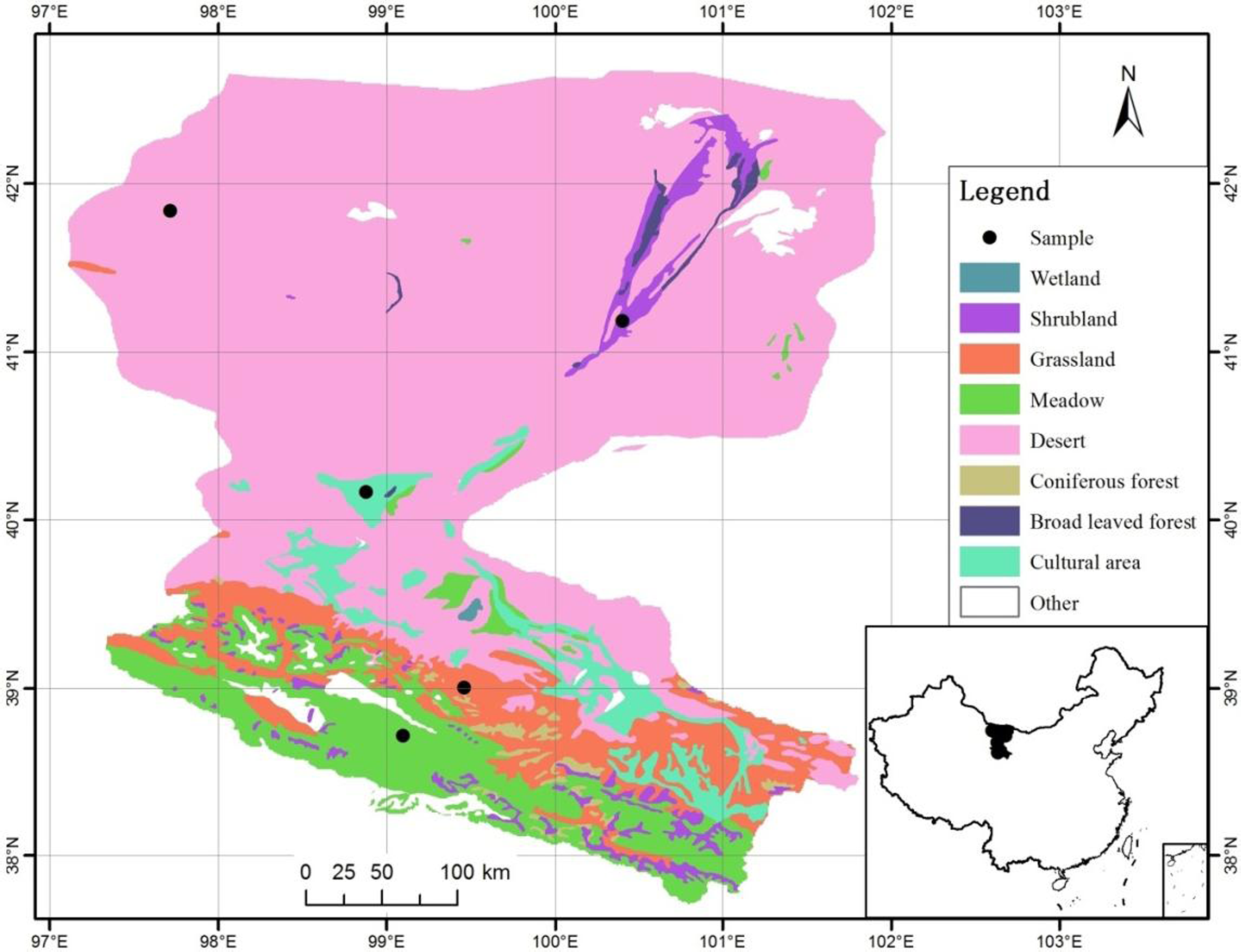
2.1. Study Area
2.2. Data and Processing
2.3. Candidate Time Series Reconstruction Techniques and Parameters
2.4. Technique Evaluation
3. Results
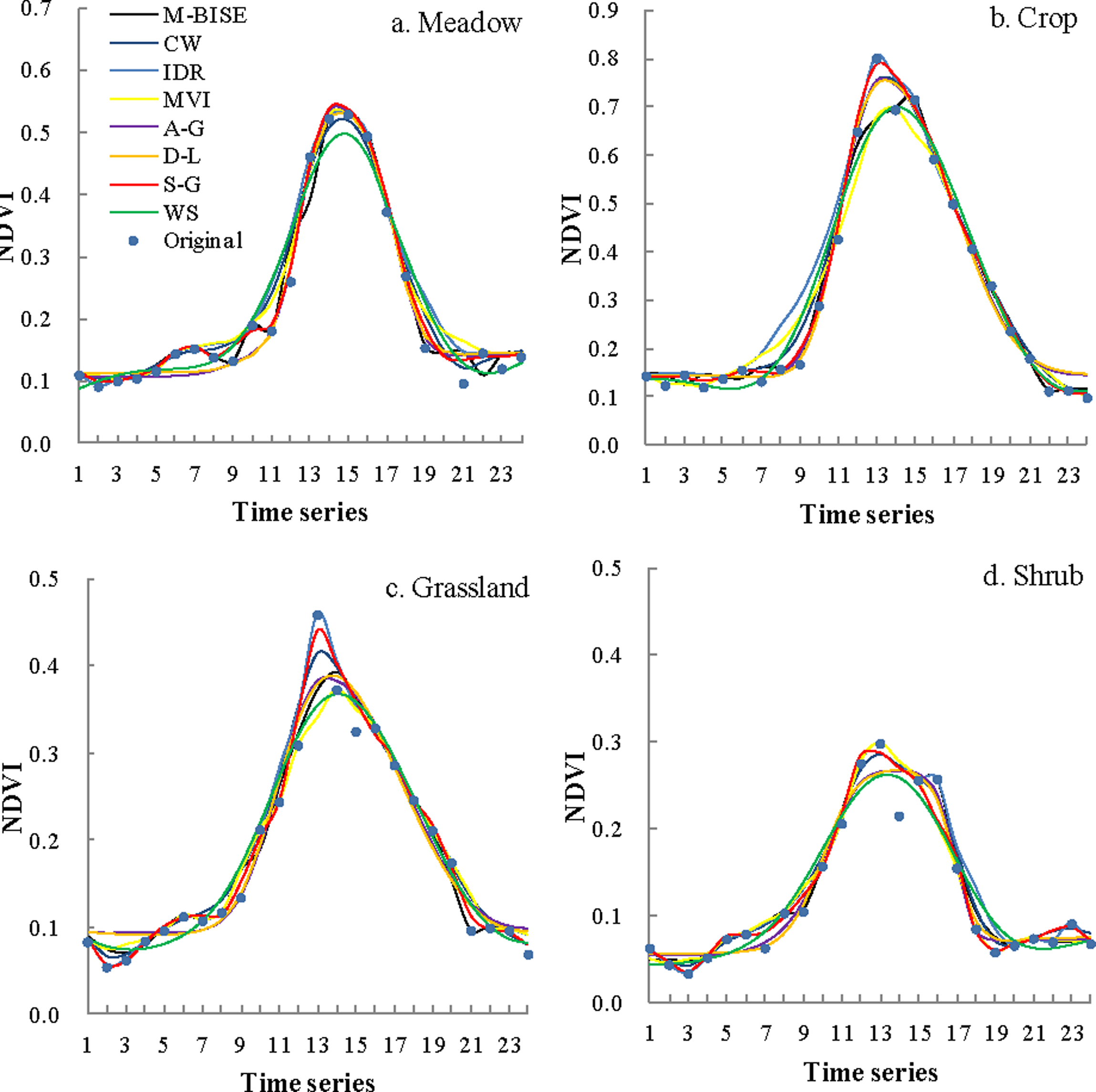
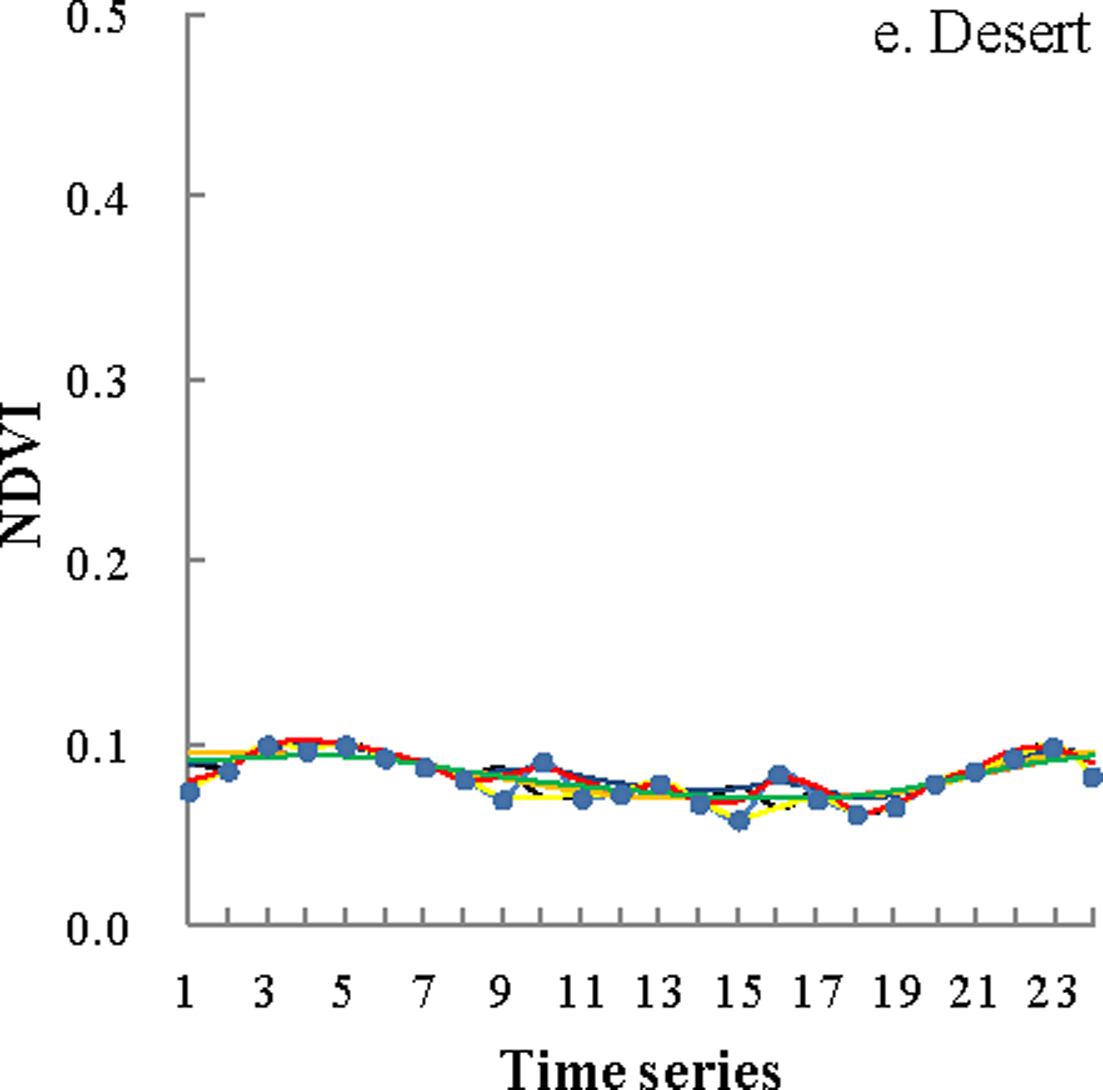
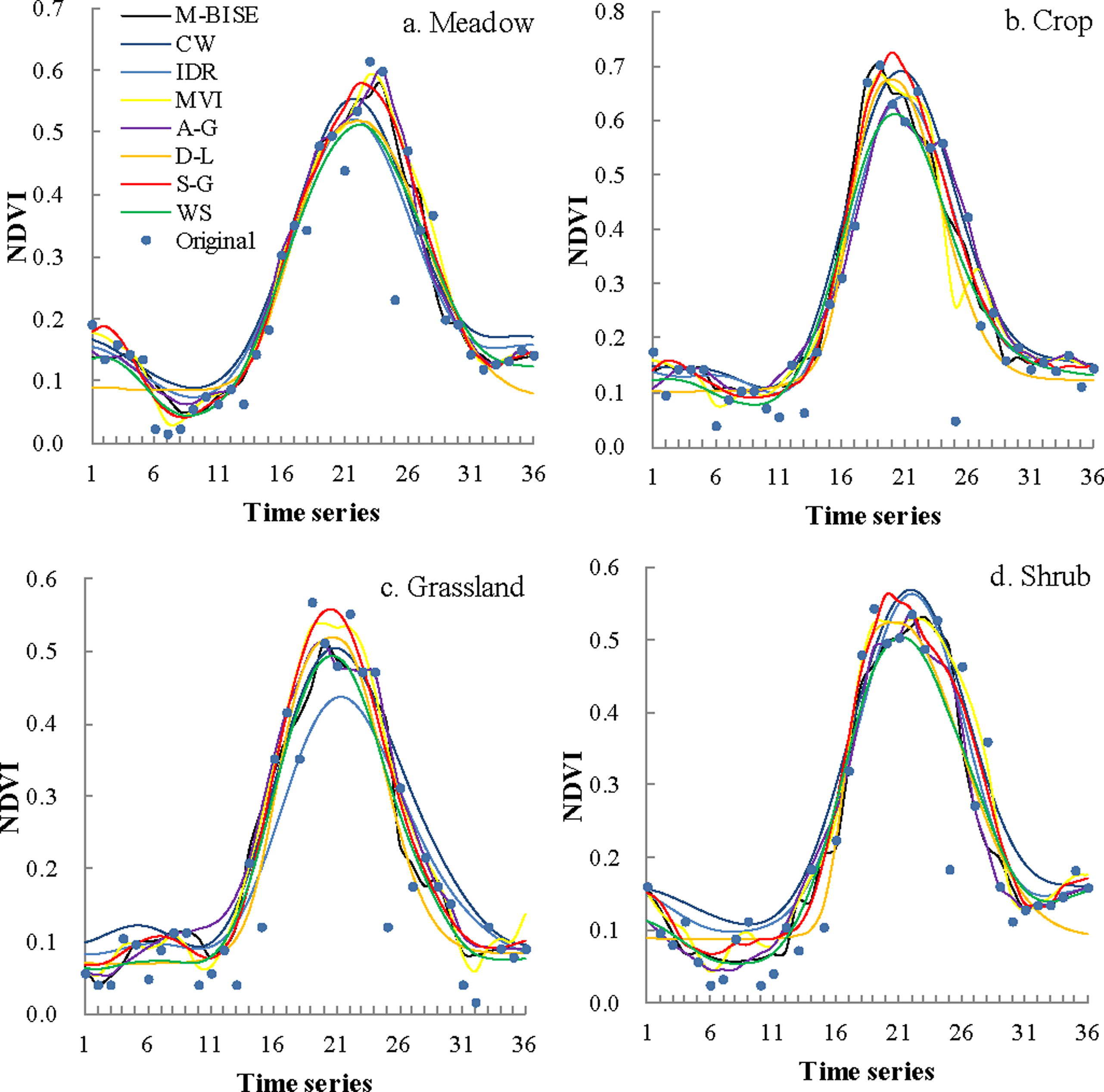
3.1. Visual Assessment of the Fitted Curves
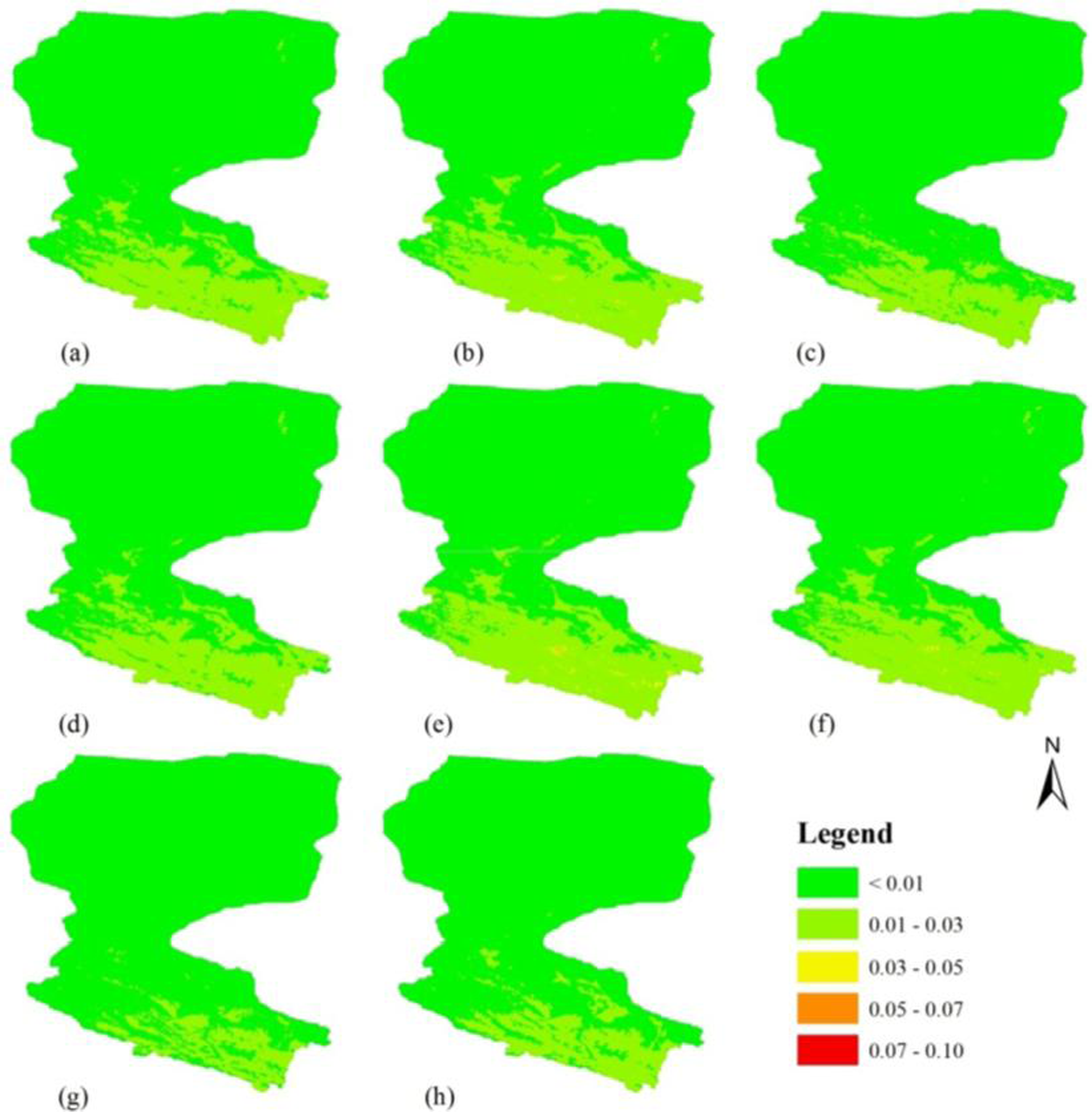
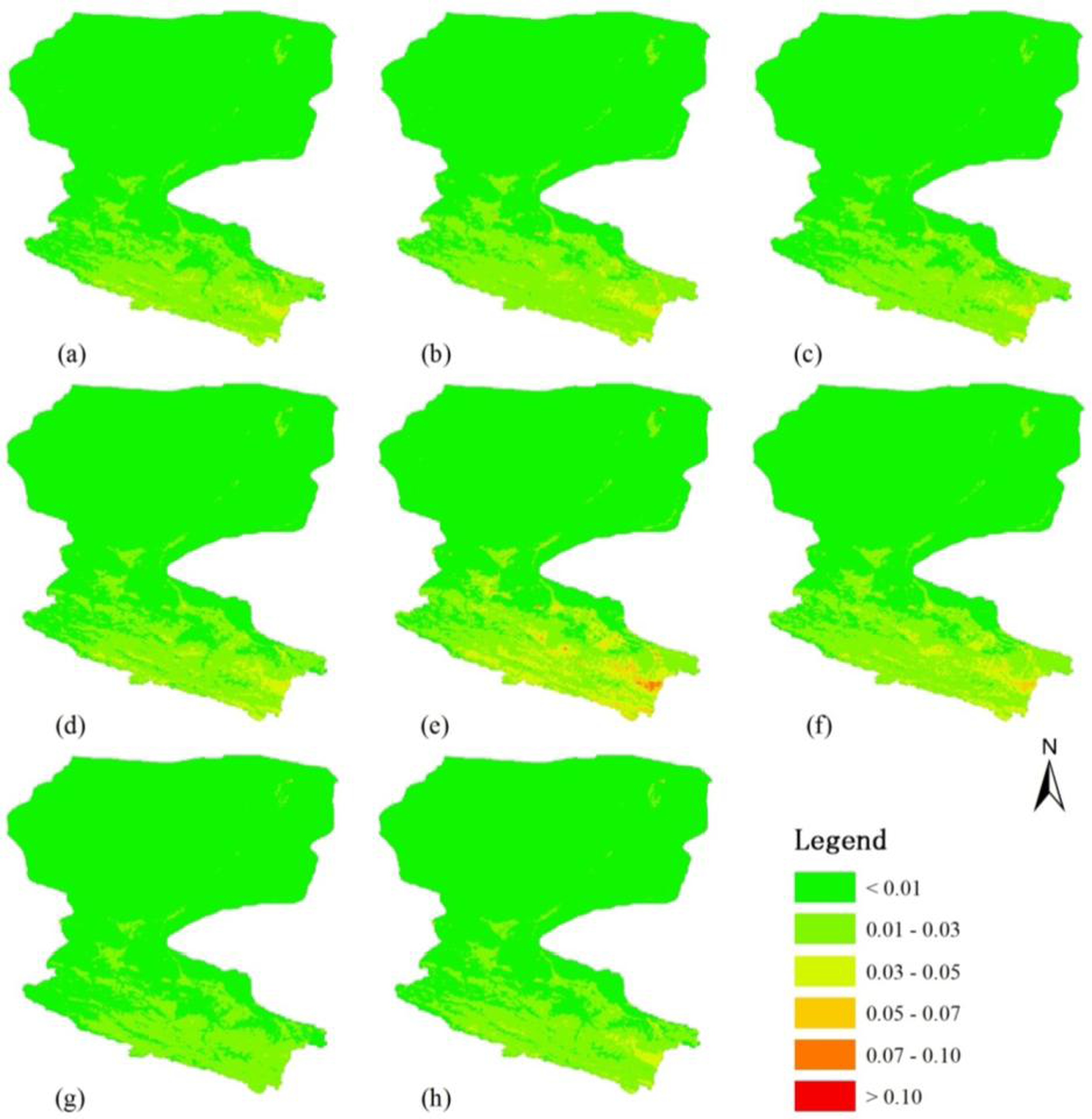
3.2. Quantitative Evaluation and Regional Application
3.2.1. GIMMS NDVI
3.2.2. PAL NDVI
3.2.3. SPOT VGT NDVI
3.2.4. MODIS NDVI
4. Discussion
4.1. Performance of the Reconstruction Techniques
4.2. Effect of Evaluation Index on the Final Reconstruction Results
4.3. Factors Influencing Performance
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Reference
- Ichii, K.; Maruyama, M.; Yamaguchi, Y. Multi-temporal analysis of deforestation in Rondonia state in Brazil using Landsat MSS, TM, ETM plus and NOAA AVHRR imagery and its relationship to changes in the local hydrological environment. Int. J. Remote Sens 2003, 24, 4467–4479. [Google Scholar]
- Roerink, G.J.; Menenti, M.; Soepboer, W.; Su, Z. Assessment of climate impact on vegetation dynamics by using remote sensing. Phys. Chem. Earth 2003, 28, 103–109. [Google Scholar]
- Zhang, G.L.; Zhang, Y.J.; Dong, J.W.; Xiao, X.M. Green-up dates in the Tibetan Plateau have continuously advanced from 1982 to 2011. Proc. Natl. Acad. Sci. USA 2013, 110, 4309–4314. [Google Scholar]
- Silveira, E.M.D.; de Carvalho, L.M.T.; Acerbi-Junior, F.W.; de Mello, J.M. The assessment of vegetation seasonal dynamics using multitemporal NDVI and EVI images derived from MODIS. Cerne 2008, 14, 177–184. [Google Scholar]
- Narasimhan, R.; Stow, D. Daily MODIS products for analyzing early season vegetation dynamics across the North Slope of Alaska. Remote Sens. Environ 2010, 114, 1251–1262. [Google Scholar]
- Li, J.L.; Zhao, H.B.; Yang, X.P. Study on the seasonal dynamics of zonal vegetation of NDVI/EVI of costal zonal vegetation based on MODIS data: A case study of Spartina alterniflora salt marsh on Jiangsu Coast, China. Afr. J. Agr. Res 2011, 6, 4019–4024. [Google Scholar]
- Fensholt, R.; Proud, S.R. Evaluation of earth observation based global long term vegetation trends—Comparing GIMMS and MODIS global NDVI time series. Remote Sens. Environ 2012, 119, 131–147. [Google Scholar]
- Forkel, M.; Carvalhais, N.; Verbesselt, J.; Mahecha, M.D.; Neigh, C.S.R.; Reichstein, M. Trend change detection in NDVI time series: Effects of inter-annual variability and methodology. Remote Sens 2013, 5, 2113–2144. [Google Scholar]
- Brown, J.C.; Kastens, J.H.; Coutinho, A.C.; Victoria, D.D.; Bishop, C.R. Classifying multiyear agricultural land use data from Mato Grosso using time-series MODIS vegetation index data. Remote Sens. Environ 2013, 130, 39–50. [Google Scholar]
- Landmann, T.; Schramm, M.; Huettich, C.; Dech, S. MODIS-based change vector analysis for assessing wetland dynamics in Southern Africa. Remote Sens. Lett 2013, 4, 104–113. [Google Scholar]
- Saito, H.; Sawada, Y.; Furuya, N.; Preap, S. Land Cover Change Mapping of the Mekong River Basin Using NOAA Pathfinder AVHRR 8-km Land Dataset. In Forest Environments in the Mekong River Basin; Sawada, H., Araki, M., Chappell, N.A., LaFrankie, J.V., Shimizu, A., Eds.; Springer Japan: Osaka, Japan, 2007; pp. 159–167. [Google Scholar]
- Kerr, J.T.; Ostrovsky, M. From space to species: Ecological applications for remote sensing. Trends Ecol. Evol 2003, 18, 299–305. [Google Scholar]
- Pettorelli, N.; Vik, J.O.; Mysterud, A.; Gaillard, J.M.; Tucker, C.J.; Stenseth, N.C. Using the satellite-derived NDVI to assess ecological responses to environmental change. Trends Ecol. Evol 2005, 20, 503–510. [Google Scholar]
- Holben, B.N. Characteristics of maximum-value composite images from temporal AVHRR data. Int. J. Remote Sens 1986, 7, 1417–1434. [Google Scholar]
- Hird, J.N.; McDermid, G.J. Noise reduction of NDVI time series: An empirical comparison of selected techniques. Remote Sens. Environ 2009, 113, 248–258. [Google Scholar]
- Carreiras, J.M.; Pereira, J.M.; Shimabukuro, Y.E.; Stroppiana, D. Evaluation of compositing algorithms over the Brazilian Amazon using SPOT-4 VEGETATION data. Int. J. Remote Sens 2003, 24, 3427–3440. [Google Scholar]
- Kobayashi, H.; Dye, D.G. Atmospheric conditions for monitoring the long-term vegetation dynamics in the Amazon using normalized difference vegetation index. Remote Sens. Environ 2005, 97, 519–525. [Google Scholar]
- Park, S. Cloud and cloud shadow effects on the MODIS vegetation index composites of the Korean Peninsula. Int. J. Remote Sens 2013, 34, 1234–1247. [Google Scholar]
- Motohka, T.; Nasahara, K.N.; Murakami, K.; Nagai, S. Evaluation of sub-pixel cloud noises on MODIS daily spectral indices based on in situ measurements. Remote Sens 2011, 3, 1644–1662. [Google Scholar]
- Viovy, N.; Arino, O.; Belward, A. The Best Index Slope Extraction (BISE): A method for reducing noise in NDVI time-series. Int. J. Remote Sens 1992, 13, 1585–1590. [Google Scholar]
- Lovell, J.L.; Graetz, R.D. Filtering pathfinder AVHRR land NDVI data for Australia. Int. J. Remote Sens 2001, 22, 2649–2654. [Google Scholar]
- Velleman, P.F. Definition and comparison of robust nonlinear data smoothing algorithms. J. Am. Stat. Assoc 1980, 75, 609–615. [Google Scholar]
- Filipova-Racheva, D.; Hall-Beyer, M. Smoothing of NDVI Time Series Curves for Monitoring of Vegetation Changes in Time. Proceedings of the Ecological Monitoring and Assessment Network National Science Meeting 2000, Toronto, ON, Canada, 17–22 January 2000.
- Chen, J.; Jönsson, P.; Tamura, M.; Gu, Z.H.; Matsushita, B.; Eklundh, L. A simple method for reconstructing a high-quality NDVI time-series data set based on the Savitzky–Golay filter. Remote Sens. Environ 2004, 91, 332–344. [Google Scholar]
- Ma, M.M.; Veroustraete, F. Reconstructing pathfinder AVHRR land NDVI time-series data for the Northwest of China. Adv. Space Res 2006, 37, 835–840. [Google Scholar]
- Zhu, W.Q.; Pan, Y.Z.; He, H.; Wang, L.L.; Mou, M.J.; Liu, J.H. A changing-weight filter method for reconstructing a high-quality NDVI time series to preserve the integrity of vegetation phenology. IEEE Trans. Geosci. Remote Sens 2012, 50, 1085–1094. [Google Scholar]
- Jiang, N.; Zhu, W.Q.; Mou, M.J.; Wang, L.L.; Zhang, J.Z. A. Phenology-Preserving Filtering Method to Reduce Noise in NDVI Time Series. Proceedings of the Geoscience and Remote Sensing Symposium (IGARSS), Munich, Genmany, 22–27 July 2012; pp. 2384–2387.
- Menenti, M.; Azzali, S.; Verhoef, W.; van Swol, R. Mapping agroecological zones and time lag in vegetation growth by means of Fourier analysis of time series of NDVI images. Adv. Space Res 1993, 13, 233–237. [Google Scholar]
- Park, J.; Tateishi, R.; Matsuoka, M. A proposal of the Temporal Window Operation (TWO) method to remove high-frequency noises in AVHRR NDVI time series data. J. Jpn. Soc. Photogramm. Remote Sens 1999, 38, 36–47. [Google Scholar]
- Roerink, G.J.; Menenti, M.; Verhoef, W. Reconstructing cloudfree NDVI composites using Fourier analysis of time series. Int. J. Remote Sens 2000, 21, 1911–1917. [Google Scholar]
- Fischer, A. A model for the seasonal variations of vegetation indices in coarse resolution data and its inversion to extract crop parameters. Remote Sens. Environ 1994, 48, 220–230. [Google Scholar]
- Fischer, A. A simple model for the temporal variations of NDVI at regional scale over agricultural countries. Validation with ground radiometric measurements. Int. J. Remote Sens 1994, 15, 1421–1446. [Google Scholar]
- Beck, P.S.A.; Atzberger, C.; Høgda, K.A.; Johansen, B.; Skidmore, A.K. Improved monitoring of vegetation dynamics at very high latitudes: A new method using MODIS NDVI. Remote Sens. Environ 2006, 100, 321–334. [Google Scholar]
- Zhang, X.Y.; Friedl, M.A.; Schaaf, C.B.; Strahler, A.H.; Hodges, J.C.F.; Gao, F.; Reed, B.C.; Huete, A. Monitoring vegetation phenology using MODIS. Remote Sens. Environ 2003, 84, 471–475. [Google Scholar]
- Jönsson, P.; Eklundh, L. Seasonality extraction by function fitting to time-series of satellite sensor data. IEEE Trans Geosci. Remote Sens 2002, 40, 1824–1832. [Google Scholar]
- Hermance, J.F.; Jacob, R.W.; Bradley, B.A.; Mustard, J.F. Extracting phenological signals from multiyear AVHRR NDVI time series: Framework for applying high-order annual splines with roughness damping. IEEE Trans. Geosci. Remote Sens 2007, 45, 3264–3276. [Google Scholar]
- Jin, Z.Y.; Xu, B. A novel compound smoother—RMMEH to reconstruct MODIS NDVI time series. IEEE Geosci. Remote Sens.Lett 2013, 10, 942–946. [Google Scholar]
- Li, Z.H. A Study on the Eco-Environment Evolution of Yangtze River Delta Region Based on the Retrieval & Reconstruction of MODIS Time Series Datasets. 2011; p. 36. [Google Scholar]
- Lu, X.L.; Liu, R.G.; Liu, J.Y.; Liang, S.L. Removal of noise by wavelet method to generate high quality temporal data of terrestrial MODIS products. Photogramm. Eng. Remote Sens 2007, 73, 1129–1139. [Google Scholar]
- Gu, J.; Li, X.; Huang, C.L.; Okin, G.S. A simplified data assimilation method for reconstructing time-series MODIS NDVI data. Adv. Space Res 2009, 44, 501–509. [Google Scholar]
- Eilers, P.H.C. A perfect smoother. Anal. Chem 2003, 75, 3631–3636. [Google Scholar]
- Atzberger, C.; Eilers, P.H.C. A time series for monitoring vegetation activity and phenology at 10-daily time steps covering large parts of South America. Int. J. Digit. Earth 2011, 4, 365–386. [Google Scholar]
- Atzberger, C.; Eilers, P.H.C. Evaluating the effectiveness of smoothing algorithms in the absence of ground reference measurements. Int. J. Remote Sens 2011, 32, 3689–3709. [Google Scholar]
- Julien, Y.; Sobrino, J.A. Comparison of cloud-reconstruction methods for time series of composite NDVI data. Remote Sens. Environ 2010, 114, 618–625. [Google Scholar]
- Atkinson, P.M.; Jeganathan, C.; Dash, J.; Atzberger, C. Inter-comparison of four models for smoothing satellite sensor time-series data to estimate vegetation phenology. Remote Sens. Environ 2012, 123, 400–417. [Google Scholar]
- Jönsson, P.; Eklundh, L. TIMESAT—A program for analyzing time-series of satellite sensor data. Comput. Geosci 2004, 30, 833–845. [Google Scholar]
- Julien, Y.; Sobrino, J.A.; Verhoef, W. Changes in land surface temperatures and NDVI values over Europe between 1982 and 1999. Remote Sens. Environ 2006, 103, 43–55. [Google Scholar]
- De Jong, R.; de Bruin, S.; de Wit, A.; Schaepman, M.E.; Dent, D.L. Analysis of monotonic greening and browning trends from global NDVI time-series. Remote Sens. Environ 2011, 115, 692–702. [Google Scholar] [Green Version]
- Ali, A.; de Bie, C.; Skidmore, A.K. Detecting long-duration cloud contamination in hyper-temporal NDVI imagery. Int. J. Appl. Earth Obs. Geoinf 2013, 24, 22–31. [Google Scholar]
- Yuan, H.; Dai, Y.J.; Xiao, Z.Q.; Ji, D.Y.; Wei, S. Reprocessing the MODIS Leaf Area Index products for land surface and climate modelling. Remote Sens. Environ 2011, 115, 1171–1187. [Google Scholar]
- A Software Package to Analyse Time-Series of Satellite Sensor Data. Available online: http://www.nateko.lu.se/timesat/timesat.asp?cat=5 (accessed on 27 February 2014).
- Long Term Vegetation Index Dataset of the Shulehe River Basin—GIMMS. Available online: http://westdc.westgis.ac.cn/data/9e962971-d782-4cbf-a96f-2cda10c3d842 (accessed on 27 February 2014).
- Cold and Arid Regions Science Data Center. Available online: http://westdc.westgis.ac.cn/data/d2338e75-e1f5-4113-a5f1-df1570cf929d (accessed on 27 February 2014).
- VITO Earth Observation. Available online: http://www.spot-vegetation.com/ (accessed on 27 February 2014).
- NASA Land Data Products and Services. Available online: https://lpdaac.usgs.gov/products/modis_products_table/mod13a2 (accessed on 27 February 2014).
- Ma, M.M.; Frank, V. Interannual variability of vegetation cover in the Chinese Heihe River Basin and its relation to meteorological parameters. Int. J. Remote Sens 2006, 27, 3473–3486. [Google Scholar]
- Zhu, G.F.; Su, Y.H.; Feng, Q. The hydrochemical characteristics and evolution of groundwater and surface water in the Heihe River Basin, northwest China. Hydrogeol. J 2008, 16, 167–182. [Google Scholar]
- Pan, X.D.; Li, X.; Shi, X.K.; Han, X.J.; Luo, L.H.; Wang, L.X. Dynamic downscaling of near-surface air temperature at the basin scale using WRF—A case study in the Heihe River Basin, China. Front. Earth Sci 2012, 6, 314–323. [Google Scholar]
- Townshend, J.R. Global data sets for land applications from the Advanced Very High Resolution Radiometer: An introduction. Int. J. Remote Sens 1994, 15, 3319–3332. [Google Scholar]
- Tucker, C.J.; Pinzon, J.; Brown, M.; Slayback, D.A.; Pak, E.W.; Mahoney, R.; Vermote, E.F.; Saleous, N.E. An extended AVHRR 8-km NDVI dataset compatible with MODIS and SPOT vegetation NDVI data. Int. J. Remote Sens 2005, 26, 4485–4498. [Google Scholar]
- James, M.; Kalluri, S.N. The Pathfinder AVHRR land data set: An improved coarse resolution data set for terrestrial monitoring. Int. J. Remote Sens 1994, 15, 3347–3363. [Google Scholar]
- MODIS Vegetation Index (MOD13): Algorithm Theoretical Basis Document, Version 3. Available online: http://modis.gsfc.nasa.gov/data/atbd/atbd_mod13.pdf (accessed on 5 March 2014).
- Maisongrande, P.; Duchemin, B.; Dedieu, G. VEGETATION/SPOT: An operational mission for the Earth monitoring; presentation of new standard products. Int. J. Remote Sens 2004, 25, 9–14. [Google Scholar]
- Hou, X.Y. Editorial Board of Vegetation Map of China, 1st ed; Science Press: Beijing, China, 2001; pp. 1–135. (In Chinese) [Google Scholar]
- Daren Harmel, R.; Smith, P.K. Consideration of measurement uncertainty in the evaluation of goodness-of-fit in hydrologic and water quality modeling. J. Hydrol 2007, 337, 326–336. [Google Scholar]
- Akaike, H. Information Theory and an Extension of the Maximum Likelihood Principle. In Proceedings of the Second International Symposium on Information Theory; Petrov, B.N., Cáski, F., Eds.; Akadémiai Kiadó: Budapest, Hungary, 1973; pp. 267–281. [Google Scholar]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat 1978, 6, 461–464. [Google Scholar]
- Jönsson, P.; Eklundh, L. Seasonality Extraction from Satellite Sensor Data. In Frontiers of Remote Sensing Information Processing; Chen, C.H., Ed.; World Scientific Publishing: Singapore, 2003; pp. 487–500. [Google Scholar]
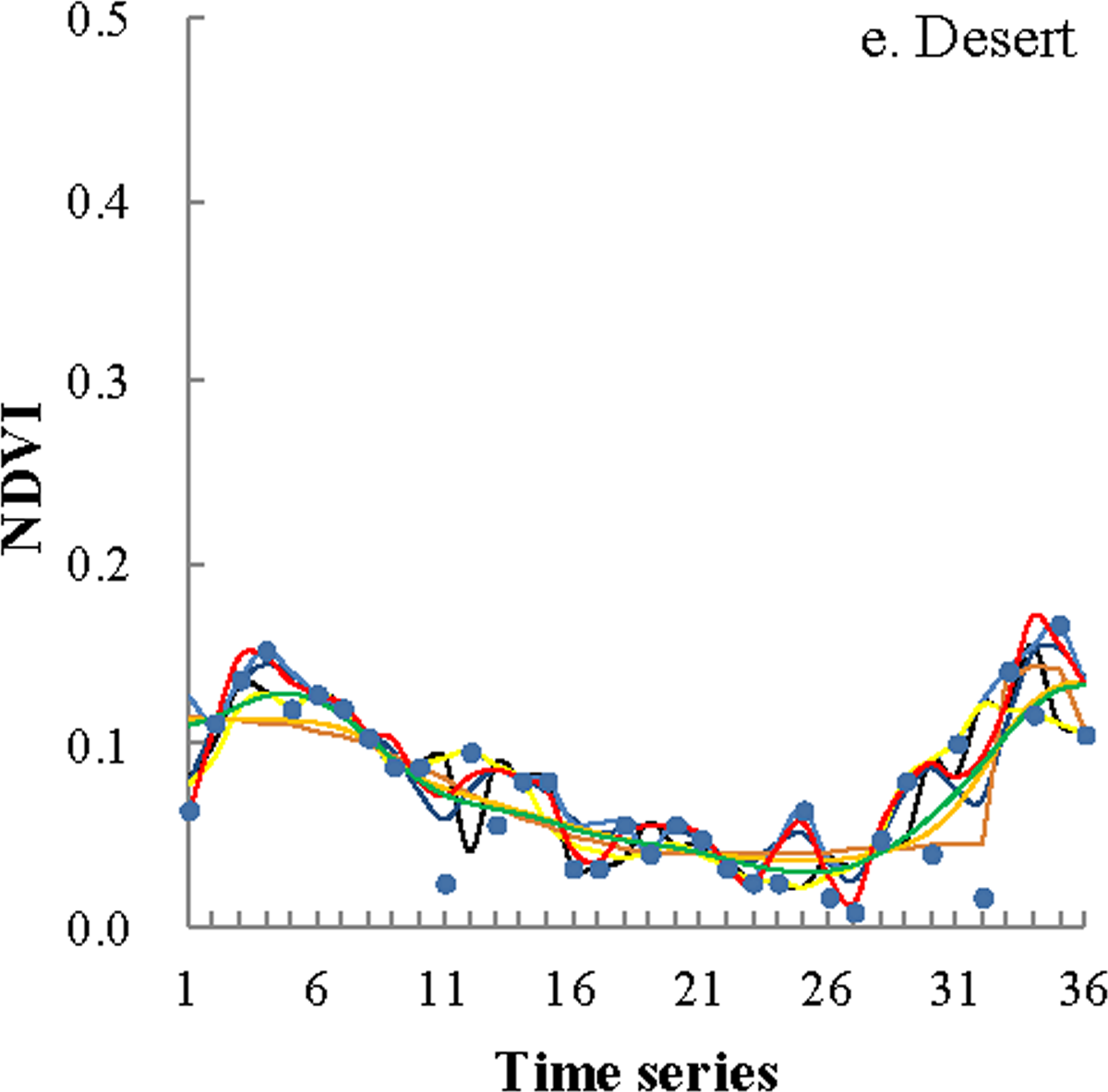
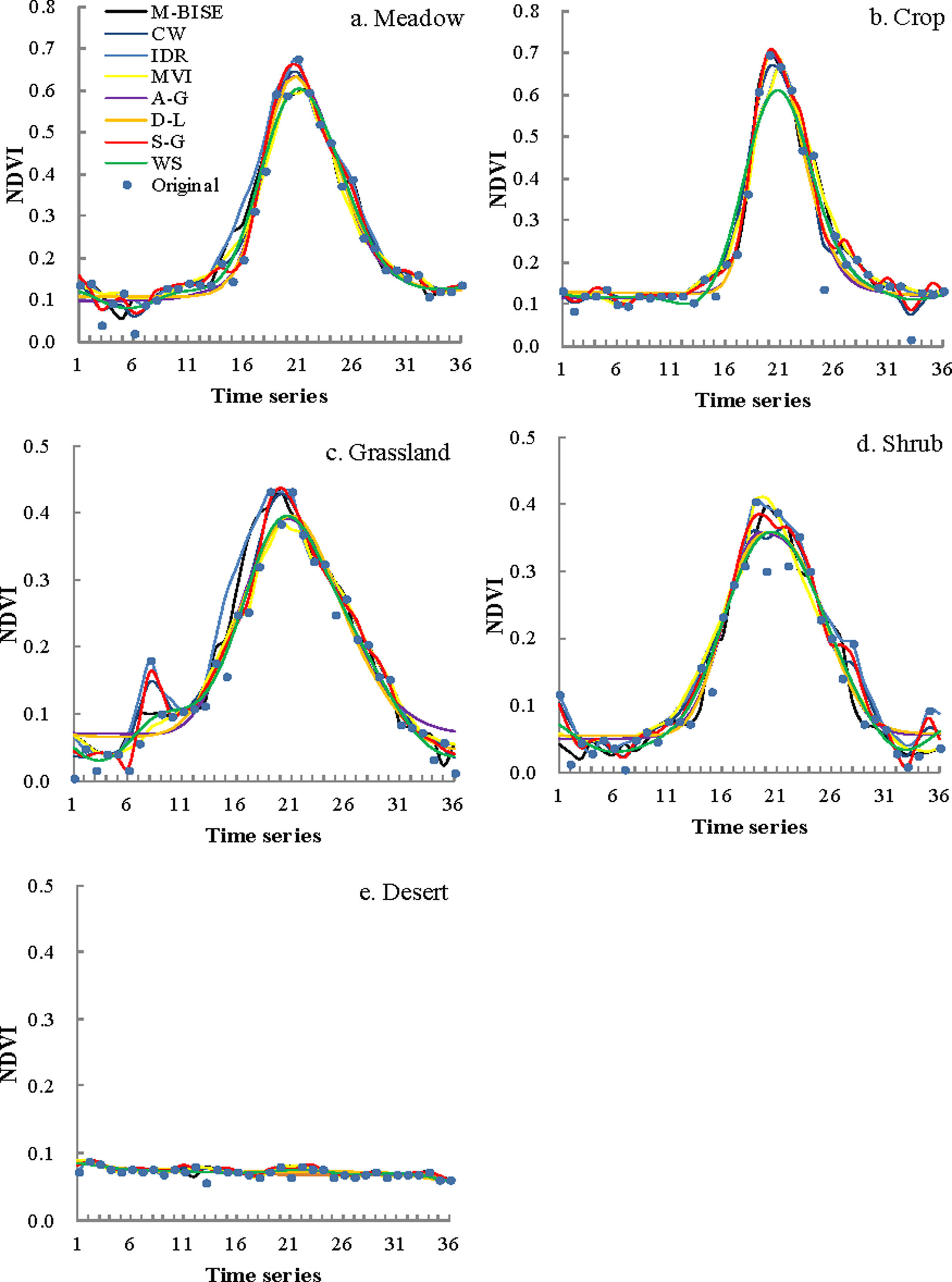
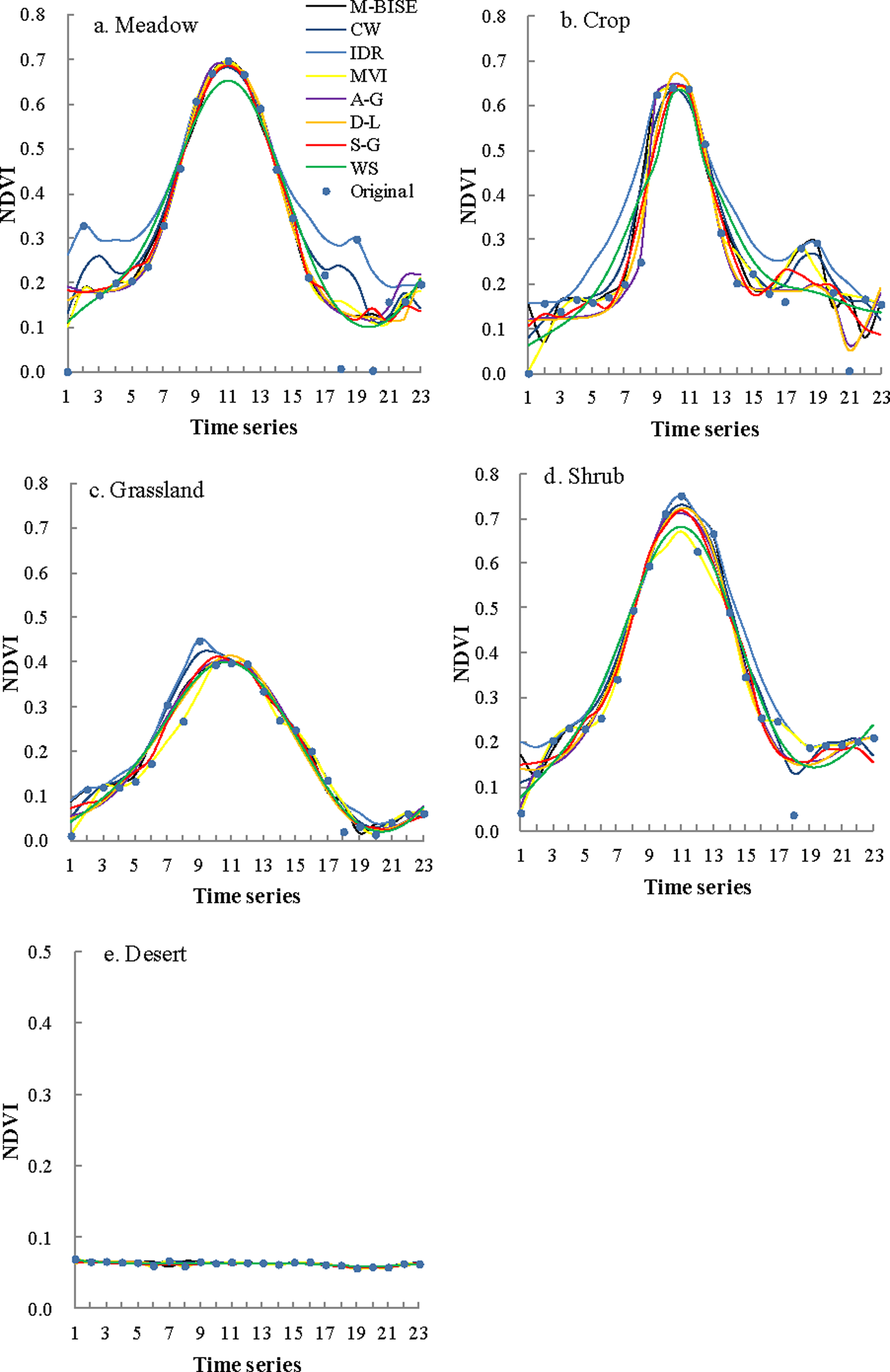
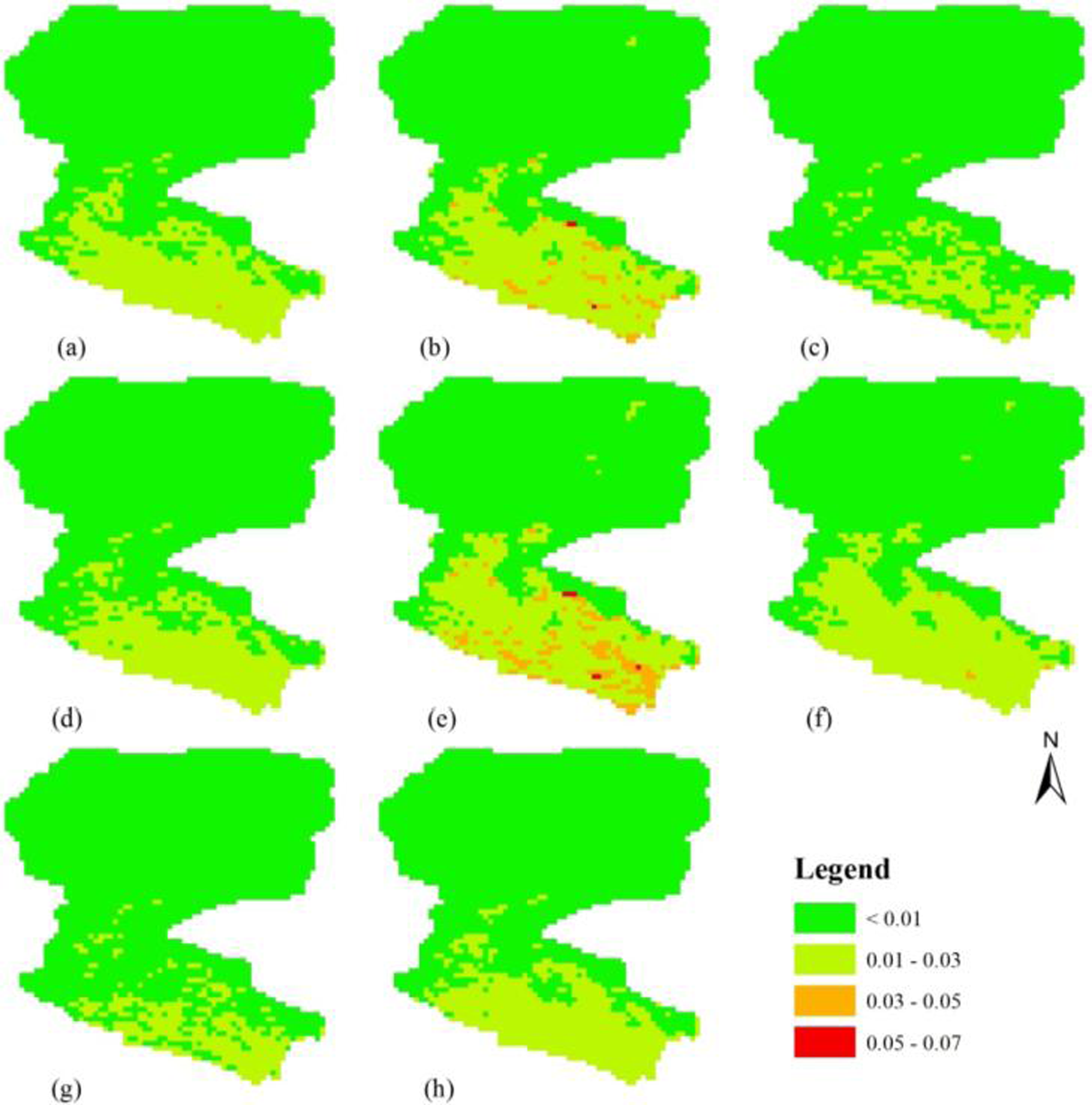

| Products | Time Period | Temporal/Spatial Resolution | Sensors | Data Source |
|---|---|---|---|---|
| GIMMS | January 1982–December 2006 | 15 d/8 km | AVHRR | Cold and Arid Regions Science Data Center [52] |
| Pathfinder | July 1981–July 1994 January 1995–December 2000 | 10 d/8 km | AVHRR | Cold and Arid Regions Science Data Center [53] |
| SPOT VEGETATION (S10) | April 1998–April 2013 | 10 d/1 km | SPOT VGT | VITO Earth observation [54] |
| MOD13A2 | February 2000–February 2013 | 16 d/1 km | Terra/MODIS | The Land Processes Distributed Active Archive Center [55] |
| Candidate Techniques (ab.) | Description | References |
|---|---|---|
| Modified-best index slope extraction (M-BISE) | Compares the current term value with the previous and the next term within a predefined sliding window, and replaces these values with the mean value of the previous and the next values if the percentage difference is greater than a predefined threshold. | [20,21] |
| Asymmetric Gaussian function-fitting (A-G) | Fits local, nonlinear functions at intervals around the local maxima and minima, then merges these into a global function describing the full NDVI time series. | [35] |
| Double logistic function fitting (D-L) | Uses six parameters to model the NDVI time series with a double logistic function. These parameters are the winter NDVI (wNDVI), maximum NDVI (mNDVI), two inflection points, one as the curve rises (S) and one as it drops (A), and the rate of increase or decrease (mS and mA) of the curve at the inflection points. | [33] |
| Savitzky-Golay filtering (S-G) | Based on a simplified least-squares-fit convolution for smoothing and computing derivatives of a set of consecutive values (a spectrum). The convolution can be understood as a weighted moving average filter with weighting given as a polynomial of a certain degree. The weight coefficients, when applied to a signal, perform a polynomial least-squares fit within the filter window. This polynomial is designed to preserve higher moments within the data and to reduce the bias introduced by the filter. | [24] |
| Mean value iteration filtering (MVI) | Iteratively compares each date with the average of the dates before and after it, replacing the date with this average if the difference is above a certain threshold. The maximum difference date value will be removed in an iteration process. Iteration will stop when all differences are less than the threshold. | [25] |
| Whittaker smoother (WS) | Based on penalized least squares, fits a discrete series to discrete data and penalizes the roughness of the smooth curve. In this way, it balances the reliability of the data and roughness of the fitted data. | [41,43,45] |
| Iterative interpolation for data reconstruction (IDR) | Creates an alternative NDVI time series by computing the mean of the immediately preceding and following observations and comparing it to that of the original time series, replacing the original data with the alternative time-series data if the maximum difference between the alternative and original time series is above a certain threshold. | [44] |
| Changing-weight filtering (CW) | Filters an NDVI time series with a three-point changing-weight filter and replaces the local maximum/minimum points in a growth cycle. | [26] |
| Evaluation Indexa | Vegetation Type | Techniqueb | |||||||
|---|---|---|---|---|---|---|---|---|---|
| A-G | M-BISE | CW | D-L | IDR | MVI | S-G | WS | ||
| RMSE | shrub | 0.0071 | 0.0081 | 0.0055 | 0.0067 | 0.0104 | 0.0082 | 0.0055 | 0.0061 |
| crop | 0.0123 | 0.0174 | 0.0093 | 0.0114 | 0.0214 | 0.0153 | 0.0087 | 0.0122 | |
| desert | 0.004 | 0.0045 | 0.0033 | 0.0038 | 0.0058 | 0.0047 | 0.0033 | 0.0031 | |
| grassland | 0.0128 | 0.0166 | 0.009 | 0.0118 | 0.0199 | 0.0152 | 0.0088 | 0.0126 | |
| meadow | 0.0162 | 0.0192 | 0.0101 | 0.0152 | 0.0238 | 0.0175 | 0.0102 | 0.0165 | |
| AIC | shrub | −2330 | −2206 | −2559 | −1421 | −2407 | −2170 | −2564 | −2600 |
| crop | −1549 | −1192 | −1833 | −802 | −1653 | −1262 | −1908 | −1619 | |
| desert | −2889 | −2791 | −3111 | −1968 | −2929 | −2728 | −3080 | −3216 | |
| grassland | −1441 | −1184 | −1851 | −759 | −1545 | −1247 | −1873 | −1493 | |
| meadow | −1161 | −996 | −1711 | −573 | −1241 | −1074 | −1696 | −1161 | |
| BIC | shrub | −6137 | −6040 | −6384 | −6219 | −5717 | −6004 | −6393 | −6429 |
| crop | −5357 | −5026 | −5658 | −5465 | −4780 | −5096 | −5737 | −5448 | |
| desert | −6697 | −6624 | −6936 | −6740 | −6304 | −6562 | −6909 | −7045 | |
| grassland | −5249 | −5018 | −5676 | −5357 | −4800 | −5081 | −5702 | −5322 | |
| meadow | −4968 | −4829 | −5536 | −5053 | −4581 | −4908 | −5525 | −4990 | |
| Evaluation index a | Vegetation type | Technique b | |||||||
|---|---|---|---|---|---|---|---|---|---|
| A-G | M-BISE | CW | D-L | IDR | MVI | S-G | WS | ||
| RMSE | shrub | 0.0143 | 0.019 | 0.0137 | 0.0131 | 0.0251 | 0.0197 | 0.0093 | 0.0103 |
| crop | 0.0198 | 0.027 | 0.0152 | 0.0181 | 0.033 | 0.024 | 0.0119 | 0.0148 | |
| desert | 0.0066 | 0.0099 | 0.0073 | 0.0062 | 0.0139 | 0.0101 | 0.0052 | 0.0048 | |
| grassland | 0.0196 | 0.0269 | 0.0173 | 0.0182 | 0.0334 | 0.0249 | 0.0119 | 0.0149 | |
| meadow | 0.0228 | 0.0277 | 0.0178 | 0.0209 | 0.0331 | 0.026 | 0.0122 | 0.0174 | |
| AIC | shrub | −1528 | −1128 | −1545 | −1656 | −788 | −1087 | −2036 | −2037 |
| crop | −950 | −580 | −1310 | −1075 | −316 | −698 | −1636 | −1377 | |
| desert | −2514 | −2038 | −2393 | −2587 | −1675 | −2053 | −2828 | −3059 | |
| grassland | −985 | −574 | −1147 | −1087 | −289 | −662 | −1648 | −1392 | |
| meadow | −777 | −536 | −1102 | −900 | −309 | −606 | −1605 | −1174 | |
| BIC | shrub | −5962 | −5589 | −5997 | −6094 | −5249 | −5547 | −6492 | −6493 |
| crop | −5383 | −5041 | −5761 | −5513 | −4777 | −5159 | −6092 | −5833 | |
| desert | −6948 | −6499 | −6844 | −7025 | −6136 | −6514 | −7284 | −7515 | |
| grassland | −5419 | −5035 | −5599 | −5525 | −4750 | −5123 | −6104 | −5848 | |
| meadow | −5211 | −4997 | −5554 | −5338 | −4770 | −5067 | −6061 | −5630 | |
| Evaluation Indexes a | Vegetation Types | Technique b | |||||||
|---|---|---|---|---|---|---|---|---|---|
| A-G | M-BISE | CW | D-L | IDR | MVI | S-G | WS | ||
| RMSE | shrub | 0.0111 | 0.0129 | 0.0089 | 0.0111 | 0.0131 | 0.0121 | 0.007 | 0.0078 |
| crop | 0.0133 | 0.0142 | 0.0091 | 0.0135 | 0.0144 | 0.0145 | 0.0084 | 0.0099 | |
| desert | 0.0043 | 0.005 | 0.0039 | 0.004 | 0.0057 | 0.0049 | 0.0033 | 0.003 | |
| grassland | 0.0128 | 0.0146 | 0.0101 | 0.0125 | 0.0147 | 0.0144 | 0.0083 | 0.0084 | |
| meadow | 0.014 | 0.0157 | 0.0108 | 0.0138 | 0.0159 | 0.0146 | 0.0086 | 0.0095 | |
| AIC | shrub | −1716 | −1563 | −1897 | −1745 | −1518 | −1605 | −2136 | −2121 |
| crop | −1369 | −1271 | −1719 | −1354 | −1270 | −1248 | −1830 | −1698 | |
| desert | −2504 | −2361 | −2607 | −2590 | −2211 | −2377 | −2801 | −2922 | |
| grassland | −1376 | −1238 | −1605 | −1408 | −1235 | −1253 | −1828 | −1839 | |
| meadow | −1292 | −1165 | −1541 | −1321 | −1144 | −1229 | −1795 | −1725 | |
| BIC | shrub | −5083 | −4957 | −5281 | −5116 | −4911 | −4998 | −5525 | −5510 |
| crop | −4737 | −4664 | −5103 | −4725 | −4663 | −4641 | −5219 | −5087 | |
| desert | −5871 | −5754 | −5992 | −5962 | −5604 | −5770 | −6190 | −6310 | |
| grassland | −4744 | −4631 | −4989 | −4779 | −4628 | −4646 | −5217 | −5228 | |
| meadow | −4659 | −4558 | −4926 | −4692 | −4537 | −4622 | −5184 | −5113 | |
| Evaluation Index a | Vegetation Type | Technique b | |||||||
|---|---|---|---|---|---|---|---|---|---|
| A-G | M-BISE | CW | D-L | IDR | MVI | S-G | WS | ||
| RMSE | shrub | 0.0138 | 0.0143 | 0.0119 | 0.0141 | 0.019 | 0.016 | 0.0089 | 0.0122 |
| crop | 0.0182 | 0.0217 | 0.0182 | 0.0194 | 0.0294 | 0.0243 | 0.0125 | 0.0181 | |
| desert | 0.0043 | 0.0041 | 0.0032 | 0.0035 | 0.0044 | 0.0041 | 0.0028 | 0.0028 | |
| grassland | 0.0142 | 0.0181 | 0.0147 | 0.0147 | 0.0219 | 0.0195 | 0.0103 | 0.0136 | |
| meadow | 0.017 | 0.0175 | 0.0142 | 0.0169 | 0.0234 | 0.02 | 0.011 | 0.0156 | |
| AIC | shrub | −1454 | −1466 | −1600 | −1538 | −1394 | −1455 | −1687 | −1654 |
| crop | −1648 | −1730 | −1884 | −1786 | −1694 | −1737 | −1923 | −1950 | |
| desert | −1301 | −1309 | −1460 | −1385 | −1241 | −1293 | −1558 | −1507 | |
| grassland | −1701 | −1758 | −1903 | −1824 | −1715 | −1764 | −1950 | −1982 | |
| meadow | −1701 | −1769 | −1910 | −1826 | −1722 | −1773 | −1952 | −1978 | |
| BIC | shrub | −2365 | −2221 | −2255 | −2326 | −2202 | −2270 | −2406 | −2283 |
| crop | −2095 | −1990 | −1994 | −2070 | −1885 | −2072 | −2254 | −1999 | |
| desert | −3091 | −2755 | −2804 | −3008 | −2801 | −2779 | −2861 | −2941 | |
| grassland | −2107 | −2016 | −2047 | −2096 | −1969 | −2072 | −2218 | −2061 | |
| meadow | −2111 | −1939 | −1943 | −2085 | −1873 | −1972 | −2095 | −2020 | |
| Data Source | Vegetation Type | The Eight Techniques in Order of Fit a | |||||||
|---|---|---|---|---|---|---|---|---|---|
| GIMMS NDVI | shrub | WS | S-G | CW | D-L | A-G | M-BISE | MVI | IDR |
| Crop | S-G | CW | D-L | WS | A-G | MVI | M-BISE | IDR | |
| desert | WS | CW | S-G | D-L | A-G | M-BISE | MVI | IDR | |
| grassland | S-G | CW | D-L | WS | A-G | MVI | M-BISE | IDR | |
| meadow | CW | S-G | D-L | WS | A-G | MVI | M-BISE | IDR | |
| PAL NDVI | shrub | WS | S-G | D-L | CW | A-G | M-BISE | MVI | IDR |
| Crop | S-G | WS | CW | D-L | A-G | MVI | M-BISE | IDR | |
| desert | WS | S-G | D-L | A-G | CW | MVI | M-BISE | IDR | |
| grassland | S-G | WS | CW | D-L | A-G | MVI | M-BISE | IDR | |
| meadow | S-G | WS | CW | D-L | A-G | MVI | M-BISE | IDR | |
| SPOT VGT NDVI | shrub | S-G | WS | CW | D-L | A-G | MVI | M-BISE | IDR |
| Crop | S-G | CW | WS | A-G | D-L | M-BISE | IDR | MVI | |
| desert | WS | S-G | CW | D-L | A-G | MVI | M-BISE | IDR | |
| grassland | WS | S-G | CW | D-L | A-G | MVI | M-BISE | IDR | |
| meadow | S-G | WS | CW | D-L | A-G | MVI | M-BISE | IDR | |
| MODIS NDVI | shrub | S-G | WS | CW | A-G | D-L | M-BISE | MVI | IDR |
| Crop | S-G | WS | CW | A-G | D-L | M-BISE | MVI | IDR | |
| desert | WS | S-G | CW | D-L | A-G | M-BISE | MVI | IDR | |
| grassland | S-G | WS | A-G | CW | D-L | M-BISE | MVI | IDR | |
| meadow | S-G | CW | WS | D-L | A-G | M-BISE | MVI | IDR | |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Geng, L.; Ma, M.; Wang, X.; Yu, W.; Jia, S.; Wang, H. Comparison of Eight Techniques for Reconstructing Multi-Satellite Sensor Time-Series NDVI Data Sets in the Heihe River Basin, China. Remote Sens. 2014, 6, 2024-2049. https://doi.org/10.3390/rs6032024
Geng L, Ma M, Wang X, Yu W, Jia S, Wang H. Comparison of Eight Techniques for Reconstructing Multi-Satellite Sensor Time-Series NDVI Data Sets in the Heihe River Basin, China. Remote Sensing. 2014; 6(3):2024-2049. https://doi.org/10.3390/rs6032024
Chicago/Turabian StyleGeng, Liying, Mingguo Ma, Xufeng Wang, Wenping Yu, Shuzhen Jia, and Haibo Wang. 2014. "Comparison of Eight Techniques for Reconstructing Multi-Satellite Sensor Time-Series NDVI Data Sets in the Heihe River Basin, China" Remote Sensing 6, no. 3: 2024-2049. https://doi.org/10.3390/rs6032024








