Vicarious Radiometric Calibration of a Multispectral Camera on Board an Unmanned Aerial System
Abstract
:1. Introduction
2. Materials
2.1. Instruments
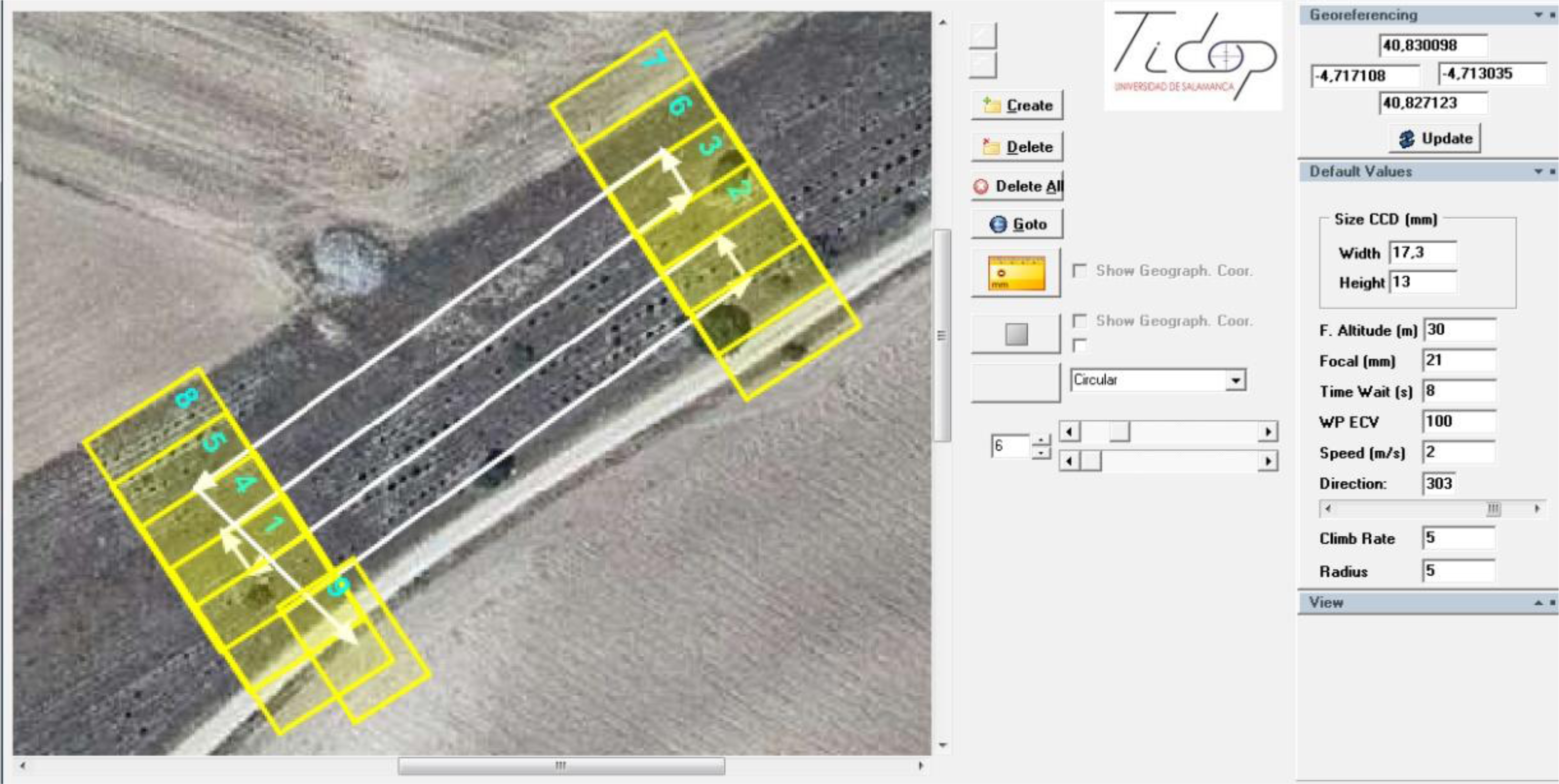
2.2. Flight Planning
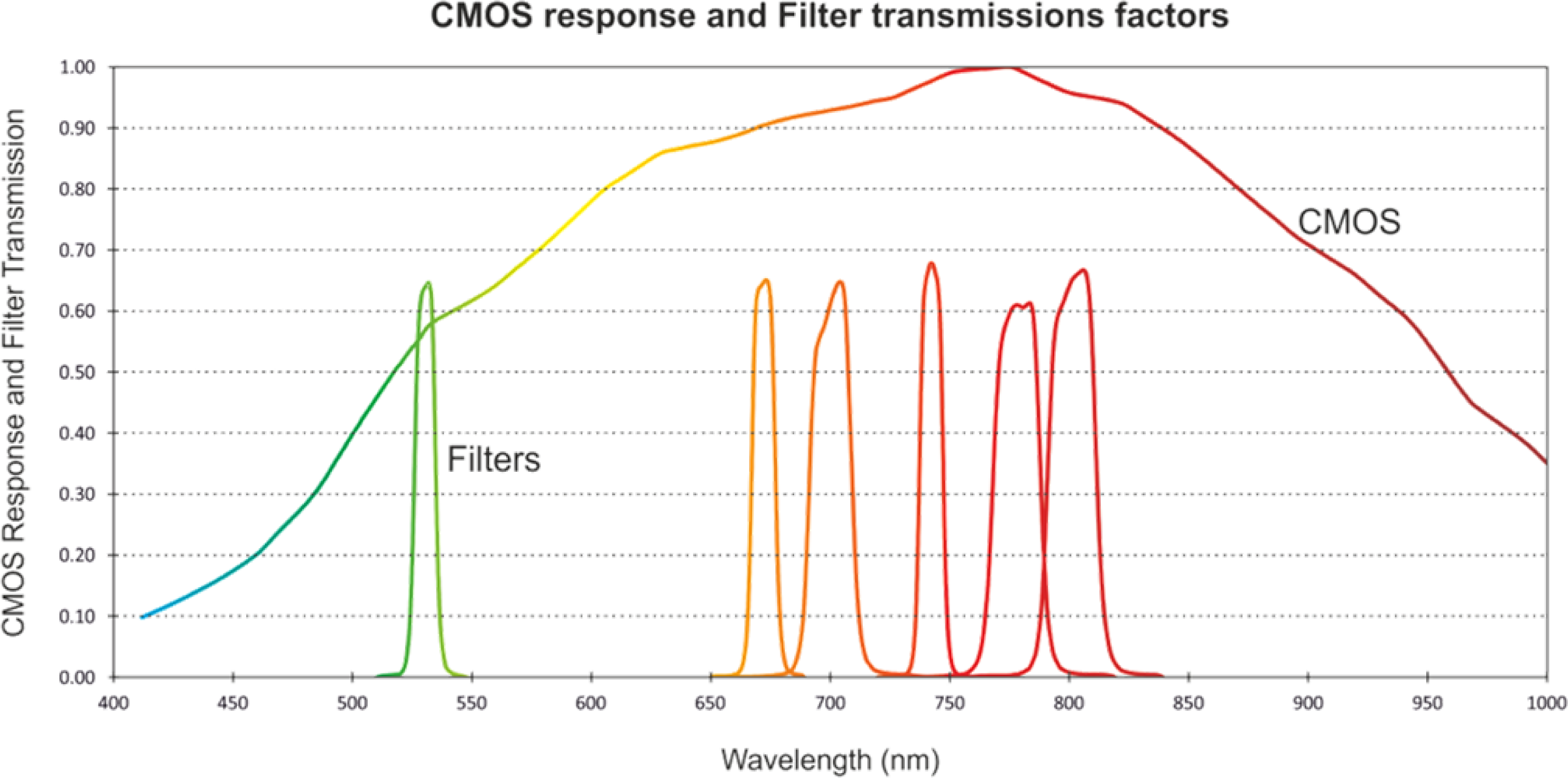
3. Multispectral Camera Correction
3.1. Background Error Correction
3.2. Vignetting
3.3. Geometric Distortion
4. Radiometric Calibration
4.1. Calibration Method
- Laboratory calibration before the flight (preflight calibration). This procedure involves a rigorous calibration of sensors.
- Satellite or airborne calibration (onboard calibration), implementing checks during image acquisition. Lamps or solar-diffuser panels are used in this kind of calibration.
- Calibration through in situ measurement campaigns (vicarious calibration). This entails an absolute radiometric calibration in flight conditions other than those found in the laboratory. Within this modality, the absolute method based on radiance or reflectance is included.
4.2. Fitting Model
- Standard deviation estimator < 0.001;
- Change in variance < 0.01;
- When there are more than 20 iterations.
5. Experimental Results
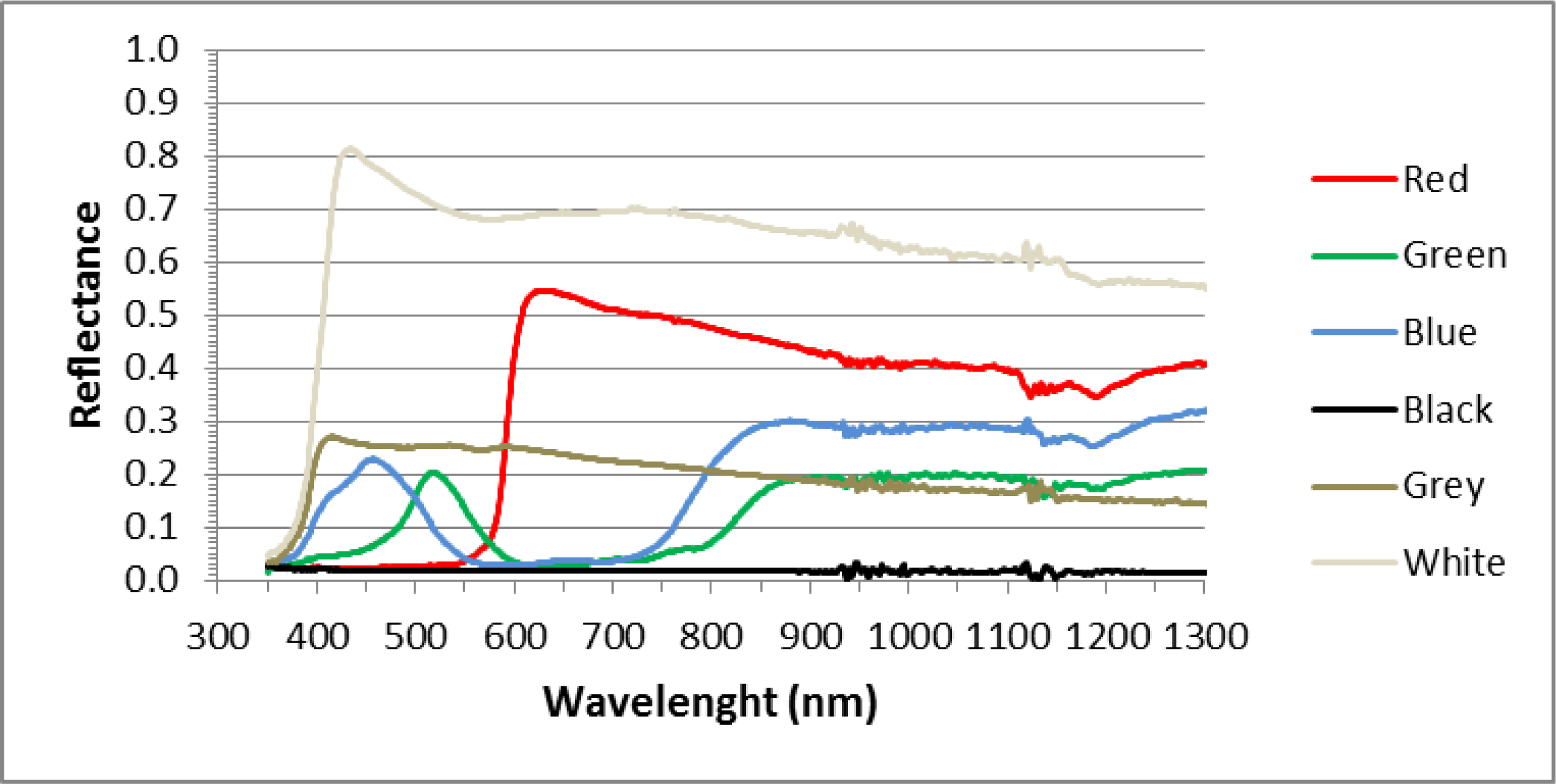
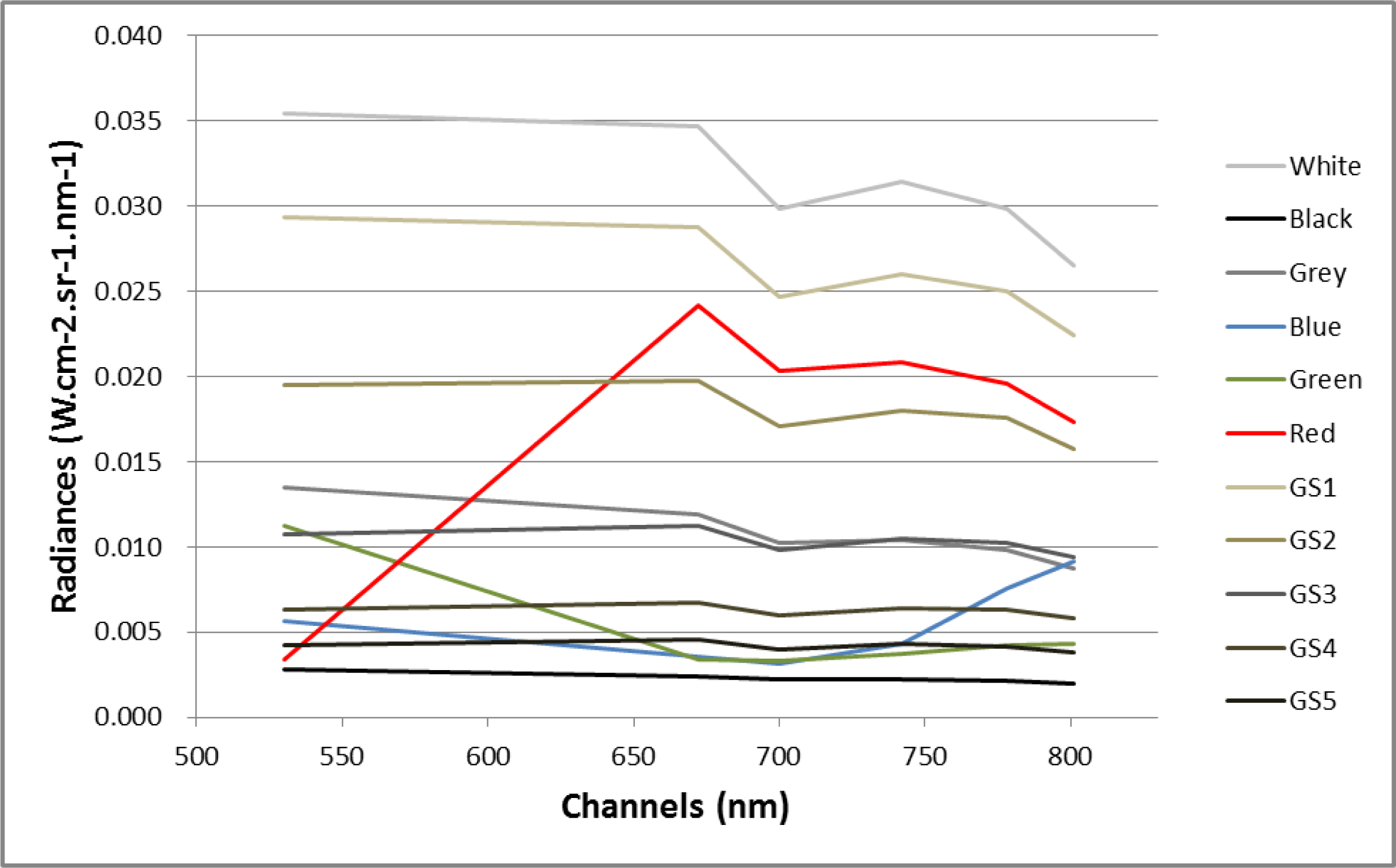
5.1. Radiometric Campaign
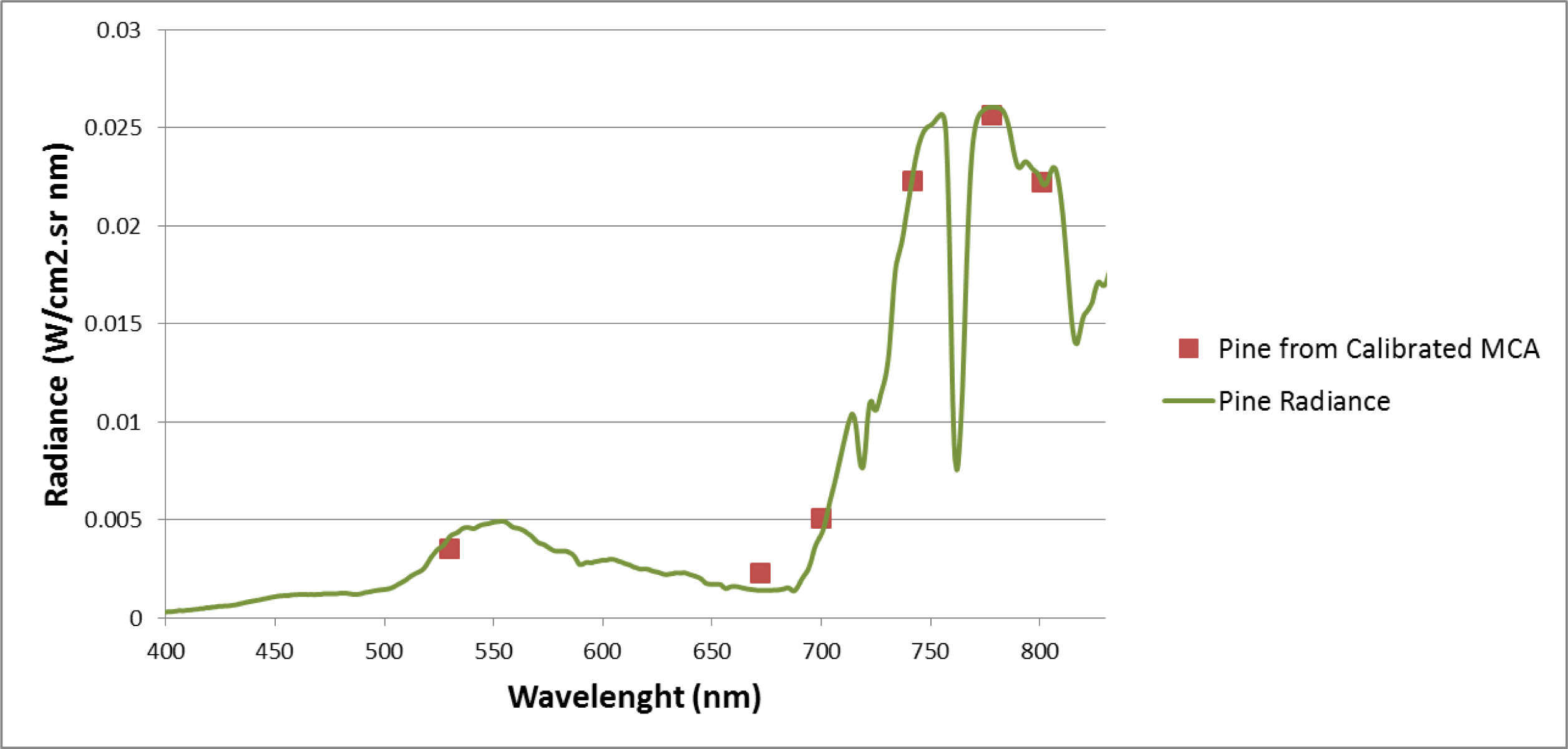
5.2. Analysis and Validation of Results
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Herwitz, S.R.; Dunagan, S.; Sullivan, D.; Higgins, R.; Johnson, L.; Jian, Z.; Slye, R.; Brass, J.; Leung, J.; Gallmeyer, B.; et al. Solar-Powered UAV Mission for Agricultural Decision Support. Proceedings of the 2003 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Worcester, MA, USA, 21–25 July 2003; pp. 1692–1694.
- Herwitz, S.R.; Johnson, L.F.; Dunagan, S.E.; Higgins, R.G.; Sullivan, D.V.; Zheng, J.; Lobitz, B.M.; Leung, J.G.; Gallmeyer, B.A.; Aoyagi, M.; et al. Imaging from an unmanned aerial vehicle: Agricultural surveillance and decision support. Comput. Electron. Agric 2004, 44, 49–61. [Google Scholar]
- Johnson, L.; Herwitz, S.; Dunagan, S.; Lobitz, B.; Sullivan, D.; Slye, R. Collection of Ultra High Spatial and Spectral Resolution Image Data over California Vineyards with a Small UAV. Proceedings of the 30th International Symposium on Remote Sensing of Environment, Honolulu, HI, USA, 10–14 November 2003.
- Dunford, R.; Michel, K.; Gagnage, M.; Piégay, H.; Trémelo, M.L. Potential and constraints of Unmanned Aerial Vehicle technology for the characterization of Mediterranean riparian forest. Int. J. Remote Sens 2009, 30, 4915–4935. [Google Scholar]
- Scaioni, M.; Barazzetti, L.; Brumana, R.; Cuca, B.; Fassi, F.; Prandi, F. RC-Heli and Structure & Motion Techniques for the 3-D Reconstruction of a Milan Dome Spire. Proceedings of the 3rd ISPRS International Workshop 3D-ARCH, Trento, Italy, 25–28 February 2009.
- Hunt, E.R.; Hively, W.D.; Fujikawa, S.; Linden, D.; Daughtry, C.S.; McCarty, G. Acquisition of NIR-Green-Blue digital photographs from unmanned aircraft for crop monitoring. Remote Sens 2010, 2, 290–305. [Google Scholar]
- Berni, J.; Zarco-Tejada, P.J.; Suarez, L.; Fereres, E. Thermal and narrowband multispectral remote sensing for vegetation monitoring from an unmanned aerial vehicle. IEEE Trans. Geosci. Remote Sens 2009, 47, 722–738. [Google Scholar]
- Laliberte, A.S.; Rango, A.; Herrick, J.E.; Fredrickson, E.L.; Burkett, L. An object-based image analysis approach for determining fractional cover of senescent and green vegetation with digital plot photography. J. Arid Environ 2007, 69, 1–14. [Google Scholar]
- Everaerts, J. The Use of Unmanned Aerial Vehicles (UAVs) for Remote Sensing and Mapping. Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Beijing, China, 5–7 July 2008; pp. 1187–1192.
- Pastor, E.; Lopez, J.; Royo, P. UAV payload and mission control hardware/software architecture. IEEE Aerosp. Electron. Syst. Mag 2007, 22, 3–8. [Google Scholar]
- Zhao, H.; Lei, Y.; Gou, Z.; Zhang, L. The Characteristic Analyses of Images from the UAV Remote Sensing System. Proceedings of the 2006 IEEE International Conference on Geoscience and Remote Sensing Symposium (IGARSS), Denver, CO, USA, 31 July–4 August 2006; pp. 3349–3351.
- Esposito, F.; Rufino, G.; Moccia, A. 1st Mini-UAV Integrated Hyperspectral/Thermal Electro-Optical Payload for Forest Fire Risk Management. Proceedings of the AIAA InfotechAerosp Conference, Rohnert Park, CA, USA, 7–10 May 2007; pp. 653–665.
- Lambers, K.; Eisenbeiss, H.; Sauerbier, M.; Kupferschmidt, D.; Gaisecker, T.; Sotoodeh, S.; Hanusch, T. Combining photogrammetry and laser scanning for the recording and modelling of the Late Intermediate Period site of Pinchango Alto, Palpa, Peru. J. Archaeol. Sci 2007, 34, 1702–1712. [Google Scholar]
- Nebiker, S.; Annen, A.; Scherrer, M.; Oesch, D. A. Light-Weight Multispectral Sensor for Micro UAV—Opportunities for Very High Resolution Airborne Remote Sensing. Proceedings of the XXIst ISPRS Congress, Beijing, China, 3–11 July 2008; pp. 1193–2000.
- Xiang, H.; Tian, L. Development of a low-cost agricultural remote sensing system based on an autonomous unmanned aerial vehicle (UAV). Biosyst. Eng 2011, 108, 174–190. [Google Scholar]
- Turner, D.; Lucieer, A.; Watson, C. Development of an Unmanned Aerial Vehicle (UAV) for Hyper Resolution Vineyard Mapping Based on Visible, Multispectral, and Thermal Imagery. Proceedings of the 34th International Symposium on Remote Sensing of Environment, Hobart, Australia, 28–29 June 2011.
- Biggar, S.F.; Thome, K.J.; Wisniewski, W. Vicarious radiometric calibration of EO-1 sensors by reference to high-reflectance ground targets. IEEE Trans. Geosci. Remote Sens 2003, 41, 1174–1179. [Google Scholar]
- Hernández López, D.; Felipe García, B.; González Piqueras, J.; Alcázar, G.V. An approach to the radiometric aerotriangulation of photogrammetric images. ISPRS J. Photogramm. Remote Sens 2011, 66, 883–893. [Google Scholar]
- Moran, M.S.; Bryant, R.; Thome, K.; Ni, W.; Nouvellon, Y.; Gonzalez-Dugo, M.P.; Qi, J.; Clarke, T.R. A refined empirical line approach for reflectance factor retrieval from Landsat-5 TM and Landsat-7 ETM+. Remote Sens. Environ 2001, 78, 71–82. [Google Scholar]
- Chuvieco, E.; Huete, A. Fundamentals of Satellite Remote Sensing; CRC Press Inc: Boca Raton, FL, USA, 2009. [Google Scholar]
- Honkavaara, E.; Arbiol, R.; Markelin, L.; Martinez, L.; Cramer, M.; Bovet, S.; Chandelier, L.; Ilves, R.; Klonus, S.; Marshal, P.; et al. Digital airborne photogrammetry—A new tool for quantitative remote sensing?—A state-of-the-art review on radiometric aspects of digital photogrammetric images. Remote Sens 2009, 1, 577–605. [Google Scholar]
- Hefele, J. Calibration Expierence with the DMC. Proceedings of the International Calibration and Orientation Workshop EuroCOW 2006, Castelldefels, Spain, 25–27 January 2006.
- Tetracam Inc. Digital Camera and Imaging Systems Design—Mini Multiple Camera Array. Available online: http://www.tetracam.com/Products-Mini_MCA.htm (accessed on 6 December 2013).
- HiSystems GmbH. Mikrokopter. Available online: http://www.mikrokopter.com/en/home (accessed on 6 December 2013).
- Fernández-Hernandez, J.; González-Aguilera, D.; Rodríguez-Gonzálvez, P.; Mancera-Taboada, J. A new trend for reverse engineering: Robotized aerial system for spatial information management. Appl. Mech. Mater 2012, 152, 1785–1790. [Google Scholar]
- Li, F.; Barabas, J.; Mohan, A.; Raskar, R. Analysis on Errors Due to Photon Noise and Quantization Process with Multiple Images. Proceedings of the 44th Annual Conference on Information Sciences and Systems (CISS), Princeton, NJ, USA, 17–19 March 2010; pp. 1–6.
- Kelcey, J.; Lucieer, A. Sensor correction of a 6-band multispectral imaging sensor for UAV remote sensing. Remote Sens 2012, 4, 1462–1493. [Google Scholar]
- Zheng, Y.; Lin, S.; Kambhamettu, C.; Yu, J.; Kang, S.B. Single-image vignetting correction. IEEE Trans. Pattern Anal. Mach. Intell 2009, 31, 2243–2256. [Google Scholar]
- Bouguet, J.-Y. Camera Calibration Toolbox for Matlab. Available online: http://www.vision.caltech.edu/bouguetj/calib_doc/ (accessed on 6 December 2013).
- Light, D.L. The new camera calibration system at the US Geological Survey. Photogramm. Eng. Remote Sens 1992, 58, 185–188. [Google Scholar]
- Gonzalez-Aguilera, D.; Gomez-Lahoz, J.; Rodriguez-Gonzalvez, P. An Automatic approach for Radial Lens distortion correction from a single image. IEEE Sens. J 2011, 11, 956–965. [Google Scholar]
- Kraus, K.; Jansa, J.; Kager, H. Advanced Methods and Applications; Dümmler: Bonn, Germany, 1997. [Google Scholar]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Dinguirard, M.; Slater, P.N. Calibration of space-multispectral imaging sensors: A review. Remote Sens. Environ 1999, 68, 194–205. [Google Scholar]
- Biggar, S.F.; Slater, P.N.; Gellman, D.I. Uncertainties in the in-flight calibration of sensors with reference to measured ground sites in the 0.4–1.1 μm range. Remote Sens. Environ 1994, 48, 245–252. [Google Scholar]
- Hiscocks, P.D.; Eng, P. Measuring Luminance with a Digital Camera. Available online: http://www.ee.ryerson.ca/∼phiscock/astronomy/light-pollution/luminance-notes.pdf (accessed on 6 February 2014).
- Moran, M.S.; Bryant, R.B.; Clarke, T.R.; Qi, J. Deployment and calibration of reference reflectance tarps for use with airborne imaging sensors. Photogramm. Eng. Remote Sens 2001, 67, 273–286. [Google Scholar]
- Pagnutti, M.; Holekamp, K.; Ryan, R.; Blonski, S.; Sellers, R.; Davis, B.; Zanoni, V. Measurement Sets and Sites Commonly Used for Characterizations. Proceedings of the Integrated Remote Sensing at the Global, Regional and Local Scale Denver, Denver, CO, USA, 10–15 November 2002; pp. 159–164.
- Moran, M.; Clarke, T.; Qi, J.; Barnes, E.; Pinter, P.J., Jr. Practical Techniques for Conversion of Airborne Imagery to Reflectances. Proceedings of the 16th Biennial Workshop on Color Photography and Videography in Resource Assessment, Weslaco, TX, USA, 29 April–1 May 1997; pp. 82–95.
- Davranche, A.; Lefebvre, G.; Poulin, B. Radiometric normalization of SPOT-5 scenes: 6S atmospheric model versus pseudo-invariant features. Photogramm. Eng. Remote Sens 2009, 75, 723–728. [Google Scholar]
- Vermote, E.F.; Tanre, D.; Deuze, J.L.; Herman, M.; Morcette, J.J. Second simulation of the satellite signal in the solar spectrum, 6S: An overview. IEEE Trans. Geosci. Remote Sens 1997, 35, 675–686. [Google Scholar]
- Hernández-López, D.; Felipe-García, B.; Sánchez, N.; González-Aguilera, D.; Gomez-Lahoz, J. Testing the radiometric performance of digital photogrammetric images: Vicarious versus laboratory CALIBRATION on the Leica ADS40, a study in Spain. Photogramm. Fernerkund. Geoinf 2012, 2012, 557–571. [Google Scholar]
- Triggs, B.; McLauchlan, P.F.; Hartley, R.I.; Fitzgibbon, A.W. Bundle Adjustment—A Modern Synthesis. In Vision Algorithms: Theory and Practice; Springer: Berlin, Germany, 2000; pp. 298–372. [Google Scholar]
- Krarup, T.; Juhl, J.; Kubik, K. Götterdammerung over Least Squares Adjustment. Proceedings of the XIV Congress of International Society of Photogrammetry, Hamburg, Germany, 13–25 July, 1980; pp. 369–378.
- Honkavaara, E.; Peltoniemi, J.; Ahokas, E.; Kuittinen, R.; Hyyppa, J.; Jaakkola, J.; Kaartinen, H.; Markelin, L.; Nurminen, K.; Suomalainen, J. A permanent test field for digital photogrammetric systems. Photogramm. Eng. Remote Sens 2008, 74, 95–106. [Google Scholar]








| Parameter | Value |
|---|---|
| Number of channels | 6 |
| Weight | 700 g |
| Geometric resolution | 1280 × 1024 |
| Radiometric resolution | 10 bits |
| Speed | 1.3 frames/s |
| Pixel size | 5.2 μm |
| Focal length | 9.6 mm |
| Channel | λmin (nm) | λmax (nm) | Band Width (nm) | Exposure Time (%) |
|---|---|---|---|---|
| 0 | 740 | 820 | 80 | 100 |
| 1 | 510 | 550 | 40 | 130 |
| 2 | 650 | 690 | 40 | 125 |
| 3 | 660 | 740 | 80 | 100 |
| 4 | 720 | 760 | 40 | 100 |
| 5 | 760 | 840 | 80 | 100 |
| Parameter | Value |
|---|---|
| Weight without batteries | 1880 g |
| Battery weight (5000 mAh-14.8 V) | 540 g |
| Multispectral camera weight | 1025 g |
| Full system weight | 3445 g |
| Maximum range transmission | 1000 m |
| Recommended range transmission | 750 m |
| Estimated flight time | 12 min |
| Maximum horizontal speed | 4 km/h |
| Channel | Balanced Principal Distance (mm) | Radial Distortion | Tangential Distortion | |||
|---|---|---|---|---|---|---|
| a0 | a1 | a2 | P1 | P2 | ||
| 778 nm | 9.971 | 0.01508 | −0.00234 | 6.16E–05 | 1.45E–04 | −2.74E–04 |
| 530 nm | 9.849 | 0.01560 | −0.00231 | 5.01E–05 | 2:06E–05 | −1.31E–04 |
| 672 nm | 9.961 | 0.01556 | −0.00177 | −1.55E–05 | 1.57E–04 | −4.82E–04 |
| 700 nm | 9.945 | 0.01464 | −0.00206 | 3.35E–05 | 3:20E–04 | −2.44E–04 |
| 742 nm | 9.974 | 0.01817 | −0.00184 | −4.55E–05 | 5.41E–05 | −1.79E–04 |
| 801 nm | 9.955 | 0.01648 | −0.00178 | −2.85E–05 | −1.02E–05 | −1.37E–04 |
| Channel | Block Adjustment | Individual Channel Adjustment | ||||
|---|---|---|---|---|---|---|
| C0 | C1 | R2 | C0 | C1 | R2 | |
| 778 nm | −0.000992 | 0.047175 | 0.9833 | −0.001510 | 0.047292 | 0.9846 |
| 530 nm | 0.000704 | 0.057802 | 0.000264 | 0.057718 | 0.9816 | |
| 672 nm | −0.000307 | 0.049919 | −0.000795 | 0.050005 | 0.9823 | |
| 700 nm | −0.000345 | 0.041242 | −0.000861 | 0.041353 | 0.9820 | |
| 742 nm | −0.000688 | 0.074146 | −0.001205 | 0.074335 | 0.9843 | |
| 801 nm | −0.000319 | 0.047655 | −0.000834 | 0.047656 | 0.9827 | |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Del Pozo, S.; Rodríguez-Gonzálvez, P.; Hernández-López, D.; Felipe-García, B. Vicarious Radiometric Calibration of a Multispectral Camera on Board an Unmanned Aerial System. Remote Sens. 2014, 6, 1918-1937. https://doi.org/10.3390/rs6031918
Del Pozo S, Rodríguez-Gonzálvez P, Hernández-López D, Felipe-García B. Vicarious Radiometric Calibration of a Multispectral Camera on Board an Unmanned Aerial System. Remote Sensing. 2014; 6(3):1918-1937. https://doi.org/10.3390/rs6031918
Chicago/Turabian StyleDel Pozo, Susana, Pablo Rodríguez-Gonzálvez, David Hernández-López, and Beatriz Felipe-García. 2014. "Vicarious Radiometric Calibration of a Multispectral Camera on Board an Unmanned Aerial System" Remote Sensing 6, no. 3: 1918-1937. https://doi.org/10.3390/rs6031918
APA StyleDel Pozo, S., Rodríguez-Gonzálvez, P., Hernández-López, D., & Felipe-García, B. (2014). Vicarious Radiometric Calibration of a Multispectral Camera on Board an Unmanned Aerial System. Remote Sensing, 6(3), 1918-1937. https://doi.org/10.3390/rs6031918







