Intercomparison of Seven NDVI Products over the United States and Mexico
Abstract
:1. Introduction
2. Data and Methods
2.1. Satellite Sensors
2.2. NDVI Datasets
2.3. NDVI Preprocessing
2.4. Definition of Phenology
2.5. Analysis Methodology
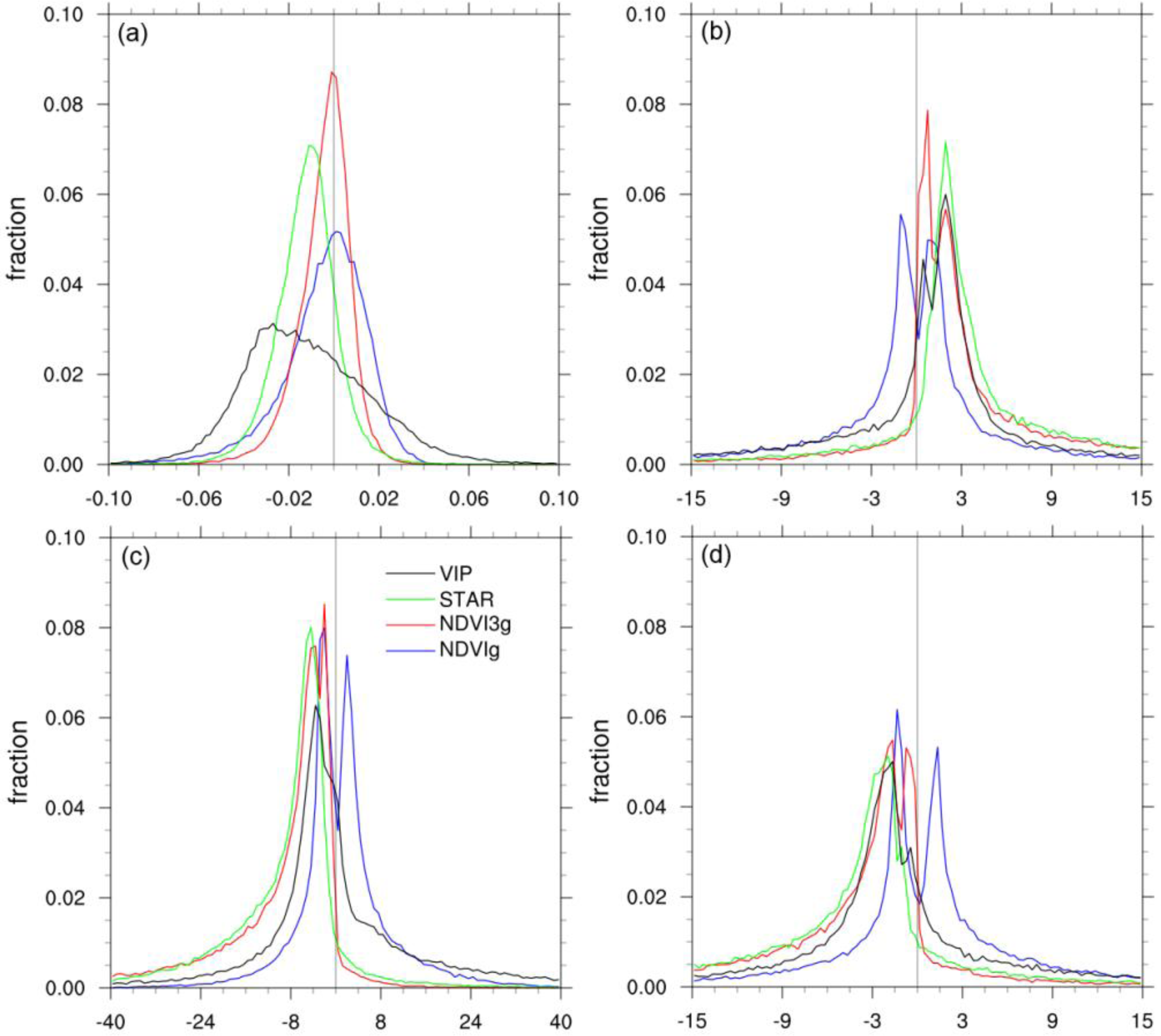
3. Results
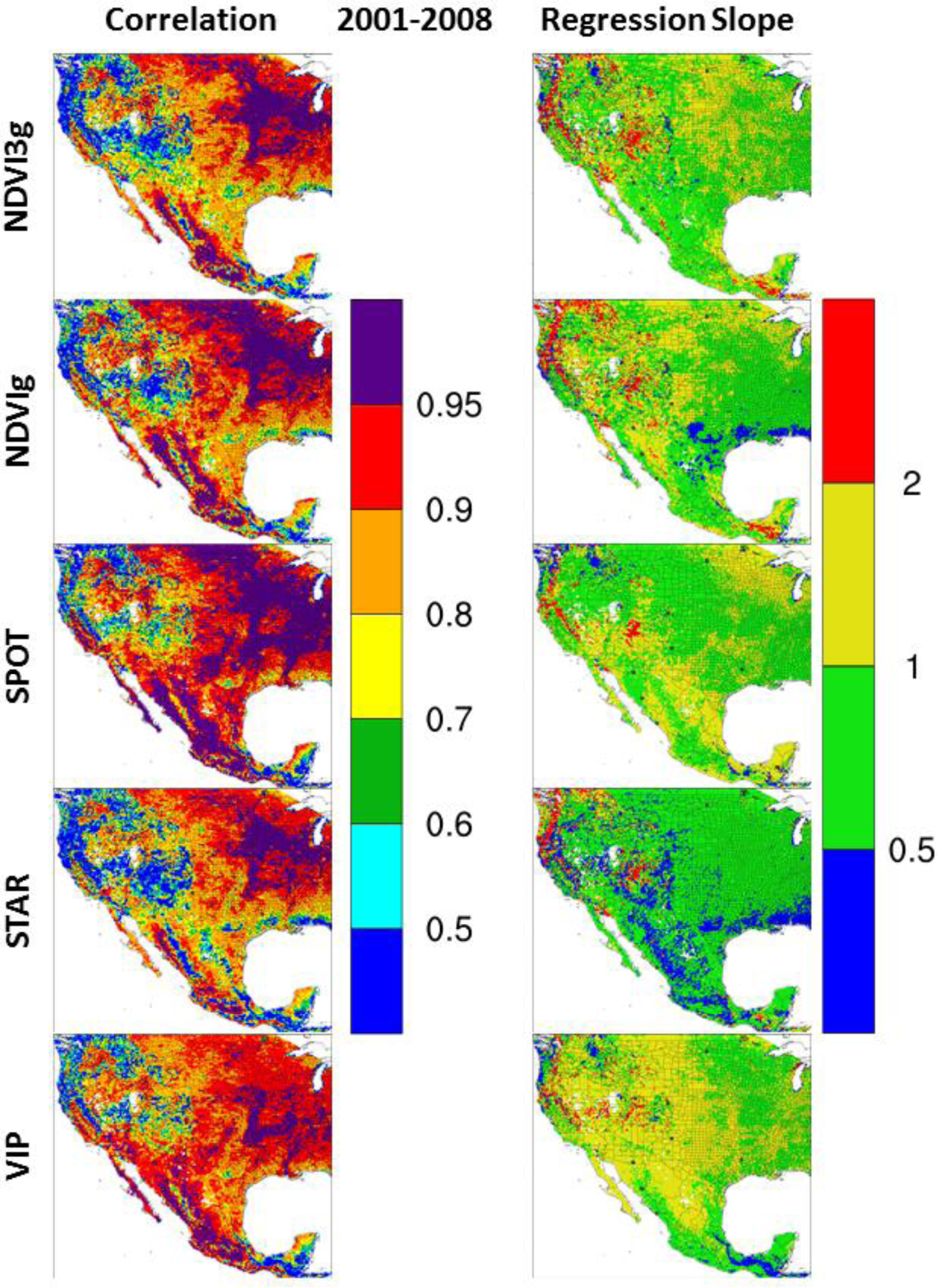
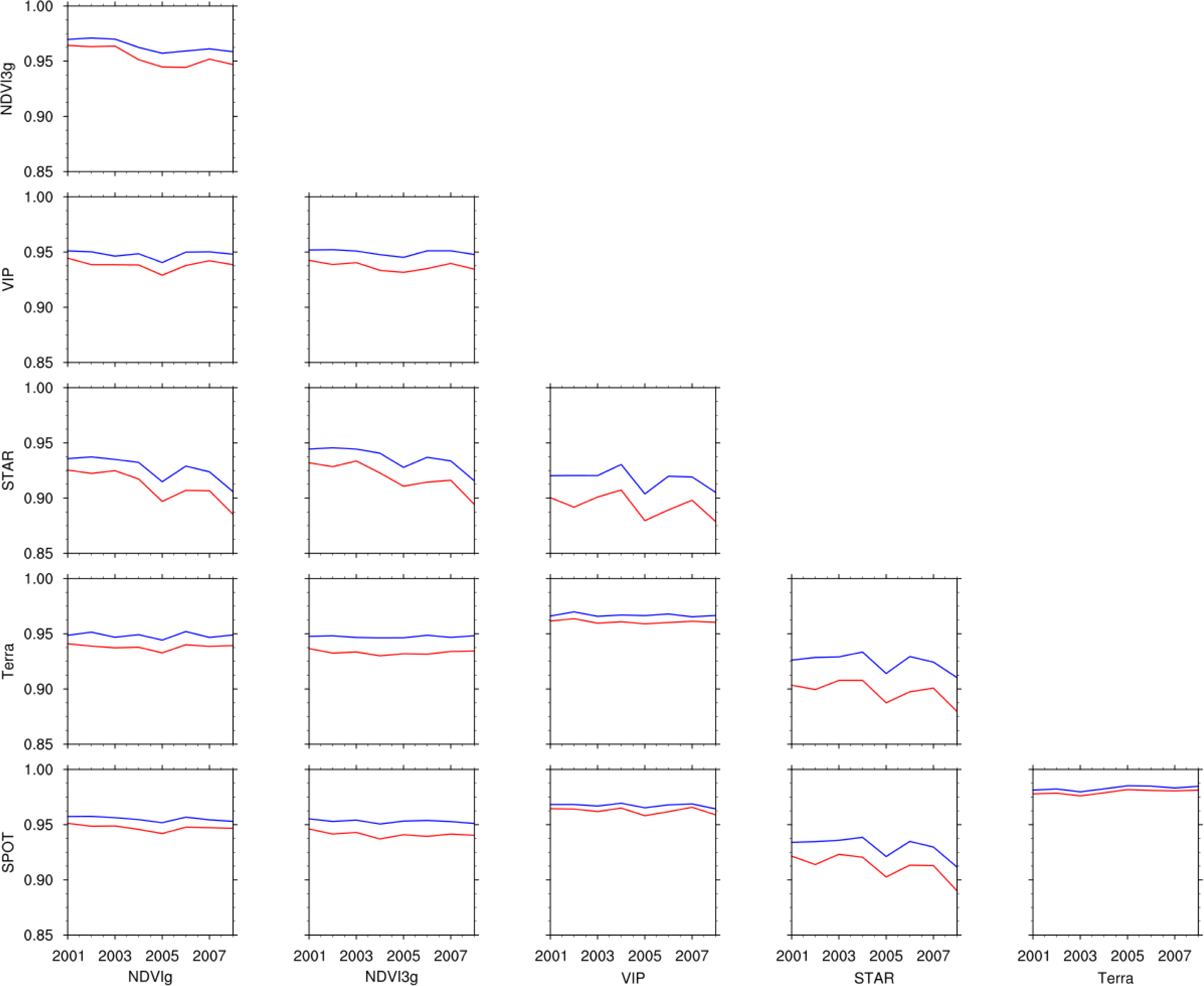
3.1. NDVI Intercomparison
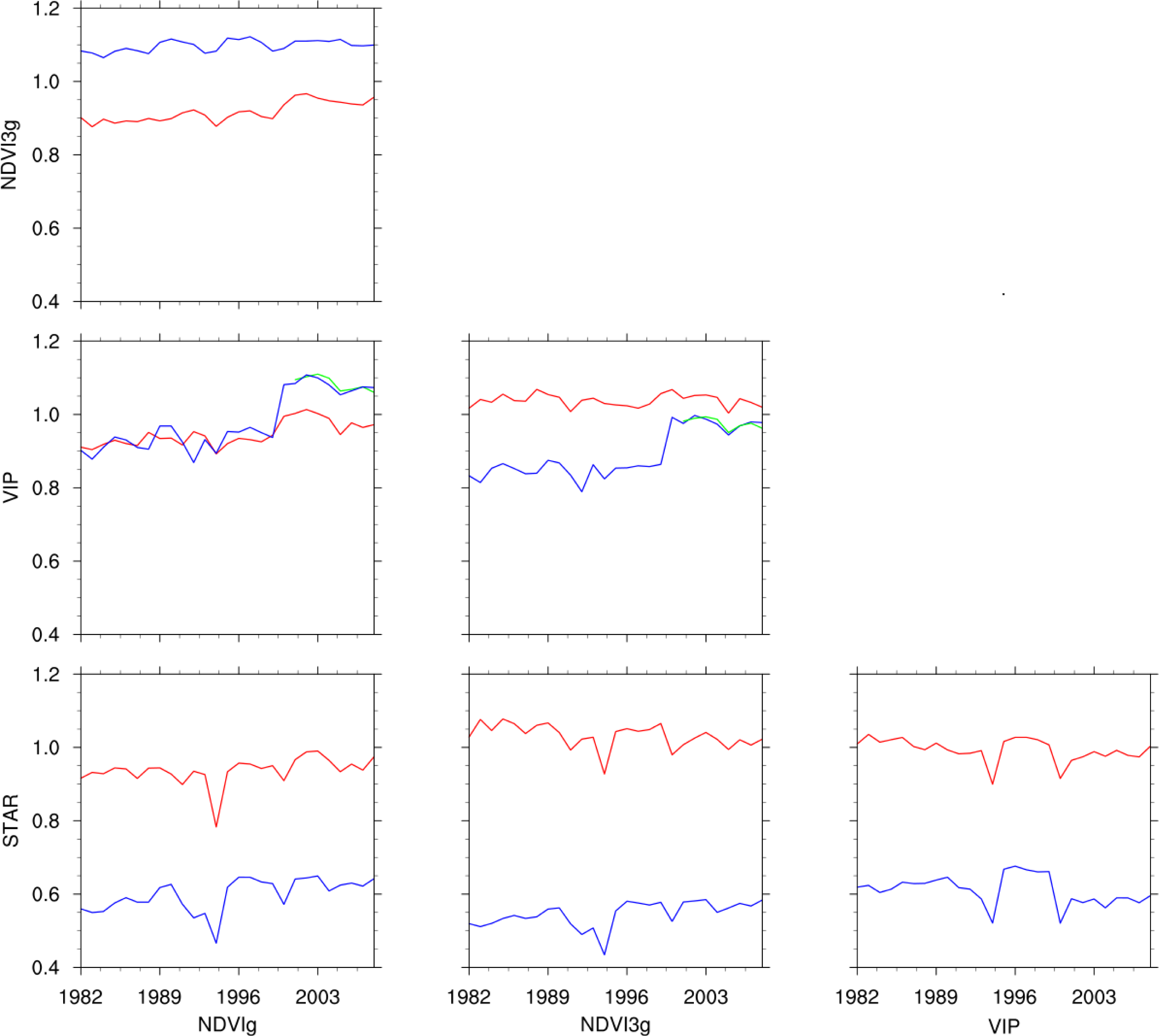
3.2. NDVI Trend Intercomparison
3.3. Calculation of Green Vegetation Fraction
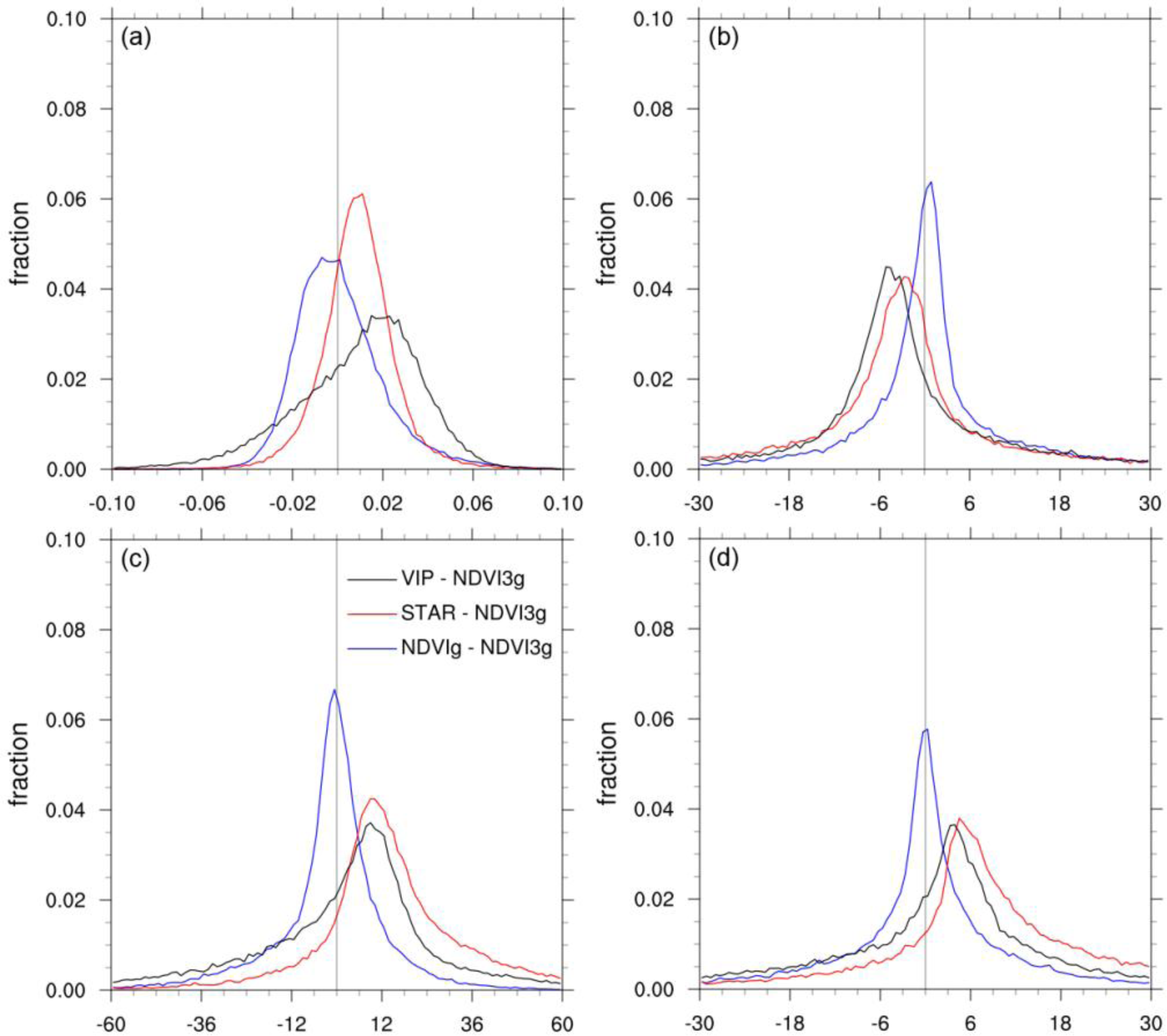
3.4. GVF to NDVI Trend Changes
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hansen, A.J.; Neilson, R.P.; Dale, V.H.; Flather, C.H.; Iverson, L.R.; Currie, D.J.; Shafer, S.; Cook, R.; Bartlein, P.J. Global change in forests: Responses of species, communities, and biomes. Bioscience 2001, 51, 765–779. [Google Scholar]
- Jackson, R.B.; Banner, J.L.; Jobbagy, E.G.; Pockman, W.T.; Wall, D.H. Ecosystem carbon loss with woody plant invasion of grasslands. Nature 2002, 418, 623–626. [Google Scholar]
- Walther, G.-R.; Post, E.; Convey, P.; Menzel, A.; Parmesan, C.; Beebee, T.J.C.; Fromentin, J.-M.; Hoegh-Guldberg, O.; Bairlein, F. Ecological responses to recent climate change. Nature 2002, 416, 389–395. [Google Scholar]
- Parmesan, C.; Yohe, G. A globally coherent fingerprint of climate change impacts across natural systems. Nature 2003, 421, 37–42. [Google Scholar]
- Donohue, R.J.; Roderick, M.L.; McVicar, T.R.; Farquhar, G.D. Impact of CO2 fertilization on maximum foliage cover across the globe's warm, arid environments. Geophys. Res. Lett 2013, 40, 3031–3035. [Google Scholar]
- Knapp, A.K.; Smith, M.D. Variation among biomes in temporal dynamics of aboveground primary production. Science 2001, 291, 481–484. [Google Scholar]
- Deering, D. Rangeland Reflectance Characteristics Measured by Aircraft and Spacecraft Sensors; Texas A & M University: College Station, TX, USA, 1978. [Google Scholar]
- Tucker, C. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ 1979, 8, 127–150. [Google Scholar]
- Wang, Q.; Adiku, S.; Tenhunen, J.; Granier, A. On the relationship of NDVI with leaf area index in a deciduous forest site. Remote Sens. Environ 2005, 94, 244–255. [Google Scholar]
- Sellers, P.J.; Tucker, C.J.; Collatz, G.J.; Los, S.O.; Justice, C.O.; Dazlich, D.A.; Randall, D.A. A revised land surface parameterization (SiB2) for atmospheric GCMS. Part II: The generation of global fields of terrestrial biophysical parameters from satellite data. J. Clim 1996, 9, 706–737. [Google Scholar]
- Gutman, G.; Ignatov, A. The derivation of the green vegetation fraction from NOAA/AVHRR data for use in numerical weather prediction models. Int. J. Remote Sens 1998, 19, 1533–1543. [Google Scholar]
- Defries, R.S.; Hansen, M.C.; Townshend, J.R.G.; Janetos, A.C.; Loveland, T.R. A new global 1-km dataset of percentage tree cover derived from remote sensing. Glob. Chang. Biol 2000, 6, 247–254. [Google Scholar]
- Lu, H.; Raupach, M.R.; McVicar, T.R.; Barrett, D.J. Decomposition of vegetation cover into woody and herbaceous components using AVHRR NDVI time series. Remote Sens. Environ 2003, 86, 1–18. [Google Scholar]
- Zeng, X.; Rao, P.; DeFries, R.S.; Hansen, M.C. Interannual variability and decadal trend of global fractional vegetation cover from 1982 to 2000. J. Appl. Meteorol 2003, 42, 1525–1530. [Google Scholar]
- Nemani, R.R.; Keeling, C.D.; Hashimoto, H.; Jolly, W.M.; Piper, S.C.; Tucker, C.J.; Myneni, R.B.; Running, S.W. Climate-driven increases in global terrestrial net primary production from 1982 to 1999. Science 2003, 300, 1560–1563. [Google Scholar]
- Baghzouz, M.; Devitt, D.A.; Fenstermaker, L.F.; Young, M.H. Monitoring vegetation phenological cycles in two different semi-arid environmental settings using a ground-based NDVI system: A potential approach to improve satellite data interpretation. Remote Sens 2010, 2, 990–1013. [Google Scholar]
- Goetz, S.J.; Prince, S.D.; Goward, S.N.; Thawley, M.M.; Small, J.; Johnston, A. Mapping net primary production and related biophysical variables with remote sensing: Application to the BOREAS region. J. Geophys. Res. Atmos 1999, 104, 27719–27734. [Google Scholar]
- Suzuki, R.; Nomaki, T.; Yasunari, T. Spatial distribution and its seasonality of satellite derived vegetation index (NDVI) and climate in Siberia. Int. J. Climatol 2001, 21, 1321–1335. [Google Scholar]
- Myneni, R.B.; Tucker, C.J.; Asrar, G.; Keeling, C.D. Interannual variations in satellite-sensed vegetation index data from 1981 to 1991. J. Geophys. Res. Atmos 1998, 103, 6145–6160. [Google Scholar]
- Julien, Y.; Sobrino, J.A. Global land surface phenology trends from GIMMS database. Int. J. Remote Sens 2009, 30, 3495–3513. [Google Scholar]
- De Jong, R.; de Bruin, S.; de Wit, A.; Schaepman, M.E.; Dent, D.L. Analysis of monotonic greening and browning trends from global NDVI time-series. Remote Sens. Environ 2011, 115, 692–702. [Google Scholar] [Green Version]
- Dahlke, C.; Loew, A.; Reick, C. Robust identification of global greening phase patterns from remote sensing vegetation products. J. Clim 2012, 25, 8289–8307. [Google Scholar]
- Fensholt, R.; Proud, S.R. Evaluation of earth observation based global long term vegetation trends—Comparing GIMMS and MODIS global NDVI time series. Remote Sens. Environ 2012, 119, 131–147. [Google Scholar]
- Beck, P.S.A.; Goetz, S.J. Satellite observations of high northern latitude vegetation productivity changes between 1982 and 2008: Ecological variability and regional differences. Environ. Res. Lett 2011. [Google Scholar] [CrossRef]
- Salinas-Zavala, C.A.; Douglas, A.V.; Diaz, H.F. Interannual variability of NDVI in northwest Mexico. Associated climatic mechanisms and ecological implications. Remote Sens. Environ 2002, 82, 417–430. [Google Scholar]
- Notaro, M.; Liu, Z.; Williams, J.W. Observed vegetation-climate feedbacks in the United States. J. Clim 2006, 19, 763–786. [Google Scholar]
- Forzieri, G.; Castelli, F.; Vivoni, E.R. Vegetation dynamics within the North American monsoon region. J. Clim 2011, 24, 1763–1783. [Google Scholar]
- Castro, C.L.; Beltrán-Przekurat, A.B.; Pielke, R.A. Spatiotemporal variability of precipitation, modeled soil moisture, and vegetation greenness in North America within the recent observational record. J. Hydrometeorol 2009, 10, 1355–1378. [Google Scholar]
- Donohue, R.J.; McVicar, T.I.M.R.; Roderick, M.L. Climate-related trends in Australian vegetation cover as inferred from satellite observations, 1981–2006. Glob. Chang. Biol 2009, 15, 1025–1039. [Google Scholar]
- Fensholt, R.; Rasmussen, K. Analysis of trends in the Sahelian “rain-use efficiency” using GIMMS NDVI, RFE and GPCP rainfall data. Remote Sens. Environ 2011, 115, 438–451. [Google Scholar]
- Xu, L.; Myneni, R.B.; Chapin, F.S., III; Callaghan, T.V.; Pinzon, J.E.; Tucker, C.J.; Zhu, Z.; Bi, J.; Ciais, P.; Tømmervik, H.; et al. Temperature and vegetation seasonality diminishment over northern lands. Nat. Clim. Chang 2013. [Google Scholar] [CrossRef]
- Wang, W.; Anderson, B.T.; Phillips, N.; Kaufmann, R.K.; Potter, C.; Myneni, R.B. Feedbacks of vegetation on summertime climate variability over the North American Grasslands. Part I: Statistical analysis. Earth Interact 2006, 10, 1–27. [Google Scholar]
- Van Leeuwen, W.J.D.; Orr, B.J.; Marsh, S.E.; Herrmann, S.M. Multi-sensor NDVI data continuity: Uncertainties and implications for vegetation monitoring applications. Remote Sens. Environ 2006, 100, 67–81. [Google Scholar]
- Fensholt, R.; Nielsen, T.T.; Stisen, S. Evaluation of AVHRR PAL and GIMMS 10-day composite NDVI time series products using SPOT-4 vegetation data for the African continent. Int. J. Remote Sens 2006, 27, 2719–2733. [Google Scholar]
- Alcaraz-Segura, D.; Liras, E.; Tabik, S.; Paruelo, J.; Cabello, J. Evaluating the consistency of the 1982–1999 NDVI trends in the Iberian Peninsula across four time-series derived from the AVHRR sensor: LTDR, GIMMS, FASIR, and PAL-II. Sensors 2010, 10, 1291–1314. [Google Scholar]
- Beck, H.E.; McVicar, T.R.; van Dijk, A.I.J.M.; Schellekens, J.; de Jeu, R.A.M.; Bruijnzeel, L.A. Global evaluation of four AVHRR-NDVI data sets: Intercomparison and assessment against Landsat imagery. Remote Sens. Environ 2011, 115, 2547–2563. [Google Scholar]
- Brown, M.E.; Pinzón, J.E.; Didan, K.; Morisette, J.T.; Tucker, C.J. Evaluation of the consistency of long-term NDVI time series derived from AVHRR,SPOT-vegetation, SeaWiFS, MODIS, and Landsat ETM+ sensors. IEEE Trans. Geosci. Remote Sens 2006, 44, 1787–1793. [Google Scholar]
- Fensholt, R.; Sandholt, I.; Stisen, S. Evaluating MODIS, MERIS, and VEGETATION vegetation indices using in situ measurements in a semiarid environment. IEEE Trans. Geosci. Remote Sens 2006, 44, 1774–1786. [Google Scholar]
- Fensholt, R.; Rasmussen, K.; Nielsen, T.T.; Mbow, C. Evaluation of earth observation based long term vegetation trends—Intercomparing NDVI time series trend analysis consistency of Sahel from AVHRR GIMMS, Terra MODIS and SPOT VGT data. Remote Sens. Environ 2009, 113, 1886–1898. [Google Scholar]
- Song, Y.; Ma, M.; Veroustraete, F. Comparison and conversion of AVHRR GIMMS and SPOT VEGETATION NDVI data in China. Int. J. Remote Sens 2010, 31, 2377–2392. [Google Scholar]
- Zeng, X.; Dickinson, R.E.; Walker, A.; Shaikh, M.; DeFries, R.S.; Qi, J. Derivation and evaluation of global 1-km fractional vegetation cover data for land modeling. J. Appl. Meteorol 2000, 39, 826–839. [Google Scholar]
- Miller, J.; Barlage, M.; Zeng, X.; Wei, H.; Mitchell, K.; Tarpley, D. Sensitivity of the NCEP/Noah land surface model to the MODIS green vegetation fraction data set. Geophys. Res. Lett 2006. [Google Scholar] [CrossRef]
- Galvao, L.S.; Vitorello, I.; Pizarro, M.A. An adequate band positioning to enhance NDVI contrasts among green vegetation, senescent biomass, and tropical soils. Int. J. Remote Sens 2000, 21, 1953–1960. [Google Scholar]
- Teillet, P.M.; Staenz, K.; William, D.J. Effects of spectral, spatial, and radiometric characteristics on remote sensing vegetation indices of forested regions. Remote Sens. Environ 1997, 61, 139–149. [Google Scholar]
- Justice, C.O.; Eck, T.F.; Tanré, D.; Holben, B.N. The effect of water vapour on the normalized difference vegetation index derived for the Sahelian region from NOAA AVHRR data. Int. J. Remote Sens 1991, 12, 1165–1187. [Google Scholar]
- Ignatov, A.; Laszlo, I.; Harrod, E.D.; Kidwell, K.B.; Goodrum, G.P. Equator crossing times for NOAA, ERS and EOS sun-synchronous satellites. Int. J. Remote Sens 2004, 25, 5255–5266. [Google Scholar]
- Maisongrande, P.; Duchemin, B.; Dedieu, G. VEGETATION/SPOT: An operational mission for the Earth monitoring; presentation of new standard products. Int. J. Remote Sens 2004, 25, 9–14. [Google Scholar]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ 2002, 83, 195–213. [Google Scholar]
- Tucker, C.J.; Pinzon, J.E.; Brown, M.E.; Slayback, D.A.; Pak, E.W.; Mahoney, R.; Vermote, E.F.; El Saleous, N. An extended AVHRR 8-km NDVI dataset compatible with MODIS and SPOT vegetation NDVI data. Int. J. Remote Sens 2005, 26, 4485–4498. [Google Scholar]
- Jiang, L.; Kogan, F.N.; Guo, W.; Tarpley, J.D.; Mitchell, K.E.; Ek, M.B.; Tian, Y.; Zheng, W.; Zou, C.-Z.-Z.; Ramsay, B.H. Real-time weekly global green vegetation fraction derived from advanced very high resolution radiometer-based NOAA operational global vegetation index (GVI) system. J. Geophys. Res 2010, 115, 1–22. [Google Scholar]
- Didan, K. Multi-Satellite Earth Science Data Record for Studying Global Vegetation Trends and Changes. Proceedings of the 2010 International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010.
- Barreto-Munoz, A. Multi-Sensor Vegetation Index and Land Surface Phenology Earth Science Data Records in Support of Global Change Studies: Data Quality Challenges and Data Explorer System. The University of Arizona, Tucson, AZ, USA, 2013. [Google Scholar]
- Wang, D.; Morton, D.; Masek, J.; Wu, A.; Nagol, J.; Xiong, X.; Levy, R.; Vermote, E.; Wolfe, R. Impact of sensor degradation on the MODIS NDVI time series. Remote Sens. Environ 2012, 119, 55–61. [Google Scholar]
- Holben, B.N. Characteristics of maximum-value composite images from temporal AVHRR data. Int. J. Remote Sens 1986, 7, 1417–1434. [Google Scholar]
- Moody, A.; Strahler, A.H. Characteristics of composited AVHRR data and problems in their classification. Int. J. Remote Sens 1994, 15, 3473–3491. [Google Scholar]
- White, M.A.; Thornton, P.E.; Running, S.W. A continental phenology model for monitoring vegetation responses to interannual climatic variability. Glob. Biogeochem. Cycles 1997, 11, 217–234. [Google Scholar]
- Carroll, R.J.; Ruppert, D. The use and misuse of orthogonal regression in linear errors-in-variables models. Am. Stat 1996, 50, 1–6. [Google Scholar]
- Fensholt, R.; Sandholt, I. Evaluation of MODIS and NOAA AVHRR vegetation indices with in situ measurements in a semi-arid environment. Int. J. Remote Sens 2005, 26, 2561–2594. [Google Scholar]
- Myneni, R. Department of Earth and Environment, Boston University, Boston, MA. Personal Communication,. 2013.
- Fensholt, R.; Langanke, T.; Rasmussen, K.; Reenberg, A.; Prince, S.D.; Tucker, C.; Scholes, R.J.; Le, Q.B.; Bondeau, A.; Eastman, R.; et al. Greenness in semi-arid areas across the globe 1981–2007—An earth observing satellite based analysis of trends and drivers. Remote Sens. Environ 2012, 121, 144–158. [Google Scholar]
- De Jong, R.; Verbesselt, J.; Schaepman, M.E.; de Bruin, S. Trend changes in global greening and browning: Contribution of short-term trends to longer-term change. Glob. Chang. Biol 2012, 18, 642–655. [Google Scholar]
- Jeong, S.-J.; Ho, C.-H.; Gim, H.-J.; Brown, M.E. Phenology shifts at start vs. end of growing season in temperate vegetation over the Northern Hemisphere for the period 1982–2008. Glob. Chang. Biol 2011, 17, 2385–2399. [Google Scholar]
- Didan, K. Department of Electrical and Computer Engineering, The University of Arizona, Tucson, AZ. Personal Communication,. 2013.
- Mao, J.; Shi, X.; Thornton, P.E.; Piao, S.; Wang, X. Causes of spring vegetation growth trends in the northern mid-high latitudes from 1982 to 2004. Environ. Res. Lett 2012. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, Y.; Dong, J.; Xiao, X. Green-up dates in the Tibetan Plateau have continuously advanced from 1982 to 2011. Proc. Natl. Acad. Sci. USA 2013, 110, 4309–4314. [Google Scholar]



| Dataset | Sensor | Temporal Span | Temporal Resolution | Spatial Resolution | Compositing |
|---|---|---|---|---|---|
| NDVIg | AVHRR | 1981–2008 | bi-monthly | 8 km | MVC |
| NDVI3g | AVHRR | 1981–2011 | bi-monthly | 1/12 deg | MVC |
| STAR | AVHRR | 1981–2011 | weekly | 16 km | MVC smoothed |
| VIP | AVHRR VEGETATION MODIS | 1981–2010 | 15-day | 0.05 deg | MVC |
| Terra | MODIS | 2000–2011 | 16-day | 1 km | CV-MVC |
| SPOT | VEGETATION | 1998–2011 | 10-day | 1 km | MVC |
| Np,max | MGVF | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IGBP Type | T | SP | g | 3g | ST | V | T | SP | G | 3g | ST | V | |
| Mean | |||||||||||||
| 1 | ENFor (3347) | 0.75 | 0.71 | 0.70 | 0.85 | 0.49 | 0.81 | 0.89 | 0.88 | 0.89 | 0.90 | 0.86 | 0.90 |
| 2 | EBFor (1463) | 0.85 | 0.81 | 0.76 | 0.87 | 0.50 | 0.86 | 0.94 | 0.96 | 0.91 | 0.93 | 0.90 | 0.95 |
| 3 | DNFor (0) | ||||||||||||
| 4 | DBFor (696) | 0.86 | 0.81 | 0.81 | 0.89 | 0.56 | 0.89 | 0.96 | 0.96 | 0.95 | 0.95 | 0.92 | 0.97 |
| 5 | MixFor (3062) | 0.82 | 0.77 | 0.76 | 0.88 | 0.52 | 0.86 | 0.94 | 0.93 | 0.92 | 0.94 | 0.90 | 0.95 |
| 6 | ClsShr (149) | 0.58 | 0.52 | 0.56 | 0.65 | 0.36 | 0.65 | 0.83 | 0.84 | 0.86 | 0.86 | 0.83 | 0.86 |
| 7 | OpnShr (8609) | 0.36 | 0.31 | 0.33 | 0.39 | 0.22 | 0.41 | 0.46 | 0.44 | 0.45 | 0.47 | 0.46 | 0.49 |
| 8 | WdySav (4562) | 0.77 | 0.71 | 0.71 | 0.82 | 0.47 | 0.81 | 0.91 | 0.91 | 0.90 | 0.91 | 0.90 | 0.93 |
| 9 | Sav (132) | 0.66 | 0.60 | 0.60 | 0.78 | 0.44 | 0.73 | 0.92 | 0.92 | 0.93 | 0.94 | 0.92 | 0.94 |
| 10 | Grass (19449) | 0.50 | 0.44 | 0.49 | 0.57 | 0.32 | 0.57 | 0.76 | 0.73 | 0.77 | 0.77 | 0.76 | 0.78 |
| 11 | Wetlnd (84) | 0.56 | 0.60 | 0.50 | 0.63 | 0.32 | 0.66 | 0.72 | 0.81 | 0.69 | 0.75 | 0.70 | 0.78 |
| 12 | Crop (8592) | 0.75 | 0.69 | 0.73 | 0.81 | 0.49 | 0.80 | 0.87 | 0.86 | 0.87 | 0.90 | 0.86 | 0.89 |
| 13 | Urban (347) | 0.52 | 0.46 | 0.49 | 0.65 | 0.35 | 0.59 | 0.73 | 0.70 | 0.69 | 0.74 | 0.68 | 0.73 |
| 14 | CrpVeg (4959) | 0.79 | 0.74 | 0.75 | 0.86 | 0.52 | 0.83 | 0.93 | 0.93 | 0.92 | 0.94 | 0.91 | 0.95 |
| 16 | Barren (543) | 0.15 | 0.13 | 0.16 | 0.20 | 0.11 | 0.18 | 0.12 | 0.11 | 0.14 | 0.19 | 0.17 | 0.14 |
| Total (55994) | 0.61 | 0.55 | 0.58 | 0.67 | 0.39 | 0.66 | 0.77 | 0.76 | 0.77 | 0.79 | 0.77 | 0.79 | |
| Range | |||||||||||||
| 1 | ENFor | 0.03 | 0.03 | 0.04 | 0.02 | 0.03 | 0.03 | 0.01 | 0.01 | 0.01 | 0.01 | 0.03 | 0.01 |
| 2 | EBFor | 0.01 | 0.04 | 0.02 | 0.02 | 0.04 | 0.02 | 0.01 | 0.01 | 0.02 | 0.01 | 0.01 | 0.01 |
| 3 | DNFor | ||||||||||||
| 4 | DBFor | 0.02 | 0.04 | 0.05 | 0.03 | 0.04 | 0.02 | 0.01 | 0.02 | 0.01 | 0.01 | 0.02 | 0.01 |
| 5 | MixFor | 0.02 | 0.04 | 0.03 | 0.01 | 0.04 | 0.03 | 0.01 | 0.01 | 0.01 | 0.01 | 0.03 | 0.01 |
| 6 | ClsShr | 0.04 | 0.06 | 0.06 | 0.04 | 0.04 | 0.06 | 0.07 | 0.04 | 0.05 | 0.02 | 0.06 | 0.03 |
| 7 | OpnShr | 0.07 | 0.11 | 0.06 | 0.04 | 0.06 | 0.11 | 0.13 | 0.12 | 0.10 | 0.05 | 0.10 | 0.13 |
| 8 | WdySav | 0.02 | 0.04 | 0.02 | 0.01 | 0.03 | 0.03 | 0.00 | 0.01 | 0.02 | 0.01 | 0.02 | 0.02 |
| 9 | Sav | 0.10 | 0.10 | 0.07 | 0.03 | 0.06 | 0.06 | 0.04 | 0.05 | 0.04 | 0.03 | 0.03 | 0.04 |
| 10 | Grass | 0.06 | 0.09 | 0.04 | 0.03 | 0.05 | 0.06 | 0.06 | 0.06 | 0.04 | 0.02 | 0.05 | 0.06 |
| 11 | Wetlnd | 0.06 | 0.04 | 0.02 | 0.02 | 0.04 | 0.06 | 0.05 | 0.02 | 0.02 | 0.02 | 0.07 | 0.05 |
| 12 | Crop | 0.03 | 0.06 | 0.02 | 0.02 | 0.05 | 0.02 | 0.02 | 0.03 | 0.02 | 0.02 | 0.04 | 0.02 |
| 13 | Urban | 0.03 | 0.04 | 0.02 | 0.02 | 0.03 | 0.02 | 0.02 | 0.02 | 0.03 | 0.02 | 0.03 | 0.02 |
| 14 | CrpVeg | 0.02 | 0.04 | 0.02 | 0.01 | 0.04 | 0.02 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 |
| 16 | Barren | 0.07 | 0.10 | 0.06 | 0.06 | 0.04 | 0.09 | 0.11 | 0.12 | 0.09 | 0.09 | 0.10 | 0.13 |
| Total | 0.03 | 0.07 | 0.02 | 0.02 | 0.04 | 0.04 | 0.04 | 0.04 | 0.03 | 0.02 | 0.03 | 0.04 | |
| Np,max (per decade) | Duration of Season (days/decade) | Start of Season (days/decade) | End of Season (days/decade) | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IGBP Type | g | 3 g | ST | V | g | 3 g | ST | V | g | 3 g | ST | V | g | 3 g | ST | V | |
| 1 | ENFor | −0.012 | 0.003 | 0.011 | −0.015 | −1.1 | 7.7 | 17.1 | −11.7 | 9.9 | 6.2 | −5.2 | 2.0 | 2.0 | 1.6 | 11.0 | −3.0 |
| 2 | EBFor | 0.002 | −0.001 | 0.016 | 0.031 | −12.5 | 3.0 | 31.3 | 42.4 | −2.8 | −4.0 | 7.8 | −5.0 | −20.1 | −11.2 | 26.3 | 16.5 |
| 3 | DNFor | ||||||||||||||||
| 4 | DBFor | −0.014 | −0.003 | 0.015 | 0.028 | 4.9 | 5.9 | 15.6 | 15.2 | −0.7 | −2.1 | −4.1 | −6.0 | 4.7 | 4.5 | 10.6 | 8.1 |
| 5 | MixFor | −0.011 | −0.001 | 0.013 | 0.016 | 6.2 | 7.5 | 21.2 | 17.6 | 1.6 | 1.4 | −2.1 | −3.9 | 8.9 | 7.9 | 15.9 | 12.2 |
| 6 | ClsShr | −0.004 | 0.000 | 0.009 | −0.010 | −2.9 | 1.5 | 23.8 | −10.6 | 32.6 | 22.3 | 35.7 | 11.2 | 27.2 | 22.0 | −55.2 | −10.1 |
| 7 | OpnShr | 0.014 | 0.001 | 0.009 | −0.009 | 3.8 | 3.9 | 13.9 | −17.8 | 25.3 | 13.2 | 33.2 | 14.3 | 29.1 | 14.8 | 42.7 | −6.2 |
| 8 | WdySav | −0.002 | 0.004 | 0.021 | 0.026 | 7.2 | 10.0 | 31.8 | 24.1 | −2.7 | −1.5 | −4.0 | −7.9 | 9.1 | 8.1 | 26.3 | 15.5 |
| 9 | Sav | −0.005 | −0.004 | 0.009 | 0.013 | −11.6 | 0.9 | 17.1 | 11.8 | −0.3 | −0.7 | −7.2 | −21.3 | −17.0 | −0.4 | 13.8 | −7.2 |
| 10 | Grass | 0.009 | 0.002 | 0.009 | 0.009 | 3.5 | 3.7 | 16.3 | 7.8 | 0.3 | 0.8 | −2.4 | −3.6 | 4.6 | 4.4 | 13.0 | 5.0 |
| 11 | Wetlnd | −0.003 | −0.001 | 0.019 | 0.031 | 16.2 | 13.9 | 30.2 | 20.7 | −4.5 | −2.6 | −11.2 | −6.9 | 20.2 | 14.8 | 25.4 | 11.2 |
| 12 | Crop | 0.014 | 0.014 | 0.021 | 0.036 | 1.2 | 0.5 | 13.0 | 11.5 | 1.8 | 1.7 | −2.4 | −4.5 | 2.4 | 1.5 | 8.5 | 6.0 |
| 13 | Urban | −0.010 | −0.001 | 0.000 | −0.012 | −3.1 | −0.3 | 11.5 | −5.2 | 2.4 | 2.6 | −1.7 | 0.9 | 2.3 | 2.3 | 12.1 | 1.4 |
| 14 | CrpVeg | −0.008 | 0.002 | 0.015 | 0.029 | 2.3 | 4.9 | 18.0 | 18.8 | −0.7 | −0.6 | −3.1 | −6.8 | 3.2 | 3.7 | 10.5 | 8.1 |
| 16 | Barren | 0.005 | −0.001 | 0.000 | −0.024 | 0.9 | −1.3 | −1.5 | −33.2 | −7.3 | −16.2 | −13.2 | 32.7 | −4.4 | −4.5 | −1.2 | 15.3 |
| Total | 0.005 | 0.004 | 0.013 | 0.013 | 2.7 | 4.2 | 17.5 | 7.6 | 3.0 | 2.2 | 0.2 | −3.4 | 7.1 | 5.7 | 13.9 | 5.0 | |
| MGVF (per decade) | Duration of Season (days/decade) | Start of Season (days/decade) | End of Season (days/decade) | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IGBP Type | g | 3 g | ST | V | g | 3 g | ST | V | g | 3 g | ST | V | g | 3 g | ST | V | |
| 1 | ENFor | 0.000 | −0.002 | 0.001 | 0.005 | 12.1 | −1.0 | 8.2 | 17.0 | 0.3 | 5.9 | 4.0 | −5.3 | 8.7 | −1.8 | 7.2 | 11.8 |
| 2 | EBFor | −0.001 | −0.001 | 0.010 | 0.006 | −16.1 | 1.2 | 18.5 | 4.3 | −1.6 | −3.7 | 20.2 | 15.6 | −21.5 | −11.7 | 22.6 | 4.5 |
| 3 | DNFor | ||||||||||||||||
| 4 | DBFor | 0.003 | 0.001 | 0.013 | 0.008 | 9.6 | 5.6 | 12.0 | 10.7 | −2.4 | −2.0 | −2.8 | −4.4 | 6.6 | 4.4 | 8.8 | 6.2 |
| 5 | MixFor | 0.004 | 0.001 | 0.012 | 0.011 | 15.1 | 6.6 | 17.0 | 15.6 | −1.4 | 1.6 | −0.5 | −3.2 | 13.4 | 7.3 | 13.6 | 11.2 |
| 6 | ClsShr | −0.001 | −0.006 | −0.001 | 0.013 | 4.0 | −7.9 | 8.9 | 21.5 | 30.4 | 23.8 | 42.1 | −2.4 | 31.1 | 12.5 | 25.1 | 13.3 |
| 7 | OpnShr | 0.029 | −0.011 | 0.005 | 0.011 | 9.2 | −17.6 | 4.6 | 0.9 | 25.2 | 20.0 | 35.9 | 5.4 | 32.6 | 4.0 | 46.9 | 4.7 |
| 8 | WdySav | 0.004 | 0.001 | 0.012 | 0.007 | 11.3 | 4.0 | 16.0 | 11.4 | −3.6 | −0.3 | −1.1 | −4.2 | 10.9 | 5.2 | 15.5 | 9.1 |
| 9 | Sav | 0.005 | −0.004 | 0.003 | 0.003 | −4.0 | −0.7 | 13.7 | 9.5 | −3.2 | 0.3 | −7.6 | −18.9 | −10.1 | −1.0 | 5.6 | −7.0 |
| 10 | Grass | 0.010 | −0.009 | 0.006 | 0.002 | 0.4 | −8.3 | 8.2 | 5.7 | 1.8 | 5.2 | 1.1 | −2.5 | 3.1 | −3.1 | 8.7 | 4.1 |
| 11 | Wetlnd | 0.002 | −0.003 | 0.007 | 0.009 | 20.6 | 11.6 | 14.3 | 2.8 | −5.0 | −2.2 | −7.6 | −4.3 | 20.5 | 12.1 | 11.7 | 2.1 |
| 12 | Crop | 0.003 | 0.001 | 0.005 | 0.009 | −2.8 | −7.0 | 4.7 | 4.2 | 3.7 | 5.2 | 1.4 | −1.0 | 0.5 | −1.7 | 5.0 | 3.0 |
| 13 | Urban | 0.001 | −0.004 | −0.006 | −0.014 | 8.2 | −6.4 | 7.8 | 0.6 | −1.9 | 4.6 | −0.6 | −1.2 | 8.9 | −0.8 | 9.8 | 4.2 |
| 14 | CrpVeg | 0.001 | 0.002 | 0.007 | 0.008 | 6.4 | 2.5 | 11.8 | 10.6 | −1.9 | 0.2 | −0.9 | −4.2 | 4.9 | 2.6 | 8.0 | 5.0 |
| 16 | Barren | 0.013 | −0.021 | −0.011 | −0.014 | 6.8 | −30.2 | −10.0 | −11.9 | −23.2 | 10.4 | −2.1 | 6.4 | 0.3 | −30.1 | −13.9 | 14.4 |
| Total | 0.009 | −0.005 | 0.006 | 0.006 | 3.9 | −5.8 | 8.8 | 6.9 | 3.1 | 5.4 | 3.4 | −2.5 | 7.5 | 0.7 | 10.1 | 4.8 | |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Scheftic, W.; Zeng, X.; Broxton, P.; Brunke, M. Intercomparison of Seven NDVI Products over the United States and Mexico. Remote Sens. 2014, 6, 1057-1084. https://doi.org/10.3390/rs6021057
Scheftic W, Zeng X, Broxton P, Brunke M. Intercomparison of Seven NDVI Products over the United States and Mexico. Remote Sensing. 2014; 6(2):1057-1084. https://doi.org/10.3390/rs6021057
Chicago/Turabian StyleScheftic, William, Xubin Zeng, Patrick Broxton, and Michael Brunke. 2014. "Intercomparison of Seven NDVI Products over the United States and Mexico" Remote Sensing 6, no. 2: 1057-1084. https://doi.org/10.3390/rs6021057






