Next Article in Journal
Training Area Concept in a Two-Phase Biomass Inventory Using Airborne Laser Scanning and RapidEye Satellite Data
Next Article in Special Issue
Intercomparison of Seven NDVI Products over the United States and Mexico
Previous Article in Journal
Actual Evapotranspiration (Water Use) Assessment of the Colorado River Basin at the Landsat Resolution Using the Operational Simplified Surface Energy Balance Model
Previous Article in Special Issue
Combined Spatial and Temporal Effects of Environmental Controls on Long-Term Monthly NDVI in the Southern Africa Savanna
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 6
Issue 1
10.3390/rs6010257
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Phenological Metrics Derived over the European Continent from NDVI3g Data and MODIS Time Series

by
Clement Atzberger
*,
Anja Klisch
,
Matteo Mattiuzzi
and
Francesco Vuolo
Institute for Surveying, Remote Sensing and Land Information, University of Natural Resources and Life Sciences (BOKU), Peter Jordan Strasse 82, A-1190 Vienna, Austria
*
Author to whom correspondence should be addressed.
Remote Sens. 2014, 6(1), 257-284; https://doi.org/10.3390/rs6010257
Submission received: 22 July 2013 / Revised: 21 November 2013 / Accepted: 25 November 2013 / Published: 27 December 2013
(This article belongs to the Special Issue Monitoring Global Vegetation with AVHRR NDVI3g Data (1981-2011))
Browse Figures
Versions Notes

Abstract

:
Time series of normalized difference vegetation index (NDVI) are important data sources for environmental monitoring. Continuous efforts are put into their production and updating. The recently released Global Inventory Modeling and Mapping Studies (GIMMS) NDVI3g data set is a consistent time series with 1/12° spatial and bi-monthly temporal resolution. It covers the time period from 1981 to 2011. However, it is unclear if vegetation density and phenology derived from GIMMS are comparable to those obtained from Moderate Resolution Imaging Spectroradiometer (MODIS) NDVI with 250 m ground resolution. To check the consistency between GIMMS and MODIS data sets, a comparative analysis was performed. For a large European window (40 × 40°), data distribution, spatial and temporal agreement were analyzed, as well as the timing of important phenological events. Overall, only a moderately good agreement of NDVI values was found. Large differences occurred during winter. Large discrepancies were also observed for phenological metrics, in particular the start of season. Information regarding the maximum of season was more consistent. Hence, both data sets should be well inter-calibrated before being used concurrently.

Graphical Abstract

1. Introduction

Time series of remotely sensed normalized difference vegetation index (NDVI) are valuable data sets in various Earth science fields. For example, NDVI time series have been successfully used for environmental monitoring [1–3], for providing agricultural outlooks and yield predictions [4–6], and for modeling wildlife occurrence/movement and biodiversity [7]. Such time series are also excellent and unique proxies for assessing possible climate change impacts across the globe [8,9] and for large scale drought monitoring [10]. A number of prominent applications are listed in Table 1 ([11–43]). Additional examples are presented within this special issue. Most applications build on the fact that NDVI is a (coarse) measure of vegetation density and more or less linearly related to the fraction of absorbed photosynthetically active radiation (fAPAR).
The value of remotely sensed time series naturally increases with the accuracy of the measurement (i.e., radiometric and geometric accuracy). Equally important are, however, the length of the time series, its consistency, and temporal and spatial resolution. With the recently released Global Inventory Modeling and Mapping Studies NDVI3g (GIMMS) data set, a major breakthrough in harmonizing Advanced Very High Resolution Radiometer (AVHRR) data from various NOAA satellites (National Oceanic and Atmospheric Administration) was made [44]. The GIMMS data set spans the time period from 1981 to 2011, in 1/12° spatial resolution, and with bi-monthly temporal resolution. This offers interesting perspectives for a joint use with other NDVI data sets with higher spatial and temporal resolution but shorter length of the series. For example MODIS products at 250 m are only available from 2000 onwards. Before combining different NDVI time series, however, their consistency has to be checked [45,46]. The current paper addresses this issue and provides a comparative analysis of the GIMMS NDVI3g dataset and MODIS NDVI time series over a 40 × 40° European window for the time frame of 2002–2011. The comparative analysis covers several aspects of such time series and explicitly distinguishes between spatial and temporal agreement:
  • data (frequency) distribution of vegetation density information (NDVI);
  • agreement/disagreement and correlation of NDVI;
  • timing of major phenological events (here start and maximum of season).
The study complements ongoing direct validation exercises, but is not intended to replace such efforts. A comparative analysis between existing Earth Observation (EO) products yields for example important information regarding the feasibility of creating historical records of NDVI and/or satellite-derived pheno-indicators. Phenological events were included in the study as pheno-indicators provide unique information for assessing possible climatic impacts on vegetation growth and the bio-sphere [1,3,13,47–49].

2. Data and Methods

The paper addresses the consistency of GIMMS and MODIS NDVI time series over Europe with a special focus on the timing of phenological events (start/maximum of season). The comparative analysis covers the years 2002–2011. Before analysis, we performed a careful harmonization of the two data sets in terms of temporal and spatial resolution. This also implied a smoothing/filtering of the two time series to remove undesired artifacts due to poor atmospheric conditions and undetected clouds, etc. Major pre-processing steps for spatial and temporal homogenization of the two time series are outlined in the following sub-sections and summarized in Table 2.
The method used for the comparison capitalizes on previous studies involving either single image acquisitions or multi-temporal data [46,50]. In addition to analyzing the ‘overall’ agreement between paired data sets, we explicitly addressed—following the work of [46]—the seasonality of their spatial coherence and the spatial variability of their temporal agreement. Thus, both spatial and temporal patterns were analyzed within the present study. On the other hand, no attempts were made to determine which of the two series is of ‘better’ quality [46]. Seriously answering this question would only be possible with an extended network of NDVI reference measurements [51,52]. Such an extended reference network is currently not available. Existing prototype reference networks have only a reduced spatial and temporal coverage and are mainly focused on biophysical variables of vegetation such as leaf area index (LAI) and fraction of absorbed photosynthetically active radiation (fAPAR) [53,54]. Moreover, direct validation of coarse-resolution satellite data against point-like reference measurements is a nontrivial task [55]. Instead, the plausibility of seasonal and spatial pattern was checked by comparing with published results of other research teams.

2.1. Study Area

The study area is depicted in Figure 1 ([56–58]) together with some environmental variables. The selected variables demonstrate a very large spatial variability of the landscape as well as climatic conditions. The study region covers an area of approximately 18 million km2 (land surface: 12 million km2). Only land pixels (see Section 2.3) are included in this study without any additional efforts to mask out inland water bodies (e.g., lakes and rivers). According to the Koeppen climate classification [59], the climate in the area ranges from polar to arid. Precipitation and temperatures show a large gradient from the fully humid to very dry Sahara desert and from polar tundra to cold/hot arid. Land cover comprises a large number of different classes (mainly cropland, forest, shrubs, grassland and bare areas), and is generally fine structured [23,60]. This highly variable environmental setting permits comparing GIMMS and MODIS NDVI time series across various eco-zones and environments. Nonetheless, the findings of this study are necessarily restricted to the selected study area.

2.2. MODIS Dataset and Temporal Smoothing

We used the MOD13Q1 and MYD13Q1 NDVI collection 5 products of the MODIS Terra and Aqua satellites from 2000 onwards from the Land Processes Distributed Active Archive Center (LP DAAC). The data of both satellites are processed in a phased production providing a global NDVI with improved temporal frequency of eight days (Terra 16-day period starting Day 001, Aqua 16-day period starting Day 009). The gridded Level-3 product offers data in approximately 250-m spatial resolution in Sinusoidal projection. The Level-3 product is calculated from the Level-2G daily surface reflectance gridded data (MOD09 and MYD09 series) using the Constrained View angle-Maximum Value Composite (CV-MVC) compositing method [61].
For processing the data, we set-up in a first step an operational processing chain that downloads, mosaics, resamples, reprojects, and performs an image cropping to a dedicated tile system on a daily basis based on the “MODIS” R package [62]. The data are reprojected to geographic coordinates (datum WGS84) using nearest neighbor resampling. One file of the dedicated tile system covers the extent of 1 × 1°. The 448 × 448 pixels per tile have thus a spatial resolution of 0.002232°. The reprojected data are archived and further processed in two different ways: (1) an on-demand simplified filtering is applied upon user’s request via a web application [63], and (2) operational filtering procedures are applied for European areas with two processing lines: (i) an enhanced near real-time (NRT) weekly processing of new/updated NDVI data, and (ii) a processing of the entire NDVI time-series at once (launched only once a year). For this study, only the last data (ii) were considered. All procedures were implemented in MATLAB and are based on the Whittaker smoother [28,64,65]. Compared to our web application [63], the operational filtering procedures have the advantage to take the MODIS quality flag during smoothing into account, as well as the exact composite day. The Whittaker smoother was shown to perform well against a number of other filters based either on curve fitting or Fast Fourier transform (FFT) [66]. In [64], it was shown that this filter permits a significant increase in the signal-to-noise ratio (SNR) of coarse resolution NDVI time series.
Besides VI usefulness information, the smoother also takes into account land/water mask layers of the VI Quality Assessment Science Data Set [61]. Pixels having a VI usefulness value lower than three were considered to be acceptable and assigned a weight of one (very good to good quality), while a VI usefulness larger than seven was excluded from further processing with a weight of zero (not acceptable). VI usefulness values between three and seven were linearly scaled between one and zero.
For the back-processing, the smoothing parameter λ of the Whittaker filter was fixed to a constant value for the entire study region. After some trial-and-error tests, a value of 30.000 was found acceptable, balancing fidelity to the MODIS data with the roughness of the resulting curve. To further reduce the possible impact of undetected clouds and poor atmospheric conditions, three filtering iterations were performed to fit the upper envelope of the NDVI. Multiple filter runs were for example recommended by [2,12]. The second parameter of the Whittaker smoother (i.e., order difference) was set after some tests to two. Based on the order difference, the smoother calculates the roughness of the smoothed curve [65]. From the resulting daily NDVI values (combining inputs from MOD13Q1 and MYD13Q1), all images corresponding to “Mondays” were extracted and stored as a 7-daily data set. This NDVI is further referred as filtered MODIS data set. The weekly data were considered sufficient for most of the analyses, reducing the computational load of the exercise. For the analysis of timing of (phenological) events, however, the (smoothed) daily NDVI series were used allowing a better retrieval of start/maximum of season.

2.3. Spatial Degradation of MODIS Data

After smoothing, the MODIS data set was spatially aggregated to fit the resolution of the GIMMS data set (1/12°). This was done by averaging the smoothed MODIS data to the GIMMS grid. Pixels flagged as water were excluded from the averaging procedure. With respect to coastal pixels, a mask was applied for the subsequent analysis. It comprises all pixels that represent water in at least one time step of either of both time series. This mask was expanded by one pixel to further reduce possible artifacts. The remaining land pixels should be largely unaffected by coastal water. However, no attempts were made to exclude inland water bodies from the two series.
As the NDVI does not scale linearly there will be a certain impact compared to aggregating the reflectances and then calculating NDVI e.g., [67]. Nevertheless, we decided to aggregate NDVI rather than the reflectances. The decision was done after having analyzed the impact of the different aggregation approaches for a test dataset (2002 to 2004) covering the Iberian Peninsula. For the exercise, MOD09Q1 reflectance data were used. From the reflectances, the two spatially aggregated NDVI were calculated. It turned out that the impact of different aggregation schemes was significantly smaller than the one caused by using different sensors (not shown).

2.4. GIMMS Dataset

The NDVI3g data set is the latest version of the Global Inventory Modeling and Mapping Studies (GIMMS) project [44]. The data set is currently under investigation by a number of research teams. Important contributions can be found in this special issue. The original GIMMS data set was produced from the AVHRR sensor data taking into account various deleterious effects, such as calibration loss, orbital drift, volcanic eruptions, etc. [68]. The third generation GIMMS NDVI is a 15-day Maximum Value Composite derived from AVHRR sensor data from NOAA 7 to 18 satellites. It covers the period 1981–2011. The data set has an improved calibration and cloud masking compared to older versions of the GIMMS data set [44]. For the purpose of our study, the extent of the GIMMS NDVI3g data set was cut to the extent of the study area (Figure 1), while preserving the original GIMMS NDVI3g grid with a spatial resolution of 1/12°.

2.5. Temporal Smoothing of GIMMS

To allow comparability between the two time series, the GIMMS data set was smoothed in a similar way as the MODIS data. As the exact composite DOY of the GIMMS data set is not known, the 8th and 23th day of the month were assigned as DOY for the 1st and 2nd compositing period of the month, respectively (Table 2). Next, the Whittaker filter was applied to the GIMMS data set to produce daily NDVI values between 2002 and 2011 (ten years). Similar to the MODIS data, the filtered GIMMS data were saved as 7-daily values (corresponding to Mondays). For detecting the phenological indicators, we made again use of the daily GIMMS values.
Regarding a suitable filter setting for the GIMMS data, different tests were performed. The tests aimed at identifying a parameter setting providing GIMMS data similar to the MODIS data in terms of curve shape, amplitude and timing of feature of the NDVI profiles. The decision was made based on the root mean square difference (RMSD) between the data sets. The selected setting was a λ of 30.000, one iteration and a second order difference. Table 2 summarizes the main choices regarding the spatio-temporal homogenization of the two data sets.
Note that filtering the GIMMS time series ending December 2011 implies that the last observations were possibly less accurately filtered compared to observations situated in the middle of the series (e.g., temporal edge effects). This was considered overall acceptable but might influence some of the results. This problem did not occur when filtering the MODIS data because the MODIS time series extends into 2013 (and starts before 2002).

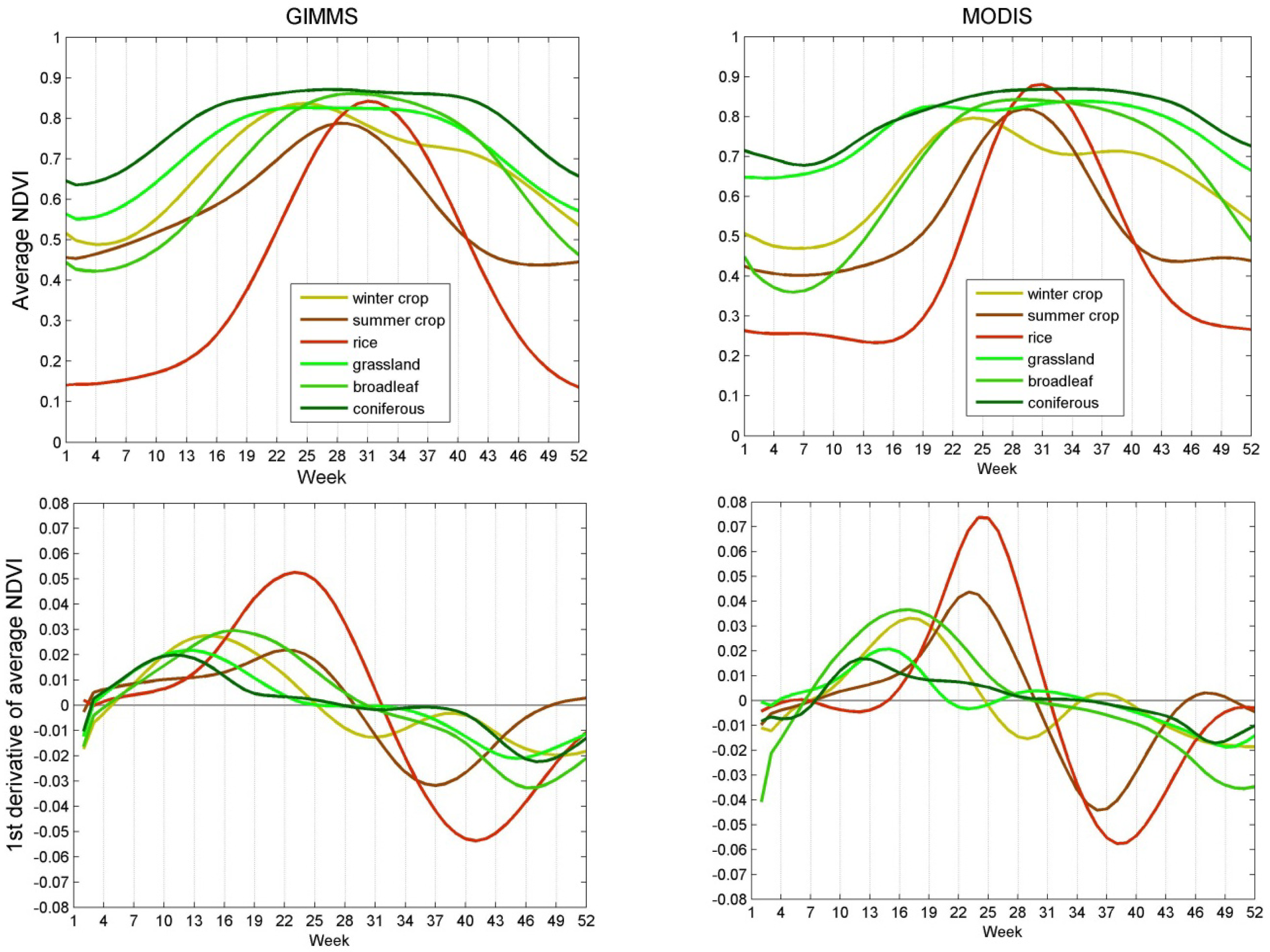
2.6. Extraction of Start (SOS) and Maximum of Season (MOS)

Phenological metrics were extracted for all pixels having a maximum NDVI of at least 0.3. An approach was implemented for detecting uni- and bi-modal growing seasons. In case of bi-modal growing seasons, only the metrics of the first season were extracted. The selected approach can also handle seasons spanning over different years. The extraction was done in four steps:
(1)
Detecting the number of cycles by means of auto-correlation information (e.g., [69]): The number of lags was chosen to be little less than two years. Next the algorithm was searching for maxima and minima on the auto-correlation function (ACF). Two cycles were detected, if a second distinct maximum in the ACF before the end of the year appeared. The maximum was accepted, if the increase before the maximum and decrease after the maximum in the ACF was more than 0.1.
(2)
Focus on the first season in case of multiple cycles: If in either of the time series two growing seasons were identified, the algorithm searched for two starts and two maxima each year, while only the first start and maximum was included in the subsequent comparison of the time series.
(3)
Defining a temporal search window for each growing season: In a first step the algorithm was searching for the maximum NDVI of each season. The growing season was considered to be centered around the maximum, while the size of the range depends on the number of detected cycles. The start (SOS) will be found between the moment of minimum and the moment of maximum. Even if filtered NDVI curves were used, there might be still several preceding minima. To identify a reasonable and reproducible minimum, the steepest preceding increase was chosen as a criterion. This criterion accounts for the number of increasing time steps and the NDVI difference.
(4)
Detecting start of season (SOS) and maximum of season (MOS): The start of season was detected using a relative threshold [3,70,71], namely when the NDVI increased 20% of the seasonal amplitude from seasonal minimum. The maximum was defined at the time of the largest NDVI in the growing season.
The extraction procedure used the entire filtered time series from 2002 to 2011 at daily time steps. However, the actual start and maximum were detected for the growing seasons from 2003 to 2011. This restriction was necessary as growing seasons might span different years. For example, valid starts of the growing season of 2003 can range from beginning of July 2002 (−183) to end of June 2003 (181) counted in days of year (DOY). The timing of the seasonal maximum is defined in a similar way, e.g., ranging from the beginning of November 2002 (DOY −60) to end of October 2003 (DOY 304). If values occurred outside the defined start and maximum ranges, they were considered misdetections and flagged as “no data”. A number of alternative algorithms for extracting phenological signals from remotely sensed time series have been described in the literature (for a review see [3,72]). However, it was out of scope of this study to explore more than one algorithm.

3. Results

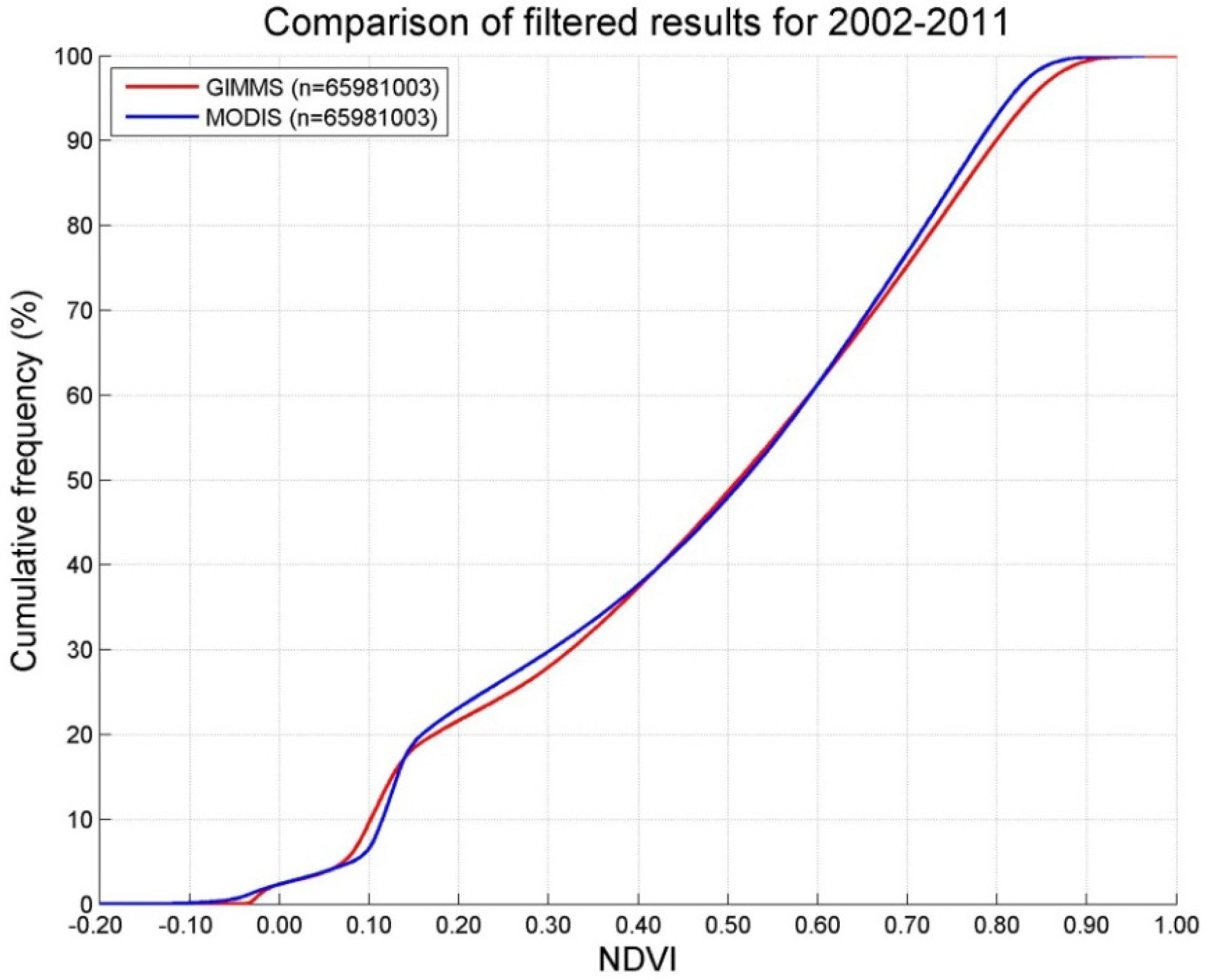
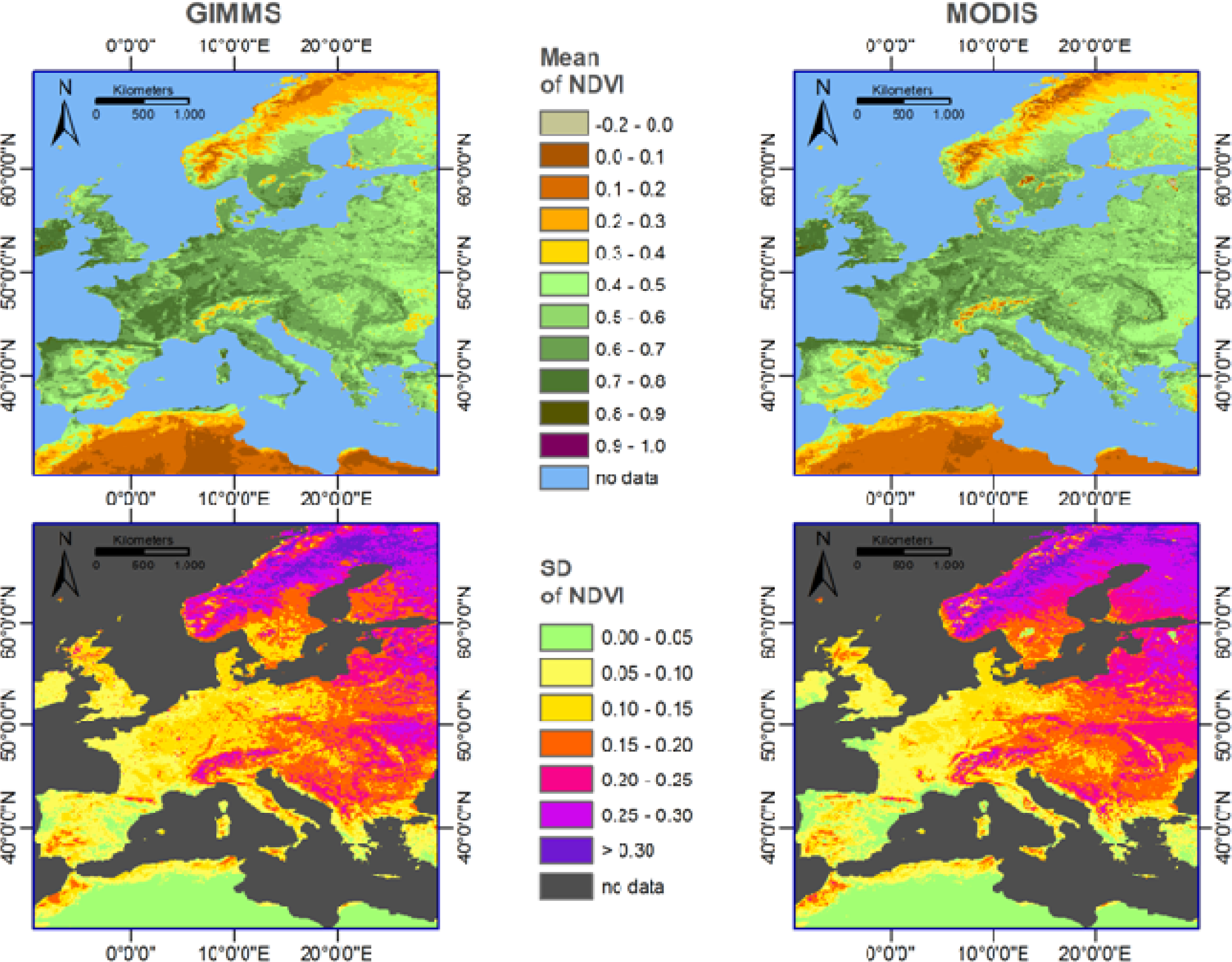
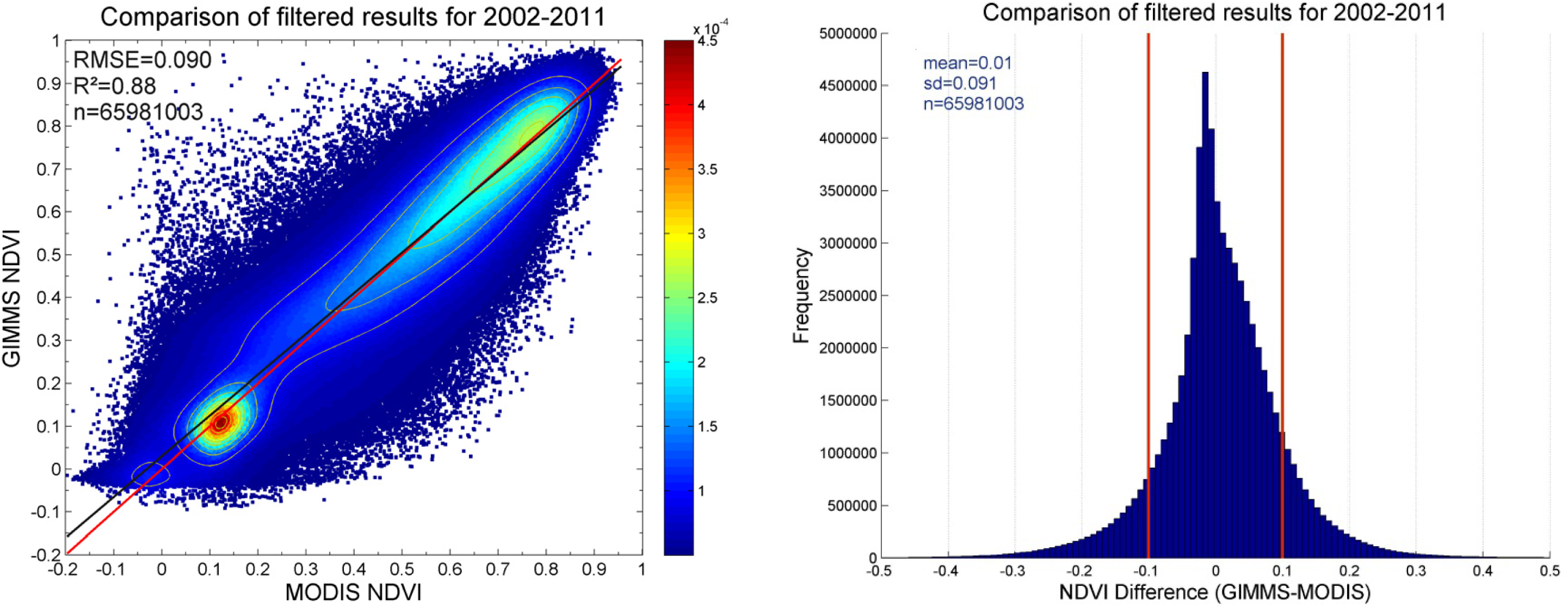
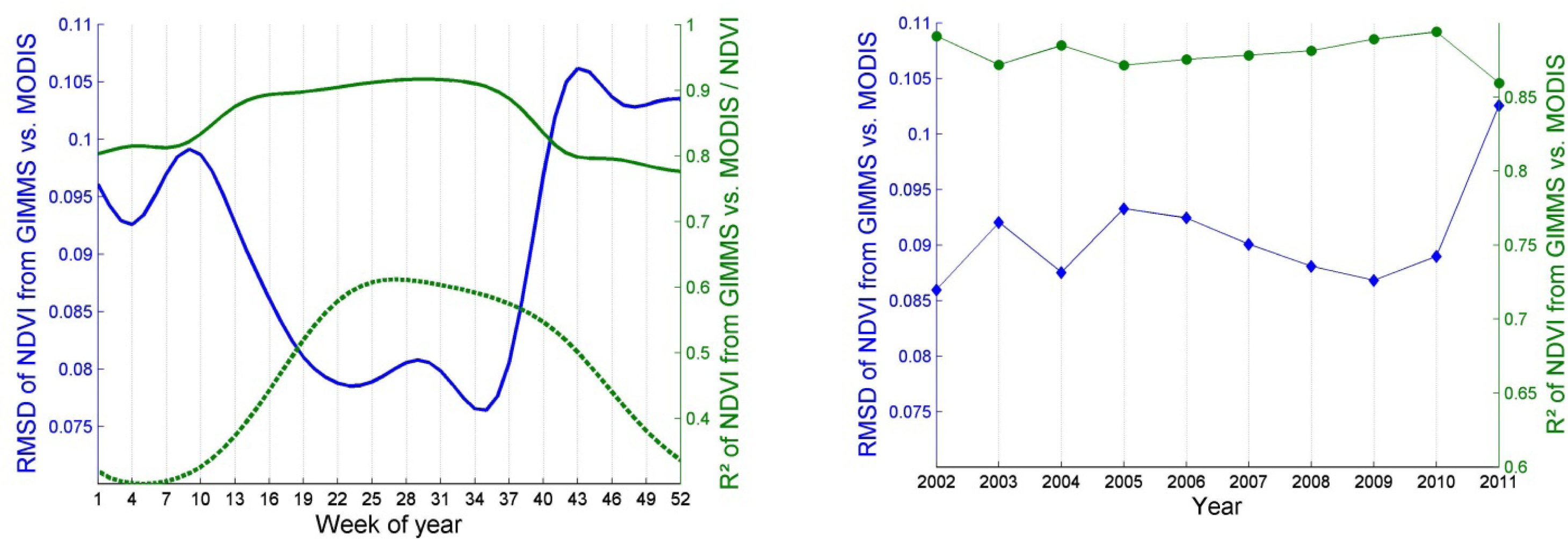
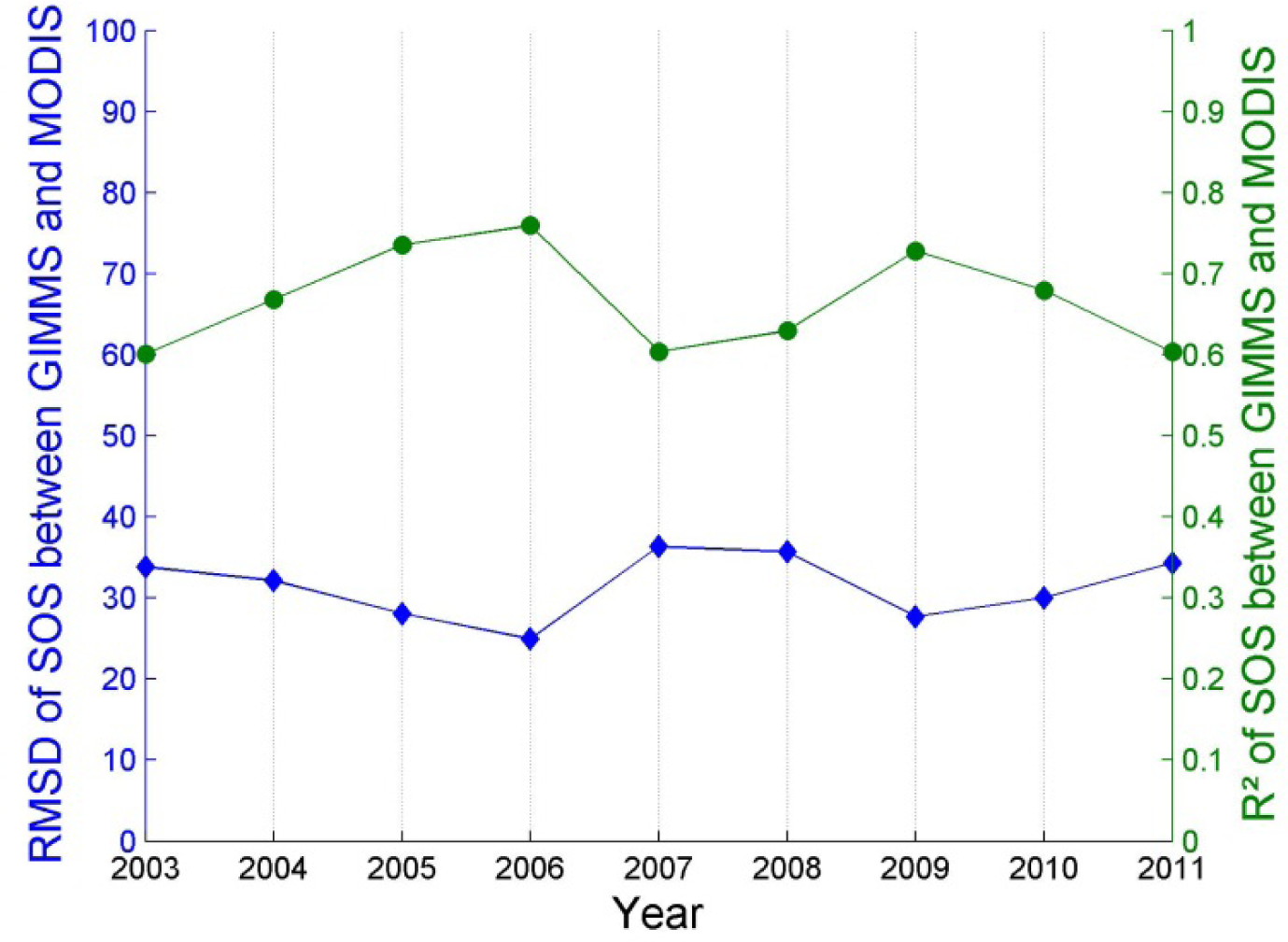
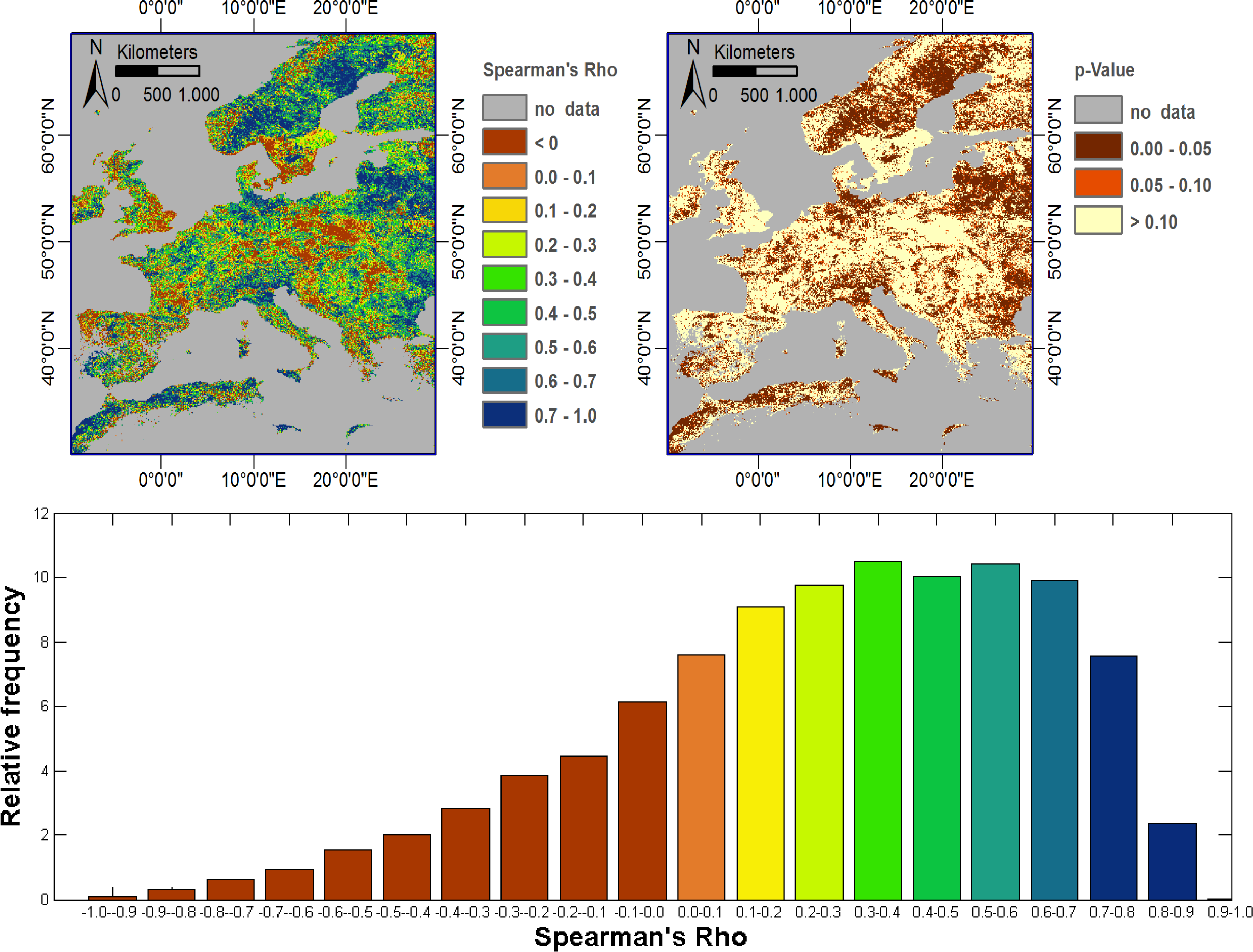
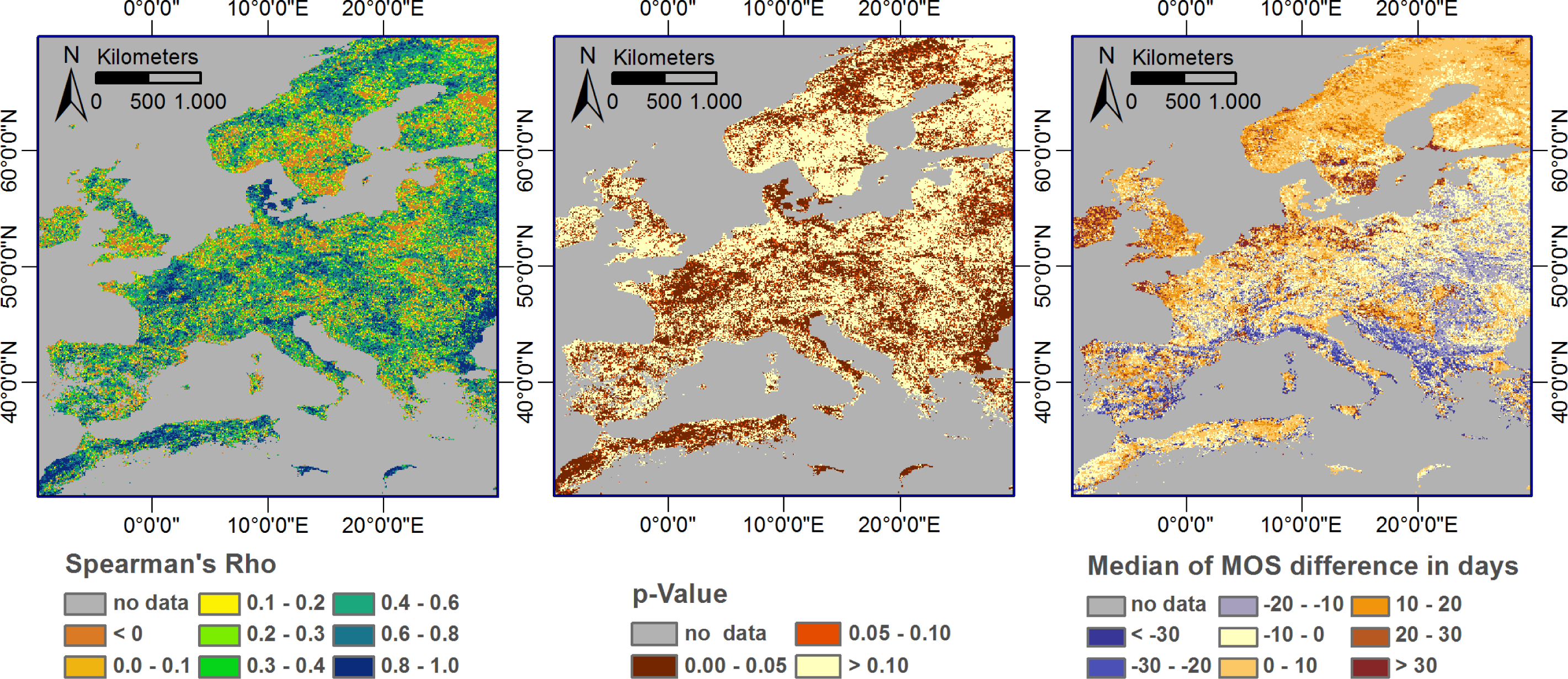
3.1. Data Distribution and Correlation

Generally, GIMMS and MODIS NDVI data sets show a reasonable agreement regarding their spatial distribution and temporal behavior. Exemplary annual profiles (averaged over the 2002–2011 time period) of the two time series are reported in Figure 2. Likewise, the two cumulated distribution functions derived from the entire time series display only little divergences (Figure 3). This also holds for the multi-annual mean and standard deviation (Figure 4). Together these findings demonstrate a generally relative good correspondence between the GIMMS and MODIS derived vegetation densities. It also demonstrates the success of the applied pre-processing and smoothing, yielding identical spatial and temporal resolutions of the originally very different data sets.
However, despite the general agreement, some persistent differences can be observed. In particular, in winter time, significant differences in the averaged NDVI of the two time series are visible in Northern and Eastern Europe (e.g., Sweden, Finland) (Figure 5). On the contrary, the agreement between the two data sets is better for these areas during summer months (June, July, and August) and (to a lesser extent) in spring and autumn. The same can be observed in Figure 2 where some of the displayed profiles reveal a stronger disagreement during winter time. However, particularly in Spain, France and Italy, one can observe higher differences in the summer and spring months than in winter.
The differences between the two time series become more evident, when plotting (pixel-by-pixel) the NDVI values against each other (Figure 6). The results indicate relatively large scatter around the 1-to-1 line with sometimes extremely large differences between individual observations. In addition, a small bias between GIMMS and MODIS is observed. The GIMMS data reveal on average a somewhat higher NDVI compared to MODIS. However, most of the observations fall well within a range of ± 0.1 NDVI units (Figure 6, right). Calculated over all pixels and all time steps (i.e., all weekly observations between 2002 and 2011), we find a correlation between GIMMS and MODIS time series of about (R2) 0.88 (Figure 6). This correlation shows a clear seasonal component (Figure 7, left). The intra-annual coefficient of determination (R2) varies between 0.78 (winter) and 0.92 (summer).
A value of R2 ≥ 0.9 is found between week 13 (end of March) and 37 (mid-September). The root mean square difference (RMSD) exceeds >0.05 throughout the year (blue line), with values approaching or exceeding 0.10 between week 40 (Beginning of October) and 13 (End of March). This confirms again that the largest differences regarding the observed vegetation densities occur during winter time. The inter-annual agreement/disagreement between the two data sets is depicted in Figure 7 (right). Results show only little variability from year to year, except for the last year in the time series (2011). Indeed, this year is the last year in the original GIMMS time series. Hence, the filtering/smoothing might be affected by the temporal edge effects mentioned before (2.5). This will in particular affect the November/December observations of GIMMS (see also weeks 49 to 52 in Figure 7 left). We tested the effect of excluding the weeks 49–52 of 2011 on the calculations of Figure 7. The biggest absolute differences for the intra-annual variation of RMSD and R2 appear in week 52 with 0.006 and 0.02, respectively. The absolute differences for the inter-annual variation of RMSD and R2 calculated for 2011 are slightly lower. As the described differences in these particular weeks are irrelevant for calculating SOS and MOS, we kept all data in our analysis.
The spatial pattern of the pixel-wise correlation between the two time series across all weekly observations is shown in Figure 8 (left). The map reveals a clear spatial pattern with high correlations (>0.8) over much of the central and eastern part of Europe as well as the northern parts of the Maghreb countries (Algeria and Morocco). Correlations are markedly lower in the coastal parts of Spain, Italy, and Greece/Turkey and to a lesser extent in France, Ireland and the UK. Particularly in Portugal, Galicia, and to a lesser extent in Brittany, very low correlations are accompanied with almost continuously high NDVI levels and a low variability (see Figures 4 and 5). In these areas, clear differences between the NDVI profiles occur (not shown). Very low correlations between the time series are also found over the arid parts of North Africa. In these areas, however, the low correlations are a direct result of the constantly low vegetation density (Figure 5). To further explore the impact of intra-annual vegetation dynamics on the derived (pixel-wise) agreement/disagreement between the two time series, Figure 8 (right) shows the RMSD between the two data sets.
The RMSD pattern displays a relatively high disagreement over Scandinavia and Eastern Europe, but also in the alpine region and Spain. The best agreement is observed over the constantly dry parts of North Africa (e.g., Sahara) and the non-coastal areas of the UK and Ireland. Some larger reddish spots (RMSD > 0.2) in Sweden and Estonia/Russia are due to inland lakes not masked out for this study.

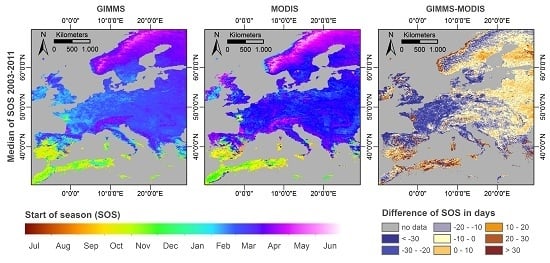
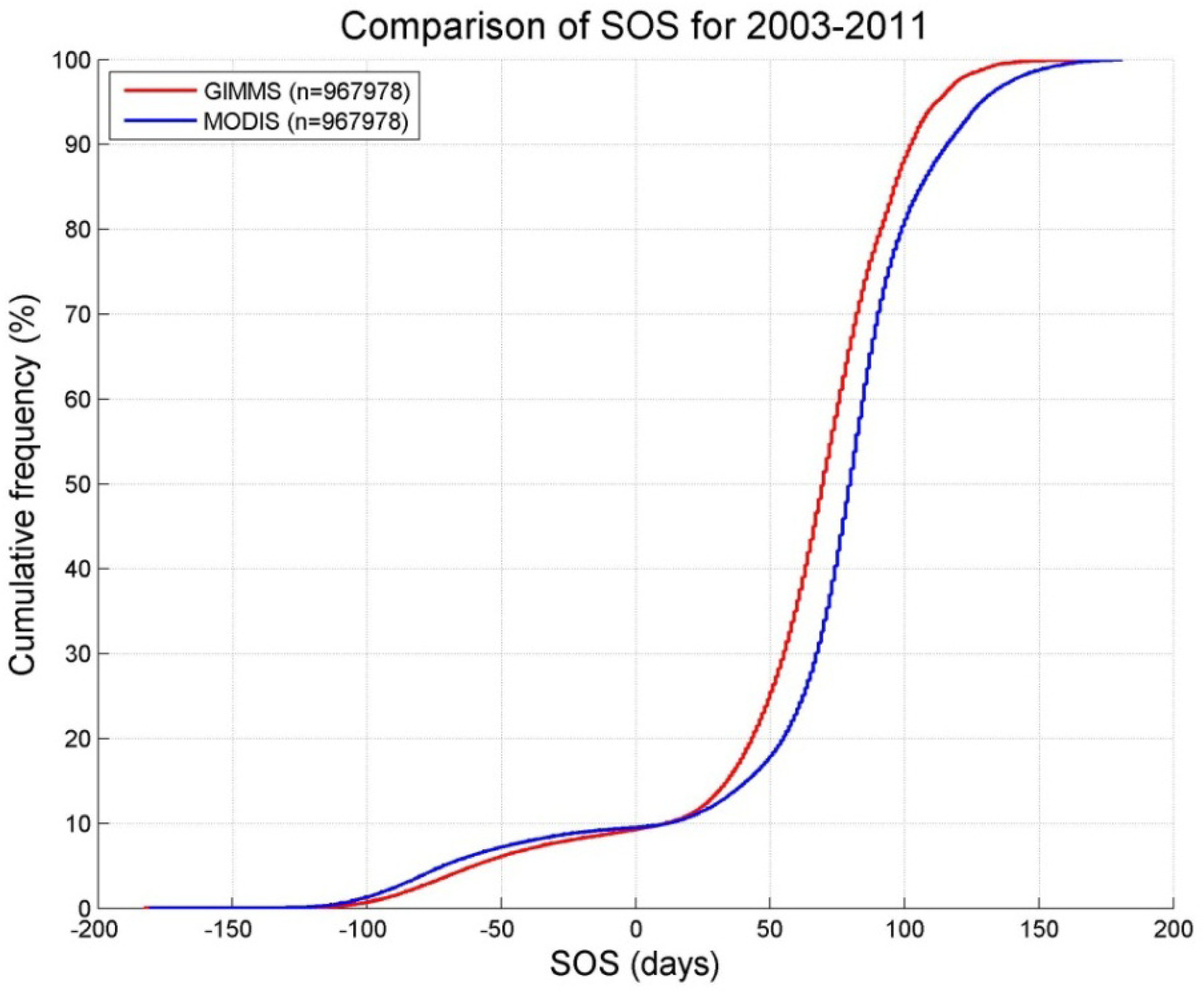
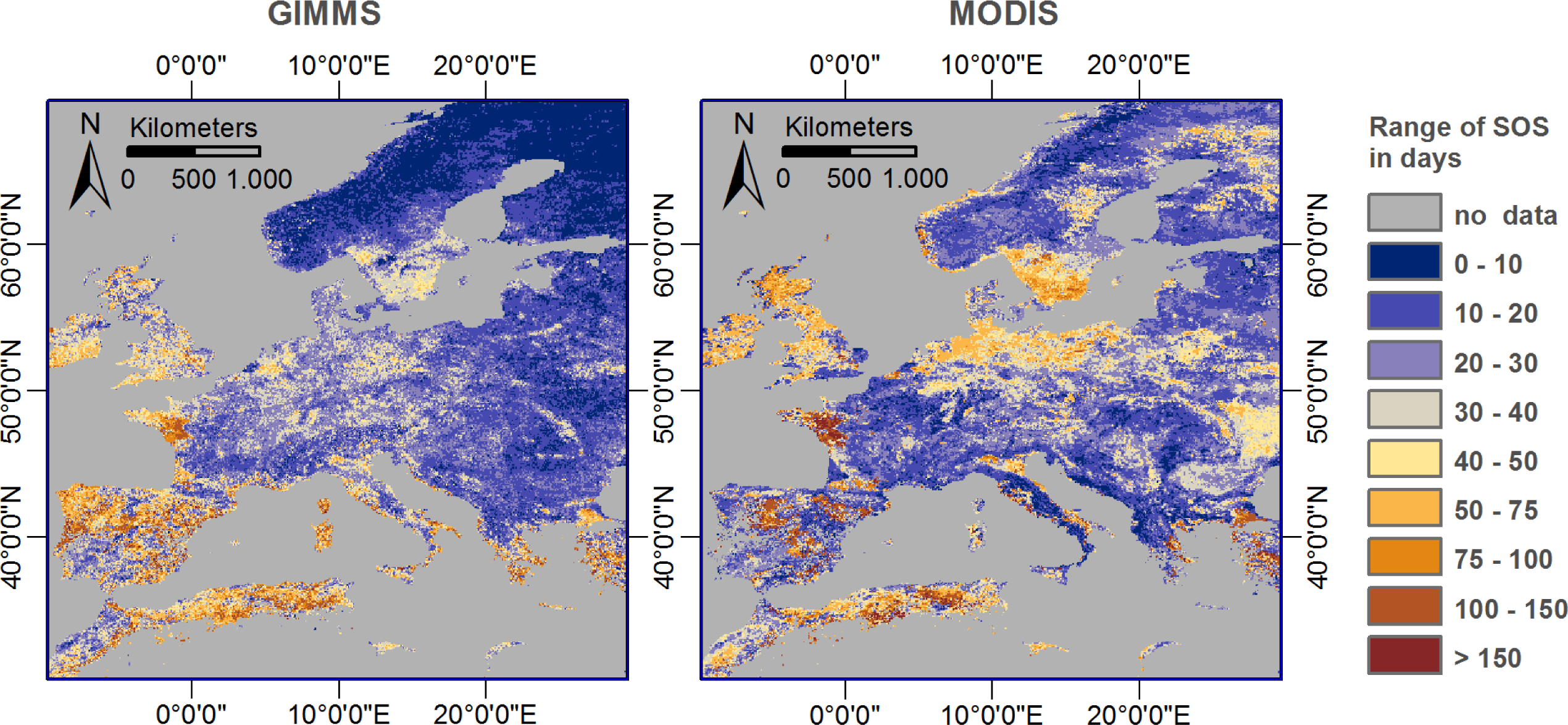
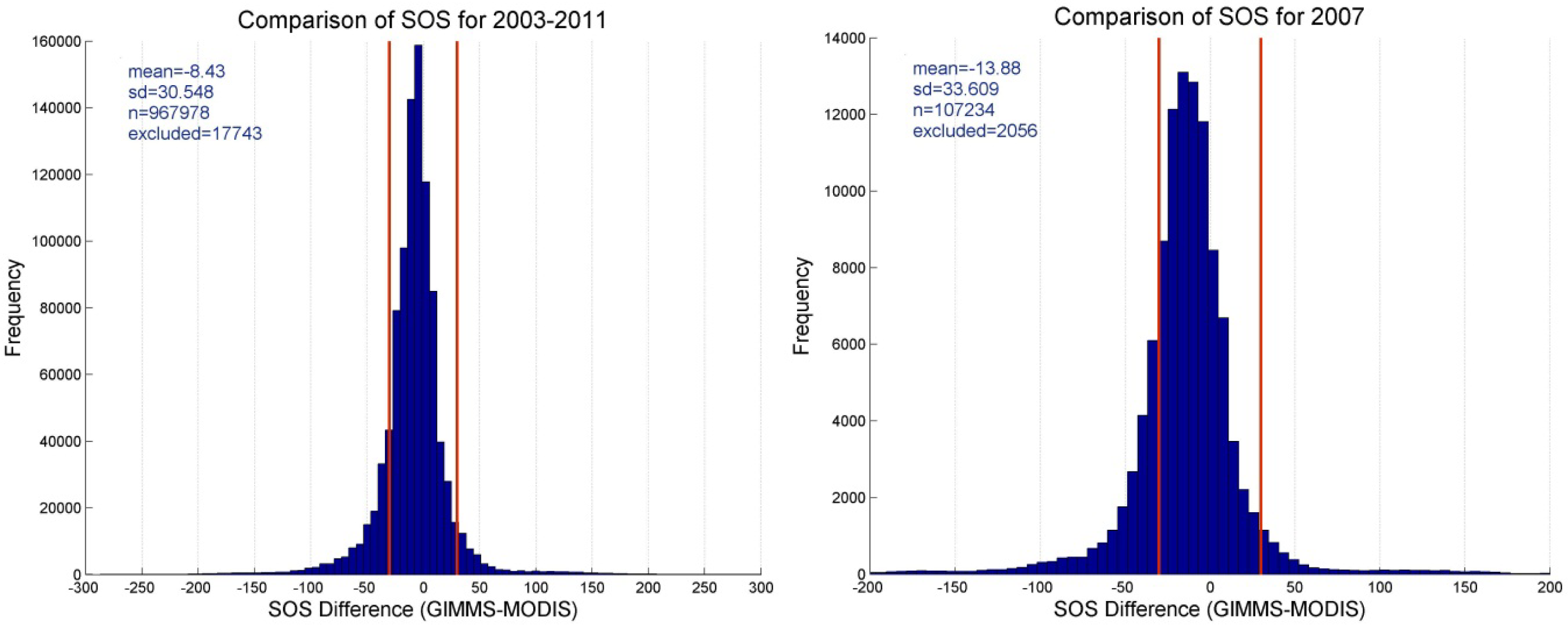
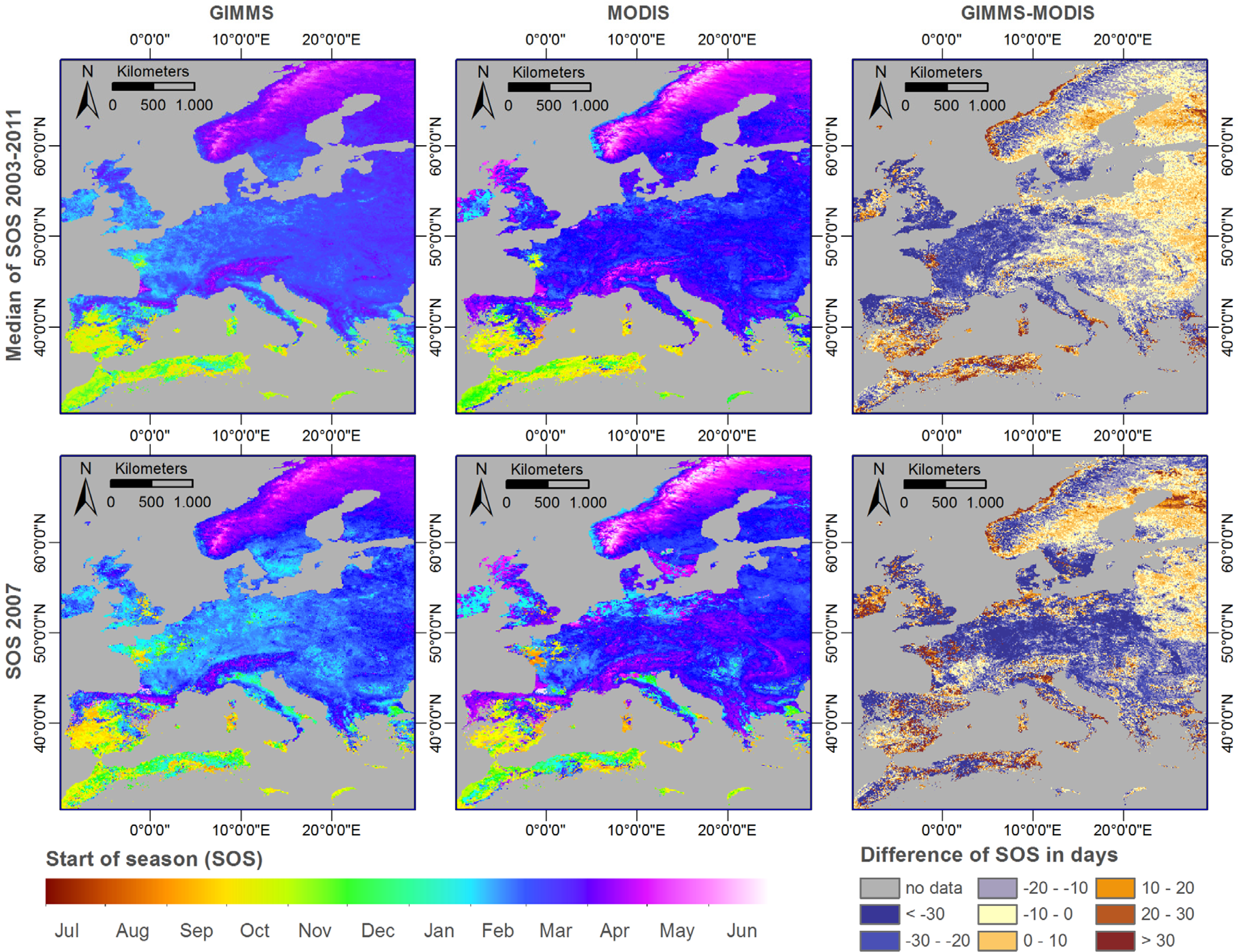
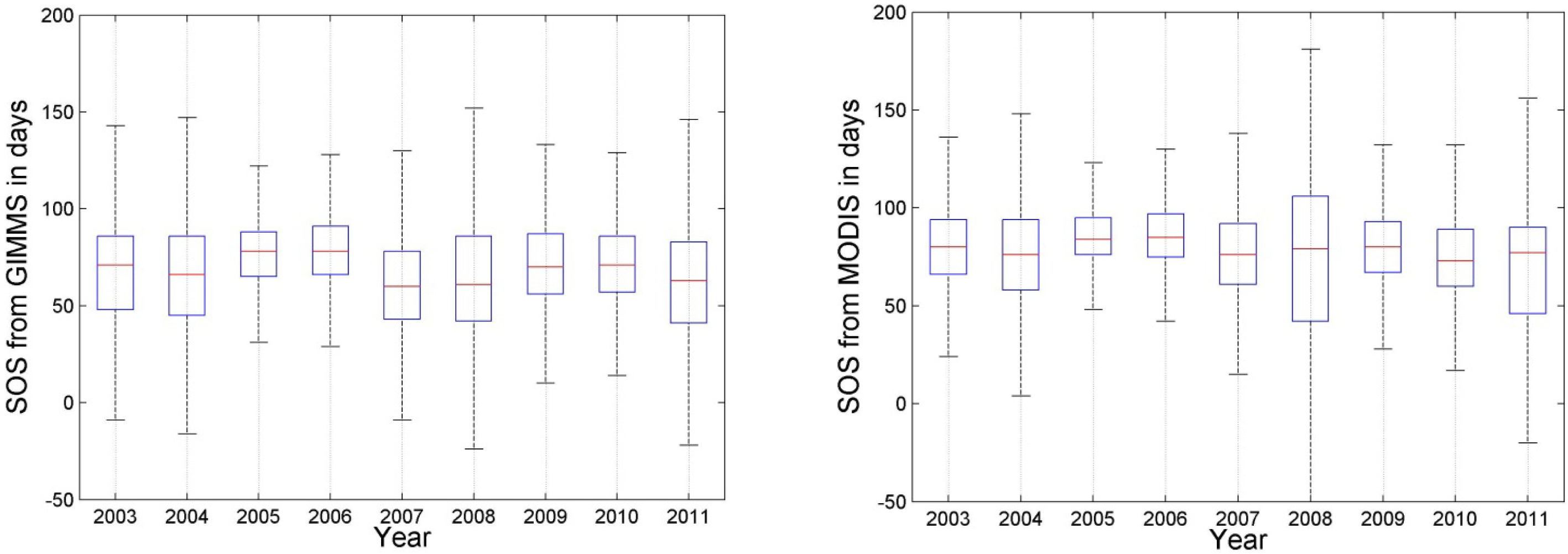
3.2. Phenology: Start of Season (SOS)

The start of the season (SOS) was determined for each pixel and each year in the time series (2003–2011) using the relative threshold approach described in Section 2.6. The algorithm yields up to nine SOS estimates per pixel. The cumulated distribution functions of SOS derived from the two time series are shown in Figure 9. Both data sets reveal a similar shape of the SOS distribution. However, GIMMS (in red) depicts SOS frequently more than one week earlier, compared to MODIS (in blue). A similar trend is already visible in Figure 2 where the NDVI profiles of the GIMMS data start rising earlier than MODIS.
The inter-annual variability (“range”: difference (in days) between maximum and minimum) of SOS exhibits a relative similar spatial distribution in both data sets (Figure 10). However, the SOS extracted from the MODIS time series shows a larger inter-annual variability compared to GIMMS in many coastal areas of the North Sea (Belgium, Netherlands, Germany, Poland, and Sweden). The opposite can be observed over the north part of Spain.
A more detailed analysis at pixel level shows that the SOS extracted from the two series often reveal high differences. Figure 11 (left) presents the frequency distribution of the SOS differences (SOSGIMMS–SOSMODIS) over the entire time series (2003–2011). It can be seen that many observations fall outside the range of ±30 days. Only 32% of the observations have (acceptable) differences ≤1 week. Generally, GIMMS depicts the SOS earlier than MODIS confirming earlier findings (Figures 2 and 9). This can be consistently observed for individual years and is exemplarily shown in Figure 11 (right) for the year 2007. In this example, MODIS data evidences a SOS on average 14 days later than GIMMS. The differences between the two time series can also be clearly seen when mapping the spatial distribution of the SOS for a particular year. For example, Figure 12 (right) displays the SOS for 2007 estimated by GIMMS (top) and MODIS (bottom). The median SOS across all years (Figure 12, left) confirms again the large differences between the two data sets regarding the SOS.
The disagreement between the two time series is further sustained when plotting the SOS of both time series against each other (Figure 13). The regression analysis between the two SOS data sets reveals only a R2 of ∼0.66, if data from all years are pooled together. A larger number of strong outliers can also be detected. They mostly correspond to cases where the detection algorithm (see Section 2.6) depicts different parts of the growth cycles of an individual pixel. This often happens if the profiles show multiple—but not well distinguished—peaks in one but not the other data set (not shown).
Analyzed separately for each individual year, some inter-annual variability in the correlation between SOS from GIMMS and MODIS are found (Figure 14). Somehow higher (spatial) correlations can be observed in 2005, 2006, and 2009, which also correspond to years with delayed onset of vegetation growth (negative North Atlantic Oscillation index) and more homogeneous growth patterns. Despite the R2 occasionally exceeding 0.7, the RMSD between the two series of SOS always remains in the range 30–40 days (blue).
At the pixel level, we find both high and low rank correlation (Spearman’s Rho) between SOS from GIMMS and MODIS (Figure 15). P-values were computed for testing the hypothesis of no correlation against correlation is greater than zero (Figure 15, upper right). In most cases, the strong positive correlations (>0.6) were significant at the 0.05 level. Low/negative correlations are often present in areas with reduced inter-annual variability of SOS and where extracting SOS is influenced by snow cover (Figure 10).

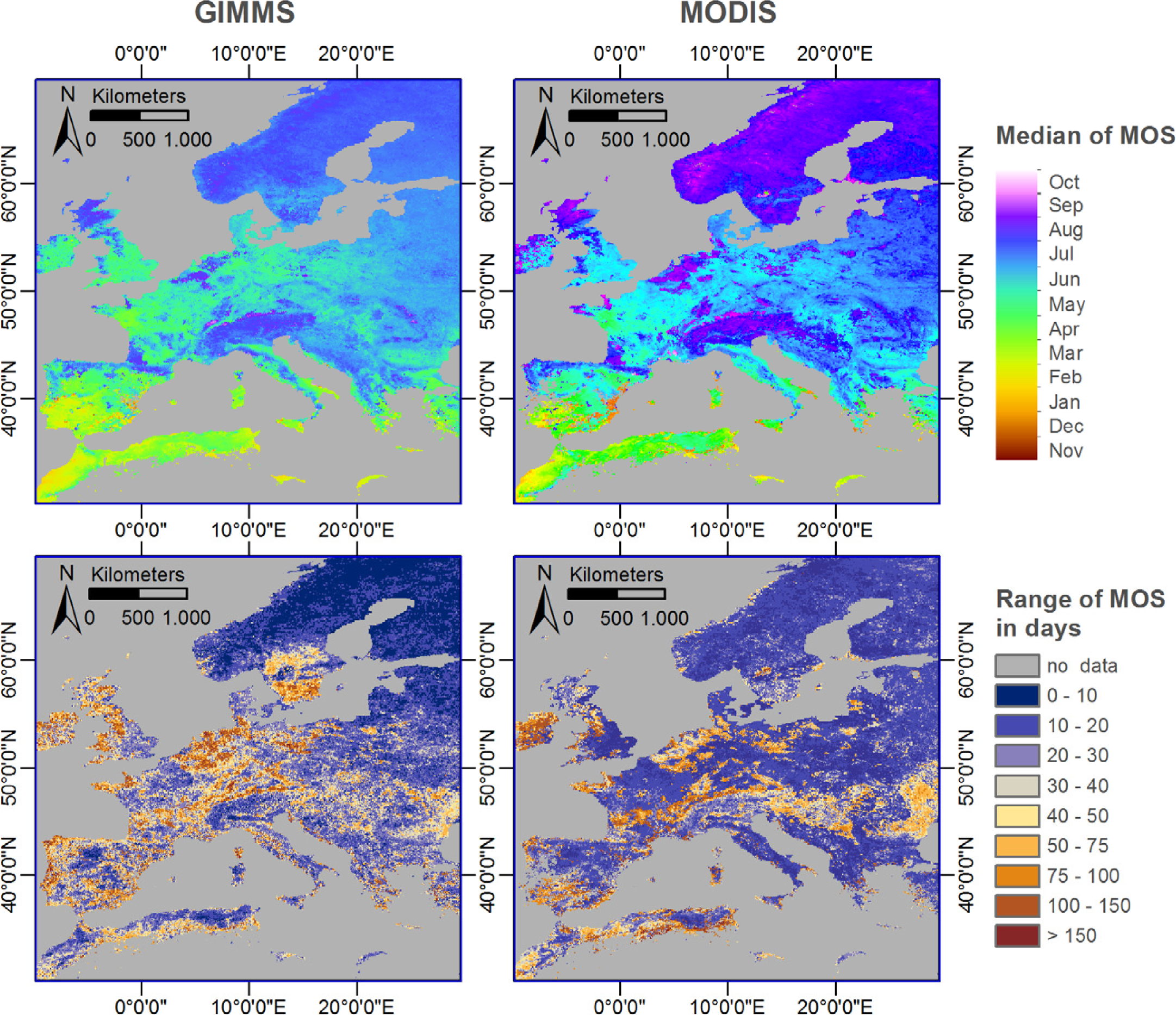
3.3. Phenology: Maximum of Season (MOS)

Similar to the SOS, the maximum of the season (MOS) was determined within the growing season for each pixel and each year in the time series (2003–2011), yielding up to nine MOS estimates per pixel. The cumulated frequency distributions of the MOS extracted from GIMMS and MODIS are shown in Figure 16 (top) demonstrating a good correspondence between the two data sets. Likewise, the co-distribution shown in the scatterplot of Figure 16 (bottom) reveals, that the majority of the pixels (in green-yellow-red) well distribute around the 1-to-1 line.
The spatial pattern in MOS is similar for the two data sets when averaged over all years (Figure 17, top). The same holds to a lesser extent for the observed inter-annual range of MOS (bottom); compared to the MODIS extracted MOS, the inter-annual variability derived from GIMMS data is often much higher. In some areas, the range between the earliest and the latest MOS exceeds 100 days where MODIS yields an inter-annual range of MOS of about 30 days (e.g., southern part of Sweden). Secondary maxima in the GIMMS data, not present in MODIS, are the main reason (not shown).
The correlation between the two MOS products at pixel level is displayed in Figure 18 (left) along with the median of differences (right). In most regions, the GIMMS and MODIS MOS values had a Spearman’s Rho exceeding 0.4. Regions with low rank correlation (left) and high p-value (center) often correspond to regions with low SOS correlation (Figure 15, top left).

4. Discussions

Before starting the comparative analysis, efforts were made to harmonize the two (originally very distinct) data sets to a common spatial (1/12°) and temporal (weekly/daily) resolution while eliminating at the same time noise and other artifacts (Table 2). Despite these efforts, we have to acknowledge that overall the two NDVI time series show only a moderately good agreement. The agreement is better between the NDVI values compared to the phenological indicators.
The overall relationship between the two weekly NDVI products (ca. 125.000 pixels × 10 years × 52 weeks) has a R2 of 0.88 and RMSE of 0.09 (Figure 6). The correlation is relatively high if one considers that the original data came with 1/12° (GIMMS) vs. 250 m resolution (MODIS) and bi-weekly vs. 8-daily temporal resolution. Comparatively analyzing fAPAR time series (fraction of absorbed photosynthetically active radiation) obtained from one single sensor (SPOT-VEGETATION), [46] found R2 between 0.60 and 0.94 for three test windows with each 10° × 10° (RMSE 0.06–0.24).
A marked seasonal component of the correlation/agreement between the two NDVI time series is observed (Figure 7, left). Disagreement between the two series is generally higher during winter (RMSE ≥ 0.10) and reduces considerably during summer (RMSE ≤ 0.08). This seems a reasonable finding as observation conditions degrade strongly during winter time leading to fewer observations with generally lower quality. This is also confirmed by analyzing the occurrence of good quality measurements in MODIS data such as VI usefulness ≤ 3 (see [61]), where fewer favorable cases are counted from November to February than in summer (not shown). Surprisingly, however, the agreement (e.g., R2) does not always go parallel with vegetation density and/or season. Instead, we observed a relatively strong asymmetry around summer. For example, the agreement in spring is relatively close to summer conditions, whereas autumn is closer to winter. Considering solely LAI, sun angle and temperatures, etc., one would expect a relatively symmetric behavior of the seasonal agreement profiles. This neglects, however, the fact that not only LAI changes during the year (with a more or less good symmetry) but also the leaf pigmentation and structure. Possibly during autumn (leaf senescence), these changes at the leaf level accentuate the (otherwise insignificant) differences in the band setting of the two sensors (AVHRR vs. MODIS).
The correlation between the two data sets shows on the other hand only a low inter-annual variability. For all years, except 2011, the R2 is close to 0.9 with RMSD of ∼0.09 showing a good correspondence in the spatial patterns of vegetation density (NDVI) of the two data sets (Figure 7, right). The significantly higher disagreement observed for 2011 is partly related to the fact that the original GIMMS series ends in 2011. Hence, when applying the smoother for noise removal, the very last observations of this data set were smoothed with a lower accuracy compared to the MODIS data for which we had observations beyond 2011 (thus, avoiding this well-known border effect). All data of year 2011 was nevertheless kept in the comparative analysis as the overall effect on NDVI differences and in particular on extracting start and maximum of season should be small.
A good agreement between the two series can also be observed regarding the spatial maps of average NDVI and corresponding standard deviation (Figure 4). The former indicator reflects the average vegetation density of a pixel, whereas the standard deviation is a proxy for vegetation dynamics/variability at a given location (combining seasonal and inter-annual dynamics). In our study, the vegetation dynamics directly influences the (pixel-wise) correlations of the temporal signatures across the continent (Figure 8). As expected, in areas with low dynamics, the R2 between the two series was considerably reduced. They fall even down to zero in the absence of any dynamics such as in the Sahara. However, we find interesting differences between the Sahara where (as expected) both R2 and RMSD approach zero, and other parts of Europe with equally low vegetation dynamics (thus, R2 ∼ 0) but with high(er) RMSD. This is for example observed in many coastal areas of the Mediterranean Sea and the NW coast of Spain/Portugal. It is currently not clear why the two data sets behave so differently in these areas.
Using the relative threshold approach similar to e.g., [3,12,49,70] two major phenological metrics were extracted for each year of the time series: start (SOS) and maximum of season (MOS). The observed spatial pattern from both data sets (Figures 12 and 17) reflects well existing gradients within Europe resulting from the combined impact of land cover, latitude, altitude, temperature, and rainfall regimes within the study area [13].
Regarding MOS, only few differences can be observed regarding the multi-annual averages (Figure 17) as well as its general frequency distribution (Figure 16). For major parts of the European continent, the Spearman’s Rho (rank) correlation coefficient between the two MOS products is ≥ 0.5 (Figure 18). The average (median) difference in MOS is often in the (acceptable) range of ±10 days. However, some striking differences can be observed. For example, lower correlations appear over the (boreonemoral) southern part of Sweden. In this area the two products differ most strongly. Whereas both products show moderate differences in terms of average MOS (10–20 days) for this region, the corresponding inter-annual variability (range) differ significantly (Figure 17); GIMMS data yielded an inter-annual range of MOS of more than 50 (sometimes more than 75) days. On the contrary, the MODIS data exhibit smaller (and possibly more reasonable) ranges of ±20 days.
The same region is again noticeable in the SOS data of GIMMS (Figure 12). Indeed, the GIMMS data show a start of season as early as for example (oceanic) Ireland (e.g., in February). This contrasts for example with maps published by [73] in which the average onset of spring for this region was reported to be April/May with similar values in a large region ranging from Denmark to Southern Finland. A very similar spatial pattern of SOS is observed in the MODIS data in the mentioned region. At the same time, the MODIS data also depict the earlier onset of vegetation growth in Ireland. The MODIS data also well reflect the spatial pattern (and absolute values) of SOS published in [74] for southern Norway. In their work the range of Birch flowering was between April and June with an earlier onset towards coastal (low level) areas.
Regarding the inter-annual variability (range) of SOS for the most northern parts of the test window (e.g., Norway, Sweden, and Finland) we could compare our maps against data published by [75]. In the mentioned publication it was shown that the SOS of the entire region could vary at least ±10 days. This is not well reflected in the GIMMS data where the range of SOS is often only 0–10 or at maximum 10–20 days (Figure 10). On the contrary, the MODIS derived SOS range is at least 10–20 days or more.
The most striking difference in SOS concerns however the (large) area of central Europe (from France/UK to Germany/Poland) (Figure 12). For the mentioned region, GIMMS maps the average SOS as early as February, whereas MODIS depicts the SOS between March and April. Although direct evidence is missing we believe that the GIMMS derived vegetation onset is probably too early. For example, maps produced by the German Weather Service (DWD) involving key tree species such as birch and apple, as well as common agricultural (winter) crops such as winter wheat and oats, defined the onset of growing season in Germany only around March/April. A more detailed study will have to correlate the remotely sensed maps with the mentioned reference maps, respectively, field observations. This is however beyond the scope of the present study.
More research is also needed to verify that the observed differences in SOS persist in case of using different detection algorithms. For MOS, there might be differences in using for example a curve fitting approach, e.g., [12]. Special attention is needed in case of flat plateaus or when secondary maxima appear near the plateau. Several studies have pointed out that huge differences can be obtained for individual phenological metrics, depending on the employed phenological algorithm [3,72]. Hence, it cannot be excluded that the observed differences in SOS and MOS patterns are solely the result of the selected detection algorithm.

5. Conclusions

The research is a first attempt to analyze in a comparative way NDVI time series from GIMMS and MODIS (2002–2011) over a large and heterogeneous study area in Europe. The intention is not to qualify one of the two data sets of being ‘better’ but to highlight existing differences and agreements. The comparison between existing products yields important information regarding the feasibility of creating “combined” historical archives of NDVI (and derived phenological indicators). With the launch of Sentinel and Proba-V satellites, such cross-sensorial studies will become more and more important as they permit to effectively address issues related to the ongoing climatic change.
The study reveals several points worth being mentioned:
  • Overall, the NDVI data sets from GIMMS and MODIS show only a moderately good agreement. Differences in observed vegetation density (NDVI) are largest in winter, followed by autumn. The best agreement is observed during summer. This highlights the need to carefully inter-calibrate the two data sets, giving special attention to autumn and winter. Without such an inter-calibration, the two data sets cannot be analyzed concurrently.
  • The maximum of season (MOS) extracted from the two time series shows a good agreement with respect to the observed spatial pattern and its inter-annual variability. However, more research is necessary to explain the observed differences in the timing of vegetation onset (start of season—SOS). GIMMS consistently shows higher vegetation densities during spring. Its temporal NDVI profiles therefore start rising very early in the year and earlier than those of MODIS. This leads to, sometimes, very large differences in the mapped SOS of both data sets. Without removing these differences, the two data sets cannot be combined for phenological studies.
  • Regarding the start of season (SOS), differences were observed regarding spatial pattern and inter-annual variation. Only a part of these differences are of systematic nature and could therefore be corrected a posteriori. This again clearly highlights the need of a well-done cross-sensor inter-calibration.
  • Future studies should focus on validating phenological indicators. At least for some countries of Europe, long lasting and relative dense phenological networks exist (e.g., Germany and Austria). This permits comparing the remotely sensed indicators against field observations as already shown by e.g., [76–78].

Acknowledgments

We thank Ranga Myneni, Jorge Pinzón and Zaichun Zhu for providing the NDVI3g of Europe for this paper, and the three reviewers for their valuable contributions. The MODIS MOD13Q1, MYD13Q1, MCD12Q1 and MOD09Q1 data were obtained through the online Data Pool at the NASA Land Processes Distributed Active Archive Center (LP DAAC), USGS/Earth Resources Observation and Science (EROS) Center, Sioux Falls, South Dakota ( https://lpdaac.usgs.gov/get_data). The computations have been partly achieved using the Vienna Scientific Cluster (VSC).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Reed, B.C.; Brown, J.F.; VanderZee, D.; Loveland, T.R.; Merchant, J.W.; Ohlen, D.O. Measuring phenological variability from satellite imagery. J. Veg. Sci 1994, 5, 703–714. [Google Scholar]
  2. Beck, P.S.A.; Atzberger, C.; Høgda, K.A.; Johansen, B.; Skidmore, A.K. Improved monitoring of vegetation dynamics at very high latitudes: A new method using MODIS NDVI. Remote Sens. Environ 2006, 100, 321–334. [Google Scholar]
  3. White, M.A.; de Beurs, K.M.; Didan, K.; Inouyes, D.W.; Richardson, A.D.; Jensen, O.P.; O’Keefe, J.; Zhang, G.; Neman, R.R.; van Leeuwen, W.J.D.; et al. Intercomparison, interpretation, and assessment of spring phenology in North America estimated from remote sensing for 1982–2006. Glob. Chang. Biol 2009, 15, 2335–2359. [Google Scholar]
  4. Tucker, C.J.; Vanpraet, C.; Sharman, M.; van Ittersum, G. Satellite remote sensing of total herbaceous biomass production in the Senegalese Sahel: 1980–1984. Remote Sens. Environ 1985, 17, 233–249. [Google Scholar]
  5. Atzberger, C. Advances in remote sensing of agriculture: Context description, existing operational monitoring systems and major information needs. Remote Sens 2013, 5, 649–981. [Google Scholar]
  6. Rembold, F.; Atzberger, C.; Savin, I.; Rojas, O. Using low resolution satellite imagery for yield prediction and yield anomaly detection. Remote Sens 2013, 5, 1704–1733. [Google Scholar]
  7. Kerr, J.T.; Ostrovsky, M. From space to species: Ecological applications for remote sensing. Trends Ecol. Evol 2003, 18, 299–305. [Google Scholar]
  8. Anyamba, A.; Eastman, R. Interannual variability of NDVI over Africa and its relation to El Niño/Southern Oscillation. Int. J. Remote Sens 1996, 17, 2533–2548. [Google Scholar]
  9. Herrmann, S.M.; Anyamba, A. Recent trends in vegetation dynamics in the African Sahel and their relationship to climate. Glob. Environ. Chang 2005, 15, 394–404. [Google Scholar]
  10. Ji, L.; Peters, A.J. Assessing vegetation response to drought in the northern Great Plains using vegetation and drought indices. Remote Sens. Environ. 2003, 87, 85–98. [Google Scholar]
  11. Moulin, S.; Kergoat, L.; Viovy, N.; Dedieu, G. Global-scale assessment of vegetation phenology using NOAA/AVHRR satellite measurements. J. Clim 1997, 10, 1154–1170. [Google Scholar]
  12. Jönsson, P.K.; Eklundh, L. Seasonality extraction by function fitting to time series of satellite sensor data. IEEE Trans. Geosci. Remote Sens 2002, 40, 1824–1832. [Google Scholar]
  13. Stöckli, R.; Vidale, P. European plant phenology and climate as seen in a 20-year AVHRR land-surface parameter dataset. Int. J. Remote Sens 2004, 25, 3303–3330. [Google Scholar]
  14. Li, Z.; Kafatos, M. Interannual variability of vegetation in the United States and its relation to El Niño/Southern Oscillation. Remote Sens. Environ 2000, 41, 239–247. [Google Scholar]
  15. Tucker, C.J.; Slayback, D.A.; Pinson, J.E.; Los, S.O.; Myneni, R.B.; Taylor, M.G. Higher northern latitude normalized difference vegetation index and growing season trends from 1982 to 1999. Int. J. Biometeorol 2001, 45, 184–190. [Google Scholar]
  16. Shabanov, N.V.; Zhou, L.; Knyazikhin, Y.; Myneni, R.B.; Tucker, C.J. Analysis of interannual changes in northern vegetation activity observed in AVHRR data from 1981 to 1994. IEEE Trans. Geosci. Remote Sens 2002, 40, 115–130. [Google Scholar]
  17. Piao, S.; Fang, J.; Zhou, L.; Ciais, P.; Zhu, B. Variations in satellite-derived phenology of China’s temperate vegetation. Glob. Chang. Biol 2006, 12, 672–685. [Google Scholar]
  18. Friedl, M.A.; Brodley, C.E.; Strahler, A.H.; R, I.N. Maximizing land cover classification accuracies produced by decision trees at continental to global scales. IEEE Trans. Geosci. Remote Sens 1999, 3, 969–977. [Google Scholar]
  19. Hansen, M.C.; Defries, R.S.; Townshend, J.R.G.; Sohlberg, R. Global land cover classification at 1 km spatial resolution using a classification tree approach. Int. J. Remote Sens 2000, 21, 1331–1364. [Google Scholar]
  20. Xiao, X.; Bolesa, S.; Liub, J.; Zhuangb, D.; Frolkinga, S.; Lia, C.; Salasc, W.; Moore, B. Mapping paddy rice agriculture in southern China using multi-temporal MODIS images. Remote Sens. Environ 2005, 95, 480–492. [Google Scholar]
  21. Xavier, A.C.; Rudorff, B.F.T.; Shimabukuro, Y.E.; Berka, L.M.S.; Moreira, M.A. Multi-temporal analysis of MODIS data to classify sugarcane crop. Int. J. Remote Sens 2006, 27, 755–768. [Google Scholar]
  22. Wardlow, B.; Egbert, S.; Kastens, J. Analysis of time-series MODIS 250 m vegetation index data for crop classification in the U.S. Central Great Plains. Remote Sens. Environ 2007, 108, 290–310. [Google Scholar]
  23. Vuolo, F.; Atzberger, C. Exploiting the classification performance of support vector machines with multi-temporal Moderate-Resolution Imaging Spectroradiometer (MODIS) data in areas of agreement and disagreement of existing land cover products. Remote Sens 2012, 4, 3143–3167. [Google Scholar]
  24. Eastman, R.J.; Fulk, M. Long sequence time series evaluation using standardized principal components. Photogramm. Eng. Remote Sens 1993, 59, 991–996. [Google Scholar]
  25. Azzali, S.; Menenti, M. Mapping vegetation-soil-climate complexes in southern Africa using temporal Fourier analysis of NOAA-AVHRR NDVI data. Int. J. Remote Sens 2000, 21, 973–996. [Google Scholar]
  26. Paruelo, J.M.; Burke, I.C.; Lauenroth, W.K. Land-use impact on ecosystem functioning in eastern Colorado, USA. Glob. Chang. Biol 2001, 7, 631–639. [Google Scholar]
  27. Martínez, B.; Gilabert, M.A. Vegetation dynamics from NDVI time series analysis using the wavelet transform. Remote Sens. Environ 2009, 113, 1823–1842. [Google Scholar]
  28. Atzberger, C.; Eilers, P.H.C. A time series for monitoring vegetation activity and phenology at 10-daily time steps covering large parts of South America. Int. J. Digit. Earth 2011, 4, 365–386. [Google Scholar]
  29. Geerken, R.A. An algorithm to classify and monitor seasonal variations in vegetation phenologies and their inter-annual change. ISPRS J. Photogramm. Remote Sens 2009, 64, 422–431. [Google Scholar]
  30. Hurlbert, A.H.; Haskell, J.P. The effect of energy and seasonality on avian species richness and community composition. Am. Nat 2003, 161, 83–97. [Google Scholar]
  31. Pettorelli, N.; F. Pelletier, A.; von Hardenberg, M.F.B.; CôTé, S.D. Early onset of vegetation growth vs. rapid green-up: Impacts on juvenile mountain ungulates. Ecology 2007, 88, 381–390. [Google Scholar]
  32. Scharlemann, J.P.W.; Benz, D.; Hay, S.I.; Purse, B.V.; Tatem, A.J.; Wint, G.R.W.; Rogers, D.J. Global data for ecology and epidemiology: A novel algorithm for temporal Fourier processing MODIS data. PLoS ONE 2008, 3, e1408. [Google Scholar]
  33. Coops, N.; Wulder, M.; Iwanicka, D. An environmental domain classification of Canada using earth observation data for biodiversity assessment. Ecol. Inform 2009, 4, 8–22. [Google Scholar]
  34. Fuller, D. Trends in NDVI time series and their relation to rangeland and crop production in Senegal, 1987–1993. Int. J. Remote Sens 1998, 19, 2013–2018. [Google Scholar]
  35. Zhang, P.; Anderson, B.; Tan, B.; Huang, D.; Myneni, R. Potential monitoring of crop production using a satellite-based Climate-Variability Impact Index. Agric. For. Meteorol 2005, 132, 344–358. [Google Scholar]
  36. McVicar, T.R.; Jupp, D.L. The current and potential operational uses of remote sensing to aid decisions on drought exceptional circumstances in Australia: A review. Agric. Syst 1998, 57, 399–468. [Google Scholar]
  37. Barbosa, P.; Stroppiana, D.; Pereira, J. An algorithm for extracting burned areas from time series of AVHRR GAC data applied at a continental scale. Remote Sens. Environ 1999, 69, 38–49. [Google Scholar]
  38. Fraser, R.H.; Li, Z.; Cihlar, J. Hotspot and NDVI Differencing Synergy (HANDS): A new technique for burned area mapping over boreal forest. Remote Sens. Environ 2000, 74, 362–376. [Google Scholar]
  39. Coops, N.C.; Wulder, M.A.; Iwanicka, D. Large area monitoring with a MODIS-based Disturbance Index (DI) sensitive to annual and seasonal variations. Remote Sens. Environ 2009, 113, 1250–1261. [Google Scholar]
  40. Spanner, M.; Pierce, L.; Running, S.; D.L., P. The seasonality of AVHRR data of temperate coniferous forests: Relationship with leaf area index. Remote Sens. Environ 1990, 33, 97–112. [Google Scholar]
  41. Sellers, P.J.; Tucker, C.J.; Collatz, G.J.; Los, S.O.; Justice, C.O.; Dazlich, D.A.; Randall, D.A. A global 1° by 1° NDVI data set for climate studies. Part 2: The generation of global fields of terrestrial biophysical parameters from the NDVI. Int. J. Remote Sens 1994, 15, 3519–3545. [Google Scholar]
  42. Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ 2002, 83, 195–213. [Google Scholar]
  43. Wang, Q.; Adiku, S.; Tenhunen, J.; Granier, A. On the relationship of NDVI with leaf area index in a deciduous forest site. Remote Sens. Environ 2005, 94, 244–255. [Google Scholar]
  44. Pinzón, J. Revisiting error, precision and uncertainty in NDVI AVHRR data: Development of a consistent NDVI3g time series. Remote Sens 2013. under review.. [Google Scholar]
  45. Van Leeuwen, W.J.D.; Orr, B.J.; Marsh, S.E.; Herrmann, S.M. Multi-sensor NDVI data continuity: Uncertainties and implications for vegetation monitoring applications. Remote Sens. Environ 2006, 100, 67–81. [Google Scholar]
  46. Meroni, M.; Atzberger, C.; Vancutsem, C.; Gobron, N.; Baret, F.; Lacaze, R.; Eerens, H.; Leo, O. Evaluation of agreement between space remote sensing SPOT-VEGETATION fAPAR time series. IEEE Trans. Geosci. Remote Sens 2013, 51, 1951–1962. [Google Scholar]
  47. Mao, J.; Shi, X.; Thornton, P.E.; Hoffman, F.M.; Zhu, Z.; Myneni, R.B. Global latitudinal-asymmetric vegetation growth trends and their driving mechanisms: 1982–2009. Remote Sens 2013, 5, 1484–1497. [Google Scholar]
  48. De Jong, R.; Verbesselt, J.; Zeileis, A.; Schaepman, M.E. Shifts in global vegetation activity trends. Remote Sens 2013, 5, 1117–1133. [Google Scholar]
  49. Vrieling, A.; de Leeuw, J.; Said, M.Y. Length of growing period over Africa: Variability and trends from 30 Years of NDVI time series. Remote Sens 2013, 5, 982–1000. [Google Scholar]
  50. Brown, M.E.; Pinzon, J.E.; Didan, K.; Morisette, J.T.; Tucker, C.J. Evaluation of the consistency of long-term NDVI time series derived from AVHRR, SPOT-Vegetation, Sea WiFS, MODIS, and LandSAT ETM+ sensors. IEEE Trans. Geosci. Remote Sens 2006, 44, 1787–1793. [Google Scholar]
  51. Justice, C.; Belward, A.; Morisette, J.; Lewis, P.; Privette, J.; Baret, F. Developments in the ‘validation’ of satellite sensor products for the study of the land surface. Int. J. Remote Sens 2000, 51, 3383–3390. [Google Scholar]
  52. Garrigues, S.; Lacaze, R.; Baret, F.; Morisette, J.T.; Weiss, M.; Nickeson, J.E.; Fernandes, R.; Plummer, S.; Shabanov, N.V.; Myneni, R.B.; et al. Validation and intercomparison of global Leaf Area Index products derived from remote sensing data. J. Geophys. Res 2008, 113, G02028. [Google Scholar]
  53. Baret, F.; Morissette, J.; Fernandes, R.; Champeaux, J.; Myneni, R.; Chen, J.; Plummer, S.; Weiss, M.; Bacour, C.; Garrigues, S.; et al. Evaluation of the representativeness of networks of sites for the global validation and intercomparison of land biophysical products: proposition of the CEOS-BELMANIP. IEEE Trans. Geosci. Remote Sens 2006, 44, 1794–1803. [Google Scholar]
  54. Morisette, J.T.; Baret, F.; Privette, J.L.; Myneni, R.B.; Nickeson, J.E.; Garrigues, S.; Shabanov, N.V.; Weiss, M.; Fernandes, R.; Leblanc, S.G.; et al. Validation of global moderate-resolution LAI products: A framework proposed within the CEOS land product validation subgroup. IEEE Trans. Geosci. Remote Sens 2006, 44, 1804–1818. [Google Scholar]
  55. Weiss, M.; Baret, F.; Garrigues, S.; Lacaze, R. LAI and fAPAR CYCLOPES global products derived from VEGETATION. Part 2: Validation and comparison with MODIS collection 4 products. Remote Sens. Environ 2007, 110, 317–331. [Google Scholar]
  56. NOAA. Data Announcement 88-MGG-02, Digital Relief of the Surface of the Earth; National Geophysical Data Center, NOAA: Boulder, CO, USA, 1988. [Google Scholar]
  57. Olson, D.; Dinerstein, E.; Wikramanayake, E.; Burgess, N.; Powell, G.; Underwood, E.; D’Amico, J.; Itoua, I.; Strand, H.; Morrison, J.; et al. Terrestrial Ecoregions of the World: A New Map of Life on Earth. BioScience 2001, 51, 933–938. [Google Scholar]
  58. Hijmans, R.; Cameron, S.; Parra, J.; Jones, P.; Jarvis, A. Very high resolution interpolated climate surfaces for global land areas. Int. J. Clim 2005, 25, 1965–1978. [Google Scholar]
  59. Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World map of Köppen-Geiger climate classification updated. Meteorol. Z 2006, 15, 259–263. [Google Scholar]
  60. Friedl, M.A.; Sulla-Menashe, D.; Tan, B.; Schneider, A.; Ramankutty, N.; Sibley, A.; Huang, X. MODIS Collection 5 global land cover: Algorithm refinements and characterization of new datasets. Remote Sens. Environ 2010, 114, 168–182. [Google Scholar]
  61. Solano, R.; Didan, K.; Jacobson, A.; Huete, A. MODIS Vegetation Index User’s Guide (MOD13 Series); Version 2.00, May 2010 (Collection 5); The University of Arizona: Tucson, AZ, USA, 2010. [Google Scholar]
  62. Mattiuzzi, M.; Verbesselt, J.; Hengl, T.; Klisch, A.; Evans, B.; Lobo, A. MODIS Multi-Temporal Data Retrieval and Processing Toolbox. Processing of First International Workshop on “Temporal Analysis of Satellite Images”, Mykonos Island, Greece, 23–25 May 2012.
  63. Vuolo, F.; Mattiuzzi, M.; Klisch, A.; Atzberger, C. Data service platform for MODIS vegetation indices time series processing at BOKU Vienna: Current status and future perspectives. Proc. SPIE 2012, 8538. [Google Scholar] [CrossRef]
  64. Atzberger, C.; Eilers, P.H.C. Evaluating the effectiveness of smoothing algorithms in the absence of ground reference measurements. Int. J. Remote Sens 2011, 32, 3689–3709. [Google Scholar]
  65. Eilers, P.H.C. A perfect smoother. Anal. Chem 2003, 75, 3631–3636. [Google Scholar]
  66. Atkinson, P.M.; Jeganathan, C.; Dash, J.; Atzberger, C. Intercomparison of four models for smoothing satellite sensor time-series data to estimate vegetation phenology. Remote Sens. Environ 2012, 123, 400–417. [Google Scholar]
  67. Fensholt, R.; Proud, S.R. Evaluation of Earth Observation based global long term vegetation trends—Comparing GIMMS and MODIS global NDVI time series. Remote Sens. Environ 2012, 119, 131–147. [Google Scholar]
  68. Tucker, C.; Pinzon, J.; Brown, M.; Slayback, D.; Pak, E.; Mahoney, R.; Vermote, E.; Saleous, E. An extended AVHRR 8-km NDVI dataset compatible with MODIS and SPOT vegetation NDVI data. Int. J. Remote Sens 2005, 26, 4485–4498. [Google Scholar]
  69. Verstraete, M.M.; Gobron, N.; Aussedat, O.; Robustelli, M.; Pinty, B.; Widlowski, J.L.; Taberner, M. An automatic procedure to identify key vegetation phenology events using the JRC-FAPAR products. Adv. Space Res 2008, 41, 1773–1783. [Google Scholar]
  70. Delbart, N.; Le Toan, L.; Kergoat, L.; Fedotova, V. Remote sensing of spring phenology in boreal regions: A free of snow-effect method using NOAA-AVHRR and SPOT-VGT data (1982–2004). Remote Sens. Environ 2006, 101, 52–62. [Google Scholar]
  71. Van Leeuwen, W.J.D. Monitoring the effects of forest restoration treatments on post-fire vegetation recovery with MODIS multitemporal data. Sensors 2008, 8, 2017–2042. [Google Scholar]
  72. De Beurs, K.; Henebry, G. Spatio-Temporal Statistical Methods for Modeling Land Surface Phenology. In Phenological Research: Methods for Environmental and Climate Change Analysis; Hudson, I.L., Keatley, M.R., Eds.; Springer: Berlin, Germany, 2010; pp. 177–208. [Google Scholar]
  73. Karlsen, S.R.; Høgda, K.; Johansen, B.; Elvebakk, A.; Tømmervik, H. Use of AVHRR NDVI Data to Map Vegetation Zones in North-Western Europe. Proceedings of the 29th International Symposium on Remote Sensing Environment (ISRSE), Buenos Aires, Argentina, 8–12 April 2002.
  74. Karlsen, S.R.; Ramfjord, H.; Høgda, K.A.; Johansen, B.; Danks, F.S.; Brobakk, T.E. A satellite-based map of onset of birch (Betula) flowering in Norway. Aerobiologica 2009, 25, 15–25. [Google Scholar]
  75. Beck, P.S.A.; Jönsson, P.; Høgda, K.A.; Karlsen, S.R.; Eklundh, L.; Skidmore, A.K. A ground-validated NDVI dataset for monitoring vegetation dynamics and mapping phenology in Fennoscandia and the Kola Peninsula. Int. J. Remote Sens 2007, 28, 4311–4330. [Google Scholar]
  76. Soudani, K.; le Maire, G.; Dufrêne, E.; Francois, C.; Delpierre, N.; Ulrich, E.; Cecchini, S. Evaluation of the onset of green-up in temperate deciduous broadleaf forests derived from Moderate Resolution Imaging Spectroradiometer (MODIS) data. Remote Sens. Environ 2008, 112, 2643–2655. [Google Scholar]
  77. Bradley, C.; Schwartz, M.; Xiao, X. Remote Sensing Phenology: Status and Way forward. In Phenology of Ecosystem Processes—Applications in Global Change Research; Springer: Berlin, Germany, 2009; pp. 231–246. [Google Scholar]
  78. Liang, L.; Schwartz, M.D.; Fei, S. Validating satellite phenology through intensive ground observation and landscape scaling in a mixed seasonal forest. Remote Sens. Environ 2011, 115, 143–157. [Google Scholar]
Remotesensing 06 00257f1a 1024Remotesensing 06 00257f1b 1024
Figure 1. Study area and general environmental conditions. (top left) typical NDVI values in the study area in July, (top right) mean elevation [56], (center left) recoded land cover type 1 product MCD12Q1 v005 from MODIS [23,60], (center right) terrestrial ecoregions of World Wildlife Fund (WWF) [57], (bottom left) annual mean temperature [58], (bottom right) annual mean precipitation [58].
Figure 1. Study area and general environmental conditions. (top left) typical NDVI values in the study area in July, (top right) mean elevation [56], (center left) recoded land cover type 1 product MCD12Q1 v005 from MODIS [23,60], (center right) terrestrial ecoregions of World Wildlife Fund (WWF) [57], (bottom left) annual mean temperature [58], (bottom right) annual mean precipitation [58].
Remotesensing 06 00257f1aRemotesensing 06 00257f1b
Remotesensing 06 00257f2 1024
Figure 2. NDVI profiles (top) and first derivatives (bottom) for individual pixels from GIMMS (left) and MODIS (right). Example pixels were selected to represent different land cover types. Curves were obtained by averaging the respective NDVI of sample locations over the period of 2002–2011.
Figure 2. NDVI profiles (top) and first derivatives (bottom) for individual pixels from GIMMS (left) and MODIS (right). Example pixels were selected to represent different land cover types. Curves were obtained by averaging the respective NDVI of sample locations over the period of 2002–2011.
Remotesensing 06 00257f2
Remotesensing 06 00257f3 1024
Figure 3. Data distribution of GIMMS and MODIS time series (weekly data) extracted from the full image extent and pooled across all years (2002–2011).
Figure 3. Data distribution of GIMMS and MODIS time series (weekly data) extracted from the full image extent and pooled across all years (2002–2011).
Remotesensing 06 00257f3
Remotesensing 06 00257f4 1024
Figure 4. Spatial distribution of NDVI from GIMMS (left) and MODIS (right) time series. Displayed are the average NDVI (top) and standard deviation (bottom) calculated from weekly data over the full time period (2002–2011).
Figure 4. Spatial distribution of NDVI from GIMMS (left) and MODIS (right) time series. Displayed are the average NDVI (top) and standard deviation (bottom) calculated from weekly data over the full time period (2002–2011).
Remotesensing 06 00257f4
Remotesensing 06 00257f5a 1024Remotesensing 06 00257f5b 1024
Figure 5. Spatial distribution of weekly NDVI from GIMMS (left) and MODIS (center) time series averaged over 2002–2011 for each of the four climatological seasons. (right) Differences between the mean NDVI of GIMMS and MODIS.
Figure 5. Spatial distribution of weekly NDVI from GIMMS (left) and MODIS (center) time series averaged over 2002–2011 for each of the four climatological seasons. (right) Differences between the mean NDVI of GIMMS and MODIS.
Remotesensing 06 00257f5aRemotesensing 06 00257f5b
Remotesensing 06 00257f6 1024
Figure 6. Co-distribution of NDVI values from GIMMS and MODIS derived from the full image extent and weekly observations across all weeks between 2002 and 2011. (left) scatterplot with 1-to-1 line (red) and regression line (black); (right) frequency distribution of the differences between GIMMS and MODIS NDVI.
Figure 6. Co-distribution of NDVI values from GIMMS and MODIS derived from the full image extent and weekly observations across all weeks between 2002 and 2011. (left) scatterplot with 1-to-1 line (red) and regression line (black); (right) frequency distribution of the differences between GIMMS and MODIS NDVI.
Remotesensing 06 00257f6
Remotesensing 06 00257f7 1024
Figure 7. Agreement/disagreement between weekly GIMMS and MODIS NDVI values. (left) Intra-annual analysis; (right) inter-annual analysis. (solid green) coefficient of determination (R2), (blue) root mean square difference (RMSD), (dashed green) time course of the average NDVI. Per week, or year, one value is shown per indicator. Lines are only shown for reader’s convenience.
Figure 7. Agreement/disagreement between weekly GIMMS and MODIS NDVI values. (left) Intra-annual analysis; (right) inter-annual analysis. (solid green) coefficient of determination (R2), (blue) root mean square difference (RMSD), (dashed green) time course of the average NDVI. Per week, or year, one value is shown per indicator. Lines are only shown for reader’s convenience.
Remotesensing 06 00257f7
Remotesensing 06 00257f8 1024
Figure 8. (left) Coefficient of determination (R2) and (right) root mean square difference (RMSD) between the temporal GIMMS and MODIS series calculated across all weekly observations between 2002 and 2011.
Figure 8. (left) Coefficient of determination (R2) and (right) root mean square difference (RMSD) between the temporal GIMMS and MODIS series calculated across all weekly observations between 2002 and 2011.
Remotesensing 06 00257f8
Remotesensing 06 00257f9 1024
Figure 9. Cumulated distribution function of the pixel-wise estimated start of season (SOS) for GIMMS (red) and MODIS (blue) for all years (2003–2011) using the relative threshold approach. Smoothed products at daily temporal resolution were used for the calculations. SOS of zero corresponds to a turn of the year.
Figure 9. Cumulated distribution function of the pixel-wise estimated start of season (SOS) for GIMMS (red) and MODIS (blue) for all years (2003–2011) using the relative threshold approach. Smoothed products at daily temporal resolution were used for the calculations. SOS of zero corresponds to a turn of the year.
Remotesensing 06 00257f9
Remotesensing 06 00257f10 1024
Figure 10. Range of estimated start of season (SOS) across nine years (2003–2011) for two time series (GIMMS and MODIS). The ranges are expressed in days.
Figure 10. Range of estimated start of season (SOS) across nine years (2003–2011) for two time series (GIMMS and MODIS). The ranges are expressed in days.
Remotesensing 06 00257f10
Remotesensing 06 00257f11 1024
Figure 11. Frequency distribution of differences in the start of season (SOS) from 2003 to 2011 (left) and for 2007 (right). Differences in SOS are expressed in days.
Figure 11. Frequency distribution of differences in the start of season (SOS) from 2003 to 2011 (left) and for 2007 (right). Differences in SOS are expressed in days.
Remotesensing 06 00257f11
Remotesensing 06 00257f12 1024
Figure 12. Spatial distribution of start of season (SOS) for GIMMS and MODIS time series. (top) averaged SOS (median) over all years (2003–2011) and (bottom) SOS of 2007.
Figure 12. Spatial distribution of start of season (SOS) for GIMMS and MODIS time series. (top) averaged SOS (median) over all years (2003–2011) and (bottom) SOS of 2007.
Remotesensing 06 00257f12
Remotesensing 06 00257f13 1024
Figure 13. Scatterplots between the start of season from GIMMS vs. MODIS for full image extent and all observations. (left) data from 2003 to 2011 (right) only data from 2007. The 1-to-1 line (red) and the regression line (black) are also shown. Densities increase from blue to red.
Figure 13. Scatterplots between the start of season from GIMMS vs. MODIS for full image extent and all observations. (left) data from 2003 to 2011 (right) only data from 2007. The 1-to-1 line (red) and the regression line (black) are also shown. Densities increase from blue to red.
Remotesensing 06 00257f13
Remotesensing 06 00257f14a 1024Remotesensing 06 00257f14b 1024
Figure 14. (top) annual analysis of the pixel-wise correlation between SOS from GIMMS and MODIS with coefficient of determination (R2) and root mean square difference (RMSD). (bottom) inter-annual distribution of SOS for GIMMS (left) and MODIS (right). The box-and-whisker plots show the median in red. Box edges represent the 25th and 75th percentiles. The whiskers extend to data points still within the 1.5 interquartile range.
Figure 14. (top) annual analysis of the pixel-wise correlation between SOS from GIMMS and MODIS with coefficient of determination (R2) and root mean square difference (RMSD). (bottom) inter-annual distribution of SOS for GIMMS (left) and MODIS (right). The box-and-whisker plots show the median in red. Box edges represent the 25th and 75th percentiles. The whiskers extend to data points still within the 1.5 interquartile range.
Remotesensing 06 00257f14aRemotesensing 06 00257f14b
Remotesensing 06 00257f15 1024
Figure 15. Correlation (at pixel level) between the start of season (SOS) estimated form GIMMS and MODIS time series. (top left) rank correlation coefficient, (top right) p-value, (bottom) the frequency distribution of Spearman’s Rho. The correlation was only calculated if the relative threshold algorithm could at least detect five valid SOS observations (out of nine). In the maps (top) areas not fulfilling these conditions are shown as ‘no data’.
Figure 15. Correlation (at pixel level) between the start of season (SOS) estimated form GIMMS and MODIS time series. (top left) rank correlation coefficient, (top right) p-value, (bottom) the frequency distribution of Spearman’s Rho. The correlation was only calculated if the relative threshold algorithm could at least detect five valid SOS observations (out of nine). In the maps (top) areas not fulfilling these conditions are shown as ‘no data’.
Remotesensing 06 00257f15
Remotesensing 06 00257f16 1024
Figure 16. Maximum of season (MOS) derived from GIMMS and MODIS (full image extent and all data from 2003–2011. (top) cumulated frequency distribution, (bottom) scatterplot. In addition, also shown are the 1-to-1 line (red) and the regression line (black).
Figure 16. Maximum of season (MOS) derived from GIMMS and MODIS (full image extent and all data from 2003–2011. (top) cumulated frequency distribution, (bottom) scatterplot. In addition, also shown are the 1-to-1 line (red) and the regression line (black).
Remotesensing 06 00257f16
Remotesensing 06 00257f17 1024
Figure 17. Spatial distribution of the maximum of season (MOS) from GIMMS (left) and MODIS (right). (top) median across nine years, (bottom) inter-annual range.
Figure 17. Spatial distribution of the maximum of season (MOS) from GIMMS (left) and MODIS (right). (top) median across nine years, (bottom) inter-annual range.
Remotesensing 06 00257f17
Remotesensing 06 00257f18 1024
Figure 18. Correlation (at pixel level) between the maximum of season (MOS) from GIMMS, respectively, MODIS time series. The rank correlation coefficient is shown on the left whereas the corresponding p-value is shown in the center. The median of differences (in days) is shown on the right.
Figure 18. Correlation (at pixel level) between the maximum of season (MOS) from GIMMS, respectively, MODIS time series. The rank correlation coefficient is shown on the left whereas the corresponding p-value is shown in the center. The median of differences (in days) is shown on the right.
Remotesensing 06 00257f18
Table
Table 1. Prominent applications building on time series of vegetation indices.
Table 1. Prominent applications building on time series of vegetation indices.
Type of ApplicationReference
Seasonality extraction and vegetation dynamics[1–3,11–13]
Environmental monitoring and climate change[8,9,14–17]
Land use and land cover mapping[18–23]
Vegetation and landscape characterization[24–29]
Biodiversity and wildlife distribution[4,7,30–33]
Primary production and yield/production estimates[4,6,34,35]
Drought monitoring and food security[10,36]
Change detection (incl. natural disasters, forest fires)[37–39]
Characterizing vegetation’s biophysical variables[40–43]
Table
Table 2. Specification of the spatial and temporal pre-processing steps for homogenizing GIMMS and MODIS NDVI time series. The smoothing parameter (λ) of the Whittaker smoother determines the roughness of the smoothed curve. See text for further details.
Table 2. Specification of the spatial and temporal pre-processing steps for homogenizing GIMMS and MODIS NDVI time series. The smoothing parameter (λ) of the Whittaker smoother determines the roughness of the smoothed curve. See text for further details.
Parameterization of the Whittaker Smoother for Providing Smoothed Weekly DataSpatial ResamplingLand/Water Masking
λ ×103Degreen° of IterationsCompositing DayQuality Flags
GIMMS302nd1Not availableNot consideredOriginal sampling at 1/12 degrees is keptCommon masks applied to both data sets
MODIS302nd3True DOY consideredConsideredAverage resampling to 1/12 degrees

Share and Cite

MDPI and ACS Style

Atzberger, C.; Klisch, A.; Mattiuzzi, M.; Vuolo, F. Phenological Metrics Derived over the European Continent from NDVI3g Data and MODIS Time Series. Remote Sens. 2014, 6, 257-284. https://doi.org/10.3390/rs6010257

AMA Style

Atzberger C, Klisch A, Mattiuzzi M, Vuolo F. Phenological Metrics Derived over the European Continent from NDVI3g Data and MODIS Time Series. Remote Sensing. 2014; 6(1):257-284. https://doi.org/10.3390/rs6010257

Chicago/Turabian Style

Atzberger, Clement, Anja Klisch, Matteo Mattiuzzi, and Francesco Vuolo. 2014. "Phenological Metrics Derived over the European Continent from NDVI3g Data and MODIS Time Series" Remote Sensing 6, no. 1: 257-284. https://doi.org/10.3390/rs6010257

Article Metrics

Back to TopTop