Evaluation of Land Surface Models in Reproducing Satellite Derived Leaf Area Index over the High-Latitude Northern Hemisphere. Part II: Earth System Models
Abstract
:1. Introduction
2. Material and Methods
2.1. Coupled Model Intercomparison Project Phase 5 (CMIP5) Simulations
2.2. Satellite Data
2.3. Leaf Phenology Analysis
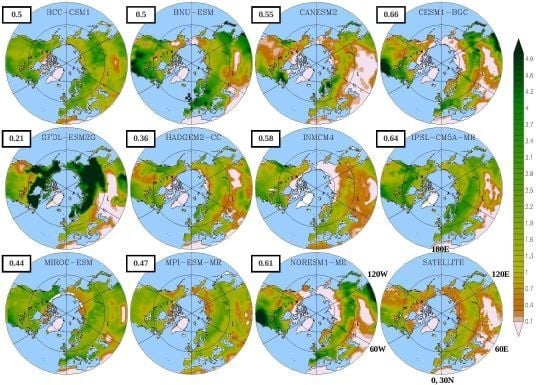
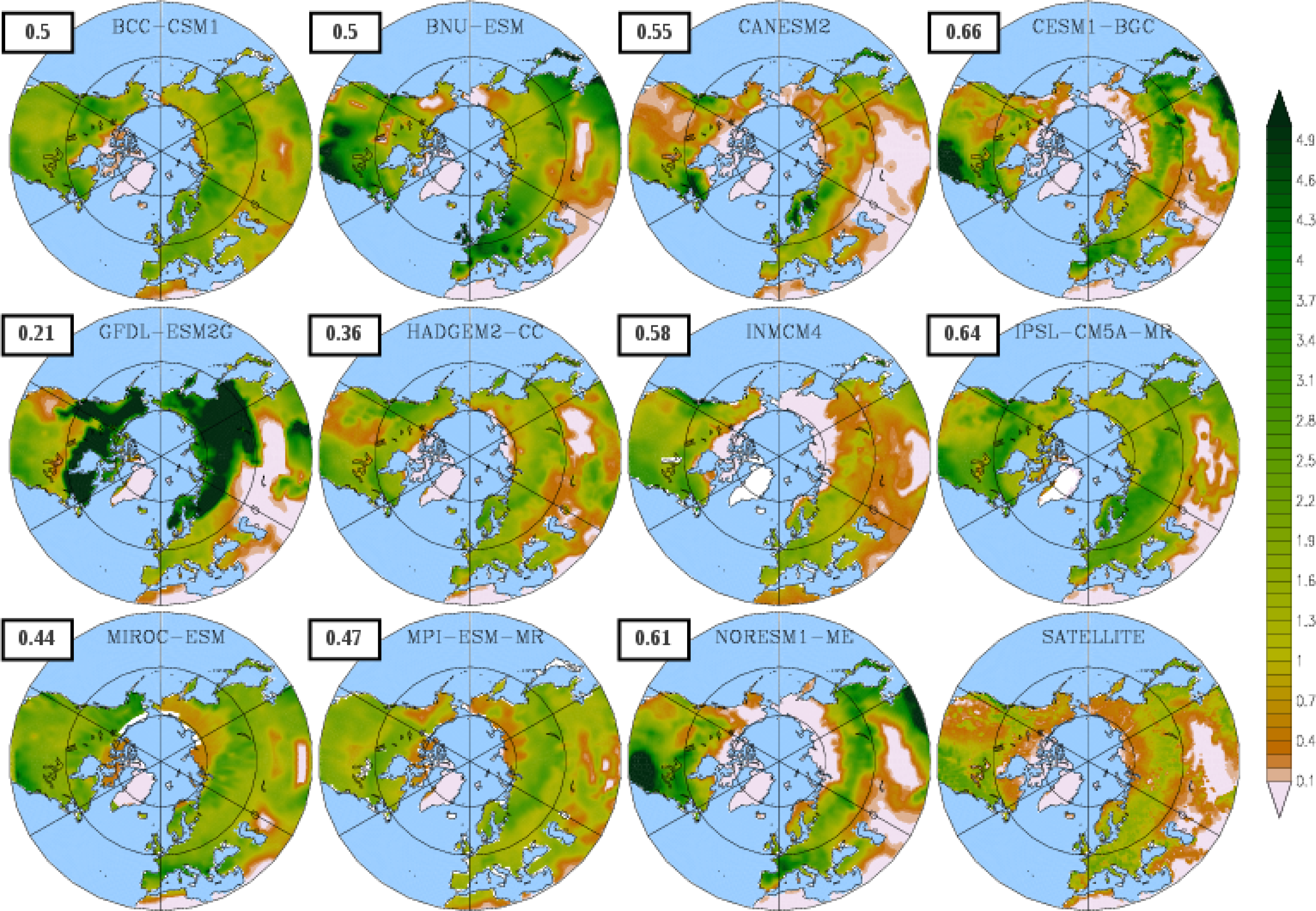
3. Results
3.1. Mean Leaf Area Index (LAI)
3.2. Growing Season
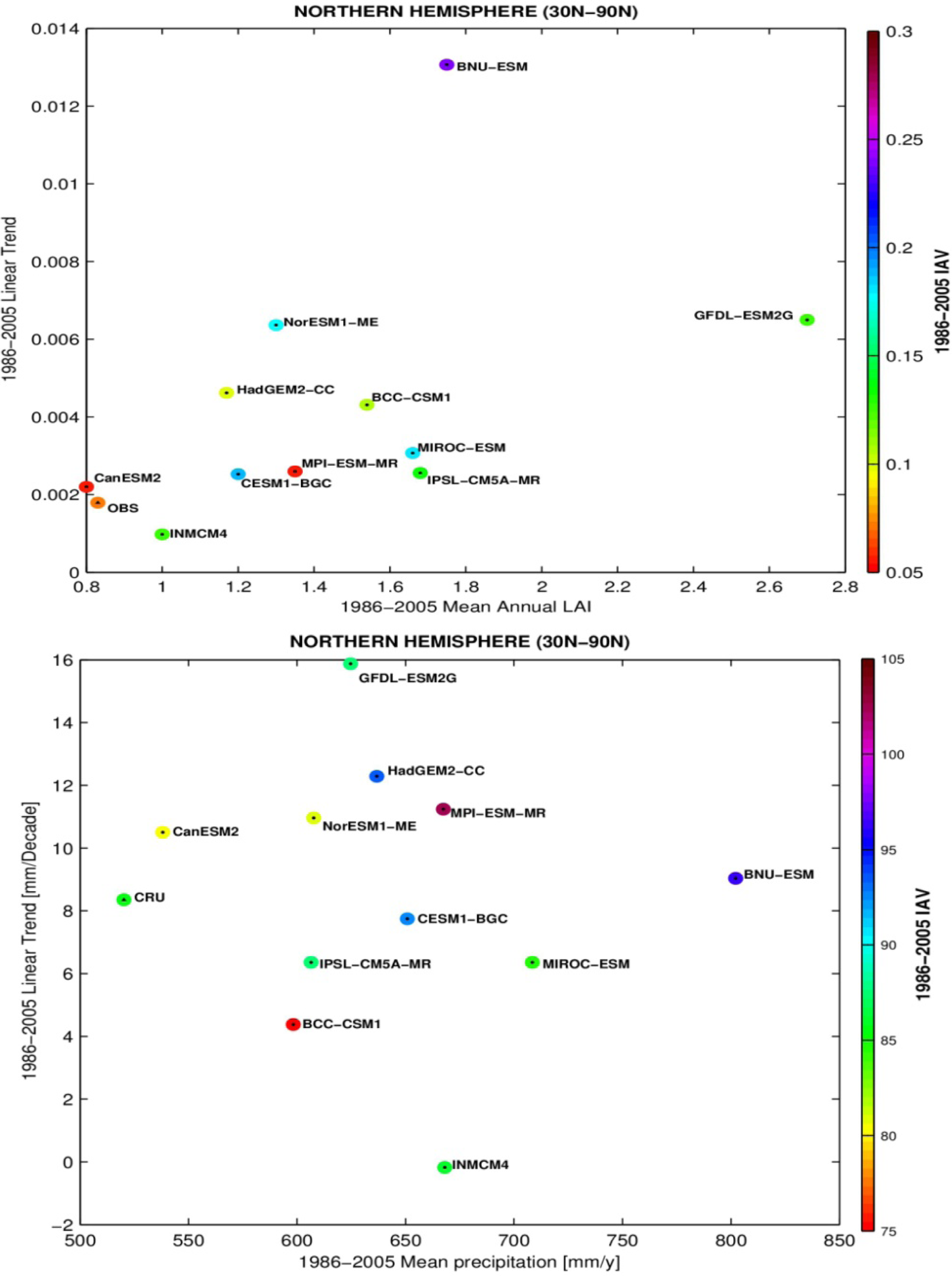
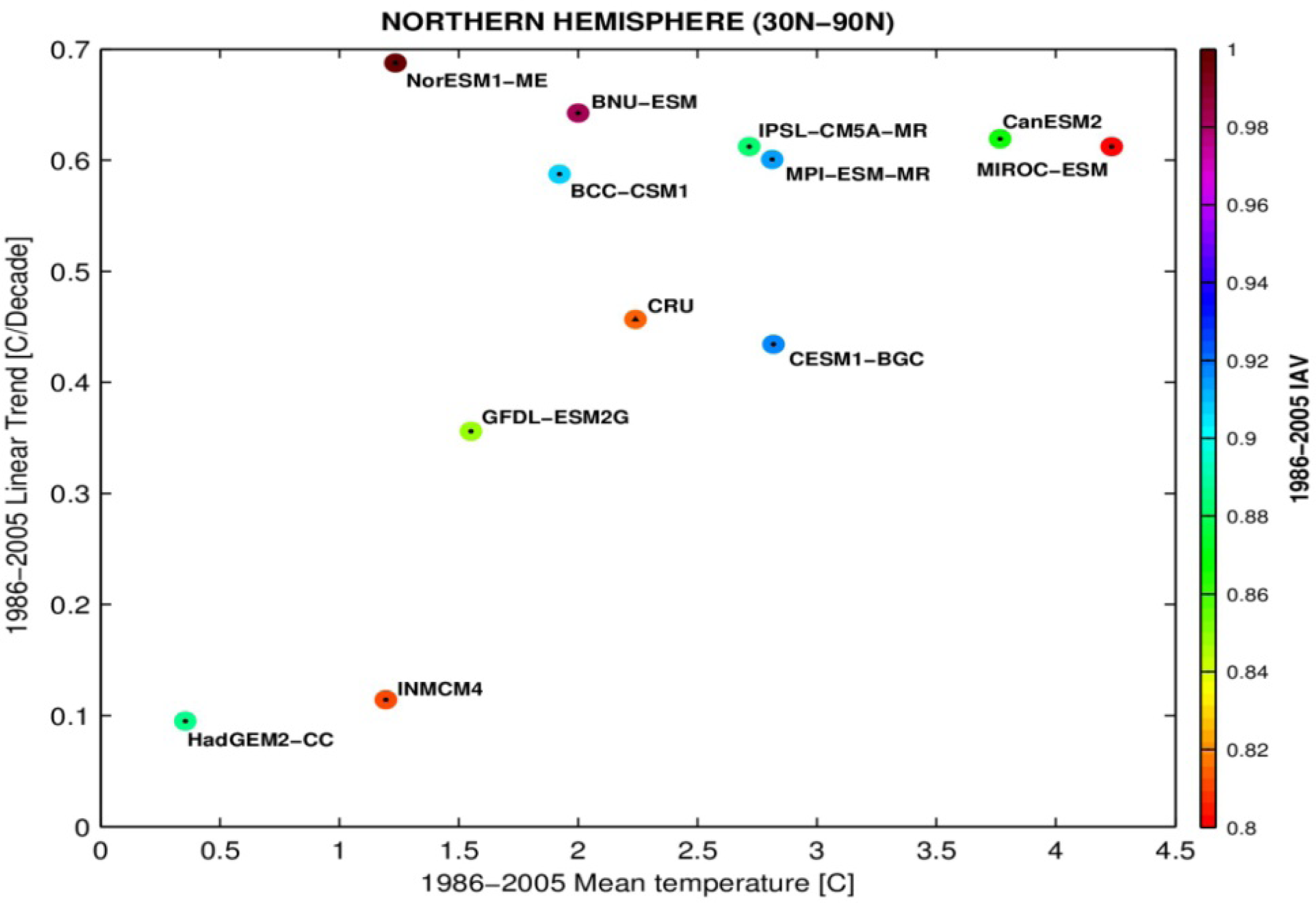
3.3. Temporal Trends
4. Discussion
5. Conclusions
Acknowledgments
Conflict of Interest
References and Notes
- Myneni, R.B.; Hoffman, S.; Knyazikhin, Y.; Privette, J.L.; Glassy, J.; Tian, Y.; Wang, Y.; Song, X.; Zhang, Y.; Smith, G.; et al. Global products of vegetation leaf area and fraction absorbed PAR from year one of MODIS data. Remote Sens. Environ 2002, 83, 214–231. [Google Scholar]
- Sellers, P.J.; Randall, D.A.; Betts, A.K.; Hall, F.G.; Berry, J.A.; Collatz, G.J.; Denning, A.S.; Mooney, H.A.; Nobre, C.A.; Sato, N.; et al. Modeling the exchanges of energy, water, and carbon between continents and the atmosphere. Science 1997, 275, 502–509. [Google Scholar]
- Botta, A.; Viovy, N.; Ciais, P.; Friedlingstein, P. A global prognostic scheme of leaf onset using satellite data. Glob. Change Biol 2000, 6, 709–726. [Google Scholar]
- Pielke, R.A.; Avissar, R.; Raupach, M.; Dolman, A.J.; Zeng, X.; Denning, A.S. Interactions between the atmosphere and terrestrial ecosystems: Influence on weather and climate. Glob. Change Biol 1998, 4, 461–475. [Google Scholar]
- Brovkin, V. Climate-vegetation interaction. J. Phys 2002, 4, 57–72. [Google Scholar]
- Chase, T.N.; Pielke, R.; Kittel, T.; Nemani, R.; Running, S. Sensitivity of a general circulation model to global changes in leaf area index. J. Geophys. Res 1996, 101, 7393–7408. [Google Scholar]
- Betts, R.A.; Cox, P.M.; Lee, S.E.; Woodward, F.I. Contrasting physiological and structural vegetation feedback in climate change simulations. Nature 1997, 387, 796–799. [Google Scholar]
- Piao, S.; Friedlingstein, P.; Ciais, P.; Viovy, N.; Demarty, J. Growing season extension and its impact on terrestrial carbon cycle in the Northern Hemisphere over the past 2 decades. Glob. Biogeochem. Cy 2007, 21, GB3018. [Google Scholar]
- Guenther, A.; Karl, T.; Harley, P.; Wiedinmyer, C.; Palmer, P.I.; Geron, C. Estimates of global terrestrial isoprene emissions using MEGAN (Model of Emissions of Gases and Aerosols from Nature). Atmos. Chem. Phys 2006, 6, 3181–3210. [Google Scholar]
- Lathière, J.; Hauglustaine, D.A.; Friend, A.D.; De Noblet-Ducoudré, N.; Viovy, N.; Folberth, G.A. Impact of climate variability and land use changes on global biogenic volatile organic compound emissions. Atmos. Chem. Phys 2006, 6, 2129–2146. [Google Scholar]
- Petroff, A.; Mailliat, A.; Amielh, M.; Anselmet, F. Aerosol dry deposition on vegetative canopies. Part 1: Review of present knowledge. Atmos. Environ 2008, 42, 3625–3653. [Google Scholar]
- Anav, A.; Menut, L.; Khvorostyanov, D.; Viovy, N. A comparison of two canopy conductance parameterizations to quantify the interactions between surface ozone and vegetation over Europe. J. Geophys. Res 2012, 117, G03027. [Google Scholar]
- Menzel, A.; Fabian, P. Growing season extended in Europe. Nature 1999, 397, 659. [Google Scholar]
- Ahas, R.; Jaagus, J.; Aasa, A. The phenological calendar of Estonia and its correlation with mean air temperature. Int. J. Biometeorol 2000, 44, 159–166. [Google Scholar]
- Myneni, R.B.; Keeling, C.D.; Tucker, C.J.; Asrar, G.; Nemani, R.R. Increased plant growth in the northern latitudes from 1981–1991. Nature 1997, 386, 698–702. [Google Scholar]
- Zhou, L.; Tucker, C.J.; Kaufmann, R.K.; Slayback, D.; Shabanov, N.V.; Myneni, R.B. Variations in northern vegetation activity inferred from satellite data of vegetation index during 1981 to 1999. J. Geophys. Res 2001, 106, 20069–20083. [Google Scholar]
- Tucker, C.J.; Slayback, D.; Pinzon, J.E.; Los, S.O.; Myneni, R.B.; Taylor, M.G. Higher northern latitude normalized difference vegetation index and growing season trends from 1982 to 1999. Int. J. Biometeorol 2001, 45, 184–190. [Google Scholar]
- Suzuki, R.; Nomaki, T.; Yasunari, T. West-east contrast of phenology and climate in northern Asia revealed using a remotely sensed vegetation index. Int. J. Remote Sens 2003, 47, 126–138. [Google Scholar]
- Stöckli, R.; Vidale, P.L. European plant phenology and climate as seen in a 20-year AVHRR land-surface parameter dataset. Int. J. Remote Sens 2004, 25, 3303–3330. [Google Scholar]
- Keeling, C.D.; Chin, J.F.S.; Whorf, T.P. Increased activity of northern vegetation in inferred from atmospheric CO2 measurements. Nature 1996, 382, 146–149. [Google Scholar]
- Lucht, W.; Prentice, I.C.; Myneni, R.B.; Sitch, S.; Friedlingstein, P.; Cramer, W.; Bousquet, P.; Buermann, W.; Smith, B. Climatic control of the high-latitude vegetation greening trend and Pinatubo effect. Science 2002, 296, 1687–1689. [Google Scholar]
- Barichivich, J.; Briffa, K.R.; Osborn, T.J.; Melvin, T.M.; Caesar, J. Thermal growing season and timing of biospheric carbon uptake across the Northern Hemisphere. Glob. Biogeochem. Cy 2012, 26, GB4015. [Google Scholar]
- Kimball, J.; McDonald, K.; Running, S.; Frolking, S. Satellite radar remote sensing of seasonal growing seasons for boreal and subalpine evergreen forests. Remote Sens. Environ 2004, 90, 243–258. [Google Scholar]
- Euskirchen, E.S.; McGuire, A.D.; Kicklighter, D.W.; Zhuang, Q.; Clein, J.S.; Dargaville, R.J.; Dye, D.G.; Kimball, J.S.; McDonald, K.C.; Melillo, J.M.; Romanovsky, V.E.; et al. Importance of recent shifts in soil thermal dynamics on growing season length, productivity, and carbon sequestration in terrestrial high-latitude ecosystems. Glob. Change Biol 2006, 12, 731–750. [Google Scholar]
- Linderholm, H. Growing season changes in the last century. Agric. For. Meteorol 2006, 137, 1–14. [Google Scholar]
- Churkina, G.; Schimel, D.; Braswell, B.; Xiao, X. Spatial analysis of growing season length control over net ecosystem exchange. Glob. Change Biol 2005, 11, 1777–1787. [Google Scholar]
- Richardson, A.D.; Black, T.A.; Ciais, P.; Delbart, N.; Friedl, M.A.; Gobron, N.; Hollinger, D.Y.; Kutsch, W.L.; Longdoz, B.; Luyssaert, S.; et al. Influence of spring and autumn phenological transitions on forest ecosystem productivity. Philos. T. R. Soc. B 2010, 365, 3227–3246. [Google Scholar] [Green Version]
- Mao, J.; Shi, X.; Thornton, P.E.; Piao, S.; Wnag, X. Causes of spring vegetation growth trends in the northern mid–high latitudes from 1982 to 2004. Environ. Res. Lett 2012, 7, 014010. [Google Scholar]
- Mao, J.; Shi, X.; Thornton, P.E.; Hoffman, F.M.; Zhu, Z.; Myneni, R.B. Global latitudinal-asymmetric vegetation growth trends and their driving mechanisms: 1982–2009. Remote Sens 2013, 5, 1484–1497. [Google Scholar]
- Smith, N.V.; Saatchi, S.S.; Randerson, J.T. Trends in high northern latitude soil freeze and thaw cycles from 1988 to 2002. J. Geophys. Res 2004, 109, D12101. [Google Scholar]
- Christidis, N.; Stott, P.; Brown, S.; Karoly, D.; Caesar, J. Human contribution to the lengthening of the growing season during 1950–99. J. Clim 2007, 20, 5441–5454. [Google Scholar]
- Suni, T.; Berninger, F.; Markkanen, T.; Keronen, P.; Rannik, Ü.; Vesala, T. Interannual variability and timing of growing-season CO2exchange in a boreal forest. J. Geophys. Res 2003. [Google Scholar] [CrossRef]
- Hänninen, H.; Tanino, K. Tree seasonality in a warming climate. Trends Plant Sci 2011, 16, 412–416. [Google Scholar]
- Charney, J.; Quirk, W.J.; Chow, S.-H.; Kornfield, J. A comparative study of the effects of albedo change on drought in semi-arid regions. J. Atmos. Sci 1977, 34, 1366–1385. [Google Scholar]
- Sud, Y.C.; Fennessy, M.J. A study of the influence of surface albedo on July circulation in semi-arid regions using the GLAS GCM. J. Climatol 1982, 2, 105–125. [Google Scholar]
- Dirmeyer, P.A.; Shukla, J. Albedo as a modulator of climate response to tropical deforestation. J. Geophys. Res 1994, 99, 20863–20877. [Google Scholar]
- Shukla, J.; Mintz, Y. Influence of land-surface evapotranspiration on the Earth’s climate. Science 1982, 215, 1498–1501. [Google Scholar]
- Douville, H.; Chauvin, F.; Broqua, H. Influence of soil moisture on the Asian and African monsoons. Part I: Mean monsoon and daily precipitation. J. Climate 2001, 14, 2381–2403. [Google Scholar]
- Zampieri, M.; D’Andrea, F.; Vautard, R.; Ciais, P.; de Noblet-Ducoudré, N.; Yiou, P. Hot european summers and the role of soil moisture in the propagation of mediterranean drought. J. Climate 2009, 22, 4747–4758. [Google Scholar]
- Sud, Y.C.; Shukla, J.; Mintz, Y. Influence of land surface roughness on atmospheric circulation and precipitation: A sensitivity study with a general circulation model. J. Appl. Meteor 1988, 27, 1036–1054. [Google Scholar]
- Bounoua, L.; Collatz, G.J.; Los, S.O.; Sellers, P.J.; Dazlich, D.A.; Tucker, C.J.; Randall, D.A. Sensitivity of climate to changes in NDVI. J. Climate 2000, 13, 2277–2292. [Google Scholar]
- Oleson, K.W.; Bonan, G.B. The effects of remotely sensed plant functional type and leaf area index in simulations of boreal forest surface fluxes by the NCAR land surface model. J. Hydrometeor 2000, 1, 431–446. [Google Scholar]
- Buermann, W.; Dong, J.; Zeng, X.; Myneni, R.B.; Dickinson, R.E. Evaluation of the utility of satellite-based leaf area index data for climate simulation. J. Climate 2001, 14, 3536–3550. [Google Scholar]
- Van den Hurk, B.J.J.M.; Viterbo, P.; Los, S.O. Impact of leaf area index seasonality on the annual land surface evaporation in a global circulation model. J. Geophys. Res 2003, 108, 4191. [Google Scholar]
- Tian, Y.; Dickinson, R.E.; Zhou, L.; Myneni, R.B.; Friedl, M.; Chaaf, C.B.; Carroll, M.; Gao, F. Land boundary conditions from MODIS data and consequences for the albedo of a climate model. Geophys. Res. Lett 2004, 31, L05504. [Google Scholar]
- Kang, H.-S.; Xue, Y.; Collatz, G.J. Impact assessment of satellite-derived leaf area index datasets using a general circulation model: Seasonal variability. J. Climate 2007, 20, 993–1015. [Google Scholar]
- Dickinson, R.E.; Henderson-Sellers, A.; Kennedy, P.J. Biosphere-Atmosphere Transfer Scheme (BATS) Version 1e as Coupled to the NCAR Community Climate Model; NCAR Technical Note, NCAR/TN-387+ STR; National Center for Atmospheric Research: Boulder, CO, USA, 1993. [Google Scholar]
- Giorgi, F.; Marinucci, M.R.; Bates, G.T. Development of a second generation regional climate model (RegCM2). I. Boundary-layer and radiative transfer processes. Mon. Wea. Rev 1993, 121, 2794–2813. [Google Scholar]
- Schulz, J.-P.; Dümenil, L.; Polcher, J.; Schlosser, C.A.; Xue, Y. Land surface energy and moisture fluxes: Comparing three models. J. Appl. Meteor 1998, 37, 288–307. [Google Scholar]
- Lawrence, D.M.; Slingo, J.M. An annual cycle of vegetation in a GCM. Part II: Global impacts on climate and hydrology. Clim. Dyn 2004, 22, 107–122. [Google Scholar]
- Stier, P.; Feichter, J.; Kinne, S.; Kloster, S.; Vignati, E.; Wilson, J.; Ganzeveld, L.; Tegen, I.; Werner, M.; Balkanski, Y.; et al. The aerosol-climate model ECHAM5-HAM. Atmos. Chem. Phys 2005, 5, 1125–1156. [Google Scholar]
- Hourdin, F.; Musat, I.; Bony, S.; Braconnot, P.; Codron, F.; Dufresne, J.-L.; Fairhead, L.; Filiberti, M.A.; Friedlingstein, P.; Grandpeix, J.-Y.; et al. The LMDZ4 general circulation model: Climate performance and sensitivity to parametrized physics with emphasis on tropical convection. Clim. Dyn 2006, 19, 3445–3482. [Google Scholar]
- Foley, J.A.; Prentice, I.C.; Ramankutty, N.; Levis, S.; Pollard, D.; Sitch, S.; Haxeltine, A. An integrated biosphere model of land surface processes, terrestrial carbon balance, and vegetation dynamics. Glob. Biogeochem. Cy 1996, 10, 603–628. [Google Scholar]
- Sellers, P.J.; Randall, D.A.; Collatz, G.J.; Berry, J.A.; Field, C.B.; Dazlich, D.A.; Zhang, C.; Collelo, G.D.; Bounoua, L. A revised land surface parameterization (SiB2) for atmospheric GCMs, Part I : Model Formulation. J. Climate 1996, 9, 676–705. [Google Scholar]
- Foley, J.A.; Levis, S.; Prentice, I.C.; Pollard, D.; Thompson, S.L. Coupling dynamic models of climate and vegetation. Glob. Change Biol 1998, 4, 561–579. [Google Scholar]
- Foley, J.A.; Levis, S.; Costa, M.H.; Cramer, W.; Pollard, D. Incorporating dynamic vegetation cover within global climate models. Ecol. Appl 2000, 10, 1620–1632. [Google Scholar]
- Bonan, G.; Levis, S.; Sitch, S.; Vertenstein, M.; Oleson, K.W. A dynamic global vegetation model for use with climate models: Concepts and description of simulated vegetation dynamics. Glob. Change Biol 2003, 9, 1543–1566. [Google Scholar]
- Pitman, A.J. The evolution of, and revolution in, land surface schemes designed for climate models. Int. J. Climatol 2003, 23, 479–510. [Google Scholar]
- Sitch, S.; Smith, B.; Prentice, I.C.; Arneth, A.; Bondeau, A.; Cramer, W.; Kaplan, J.O.; Levis, S.; Lucht, W.; Sykes, M.T.; et al. Evaluation of ecosystem dynamics, plant geography and terrestrial carbon cycling in the LPJ dynamic global vegetation model. Glob. Change Biol 2003, 9, 161–185. [Google Scholar]
- Krinner, G.; Viovy, N.; de Noblet-Ducoudré, N.; Ogée, J.; Polcher, J.; Friedlingstein, P.; Ciais, P.; Sitch, S.; Prentice, I.C. A dynamic global vegetation model for studies of the coupled atmosphere-biosphere system. Glob. Biogeochem. Cy 2005, 19, GB1015. [Google Scholar]
- Alessandri, A.; Gualdi, S.; Polcher, J.; Navarra, A. Effects of Land Surface-Vegetation on the Boreal Summer Surface Climate of a GCM. J. Climate 2007, 20, 225–278. [Google Scholar]
- Taylor, K.; Stouffer, R.; Meehl, G. An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc 2012, 93, 485–498. [Google Scholar]
- Collins, W.J.; Bellouin, N.; Doutriaux-Boucher, M.; Gedney, N.; Halloran, P.; Hinton, T.; Hughes, J.; Jones, C.D.; Joshi, M.; Liddicoat, S.; et al. Development and evaluation of an Earth-System model—HadGEM2. Geosci. Model Dev 2011, 4, 1051–1075. [Google Scholar]
- Charlson, R.J.; Lovelock, J.E.; Andreae, M.O.; Warren, S.G. Oceanic phytoplankton, atmospheric sulphur, cloud albedo and climate. Nature 1987, 326, 655–661. [Google Scholar]
- Cox, P.M.; Betts, R.A.; Jones, C.D.; Spall, S.A.; Totterdell, I.J. Acceleration of global warming due to carbon-cycle feedbacks in a coupled climate model. Nature 2000, 408, 184–187. [Google Scholar]
- Rea, J.; Ashley, M. Phenological evaluations using Landsat-1 sensors. Int. J. Biometeorol 1976, 20, 240–248. [Google Scholar]
- Girard, C.M. Estimation of phenological stages and physiological states of grasslands from remote-sensing data. Vegetatio 1982, 48, 219–226. [Google Scholar]
- White, M.A.; Thornton, P.E.; Running, S.W. A continental phenology model for monitoring vegetation responses to interannual climatic variability. Glob. Biogeochem. Cy 1997, 11, 217–234. [Google Scholar]
- Zhang, X.; Friedl, M.A.; Schaaf, C.B.; Strahler, A.H.; Hodges, J.C.F.; Gao, F.; Reed, B.C.; Huete, A. Monitoring vegetation phenology using MODIS. Remote Sens. Environ 2003, 84, 471–475. [Google Scholar]
- Zhou, L.; Kaufmann, R.K.; Tian, Y.; Myneni, R.B.; Tucker, C.J. Relation between interannual variations in satellite measures of northern forest greeness and climate between 1982 and 1999. J. Geophys. Res 2003, 108, 4004. [Google Scholar]
- Zhang, P.; Anderson, B.; Barlow, M.; Tan, B.; Myneni, R.B. Climate-related vegetation characteristics derived from Moderate Resolution Imaging Spectroradiometer (MODIS) leaf area index and normalized difference vegetation index. J. Geophys. Res 2004, 109, D20105. [Google Scholar]
- Ahl, D.E.; Gower, S.T.; Burrows, S.N.; Shabanov, N.V.; Myneni, R.B.; Knyazikhin, Y. Monitoring spring canopy phenology of a deciduous broadleaf forest using MODIS. Remote Sens. Environ 2006, 104, 88–95. [Google Scholar]
- Murray-Tortarolo, G.; Anav, A.; Friedlingstein, P.; Sitch, S.; Piao, S.; Zhu, Z. Evaluation of DGVMs in reproducing satellite derived LAI over the Northern Hemisphere. Part I: Uncoupled DGVMs. Remote Sens. 2013. submitted. [Google Scholar]
- Earth System Grid Federation (ESGF). Available online: http://pcmdi9.llnl.gov/esgf-web-fe/ (accessed on 1 June 2013).
- Wu, T.; Li, W.; Ji, J.; Xin, X.; Li, L.; Wang, Z.; Zhang, Y.; Li, J.; Zhang, F.; Wei, M.; Shi, X.; et al. Global carbon budgets simulated by the beijing climate center climate system model for the last century. J. Geophys. Res. 2013. [Google Scholar] [CrossRef]
- BNU-ESM. Available online: http://esg.bnu.edu.cn/BNU_ESM_webs/htmls/index.html (accessed on 1 June 2013).
- Arora, V.K.; Scinocca, J.F.; Boer, G.J.; Christian, J.R.; Denman, K.L.; Flato, G.M.; Kharin, V.V.; Lee, W.G.; Merryfield, W.J. Carbon emission limits required to satisfy future representative concentration pathways of greenhouse gases. Geophys. Res. Lett 2011, 38, L0580. [Google Scholar]
- Lindsay, K.; Bonan, G.B.; Doney, S.C.; Hoffman, F.M.; Lawrence, D.M.; Long, M.C.; Mahowald, N.M.; Moore, J.K.; Randerston, J.T.; Thornton, P.E. Preindustrial control and 20th century carbon cycle experiments with the earth system model CESM1-(BGC). J. Climate 2013. submitted. [Google Scholar]
- Dunne, J.P.; John, J.G.; Shevliakova, E.; Stouffer, R.J.; Krasting, J.P.; Malyshev, S.L.; Milly, P.C.D.; Sentman, L.T.; Adcroft, A.J.; Cooke, W.; et al. GFDL’s ESM2 global coupled climate-carbon Earth system models. Part II: Carbon system formation and baseline simulation characteristics. J Climate 2013, 26, 2247–2267. [Google Scholar]
- Volodin, E.M.; Dianskii, N.A.; Gusev, A.V. Simulating present day climate with the INMCM4.0 coupled model of the atmospheric and oceanic general circulations. Izv. Ocean. Atmos. Phys 2010, 46, 414–431. [Google Scholar]
- Dufresne, J.-L.; Foujols, M.-A.; Denvil, S.; Caubel, A.; Marti, O.; Aumont, O.; Balkanski, Y.; Bekki, S.; Bellenger, H.; Benshila, R.; et al. Climate change projections using the IPSL-CM5 Earth system model: From CMIP3 to CMIP5. Clim. Dyn 2013, 40, 2123–2165. [Google Scholar]
- Watanabe, S.; Hajima, T.; Sudo, K.; Nagashima, T.; Takemura, T.; Okajima, H.; Nozawa, T.; Kawase, H.; Abe, M.; Yokohata, T.; et al. MIROC-ESM 2010: Model description and basic results of CMIP5–20c3m experiments. Geosci. Model Dev 2011, 4, 845–872. [Google Scholar]
- Raddatz, T.; Reick, C.H.; Knorr, W.; Kattge, J.; Roeckner, E.; Schnur, R.; Schnitzler, K.-G.; Wetzel, P.; Jungclaus, J. Will the tropical land biosphere dominate the climate-carbon cycle feedback during the twenty-first century? Clim. Dyn 2007, 29, 565–574. [Google Scholar]
- Bentsen, M.; Bethke, I.; Debernard, J.B.; Iversen, T.; Kirkevåg, A.; Seland, Ø.; Drange, H.; Roelandt, C.; Seierstad, I.A.; Hoose, C.; et al. The Norwegian earth system model, NorESM1-M. Part 1: Description and basic evaluation. Geosci. Model Dev. Discuss 2012, 5, 2843–2931. [Google Scholar]
- Anav, A.; Friedlingstein, P.; Kidston, M.; Bopp, L.; Ciais, P.; Cox, P.M.; Jones, C.D.; Jung, M.; Myneni, R.B.; Zhu, Z. Evaluating the land and ocean components of the global carbon cycle in the CMIP5 Earth System Models. J Climate 2013, in press. [Google Scholar]
- Zhu, Z.; Bi, J.; Pan, Y.; Ganguly, S.; Anav, A.; Xu, L.; Samanta, A.; Piao, S.; Nemani, R.R.; Myneni, R.B. Global data sets of vegetation leaf area index (LAI)3g and Fraction of photosynthetically active radiation (FPAR)3g derived from global inventory modeling and mapping studies (GIMMS) normalized difference vegetation index (NDVI3g) for the period 1981 to 2011. Remote Sens 2013, 5, 927–948. [Google Scholar]
- Fang, H.; Jiang, C.; Li, W.; Wei, S.; Baret, F.; Chen, J.M.; Haro, J.G.; Liang, S.; Liu, R.; Myneni, R.B.; et al. Characterization and intercomparison of global moderate resolution leaf area index (LAI) products: Analysis of climatologies and theoretical uncertainties. J. Geophys. Res 2013, 118, 529–548. [Google Scholar]
- Zhu, W.; Tian, H.; Xu, X.; Pan, Y.; Chen, G.; Lin, W. Extension of the growing season due to delayed autumn over mid and high latitudes in North America during 1982–2006. Global Ecol. Biogeogr 2012, 21, 260–271. [Google Scholar]
- Mitchell, T.D.; Jones, P.D. An improved method of constructing a database of monthly climate observations and associated high-resolution grids. Int. J. Climatol 2005, 25, 693–712. [Google Scholar]
- McGuire, A.D.; Christensen, T.R.; Hayes, D.; Heroult, A.; Euskirchen, E.; Yi, Y.; Kimball, J.S.; Koven, C.; Lafleur, P.; Miller, P.A.; et al. An assessment of the carbon balance of arctic tundra: Comparisons among observations, process models, and atmospheric inversions. Biogeosciences 2012, 9, 3185–3204. [Google Scholar]
- Nemani, R.R.; Keeling, C.D.; Hashimoto, H.; Jolly, W.M.; Piper, S.C.; Tucker, C.J.; Myneni, R.B.; Running, S.W. Climate-driven increases in global terrestrial net primary production from 1982 to 1999. Science 2003, 300, 1560–1563. [Google Scholar]
- Piao, S.; Ciais, P.; Friedlingstein, P.; de Noblet-Ducoudre, N.; Cadule, P.; Viovy, N.; Wang, T. Spatiotemporal patterns of terrestrial carbon cycle during the 20th century. Glob. Biogeochem. Cy 2009, 23, GB4026. [Google Scholar]
- Zeng, H.; Jia, G.; Epstein, H. Recent changes in phenology over the northern high latitudes detected from multi-satellite data. Environ. Res. Lett 2011, 6, 045508. [Google Scholar]
- Richardson, A.D.; Anderson, R.S.; Arain, M.A.; Barr, A.G.; Bohrer, G.; Chen, G.; Chen, J.M.; Ciais, P.; Davis, K.J.; Desai, A.R.; et al. Terrestrial biosphere models need better representation of vegetation phenology: Results from the North American carbon program site synthesis. Glob. Change Biol 2011, 18, 566–584. [Google Scholar]
- Jeong, S.-J.; Ho, C.-H.; Gim, H.J.; Brown, M.E. Phenology shifts at start vs. end of growing season in temperate vegetation over the Northern Hemisphere for the period 1982–2008. Glob. Change Biol 2011, 17, 2385–2399. [Google Scholar]


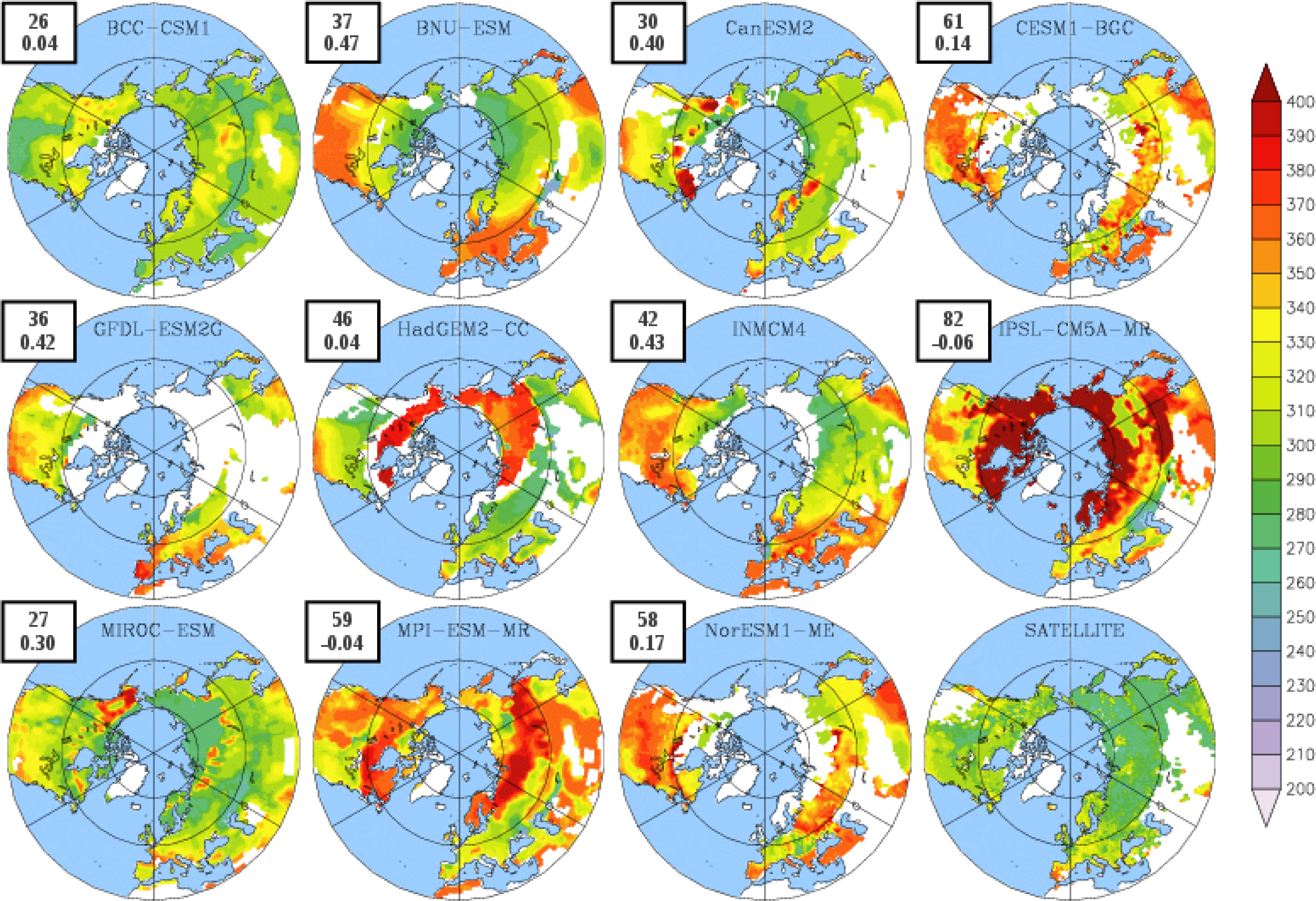
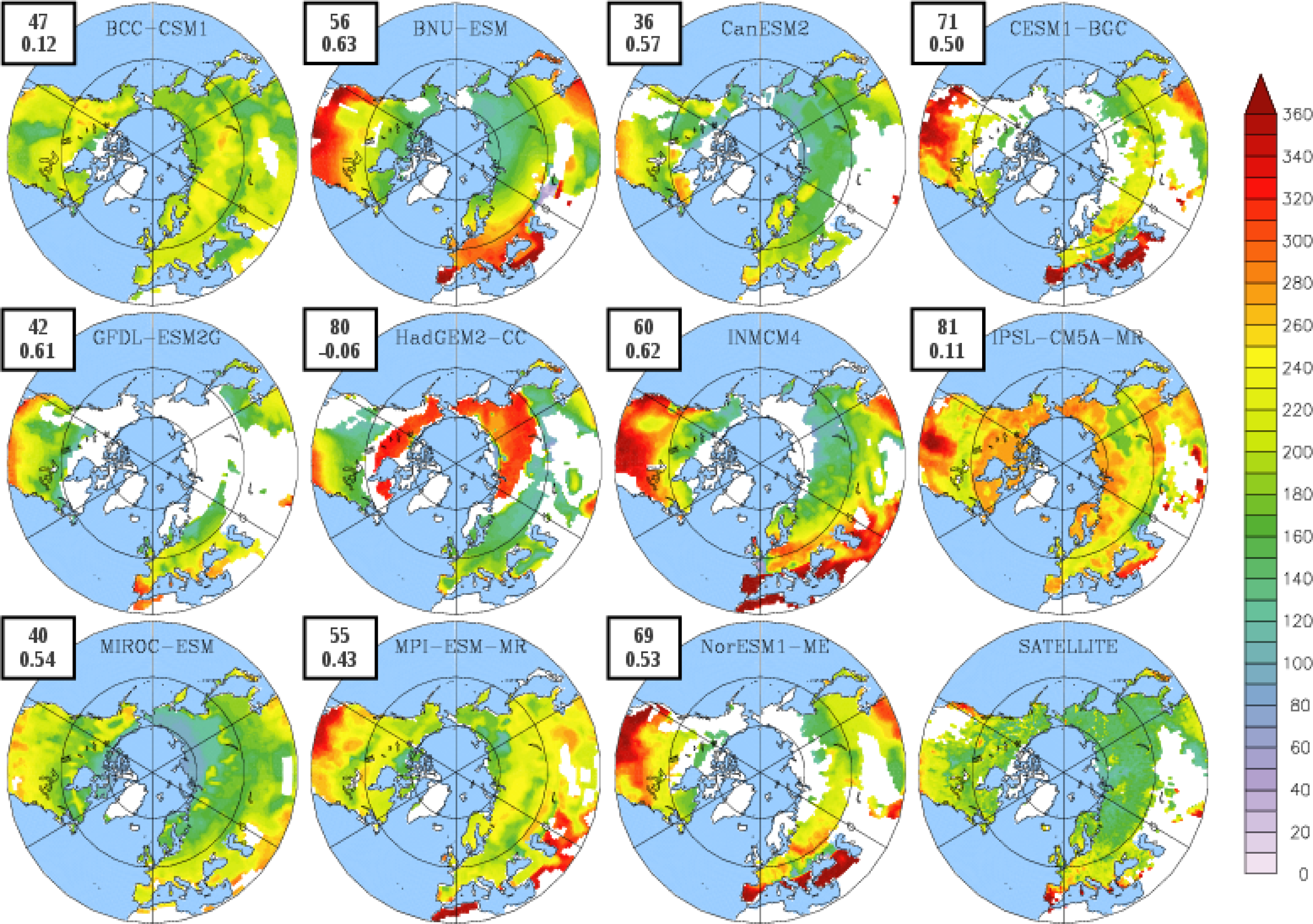
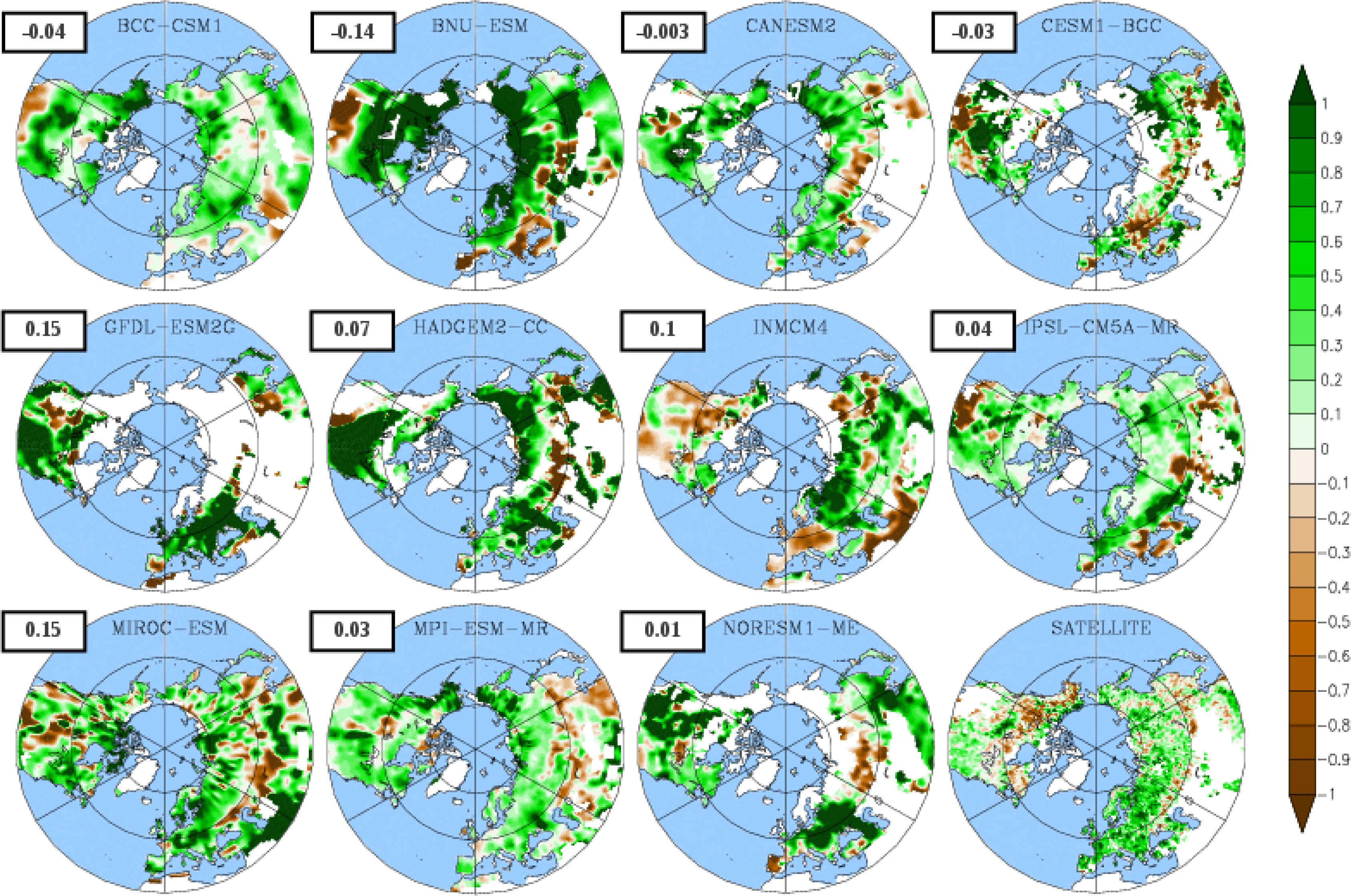
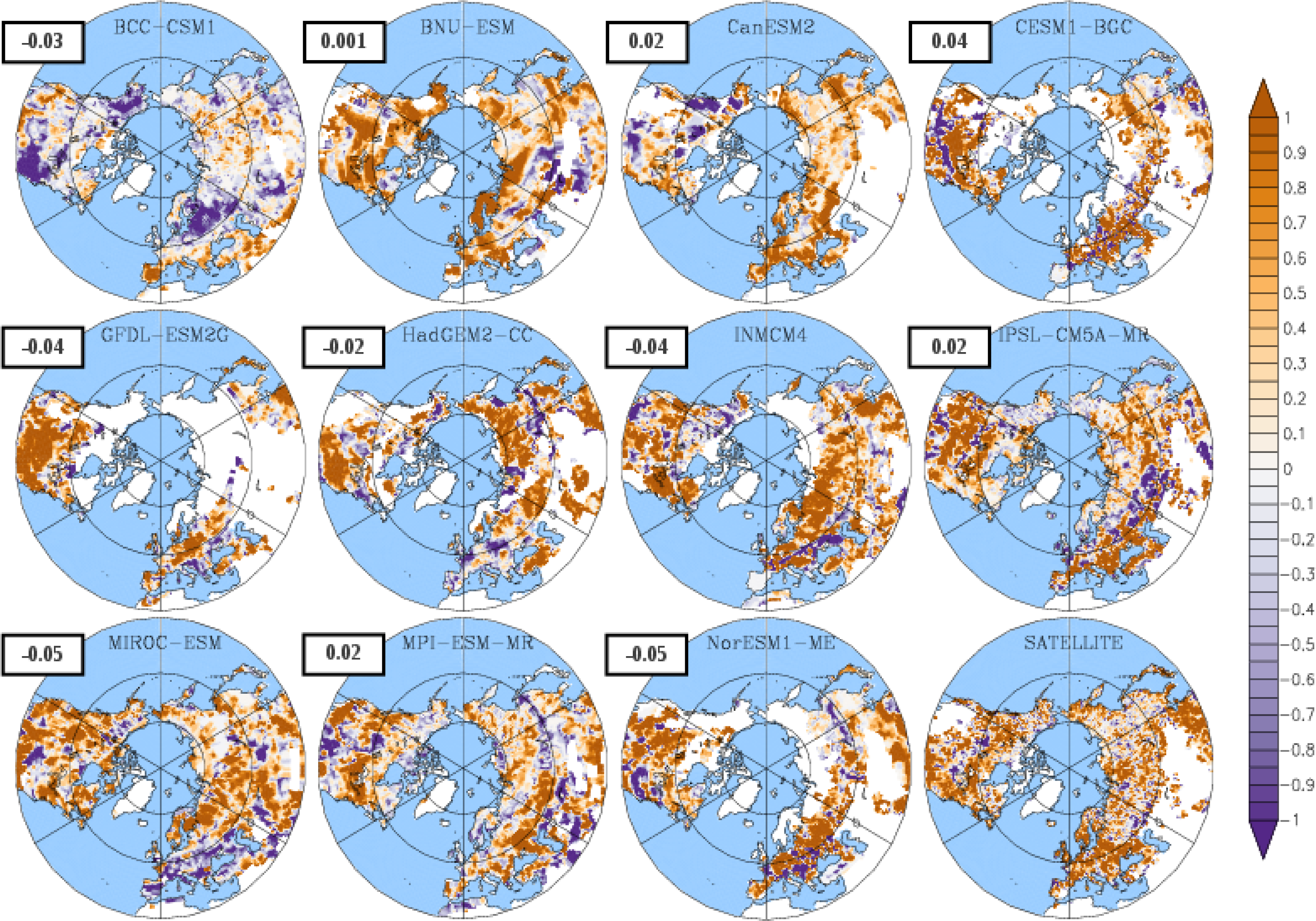

| Models | Source | Land Models | Dynamic Vegetation | #PFTs | N Cycle | Resolution (Lat. × Lon.) | Reference |
|---|---|---|---|---|---|---|---|
| BCC-CSM1 | Beijing Climate Center, China | BCC_AVIM1.0 | N | 15 | N | ∼2.8125° × 2.8125° | [75] |
| BNU-ESM | Beijing Normal University, China | CoLM | Y | n/a | Y | ∼2.8125° × 2.8125° | [76] |
| CanESM2 | Canadian Centre for Climate Modelling and Analysis, Canada | CLASS2.7 + CTEM1 | N | 9 | N | ∼2.8125° × 2.8125° | [77] |
| CESM1-BGC | National Center for Atmospheric Research, USA | CLM4 | N | 15 | Y | 1.25° × 0.9 | [78] |
| GFDL-ESM2G | Geophysical Fluid Dynamics Laboratory, USA | LM3 | Y | 5 | N | 2° × 2.5° | [79] |
| HadGEM2-CC | Met Office Hadley Centre, UK | JULES + TRIFFID | Y | 5 | N | 1.25° × 1.875° | [63] |
| INMCM4 | Institute for Numerical Mathematics, Russia | Simple model | N | n/a | N | 1.5° × 2 | [80] |
| IPSL-CM5A-MR | Institut Pierre Simon Laplace, France Japan Agency for Marine-Earth Science and Technology, Japan; | ORCHIDEE | N | 13 | N | 1.25° × 2.5° | [81] |
| MIROC-ESM | Atmosphere and Ocean Research Institute, Japan; National Institute for Environmental Studies, Japan | MATSIRO + SEIB-DGVM | Y | 13 | N | ∼2.8125° × 2.8125° | [82] |
| MPI-ESM-MR | Max Planck Institute for Meteorology, Germany | JSBACH + BETHY | Y | 12 | N | 1.875° × 1.875° | [83] |
| NorESM1-ME | Norwegian Climate Centre, Norway | CLM4 | N | 16 | Y | 1.9° × 2.5° | [84] |
| Model | LAI | Onset | Dormancy | Length |
|---|---|---|---|---|
| BCC-CSM1 | 1.54 | 102 | 304 (274) | 203 (146) |
| BNU-ESM | 1.75 | 109 | 323 (280) | 214 (148) |
| CanESM2 | 0.80 | 140 | 318 (295) | 178 (149) |
| CESM1-BGC | 1.20 | 109 | 343 (305) | 233 (190) |
| GFDL-ESM2G | 2.70 | 131 | 330 (304) | 199 (152) |
| HadGEM2-CC | 1.17 | 115 | 325 (279) | 210 (132) |
| INMCM4 | 1.00 | 106 | 329 (289) | 223 (164) |
| IPSL-CM5A-MR | 1.68 | 121 | 370 (276) | 249 (131) |
| MIROC-ESM | 1.66 | 124 | 307 (276) | 183 (130) |
| MPI-ESM-MR | 1.35 | 121 | 347 (274) | 227 (147) |
| NorESM1-ME | 1.30 | 109 | 342 (303) | 219 (186) |
| LAI3g | 0.83 | 111 | 295 | 184 |
| LAI | Onset | Dormancy | Length | |
|---|---|---|---|---|
| Uncoupled | 1.55 ± 0.45 | 131 ± 10 | 339 ± 20 (277±7) | 208 ± 25 (137±20) |
| Coupled | 1.47 ± 0.51 | 117 ± 12 | 331 ± 19 (287±13) | 214 ± 22 (152±20) |
| LAI3g | 0.83 | 111 | 295 | 184 |
© 2013 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Anav, A.; Murray-Tortarolo, G.; Friedlingstein, P.; Sitch, S.; Piao, S.; Zhu, Z. Evaluation of Land Surface Models in Reproducing Satellite Derived Leaf Area Index over the High-Latitude Northern Hemisphere. Part II: Earth System Models. Remote Sens. 2013, 5, 3637-3661. https://doi.org/10.3390/rs5083637
Anav A, Murray-Tortarolo G, Friedlingstein P, Sitch S, Piao S, Zhu Z. Evaluation of Land Surface Models in Reproducing Satellite Derived Leaf Area Index over the High-Latitude Northern Hemisphere. Part II: Earth System Models. Remote Sensing. 2013; 5(8):3637-3661. https://doi.org/10.3390/rs5083637
Chicago/Turabian StyleAnav, Alessandro, Guillermo Murray-Tortarolo, Pierre Friedlingstein, Stephen Sitch, Shilong Piao, and Zaichun Zhu. 2013. "Evaluation of Land Surface Models in Reproducing Satellite Derived Leaf Area Index over the High-Latitude Northern Hemisphere. Part II: Earth System Models" Remote Sensing 5, no. 8: 3637-3661. https://doi.org/10.3390/rs5083637