A Remote-Sensing Driven Tool for Estimating Crop Stress and Yields
Abstract
:1. Introduction
2. Methods and Materials
- (1)
- Estimation of surface and root zone soil moisture proxy values from ALEXI over the period April 2000 to September 2009. Daily values of either surface or root zone soil moisture were obtained on clear days for which ALEXI simulations were available.
- (2)
- Computation of a vertical soil moisture profile from the ALEXI data consistent with the profile depths required by DSSAT.
- (3)
- Comparison of ALEXI soil moisture values with both rainfed DSSAT values and soil moisture estimates from a simulation using Noah land surface model processed from NASA’s Land Information System (LIS) over the same period.
- (4)
- Integration of ALEXI derived soil moisture profiles within the DSSAT model, used in lieu of precipitation data.
- (5)
- Comparison of yield estimates from the ALEXI soil moisture driven model and the DSSAT model driven by the recorded precipitation, and with measured yields.
2.1. Study Site
2.2. ALEXI Modeling Framework
2.2.1. Two-Source Energy Balance Model
2.2.2. Regional Implementation
2.2.3. ALEXI Input Datasets
(i) Surface radiometric temperature and solar insolation data
(ii) Surface and upper air meteorological data
(iii) Land surface and canopy data
2.3. Available Water Derived from ALEXI
2.4. Agricultural Simulation Model
2.5. Development of Soil Moisture Profiles from ALEXI AW
3. Integration of ALEXI SM within DSSAT
3.1. Gap-Filling ALEXI SM Time Series
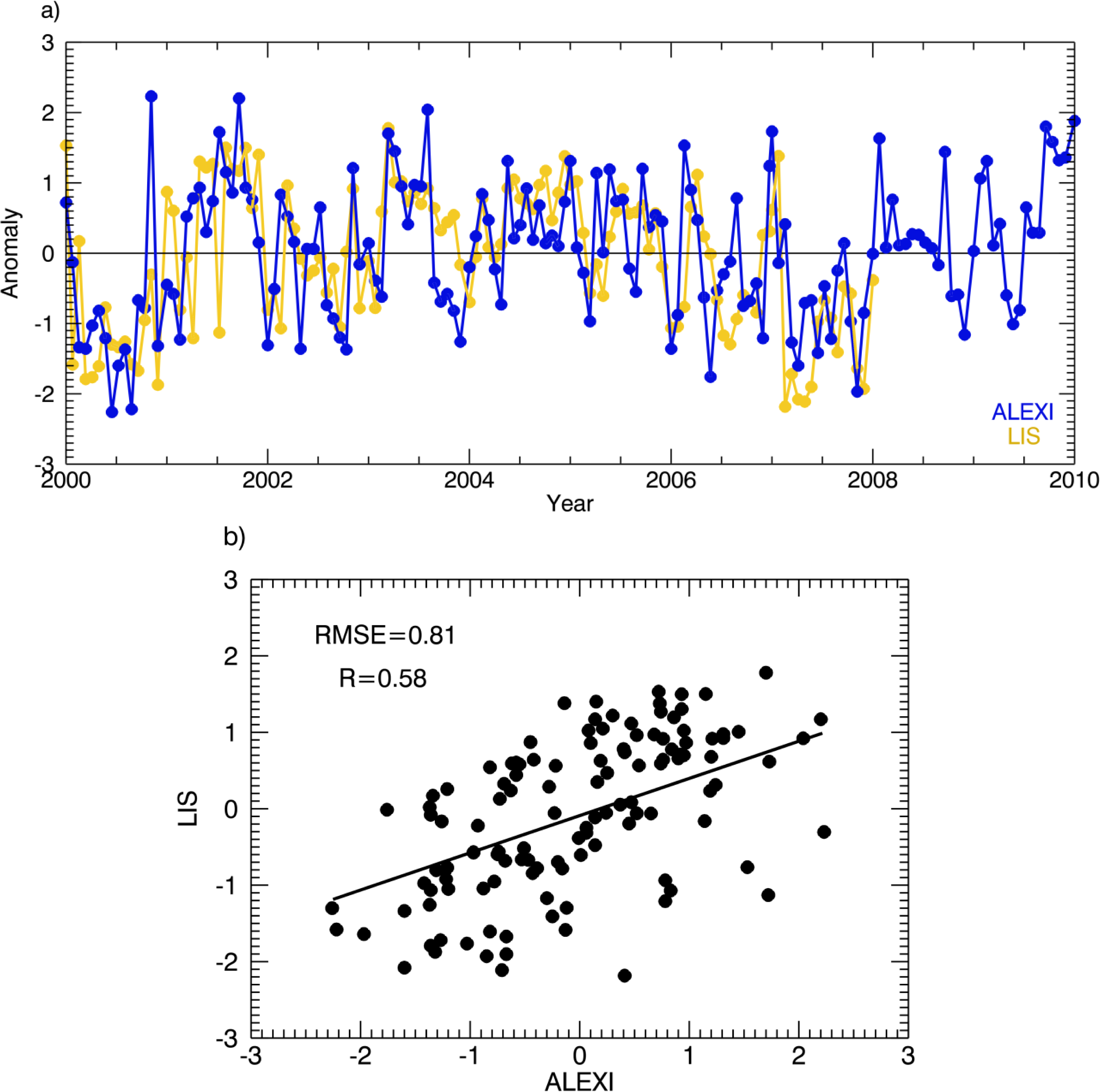
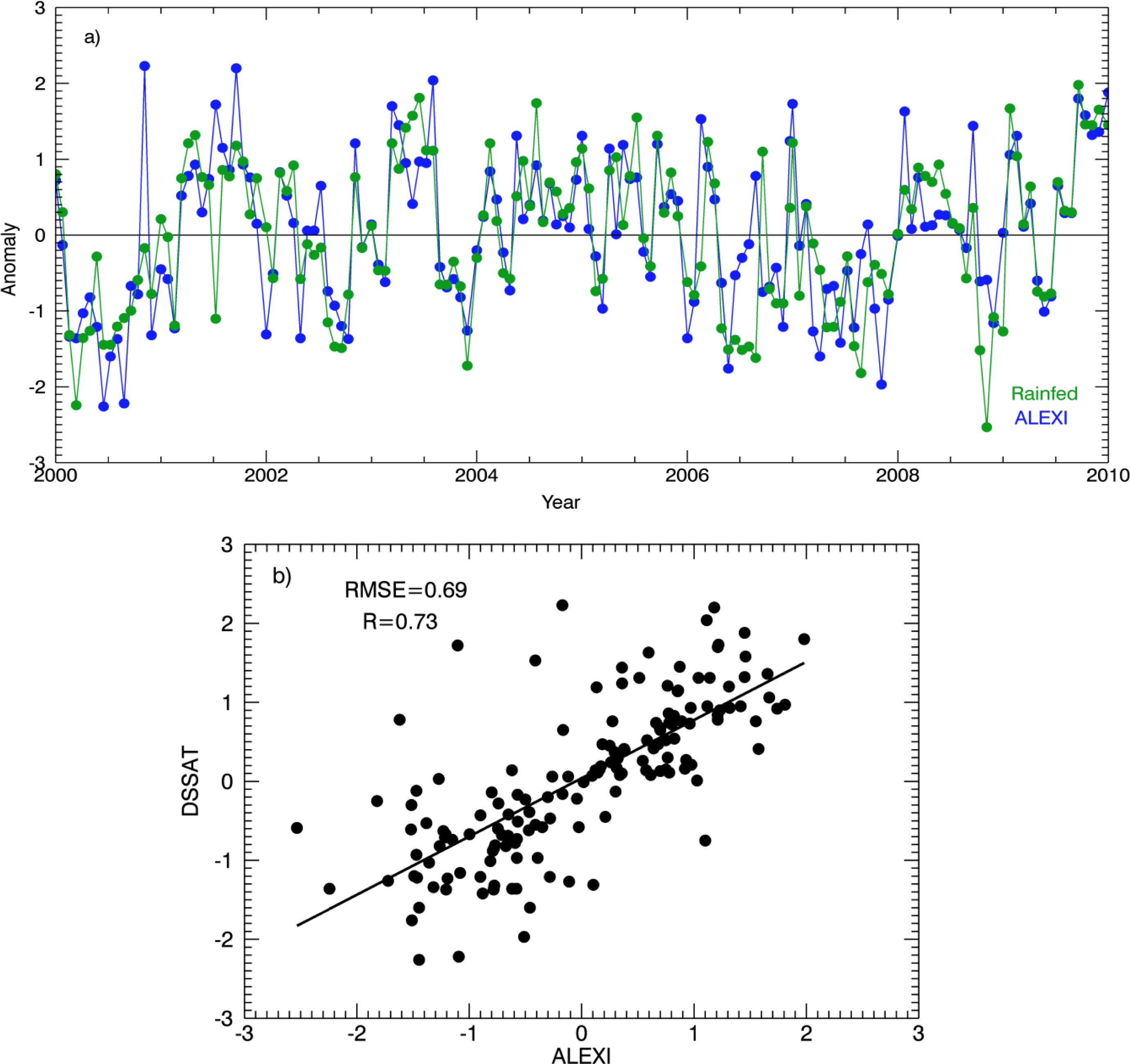
3.2. Intercomparison of Soil Moisture Time Series
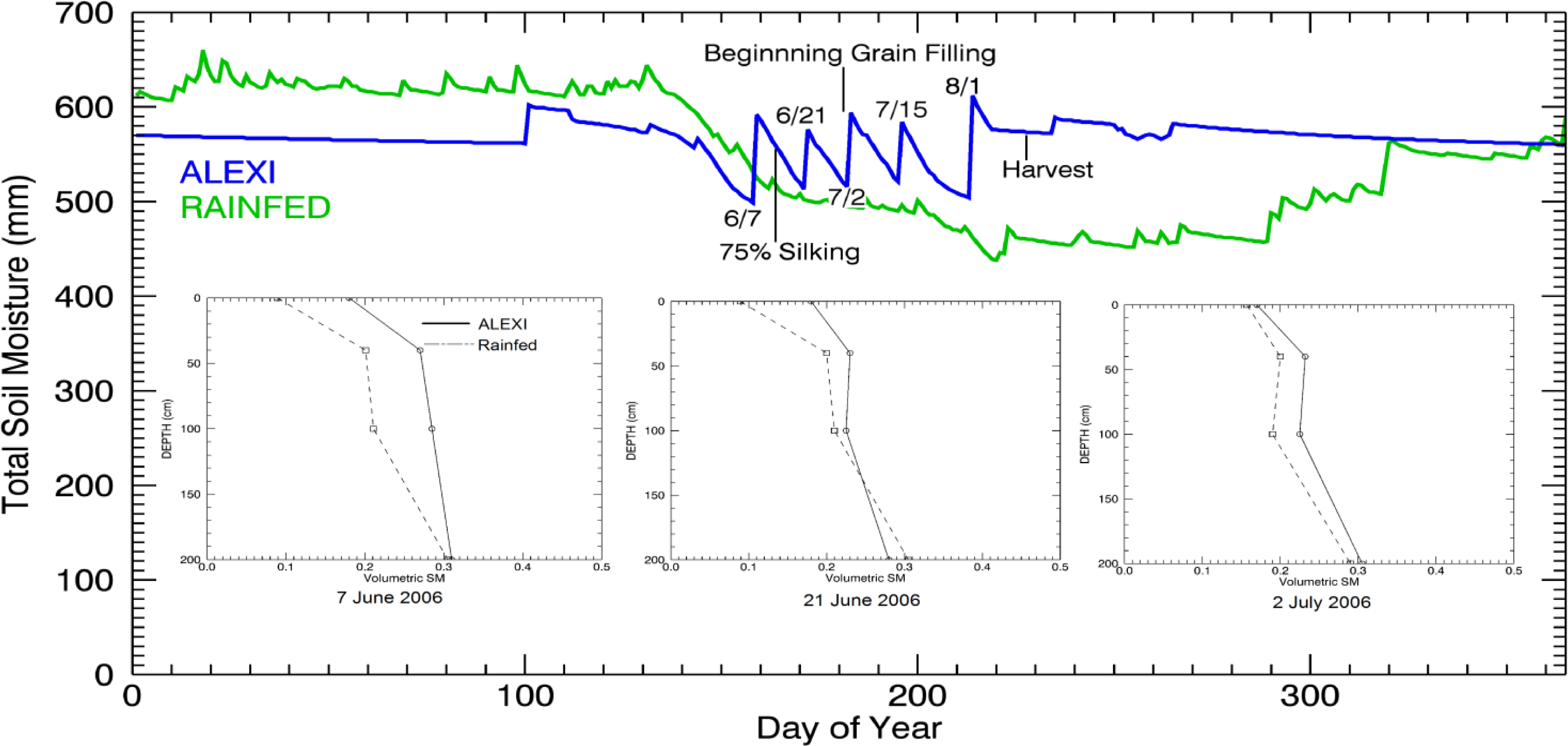
3.3. Updating DSSAT with ALEXI Soil Moisture
4. Results and Discussion
5. Errors and Uncertainties in the Study
6. Conclusions
Acknowledgments
Conflict of Interest
References
- Wood, S.J.; Jones, D.A.; Moore, R.J. Accuracy of rainfall measurement for scales of hydrological interest. Hydrol. Earth Syst. Sci. Discuss 2000, 4, 531–543. [Google Scholar]
- Levizzani, V.; Bauer, P.; Turk, J. (Eds.) Measuring Precipitation from Space, Advances in Global Change Research; Springer Publishers: Amsterdam, The Netherlands, 2007; Volume 28, p. 223.
- Simpson, J.; Kummerow, C.; Tao, W.K.; Adler, R.F. On the tropical rainfall measuring mission (TRMM). Meteorol. Atmos. Phys 1996, 60, 19–36. [Google Scholar]
- Arkin, P.A.; Meisner, B.N. The relationship between large-scale convective rainfall and cold cloud over the western hemisphere during 1982–84. Mon. Wea. Rev 1987, 115, 51–74. [Google Scholar]
- Scofield, R.A.; Naimeng, L. The Use of Satellite Imagery during the Great Floods of 1993. Proceedings of 7th Conference Satellite Meteorology and Oceanography, Monterey, CA, USA, 6–10 June 1994; pp. 345–350.
- Lovejoy, S.; Austin, G.L. The delineation of rain areas from visible and IR satellite data for GATE and mid-latitudes. Atmos.-Ocean 1979, 17, 77–92. [Google Scholar]
- Gebregiorgis, A.S.; Tian, Y.; Peters-Lidard, C.; Hossain, F. Tracing hydrologic model simulation error as a function of satellite rainfall estimation bias components and land use and land cover conditions. Water Resour. Res 2012, 48, W11509. [Google Scholar]
- Joyce, R.J.; Xie, P. Kalman filter-based CMORPH. J. Hydrometeorol 2011, 12, 1547–1563. [Google Scholar]
- Sorooshian, S.; Hsu, K.L.; Gao, X.; Gupta, H.V.; Imam, B.; Braithwaite, D. Evaluation of PERSIANN system satellite based estimates of tropical rainfall. Bull. Am. Meteorol. Soc 2000, 81, 2035–2046. [Google Scholar]
- Hong, Y.; Adler, R.F.; Hossain, F.; Curtis, S.; Huffman, G.J. A first approach to global runoff simulation using satellite rainfall estimation. Water Resour. Res 2007, 43, W08502. [Google Scholar]
- Hsu, K.; Behrangi, A.; Imam, B.; Sorooshian, S. Extreme Precipitation Estimation Using Satellite-Based PERSIANN-CCS Algorithm. In Satellite Rainfall Applications for Surface Hydrology; Gebremichael, M., Hossain, F., Eds.; Springer: New York, NY, USA, 2010. [Google Scholar]
- Ulaby, F.T.; Dubois, P.C.; Zyl, J.V. Radar mapping of surface soil moisture. J. Hydrol 1996, 184, 57–84. [Google Scholar]
- Reichle, R.H.; Crow, W.T.; Keppenne, C.L. An adaptive ensemble Kalman filter for soil moisture data assimilation. Water Resour. Res 2008, 44, W03423. [Google Scholar]
- Anderson, M.C.; Norman, J.M.; Mecikalski, J.R.; Otkin, J.A.; Kustas, W.P. A climatological study of evapotranspiration and moisture stress across the continental United States based on thermal remote sensing: 1. Model formulation. J. Geophys. Res 2007, 112, D10117. [Google Scholar]
- Norman, J.M.; Kustas, W.P.; Humes, K.S. Source approach for estimating soil and vegetation energy fluxes in observations of directional radiometric surface temperature. Agric. For. Meteorol 1995, 77, 263–293. [Google Scholar]
- Anderson, M.C.; Hain, C.; Wardlow, B.; Pimstein, A.; Mecikalski, J.R.; Kustas, W.P. Evaluation of drought indices based on thermal remote sensing of evapotranspiration over the continental United States. J. Climate 2011, 24, 2025–2044. [Google Scholar]
- Anderson, M.C.; Norman, J.M.; Diak, G.R.; Kustas, W.P.; Mecikalski, J.R. A two-source time-integrated model for estimating surface fluxes using thermal infrared remote sensing. Remote Sens. Environ 1997, 60, 195–216. [Google Scholar]
- Jones, J.W.; Hoogenboom, G.; Porter, C.H.; Boote, K.J.; Batchelor, W.D.; Hunt, L.A.; Wilkens, P.W.; Singh, U.; Gijsman, A.J.; Ritchie, J.T. The DSSAT cropping system model. Eur. J. Agron 2003, 18, 235–265. [Google Scholar]
- Clapp, R.B.; Hornberger, G.M. Emperical equations for some soil hydraulic properties. Water Resour. Res 1978, 14, 601–604. [Google Scholar]
- Twarakavi, N.K.C.; Sakai, M.; Simunek, J. An objective analysis of the dynamic nature of field capacity. Water Resour. Res 2009, 45, W10410. [Google Scholar]
- Cruise, J.F.; Arora, K. A hydroclimatic application strategy for the Poisson partial duration model. J. Am. Water Resour. Assoc 1990, 26, 431–442. [Google Scholar]
- Anderson, M.C.; Norman, J.M.; Mecikalski, J.R.; Otkin, J.A.; Kustas, W.P. A climatological study of evapotranspiration and moisture stress across the continental United States based on thermal remote sensing: 2. Surface moisture climatology. J. Geophys. Res 2007, 112, D11112. [Google Scholar]
- Anderson, M.C.; Norman, J.M.; Kustas, W.P.; Li, F.; Prueger, J.H.; Mecikalski, J.R. Effects of vegetation clumping on two–source model estimates of surface energy fluxes from an agricultural landscape during SMACEX. J. Hydrometeorol 2005, 6, 892–909. [Google Scholar]
- Kustas, W.P.; Norman, J.M. Evaluation of soil and vegetation heat flux predictions using a simple two-source model with radiometric temperatures for partial canopy cover. Agric. For. Meteorol 1999, 94, 13–29. [Google Scholar]
- Kustas, W.P.; Norman, J.M. Reply to comments about the basic equations of dual-source vegetation-atmosphere transfer models. Agric. For. Meteorol 1999, 94, 275–278. [Google Scholar]
- Kustas, W.P.; Norman, J.M. Evaluating the effects of subpixel heterogeneity on pixel average fluxes. Remote Sens. Environ 2000, 74, 327–342. [Google Scholar]
- Kustas, W.P.; Norman, J.M. A two-source energy balance approach using directional radiometric temperature observations for sparse canopy covered surfaces. Agron. J 2000, 92, 847–854. [Google Scholar]
- Priestley, C.H.B.; Taylor, R.J. On the assessment of surface heat flux and evaporation using large-scale parameters. Mon. Wea. Rev 1972, 100, 81–92. [Google Scholar]
- Agam, N.; Kustas, W.P.; Anderson, M.C.; Norman, J.M.; Colaizzi, P.D.; Prueger, J.H. Application of the Priestley-Taylor approach in a two-source surface energy balance model. J. Hydrometeorol 2010, 11, 185–198. [Google Scholar]
- Santanello, J.A.; Friedl, M.A. Diurnal variation in soil heat flux and net radiation. J. Appl. Meteorol 2003, 42, 851–862. [Google Scholar]
- Norman, J.M.; Divakarla, M.; Goel, N.S. Algorithms for extracting information from remote thermal-IR observations of the Earth’s surface. Remote Sens. Environ 1995, 51, 157–168. [Google Scholar]
- Mecikalski, J.R.; Diak, G.R.; Anderson, M.C.; Norman, J.M. Estimating fluxes on continental scales using remotely sensed data in an atmospheric–land exchange model. J. Appl. Meteorol 1999, 38, 1352–1369. [Google Scholar]
- Carlson, T.N.; Dodd, J.K.; Benjamin, S.G.; Cooper, J.N. Satellite Estimation of the Surface Energy Balance, Moisture Availability and Thermal Inertia. J. Appl. Meteorol 1981, 20, 67–87. [Google Scholar]
- Norman, J.M.; Anderson, M.C.; Kustas, W.P.; French, A.N.; Mecikalski, J.; Torn, R.; Diak, G.R.; Schmugge, T.J.; Tanner, B.C.W. Remote sensing of surface energy fluxes at 101-m pixel resolutions. Water Resour. Res 2003, 39, 1221. [Google Scholar]
- Kustas, W.P.; Diak, G.R.; Norman, J.M. Time Difference Methods for Monitoring Regional Scale Heat Fluxes with Remote Sensing. In Land Surface Hydrology, Meteorology, and Climate: Observations and Modeling; Lakshmi, V., Albertson, J., Schaake, J., Eds.; AGU: Washington, DC, USA, 2001; Volume 3, pp. 15–29. [Google Scholar]
- McNaughton, K.G.; Spriggs, T.W. A mixed-layer model for regional evaporation. Bound.-Lay. Meteorol 1986, 34, 243–262. [Google Scholar]
- Hain, C.R.; Crow, W.T.; Mecikalski, J.R.; Anderson, M.C.; Holmes, T. An intercomparison of available soil moisture estimates from thermal infrared and passive microwave remote sensing and land surface modeling. J. Geophys. Res 2011, 116, D15107. [Google Scholar]
- Otkin, J.A.; Anderson, M.C.; Mecikalski, J.R.; Diak, G.R. Validation of GOES-based insolation estimates using data from the United States Climate Reference Network. J. Hydrometeorol 2005, 6, 460–475. [Google Scholar]
- Michalakes, J.; Dudhia, J.; Gill, D.; Henderson, T.; Klemp, J.; Skamarock, W.; Wang, W. The Weather Research and Forecast Model: Software Architecture and Performance. In Proceedings of the Eleventh ECMWF Workshop on the Use of High Performance Computing in Meteorology, Reading, UK, 25–29 October 2004; Zwieflhofer, W., Mozdzynski, G., Eds.; World Scientific: Hackensack, NJ, USA, 2005; pp. 156–168. [Google Scholar]
- Hansen, M.C.; Defries, R.S.; Townshend, J.R.G.; Sohlberg, R. Global land cover classification at 1 km spatial resolution using a classification tree approach. Int. J. Remote Sens 2000, 21, 1331–1364. [Google Scholar]
- Hain, C.R.; Mecikalski, J.R.; Anderson, M.C. Retrieval of an available water-based soil moisture proxy from thermal infrared remote sensing. Part I: Methodology and validation. J. Hydrometeorol 2009, 10, 665–683. [Google Scholar]
- Crow, W.T.; Zhan, X. Continental-scale evaluation of remotely-sensed soil moisture products. IEEE Geosci. Remote Sens. Lett 2007, 4, 451–455. [Google Scholar]
- Tsuji, G.; Hoogenboom, G.; Thornton, P. (Eds.) Understanding Options for Agricultural Production; Kluwer Academic Publishers: Boston, MA, USA, 1998; p. 399.
- Hoogenboom, G.; Jones, J.W.; Wilkens, P.W.; Porter, C.H.; Batchelor, W.D.; Hunt, L.A.; Boote, K.J.; Singh, U.; Uryasev, O.; Bowen, W.T.; et al. Decision Support System for Agrotechnology Transfer Version 4.0; University of Hawaii: Honolulu, HI, USA, 2004; [CD-ROM]. [Google Scholar]
- Zhang, H.; Oweis, T. Water–yield relations and optimal irrigation scheduling of wheat in the Mediterranean region. Agr. Water Manage 1999, 38, 195–211. [Google Scholar]
- Guereña, A.; Ruiz-Ramos, M.; Díaz-Ambrona, C.H.; Conde, J.R.; Mínguez, M.I. Assessment of climate change and agriculture in Spain using climate models. Agron. J 2001, 93, 237–249. [Google Scholar]
- Lopez-Cedron, F.X.; Boote, K.J.; Pineiro, J.; Sau, F. Improving the CERES-maize model ability to simulate water deficit impact on maize production and yield components. Agron. J 2008, 100, 296–307. [Google Scholar]
- Garcia y Garcia, A.; Hoogenboom, G.; Guerra, L.C.; Paz, J.O.; Fraisse, C.W. Analysis of the interannual variation of peanut yield in Georgia using a dynamic crop simulation model. Trans. Amer. Soc. Agric. Biol. Eng 2006, 49, 2005–2015. [Google Scholar]
- McNider, R.T.; Christy, J.R.; Moss, D.; Doty, K.; Handyside, C.; Limaye, A.S.; Garcia y Garcia, A.; Hoogenboom, G. A real-time gridded crop model for assessing spatial drought stress on crops in the Southeastern United States. J. Appl. Meteorol 2011, 50, 1459. [Google Scholar]
- Ellenburg, W.L.; Cruise, J.F.; McNider, R.T. Assessment and Mitigation of Agricultural Drought and Water Availability in the Southeastern United States Using Space Science Technology. Proceedings of 63rd International Astronautical Congress, Naples, Italy, 1–5 October 2012; paper number IAC-12-B5.2.3. p. 13.
- Heinemann, A.B.; Hoogenboom, G.; de Faria, R.T. Determination of spatial water requirements at county and regional levels using crop models and GIS: An example for the state of Parana, Brazil. Agr. Water Manage 2002, 52, 177–196. [Google Scholar]
- Fang, H.; Liang, S.; Hoogenboom, G. Corn yield estimation through assimilation of remotely sensed data into the CSM CERES Maize model. J. Remote Sens 2008, 29, 3011–3032. [Google Scholar]
- Fang, H.S.; Hoogenboom, G. Integration of MODIS LAI and vegetation index products with the CSM–CERES–Maize model for corn yield estimation. Int. J. Remote Sens 2011, 32, 1039–1065. [Google Scholar]
- Gijsman, A.J.; Thornton, P.K.; Hoogenboom, G. Using the WISE database to parameterize soil inputs for crop simulation models. Comput. Electron. Agric 2007, 56, 85–100. [Google Scholar]
- White, J.W.; Hoogenboom, G.; Kimball, B.A.; Wall, G.W. Methodologies for simulating impacts of climate change on crop production. Field Crop. Res 2011, 124, 357–368. [Google Scholar]
- Howell, T.; Evett, S. The Penman-Monteith Method, Section 3. In Evapotranspiration; Determination of consumptive use in water rights; Denver, CO, USA, 2004. [Google Scholar]
- Ritchie, J.T.; Porter, C.H.; Judge, J.; Jones, J.W.; Suleiman, A.A. Extension of an existing model for soil water evaporation and redistribution under high water content conditions. Soil. Sci. Soc. Amer. J 2009, 73, 792–801. [Google Scholar]
- Kostov, K.G.; Jackson, T.J. Estimating profile soil moisture from surface layer measurements. A review. Proc. SPIE 1993, 1941, 125–136. [Google Scholar]
- Al-Hamdan, O.Z.; Cruise, J.F. Soil moisture profile development from surface observations by principle of maximum entropy. J. Hydrol. Eng 2010, 15, 327–337. [Google Scholar]
- Singh, V.P. Entropy theory for movement of moisture in soils. Water Resour. Res 2010, 46, W03516. [Google Scholar]
- Singh, V.P. Hydrologic synthesis using entropy theory: Review. J. Hydrol. Eng 2011, 16, 421–433. [Google Scholar]
- Jaynes, E.T. Information theory and statistical mechanics. Phys. Rev 1957, 106, 620–630. [Google Scholar]
- Jaynes, E.T. Information theory and statistical mechanics. II. Phys. Rev 1957, 108, 171–190. [Google Scholar]
- Chiu, C. Entropy and probability concepts in hydraulics. J. Hydraul. Eng 1987, 113, 583–599. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J 1948, 27, 379–423. [Google Scholar]
- Barbé, D.; Cruise, J.; Singh, V. Solution of Three-Constraint Entropy–Based Velocity Distribution. J. Hydraul. Eng 1991, 117, 1389–1396. [Google Scholar]
- Ek, M.B.; Mitchell, K.E.; Lin, Y.; Rogers, E.; Grummann, P.; Koren, V.; Gayno, G.; Tarpley, J.D. Implementation of Noah land surface model advances in the national centers for environmental prediction operational mesoscale Eta model. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Kumar, S.V.; Peters-Lidard, C.D.; Tian, Y.; Houser, P.R.; Geiger, J.; Olden, S.; Lighty, L.; Eastman, J.L.; Doty, B.; Dirmeyer, P.; et al. Land information system: An interoperable framework for high-resolution land surface modeling. Environ. Model. Softw 2006, 21, 1402–1415. [Google Scholar]
- Peters-Lidard, C.D.; Houser, P.R.; Tian, Y.; Kumar, S.V.; Geiger, J.; Olden, S.; Lighty, L.; Doty, B.; Dirmeyer, P.; Adams, J.; et al. High-performance Earth system modeling with NASA/GSFC’s Land Information System. Innov. Syst. Softw. Eng 2007, 3, 157–165. [Google Scholar]
- National Resources Conservation Service (NRCS). Urban Hydrology for Small Watersheds; Technical Release 55; Conservation Engineering Division, Soil Conservation Service, US Dept. of Agriculture: Washington, DC, USA, 1986. [Google Scholar]
- Silveira, L.; Charbonnier, F.; Genta, J.L. The antecedent soil moisture condition of the curve number procedure. Hydrol. Sci 2000, 45, 3–12. [Google Scholar]
- Paudel, K.; Limaye, A.; Hatch, U.; Cruise, J.; Musleh, F. Development of an optimal water allocation decision tool for the major crops during the water deficit period in the Southeast U.S. Nat. Resour. Model 2005, 18, 281–306. [Google Scholar]
| DSSAT Input Soil Parameters | ALEXI Soil Parameters | ||||||
|---|---|---|---|---|---|---|---|
| Depth (cm) | Clay % | Silt % | Sand % | pH | Cation Exchange Capacity (cmol/Kg) | WP (cm3/cm3) | FC (cm3/cm3) |
| 0–10 | 21.0 | 52.7 | 26.3 | 5.3 | 5.0 | 0.084 | 0.360 |
| 10–40 | 34.4 | 47.8 | 11.6 | 5.3 | 6.2 | 0.103 | 0.382 |
| 40–100 | 45.9 | 29.2 | 23.3 | 5.3 | 5.9 | 0.138 | 0.412 |
| 100–200 | 47.5 | 29.2 | 23.3 | 5.3 | 5.9 | 0.138 | 0.412 |
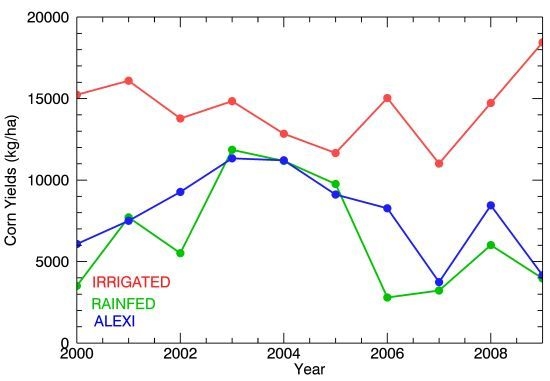
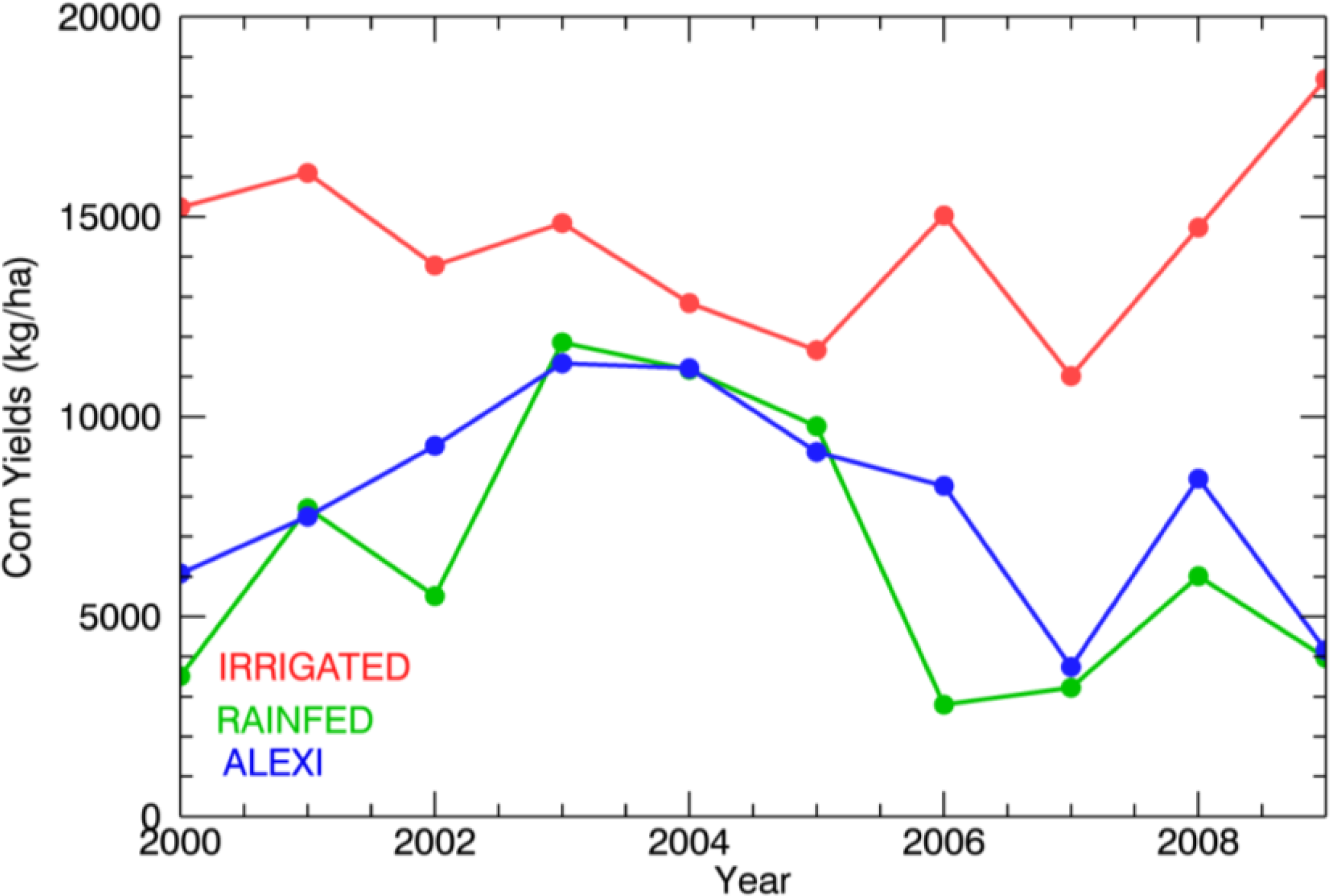
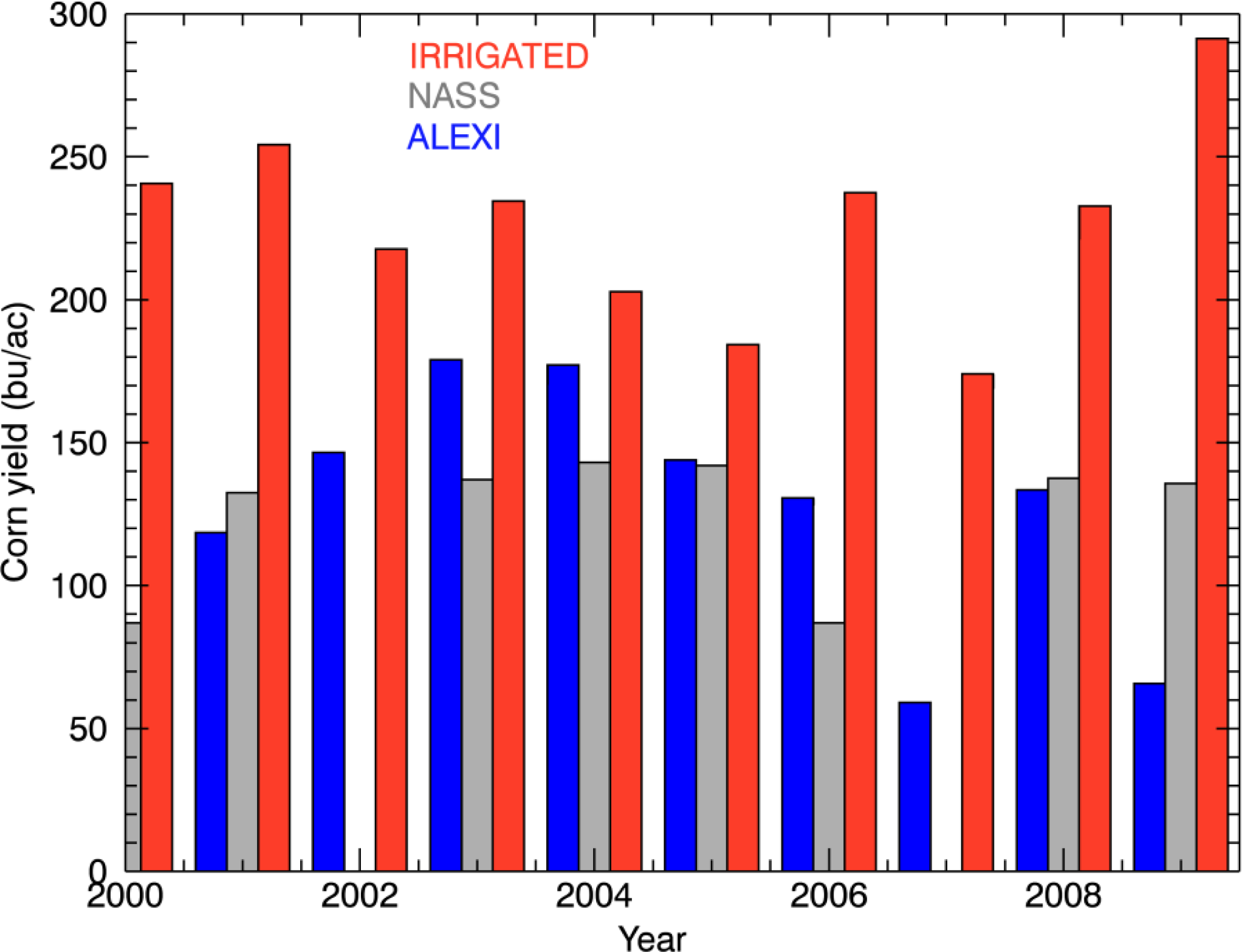
| Year | Planting Day | Rainfed Yields (kg/ha) | Irrigated Yields (kg/ha) | ALEXI Yields (kg/ha) | Number of Updates |
|---|---|---|---|---|---|
| 2000 | 07-Mar | 3,512 | 15,234 | 6,078 | 7 |
| 2001 | 27-Apr | 7,711 | 16,095 | 7,501 | 8 |
| 2002 | 17-Apr | 5,516 | 13,781 | 9,272 | 8 |
| 2003 | 30-Apr | 11,856 | 14,844 | 11,332 | 11 |
| 2004 | 23-Mar | 11,173 | 12,839 | 11,211 | 11 |
| 2005 | 20-Apr | 9,761 | 11,661 | 9,112 | 10 |
| 2006 | 17-Apr | 2,797 | 15,033 | 8,269 | 12 |
| 2007 | 04-May | 3,223 | 11,013 | 3,741 | 9 |
| 2008 | 24-Apr | 6,011 | 14,729 | 8,449 | 12 |
| 2009 | 23-Mar | 3,967 | 18,443 | 4,159 | 9 |
| Mean | 6,552.7 | 14,367.2 | 7,912.4 |
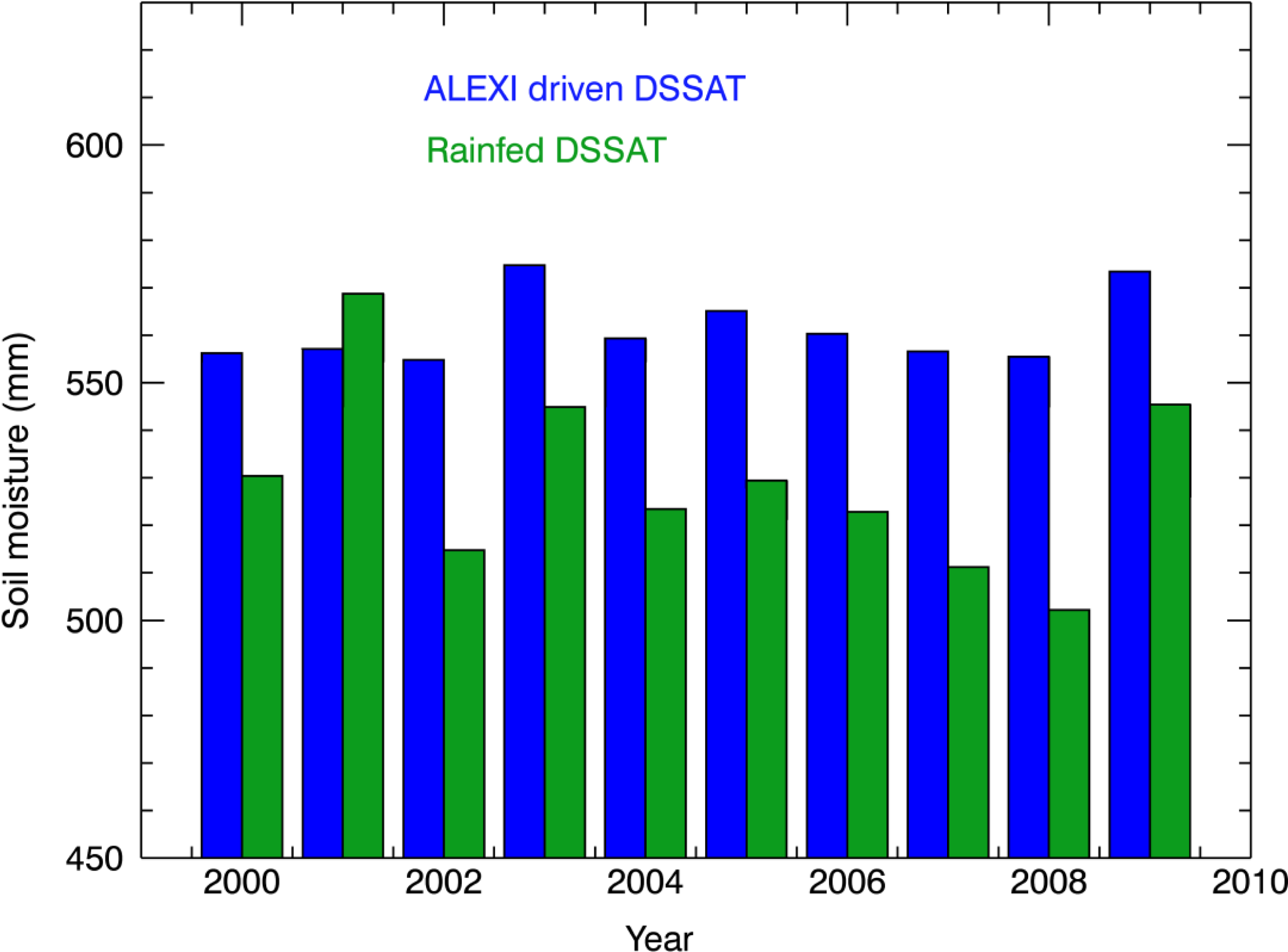
| Year | Rainfed S.M. (mm) | ALEXI S.M. (mm) | % Diff |
|---|---|---|---|
| 2000 | 530.40 | 556.16 | 4.64 |
| 2001 | 568.70 | 557.18 | −2.08 |
| 2002 | 514.81 | 554.82 | 7.21 |
| 2003 | 544.94 | 574.74 | 5.19 |
| 2004 | 523.43 | 559.30 | 6.42 |
| 2005 | 529.51 | 565.12 | 6.32 |
| 2006 | 522.86 | 560.30 | 6.69 |
| 2007 | 511.29 | 556.67 | 8.15 |
| 2008 | 502.21 | 555.55 | 9.95 |
| 2009 | 545.46 | 573.43 | 4.88 |
© 2013 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Mishra, V.; Cruise, J.F.; Mecikalski, J.R.; Hain, C.R.; Anderson, M.C. A Remote-Sensing Driven Tool for Estimating Crop Stress and Yields. Remote Sens. 2013, 5, 3331-3356. https://doi.org/10.3390/rs5073331
Mishra V, Cruise JF, Mecikalski JR, Hain CR, Anderson MC. A Remote-Sensing Driven Tool for Estimating Crop Stress and Yields. Remote Sensing. 2013; 5(7):3331-3356. https://doi.org/10.3390/rs5073331
Chicago/Turabian StyleMishra, Vikalp, James F. Cruise, John R. Mecikalski, Christopher R. Hain, and Martha C. Anderson. 2013. "A Remote-Sensing Driven Tool for Estimating Crop Stress and Yields" Remote Sensing 5, no. 7: 3331-3356. https://doi.org/10.3390/rs5073331