Segmentation for High-Resolution Optical Remote Sensing Imagery Using Improved Quadtree and Region Adjacency Graph Technique
Abstract
:1. Introduction
2. Methodology
2.1. Quadtree Initial Segmentation
2.1.1. Fast Calculation of Standard Deviation Criterion
2.1.2. Quadtree Segmentation and Spatial Indexing Creation
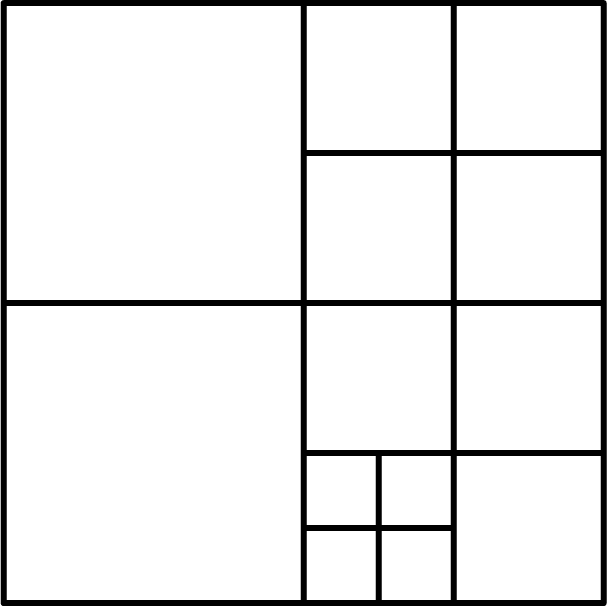
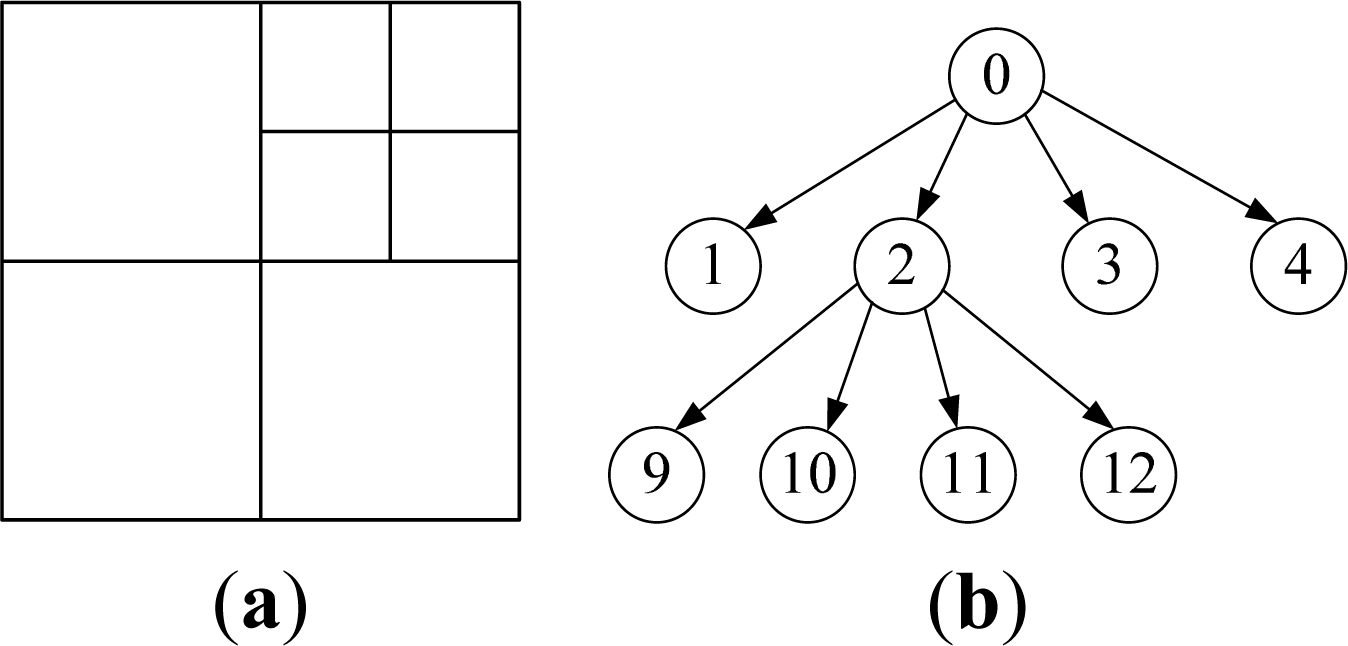
Quadtree Segmentation
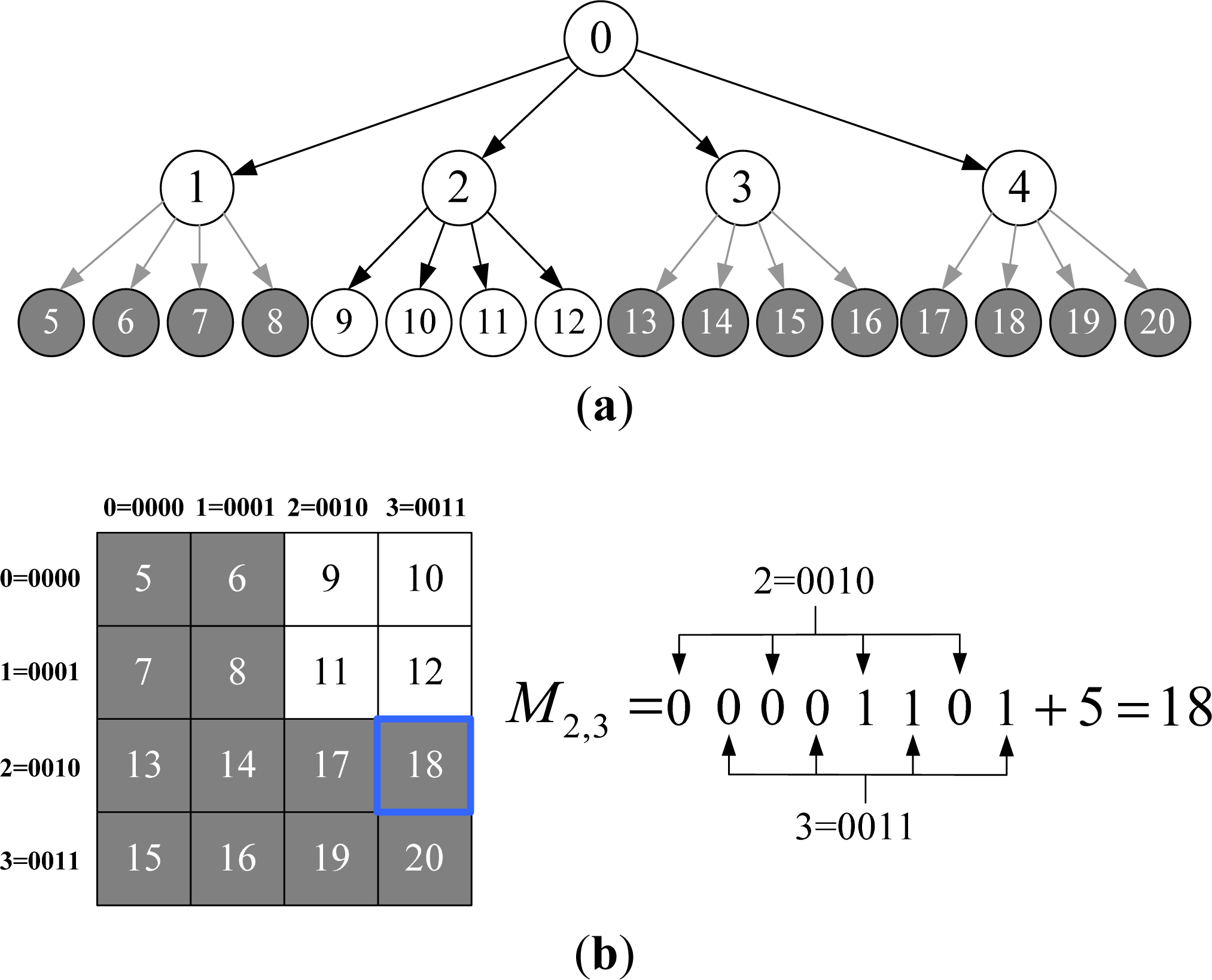
Spatial Indexing Based on Improved Morton Coding
- RI: Real inner nodes in VCQ. Also include the real nodes having virtual offspring.
- RL: Real leaf nodes in VCQ (real nodes at deepest layer).
- VN: Virtual nodes in VCQ. Also include virtual inner nodes.
- Step 1-Uniform grid mapping: If the layer of MD is n, directly map it to a single cell in uniform grid. Otherwise, if the layer is less than n, map it to a rectangular region consisting of multiple cells by down-traversing to all its virtual nodes at layer n. For example, MD = 9 in Figure 4 will be mapped to a single cell with code 9, and MD = 1 will be mapped to a rectangular region containing cells with codes 5, 6, 7 and 8 in the uniform grid, respectively.
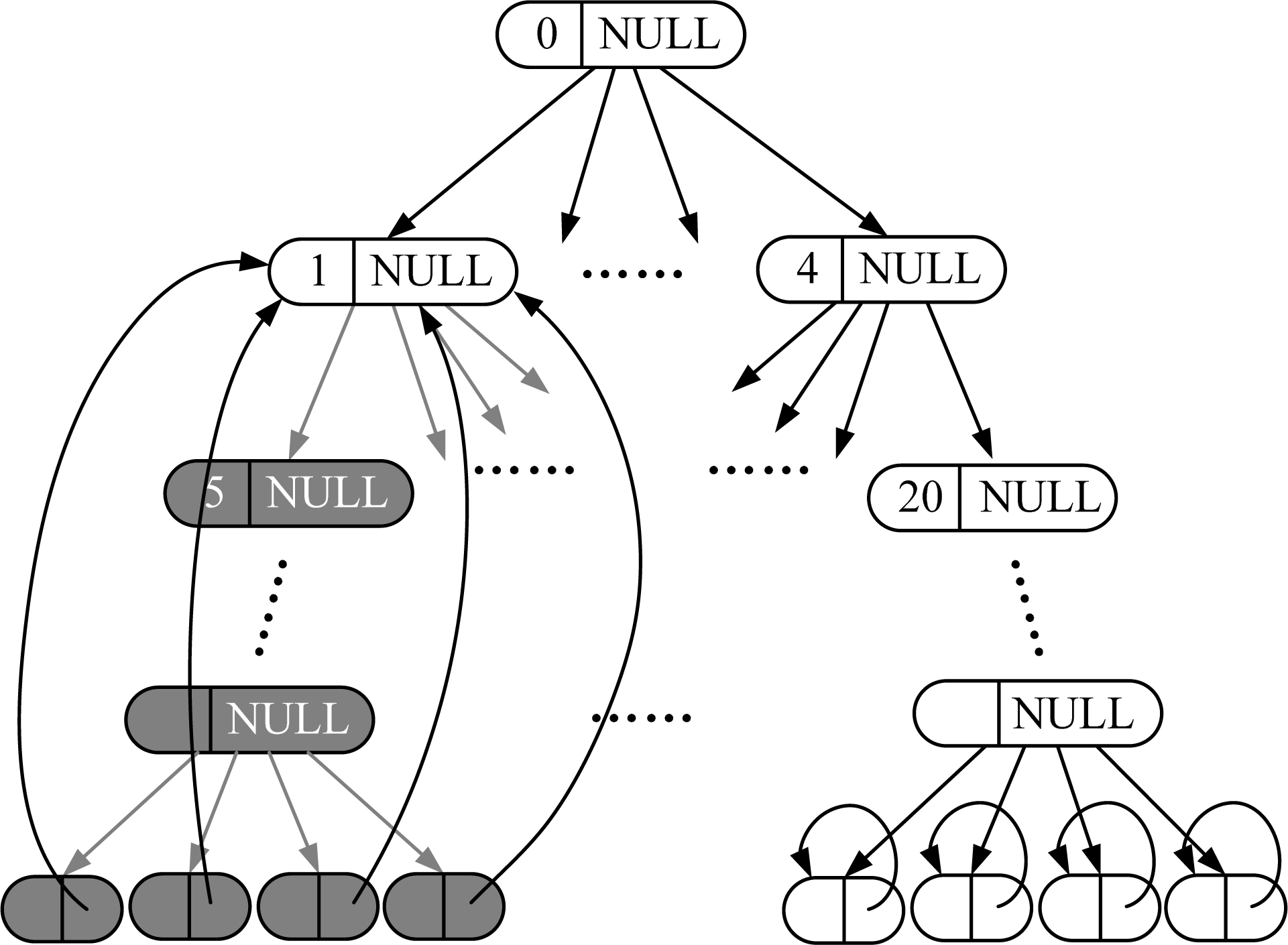
- Step 2-Neighborhood searching: Perform normal neighborhood searching on uniform grid, finding all the cells neighboring to the mapped cell(s). Then judge the states of them one by one via SLT: If the state is RL, then add this node to the neighbor list. If the state of node is VN, then up-traverse to all its ancestor nodes until the ancestor node is found which state is RI. If the ancestor node is not in the neighbor list, then add it to the neighbor list.
- Case 1: If the current node state is RI, then the pointer is set to NULL;
- Case 2: If the current node state is RL, then the pointer points to itself;
- Case 3: If the current node state is VN and at the deepest layer, then the pointer points to its nearest ancestor node with state RI. If the node is not at the deepest layer, then the pointer is set to NULL.
2.1.3. Region Feature Calculation
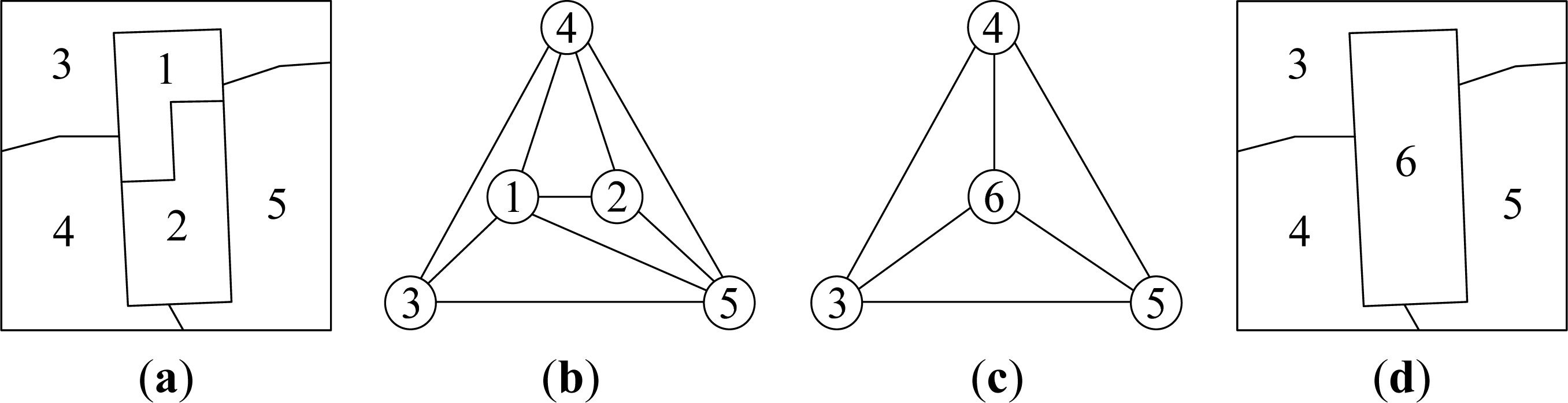
2.2. Region Merging Based on RAG
2.2.1. RAG Criterion
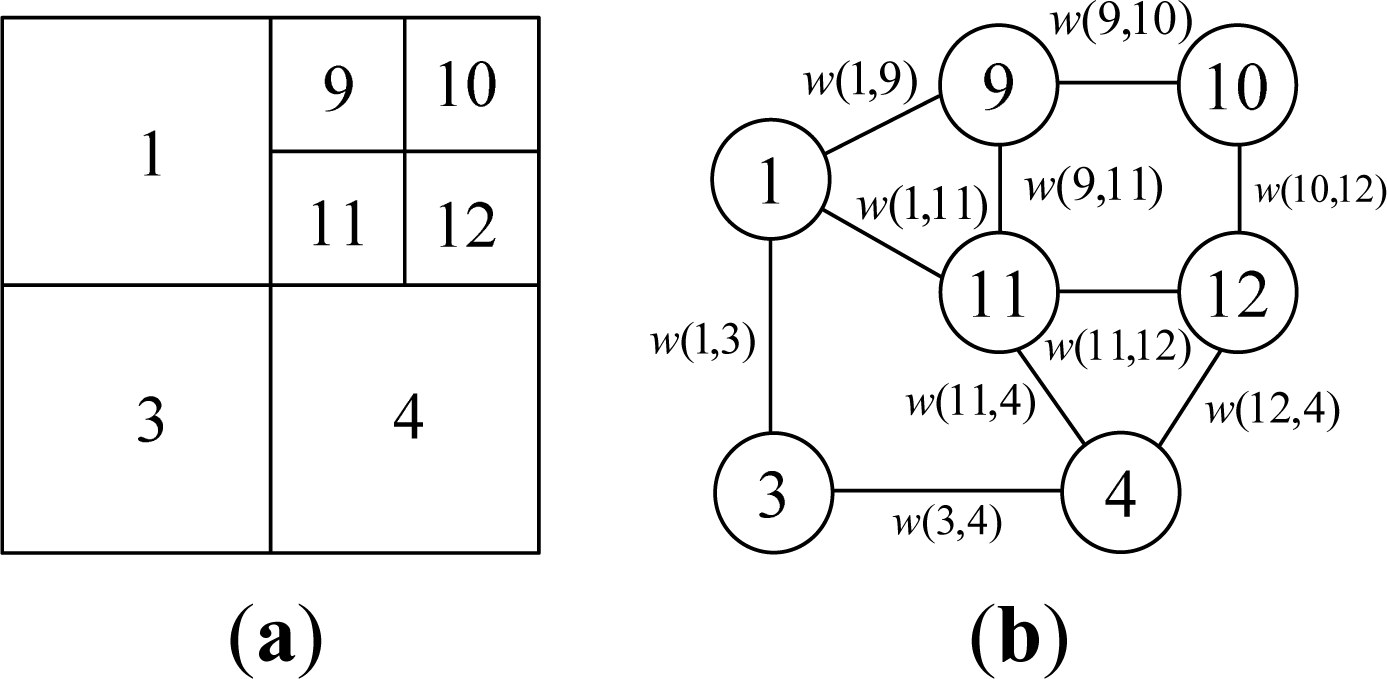
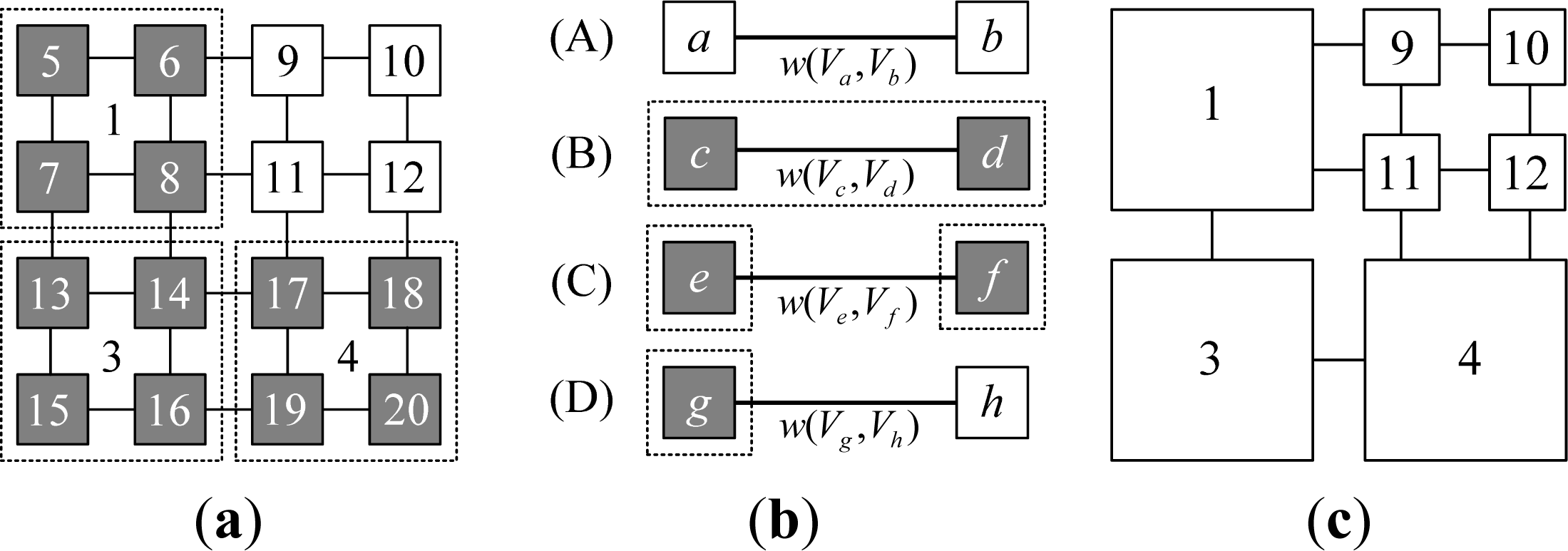
- Step 1. Virtual edge construction: Virtual edges are constructed on the uniform grid mapped from the VCQ in horizontal and vertical directions. For a quadtree with depth n, 22n + 1 − 2n + 1 virtual edges need to be constructed. There are 24 virtual edges in the example depicted in Figure 7a;
- Step 2. Graph reformation: Traverse all virtual edges, and each edge is processed by its case. Suppose the current virtual edge is e, if:
- Case B: The states of two nodes connected by e are all VN, and they are descendants of the same ancestor. See case (B) in Figure 7b. It does not need to be processed. In the example in Figure 7a, the satisfied edges are w(5,6), w(5,7), w(6,8), w(7,8), w(13,14), w(13,15), w(14,16), w(15,16), w(17,18), w(17,19), w(18,20) and w(19,20);
- Case C: The states of two nodes connected by e are VN, but they are descendants of different ancestors. See case (C) in Figure 7b. Reform it to e′ by connecting their respective ancestor nodes. Check the existence of e′. If it does not exist, then add e′ to edge set E, and the two ancestor nodes to vertex set V. In the example in Figure 7a, the edges satisfied include: w(1,3) reformed from w(7,13) and w(8,14) and w(3,4) reformed from w(14,17) and w(16,19).
- Case D: The states of two nodes connected by e are VN and RL. See case (D) in Figure 7b. Reform it to e′, which is a connection between the ancestor of VN node and the original RL node. Then add e′ to edge set E, and the two nodes after reformation to vertex set V. In the example shown in Figure 7a, the satisfied edges include: w(1,9) reformed from w(6,9), w(1,11) reformed from w(8,11), w(11,4) reformed from w(11,17), and w(12,4) reformed from w(12,18).
2.2.2. Region Merging
3. Algorithm Experiment and Analysis
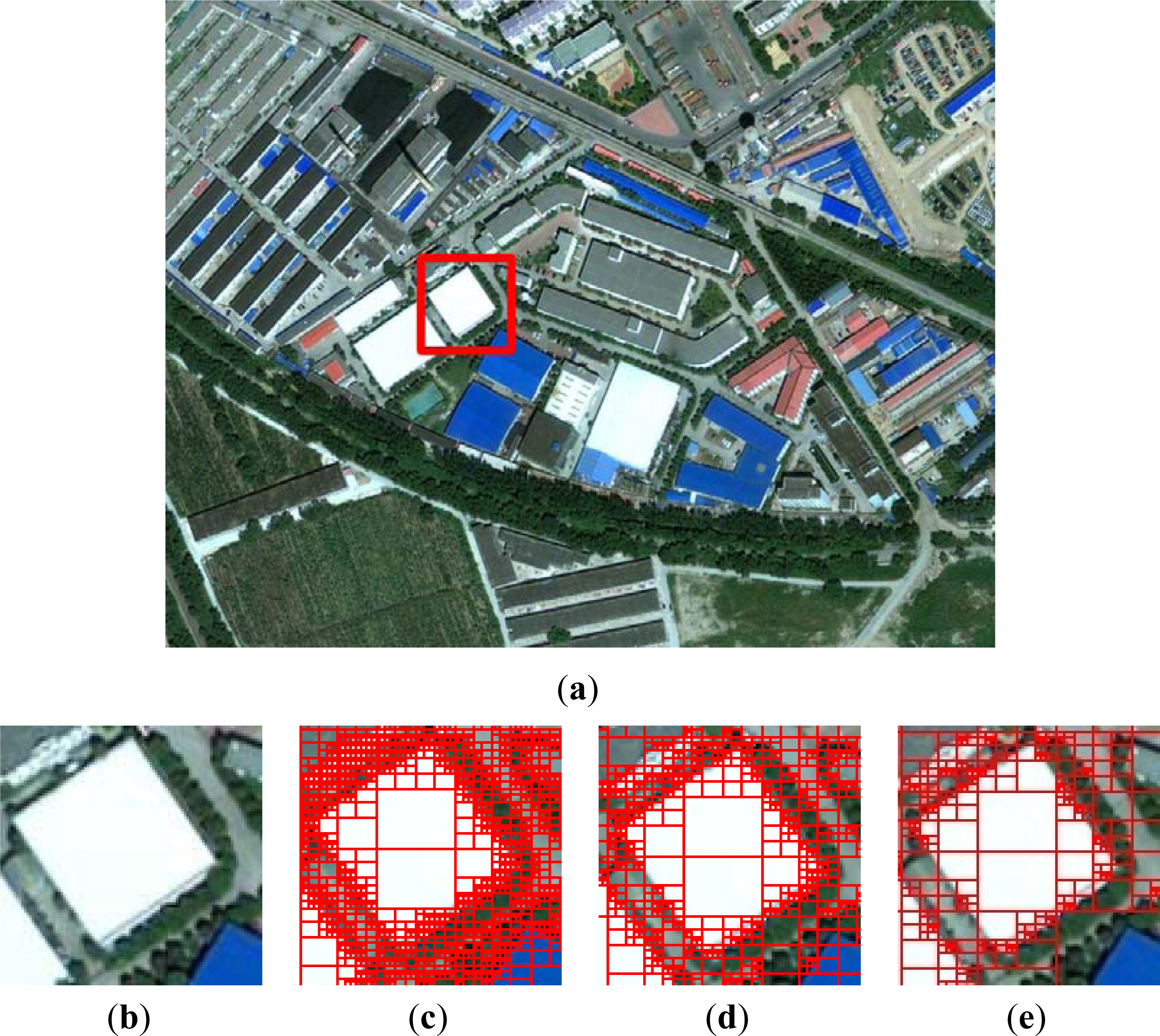
3.1. Step 1: Initial Segmentation Based on Quadtree
| Experiment | Ts | Time of Quadtree Segmentation (s) | Time of Spatial Indexing Creation (s) | Total Time (s) | Quadtree Depth | Segment Count |
|---|---|---|---|---|---|---|
| Exp. A | 3 | 2.3872 | 0.5140 | 2.9012 | 9 | 147586 |
| 10 | 1.2793 | 0.3252 | 1.6045 | 8 | 98185 | |
| 30 | 0.5634 | 0.1173 | 0.6807 | 8 | 18147 | |
| Exp. B | 4 | 2.0366 | 0.6102 | 2.6468 | 9 | 186034 |
| 12 | 1.4622 | 0.5615 | 2.0237 | 9 | 97336 | |
| 25 | 0.4621 | 0.2614 | 0.7235 | 8 | 33859 | |
3.2. Step 2: Region Merging Based on RAG
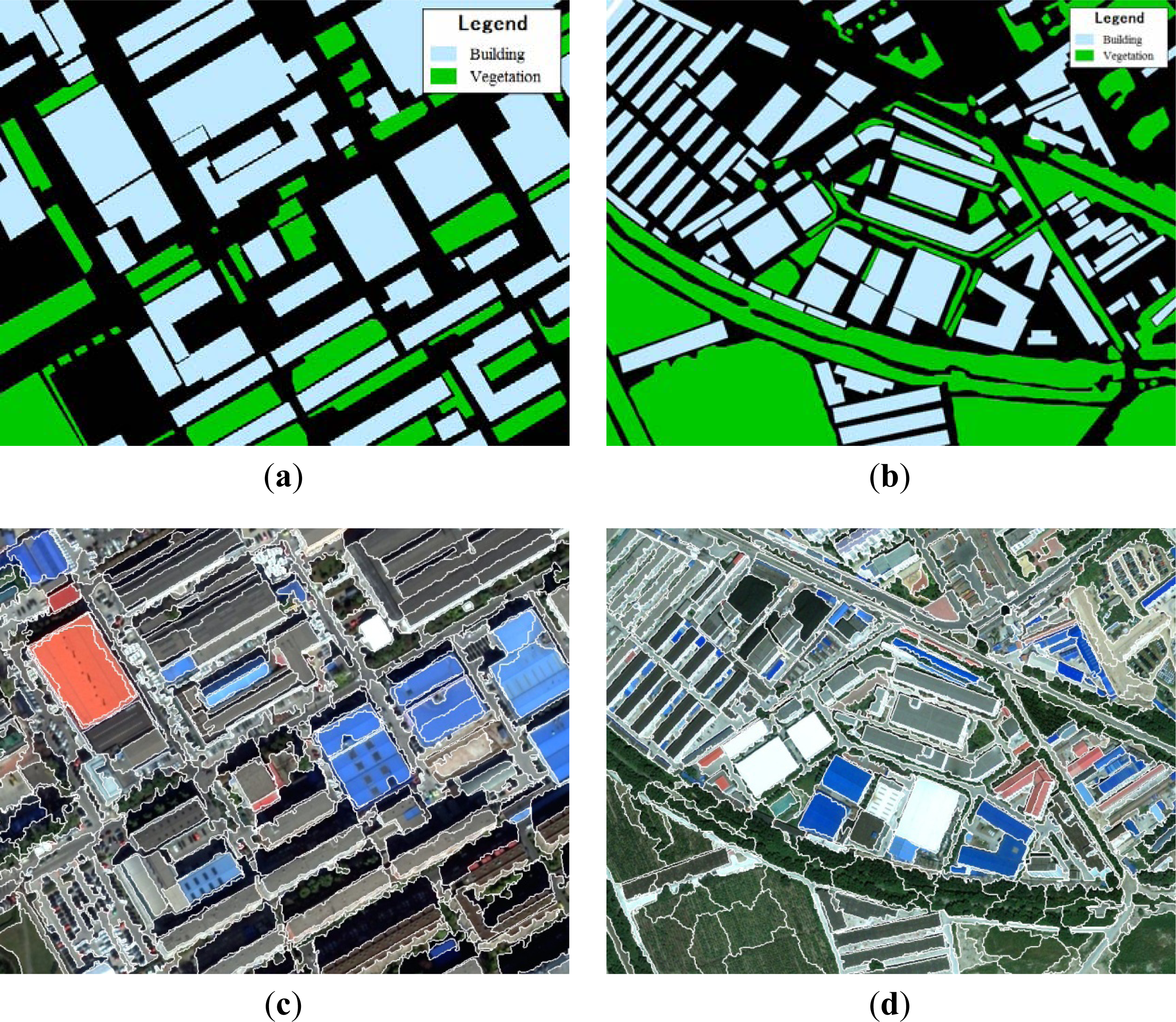
3.3. Method Comparison and Discussion
3.3.1. Method Comparison
| Experiment | Method | Segmentation Accuracy | Object Integrity |
|---|---|---|---|
| Exp. A | MR method | 90.50% | 31.79% |
| MS method | 90.77% | 29.35% | |
| Our method | 92.45% | 51.63% | |
| Exp. B | MR method | 91.36% | 27.92% |
| MS method | 89.32% | 25.11% | |
| Our method | 95.74% | 48.44% | |
3.3.2. Discussion
4. Conclusions
Acknowledgments
Conflict of Interest
References
- Shapiro, L.G.; Stockman, G.C. Computer Vision; Prentice-Hall: Upper Saddle River, NJ, USA, 2011; pp. 279–325. [Google Scholar]
- Willhauck, G.; Schneider, T.; de Kok, R.; Ammer, U. Comparison of Object Oriented Classification Techniques and Standard Image Analysis for the Use of Change Detection between SPOT Multispectral Satellite Images and Aerial Photos. Proceedings of XIXth ISPRS Congress—Technical Commission III: Systems for Data Processing, Analysis and Representation, Amsterdam, The Netherlands, 16–23 July 2000; pp. 35–42.
- Geneletti, D.; Gorte, B. A method for object-oriented land cover classification combining Landsat TM data and aerial photographs. Int. J. Remote Sens 2003, 24, 1273–1286. [Google Scholar]
- Tan, Y.M.; Huai, J.Z.; Tang, Z.S. Edge-guided segmentation method for multiscale and high resolution remote sensing image. J. Infrared Millim. Waves 2010, 29, 312–315. [Google Scholar]
- Cheng, Y. Mean shift, mode seeking, and clustering. IEEE Trans. Pat. Anal. Mach. Intell 1995, 17, 790–799. [Google Scholar]
- Comaniciu, D.; Meer, P. Mean shift: A robust approach toward feature space analysis. IEEE Trans. Pat. Anal. Mach. Intell 2002, 24, 603–619. [Google Scholar]
- Georgescu, B.; Shimshoni, I.; Meer, P. Mean Shift based Clustering in High Dimensions: A Texture Classification Example. Proceedings of the Ninth IEEE International Conference on Computer Vision, Nice, France, 13–16 October 2003; pp. 456–463.
- Xiao, C.; Liu, M. Efficient mean-shift clustering using gaussian KD-tree. Comput. Graph. Forum 2010, 29, 2065–2073. [Google Scholar]
- Wang, L.C.; Zheng, L.; Lin, R.; Chen, T.; Mei, T.C. Fast segmentation algorithm of high resolution remote sensing image based on multiscale mean shift. Spectrosc. Spectr. Anal 2011, 31, 177. [Google Scholar]
- Roerdink, J.B.; Meijster, A. The watershed transform: Definitions, algorithms and parallelization strategies. Fundam. Informa 2000, 41, 187–228. [Google Scholar]
- Bleau, A.; Leon, L.J. Watershed-based segmentation and region merging. Comput. Vis. Image Underst 2000, 77, 317–370. [Google Scholar]
- Pun, C.M.; An, N.Y.; Chen, C.L.P. Region-based image segmentation by watershed partition and DCT energy compaction. Int. J. Comput. Intell. Syst 2012, 5, 53–64. [Google Scholar]
- Baatz, M.; Schäpe, A. Multiresolution Segmentation: An Optimization Approach for High Quality Multi-scale Image Segmentation. Proceedings of the Angewandte Geographische Information Sverarbeitung XII, Heidelberg, Germany, 5–7 July 2000; pp. 12–23.
- Definients Image. eCognition User’s Guide 4; Definients Image: Bernhard, Germany, 2004. [Google Scholar]
- Shi, J.; Malik, J. Normalized cuts and image segmentation. IEEE Trans. Pat. Anal. Mach. Intell 2000, 22, 888–905. [Google Scholar]
- Feature Extraction Module Version 4.6. In ENVI Feature Extraction Module User’s GuideDecember, 2008th ed.; ITT Corporation: Boulder, Colorado, USA, 2008.
- Robinson, D.J.; Redding, N.J.; Crisp, D.J. Implementation of a Fast Algorithm for Segmenting SAR Imagery; DSTO Electronics and Surveillance Research Laboratory: Edinburgh, SA, Australia, 2002. [Google Scholar]
- Finkel, R.; Bentley, J.L. Quad trees: A data structure for retrieval on composite keys. Acta Inform 1974, 4, 1–9. [Google Scholar]
- Choi, H.; Baraniuk, R.G. Multiscale image segmentation using wavelet-domain hidden Markov models. IEEE Trans. Image Process 2001, 10, 1309–1321. [Google Scholar]
- Pavlidis, T.; Liowm, Y.T. Integrating region growing and edge detection. IEEE Trans. Pat. Anal. Mach. Intell 1990, 12, 225–233. [Google Scholar]
- Kelkar, D.; Gupta, S. Improved Quadtree Method for Split Merge Image Segmentation. Proceedings of the 1st International Conference on Emerging Trends in Engineering and Technology, (ICETET’08), Nagpur, India, 16–18 July 2008; pp. 44–47.
- Viola, P.; Jones, M.J. Robust real-time face detection. Int. J. Comput. Vis 2004, 57, 137–154. [Google Scholar]
- Abel, D.J.; Smith, J. A data structure and algorithm based on a linear key for a rectangle retrieval problem. Comput. Vis. Graph. Image Process 1983, 24, 1–13. [Google Scholar]
- Tamura, H.; Mori, S.; Yamawaki, T. Texture features corresponding to visual perception. IEEE Trans. Syst. Man Cybern 1978, 8, 202–215. [Google Scholar]






| Method | Addition and Subtraction | Multiplication and Division | Pixel Accesses |
|---|---|---|---|
| Traditional method | 2015198 | 671778 | 1572864 |
| Our method | 524422 | 102 | 524228 |
| Node code | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| State | RI | RI | RI | RI | RI | VN | VN | VN | VN | RL | RL |
| Node code | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
| State | RL | RL | VN | VN | VN | VN | VN | VN | VN | VN | |
| Experiment | Method | Region Count | Time (s) |
|---|---|---|---|
| Exp. A | MR method | 1487 | about 8 |
| MS method | 1853 | 29.77 | |
| Our method | 657 | 3.7530 | |
| Exp. B | MR method | 1659 | about 10 |
| MS method | 1968 | 22.13 | |
| Our method | 711 | 4.57 | |
© 2013 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Fu, G.; Zhao, H.; Li, C.; Shi, L. Segmentation for High-Resolution Optical Remote Sensing Imagery Using Improved Quadtree and Region Adjacency Graph Technique. Remote Sens. 2013, 5, 3259-3279. https://doi.org/10.3390/rs5073259
Fu G, Zhao H, Li C, Shi L. Segmentation for High-Resolution Optical Remote Sensing Imagery Using Improved Quadtree and Region Adjacency Graph Technique. Remote Sensing. 2013; 5(7):3259-3279. https://doi.org/10.3390/rs5073259
Chicago/Turabian StyleFu, Gang, Hongrui Zhao, Cong Li, and Limei Shi. 2013. "Segmentation for High-Resolution Optical Remote Sensing Imagery Using Improved Quadtree and Region Adjacency Graph Technique" Remote Sensing 5, no. 7: 3259-3279. https://doi.org/10.3390/rs5073259





