Data Assimilation of the High-Resolution Sea Surface Temperature Obtained from the Aqua-Terra Satellites (MODIS-SST) Using an Ensemble Kalman Filter
Abstract
:1. Introduction
2. Data Assimilation of Satellite Sea Surface Temperature
2.1. Ensemble Kalman Filter (EnKF) for the Kuroshio Variation South of Japan
2.2. Moderate Resolution Imaging Spectroradiometer (MODIS) Sensors—SST
2.3. Data Assimilation Experiments
3. Results and Discussions
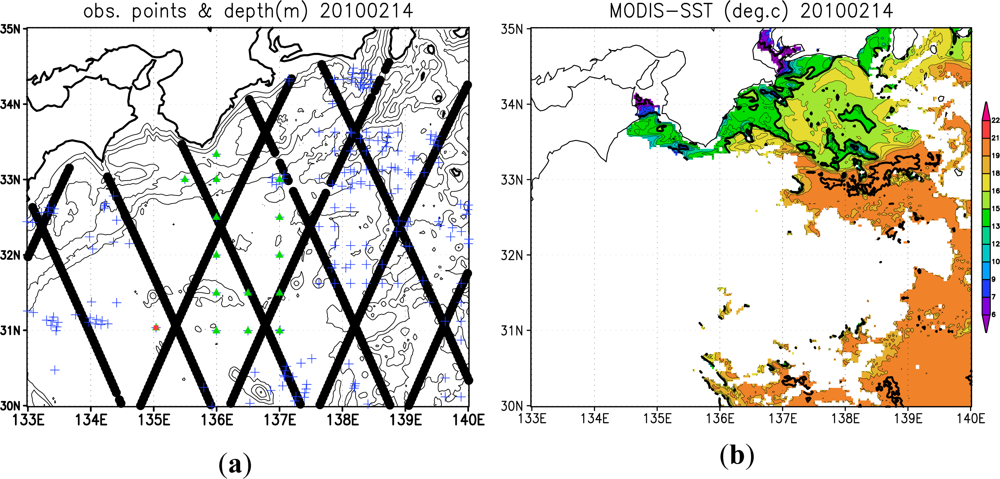
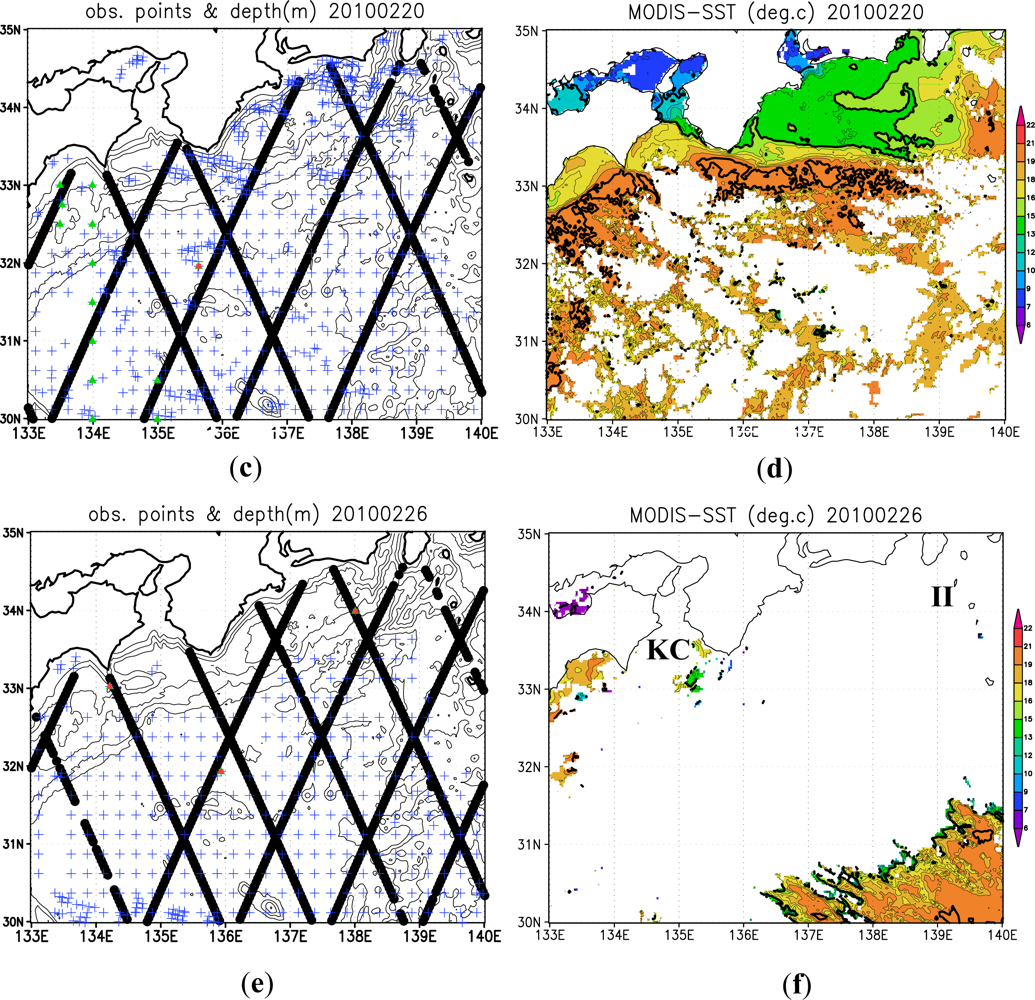
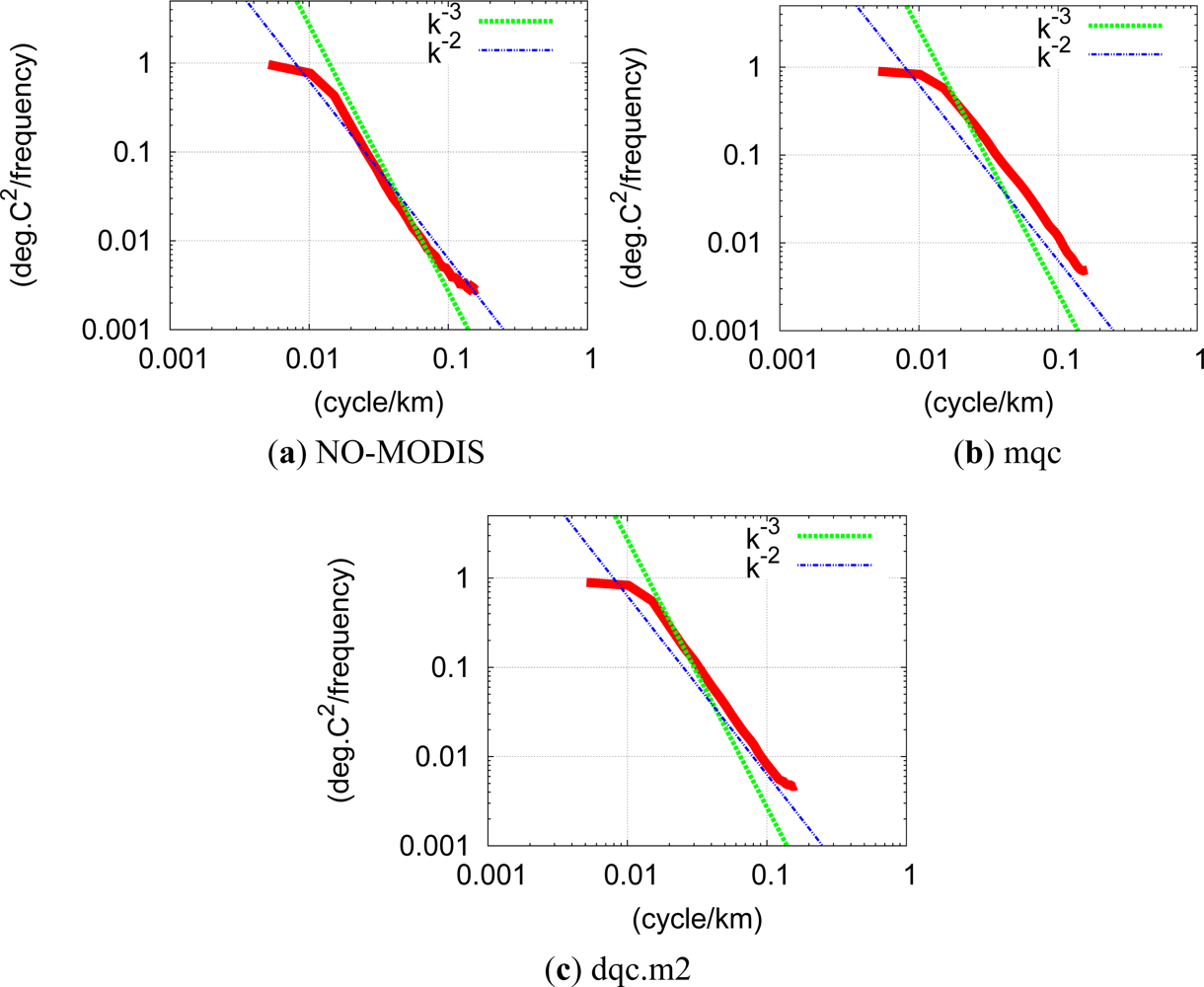
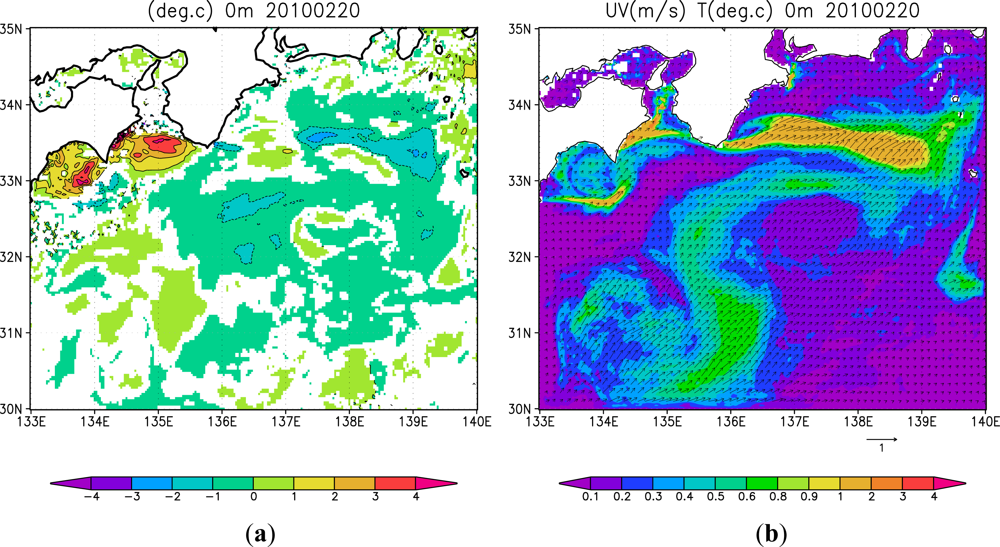
3.1. Quality Control of MODIS-SST
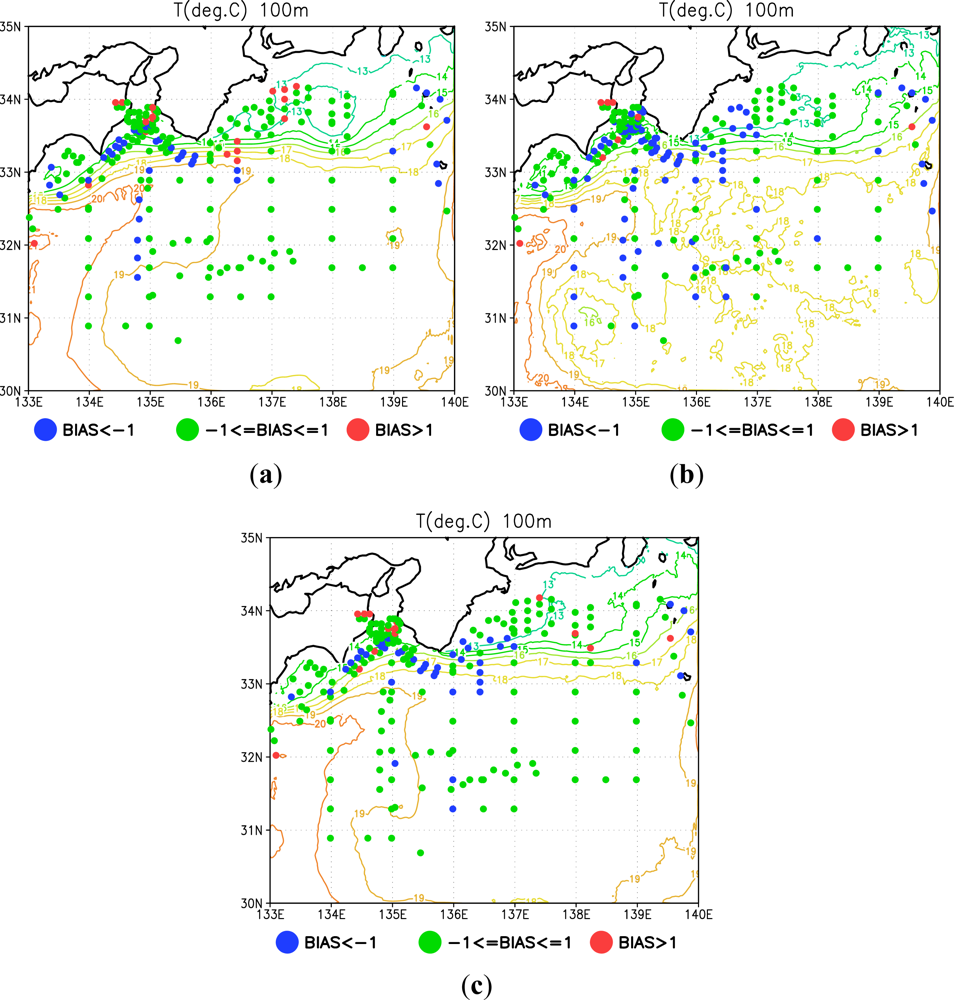
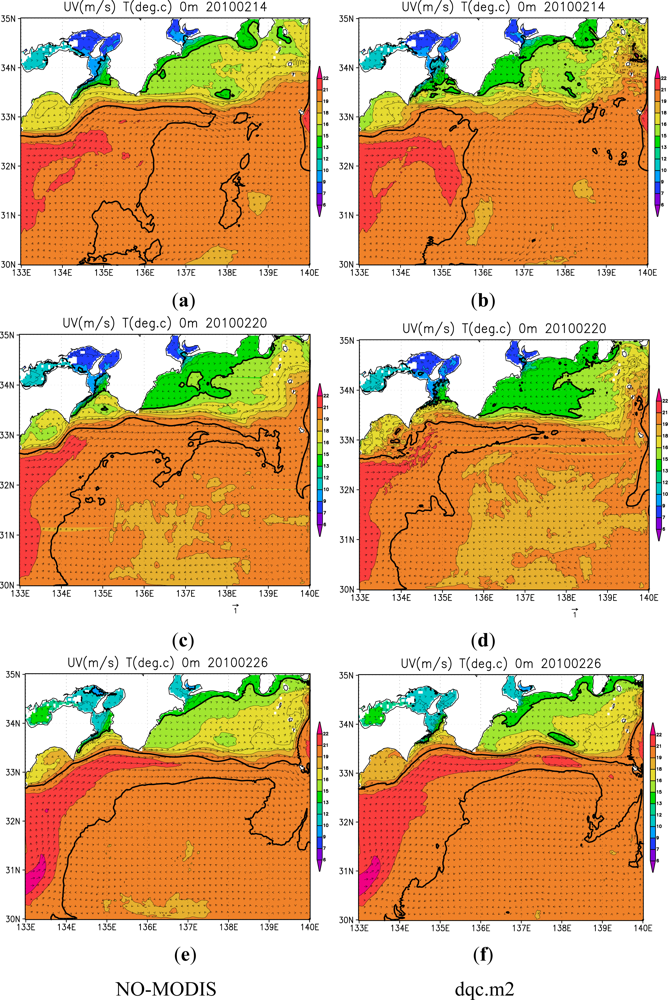
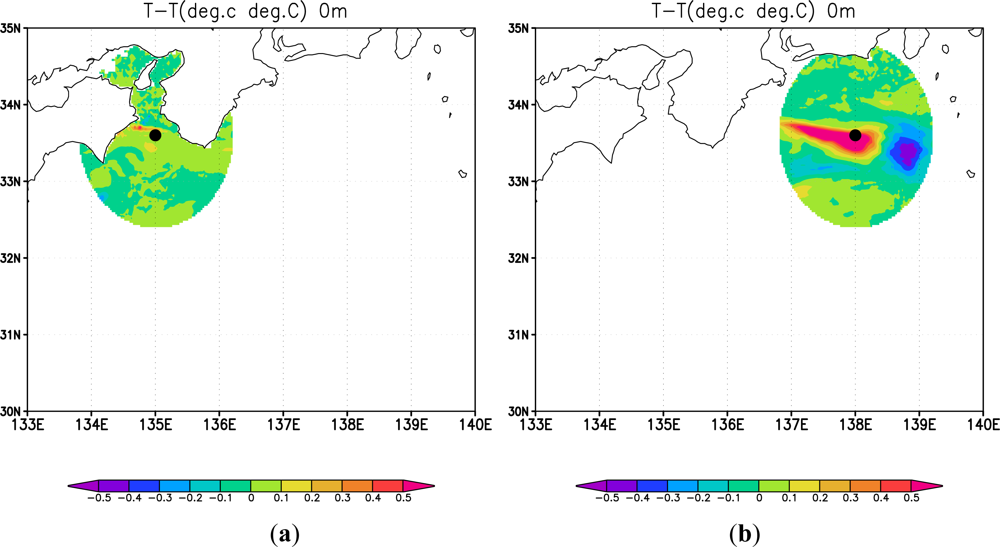
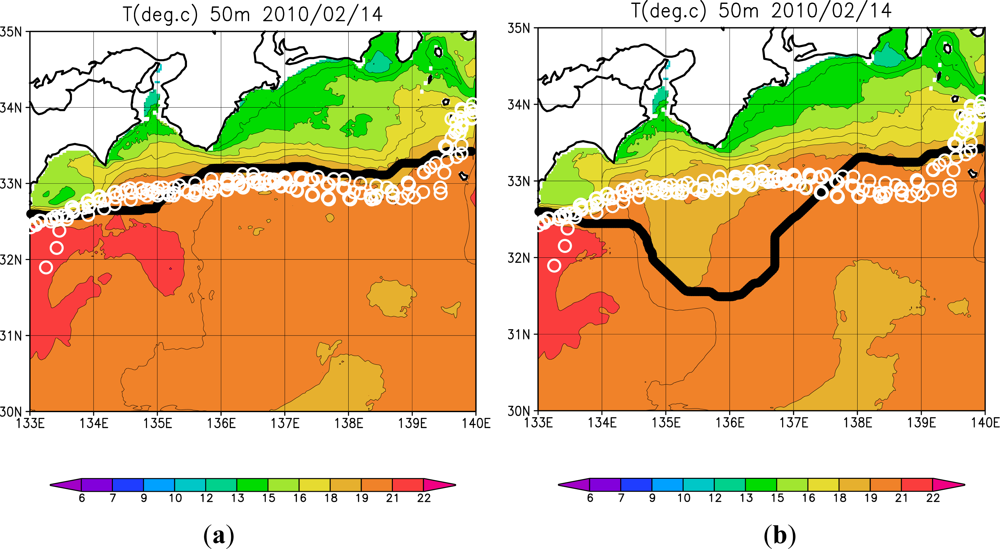
3.2. Effects of High-Resolution SST
3.3. Roles of High-Resolution SST and Sea Surface Height Anomaly (SSHA) Data
3.4. Discussion
4. Conclusions
Acknowledgments
- Conflict of InterestThe authors declare no conflict of interest.
References
- Miyama, T.; Nonaka, M.; Nakamura, H.; Kuwano-Yoshida, A. A striking early-summer event of convective rainband persistent along the warm Kuroshio in the East China Sea. Tellus A 2012. [Google Scholar] [CrossRef]
- Hosoda, K.; Murakami, H.; Sakaida, F.; Kawamura, H. Algorithm and validation of sea surface temperature observation using MODIS sensors aboard Terra and Aqua in the Western North Pacific. J. Oceanogr 2007, 63, 267–280. [Google Scholar]
- Hosoda, K. Algorithm for estimating sea surface temperature based on Aqua/MODOS global ocean data. 2. Automated quality check process for eliminating cloud contamination. J. Oceanogr 2010, 67, 791–805. [Google Scholar]
- Haines, S.L.; Jedlovec, G.J.; Lazarus, S.M. A MODIS sea surface temperature composite for regional applications. IEEE Trans. Geosci. Remot. Sens 2007, 45, 2919–2927. [Google Scholar]
- Everson, R.; Cornillon, P.; Sirovich, L.; Webber, A. An empirical eigenfunction analysis of sea surface temperatures in the western North Atlantic. J. Phys. Oceanogr 1997, 27, 468–479. [Google Scholar]
- Chu, P.C.; Tseng, H.-C.; Chang, C.P.; Chen, J.M. South China Sea warm pool detected in spring from the Navy's Master Oceanographic Observational Data Set (MOODS). J. Geophys. Res 1997, 102, 15761–15771. [Google Scholar]
- Alvera-Azcarate, A.; Barth, A.; Rixen, M.; Beckers, J.M. Reconstruction of incomplete oceanographic data sets using empirical orthogonal functions: Application to the Adriatic Sea surface temperature. Ocean Model 2005, 9, 325–346. [Google Scholar]
- Guan, L.; Kawamura, H. Merging satellite infrared and microwave SSTs: Methodology and evaluation of the new SST. J. Oceanogr 2004, 60, 905–912. [Google Scholar]
- Sakaida, F.; Kawamura, H.; Takahashi, S.; Shimada, T.; Kawai, Y.; Hosoda, K.; Guan, L. Research and development of the New Generation Sea Surface Temperature for Open Ocean (NGSST-O) product and its demonstration operation. J. Oceanogr 2009, 65, 859–870. [Google Scholar]
- Miyazawa, Y.; Miyama, T.; Varlamov, S.M.; Guo, X.; Waseda, T. Open and coastal seas interactions represented by an Ensemble Kalman Filter. Ocean Dyn 2012, 62, 645–659. [Google Scholar]
- Ezer, T.; Mellor, G.L. Data assimilation experiments in the Gulf Stream region: How useful are satellite-derived surface data for nowcasting the subsurface Fields? J. Atmos. Ocean Tech. 1997, 1379–1391. [Google Scholar]
- Takahashi, W.; Kawamura, H. Detection method of the Kuroshio front using the satellite-derived chlorophyll-a images. Remote Sens. Environ 2005, 97, 83–91. [Google Scholar]
- Evensen, G. Sequential data assimilation with a nonlinear quasigeostrophic model using Monte-Carlo methods to forecast error statistics. J. Geophys. Res 1994, 99, 10143–10162. [Google Scholar]
- Hunt, B.R.; Kostelich, E.J.; Szunyogh, I. Efficient data assimilation for spatiotemporal chaos: A local ensemble transform Kalman filter. Physica D 2007, 230, 112–126. [Google Scholar]
- Jordi, A.; Wang, D.-P. sbPOM: A parallel implementation of Princenton Ocean Model. Environ. Modell. Softw 2012, 38, 59–61. [Google Scholar]
- Berntsen, J.; Oey, L.-Y. Estimation of the internal pressure gradient in σ-coordinate ocean models: comparison of second-, fourth-, and sixth-order schemes. Ocean Dyn 2010, 60, 317–330. [Google Scholar]
- Miyoshi, T.; Sato, Y.; Kadowaki, T. Ensemble Kalman Filter and 4D-Var intercomparison with the Japanese operational global analysis and prediction system. Mon. Wea. Rev 2010, 138, 2846–2866. [Google Scholar]
- McClain, E.P.; Pichel, W.P.; Walton, C.C. Comparative performance of AVHRR-based multichannel sea surface temperatures. J. Geophys. Res 1985, 90, 11587–11601. [Google Scholar]
- May, D.A.; Parmeter, M.M.; Olszewski, D.S.; McKenzie, B.D. Operational processing of satellite sea surface temperature retrievals at the Naval Oceanographic Office. Bull. Amer. Meteor. Soc 1998, 79, 397–407. [Google Scholar]
- Capet, X.; McWilliams, J.C.; Molemaker, M.J.; Shchepetkin, A.F. Mesoscale to submesoscale transition in the California Current System: Flow structure, eddy flux, and observational tests. J. Phys. Oceanogr 2008, 38, 29–43. [Google Scholar]
- Wang, D.-P.; Jordi, A. Surface frontogenesis and thermohaline intrusion in a shelfbreak front. Ocean Model 2011, 38, 161–170. [Google Scholar]
- Moteki, Q.; Yoneyama, K.; Shirooka, R.; Kubota, H.; Yasunaga, K.; Suzuki, J.; Seiki, A.; Sato, N.; Enomoto, T.; Miyoshi, T; Yamane, S. The influence of observations propagated by convectively coupled equatorial waves. Quart. J. Royal Meteoro. Soc 2011, 137, 641–655. [Google Scholar]
- Harlim, J.; Hunt, B.R. A non-Gaussian ensemble filter for assimilating infrequent noisy observations. Tellus A 2007, 59, 225–237. [Google Scholar]
- Miyazawa, Y.; Zhang, R.; Guo, X.; Tamura, H.; Ambe, D.; Lee, J.-S.; Okuno, A.; Yoshinari, H.; Setou, T.; Komatsu, K. Water mass variability in the western North Pacific detected in a 15-year eddy resolving ocean reanalysis. J. Oceanogr 2009, 65, 737–756. [Google Scholar]


| Parameters | Values |
|---|---|
| Horizontal localization scale (σobs; number of grids) | 12 (1/3°) |
| Vertical localization scale (σobsv; m) | 2000 |
| Covariance inflation parameter (%) | 21 |
| Observation error of sea surface height anomaly (m) | 0.2 |
| Observation error of sea surface temperature (°C) | 1.0 |
| Time window of sea surface height anomaly (day) | ± 4 |
| Time window of sea surface temperature (day) | ± 1 |
| Time interval of LETKF (day) | 2 |
| Case | Quality Control (Equation (2)) | Assimilated data |
|---|---|---|
| NO-ASSIM | - | - |
| NO-MODIS | m = 10, p = 10 | RMCSST,AMSR-E,SSHA |
| mqc | m = 10, p = 10 | RMCSST,AMSR-E,MODIS,SSHA |
| 5degerr | m = 10, p = 10 (observation error = 5 °C) | RMCSST,AMSR-E,MODIS,SSHA |
| m3p4 | m = 3, p = 4 | RMCSST,AMSR-E,MODIS,SSHA |
| m2p2 | m = 2, p = 2 | RMCSST,AMSR-E,MODIS,SSHA |
| m1p2 | m = 1, p = 2 | RMCSST,AMSR-E,MODIS,SSHA |
| m2 | m = 2, p=10 | RMCSST,AMSR-E,MODIS,SSHA |
| m1 | m = 1, p = 10 | RMCSST,AMSR-E,MODIS,SSHA |
| dqc.m2p2 | m = 2sprd, p = 2sprd | RMCSST,AMSR-E,MODIS,SSHA |
| dqc.m1p2 | m = sprd, p = 2sprd | RMCSST,AMSR-E,MODIS,SSHA |
| dqc.m2 | m = 2sprd, p = 10 | RMCSST,AMSR-E,MODIS,SSHA |
| dqc.m1 | m = sprd, p = 10 | RMCSST,AMSR-E,MODIS,SSHA |
| NO-SSHA | m = sprd, p = 2sprd | RMCSST,AMSR-E,MODIS |
| Case | T-BIAS (°C), S-BIAS(psu) | T-RMSE (°C), S-RMSE(psu) | Correlation with Assimilated MODIS-SST |
|---|---|---|---|
| NO-ASSIM | −0.81, −0.039 | 1.83, 0.20 | 0.76* |
| NO-MODIS | −0.24, +0.012 | 1.20, 0.16 | 0.84* |
| mqc | −1.00, −0.068 | 1.63, 0.19 | 0.86 |
| 5degerr | −0.75, −0.041 | 1.40, 0.17 | 0.85 |
| m3p4 | −0.56, −0.022 | 1.34, 0.19 | 0.85 |
| m2p2 | −0.46, −0.015 | 1.30, 0.18 | 0.86 |
| m1p2 | −0.12, +0.024 | 1.25, 0.19 | 0.85 |
| m2 | −0.29, +0.013 | 1.23, 0.18 | 0.86 |
| m1 | +0.03, +0.053 | 1.24, 0.20 | 0.84 |
| dqc.m2p2 | −0.49, −0.002 | 1.25, 0.17 | 0.86 |
| dqc.m1p2 | −0.19, +0.030 | 1.23, 0.18 | 0.84 |
| dqc.m2 | −0.35, +0.006 | 1.17, 0.17 | 0.83 |
| dqc.m1 | −0.05, +0.037 | 1.16, 0.17 | 0.80 |
| NO-SSHA | −0.27, +0.030 | 1.28, 0.18 | 0.84 |
© 2013 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Miyazawa, Y.; Murakami, H.; Miyama, T.; Varlamov, S.M.; Guo, X.; Waseda, T.; Sil, S. Data Assimilation of the High-Resolution Sea Surface Temperature Obtained from the Aqua-Terra Satellites (MODIS-SST) Using an Ensemble Kalman Filter. Remote Sens. 2013, 5, 3123-3139. https://doi.org/10.3390/rs5063123
Miyazawa Y, Murakami H, Miyama T, Varlamov SM, Guo X, Waseda T, Sil S. Data Assimilation of the High-Resolution Sea Surface Temperature Obtained from the Aqua-Terra Satellites (MODIS-SST) Using an Ensemble Kalman Filter. Remote Sensing. 2013; 5(6):3123-3139. https://doi.org/10.3390/rs5063123
Chicago/Turabian StyleMiyazawa, Yasumasa, Hiroshi Murakami, Toru Miyama, Sergey M. Varlamov, Xinyu Guo, Takuji Waseda, and Sourav Sil. 2013. "Data Assimilation of the High-Resolution Sea Surface Temperature Obtained from the Aqua-Terra Satellites (MODIS-SST) Using an Ensemble Kalman Filter" Remote Sensing 5, no. 6: 3123-3139. https://doi.org/10.3390/rs5063123






