Using Low Resolution Satellite Imagery for Yield Prediction and Yield Anomaly Detection
Abstract
:1. Introduction and Short History
1.1. Structure of the Review
- qualitative crop monitoring
- quantitative crop yield predictions by regression modeling
- quantitative yield forecasts using (mechanistic and dynamic) crop growth models
1.2. Definition of “Low Resolution Images”
1.3. Data Quality Issues
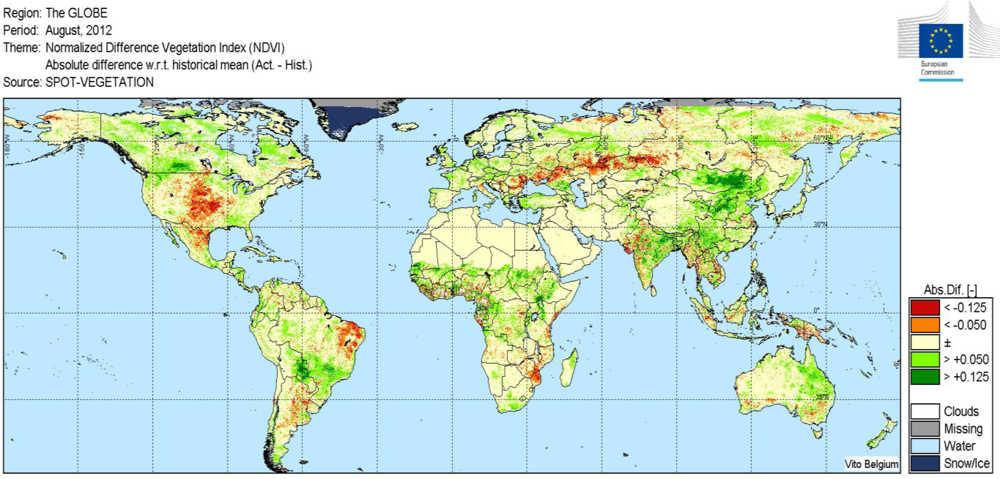
2. Qualitative Crop Monitoring
3. Quantitative Crop Yield Predictions by Regression Modeling
3.1. Use of Remotely Sensed Indicators for Crop Yield Prediction
3.2. Concomitant Use of Remotely Sensed Indicators Together with Bio-Climatic Indicators
4. Quantitative Yield Forecasts Using Crop Growth Models
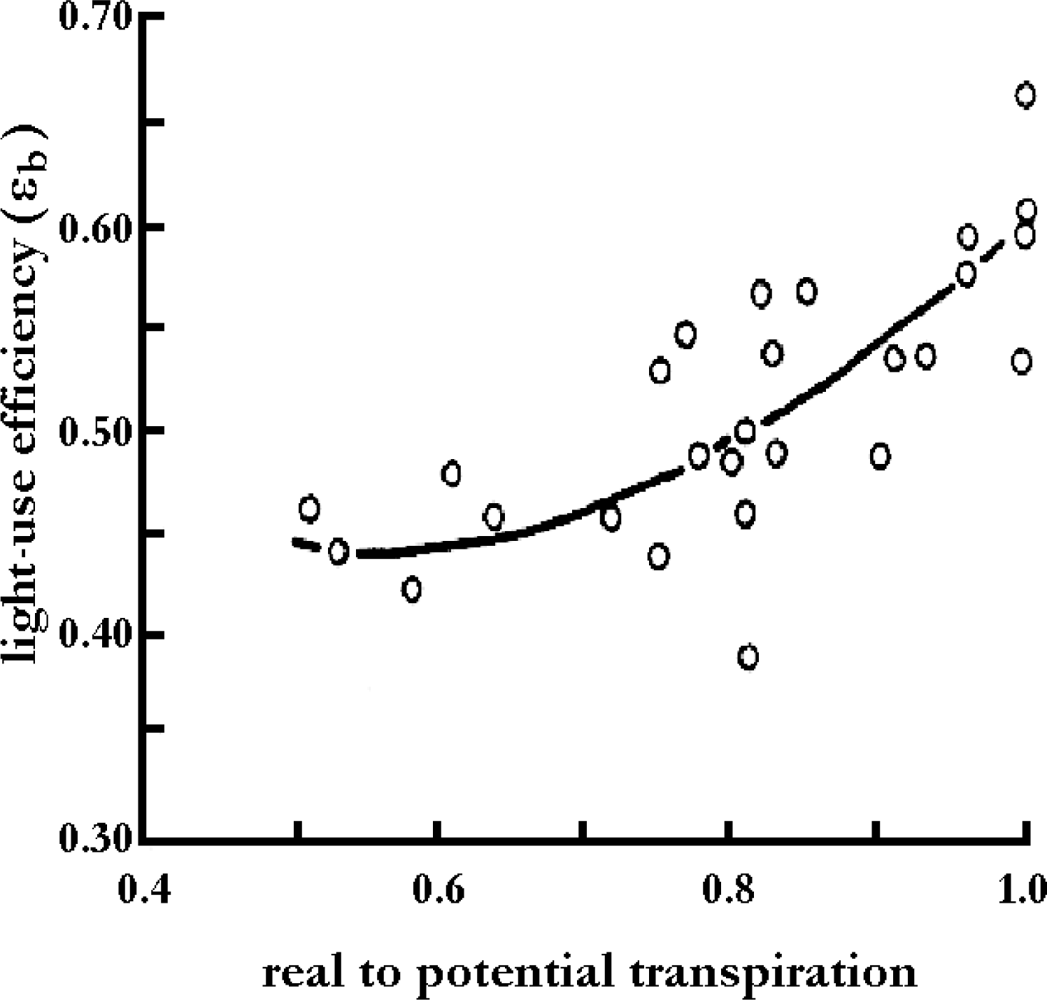
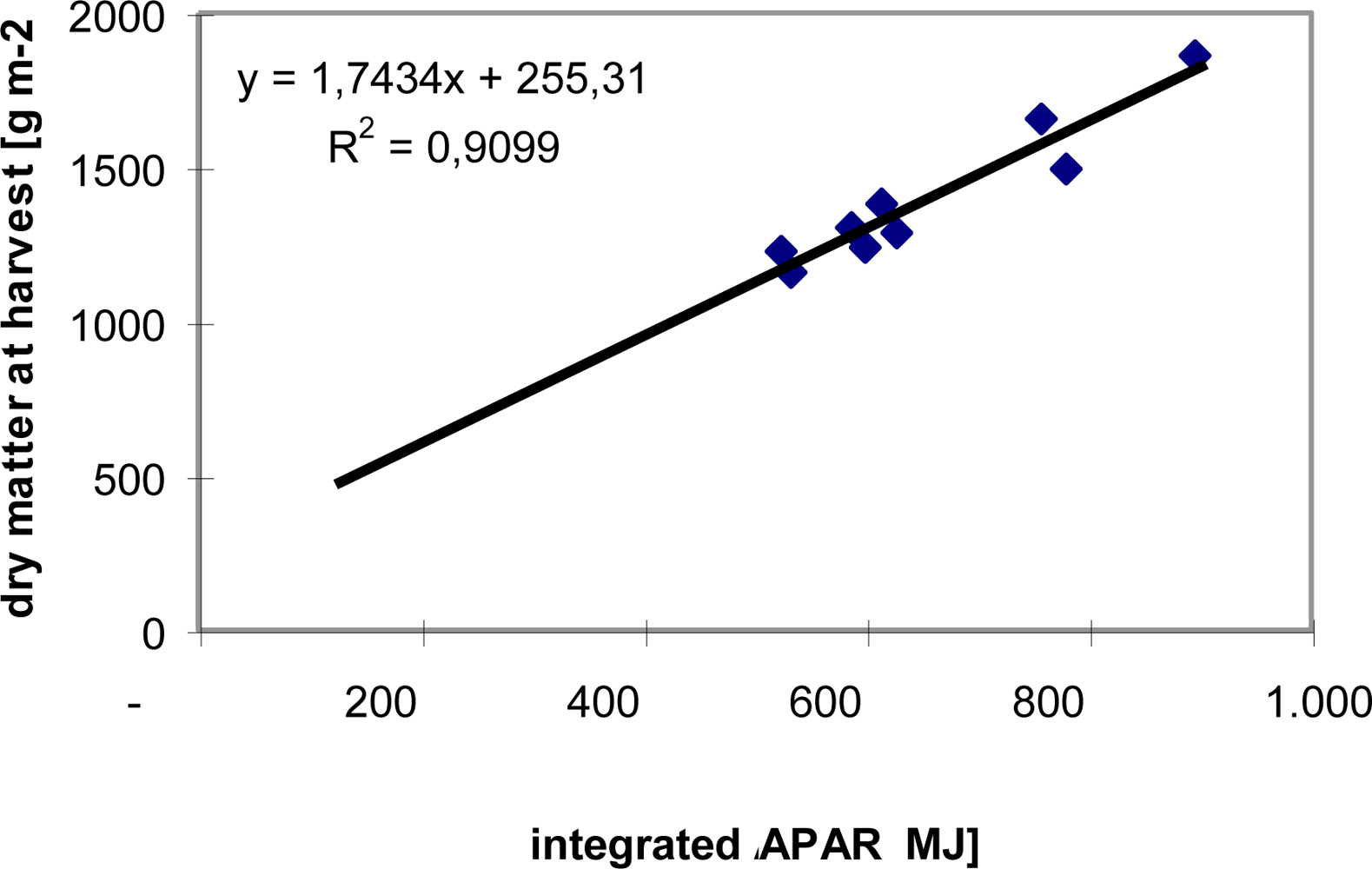
4.1. Estimation and Mapping of Absorbed Photosynthetically Active Radiation for Use in Monteith’s Efficiency Equation
- where: ΔDM: increase in dry matter (DM) or net primary production (NPP) (g·m−2·d−1)
- PAR: incident photosynthetically active solar radiation (MJ·m−2·d−1)
- fAPAR: Fraction of intercepted and absorbed PAR; fAPAR is estimated from the remotely sensed NDVI by means of a linear equation, suggested by Myneni and Williams [81] (dimensionless)
- εb: Photosynthetic efficiency, [82] (g·MJ−1)
- CO2fert: Normalized CO2 fertilization factor, [85] (dimensionless)
- r(T): fraction of assimilated photosynthesis consumed by autotrophic respiration; r is modeled as a simple linear function of daily mean air temperature, [60].
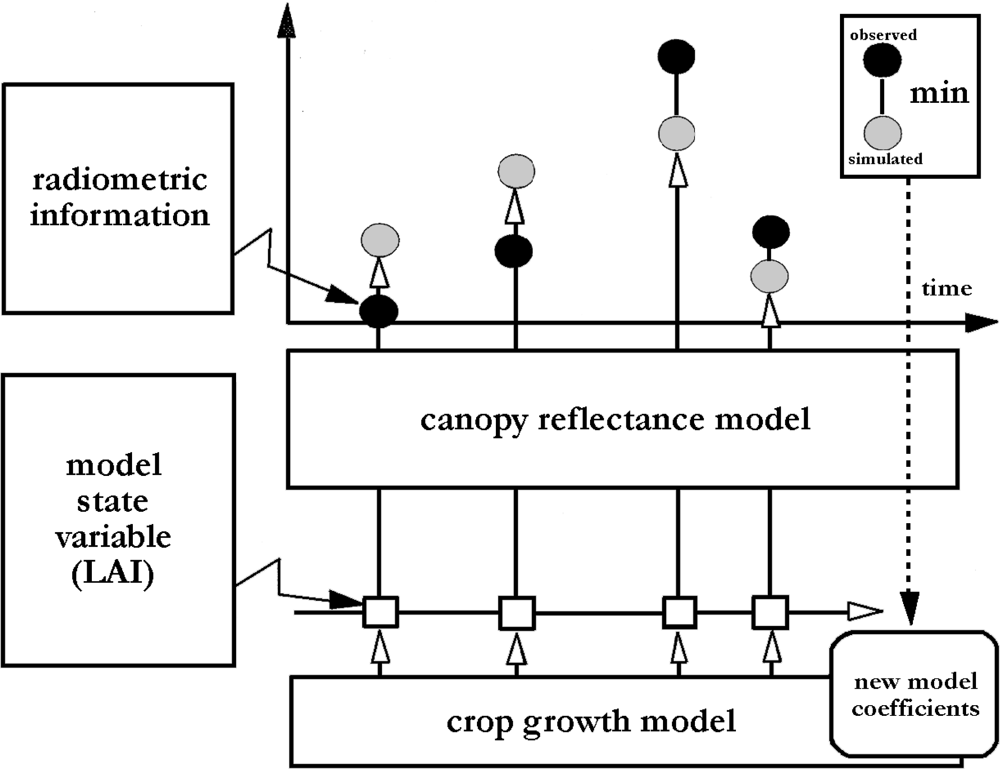
4.2. Parameterization and Re-Calibration of Crop Growth Models
- they are dynamic, in that they operate on a time step for ordering input data and updating state variables
- they contain parameters that allow a general scheme of equations to be adopted to the specific growth behavior of different crop species
- they include a strategy for describing phenological development of a crop to order organ appearance and assimilate portioning.
- Re-calibration or re-parameterization
- Re-initialization
- Forcing
- Updating
5. Conclusions
References
- Atzberger, C. Advances in remote sensing of agriculture: Context description, existing operational monitoring systems and major information needs. Remote Sens 2013, 5, 949–981. [Google Scholar]
- Johnson, G.E.; van Dijk, A.; Sakamoto, C.M. The use of AVHRR data in operational agricultural assessment in Africa. Geocarto. Int 1987, 2, 41–60. [Google Scholar]
- Hutchinson, C.F. Uses of satellite data for famine early warning in Sub-Saharan Africa. Int. J. Remote Sens 1991, 12, 1405–1421. [Google Scholar]
- Busetto, L.; Meroni, M.; Colombo, R. Combining medium and coarse spatial resolution satellite data to improve the estimation of sub-pixel NDVI time series. Remote Sens. Environ 2008, 112, 118–131. [Google Scholar]
- Atkinson, P.M.; Cutler, M.E.J.; Lewis, H. Mapping sub-pixel proportional land cover with AVHRR imagery. Int. J. Remote Sens 1997, 18, 917–935. [Google Scholar]
- Foody, G.M.; Cox, D.P. Sub-pixel land cover composition estimation using a linear mixture model and fuzzy membership functions. Int. J. Remote Sens 1994, 15, 619–631. [Google Scholar]
- Atzberger, C.; Rembold, F. Mapping the spatial distribution of winter crops at sub-pixel level using AVHRR NDVI time series and neural nets. Remote Sens 2013, 5, 1335–1354. [Google Scholar]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ 1979, 8, 127–150. [Google Scholar]
- Tucker, C.J.; Holben, B.N.; Elgin, J.H., Jr.; McMurtrey, J.E., III. Relationship of spectral data to grain yield variation. Photogramm. Eng. Remote Sensing 1980, 46, 657–666. [Google Scholar]
- Deering, D.W. Rangeland Reflectance Characteristics Measured by Aircraft and Spacecraft Sensors. 1978. [Google Scholar]
- Macdonald, R.B.; Hall, F.G. Global crop forecasting. Science 1980, 208, 670–679. [Google Scholar]
- Tucker, C.J.; Vanpraet, C.; Boerwinkel, E.; Gaston, A. Satellite remote sensing of total dry matter production in the Senegalese Sahel. Remote Sens. Environ 1983, 13, 461–474. [Google Scholar]
- Sellers, P.J. Canopy reflectance, photosynthesis and transpiration. Int. J. Remote Sens 1985, 6, 1335–1372. [Google Scholar]
- Prince, S.D. High Temporal Frequency Remote Sensing of Primary Production Using NOAA AVHRR. In Applications of Remote Sensing in Agriculture; Steven, M.D., Clark, J.A., Eds.; Butterworths: London, UK, 1990; pp. 169–183. [Google Scholar]
- Los, S.O. Linkages between Global Vegetation and Climate: An Analysis based on NOAA Advanced Very High Resolution Data. 1998. [Google Scholar]
- Tucker, C.J.; Holben, B.N.; Elgin, J.H., Jr.; McMurtrey, J.E., III. Remote sensing of total dry-matter accumulation in winter wheat. Remote Sens. Environ 1981, 11, 171–189. [Google Scholar]
- Tucker, C.J.; Sellers, P.J. Satellite remote sensing of primary production. Int. J. Remote Sens 1986, 7, 1395–1416. [Google Scholar]
- Running, S.W.; Nemani, R.R. Relating seasonal patterns of the AVHRR vegetation index to simulated photosynthesis and transpiration of forests in different climates. Remote Sens. Environ 1988, 24, 347–367. [Google Scholar]
- Prince, S.D. Satellite remote sensing of primary production: Comparison of results for Sahelian grasslands 1981–1988. Int. J. Remote Sens 1991, 12, 1301–1311. [Google Scholar]
- Pinter, P.J., Jr.; Jackson, R.D.; Idso, S.B.; Reginato, R.J. Multidate spectral reflectance as predictors of yield in water stressed wheat and barley. Int. J. Remote Sens 1981, 2, 43–48. [Google Scholar]
- Barnett, T.L.; Thompson, D.R. Large-area relation of Landsat MSS and NOAA-6 AVHRR spectral data to wheat yields. Remote Sens. Environ 1983, 13, 277–290. [Google Scholar]
- Quarmby, N.A.; Milnes, M.; Hindle, T.L.; Silleos, N. The use of multi-temporal NDVI measurements from AVHRR data for crop yield estimation and prediction. Int. J. Remote Sens 1993, 14, 199–210. [Google Scholar]
- Henricksen, B.L.; Durkin, J.W. Growing period and drought early warning in Africa using satellite data. Int. J. Remote Sens 1986, 7, 1583–1608. [Google Scholar]
- Maselli, F.; Conese, C.; Petkov, L.; Gilabert, M.A. Environmental monitoring and crop forecasting in the Sahel through the use of NOAA NDVI data. A case study: Niger 1986–89. Int. J. Remote Sens 1993, 14, 3471–3487. [Google Scholar]
- Rao, C.R.N.; Chen, J. Revised post-launch calibration of the visible and near-infrared channels of the Advanced Very High Resolution Radiometer (AVHRR) on the NOAA-14 spacecraft. Int. J. Remote Sens 1999, 20, 3485–3491. [Google Scholar]
- Meygret, A.; Briottet, X.; Henry, P.; Hagolle, O. Calibration of SPOT4 HRVIR and VEGETATION cameras over the Rayleigh scattering. Proc. SPIE 2000, 4135, 302–313. [Google Scholar]
- Yin, H.; Udelhoven, T.; Fensholt, R.; Pflugmacher, D.; Hostert, P. How NDVI trends from AVHRR and SPOT VGT time series differ in agricultural areas: An Inner Mongolian case study. Remote Sens 2012, 4, 3364–3389. [Google Scholar]
- Meroni, M.; Atzberger, C.; Vancutsem, C.; Gobron, N.; Baret, F.; Lacaze, R.; Eerens, H.; Leo, O. Evaluation of agreement between space remote sensing SPOT-VEGETATION fAPAR time series. IEEE Trans. Geosci. Remote Sens 2012, 51, 1–12. [Google Scholar]
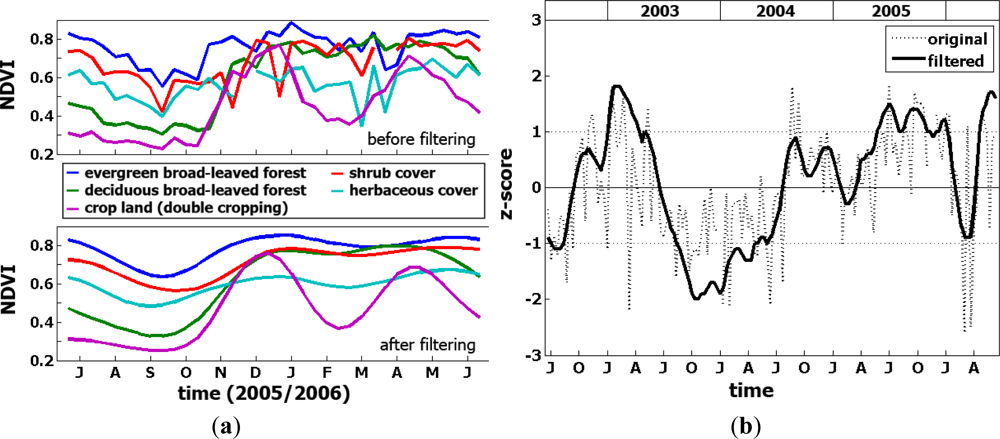
- Hird, J.N.; McDermid, G.J. Noise reduction of NDVI time series: An empirical comparison of selected techniques. Remote Sens. Environ 2009, 113, 248–258. [Google Scholar]
- Holben, B.N. Characteristics of maximum-value composite images from temporal AVHRR data. Int. J. Remote Sens 1986, 7, 1417–1434. [Google Scholar]
- Atzberger, C.; Eilers, P.H.C. Evaluating the effectiveness of smoothing algorithms in the absence of ground reference measurements. Int. J. Remote Sens 2011, 32, 3689–3709. [Google Scholar]
- Genovese, G.; Vignolles, C.; Nègre, T.; Passera, G. A methodology for a combined use of normalised difference vegetation index and CORINE land cover data for crop yield monitoring and forecasting. A case study on Spain. Agronomie 2001, 21, 91–111. [Google Scholar]
- Kerdiles, H.; Grondona, M.O. NOAA-AVHRR NDVI decomposition and subpixel classification using linear mixing in the Argentinean Pampa. Int. J. Remote Sens 1995, 16, 1303–1325. [Google Scholar]
- Kogan, F.N. Droughts of the late 1980s in the United States as derived from NOAA polar orbiting satellite data. Bull. Amer. Meteor. Soc 1995, 76, 655–668. [Google Scholar]
- Kogan, F.N. Operational space technology for global vegetation assessment. Bull. Amer. Meteor. Soc 2001, 89, 1949–1964. [Google Scholar]
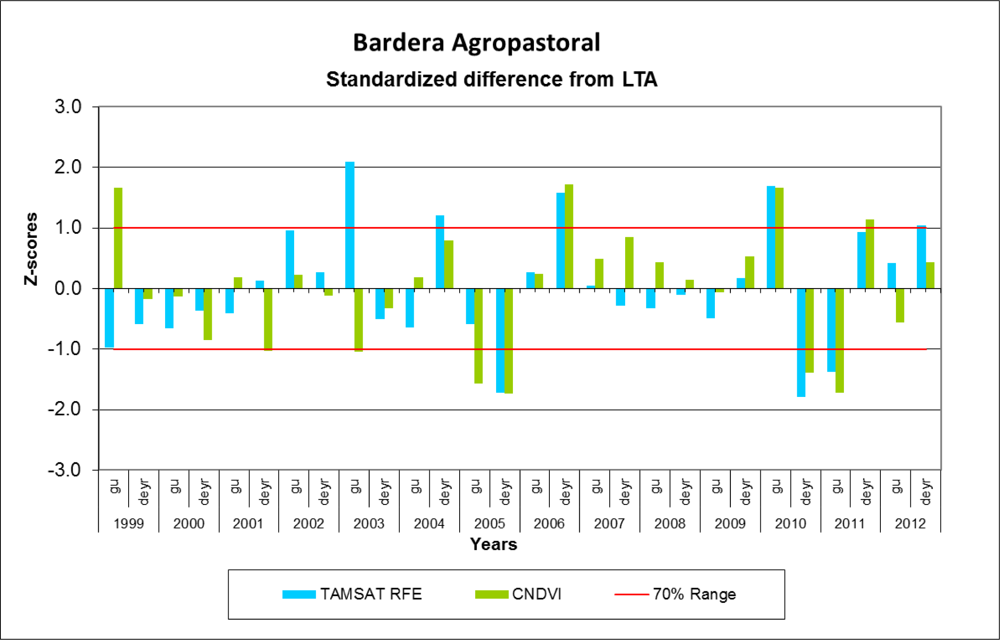
- Rojas, O.; Vrieling, A.; Rembold, F. Assessing drought probability for agricultural areas in Africa with coarse resolution remote sensing imagery. Remote Sens. Environ 2011, 115, 343–352. [Google Scholar]
- Balint, Z.; Mutua, F.M. Drought Monitoring with the Combined Drought Index; FAO-SWALIM: Nairobi, Kenya, 2011; p. 32. [Google Scholar]
- Reed, B.C.; White, M.; Brown, J.F. Remote Sensing Phenology. In Phenology: An Integrative Environmental Science; Schwartz, M.D., Ed.; Kluwer Academic Publishers: New York, NY, USA, 2003; pp. 365–382. [Google Scholar]
- White, M.A.; de Beurs, K.M.; Didan, K.; Inouye, D.W.; Richardson, A.D.; Jensen, O.P.; O’Keefe, J.; Zhang, G.; Nemani, R.R.; van Leeuwen, W.J.D.; et al. Intercomparison, interpretation, and assessment of spring phenology in North America estimated from remote sensing for 1982–2006. Glob. Chang. Biol 2009, 15, 2335–2359. [Google Scholar]
- Zhang, X.; Friedl, M.A.; Schaaf, C.B.; Strahler, A.H.; Hodges, J.C.F.; Gao, F.; Reed, B.C.; Huete, A. Monitoring vegetation phenology using MODIS. Remote Sens. Environ 2003, 84, 471–475. [Google Scholar]
- Beck, P.S.A.; Atzberger, C.; Høgda, K.A.; Johansen, B.; Skidmore, A.K. Improved monitoring of vegetation dynamics at very high latitudes: A new method using MODIS NDVI. Remote Sens. Environ 2006, 100, 321–334. [Google Scholar]
- Atzberger, C.; Eilers, P.H.C. A time series for monitoring vegetation activity and phenology at 10-daily time steps covering large parts of South America. Int. J. Appl. Earth Obs. Geoinf 2011, 4, 365–386. [Google Scholar]
- Vrieling, A.; de Beurs, K.M.; Brown, M.E. Variability of African farming systems from phenological analysis of NDVI time series. Clim. Chang 2011, 109, 455–477. [Google Scholar]
- Atkinson, P.M.; Jeganathan, C.; Dash, J.; Atzberger, C. Inter-comparison of four models for smoothing satellite sensor time-series data to estimate vegetation phenology. Remote Sens. Environ 2012, 123, 400–417. [Google Scholar]
- Food Security and Nutrition Analysis Post Deyr 2012/13; Technical Series Report No VI. 50; Food Security and Nutrition Analysis Unit: Nairobi, Kenya, 2013; p. 174.
- Maselli, F.; Rembold, F. Analysis of GAC NDVI data for cropland identification and yield forecasting in Mediterranean African countries. Photogramm. Eng. Remote Sensing 2001, 67, 593–602. [Google Scholar]
- Kastens, J.H.; Kastens, T.L.; Kastens, D.L.A.; Price, K.P.; Martinko, E.A.; Lee, R.-Y. Image masking for crop yield forecasting using AVHRR NDVI time series imagery. Remote Sens. Environ 2005, 99, 341–356. [Google Scholar]
- Baret, F.; Guyot, G.; Major, D.J. Crop biomass evaluation using radiometric measurements. Photogrammetria 1989, 43, 241–256. [Google Scholar]
- Benedetti, R.; Rossini, P. On the use of NDVI profiles as a tool for agricultural statistics: The case study of wheat yield estimate and forecast in Emilia Romagna. Remote Sens. Environ 1993, 45, 311–326. [Google Scholar]
- Delécolle, R.; Maas, S.J.; Guérif, M.; Baret, F. Remote sensing and crop production models: Present trends. ISPRS J. Photogramm 1992, 47, 145–161. [Google Scholar]
- Rasmussen, M.S. Assessment of millet yields and production in northern Burkina Faso using integrated NDVI from the AVHRR. Int. J. Remote Sens 1992, 13, 3431–3442. [Google Scholar]
- Groten, S.M.E. NDVI-crop monitoring and early yield assessment of Burkina Faso. Int. J. Remote Sens 1993, 14, 1495–1515. [Google Scholar]
- Hayes, M.J.; Decker, W.L. Using NOAA AVHRR data to estimate maize production in the United States Corn Belt. Int. J. Remote Sens 1996, 17, 3189–3200. [Google Scholar]
- Lewis, J.E.; Rowland, J.; Nadeau, A. Estimating maize production in Kenya using NDVI: Some statistical considerations. Int. J. Remote Sens 1998, 19, 2609–2617. [Google Scholar]
- Maselli, F.; Romanelli, S.; Bottai, L.; Maracchi, G. Processing of GAC NDVI data for yield forecasting in the Sahelian region. Int. J. Remote Sens 2000, 21, 3509–3523. [Google Scholar]
- Atzberger, C. Estimates of Winter Wheat Production through Remote Sensing and Crop Growth Modelling: A Case Study on the Camargue Region. 1997. [Google Scholar]
- Rudorff, B.F.T.; Batista, G.T. Spectral response of wheat and its relationship to agronomic variables in the tropical region. Remote Sens. Environ 1990, 31, 53–63. [Google Scholar]
- Atzberger, C.; Guerif, M.; Baret, F.; Werner, W. Comparative analysis of three chemometric techniques for the spectroradiometric assessment of canopy chlorophyll content in winter wheat. Comput. Electron. Agric 2010, 73, 165–173. [Google Scholar]
- Meroni, M.; Marinho, E.; Sghaier, N.; Verstrate, M.M.; Leo, O. Remote sensing based yield estimation in a stochastic framework—Case study of durum wheat in Tunisia. Remote Sens 2013, 5, 539–557. [Google Scholar]
- Goward, S.N.; Dye, D.G. Evaluating North American net primary productivity with satellite observations. Adv. Space Res 1987, 7, 165–174. [Google Scholar]
- Idso, S.B.; Pinter, P.J., Jr.; Jackson, R.D.; Reginato, R.J. Estimation of grain yields by remote sensing of crop senescence rates. Remote Sens. Environ 1980, 9, 87–91. [Google Scholar]
- Baret, F.; Guyot, G. Monitoring of the ripening period of wheat canopies using visible and near infra red radiometry [reflectance, vegetation index, senescence rate, water plateau]. Agronomie 1986, 6, 509–516. [Google Scholar]
- Rasmussen, M.S. Developing simple, operational, consistent NDVI-vegetation models by applying environmental and climatic information. Part II: Crop yield assessment. Int. J. Remote Sens 1998, 19, 119–139. [Google Scholar]
- Reynolds, C.A.; Yitayew, M.; Slack, D.C.; Hutchinson, C.F.; Huetes, A.; Petersen, M.S. Estimating crop yields and production by integrating the FAO Crop Specific Water Balance model with real-time satellite data and ground-based ancillary data. Int. J. Remote Sens 2000, 21, 3487–3508. [Google Scholar]
- Potdar, M.B.; Manjunath, K.R.; Purohit, N.L. Multi-season atmospheric normalization of NOAA AVHRR derived NDVI for crop yield modeling. Geocarto. Int 1999, 14, 51–56. [Google Scholar]
- Manjunath, K.R.; Potdar, M.B.; Purohit, N.L. Large area operational wheat yield model development and validation based on spectral and meteorological data. Int. J. Remote Sens 2002, 23, 3023–3038. [Google Scholar]
- Balaghi, R.; Tychon, B.; Eerens, H.; Jlibene, M. Empirical regression models using NDVI, rainfall and temperature data for the early prediction of wheat grain yields in Morocco. Int. J. Appl. Earth Obs. Geoinf 2008, 10, 438–452. [Google Scholar]
- Rojas, O. Operational maize yield model development and validation based on remote sensing and agro-meteorological data in Kenya. Int. J. Remote Sens 2007, 28, 3775–3793. [Google Scholar]
- Stathakis, D.; Savin, I.Y.; Nègre, T. Neuro-Fuzzy Modeling for Crop Yield Prediction. Proceedings of the ISPRS Commission VII Symposium Remote Sensing: From Pixels to Processes, Enschede, The Netherlands, 8–11 May 2006.
- Guérif, M.; Delécolle, R. Introducing Remotely Sensed Estimates of Canopy Structure into Plant Models. In Canopy Structure and Light Microclimate. Characterization and Applications; Varlet-Grancher, C., Bonhomme, R., Sinoquet, H., Eds.; INRA: Paris, France, 1993; pp. 479–490. [Google Scholar]
- Monteith, J.L. Solar radiation and productivity in tropical ecosystems. J. Appl. Ecol 1972, 9, 747–766. [Google Scholar]
- Vuolo, F.; Neugebauer, N.; Falanga, S.; Atzberger, C.; D’Urso, G. Estimation of Leaf Area Index using DEIMOS-1 data: Calibration and transferability of a semi-empirical relationship between two agricultural areas. Remote Sens 2013, 5, 1274–1291. [Google Scholar]
- Richter, K.; Atzberger, C.; Vuolo, F.; D’Urso, G. Evaluation of sentinel-2 spectral sampling for radiative transfer model based LAI estimation of wheat, sugar beet, and maize. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens 2011, 4, 458–464. [Google Scholar]
- Monteith, J.L. Climate and the efficiency of crop production in Britain. Phil. Trans. R. Soc. Lond 1977, 281, 277–294. [Google Scholar]
- Baret, F. Un modele Simplifie de Reflectance et d’absorptance d’un Couvert vegetal. Proceedings of the 4th International Colloquium on Spectral Signatures of Objects in Remote Sensing ESA SP-287, Aussois, France, 18–22 January 1988; pp. 113–120.
- Steinmetz, S.; Guerif, M.; Delecolle, R.; Baret, F. Spectral estimates of the absorbed photosynthetically active radiation and light-use efficiency of a winter wheat crop subjected to nitrogen and water deficiencies. Int. J. Remote Sens 1990, 11, 1797–1808. [Google Scholar]
- Singh, P.; Sri Rama, Y.V. Influence of water deficit on transpiration and radiation use efficiency of chickpea (Cicerarietinum L.). Agr. Forest Meteorol 1989, 48, 317–330. [Google Scholar]
- Verstraete, M.M.; Pinty, B.; Myneni, R.B. Potential and limitations of information extraction on the terrestrial biosphere from satellite remote sensing. Remote Sens. Environ 1996, 58, 201–214. [Google Scholar]
- Gobron, N.; Pinty, B.; Verstraete, M.M.; Widlowski, J.-L.; Diner, D.J. Uniqueness of multiangular measurements—Part II: Joint retrieval of vegetation structure and photosynthetic activity from MISR. IEEE Trans. Geosci. Remote Sens 2002, 40, 1574–1592. [Google Scholar]
- Eerens, H.; Piccard, I.; Royer, A.; Orlandi, S. Methodology of the MARS Crop Yield Forecasting System. Vol. 3: Remote Sensing Information, Data Processing and Analysis; Joint Research Centre European Commission: Ispra, Italy, 2004; p. 76. [Google Scholar]
- Myneni, R.B.; Williams, D.L. On the relationship between FAPAR and NDVI. Remote Sens. Environ 1994, 49, 200–211. [Google Scholar]
- Wofsy, S.C.; Goulden, M.L.; Munger, J.W.; Fan, S.-M.; Bakwin, P.S.; Daube, B.C.; Bassow, S.L.; Bazzaz, F.A. Net exchange of CO2 in a mid-latitude forest. Science 1993, 260, 1314–1317. [Google Scholar]
- Johnson, F.H.; Eyring, H.; Polissar, M.J. The Kinetic Basis of Molecular Biology; John Wiley & Sons: New York, NY, USA, 1954. [Google Scholar]
- Lommen, P.W.; Schwintzer, C.R.; Yocum, C.S.; Gates, D.M. A model describing photosynthesis in terms of gas diffusion and enzyme kinetics. Planta 1971, 98, 195–220. [Google Scholar]
- Veroustraete, F. On the use of a simple deciduous forest model for the interpretation of climate change effects at the level of carbon dynamics. Ecol. Model 1994, 75–76, 221–237. [Google Scholar]
- Savin, I. Crop Yield Prediction with SPOT VGT in Mediterranean and Central Asian Countries. Proceedings of ISPRS WG VIII/10 Workshop, Remote Sensing Support to Crop Yield Forecast and Area Estimates, Stresa, Italy, 30 November–1 December 2006; pp. 129–134.
- Gallo, K.P.; Daughtry, C.S.T.; Bauer, M.E. Spectral estimation of absorbed photosynthetically active radiation in corn canopies. Remote Sens. Environ 1985, 17, 221–232. [Google Scholar]
- Sinclair, T.R.; Seligman, N.G. Crop modeling: From infancy to maturity. Agron. J 1996, 88, 698–704. [Google Scholar]
- Boote, K.J.; Jones, J.W.; Pickering, N.B. Potential uses and limitations of crop models. Agron. J 1996, 88, 704–716. [Google Scholar]
- Jones, C.A.; Kiniry, J.R. Ceres-Maize: A Simulation Model of Maize Growth and Development, 1st ed.; Texas A&M University: College Station, TX, USA, 1986. [Google Scholar]
- Supit, I.; Hooijer, A.A.; Diepen, C.A. Van System Description of the WOFOST 6.0 Crop Simulation Model Implemented in CGMS; European Commission: Ispra, Italy, 1994. [Google Scholar]
- Villalobos, F.J.; Hall, A.J.; Ritchie, J.T.; Orgaz, F. OILCROP-SUN: A development, growth, and yield model of the sunflower crop. Agron. J 1996, 88, 403–415. [Google Scholar]
- Stöckle, C.O.; Donatelli, M.; Nelson, R. CropSyst, a cropping systems simulation model. Eur. J. Agron 2003, 18, 289–307. [Google Scholar]
- Brisson, N.; Mary, B.; Ripoche, D.; Jeuffroy, M.H.; Ruget, F.; Nicoullaud, B.; Gate, P.; Devienne-Barret, F.; Antonioletti, R.; Durr, C.; et al. STICS: A generic model for the simulation of crops and their water and nitrogen balances. I. Theory and parameterization applied to wheat and corn. Agronomie 1998, 18, 311–346. [Google Scholar]
- Maas, S.J. GRAMI: A Crop Growth Model that can Use Remotely Sensed Information ARS 91; US Department of Agriculture: Washington, DC, USA, 1992; p. 78. [Google Scholar]
- Atzberger, C.; Guérif, M.; Delecolle, R. The use of GRAMI Crop Growth Model and SPOT Data for Biomass Estimations in Winter Wheat. Proceedings of 8th International Symposium Physical Measurements and Signatures in Remote Sensing, Aussois, France, 8–12 January 2001; pp. 705–711.
- Donatelli, M.; Russell, G.; Rizzoli, A.E.; Acutis, M.; Adam, M.; Athanasiadis, I.N.; Balderacchi, M.; Bechini, L.; Belhouchette, H.; Bellocchi, G.; et al. A Component-Based Framework for Simulating Agricultural Production and Externalities. In Environmental and Agricultural Modelling; Brouwer, F.M., Ittersum, M.K., Eds.; Springer: Dordrecht, The Netherland, 2010; pp. 63–108. [Google Scholar]
- Bellocchi, G.; Rivington, M.; Donatelli, M.; Matthews, K. Validation of biophysical models: Issues and methodologies. A review. Agron. Sustain. Dev 2010, 30, 109–130. [Google Scholar]
- Padilla, F.M.; Maas, S.; Gonzales-Dugo, M.P.; Raja, N.; Mansilla, F.; Gavilan, P.; Dominguez, J. Wheat yield monitoring in Southern Spain using the GRAMI model and a series of satellite images. Field Crop. Res 2012, 130, 145–154. [Google Scholar]
- Doraiswamy, P.C.; Hatfield, J.L.; Jackson, T.J.; Akhmedov, B.; Prueger, J.; Stern, A. Crop condition and yield simulations using Landsat and MODIS. Remote Sens. Environ 2004, 92, 548–559. [Google Scholar]
- Weiss, M.; Troufleau, D.; Baret, F.; Chauki, H.; Prévot, L.; Olioso, A.; Bruguier, N.; Brisson, N. Coupling canopy functioning and radiative transfer models for remote sensing data assimilation. Agr. Forest Meteorol 2001, 108, 113–128. [Google Scholar]
- Moulin, S.; Bondeau, A.; Delécolle, R. Combining agricultural crop models and satellite observations: From field to regional scales. Int. J. Remote Sens 1998, 19, 1021–1036. [Google Scholar]
- Guérif, M.; Duke, C.L. Adjustment procedures of a crop model to the site specific characteristics of soil and crop using remote sensing data assimilation. Agr. Ecosyst. Environ 2000, 81, 57–69. [Google Scholar]
- Thornton, P.E.; Running, S.W.; White, M.A. Generating surfaces of daily meteorological variables over large regions of complex terrain. J. Hydrol 1997, 190, 214–251. [Google Scholar]
- Clevers, J.G.P.W.; van Leeuwen, H.J.C. Combined use of optical and microwave remote sensing data for crop growth monitoring. Remote Sens. Environ 1996, 56, 42–51. [Google Scholar]
- Maas, S.J. Use of remotely-sensed information in agricultural crop growth models. Ecol. Model 1988, 41, 247–268. [Google Scholar]
- Mulder, V.L.; de Bruin, S.; Schaepman, M.E.; Mayr, T.R. The use of remote sensing in soil and terrain mapping—A review. Geoderma 2011, 162, 1–19. [Google Scholar]
- Lagacherie, P.; Baret, F.; Feret, J.-B.; Madeira Netto, J.; Robbez-Masson, J.M. Estimation of soil clay and calcium carbonate using laboratory, field and airborne hyperspectral measurements. Remote Sens. Environ 2008, 112, 825–835. [Google Scholar]
- Ben-Dor, E. Quantitative remote sensing of soil properties. Adv. Agron 2002, 75, 173–243. [Google Scholar]
- Viscarra Rossel, R.A.; Cattle, S.R.; Ortega, A.; Fouad, Y. In situ measurements of soil colour, mineral composition and clay content by VIS-NIR spectroscopy. Geoderma 2009, 150, 253–266. [Google Scholar]
- Ungaro, F.; Calzolari, C.; Busoni, E. Development of pedotransfer functions using a group method of data handling for the soil of the PianuraPadano-Veneta region of North Italy: Water retention properties. Geoderma 2005, 124, 293–317. [Google Scholar]
- Wagner, W.; Naeimi, V.; Scipal, K.; Jeu, R.; Martínez-Fernández, J. Soil moisture from operational meteorological satellites. Hydrogeol. J 2007, 15, 121–131. [Google Scholar]
- Taylor, T.W. Agricultural Analysis for a Worldwide Crop Assessment. Proceedings of SPOT Conference, Paris, France, 15–18 April 1996; pp. 485–488.
- Allen, R.; Hanuschak, G.; Craig, M. Limited Use of Remotely Sensed Data for Crop Condition Monitoring and Crop Yield Forecasting in NASS; US Department of Agriculture: Washington, DC, USA, 2002. [Google Scholar]
- Vossen, P.; Rijks, D. Issues Related to Agrometeorological Models when Applying Them for Yield Forecasting at a European Scale. In Agrometeorological Applications for Regional Crop Monitoring and Production Assessment: Accounts of the EU Support Group on Agrometeorology (SUGRAM) 1991–1996; Rijks, D., Terres, J.M., Vossen, P., Eds.; Joint Research Centre, European Commission: Ispra, Italy, 1998; pp. 5–30. [Google Scholar]
- Nègre, T.; Rembold, F.; Savin, I.Y.; Rojas, O. Use of SPOT/VEGETATION Data for Food Security Oriented Crop Growth Monitoring: The MARS-FOOD Approach. Proceedings of the 2nd International SPOT/VEGETATION Users Conference, Antwerp, Belgium, 24–26 March 2004; p. 83.
- Brown, M.E. Famine Early Warning Systems and Remote Sensing Data; Springer Verlag: Heidelberg, Germany, 2008. [Google Scholar]
- De Bruin, H.A.R.; Trigo, I.F.; Lorite, I.J.; Cruz-Blanco, M.; Gavilán, P. Reference Crop Evapotranspiration Obtained from the Geostationary Satellite MSG (METEOSAT). Proceedings of EGU General Assembly 2012, Vienna, Austria, 22–27 April 2012; p. 11453.
- Mu, Q.; Zhao, M.; Running, S.W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sens. Environ 2011, 115, 1781–1800. [Google Scholar]
- Fritz, S.; Purgathofer, P.; Kayali, F.; Fellner, M.; Wimmer, M.; Sturn, T.; Triebnig, G.; Krause, S.; Schindler, F.; Kollegger, M.; et al. Landspotting: Social gaming to collect vast amounts of data for satellite validation. Geophys. Res. Abstr 2012, 14, EGU2012–13173. [Google Scholar]



| Sensor | Platform | Spectral Range | Number of Bands | Resolution | Swath Width | Repeat Coverage | Launch |
|---|---|---|---|---|---|---|---|
| AVHHR | NOAA POES 6–19 | VIS, NIR, MIR | 5 | 1,100 m | 2,400 km | 12 h | 1978 |
| AVHRR | METOP | VIS, NIR, SWIR, MIR | 5 | 1,100 m | 2,400 km | 12 h | 2007 |
| SEAWIFS | Orbview-2 | VIS, NIR | 8 | 1,100 m 4,500 m | 1,500 km 2,800 km | 1 day | 1997 |
| VEGETATION | SPOT 4, 5 | VIS, NIR, SWIR | 4 | 1,100 m | 2,200 km | 1 day | 1998 |
| MODIS | EOS AM1/PM1 | VIS, NIR, SWIR, TIR | 36 | 250–1,000 m | 2,330 km | <2 days | 1999 |
| MERIS | ENVISAT | VIS, NIR | 15 | 300 m (1,200 m) | 1,150 km | <3 days | 2000 |
| PROBA-V | PROBA-V | VIS, NIR, SWIR | 4 | 300 m (1,000 m) | 2,250 km | 1 day | Foreseen 2014 |
| SENTINEL 3 | SENTINEL | VIS, NIR, SWIR | 21 | 300 m | 1,270 km | <2 days | Foreseen 2014 |
| No. | Model Parameters | Year | r2 | Standard Error of Estimate kg·ha−a | Residual Mean Square | F-ratio | Tabled F at P < 0.05 | n |
|---|---|---|---|---|---|---|---|---|
| 1 | aiNDVIb | 1990 | 0.606 | 254 | 64,745 | 15.38 | 4.96 | 12 |
| 2 | aiNDVI + b | 1991 | 0.738 | 186 | 34,639 | 39.43 | 4.60 | 16 |
| 3 | aiNDVI + b | 90 + 91 | 0.645 | 220 | 48,349 | 47.20 | 4.23 | 28 |
| 4 | a ∑8iNDVI PAR) + b | 1990 | 0.523 | 280 | 78,358 | 10.97 | 4.96 | 12 |
| 5 | a ∑2iNDVI PAR) + b | 1991 | 0.690 | 202 | 40,995 | 31.15 | 4.60 | 16 |
| 6 | a ∑6iNDVI PAR) + b | 90 + 91 | 0.202 | 329 | 108,570 | 6.60 | 4.23 | 28 |
| 7 | aiNDVI + b AGRIPRC + c | 90 + 91 | 0.660 | 208 | 43,246 | 22.30 | 3.42 | 26 |
| 8 | aiNDVI + b > TLUDEN + c | 90 + 91 | 0.695 | 197 | 38,815 | 26.16 | 3.42 | 26 |
| 9 | AGRIPRC > 22.5 aiNDVI+b | 90 + 91 | 0.729 | 166 | 27,534 | 35.04 | 4.67 | 26 |
| 10 | AGRIPRC> 22.5 aiNDVI + b AGRIPRC + c | 90 + 91 | 0.814 | 143 | 20,530 | 26.22 | 3.89 | 15 |
| 11 | AGRIPRC > 22.5 aiNDVI + b TLUDEN + c | 90 + 91 | 0.883 | 113 | 12,858 | 45.44 | 3.89 | 15 |
| 12 | AGRIPRC < 22.5 aiNDVI + b | 90 + 91 | 0.663 | 244 | 59,637 | 21.68 | 4.84 | 13 |
| 13 | AGRIPRC < 22.5 aiNDVI + b AGRIPRC + c | 90 + 91 | 0.763 | 212 | 44,846 | 12.87 | 4.46 | 11 |
| 14 | AGRIPRC < 22.5 aiNDVI + b TLUDEN + c | 90 + 91 | 0.685 | 244 | 59,537 | 8.70 | 4.46 | 11 |
Share and Cite
Rembold, F.; Atzberger, C.; Savin, I.; Rojas, O. Using Low Resolution Satellite Imagery for Yield Prediction and Yield Anomaly Detection. Remote Sens. 2013, 5, 1704-1733. https://doi.org/10.3390/rs5041704
Rembold F, Atzberger C, Savin I, Rojas O. Using Low Resolution Satellite Imagery for Yield Prediction and Yield Anomaly Detection. Remote Sensing. 2013; 5(4):1704-1733. https://doi.org/10.3390/rs5041704
Chicago/Turabian StyleRembold, Felix, Clement Atzberger, Igor Savin, and Oscar Rojas. 2013. "Using Low Resolution Satellite Imagery for Yield Prediction and Yield Anomaly Detection" Remote Sensing 5, no. 4: 1704-1733. https://doi.org/10.3390/rs5041704
APA StyleRembold, F., Atzberger, C., Savin, I., & Rojas, O. (2013). Using Low Resolution Satellite Imagery for Yield Prediction and Yield Anomaly Detection. Remote Sensing, 5(4), 1704-1733. https://doi.org/10.3390/rs5041704








