Assimilation of MODIS Snow Cover Area Data in a Distributed Hydrological Model Using the Particle Filter
Abstract
:1. Introduction
2. Data Assimilation
3. Satellite Snow Cover Area
3.1. The Data
3.2. Preprocessing of SCA Data
3.3. Conversion from SWE to SCA
4. Hydrological Model and Setting Up of the Assimilation System
4.1. The LISFLOOD Model
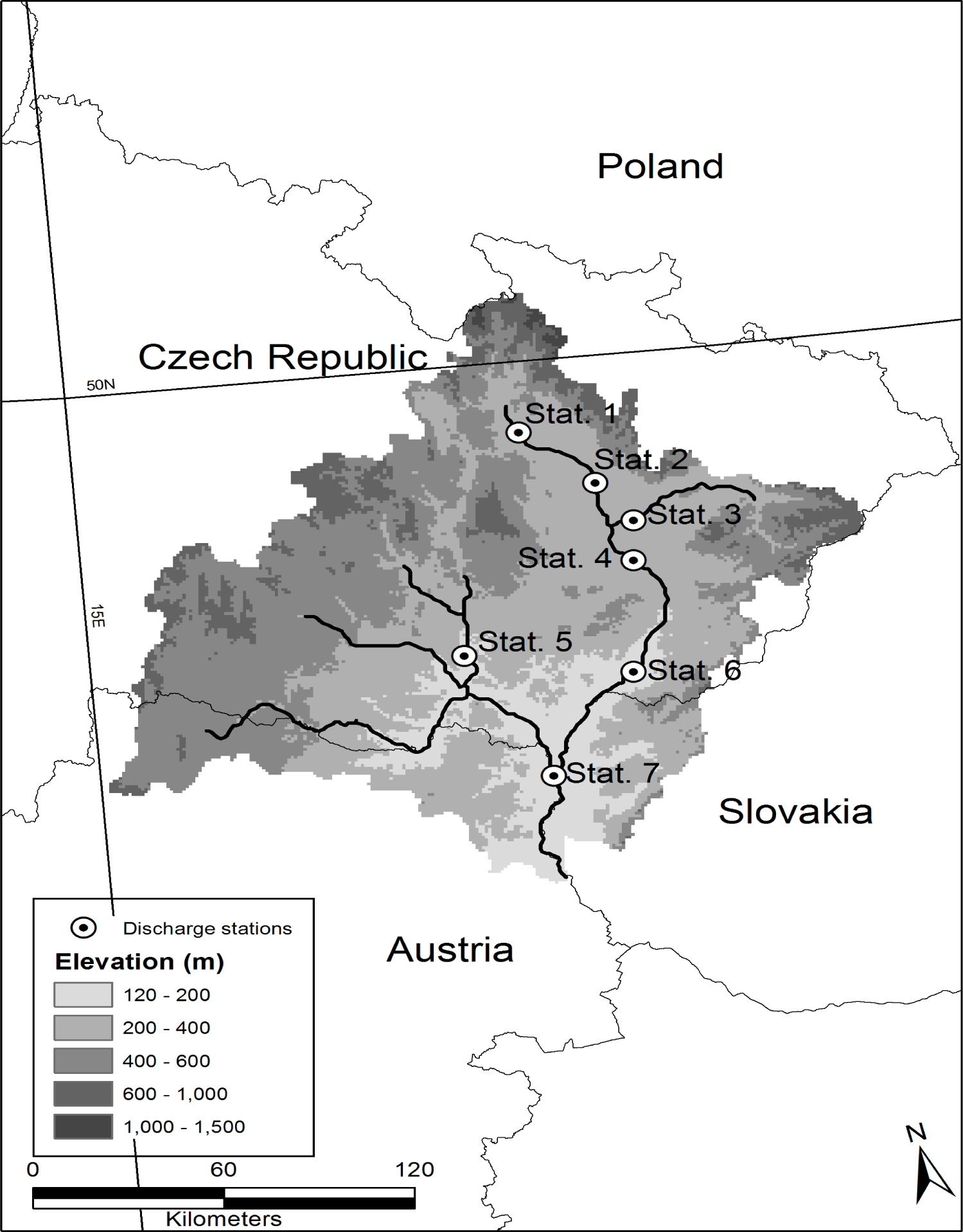
4.2. Case Study
4.3. Sources of Errors
4.4. Definition of the Scores Used
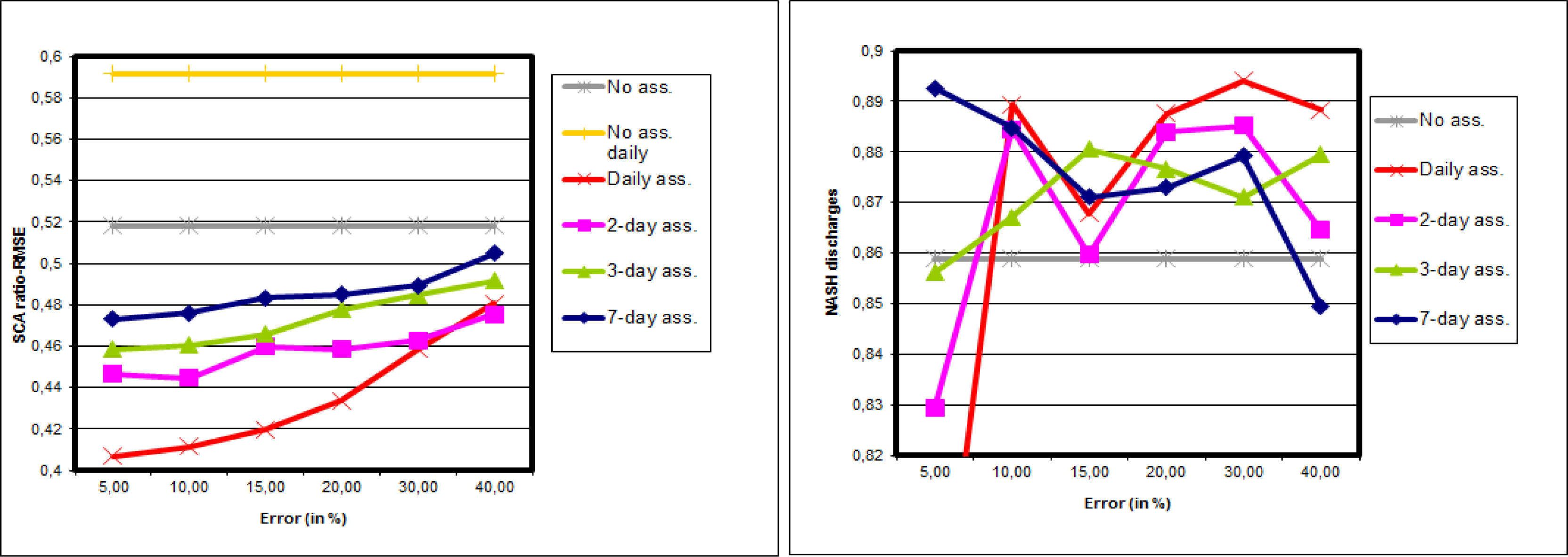
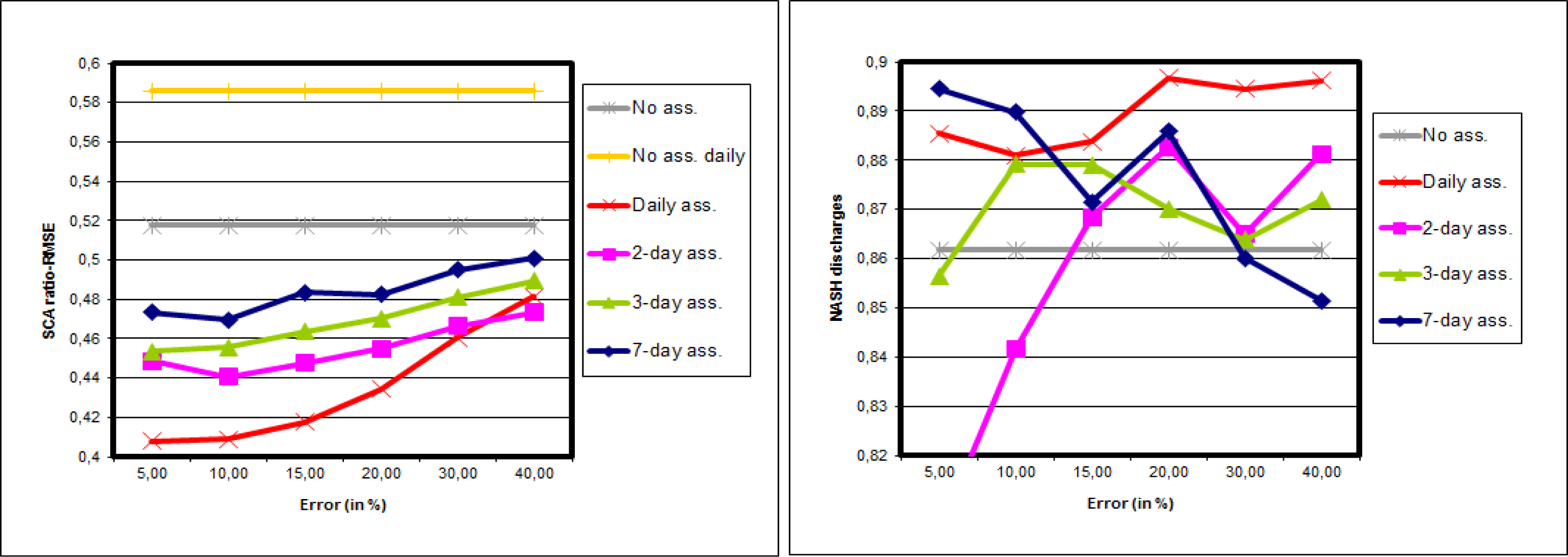
5. Assimilation of the Area Upstream of the Kromericz Station
5.1. Synthetic Experiments
5.2. Real Experiments
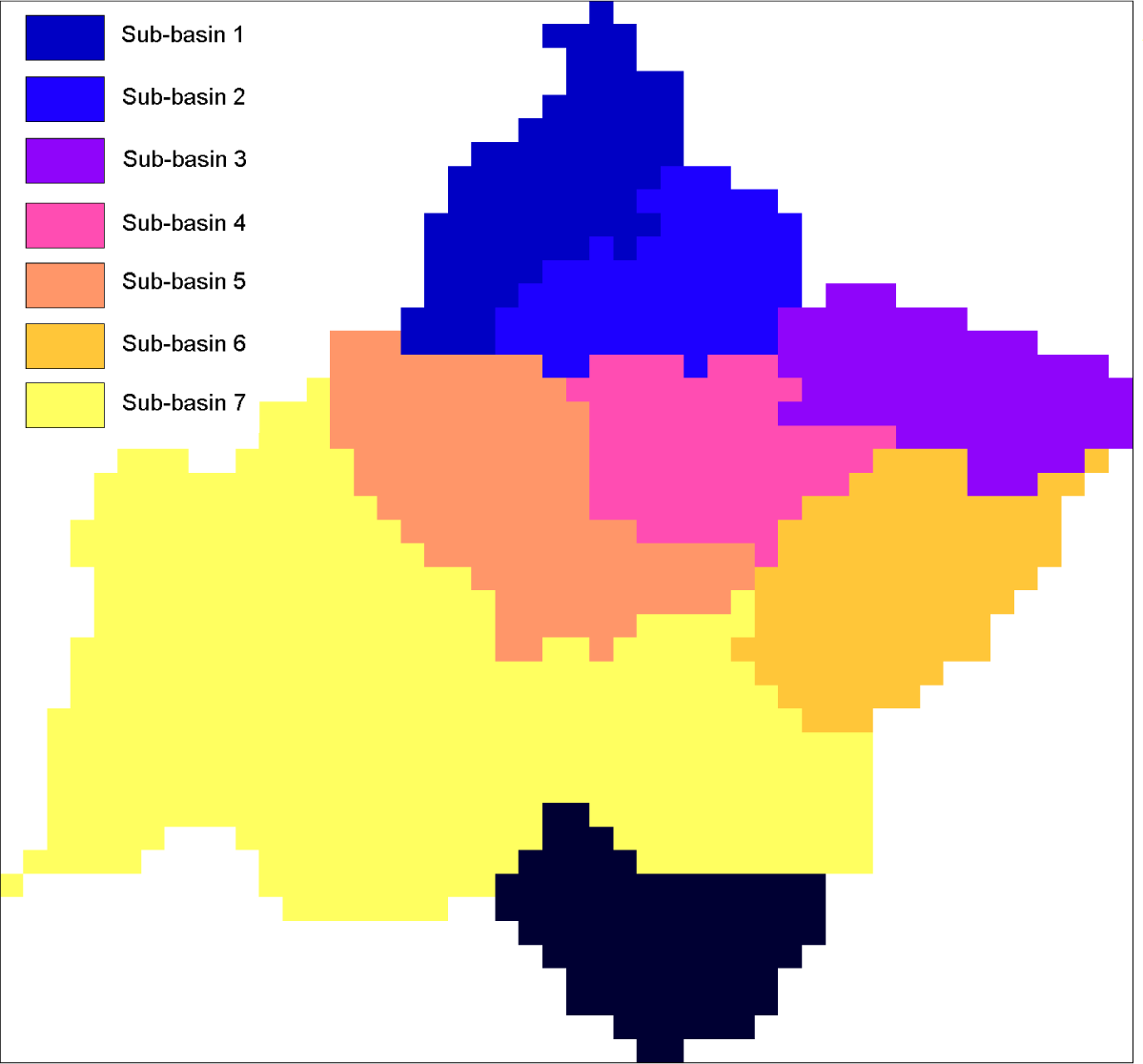
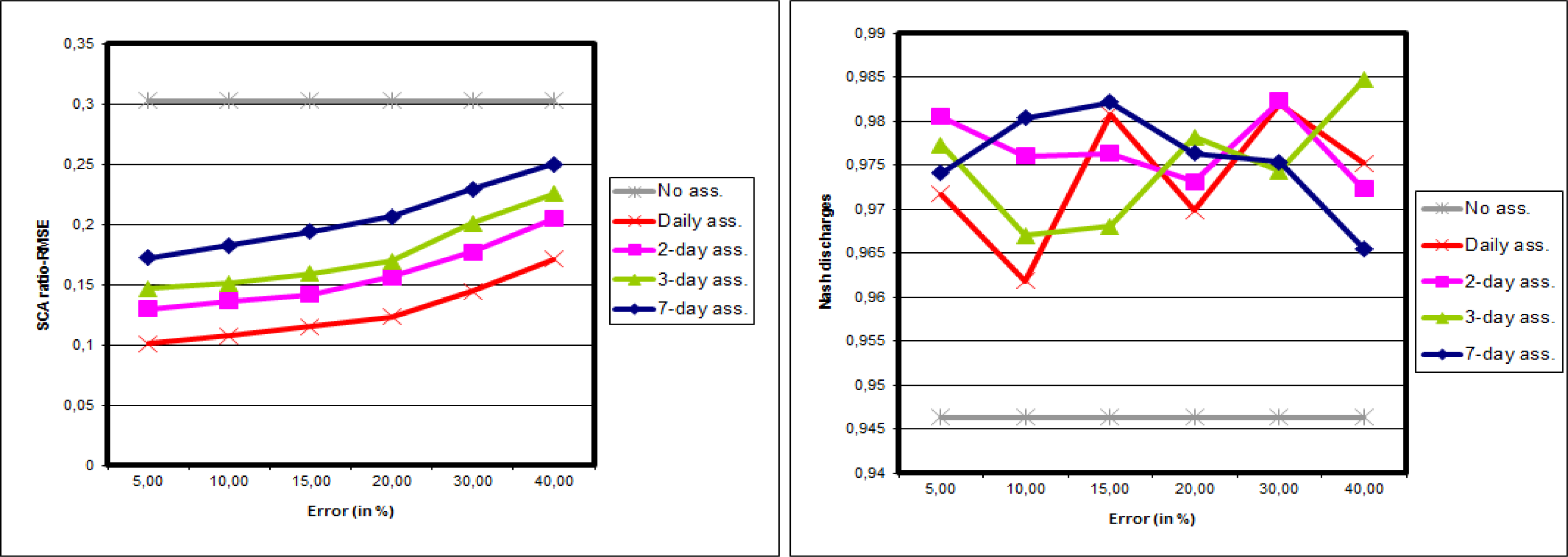
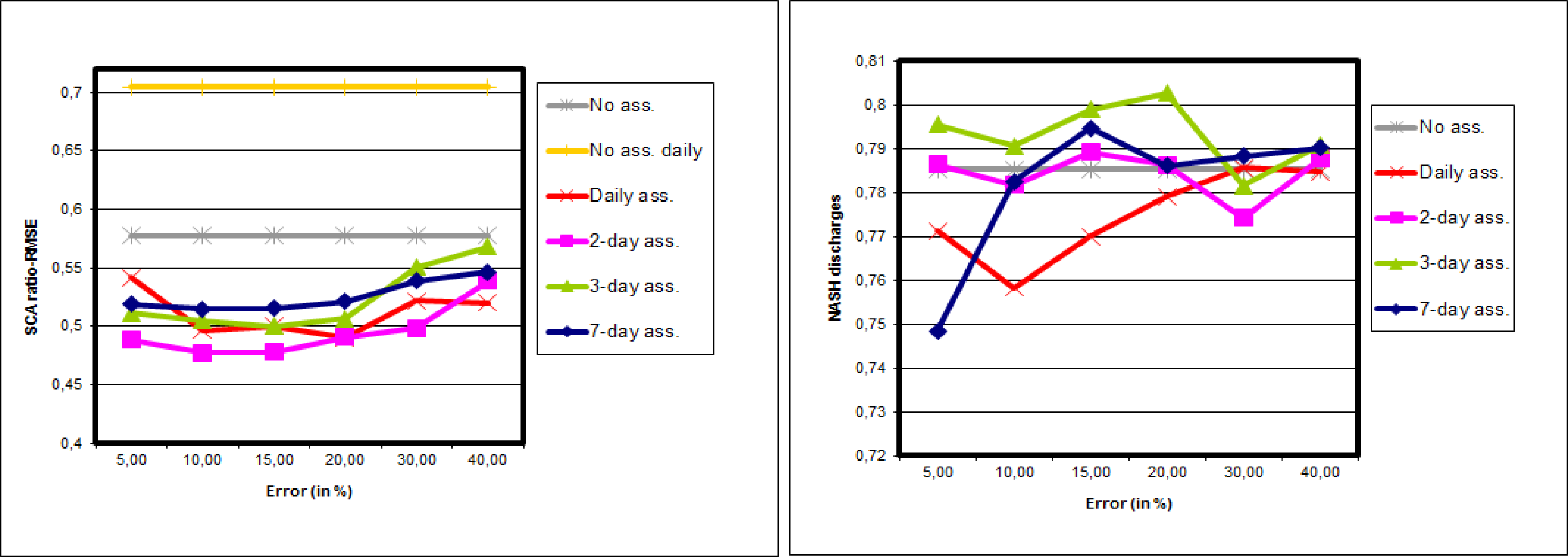
6. Assimilation on the Whole Morava Basin
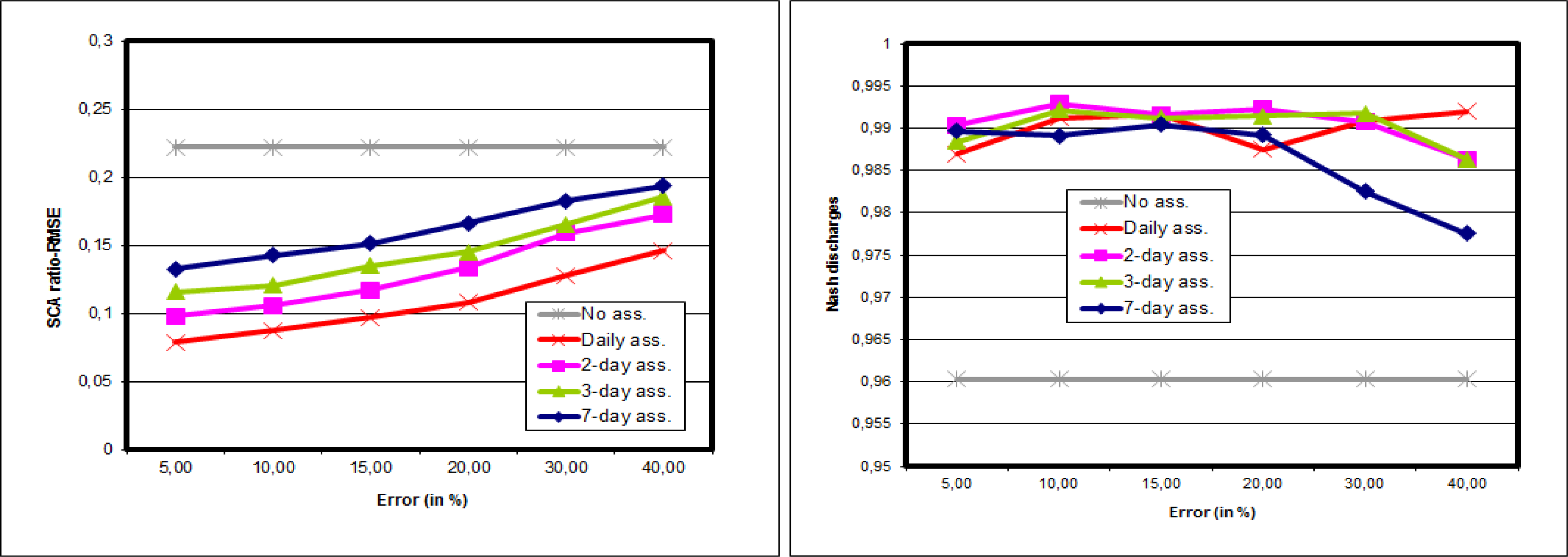
6.1. Synthetic Experiments
6.2. Real Experiments
7. Discussions
8. Conclusions
Acknowledgments
Conflicts of Interest
References
- Nelson, K.; Kurc, S.A.; John, G.; Minor, R.; Barron-Gafford, G.A. Influence of snow cover duration on soil evaporation and respiration efflux in mixed-conifer ecosystems. Ecohydrology 2013. [Google Scholar] [CrossRef]
- Barnett, T.P.; Dumenil, L.; Schlese, U.; Roechner, E.; Latif, M. The effects of Eurasian snow cover on regional and global climate variations. J. Atmos. Sci 1989, 46, 66–685. [Google Scholar]
- Boone, A.; Etchevers, P. An intercomparison of three snow schemes of varying complexity coupled to the same land-surface model: Local scale evaluation at an Alpine site. J. Hydrometeorol 2001, 2, 374–394. [Google Scholar]
- Decker, K.L.M.; Wang, D.; Waite, C.; Scherbatskoy, T. Snow removal and ambient air temperature effects on forest soil temperatures in northern Vermont. Soil Sci. Soc. Am. J 2003, 67, 1234–1242. [Google Scholar]
- Clark, M.P.; Slater, A.G.; Barrett, A.P.; Hay, L.E.; McCabe, G.J.; Rajagopalan, B.; Leavesley, G.H. Assimilation of snow covered area information into hydrologic and land-surface models. Adv. Water Resour 2006, 29, 1209–1221. [Google Scholar]
- Zaitchik, B.; Rodell, M. Forward-looking assimilation of MODIS-derived snow-covered area into a land surface model. J. Hydrometeorol 2009, 10, 130–148. [Google Scholar]
- Aksoy, A.; Aberson, S.D.; Vukicevic, T.; Sellwood, K.J.; Lorsolo, S.; Zhang, X. Assimilation of high-resolution tropical cyclone observations with an ensemble kalman filter using NOAA/AOML/HRD’s HEDAS: Evaluation of the 2008–11 vortex-scale analyses. Mon. Wea. Rev 2013, 141, 1842–1865. [Google Scholar]
- Pu, Z.; Zhang, H.; Anderson, J. Ensemble Kalman filter assimilation of near-surface observations over complex terrain: Comparison with 3DVAR for short-range forecasts. Dyn. Meteorol. Oceanogr. 2013, 65. art. no. 19620.. [Google Scholar]
- Sun, C.; Hao, Z.; Ghil, M.; Neelin, J.D. Data assimilation for a coupled ocean-atmosphere model. Part I: Sequential state estimation. Mon. Wea. Rev 2002, 130, 1073–1099. [Google Scholar]
- Reichle, R.H.; McLaughlin, D.B.; Entekhabi, D. Hydrologic data assimilation with the Ensemble Kalman Filter. Mon. Wea. Rev 2002, 130, 103–114. [Google Scholar]
- Crow, W.T.; Ryu, D. A new data assimilation approach for improving runoff prediction using remotely-sensed soil moisture retrievals. Hydrol. Earth Syst. Sci 2009, 13, 1–16. [Google Scholar]
- Salamon, P.; Feyen, L. Assessing parameter, precipitation, and predictive uncertainty in a distributed hydrological model using sequential data assimilation with the particle filter. J. Hydrol 2009, 376, 428–442. [Google Scholar]
- Thirel, G.; Martin, E.; Mahfouf, J.-F.; Massart, S.; Ricci, S.; Habets, F. A past discharges assimilation system for ensemble streamflow forecasts over France—Part 1: Description and validation of the assimilation system. Hydrol. Earth Syst. Sci 2010, 14, 1623–1637. [Google Scholar]
- Liu, Y.; Weerts, A.H.; Clark, M.; Franssen, H.-J.H.; Kumar, S.; Moradkhani, H.; Seo, D.-J.; Schwanenberg, D.; Smith, P.; van Dijk, A.I.J.M.; et al. Advancing data assimilation in operational hydrologic forecasting: progresses, challenges, and emerging opportunities. Hydrol. Earth Syst. Sci 2012, 16, 3863–3887. [Google Scholar]
- Rodell, M.; Houser, P.R. Updating a land surface model with MODIS-derived snow cover. J. Hydrometeorol 2004, 8, 1064–1075. [Google Scholar]
- Andreadis, K.M.; Lettenmaier, D.P. Assimilating remotely sensed snow observations into a macroscale hydrology model. Adv. Water Resour 2006, 29, 872–886. [Google Scholar]
- Su, H.; Yang, Z.-L.; Niu, G.-Y.; Dickinson, R.E. Enhancing the estimation of continental-scale snow water equivalent by assimilating MODIS snow cover with the ensemble Kalman filter. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Bavera, D.; de Michele, C. Snow water equivalent estimation in the Mallero basin using snow gauge data and MODIS images and fieldwork validation. Hydrol. Process 2009, 23, 1961–1972. [Google Scholar]
- Roy, A.; Royer, A.; Turcotte, R. Improvement of springtime streamflow simulations in a boreal environment by incorporating snow-covered area derived from remote sensing data. J. Hydrol 2010, 390, 35–44. [Google Scholar]
- Yatheendradas, S.; Peters-Lidard, C.D.; Koren, V.; Cosgrove, B.A.; De Goncalves, L.G.G.; Smith, M.; Geiger, J.; Cui, Z.; Borak, J.; Kumar, S.; et al. Distributed assimilation of satellite-based snow extent for improving simulated streamflow in mountainous, dense forests: An example over the DMIP2 western basins. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Liu, Y.; Peters-Lidard, C.D.; Kumar, S.; Foster, J.L.; Shaw, M.; Tian, Y.; Fall, G.M. Assimilating satellite-based snow depth and snow cover products for improving snow predictions in Alaska. Adv. Water Resour 2013, 54, 208–227. [Google Scholar]
- Pulliainen, J.; Hallikainen, M. Retrieval of regional snow water equivalent from space-borne passive microwave observations. Remote Sens. Environ 2001, 75, 76–85. [Google Scholar]
- Dong, J.; Walker, J.P.; Houser, P.R. Factors affecting remotely sensed snow water equivalent uncertainty. Remote Sens. Environ 2005, 97, 68–82. [Google Scholar]
- Parajka, J.; Blöschl, G. Validation of MODIS snow cover images over Austria. Hydrol. Earth Syst. Sci 2006, 10, 679–689. [Google Scholar]
- Gafurov, A.; Bàrdossy, A. Cloud removal methodology from MODIS snow cover product. Hydrol. Earth Syst. Sci 2009, 13, 1361–1373. [Google Scholar]
- Gao, Y.; Xie, H.; Lu, N.; Yao, T.; Liang, T. Toward advanced daily cloud-free snow cover and snow water equivalent products from Terra-Aqua MODIS and Aqua AMSR-E measurements. J. Hydrol 2010, 385, 23–35. [Google Scholar]
- Parajka, J.; Blöschl, G. Spatio-temporal combination of MODIS images—Potential for snow cover mapping. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Parajka, J.; Pepe, M.; Rampini, A.; Rossi, S.; Blöschl, G. A regional snow-line method for estimating snow cover from MODIS during cloud cover. J. Hydrol 2009, 381, 203–212. [Google Scholar]
- Slater, A.G.; Clark, M.P. Snow data assimilation via an Ensemble Kalman Filter. J. Hydrometeorol 2006, 7, 478–493. [Google Scholar]
- Clark, M.P.; Vrugt, J.A. Unraveling uncertainties in hydrologic model calibration: Addressing the problem of compensatory parameters. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol 1970, 10, 282–290. [Google Scholar]
- Lindström, G.; Johansson, B.; Persson, M.; Gardelin, M.; Bergström, S. Development and test of the distributed HBV-96 hydrological model. J. Hydrol 1997, 201, 272–288. [Google Scholar]
- Thielen, J.; Bartholmes, J.; Ramos, M.-H.; de Roo, A. The European Flood Alert System—Part 1: Concept and development. Hydrol. Earth Syst. Sci 2009, 13, 125–140. [Google Scholar]
- Doucet, A.; de Freitas, N.; Gordon, N. Sequential Monte Carlo Methods in Practice; Springer: New York, NY, USA, 2001. [Google Scholar]
- Simon, D. Optimal State Estimation: Kalman, H Infinity, and Nonlinear Approaches; Wiley-Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]
- Van Leeuwen, P.J. Particle filtering in geophysical systems. Mon. Wea. Rev 2009, 137, 4089–4114. [Google Scholar]
- Arulampalam, M.S.; Markell, S.; Gordon, N.; Clapp, T. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking. IEEE Trans. Signal Process 2002, 50, 174–188. [Google Scholar]
- Chin, T.M.; Turmon, M.J.; Jewell, J.B.; Ghil, M. An ensemble-based smoother with retrospectively updated weights for highly nonlinear systems. Mon. Wea. Rev 2007, 135, 186–202. [Google Scholar]
- Baker, J.E. Reducing Bias and Inefficiency in the Selection Algorithm. Proceedings of the Second International Conference on Genetic Algorithms and their Application; Lawrence Erlbaum Associates: Hillsdale, NJ, USA, 1987; pp. 14–21. [Google Scholar]
- Moradkhani, H.; Hsu, K.-L.; Gupta, H.; Sorooshian, S. Uncertainty assessment of hydrologic model states and parameters. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- Hall, D.K.; Riggs, G.A.; Salomonson, V.V. MODIS/Aqua Snow Cover Daily L3 Global 500m Grid V005; July 2003 to December 2006; National Snow and Ice Data Center: Boulder, CO, USA, 2006. [Google Scholar]
- Hall, D.K.; Riggs, G.A.; Salomonson, V.V. MODIS/Terra Snow Cover Daily L3 Global 500m Grid V005; July 2003 to December 2006; National Snow and Ice Data Center: Boulder, CO, USA, 2006. [Google Scholar]
- Sirguey, P.; Mathieu, R.; Arnaud, Y. Subpixel monitoring of the seasonal snow cover with MODIS at 250 m spatial resolution in the Southern Alps of New Zealand: Methodology and accuracy assessment. Remote Sens. Environ 2009, 113, 160–181. [Google Scholar]
- Painter, T.H.; Rittger, K.; McKenzie, C.; Slaughter, P.; Davis, R.E.; Dozier, J. Retrieval of subpixel snow-covered area, grain size, and albedo from MODIS. Remote Sens. Environ 2009, 113, 868–879. [Google Scholar]
- Niu, G.-Y.; Yang, Z.-L. An observation-based formulation of snow cover fraction and its evaluation over large North American river basins. J. Geophys. Res. 2007, 112. [Google Scholar] [CrossRef]
- Koren, V.; Schaake, J.; Mitchell, K.; Duan, Q.Y.; Chen, F.; Baker, J.M. A parameterization of snowpack and frozen ground intended for NCEP weather and climate models. J. Geophys. Res 1999, 104, 19569–19585. [Google Scholar]
- De Roo, A. LISFLOOD: A Rainfall-runoff Model for Large River Basins to Assess the Influence of Land Use Changes on Flood Risk. In Ribamod: river basin modelling, management and flood mitigation; Balabanis, P., Ed.; European Commission: Wallingford, UK, 1999; pp. 349–357. [Google Scholar]
- Van der Knijff, J.; Younis, J.; de Roo, A. LISFLOOD—A GIS-based distributed model for river basin scale water balance and flood simulation. Int. J. Geogr. Inf. Sci 2010, 24, 189–212. [Google Scholar]
- Karssenberg, D. The value of environmental modelling languages for building distributed hydrological models. Hydrol. Process 2002, 16, 2751–2766. [Google Scholar]
- Wösten, J.H.M.; Lilly, A.; Nemes, A.; Le Bas, C. Development and use of a database of hydraulic properties of European soils. Geoderma 1999, 90, 169–185. [Google Scholar]
- European Environment Agency. The European Topic Centre on Terrestrial Environment: Corine Land Cover raster database 2000–100m; European Environment Agency: Copenhagen, Denmark, 2000. [Google Scholar]
- King, D.; Daroussin, J.; Tavernier, R. Development of a soil geographical database from the soil map of the European communities. Catena 2004, 21, 37–56. [Google Scholar]
- Rijks, D.; Teres, J.M.; Vossen, P. Agrometeorological Applications for Regional Crop Monitoring and Production Assessment; Tech. Rep. EUR 17735 EN; Eur. Comm. Joint Res. Cent.: Ispra, Italy, 1998. [Google Scholar]
- Zhao, R.J.; Liu, X.R. The Xinanjiang Model. In Computer Models of Watershed Hydrology; Singh, V.P., Ed.; Water Resources Publications: Colorado, CO, USA, 1995; pp. 215–232. [Google Scholar]
- Todini, E. The ARNO rainfall-runoff. J. Hydrol 1996, 175, 339–382. [Google Scholar]
- Chow, V.T.; Maidment, D.R.; Mays, L.M. Applied Hydrology; McGraw-Hill: Singapore, 1988; p. 572. [Google Scholar]
- Viviroli, D.; Zappa, M.; Gurtz, J.; Weingartner, R. An introduction to the hydrological modelling system PREVAH and its pre- and post-processing tools. Environ. Model. Softw 2009, 24, 1209–1222. [Google Scholar]
- Finger, D.; Pellicciotti, F.; Konz, M.; Rimkus, S.; Burlando, P. The value of glacier mass balance, satellite snow cover images, and hourly discharge for improving the performance of a physically based distributed hydrological model. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Speers, D.D.; Versteeg, J.D. Runoff Forecasting for Reservoir Operations—The Past and the Future. In Proceedings of the 52nd Western Snow Conference; Western Snow Conference: Fort Collins, CO, USA, 1982; pp. 149–156. [Google Scholar]
- Anderson, E. Snow Accumulation and Ablation Model—SNOW-17; Technical Report; NWSRFS: Silver Spring, MD, USA, 2006; p. 61. [Google Scholar]
- Burek, P.; de Roo, A. LISFLOOD—Distributed Water Balance and Flood Simulation Model; User Manual Version December 2010; European Commission: Ispra, Italy, 2011. [Google Scholar]
- Quintana Seguí, P.; Le Moigne, P.; Durand, Y.; Martin, E.; Habets, F.; Baillon, M.; Canellas, C.; Franchisteguy, L.; Morel, S. Analysis of near surface atmospheric variables: Validation of the SAFRAN analysis over France. J. Appl. Meteorol. Climatol 2008, 47, 92–107. [Google Scholar]
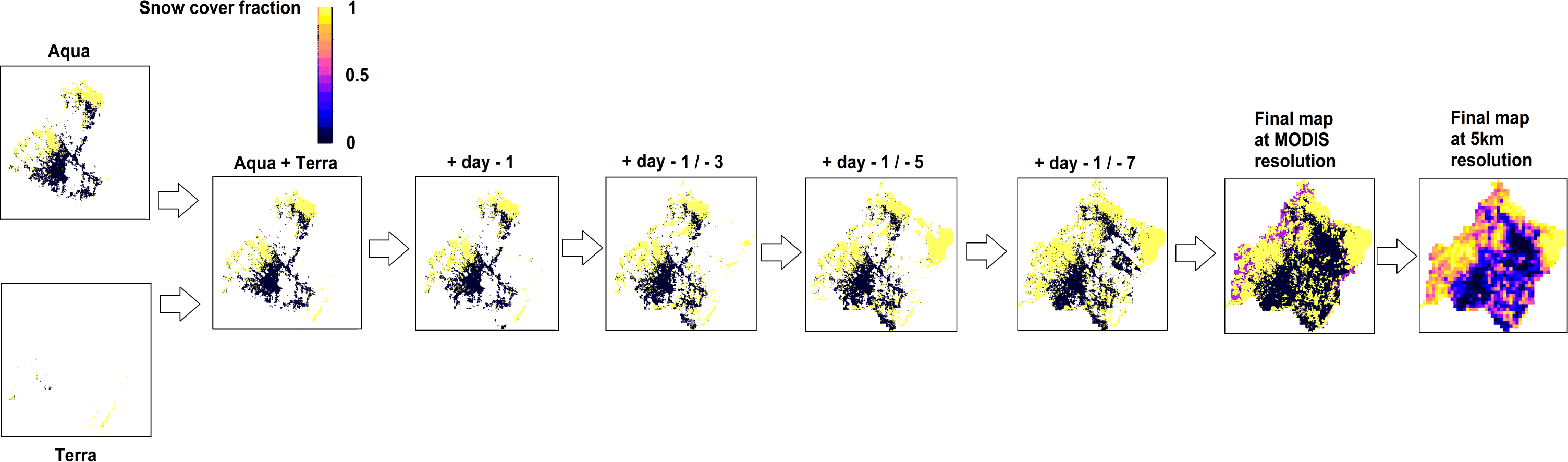



| MODIS Classification | Used Classification | ||
|---|---|---|---|
| Value | Data | Value | Data |
| 0 | Missing | ||
| 1 | No decision | ||
| 11 | Night | Missing value | “we don’t know” |
| 50 | Cloud obscured | ||
| 254 | Detector saturated | ||
| 255 | Fill | ||
| 25 | Snow-free land | 0 | No snow |
| 37 | Lake or inland water | ||
| 39 | Open water (ocean) | ||
| 100 | Snow-covered lake ice | 1 | Snow |
| 200 | Snow | ||
| Aqua+Terra | +Day-1 | +Days-2/-3 | +Days-4/-5 | +Days-6/-7 |
|---|---|---|---|---|
| 48.6 | 33.2 | 16.8 | 9.0 | 4.9 |
| Area | Method | Observations | Obs. Error Range | Frequency | |
|---|---|---|---|---|---|
| Section 5.1 | Upstr. Kromericz | Synthetic | |||
| Section 5.2 | Particle filter | MODIS | From 5% to 40% | 1,2,3,7 days | |
| Section 6.1 | Morava basin | Synthetic | |||
| Section 6.2 | MODIS |
© 2013 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Thirel, G.; Salamon, P.; Burek, P.; Kalas, M. Assimilation of MODIS Snow Cover Area Data in a Distributed Hydrological Model Using the Particle Filter. Remote Sens. 2013, 5, 5825-5850. https://doi.org/10.3390/rs5115825
Thirel G, Salamon P, Burek P, Kalas M. Assimilation of MODIS Snow Cover Area Data in a Distributed Hydrological Model Using the Particle Filter. Remote Sensing. 2013; 5(11):5825-5850. https://doi.org/10.3390/rs5115825
Chicago/Turabian StyleThirel, Guillaume, Peter Salamon, Peter Burek, and Milan Kalas. 2013. "Assimilation of MODIS Snow Cover Area Data in a Distributed Hydrological Model Using the Particle Filter" Remote Sensing 5, no. 11: 5825-5850. https://doi.org/10.3390/rs5115825
APA StyleThirel, G., Salamon, P., Burek, P., & Kalas, M. (2013). Assimilation of MODIS Snow Cover Area Data in a Distributed Hydrological Model Using the Particle Filter. Remote Sensing, 5(11), 5825-5850. https://doi.org/10.3390/rs5115825




