Derivation of Daily Evaporative Fraction Based on Temporal Variations in Surface Temperature, Air Temperature, and Net Radiation
Abstract
:1. Introduction
2. Method
2.1. Background of Theory
2.1.1. Radiometric Heat Conductance Prad
2.1.2. Diurnal Cycle of EF
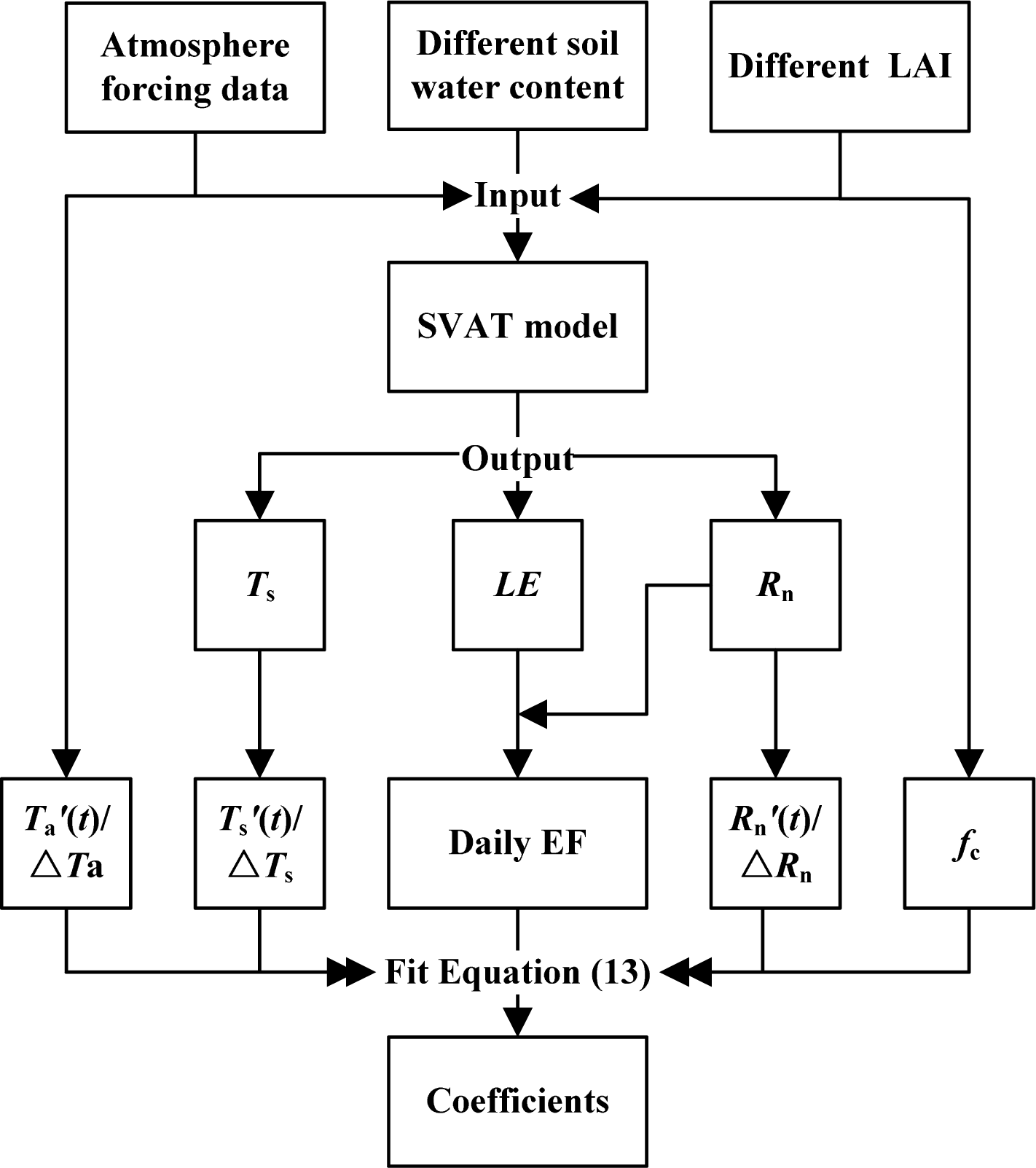
2.2. Parameterization for EF Based on SVAT Modeling
3. Data
3.1. In situ Measurements
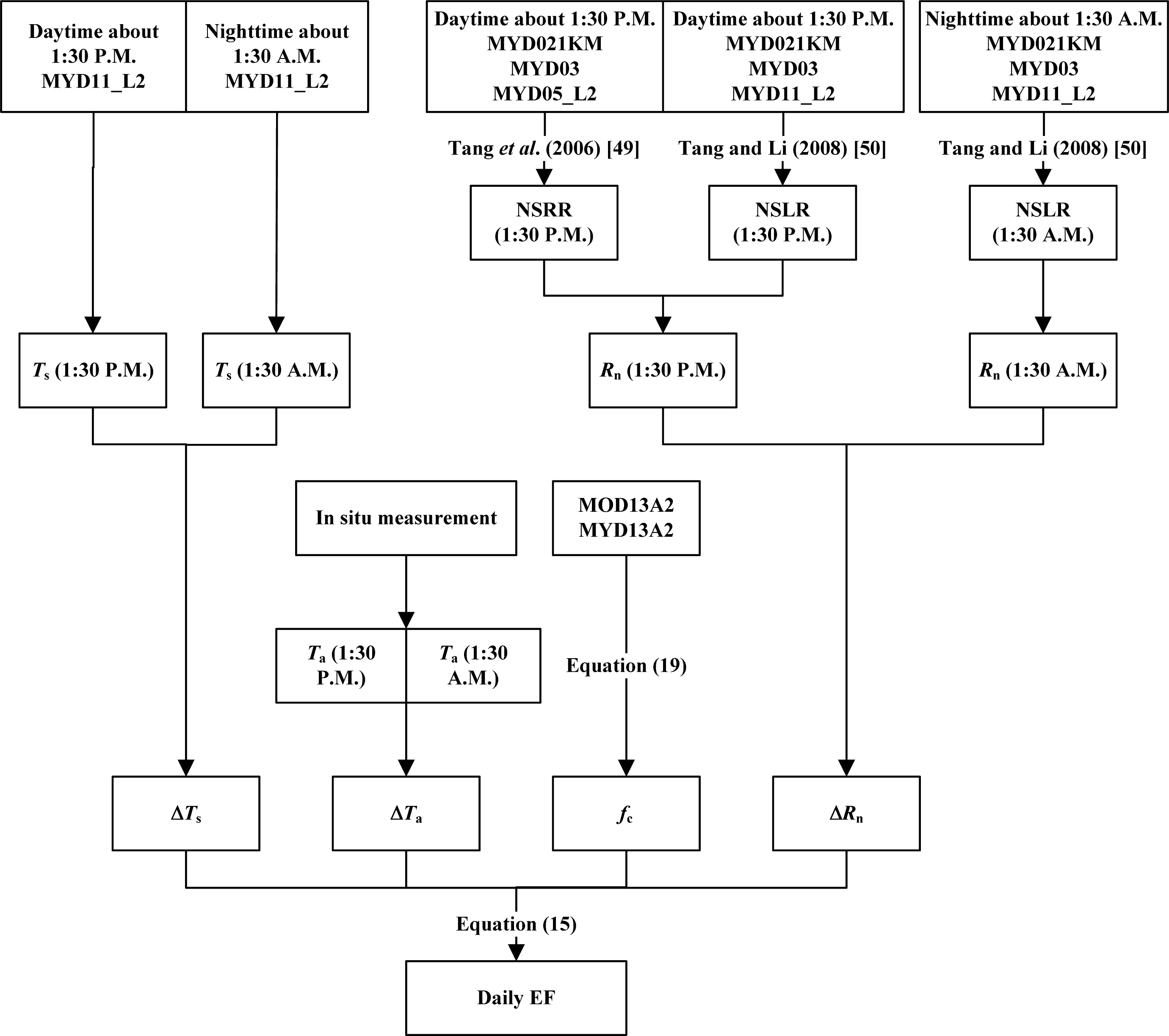
3.2. Remotely Sensed Data
4. Results and Discussions
4.1. Daily EF Estimates with In situ Measurements as Inputs
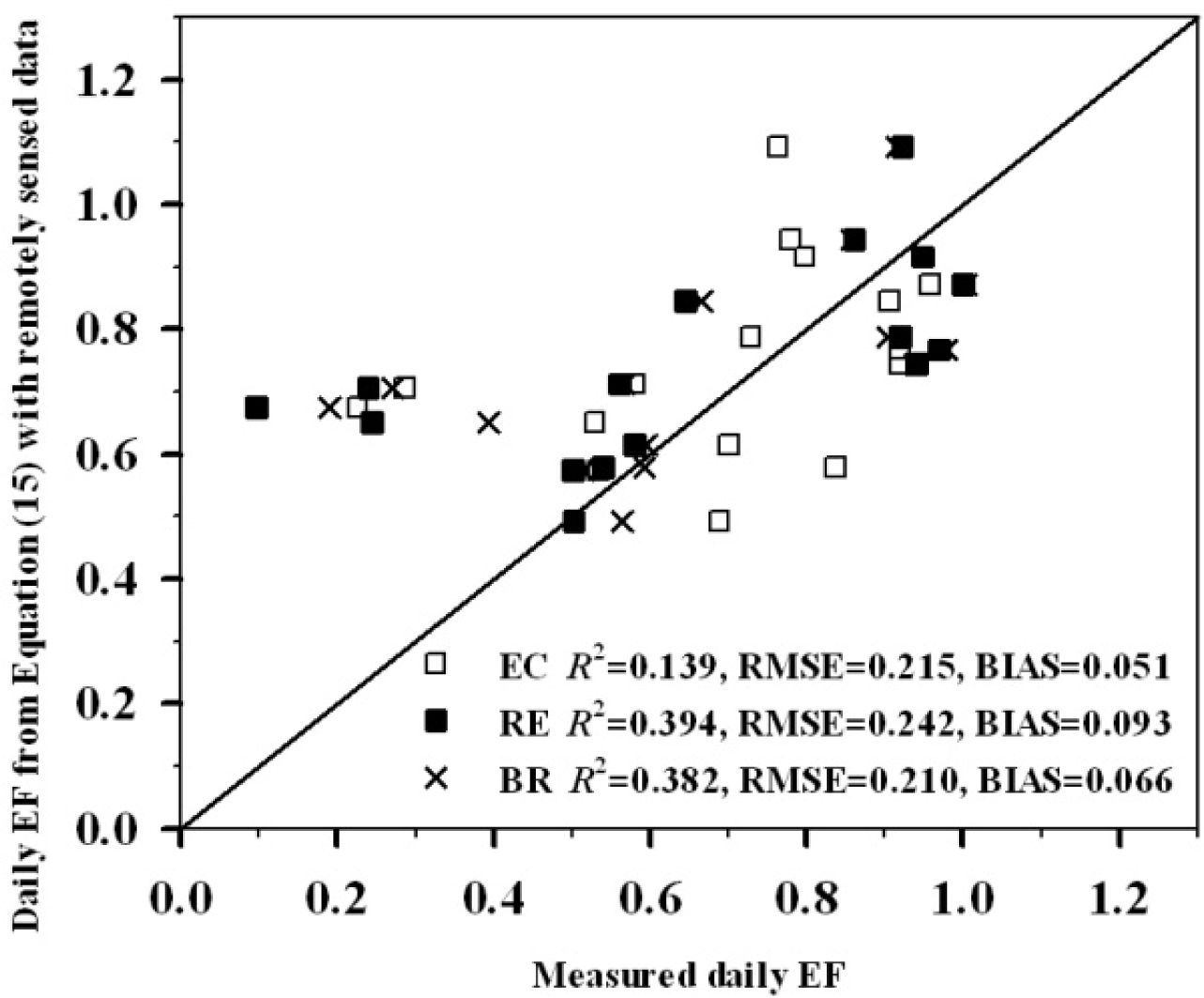
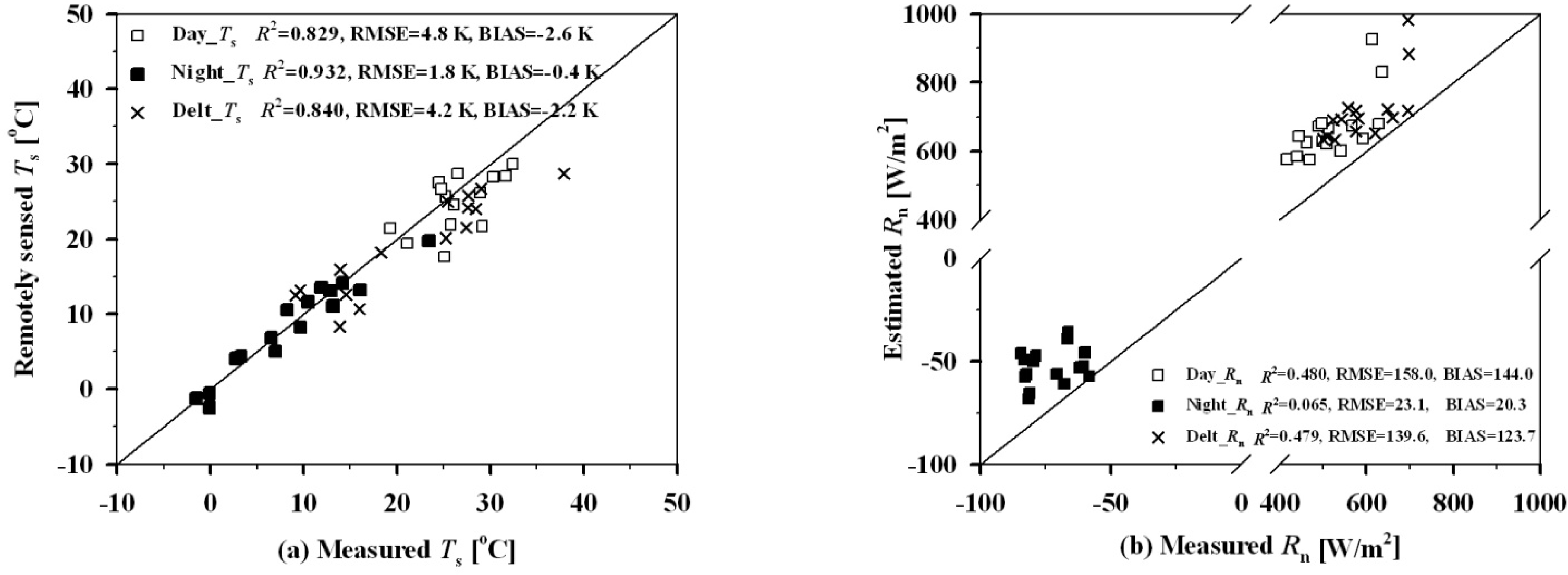
4.2. Application to Satellite Data
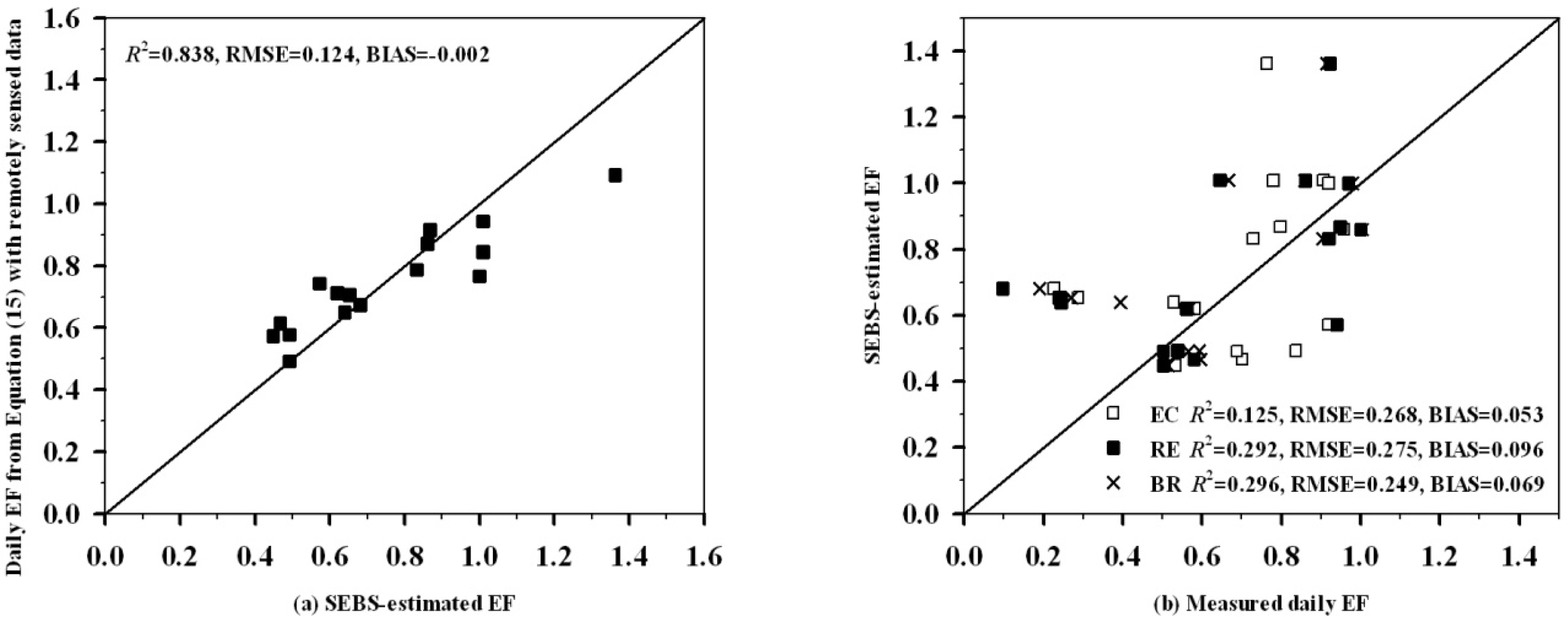
4.3. Comparison with SEBS-Estimated EF
5. Conclusion
Acknowledgments
Conflict of Interest
References
- Vinukollu, R.K.V.R.K.; Wood, E.F.; Ferguson, C.R.; Fisher, J.B. Global estimates of evapotranspiration for climate studies using multi-sensor remote sensing data: Evaluation of three process-based approaches. Remote Sens. Environ 2011, 115, 801–823. [Google Scholar]
- Anderson, M.C.; Allen, R.G.; Morse, A.; Kustas, W.P. Use of Landsat thermal imagery in monitoring evapotranspiration and managing water resources. Remote Sens. Environ 2012, 122, 50–65. [Google Scholar]
- Tang, R.L.; Li, Z.-L.; Jia, Y.; Li, C.; Sun, X.; Kustas, W.P.; Anderson, M.C. An intercomparison of three remote sensing-based energy balance models using Large Aperture Scintillometer measurements over a wheat-corn production region. Remote Sens. Environ 2011, 115, 3187–3202. [Google Scholar]
- Teixeira, A.H. de C.; Bastiaanssen, W.G.M.; Ahmad, M.D.; Bos, M.G. Determining regional actual evapotranspiration of irrigated crops and natural vegetation in the São Francisco River Basin (Brazil) using remote sensing and penman-monteith equation. Remote Sens 2010, 2, 1287–1319. [Google Scholar]
- Ruhoff, A.L.; Paz, A.R.; Collischonn, W.; Aragao, L.E.O.C.; Rocha, H.R.; Malhi, Y.S. A MODIS-based energy balance to estimate evapotranspiration for clear-sky days in Brazilian Tropical Savannas. Remote Sens 2012, 4, 703–725. [Google Scholar]
- Johnson, L.F.; Trout, T.J. Satellite NDVI assisted monitoring of vegetable crop evapotranspiration in California’s San Joaquin Valley. Remote Sens 2012, 4, 439–455. [Google Scholar]
- Long, D.; Singh, V.P. A two-source trapezoid model for evapotranspiration (TTME) from satellite imagery. Remote Sens. Environ 2012, 121, 370–388. [Google Scholar]
- Bastiaanssen, W.; Menenti, M.; Feddes, R.; Holtslag, A. A remote sensing surface energy balance algorithm for land (SEBAL). 1. Formulation. J. Hydrol 1998, 212, 198–212. [Google Scholar]
- Su, Z. The surface energy balance system (SEBS) for estimation of turbulent heat fluxes. Hydrol. Earth Syst. Sci 2002, 6, 85–99. [Google Scholar]
- Norman, J.M.; Kustas, W.P.; Humes, K.S. Source approach for estimating soil and vegetation energy fluxes in observations of directional radiometric surface-temperature. Agric. For. Meteorol 1995, 77, 263–293. [Google Scholar]
- Li, Z.-L.; Tang, B.H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ 2013, 131, 14–37. [Google Scholar]
- Wu, H.; Li, Z.-L. Scale issues in remote sensing: A review on analysis, processing and modeling. Sensors 2009, 9, 1768–1793. [Google Scholar]
- Li, Z.-L.; Wu, H.; Wang, N.; Qiu, S.; Sobrino, J.A.; Wan, Z.; Tang, B.H.; Yan, G. Land surface emissivity retrieval from satellite data. Int. J. Remote Sens 2013, 34, 3084–3127. [Google Scholar]
- Li, Z.-L.; Tang, R.L.; Wan, Z.; Bi, Y.; Zhou, C.; Tang, B.H.; Yan, G.; Zhang, X. A review of current methodologies for regional evapotranspiration estimation from remotely sensed data. Sensors 2009, 9, 3801–3853. [Google Scholar]
- Kalma, J.D.; McVicar, T.R.; McCabe, M.F. Estimating land surface evaporation: A review of methods using remotely sensed surface temperature data. Surv. Geophys 2008, 29, 421–469. [Google Scholar]
- Wang, K.C.; Dickinson, R.E. A review of global terrestrial evapotranspiration: Observation, modeling, climatology, and climatic variability. Rev. Geophys. 2012. [Google Scholar] [CrossRef]
- Crago, R.D. Conservation and variability of the evaporative fraction during the daytime. J. Hydrol 1996, 180, 173–194. [Google Scholar]
- Lhomme, J.P.; Elguero, E. Examination of evaporative fraction diurnal behaviour using a soil-vegetation model coupled with a mixed-layer model. Hydrol. Earth Syst. Sci 1999, 3, 259–270. [Google Scholar]
- Gentine, P.; Entekhabi, D.; Polcher, J. The diurnal behavior of evaporative fraction in the soil-vegetation-atmospheric boundary layer continuum. J. Hydrometeorol 2011, 12, 1530–1546. [Google Scholar]
- Lu, J.; Li, Z.-L.; Tang, R.L.; Tang, B.H.; Wu, H.; Yang, F.; Labed, J.; Zhou, G. Evaluating the SEBS-estimated evaporative fraction from MODIS data for a complex underlying surface. Hydrol. Process. 2012. [Google Scholar] [CrossRef]
- Nichols, W.E.; Cuenca, R.H. Evaluation of the evaporative fraction for parameterization of the surface energy balance. Water Resour. Res 1993, 29, 3681–3690. [Google Scholar]
- Colaizzi, P.; Evett, S.; Howell, T.; Tolk, J. Comparison of five models to scale daily evapotranspiration from one-time-of-day measurements. Trans. ASAE 2006, 49, 1409–1417. [Google Scholar]
- Sugita, M.; Brutsaert, W. Daily evaporation over a region from lower boundary layer profiles measured with radiosondes. Water Resour. Res 1991, 27, 747–752. [Google Scholar]
- Tang, R.L.; Li, Z.-L.; Sun, X. Temporal upscaling of instantaneous evapotranspiration: An intercomparison of fourmethods using eddy covariance measurements and MODIS data. Remote Sens. Environ. 2013. [Google Scholar] [CrossRef]
- Cammalleri, C.; Anderson, M.; Kustas, W. Upscaling of evapotranspiration fluxes from instantaneous to daytime scales for thermal remote sensing applications. Hydrol. Earth Syst. Sci 2013, 10, 7325–7350. [Google Scholar]
- Jiang, L.; Islam, S. A methodology for estimation of surface evapotranspiration over large areas using remote sensing observations. Geophys. Res. Lett 1999, 26, 2773–2776. [Google Scholar]
- Roerink, G.; Su, Z.; Menenti, M. S-SEBI: A simple remote sensing algorithm to estimate the surface energy balance. Phys. Chem. Earth Part. B Hydrol. Oceans Atmos 2000, 25, 147–157. [Google Scholar]
- Tang, R.L; Li, Z.-L.; Tang, B.H. An application of the Ts-VI triangle method with enhanced edges determination for evapotranspiration estimation from MODIS data in arid and semi-arid regions: Implementation and validation. Remote Sens. Environ 2010, 114, 540–551. [Google Scholar]
- Anderson, M.C.; Norman, J.M.; Diak, G.R.; Kustas, W.P.; Mecikalski, J.R. A two-source time-integrated model for estimating surface fluxes using thermal infrared remote sensing. Remote Sens. Environ 1997, 60, 195–216. [Google Scholar]
- Norman, J.M.; Kustas, W.P.; Prueger, J.H.; Diak, G.R. Surface flux estimation using radiometric temperature: A dual temperature-difference method to minimize measurement errors. Water Resour. Res 2000, 36, 2263–2274. [Google Scholar]
- Wang, K.C.; Li, Z.Q.; Cribb, M. Estimation of evaporative fraction from a combination of day and night land surface temperatures and NDVI: A new method to determine the Priestley-Taylor parameter. Remote Sens. Environ 2006, 102, 293–305. [Google Scholar]
- Stisen, S.; Sandholt, I.; Norgaard, A.; Fensholt, R.; Jensen, K.H. Combining the triangle method with thermal inertia to estimate regional evapotranspiration—Applied to MSG-SEVIRI data in the Senegal River basin. Remote Sens. Environ 2008, 112, 1242–1255. [Google Scholar]
- Shu, Y.Q.; Stisen, S.; Jensen, K.H.; Sandholt, I. Estimation of regional evapotranspiration over the North China Plain using geostationary satellite data. Int. J. Appl. Earth Obs 2011, 13, 192–206. [Google Scholar]
- Long, D.; Singh, V.P.; Scanlon, B.R. Deriving theoretical boundaries to address scale dependencies of triangle models for evapotranspiration estimation. J. Geophys. Res 2012, 117, D05113. [Google Scholar]
- Long, D.; Singh, V.P. Assessing the impact of end-member selection on the accuracy of satellite-based spatial variability models for actual evapotranspiration estimation. Water Resour. Res 2013, 49, 2601–2618. [Google Scholar]
- Anderson, M.C.; Norman, J.M.; Meyers, T.P.; Diak, G.R. An analytical model for estimating canopy transpiration and carbon assimilation fluxes based on canopy light-use efficiency. Agric. For. Meteorol 2000, 101, 265–289. [Google Scholar]
- Brutsaert, W. Evaporation into the Atmosphere: Theory, History, and Applications; D. Reidel: Dordrecht, The Netherlands, 1982. [Google Scholar]
- Kalma, J.; Jupp, D. Estimating evaporation from pasture using infrared thermometry: Evaluation of a one-layer resistance model. Agric. For. Meteorol 1990, 51, 223–246. [Google Scholar]
- Chehbouni, A.; Lo Seen, D.; Njoku, E.; Monteny, B. Examination of the difference between radiative and aerodynamic surface temperatures over sparsely vegetated surfaces. Remote Sens. Environ 1996, 58, 177–186. [Google Scholar]
- Lhomme, J.; Chehbouni, A.; Monteny, B. Sensible heat flux-radiometric surface temperature relationship over sparse vegetation: Parameterizing B-1. Bound.-Lay. Meteorol 2000, 97, 431–457. [Google Scholar]
- Sun, J.; Mahrt, L. Determination of surface fluxes from the surface radiative temperature. J. Atmos. Sci 1995, 52, 1096–1106. [Google Scholar]
- Carlson, T.N.; Buffum, M.J. On estimating total daily evapotranspiration from remote surface temperature measurements. Remote Sens. Environ 1989, 29, 197–207. [Google Scholar]
- Lagouarde, J.-P.; McAneney, K. Daily sensible heat flux estimation from a single measurement of surface temperature and maximum air temperature. Bound.-Lay. Meteorol 1992, 59, 341–362. [Google Scholar]
- Carlson, T.N.; Capehart, W.J.; Gillies, R.R. A new look at the simplified method for remote sensing of daily evapotranspiration. Remote Sens. Environ 1995, 54, 161–167. [Google Scholar]
- Brutsaert, W.; Sugita, M. Application of self-preservation in the diurnal evolution of the surface energy budget to determine daily evaporation. J. Geophys. Res 1992, 97, 18377–18382. [Google Scholar]
- Daughtry, C.; Kustas, W.; Moran, M.; Pinter, P.; Jackson, R.; Brown, P.; Nichols, W.; Gay, L. Spectral estimates of net radiation and soil heat flux. Remote Sens. Environ 1990, 32, 111–124. [Google Scholar]
- Choudhury, B.J.; Idso, S.B.; Reginato, R.J. Analysis of an empirical model for soil heat flux under a growing wheat crop for estimating evaporation by an infrared-temperature based energy balance equation. Agric. For. Meteorol 1987, 39, 283–297. [Google Scholar]
- Van de Griend, A.A.; Camillo, P.J.; Gurney, R.J. Discrimination of soil physical parameters, thermal inertia, and soil moisture from diurnal surface temperature fluctuations. Water Resour. Res 1985, 21, 997–1009. [Google Scholar]
- Tang, B.H.; Li, Z.-L.; Zhang, R. A direct method for estimating net surface shortwave radiation from MODIS data. Remote Sens. Environ 2006, 103, 115–126. [Google Scholar]
- Tang, B.H.; Li, Z.-L. Estimation of instantaneous net surface longwave radiation from MODIS cloud-free data. Remote Sens. Environ 2008, 112, 3482–3492. [Google Scholar]
- Carlson, T.N.; Ripley, D.A. On the relation between NDVI, fractional vegetation cover, and leaf area index. Remote Sens. Environ 1997, 62, 241–252. [Google Scholar]
- Prihodko, L.; Goward, S.N. Estimation of air temperature from remotely sensed surface observations. Remote Sens. Environ 1997, 60, 335–346. [Google Scholar]
- Twine, T.; Kustas, W.; Norman, J.; Cook, D.; Houser, P.; Meyers, T.; Prueger, J.; Starks, P.; Wesely, M. Correcting eddy-covariance flux underestimates over a grassland. Agric. For. Meteorol 2000, 103, 279–300. [Google Scholar]
- McCabe, M.F.; Wood, E.F. Scale influences on the remote estimation of evapotranspiration using multiple satellite sensors. Remote Sens. Environ 2006, 105, 271–285. [Google Scholar]
- Wan, Z.; Dozier, J. A generalized split-window algorithm for retrieving land-surface temperature from space. IEEE T. Geosci. Remot 1996, 34, 892–905. [Google Scholar]
- Campbell, G.S.; Norman, J.M. Introduction to Environmental Biophysics; Springer Verlag: New York, NY, USA, 1998. [Google Scholar]
Appendix

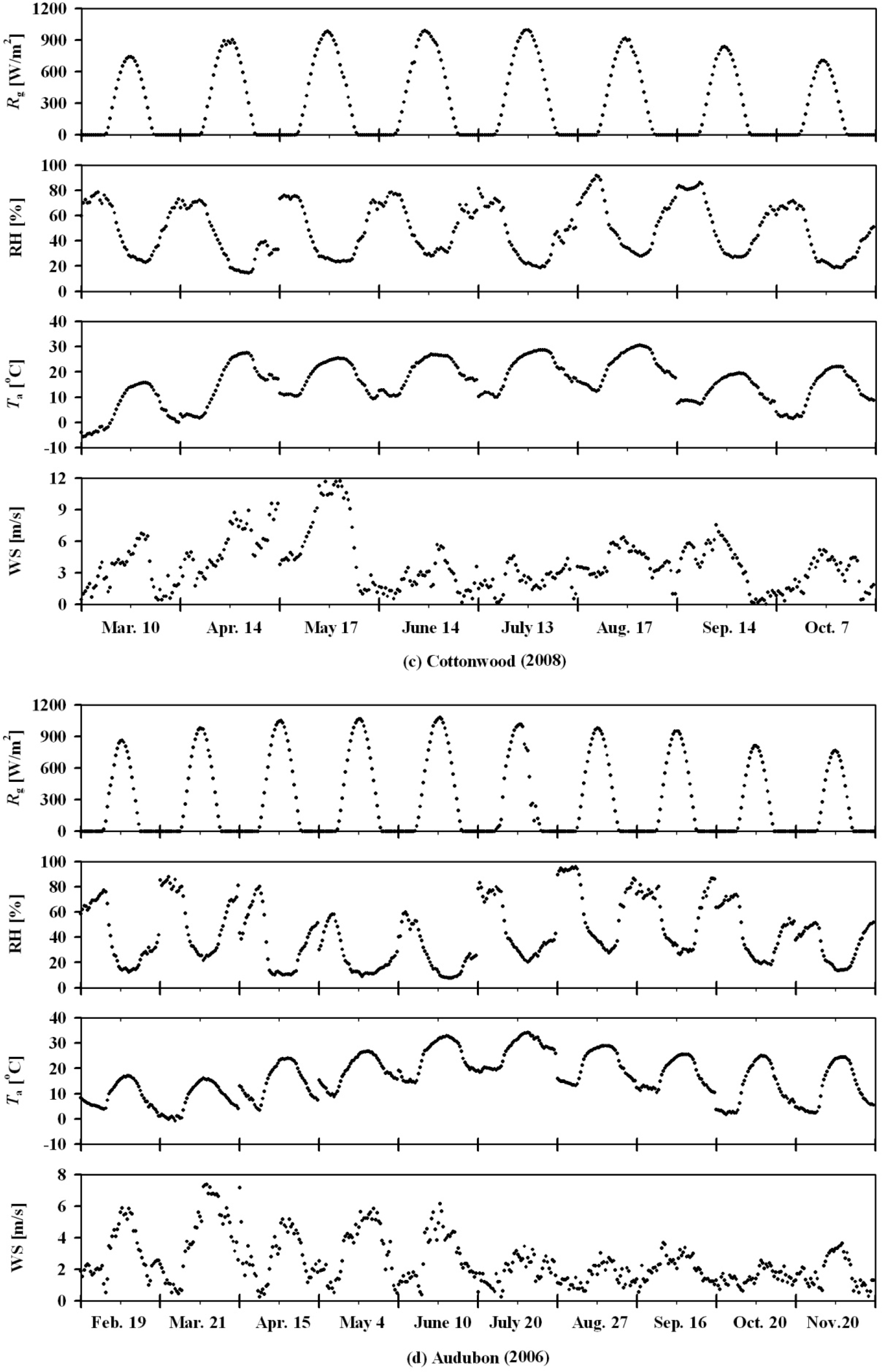
| (a) | ||||
|---|---|---|---|---|
| Quantities | Units | Values | ||
| Site | Yucheng | |||
| Longitude | 116.5703 | |||
| Latitude | 36.8291 | |||
| Year | 2010 | |||
| Date | 26 Mar, 24 Apr, 29 May, 28 June, 21 July | 17 Aug, 11 Sep, 4 Oct. | ||
| Measure height | m | 2.93 | 4.2 | |
| Vegetation type | C3 grass | corn | ||
| Vegetation height | m | 0–0.6 | 0–2.4 | |
| Leaf area index | m2/m2 | 0–10 | ||
| Rooting depth | m | 0.5 | ||
| Soil texture | loam | |||
| sand | 0.42 | |||
| silt | 0.4 | |||
| clay | 0.18 | |||
| Bulk density | g/cm3 | 1.5 | ||
| Moisture release parameter | 4.5 | |||
| Air entry potential | J/kg | −1.1 | ||
| Saturated hydraulic conductivity | K·g·s/m3 | 3.7 × 10−4 | ||
| soil water content (0–2 m) | m3/m3 | 0.09–0.21, 0.43 | ||
| (b) | ||||
|---|---|---|---|---|
| Quantities | Units | Values | ||
| Site | Goodwin | Cottonwood | Audubon | |
| Longitude | −89.7735 | −101.8466 | −110.5092 | |
| Latitude | 34.2547 | 43.95 | 31.5907 | |
| Year | 2006 | 2008 | 2006 | |
| Date | 9 Feb, 14 Mar, 12 Apr, 12 May, 15 June, 17 July, 17 Aug, 13 Sep, 7 Oct | 10 Mar, 14 Apr, 17 May, 14 June, 13 July, 17 Aug, 14 Sep, 7 Oct | 19 Feb, 21 Mar, 15 Apr, 4 May, 10 June, 20 July, 27 Aug, 16 Sep, 20 Oct, 2 Nov | |
| Measure height | m | 4 | 5 | 4 |
| Vegetation type | C3 grass | soybean | desert C3-type shrubs | |
| Vegetation height | m | 0–1 | 0–1 | 0–0.6 |
| Leaf area index | m2/m2 | 0–10 | 0–10 | 0–10 |
| Rooting depth | m | 1 | 2 | 0.5 |
| Soil texture | clay loam | clay loam | silt loam | |
| sand | 0.32 | 0.32 | 0.2 | |
| silt | 0.34 | 0.34 | 0.65 | |
| clay | 0.34 | 0.34 | 0.15 | |
| Bulk density | g/cm3 | 1.5 | 1.5 | 1.5 |
| Moisture release parameter | 5.2 | 5.2 | 4.7 | |
| Air entry potential | J/kg | −2.6 | −2.6 | −2.1 |
| Saturated hydraulic conductivity | K·g·s/m3 | 6.4 × 10−4 | 6.4 × 10−4 | 1.9 × 10−4 |
| soil water content (0–2 m) | m3/m3 | 0.13–0.25, 0.43 | 0.13–0.25, 0.43 | 0.11–0.23, 0.43 |
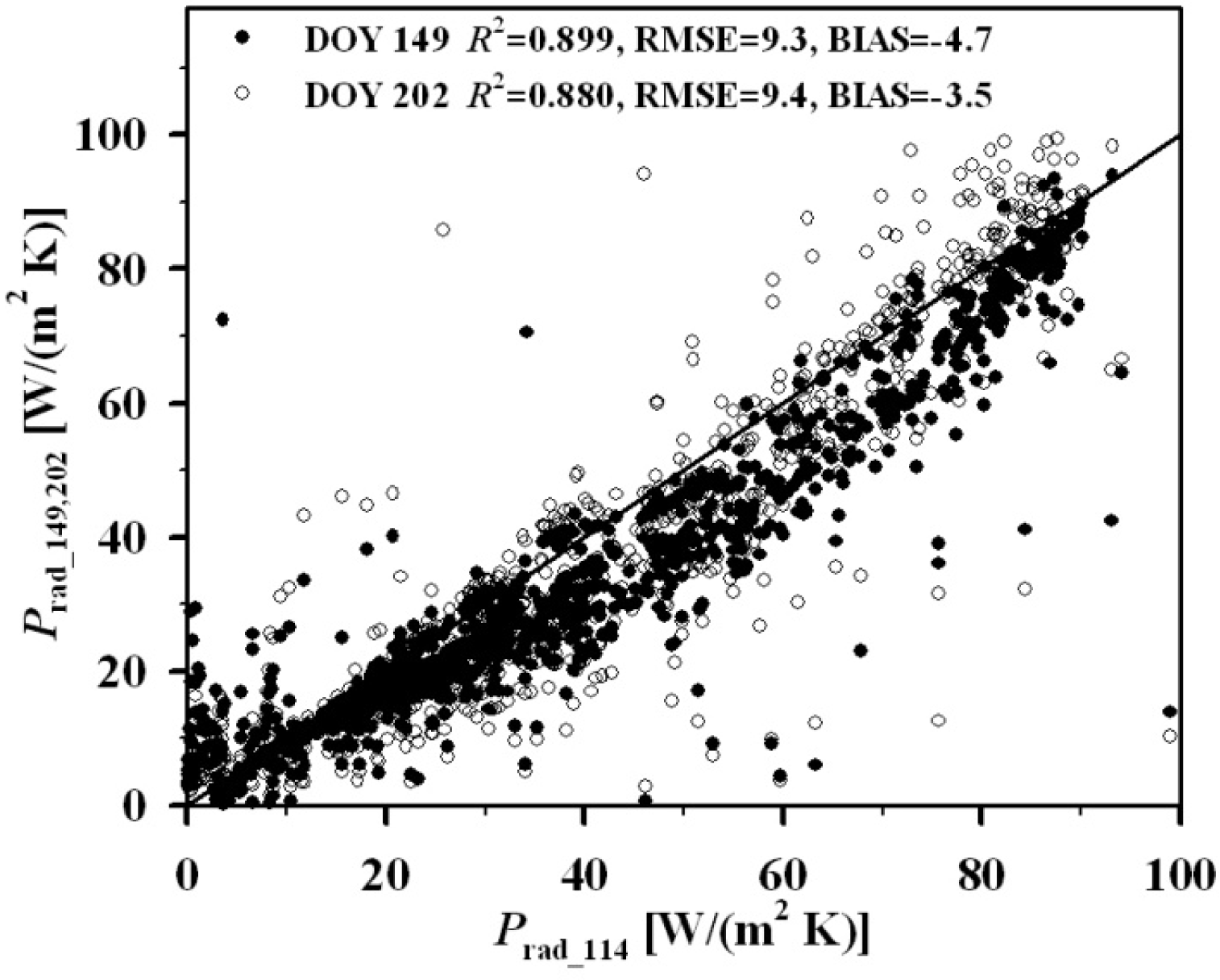
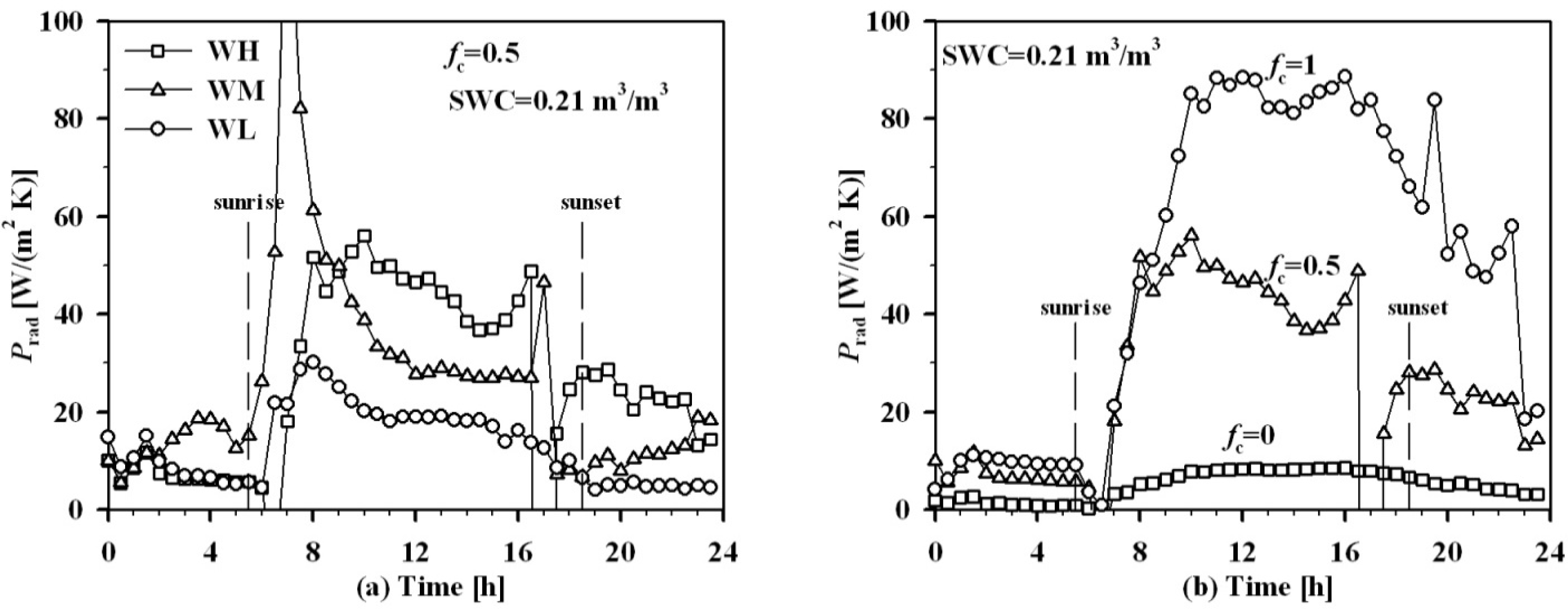
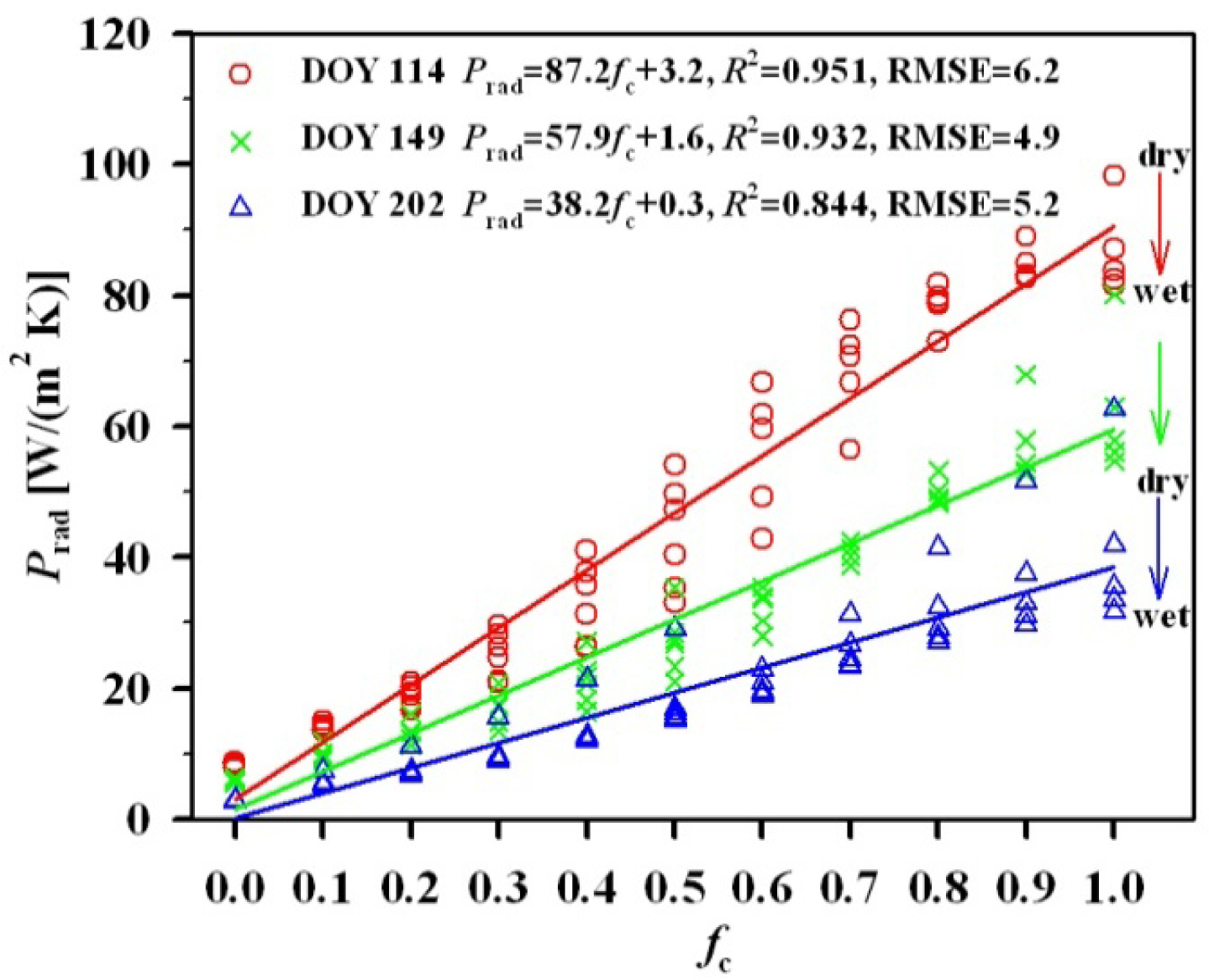
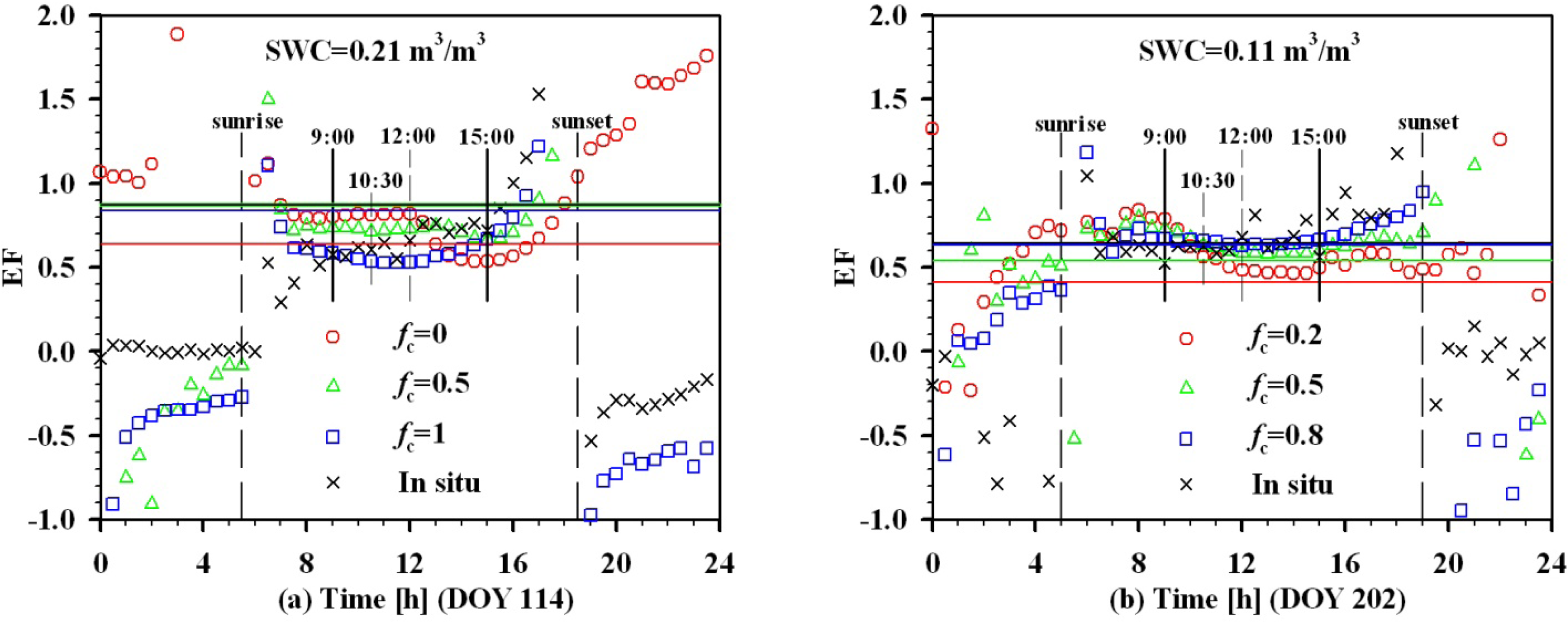
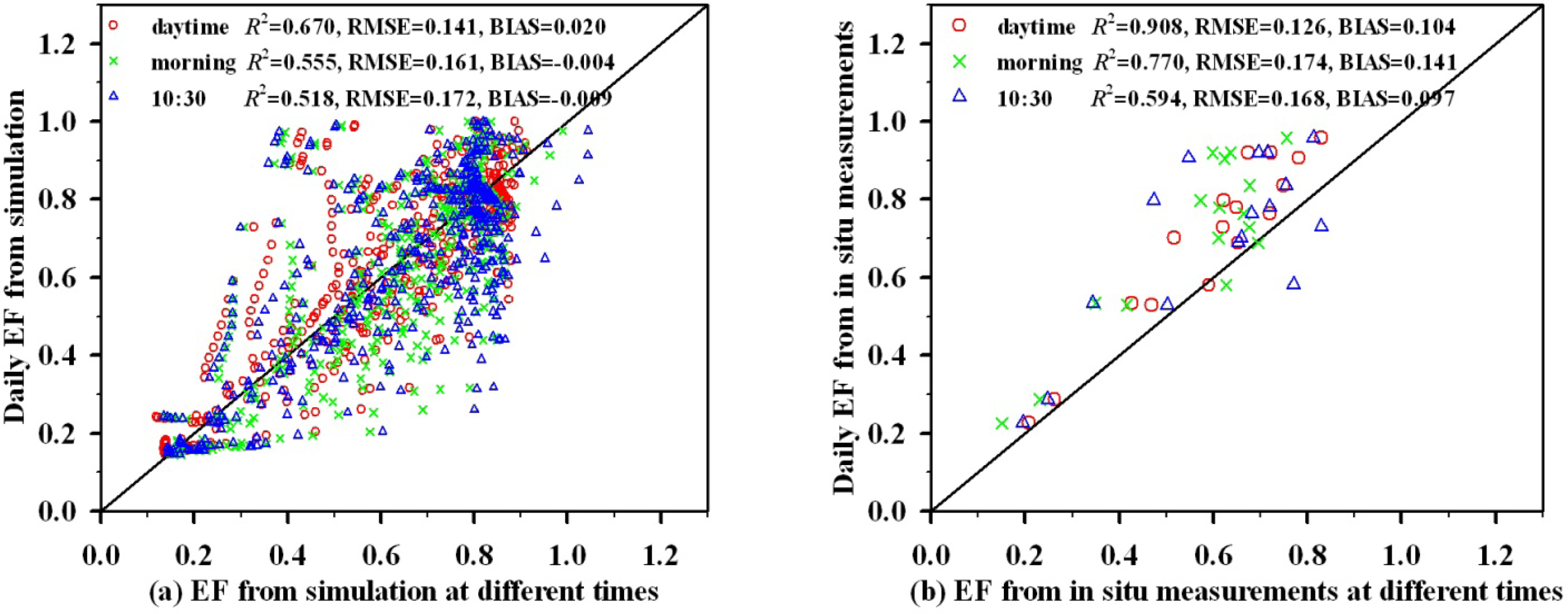

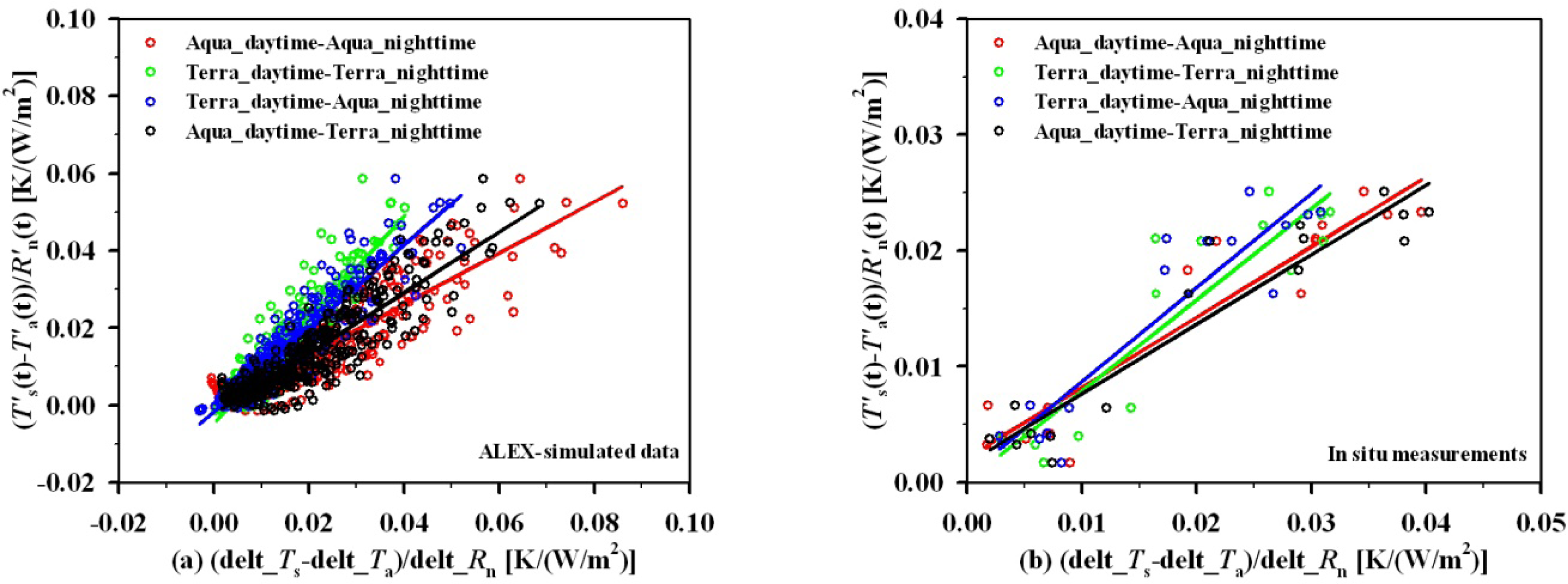

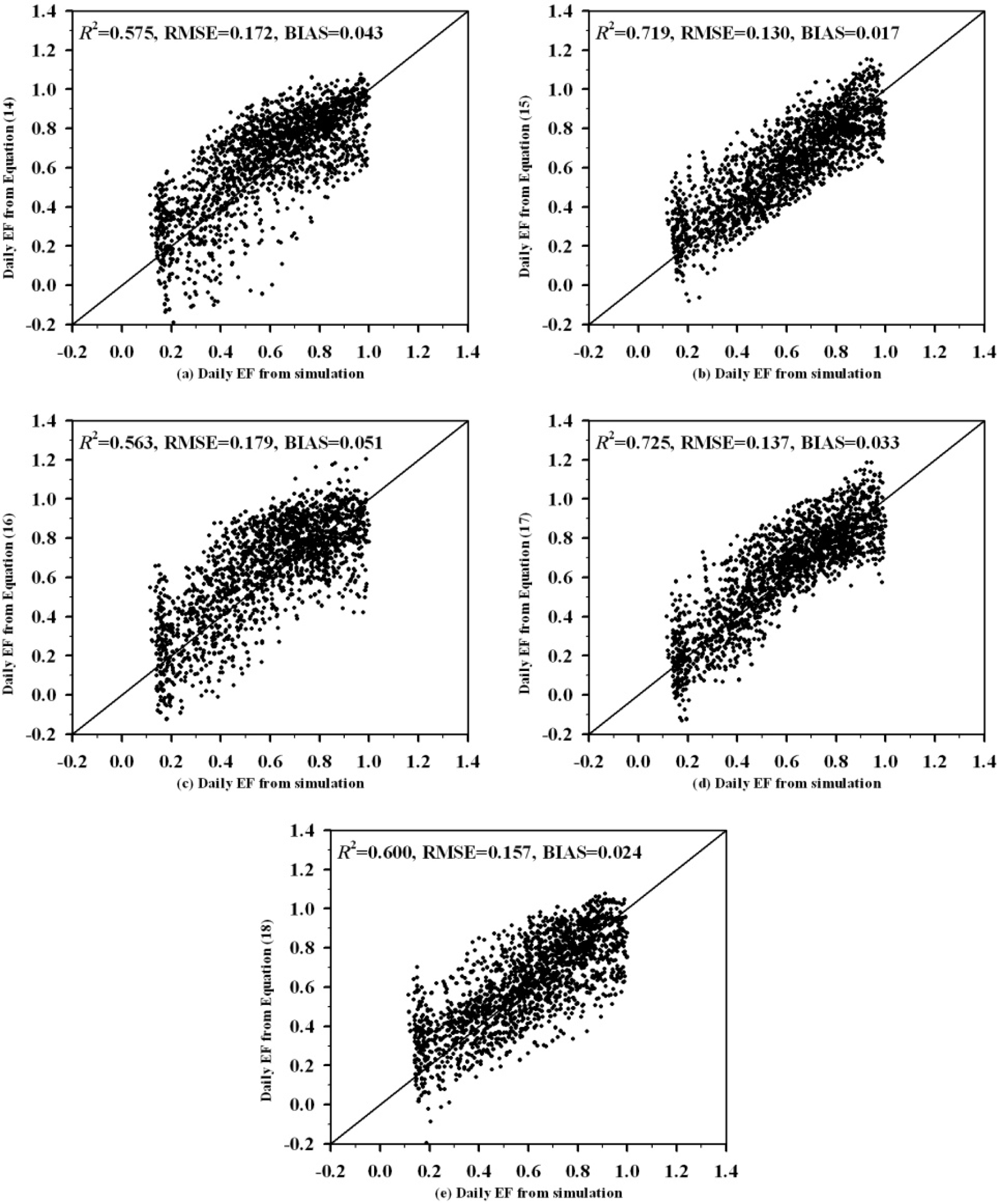

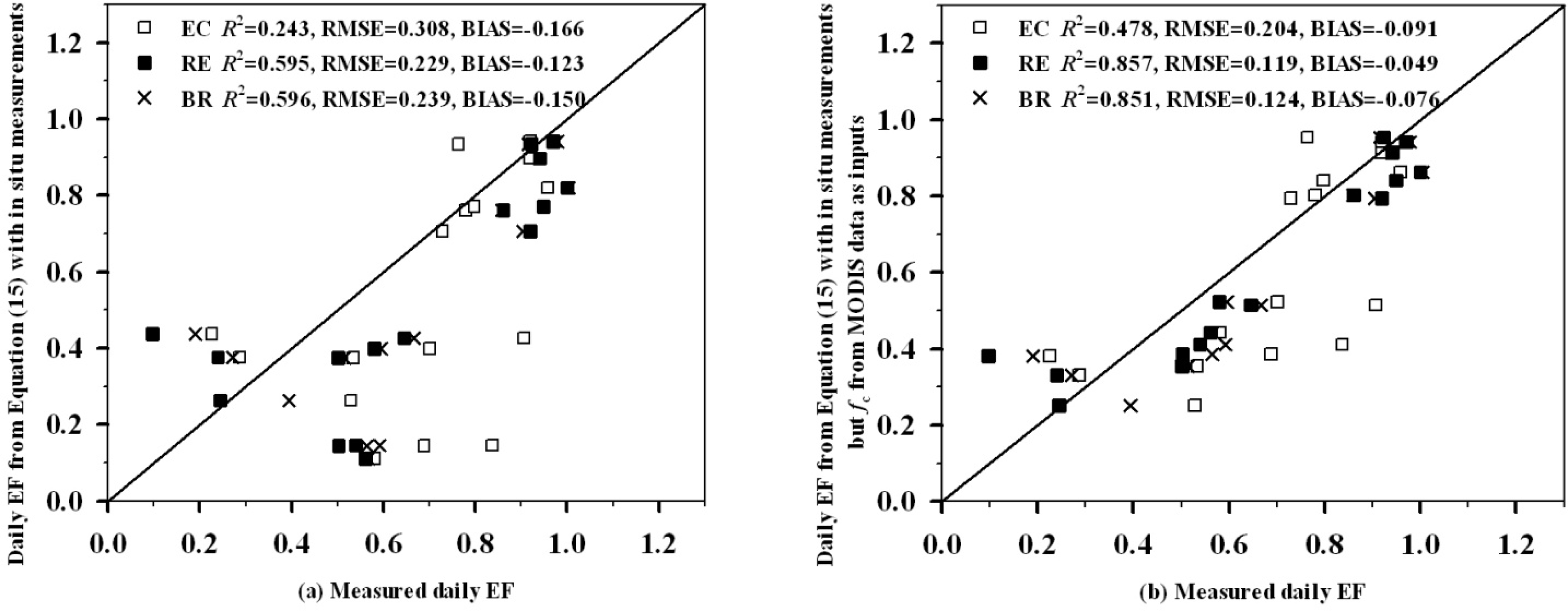
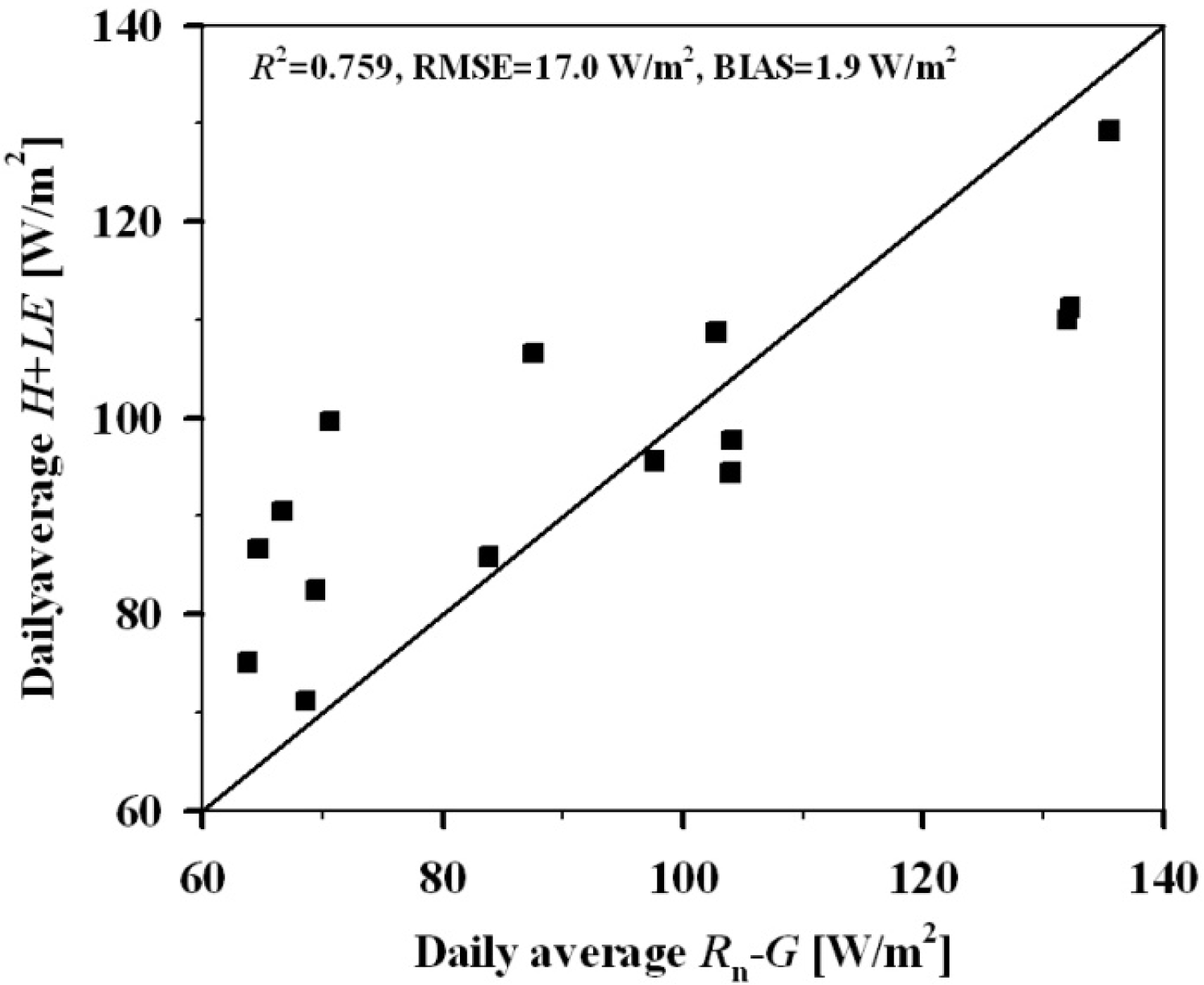
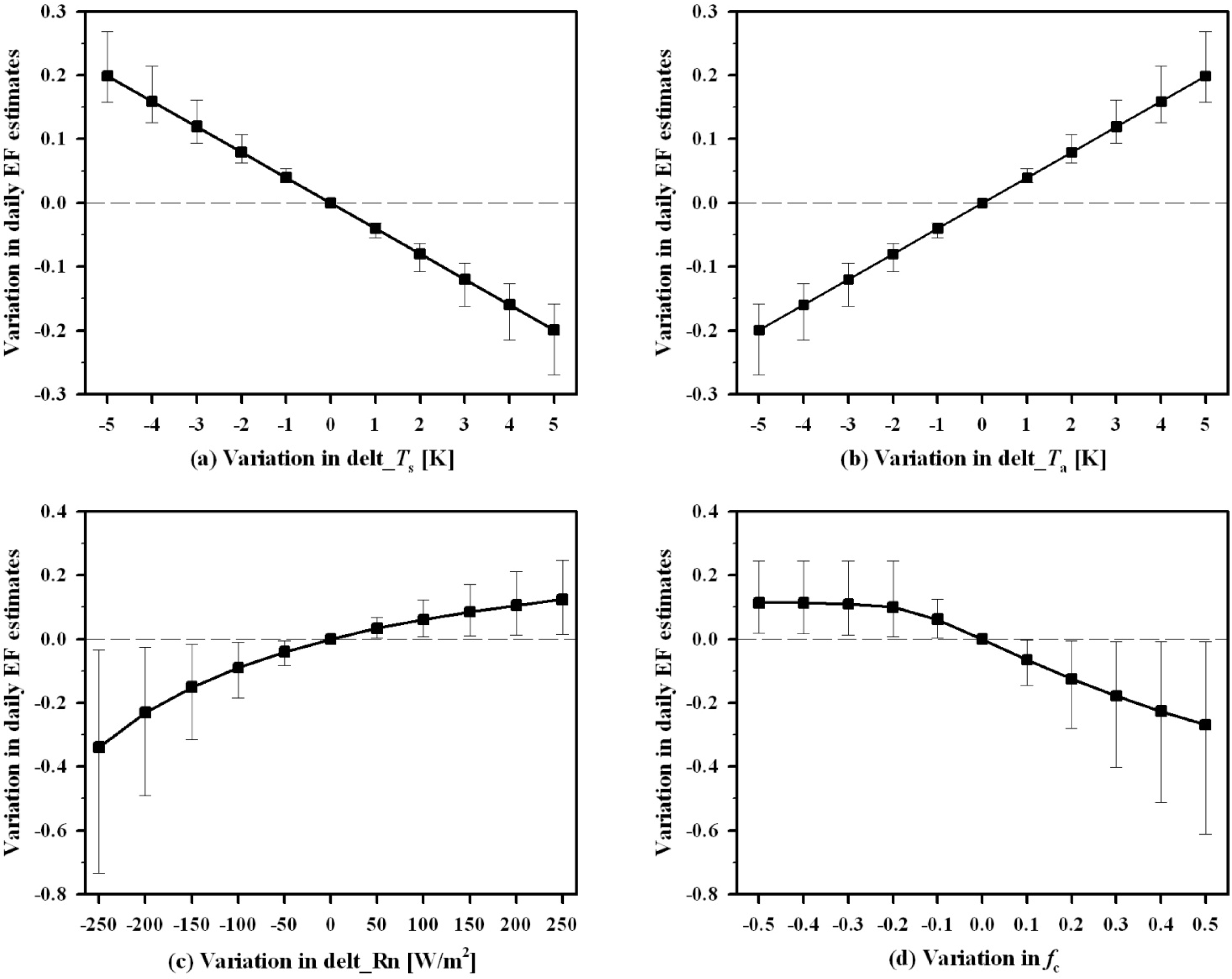
| Data | Inputs | Linear Relationships | R2 | RMSE |
|---|---|---|---|---|
| ALEX-simulated data | Aqua daytime-Aqua nighttime | Y = 0.6619X − 0.0003 | 0.808 | 0.0047 |
| Terra daytime-Terra nighttime | Y = 1.3435X − 0.0046 | 0.874 | 0.0038 | |
| Terra daytime-Aqua nighttime | Y = 1.0790X − 0.0017 | 0.882 | 0.0037 | |
| Aqua daytime-Terra nighttime | Y = 0.7858X − 0.0023 | 0.821 | 0.0045 | |
| In situ measurements | Aqua daytime-Aqua nighttime | Y = 0.6066X − 0.0021 | 0.891 | 0.0029 |
| Terra daytime-Terra nighttime | Y = 0.7854X − 0.0001 | 0.827 | 0.0036 | |
| Terra daytime-Aqua nighttime | Y = 0.8130X − 0.0006 | 0.853 | 0.0033 | |
| Aqua daytime-Terra nighttime | Y = 0.5996X − 0.0017 | 0.894 | 0.0028 |
| Sites | Inputs | R2 | RMSE | BIAS |
|---|---|---|---|---|
| Yucheng | Change rate during the morning | 0.817 | 0.107 | 0.020 |
| Aqua daytime-Aqua nighttime | 0.878 | 0.083 | −0.002 | |
| Terra daytime-Terra nighttime | 0.810 | 0.103 | −0.001 | |
| Terra daytime-Aqua nighttime | 0.869 | 0.086 | 0.007 | |
| Aqua daytime-Terra nighttime | 0.835 | 0.098 | −0.009 | |
| Goodwind | Change rate during the morning | 0.806 | 0.106 | 0.023 |
| Aqua daytime-Aqua nighttime | 0.847 | 0.093 | 0.019 | |
| Terra daytime-Terra nighttime | 0.787 | 0.129 | 0.045 | |
| Terra daytime-Aqua nighttime | 0.826 | 0.106 | 0.029 | |
| Aqua daytime-Terra nighttime | 0.840 | 0.098 | 0.023 | |
| Cottonwood | Change rate during the morning | 0.787 | 0.124 | 0.029 |
| Aqua daytime-Aqua nighttime | 0.877 | 0.087 | 0.008 | |
| Terra daytime-Terra nighttime | 0.839 | 0.100 | 0.009 | |
| Terra daytime-Aqua nighttime | 0.850 | 0.111 | 0.033 | |
| Aqua daytime-Terra nighttime | 0.860 | 0.093 | −0.007 | |
| Audubon | Change rate during the morning | 0.827 | 0.101 | 0.001 |
| Aqua daytime-Aqua nighttime | 0.858 | 0.092 | −0.005 | |
| Terra daytime-Terra nighttime | 0.737 | 0.137 | 0.034 | |
| Terra daytime-Aqua nighttime | 0.837 | 0.104 | 0.019 | |
| Aqua daytime-Terra nighttime | 0.823 | 0.103 | −0.005 |
| Inputs | Equations |
|---|---|
| Change rate during the morning | |
| Aqua daytime-Aqua nighttime | |
| Terra daytime-Terra nighttime | |
| Terra daytime-Aqua nighttime | |
| Aqua daytime-Terra nighttime |
| EC | RE | BR | |||||||
|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | BIAS | R2 | RMSE | BIAS | R2 | RMSE | BIAS | |
| New method | 0.139 | 0.215 | 0.051 | 0.394 | 0.242 | 0.093 | 0.382 | 0.210 | 0.066 |
| SEBS | 0.125 | 0.268 | 0.053 | 0.292 | 0.275 | 0.096 | 0.296 | 0.249 | 0.069 |
© 2013 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Lu, J.; Tang, R.; Tang, H.; Li, Z.-L. Derivation of Daily Evaporative Fraction Based on Temporal Variations in Surface Temperature, Air Temperature, and Net Radiation. Remote Sens. 2013, 5, 5369-5396. https://doi.org/10.3390/rs5105369
Lu J, Tang R, Tang H, Li Z-L. Derivation of Daily Evaporative Fraction Based on Temporal Variations in Surface Temperature, Air Temperature, and Net Radiation. Remote Sensing. 2013; 5(10):5369-5396. https://doi.org/10.3390/rs5105369
Chicago/Turabian StyleLu, Jing, Ronglin Tang, Huajun Tang, and Zhao-Liang Li. 2013. "Derivation of Daily Evaporative Fraction Based on Temporal Variations in Surface Temperature, Air Temperature, and Net Radiation" Remote Sensing 5, no. 10: 5369-5396. https://doi.org/10.3390/rs5105369




