2.1. Outline
The physical process being modelled can be summarised as follows: incoming solar irradiance passes through the atmosphere, reflects off the Earth’s surface, passes through the atmosphere again and is observed by the satellite sensor above the atmosphere.
Atmospheric effects on the signal include a range of scattering and absorption processes, and are a function of the various angles relating the sun, surface and satellite. These effects are assumed to be well modelled by widely available atmospheric radiative transfer models. We have used Second Simulation of the Satellite Signal in the Solar Spectrum (widely known as 6S) [
17] for this component. This is described in more detail in Section 2.2.
Reflection from the Earth’s surface is also a function of the angular configuration of the sun, surface and satellite. The surface is characterised by the proportion of light it reflects, but this depends on the angles at which it is illuminated and viewed. The terminology for different reflectance quantities used here is that defined by Martonchik
et al.[
18]. When not otherwise specified, we have used the term “reflectance” to mean the bi-directional reflectance factor.
The atmospheric modelling with 6S yields an estimate of the surface reflectance assuming a horizontal surface. We have then modelled the effects of the bi-directional reflectance distribution function (BRDF) to estimate the surface reflectance for a surface oriented as per the topography for each pixel, as it would be if viewed with a standard illumination and viewing geometry. This we refer to generically as standardised surface reflectance. This is described in more detail in Sections 2.3 and 2.4.
2.2. Atmospheric Radiative Transfer Modelling
The atmospheric radiative transfer modelling software, 6S [
17], provides estimates of direct and diffuse irradiance onto a horizontal surface,
and
respectively. 6S also provides estimates of apparent surface bi-directional reflectance,
ρh, for a horizontal surface, given the observed top of atmosphere radiance. The top of atmosphere radiance was obtained from the satellite imagery by applying the supplied gains and offsets to each pixel digital number. All of these quantities are specific to the wavelength in question, but for notational clarity we have omitted the explicit band dependency in what follows.
6S was run at a range of angle combinations, with the resolution of angle change (in radians) being 0.01 for sun zenith, 0.02 for satellite zenith and azimuth, and 0.04 for sun azimuth. 6S was also run for a range of altitudes, for each angle combination, with an altitude step size of 200 m starting at sea level up to the maximum ground elevation required. Each pixel is then corrected using the resulting 6S parameters for the nearest corresponding elevation and angles. Ozone concentration was taken from the Total Ozone Mapping Spectrometer (TOMS) monthly climatology (1996–2003) [
19]. Precipitable water was estimated by a simple regression from interpolated daily surface humidity measurements [
20]. Aerosol optical depth (at 550 nm wavelength) was assumed to be a fixed value of 0.05, for the reasons discussed by Gillingham
et al.[
21], most notably the difficulty in obtaining accurate estimates of it directly from imagery over the relatively bright Australian landscape. Australia is frequently blessed with sufficiently clear skies that this is reasonable for the purposes of monitoring vegetation cover [
22]. Aerosol was assumed to follow the continental aerosol model available in 6S. Surface elevation was given by the Shuttle Radar Topography Mission (SRTM), at 30 m resolution [
23–
25].
6S includes some capacity for modelling BRDF, but since it does not allow for a non-horizontal surface, we chose not to use this. We did this by setting it to use a homogeneous surface, with no directional effects, i.e. a uniform Lambertian surface. This effectively “switches off” BRDF modelling within 6S, leaving us free to model it separately.
2.3. Standardised Reflectance
The bi-directional reflectance factor is a measure of how much light the surface would reflect, when illuminated from a single direction, and observed from some particular direction. While this is a measure of how reflective the surface is, it does vary with the illumination and viewing geometry [
18]. Expressing the reflectance of a pixel as a function of this geometry gives the bi-directional reflectance distribution function (BRDF). This function depends on the sub-pixel scale scattering and shadowing behaviour of the surface. Since the illumination and viewing geometry do vary between acquisitions of satellite imagery, this represents an extra source of variation in the measurements. To remove this extra variation, we seek to express the surface reflectance as it would be observed if seen under a standard configuration (
i.e., a standard set of azimuth and zenith angles for both sun and satellite). We refer to this as standardised reflectance. For operational purposes we have standardised to a nadir view (
i.e., satellite zenith angle is zero) and a solar zenith angle of 45°. This is also commonly known as Nadir BRDF-Adjusted Reflectance (NBAR) at 45°.
The output of 6S is an estimate of the surface bi-directional reflectance factor for a horizontal surface,
ρh. However, as discussed above, we have switched off 6S’s BRDF modelling, so we must still apply a correction for this, for the angles appropriate for the orientation of the given pixel. The simplest approach is to define the ratio between reflectances at two sets of angles
A and
BIf we have a reflectance at angles
A, and we can estimate
γ(
A,
B) (using a model of BRDF), then we can estimate the reflectance at angles
B as
This general approach has been used successfully by other authors [
13,
26,
27]. However, while this approach works well on horizontal surfaces, it performs less well as the terrain slopes further away from the sun. This is due at least in part to the reduced importance of direct illumination, and the increased importance of diffuse illumination. So, following Shepherd and Dymond [
28], we take a slightly more complicated approach.
We define a second reflectance factor
ρdif, the diffuse reflectance, which is similar in character to the hemispherical-directional reflectance factor defined by Martonchik
et al.[
18], but considering
only the diffuse irradiance, with no direct illumination. We then assume that the surface-leaving radiance (in a given direction) can be modelled as
Since 6S does not directly supply an estimate of the surface-leaving radiance, only the surface reflectance for a horizontal surface, we approximate the observed surface-leaving radiance
L from the outputs of 6S (
ρh,
and
) as
This represents the actual radiance leaving the pixel, in the direction of the sensor, regardless of the orientation of the surface.
Following Shepherd and Dymond [
28], the direct and diffuse irradiances illuminating a sloping surface can be written in terms of the irradiances illuminating a horizontal surface
where
i is the incidence angle between the surface normal and the sun vector;
ih is the incidence angle for a horizontal surface (
i.e., the solar zenith angle);
Vd is a sky-view factor;
Vt is a terrain view factor; and
ρavg is the average reflectance of surrounding pixels.
Vd and
Vt describe (in relative terms) how much sky and terrain are visible to the sloping pixel surface, to serve as a source of diffuse illumination.
Edir is set to zero when
i ≥ 90°.
Equation (5) is just the usual correction for sun angle (widely known as a cosine correction), and
Equation (6) expresses the diffuse illumination as the sum of the diffuse light coming from the sky, and that reflected from surrounding terrain. No account is taken of the orientation of the surrounding terrain, and whether it would be directing light onto the pixel in question.
The sky view factor,
Vd, is the proportion of sky visible to a given pixel, relative to a hemisphere of sky which would be visible if no surrounding terrain obstructed the view. The hemisphere can be thought of as having its base aligned with the slope of the pixel. The sky view factor was calculated using the horizon search methods detailed by Dozier and Frew [
29]. For each pixel, the angle to the horizon is found in 16 equally spaced search directions, and a sky view factor along that azimuth is computed. The sky view factor for the whole hemisphere is approximated as the average of these 16 azimuthal view factors. The terrain view factor,
Vt, is assumed to be whatever remains of the hemisphere over the slope at that point, thus
Vt = 1 −
Vd. The sky view factor,
Vd, was pre-computed for every pixel, using the Shuttle Radar Topography Mission (SRTM) digital elevation model (DEM) at 30 m resolution.
The slope and aspect of the terrain are calculated directly from the 30 m SRTM using Fleming and Hoffer’s algorithm, as described by Jones [
30]. This means that the effective resolution of the slope is 90 m, as it uses a 3 × 3 pixel window.
Solving
Equation (3) requires an estimate of the diffuse reflectance. This seems likely to be closely related to the direct reflectance, so it was modelled as directly proportional to the direct reflectance [
28].
Shepherd and Dymond [
28] modelled this with a constant
β, but we have chosen to model
β as a function of the angles, by integrating the BDRF model over the hemisphere. This is detailed in Section 2.4.
Using
Equation (2), we define a reflectance correction factor
γstd to adjust a reflectance from a given set of angles to a standard angular configuration
This gives an estimate of the bi-directional reflectance factor for a surface at a standard angular configuration. We can substitute
L =
Lobs from
Equation (4), and
Edir and
Edif from
Equations (5) and
(6) respectively. The only remaining unknowns are
γstd and
β, which are modelled using the BRDF model, as described in Section 2.4.
2.4. Topographic and Bi-Directional Reflectance Modelling
The viewing geometry varies with the sun and satellite positions, relative to the pixel under observation, and also with the orientation of the pixel surface, due to topography. We have chosen to model both these variations with a single BRDF model. This implicitly assumes that canopy roughness is the same for both horizontal and inclined surfaces. Laboratory work by Dymond and Shepherd [
31] suggests that this may be valid, at least for closed canopies.
The kernel-driven RossThick-LiSparse reciprocal (RTLSR) BRDF model was chosen as it has been found to perform well for a range of land cover types [
32], and has been used very successfully with data from the MODIS instrument [
27,
33].
This is expressed in terms of two kernel functions
Kvol and
Kgeo, and three parameters
fiso,
fvol and
fgeowhere
i,
e and
ω are the incidence, exitance and relative azimuth angles respectively [
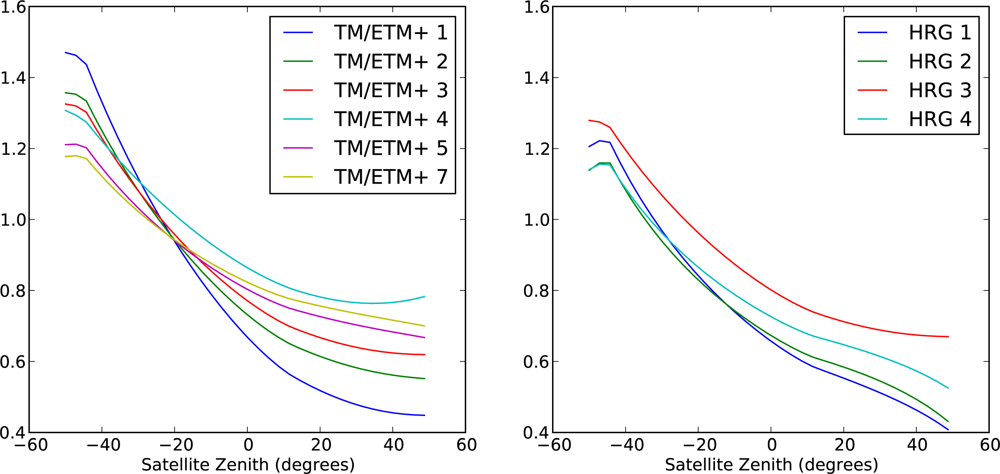
34]. (Note that the relative azimuth is calculated about the surface normal, so for sloping pixels this is not the same as the difference between the sun and satellite azimuth angles. This distinction disappears if the kernels are expressed in terms of phase angle.)
When used with the MODIS sensor, the model can be parameterised on a per-pixel basis. This is possible because each pixel is observed from multiple directions at multiple sun angles over a short time period (twice daily, typically over 16 days). The short time period means that there is very little variation on the ground itself, and so all variation is assumed to be due to the angular configuration. The range of angular configurations can be used to invert the model to provide a set of parameters which characterise the BRDF, for that pixel, in that 16 day period.
However, this is not possible with the Landsat or SPOT sensors. Because their orbits are sun-synchronous, the overpass time is roughly the same each day, and so the sun position does not vary in the short term. In the case of Landsat, the view geometry is also constant for each pass, so in general any given pixel is always viewed from the same angle. In the case of SPOT, the sensor is pointable, and so multiple view angles are possible, if image capture is appropriately tasked, although it would be difficult to obtain a large number of such views within a short period.
Because of these limitations, we have made the assumption that there is at least a major component of the BRDF which can be assumed to be the same across all pixels. This assumption is supported by the validation presented in Section 2.7. This global BRDF can be characterised with a single set of model parameters, which are then used for all pixels. There would, of course, remain a component of BRDF effect which is specific to each pixel, which we are not able to address with this approach. The correction for BRDF effects will only be successful in areas that satisfy the assumption that this global BRDF is the major component. With this assumption in place, we can address the orbital limitations of Landsat and SPOT by noting the following points:
Areas in the overlap between two Landsat paths are viewed with different view angles;
Images which are chosen to be within a few weeks of each other but across the equinoxes (Mar 21 & Sep 23) will have the largest range of sun zenith angles for the shortest time period, thus minimising on-ground change;
Pixels on hill slopes will have different sun and view angles to horizontal pixels.
By selecting pairs of pixels in overlap areas, between dates chosen as above, on a range of pixel surface orientations, we obtain a set of pairs of reflectances across a whole range of angular configurations. Pixels in shadow, or with sun incidence angle >80°, were excluded because the BRDF model is believed to perform poorly at these extremes (it tends to infinity as incidence angle approaches 90°). In the case of SPOT we selected pairs of images which were taken off-nadir from opposite view directions. We also selected pixels across a range of land cover types, as represented by the foliage projective cover (FPC) class, and a range of slope classes. The image overlap locations were chosen to cover a number of the different land types in eastern Australia, to avoid being biased by any particular type of land surface. A total of 12,000 pixels were selected for parameter fitting for Landsat TM, and 10,400 for SPOT.
Because of our assumption of a global BRDF we did not attempt to solve
Equation (11) for a full set of parameters. Rather, we solved for a ratio of reflectances, which would model the
γ parameter we need. Combining
Equations (1) and
(11)Because we solve only for this ratio, it is necessary to cancel out the
fiso parameter in order to guarantee a unique solution for the parameters. So, we define
f′vol =
fvol/
fiso and
f′geo =
fgeo/
fiso and so
For each pair of pixel observations we have an instance of
Equation (2), and we solve the whole set together to give a single set of parameters
f′vol and
f′geo. The inversion process is detailed in Section 2.6. This is done independently for each wavelength, for each instrument. The resulting
f′
vol and
f′
geo, together with
Equation (13), gives us a correction factor
γ(
A,
B) to adjust a reflectance from any set of angles to any other set of angles.
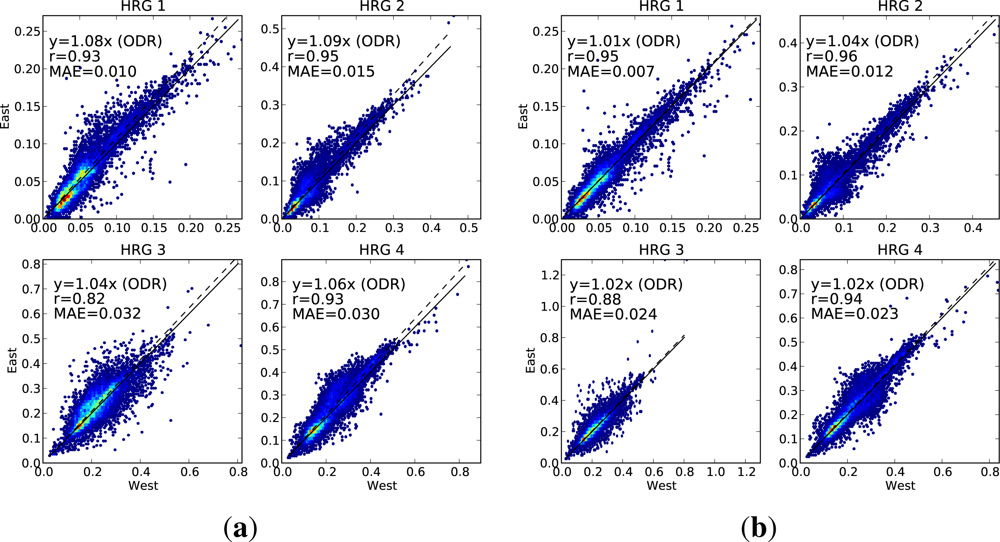
2.7. Validation of BRDF Modelling
To test the value of the BRDF correction, we used paired observations of a second set of pixels, chosen in the same way as those used for parameter fitting, as described in Section 2.4. Following the same logic as used to fit the parameters, the fitted BRDF model should be able to adjust the reflectance from one set of angles to the other. The selection of pixels allows us to test the correction on a large range of angular configurations.
Given a pair of reflectances ρA and ρB, for a pixel, observed from two different sets of angles A and B, we can adjust ρB to the angles A. As in Section 2.6, ρB,A is ρB adjusted to the angles for ρA. We can treat this pair (ρA, ρB,A) as an observed-predicted pair, and assess the performance of the prediction accordingly. The extent to which they are equal gives a measure of the merit of the correction.
We have presented validation scatter plots for a wide range of situations, as experience has suggested that a poorly tuned parameterisation can perform well on one or two of these situations, but badly on others. Scatter plots are presented for the following cases.
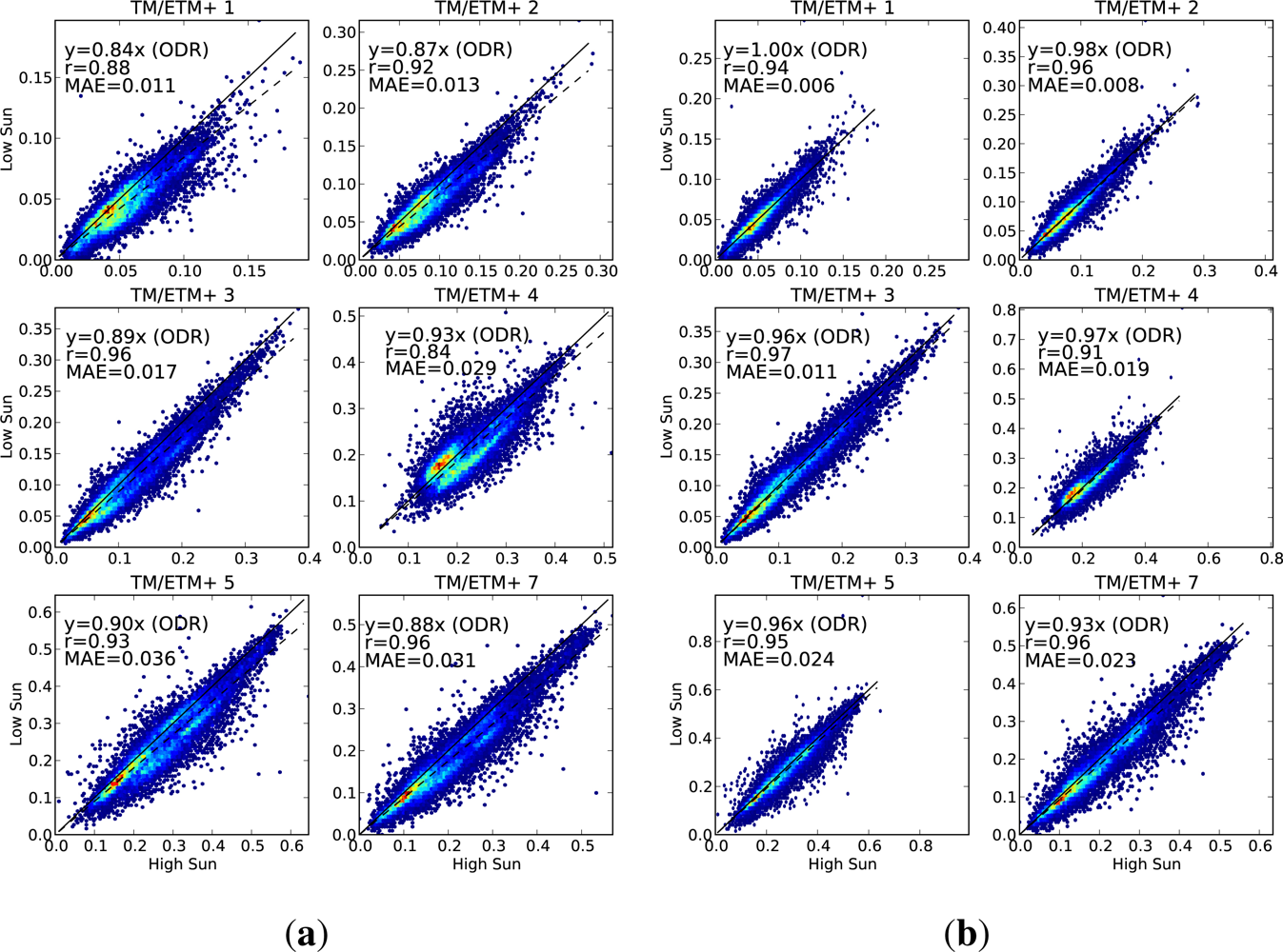
Case 1. Landsat pixels on a mixture of horizontal and sloping terrain, with sloping pixels in a range of orientations, and some with and some without tree cover. This dataset has a large range of incidence/exitance angle combinations, on a range of land cover types. Pairs are divided into the low-sun and high-sun observations, with the low-sun value being used to predict the high-sun value. This tests how well we correct for the difference in sun angle. Sample size = 20,217 pixels (9,459 Landsat-5, 10,758 Landsat-7).
Case 2. As for Case 1, but the pixels are split between the view from the east side of the overlap, and the view from the west side. The view from the east is used to predict the view from the west. This tests how well we are correcting for the difference in view angle. Sample size = 20,217 pixels (9,459 Landsat-5, 10,758 Landsat-7).
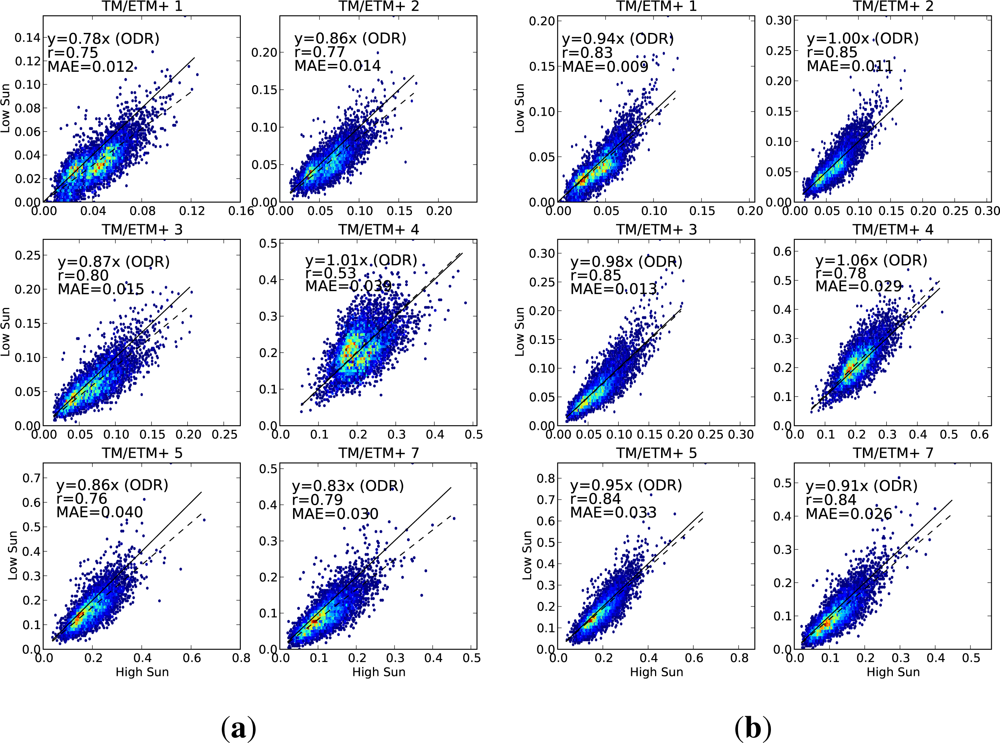
Case 3. Landsat pixels on steep slopes facing away from the sun (slope > 50%, terrain aspect is within 60° of directly away from the sun). This is the situation when the diffuse illumination becomes important. Pairs are divided into low-sun and high-sun, and the low-sun value is used to predict the high-sun value. Sample size = 6,353 pixels (3,679 Landsat-5, 1,610 Landsat-7).
Case 4. SPOT pixels on a range of orientations, split between high-sun and low-sun observations. Due to a limited number of overlap areas available with a large sun angle difference, other pairs were excluded from these plots (pairs used were those with Δ
θi > 10° from
Table 5). This tests the correction for sun angle change, for the SPOT sensor. Sample size = 2,367 pixels.
Case 5. SPOT pixels as for case 4, but including all overlap pairs. Pixels divided into those viewed from the east, and those viewed from the west. The view from the east is used to predict the view from the west. Sample size = 12,278 pixels.
Case 6. SPOT pixels from scenes pointed well off nadir view, from opposite sides, but within only a few days of each other. The largest date gap is 5 days, so we can reasonably assume no on-ground change, but the view angle differences are much larger than is possible with Landsat. This provides a more challenging test of the correction for view angle, because of the larger view angle difference, and with data less contaminated by possible change in vegetation between dates. Sample size = 4,117 pixels.
On each scatter plot, we include three measures of the performance. The linear correlation (r) is used to measure how closely related the observed and predicted values are. We also fit a regression line (using orthogonal distance regression (ODR), because there is equal uncertainty in both variables) and constrain it to pass through the origin. The slope of this regression line is a measure of any bias between the observed and predicted values. The third measure of performance is the mean absolute error (MAE), showing the absolute difference, in reflectance units, between the observed and predicted values. A perfect prediction would have both the correlation and the regression slope being equal to 1, and the mean absolute error would be zero.
For each of the cases, we present scatter plots for the data with no BRDF adjustment alongside the same scatter plot for the adjusted data, showing the extent to which the agreement is improved by applying the BRDF correction.
2.8. NDVI Improvement
The ratios of spectral reflectances provide an opportunity to test the atmospheric correction. In particular, the normalised difference vegetation index (NDVI) is, on the one hand, strongly affected by relative offsets between the red and near infra-red bands, but is relatively stable under variation in illumination. Since one effect of the atmosphere is to increase the amount of radiance at the sensor by different amounts in different wavelengths (so-called path radiance), correcting for atmospheric effects will remove this path radiance offset and improve the stability of NDVI [
36].
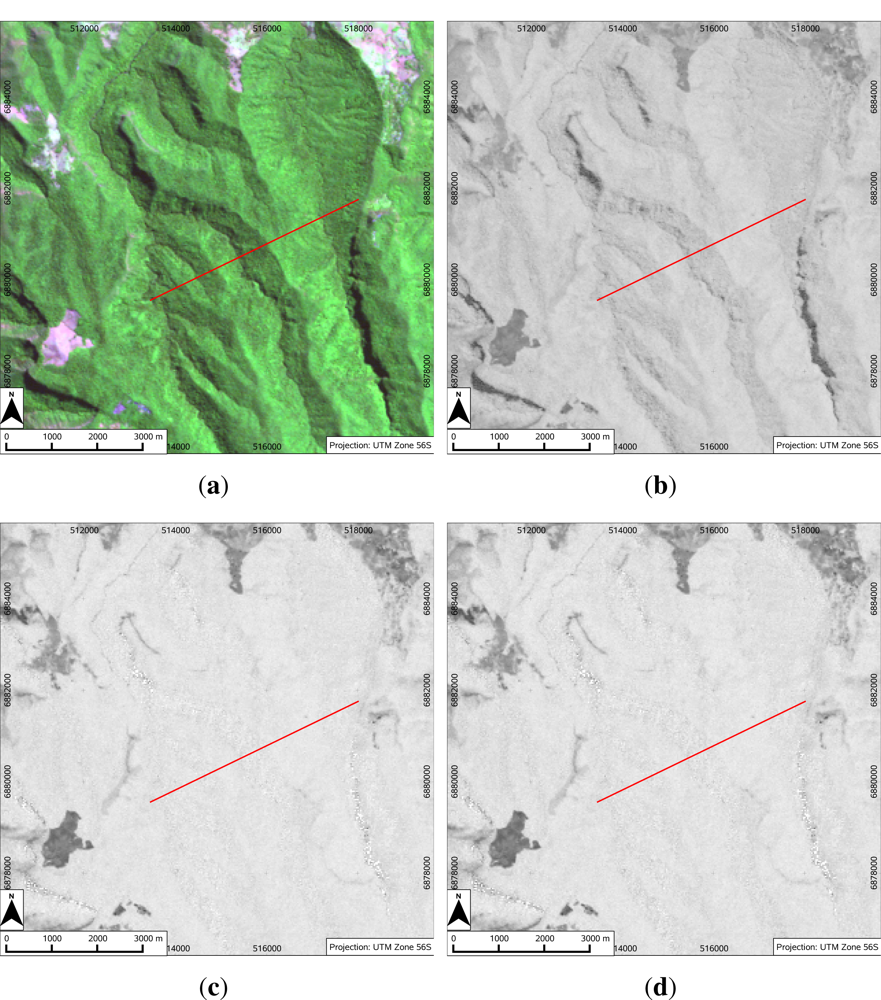
If NDVI is calculated from at-sensor reflectance values, this path radiance is still present in the signal and reduces the resilience of the NDVI to illumination changes. We can see this effect as topographic variation in NDVI when calculated from at-sensor reflectances.
A transect is defined through an area of apparently homogeneous forest, with marked topographic variation in illumination along the transect. Values along this transect are extracted from images of at-sensor reflectance, atmospherically corrected reflectance and standardised, topographically corrected reflectance. NDVI is calculated for each of these cases, and the result plotted against distance along the transect, to show how NDVI is affected by the different stages in the correction process, and by implication the effect of the correction on the relative magnitudes of the spectral reflectances. The corresponding imagery is also presented.