4.1. Optimization of the k-Means Parameterization
We compared the influence of
k on the sensitivity, specificity and BAC of the two semi-supervised classifiers, and observed several common responses. First, lower values of
k resulted in decreased sensitivity, regardless of the classifier, while higher values of
k resulted in higher specificity, (
Table 2). A value of
k =
10 maximized sensitivity for the tensor summation kernel, and a value of
k = 5 for the tensor product kernel (
Table 2). Furthermore, for both semi-supervised methods specificity increased with
k, reaching its maximum value for
k = 40. Despite these similarities, the optimal BAC differed substantially for the two methods: the maximum BAC for the tensor summation and tensor product kernels were obtained for
k = 35 and
k = 10, respectively. This is in agreement with the results obtained by Tuia
et al. [
37], who conclude that the optimal results for the tensor summation kernel are obtained for larger values of
k, while the tensor product kernel performs better at small values of
k.
The optimal
k value for the tensor product kernel was most influenced by sensitivity, which decreased faster than the increase in specificity for higher values of
k; while the optimal
k value for the tensor summation kernel was most influenced by specificity, which increased faster than the reduction in sensitivity for higher values of
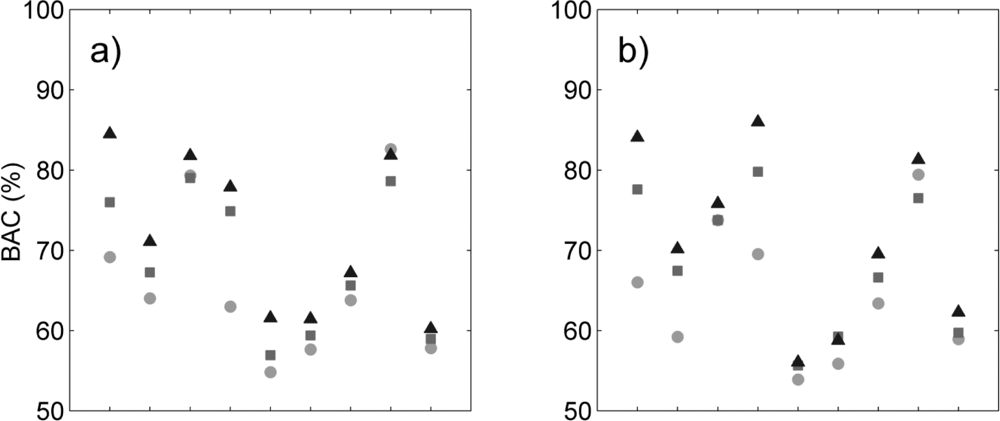
k. Strong discrepancies were also observed between the two semi-supervised methods: the most important difference was that sensitivity was 9–16 percentage points higher with the tensor summation kernel. This difference was balanced by the lower specificity of this method (3–4 percentage points). Despite this reduction in specificity, the tensor summation kernel outperformed the tensor product kernel by 3–6 percentage points based on BAC values (
Table 2).The average specificity exceeded 90% for the value of
k selected in our experiment. This result is encouraging because it means that the number of species incorrectly identified as a target species was usually very low. Based on these results, we selected
k =35 clusters for the tensor summation kernel, and
k =10 clusters for the tensor product kernel, for all following classifications.
4.2. Classification Method and Data Type
We found that the summation-bagged kernel outperformed the product-bagged kernel of 4.2 percentage points, and the supervised SVM of 6.5 percentage points, based on BAC averaged over 100 iterations performed on the nine species. Both semi-supervised methods improved the sensitivity to target species:they outperformed the supervised method by 7–15 percentage points in terms of sensitivity (
Table 3). Among the two semi-supervised classifiers, the tensor summation kernel obtained 5–9 percentage points greater sensitivity than the tensor product kernel, depending on the data type used (
Table 3).
From these results we conclude that the tensor summation kernel offers the best performance for target species discrimination in the forests studied here. Furthermore, fusing hyperspectral measurements with LiDAR canopy height and intensity data increased classification accuracy (BAC,
Table 3), as averaged over all species. Combining hyperspectral data with either of the LiDAR data types alone, however, resulted in similar or slightly reduced accuracy in most of the cases, mainly due to lower sensitivity.
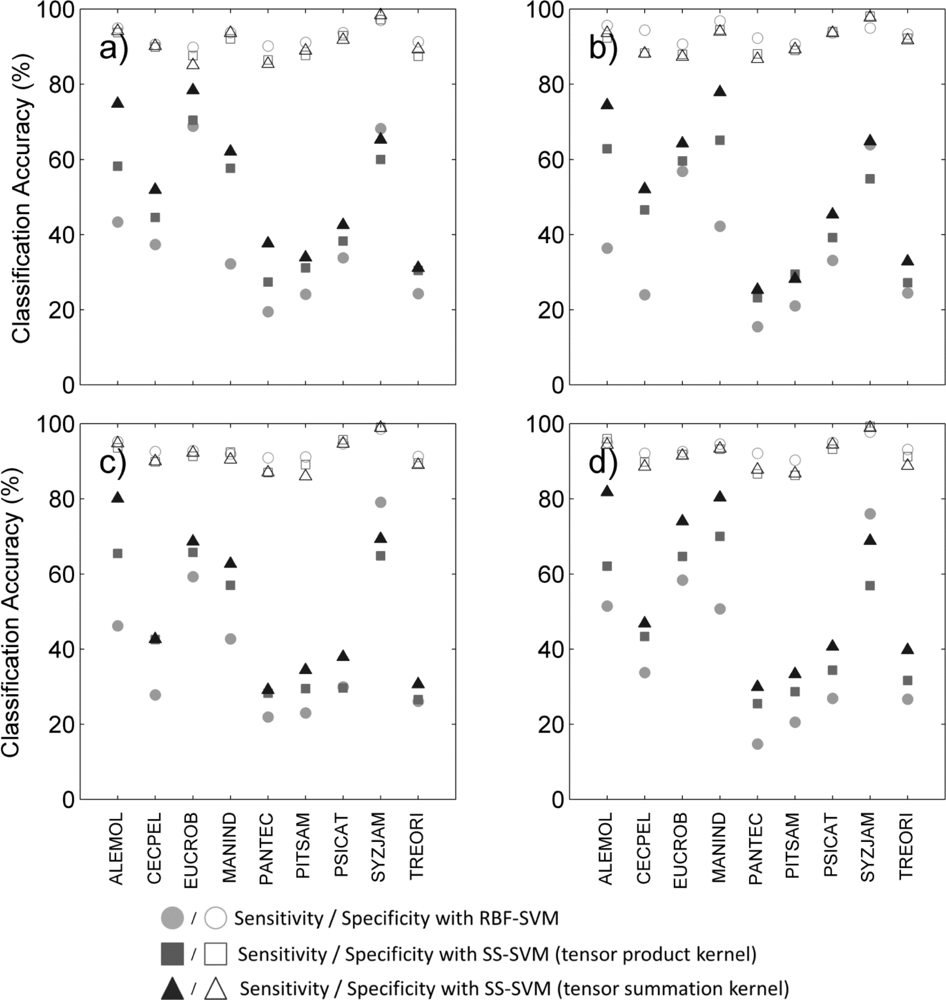
We reviewed species-specific results throughout our analysis. First we compared the different classifiers for a given data type. As observed overall species, the individual difference in BAC between classifiers (
Figure 2) was mainly driven by the difference in sensitivity of the classifier for all data types (
Figure 3). The increased overall sensitivity obtained with the tensor summation kernel (
Table 3)was also observed when studying species separately, with the exception of
Syzygium jambos which was usually classified more accurately when using a supervised method (
Figure 3,
Table 2). This result was observed for all four data types, but the difference in sensitivity between the three classification methods was species-dependent, with
Aleurites moluccana showing the highest increase in sensitivity of all species when using semi-supervised classification.
The influence of data type on the classification varied with the species targeted, and no common trend was observed. For example,
Cecropia pelata was classified more accurately with hyperspectral data alone when using supervised classification. However, combining hyperspectral data with LiDAR intensity slightly improved the sensitivity obtained for this species for semi-supervised methods, but combining hyperspectral data with LiDAR canopy height reduced sensitivity. Another example is
Mangifera indica, for which combining hyperspectral data and LiDAR intensity resulted in a greater than 15 percentage points improvement in sensitivity (
Figure 3(a, b)) and 8 percentage points improvement in BAC (
Figure 2(a,b)) when using a tensor summation kernel. In contrast, combining LiDAR intensity with hyperspectral data reduced the BAC for
Aleurites moluccana and
Syzygium jambos, but combining canopy height with hyperspectral data improved their classification accuracy (
Figure 2(a,c)).
These species-specific differences were partly explained by further examining the LiDAR canopy height and intensity values. Among the nine species studied here, some show very specific behavior in terms of intensity or height, which may help with the discrimination of these species despite their high within-species variability (
Table 4). For example, in the case of
Mangifera indica, the large difference measured between the mean intensity value of the first and only returns (the highest of all species) and the mean intensity value of the first of many returns (the lowest of all species) explains the significant improvement observed for its discrimination when including LiDAR intensity to the classification (see
Table 4). Almost no first of many returns points were recorded for
Mangifera indica, leading to very low intensity values. The low mean height measured for
Aleurites moluccana and
Syzygium jambos also explains their improved discrimination when combining canopy height with hyperspectral data.
Finally we studied which combination of data significantly improved BAC compared to any given data type (
Table 5). We tested all classifiers and data types, but the results showed here are obtained with semi-supervised classification and tensor summation kernel. The classification accuracy for
Pandanus tectorius was significantly higher when LiDAR information was not used, but this species exhibits the lowest BAC of all nine species (
Figure 2), which suggests that this is an inappropriate candidate for species targeting. The classification accuracy for
Cecropia peltata was also significantly improved when the LiDAR height was not used, either by itself or in combination with intensity, but LiDAR intensity did not impact the classification. This LiDAR intensity data significantly improved the classification of
Mangifera indica,
Trema orientalis and
Psidium cattleianum; for the latter, however, adding LiDAR height did not lead to any improvement. The addition of either one or the other LiDAR variable did not improve the classification accuracy of the same species, highlighting the different discriminating capabilities related to each of these data types. Finally these results show that the accuracy obtained when using all data types was comparable to or significantly better than when the LiDAR data were not used or only partly used for six species whereas only three species were significantly better classified when not using all data types together:
Cecropia peltata,
Pandanus tectorius,
Psidium cattleianum. Notice that these three species show a relatively low BAC, suggesting that they would not be good candidates for target species classification. These results obtained on these three species are not surprising as Féret and Asner [
5] obtained particularly low producer’s and user’s accuracy with these species (40 to 60%) when performing multiclass discrimination including these nine species and eight other ones. These results confirm the adding of multi-sensor information combining LiDAR and hyperspectral imagery for species classification.
4.3. Application to a Practical Situation
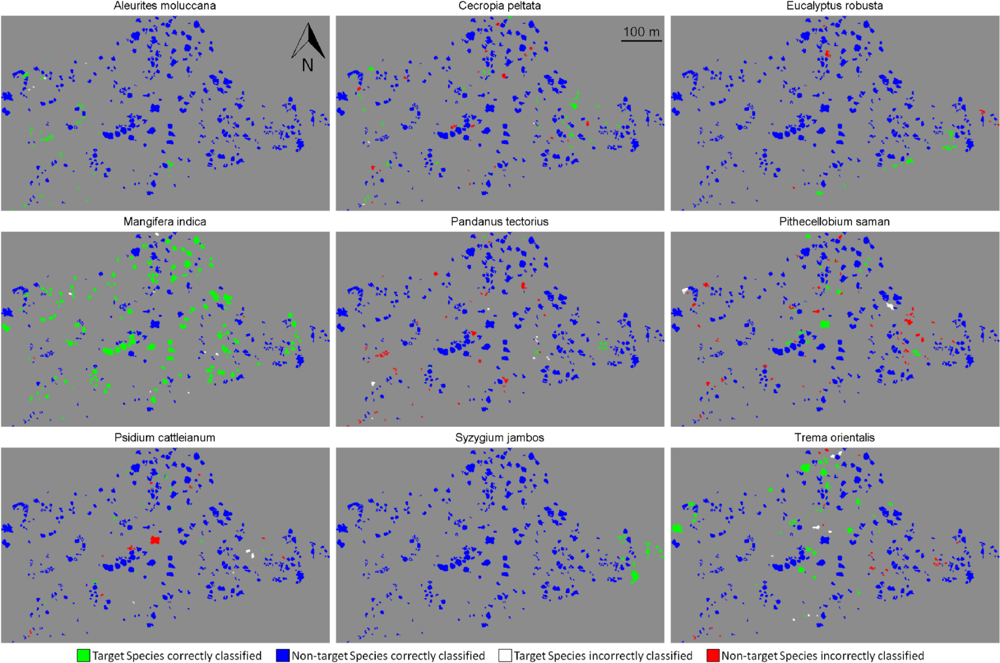
We performed target species classification on the whole site for each species, using semi-supervised classification with tensor summation kernels on the 333 ITCs available, with the full data combination (
Figure 4). For each species, we used the classification model that produced the highest BAC among the 100 iterations performed in Section 4.2. All species except
Pandanus tectorius showed sensitivity values greater than 80% ITCs (
Table 6). These values were surprisingly high for some species such as
Pithecellobium saman,
Psidium cattleianum and
Trema orientalis, as they were dramatically higher than the mean sensitivity measured after 100 iterations, which is about 40% for these three species (
Figure 3(d)). These findings confirm the importance of the training dataset, and the very high variability of the discriminating capabilities of individual tree crowns from the same species. The specificity was also higher than 80% for all species, and superior to 95% for five of them, which was expected given the results obtained previously (see
Figure 3(d)).The high specificity observed here is promising for future applications targeting individual species, but these findings must be placed in the perspective of operational applications.