Road Target Search and Tracking with Gimballed Vision Sensor on an Unmanned Aerial Vehicle
Abstract
:1. Introduction
- search new target
- follow target
- locate known target.
- Search theory and multi-target tracking are large, but separate, research areas. The problem where search and target tracking are combined has received much less attention, especially in vision-based applications. One of the objectives of this study is to fill this gap.
- There are few studies that examines both high-level and low-level aspects of tracking, planning and searching. In this paper, the state-machine framework adopted uses sub-blocks that achieve low-level tracking, planning and searching tasks while a high-level decision maker chooses among these sub-tasks to obtain an overall situational awareness.
- A useful utility measure for the combined search and target tracking performance is proposed.
- The use of road networks has been used widely to improve the tracking performance of road-bound targets, but in this study we are also utilizing the road network for improved search performance.
- We investigate the effect of the multi-target assumption on the search and show that it results in the same planning scheme as in the single target case.
- There are few studies where both PFs and PMFs are examined. We show the utilization of each algorithm and discuss the merits and the disadvantages with the appropriate applications.
1.1. Background and Literature Survey
1.2. Outline
2. The Multiple Target Search and Tracking Problem
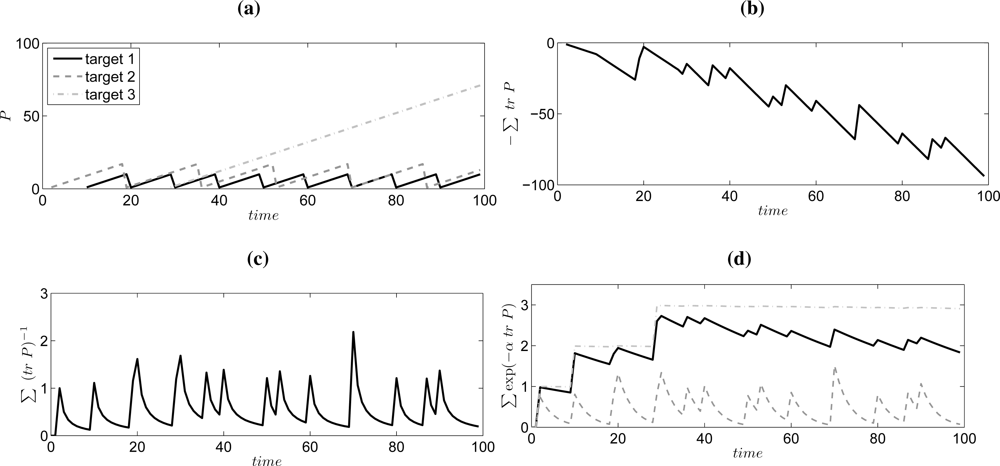
2.1. Objective Function
- It increases with each observation.
- It does not decrease unlimited for unobserved or lost targets, i.e., each target should have a limited influence.
- It should favor strategies that find many targets.
- It should give a fair compromise between splitting the observation resource among the different targets.
2.2. The Planning Problem
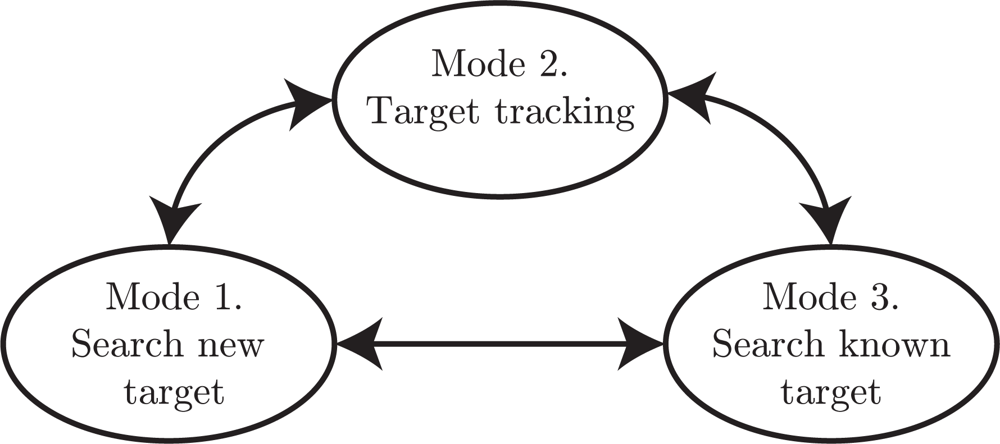
2.3. State-Machine Framework
- Mode 1: Search for new targets. In this search mode the roads are explored to discover new unknown targets. This search will stop once a target is detected and a mode transition to mode 2 will be performed. To know which road segments that have been searched, a probability grid on the roads is maintained. In the update step the weights are decreased for grid points in the current sensor footprint, see Section 5 for details.
- Mode 2: Target tracking. When the target tracking mode is active it is assumed that a target has been detected in the current sensor frame. The task of this mode is just to keep track of the current target in the sensor view. The default case in this work is that the target tracking mode is active for a fixed number of time steps, and then the high-level planner decides a transition to either mode 1 or mode 3.
- Mode 3: Search for known target. When a previously discovered target is not observed for some time, its position uncertainty grows. Thus, when the target must be re-discovered it might not be possible to point the sensor in the correct direction since the uncertainty is too large. In such cases, this mode will be active to perform a search on road segments where the target is likely to be.
- High-level planner. The high-level planner decides which mode is active. Basically, the task is to decide if any known target needs to be re-discovered and updated, or if there is time to conduct search for new targets. There is an obvious conflict in this problem, when one target is tracked, or searched for, then the uncertainty of the other targets will grow, and with increasing uncertainty the expected search time for re-discover is also increasing.
3. Elements of Single Target Bayesian Search
3.1. The General Estimation Solution
3.2. Cumulative Probability of No Detection
4. Single Road Target Search based on a Particle Filter
4.1. Particle Filter
4.2. Calculation of the Cost Function with the PF
- Let t = 1. Initialize the particle mixture weights used in the planning as for i = 1, 2, ..., N where is the set of current target probability density in the tracking filter.
- Simulate the evolution of the particles according to the target model
- Compute the probability of detection, PD(xt), and update the target density given a non-detection. Thus, for all particles i, calculateand then compute the non-detection probability and normalize the weights according to
- Set t := t +1. If t ≤ n, then go to step (ii), otherwise go to the next step.
- Set the cost function value as the cumulative probability of non-detection
5. Multi-Road-Target Search Based on PMF
5.1. Generalization of the Single Target Search to Multiple Targets
5.2. Point-Mass Filter
5.3. Target Search on a Road Network Grid
6. Multiple Road Target Search and Tracking
- New target search; search for new targets that have not been discovered before. This mode is further explained in Section 6.1.
- Tracking Tracking; a detected target is followed in the current sensor frame, Section 6.2.
- Known target search; search for an earlier discovered target that is not in the current sensor frame, Section 6.3.
6.1. New Target Search
6.2. Target Tracking
6.3. Known Target Search
6.4. High-Level Planner
- Compute the valuewhere m is the expected number of targets in the surveillance area, τ is a mode transition time constant, ν is the search speed on the road and L is the total length of all roads in the surveillance area.
- Compute the valuefor all targets j = 1, 2,...,Mt. Pxy is the covariance of the target position state and αp is a design parameter.
- LetIf q = 0 then select the New target search mode, otherwise select the Known target search mode for target q.
6.5. UAV Path Planner
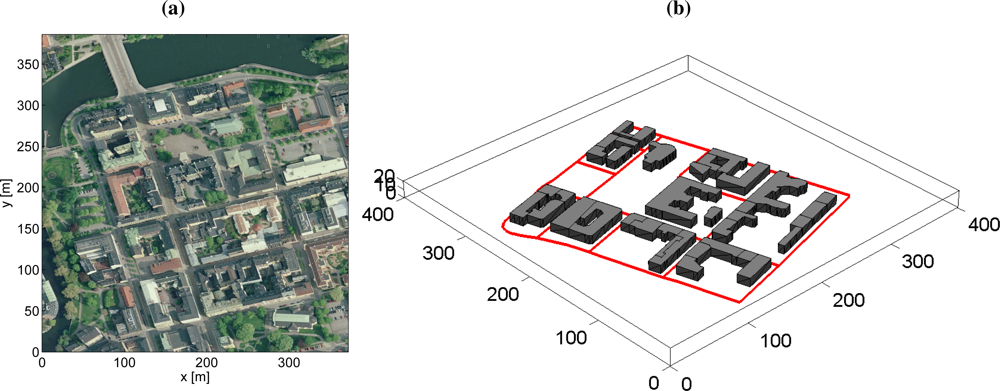
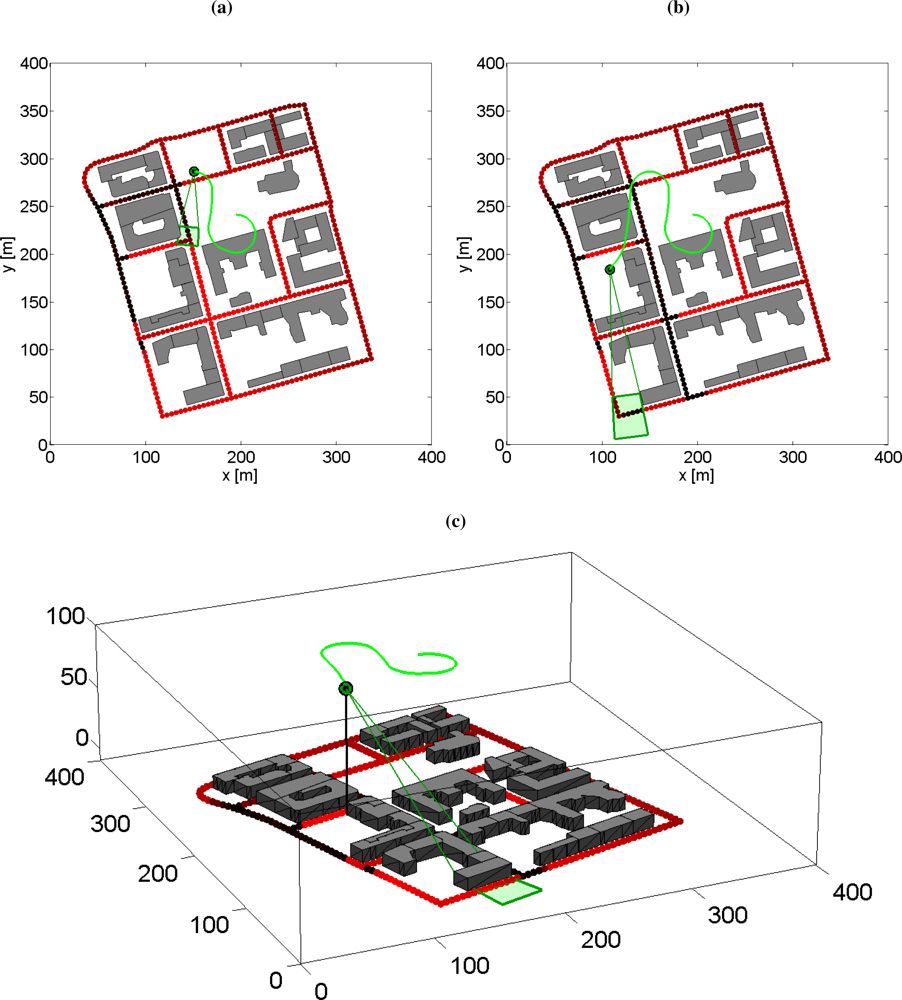
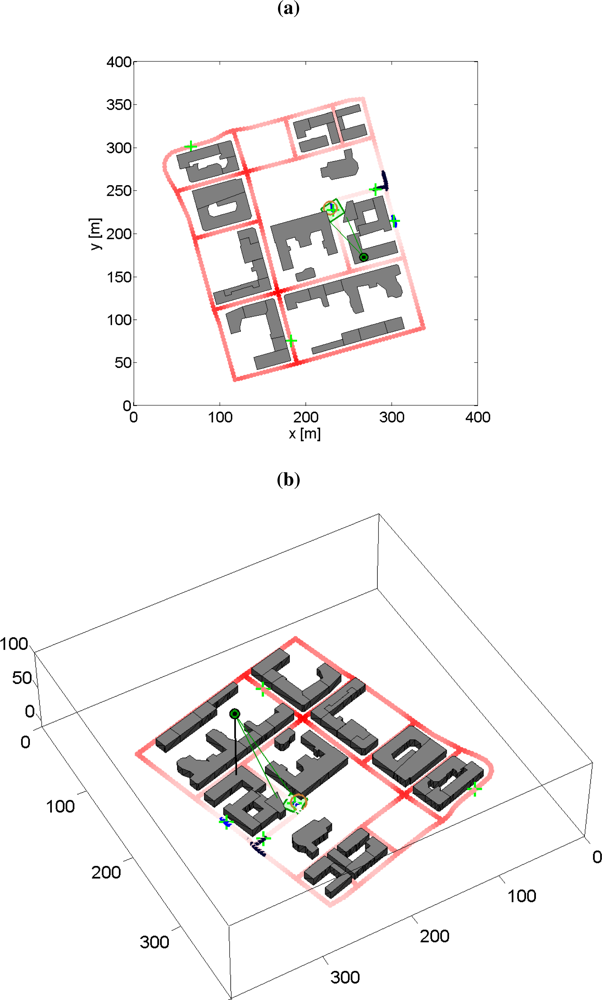
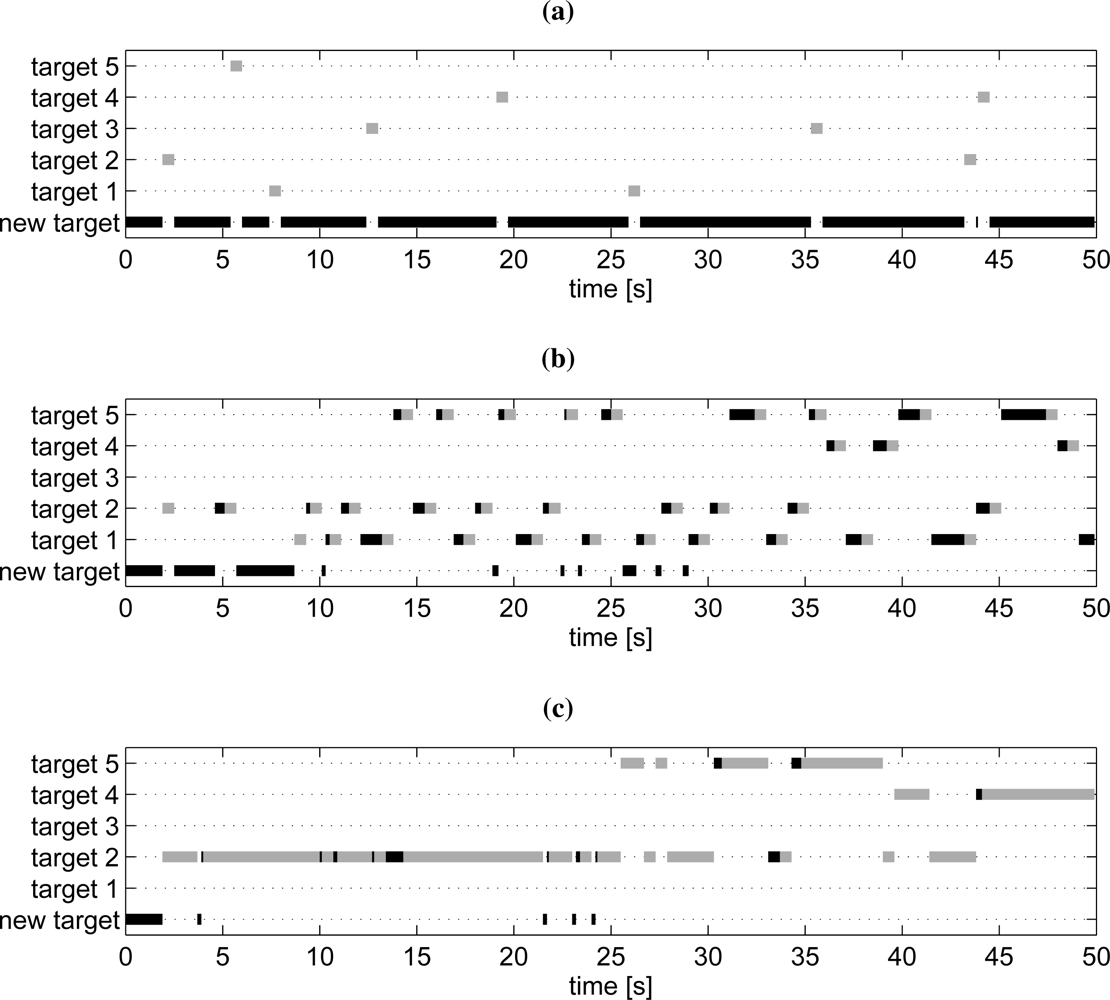
6.6. Simulation Examples: Moving Sensor Platform with Occlusion
6.7. Experiences from Real-World Experiments with a Pan/Tilt-Camera
7. Conclusions
Acknowledgments
References
- Rydell, J.; Haapalahti, G.; Karlholm, J.; Nsstrm, F.; Skoglar, P.; Stenborg, K.G.; Ulvklo, M. Autonomous Functions for UAV Surveillance. Proceedings of International Conference on Intelligent Unmanned Systems, Bali, Indonesia, 3–5 November 2010. number ICIUS-2010-0145..
- Watts, A.C.; Ambrosia, V.G.; Hinkley, E.A. Unmanned aircraft systems in remote sensing and scientific research: Classification and considerations of use. Remote Sens 2012, 4, 1671–1692. [Google Scholar]
- Ng, G.; Ng, K. Sensor management—What, why and how. Inf. Fusion 2000, 1, 67–75. [Google Scholar]
- Hero, A.; Castas, D.; Cochran, D.; Kastella, K. (Eds.) Foundations and Applications of Sensor Management; Springer: New York, NY, USA, 2007.
- Puterman, M.L. Markov Decision Processes: Discrete Stochastic Dynamic Programming; Wiley-Interscience: New York, NY, USA, 1994. [Google Scholar]
- Russell, S.J.; Norvig, P. Artificial Intelligence: A Modern Approach, 2nd ed; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Bellman, R. Adaptive Control Processes; Princeton University Press: Princeton, NJ, USA, 1961. [Google Scholar]
- Bertsekas, D.P. Dynamic Programming and Optimal Control, 2nd ed; Athena Scientific: Belmont, MA, USA, 2001; Volume 2. [Google Scholar]
- Sondik, E. The Optimal Control of Partially Observable Markov Processes, 1971.
- Pineau, J.; Gordon, G.; Thrun, S. Point-Based Value Iteration: An Anytime Algorithm for POMDPs. Proceedings of International Joint Conference on Artificial Intelligence, Acapulco, Mexico, 9–15 August 2003; pp. 1025–1032.
- Smith, T.; Simmons, R.G. Point-Based POMDP Algorithms: Improved Analysis and Implementation. Proceedings of the Conference on Uncertainty in Artificial Intelligence, Edinburgh, UK, 26–29 July 2005; pp. 542–547.
- Kurniawati, H.; Hsu, D.; Lee, W. SARSOP: Efficient Point-Based POMDP Planning by Approximating Optimally Teachable Belief Spaces. Proceedings of Robotics: Science and Systems Conference, Zurich, Switzerland, 25–28 June 2008.
- He, Y.; Chong, E.K.P. Sensor scheduling for target tracking: A Monte Carlo sampling approach. Digital Signal Processing 2006, 16, 533–545. [Google Scholar]
- Miller, S.A.; Harris, Z.A.; Chong, E.K.P. Coordinated Guidance of Autonomous UAVs via Nominal Belief-State Optimization. Proceedings of ACC’09 American Control Conference, St. Louis, MO, USA, 10–12 June 2009; pp. 2811–2818.
- He, R.; Bachrach, A.; Roy, N. Efficient Planning under Uncertainty for a Target-Tracking Micro-Aerial Vehicle. Proceedings of 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–8 May 2010.
- Whittle, P. Restless Bandits: Activity Allocation in a Changing World. J. Appl. Probabil 1988, 25, 287–298. [Google Scholar]
- Ny, J.; Dahleh, M.; Feron, E. Multi-UAV Dynamic Routing with Partial Observations Using Restless Bandit Allocation Indices. Proceedings of American Control Conference 2008, Seattle, WA, USA, 11–13 June 2008; pp. 4220–4225.
- Ding, Z. A. Survey of Radar Resource Management Algorithms. Proceedings of 21st Canadian Conference on Electrical and Computer Engineering, Dundas, ON, Canada, 4–7 May 2008; pp. 001559–001564.
- Stone, L.D. Theory of Optimal Search; Academic Press: New York, NY, USA, 1975. [Google Scholar]
- Frost, J.R.; Stone, L.D. Review of Search Theory: Advances and Applications to Search and Rescue Decision Support; Technical Report CG-D-15-01; US Coast Guard Research and Development Center: Groton, CT, USA, 2001. [Google Scholar]
- Koopman, B.O. Search and Screening: General Principles with Historical Applications; Pergamon Press: New York, USA, 1980. [Google Scholar]
- Washburn, A.R. Search for a moving target: The FAB Algorithm. Operations Res 1983, 29, 1227–1230. [Google Scholar]
- Brown, S.S. Optimal search for a moving target in discrete time and space. Operations Res 1980, 28, 1275–1289. [Google Scholar]
- Washburn, A.R. Branch and bound methods for a search problem. Nav. Res. Log 1997, 45, 243–257. [Google Scholar]
- Bourgault, F.; Göktoĝan, A.; Furukawa, T.; Durrant-Whyte, H.F. Coordinated search for a lost target in a Bayesian world. Adv. Robot 2004, 18, 979–1000. [Google Scholar]
- Furukawa, T.; Bourgault, F.; Lavis, B.; Durrant-Whyte, H.F. Recursive Bayesian Search-and-Tracking Using Coordinated UAVs for Lost Targets. Proceedings of IEEE International Conference on Robotics and Automation, Orlando, FL, USA, 15–19 May 2006; pp. 2521–2526.
- Geyer, C. Active Target Search from UAVs in Urban Environments. Proceedings of IEEE International Conference on Robotics and Automation 2008, Pasadena, CA, USA, 19–23 May 2008; pp. 2366–2371.
- Tisdale, J.; Ryan, A.; Kim, Z.; Tornqvist, D.; Hedrick, J.K. A Multiple UAV System for Vision-Based Search and Localization. Proceedings of American Control Conference 2008, Seattle, WA, USA, 11–13 June 2008; pp. 1985–1990.
- Chung, C.F.; Furukawa, T. Coordinated Search-and-Capture Using Particle Filters. Proceedings of 9th International Conference on Control, Automation, Robotics and Vision (ICARCV ’06), Singapore, 5–8 December 2006; pp. 1–6.
- Riehl, J.; Collins, G.; Hespanha, J. Cooperative search by UAV teams: A model predictive approach using dynamic graphs. IEEE Trans. Aerosp. Electron. Syst 2011, 47, 2637–2656. [Google Scholar]
- Collins, G.E.; Riehl, J.R.; Vegdahl, P.S. A UAV routing and sensor control optimization algorithm for target search. Proc. SPIE 2007, 6561, 6561D. [Google Scholar]
- Arulampalam, S.; Maskell, S.; Gordon, N.; Clapp, T. A tutorial on particle filters for On-line Non-linear/Non-Gaussian Bayesian tracking. IEEE Trans. Signal Process 2002, 50, 174–188. [Google Scholar]
- Blackman, S.; Popoli, R. Design and Analysis of Modern Tracking Systems; Artech House: Inc.: Norwood, MA, USA, 1999. [Google Scholar]
- Bar-Shalom, Y.; Li, X.R. Estimation and Tracking: Principles, Techniques and Software; Artech House, Inc: Norwood, MA, USA, 1993. [Google Scholar]
- Rodrguez-Canosa, G.R.; Thomas, S.; del Cerro, J.; Barrientos, A.; MacDonald, B. A real-time method to Detect and Track Moving Objects (DATMO) from Unmanned Aerial Vehicles (UAVs) using a single camera. Remote Sens 2012, 4, 1090–1111. [Google Scholar]
- Kirubarajan, T.; Bar-Shalom, Y.; Pattipati, K.R.; Kadar, I. Ground target tracking with variable structure IMM estimator. IEEE Trans. Aerosp. Electron. Syst 2000, 36, 26–46. [Google Scholar]
- Shea, P.J.; Zadra, T.; Klamer, D.; Frangione, E.; Brouillard, R. Improved state estimation through use of roads in ground tracking. Proc. SPIE 2000, 4048, 312–332. [Google Scholar]
- Shea, P.J.; Zadra, T.; Klamer, D.; Frangione, E.; Brouillard, R. Precision Tracking of ground targets. Proceedings of 2000 IEEE Aerospace Conferance, Big Sky, MT, USA, 18–25 March 2000; 3, pp. 473–482.
- Blom, H.; Bar-Shalom, Y. The interacting multiple model algorithm for systems with Markov switching coefficients. IEEE T. Automat. Contr 1988, 33, 780–783. [Google Scholar]
- Li, X.R.; Bar-Shalom, Y. Multiple-model estimation with variable structure. IEEE T. Automat. Contr 1996, 41, 478–493. [Google Scholar]
- Arulampalam, M.S.; Gordon, N.; Orton, M.; Ristic, B. A Variable Structure Multiple Model Particle Filter for GMTI Tracking. Proceedings of International Conference on Information Fusion, Annapolis, MD, USA, 8–11 July 2002; 2, pp. 927–934.
- Ristic, B.; Arulampalam, S.; Gordon, N. Beyond the Kalman Filter—Particle Filters for Tracking Applications; Artech House: Norwood, MA, USA, 2004. [Google Scholar]
- Ulmke, M.; Koch, W. Road-Map Assisted Ground Target Tracking. IEEE Trans. Aerosp. Electron. Syst 2006, 42, 1264–1274. [Google Scholar]
- Skoglar, P.; Orguner, U.; Törnqvist, D.; Gustafsson, F. Pedestrian tracking with an infrared sensor using road network information. EURASIP J. Adv. Signal Process 2012, 2012, 26. [Google Scholar]
- Jazwinski, A. Stochastic Processes and Filtering Theory; Academic Press: New York, NY, USA, 1970; Volume 63. [Google Scholar]
- Morawski, T.; Drury, C.; Karwan, M. Predicting search performance for multiple targets. Human Factors: The Journal of the Human Factors and Ergonomics Society 1980, 22, 707–718. [Google Scholar]
- Gordon, N.J.; Salmond, D.J.; Smith, A.F.M. Novel approach to nonlinear/non-Gaussian Bayesian state estimation. IEE Proc.-F 1993, 140, 107–113. [Google Scholar]
- Gustafsson, F. Particle filter theory and practice with positioning applications. IEEE Trans. Aerosp. Electron. Syst 2010, 25, 53–82. [Google Scholar]
- Mahler, R. Statistical Multisource-Multitarget Information Fusion; Artech House: Norwood, MA, USA, 2007. [Google Scholar]
- Miller, S.; Childers, D. Probability and Random Processes: With Applications to Signal Processing and Communications; Elsevier: Burlington, MA, USA, 2004. [Google Scholar]
- Bergman, N. Recursive Bayesian Estimation: Navigation and Tracking Applications. 1999. [Google Scholar]
- Skoglar, P. MTST Movies. 2012. Available online: http://www.control.isy.liu.se/~skoglar/mtstMovies2012/ (accessed on 28 June 2012).
- Ross, S.M. Introduction to Stochastic Dynamic Programming; Academic Press: London, UK, 1983. [Google Scholar]
- Holst, G.C. Electro-Optical Imaging System Performance, 4 ed; SPIE Press: Bellingham, WA, USA, 2006. [Google Scholar]
- Hagfalk, E.; Eriksson Ianke, E. Vision Sensor Scheduling for Multiple Target Tracking. 2010. [Google Scholar]
- Salmond, D.; Clark, M.; Vinter, R.; Godsill, S. Ground Target Modelling, Tracking and Prediction with Road Networks. Proceedings of International Conference on Information Fusion, Quebec, QC, Canada, 9–12 July 2007.
Appendix
A. System Models
A.1. UAV Motion Model
A.2. Dynamic Sensor Gimbal Model
A.3. Road Target Motion Model
A.4. Bearings-only Observation Model
A.5. Probability of Detection Model
B. Proof of Theorem 1






Share and Cite
Skoglar, P.; Orguner, U.; Törnqvist, D.; Gustafsson, F. Road Target Search and Tracking with Gimballed Vision Sensor on an Unmanned Aerial Vehicle. Remote Sens. 2012, 4, 2076-2111. https://doi.org/10.3390/rs4072076
Skoglar P, Orguner U, Törnqvist D, Gustafsson F. Road Target Search and Tracking with Gimballed Vision Sensor on an Unmanned Aerial Vehicle. Remote Sensing. 2012; 4(7):2076-2111. https://doi.org/10.3390/rs4072076
Chicago/Turabian StyleSkoglar, Per, Umut Orguner, David Törnqvist, and Fredrik Gustafsson. 2012. "Road Target Search and Tracking with Gimballed Vision Sensor on an Unmanned Aerial Vehicle" Remote Sensing 4, no. 7: 2076-2111. https://doi.org/10.3390/rs4072076



