Adaptive Slope Filtering of Airborne LiDAR Data in Urban Areas for Digital Terrain Model (DTM) Generation
Abstract
:1. Introduction
2. Algorithm
3. Data Characteristics
4. Experiments
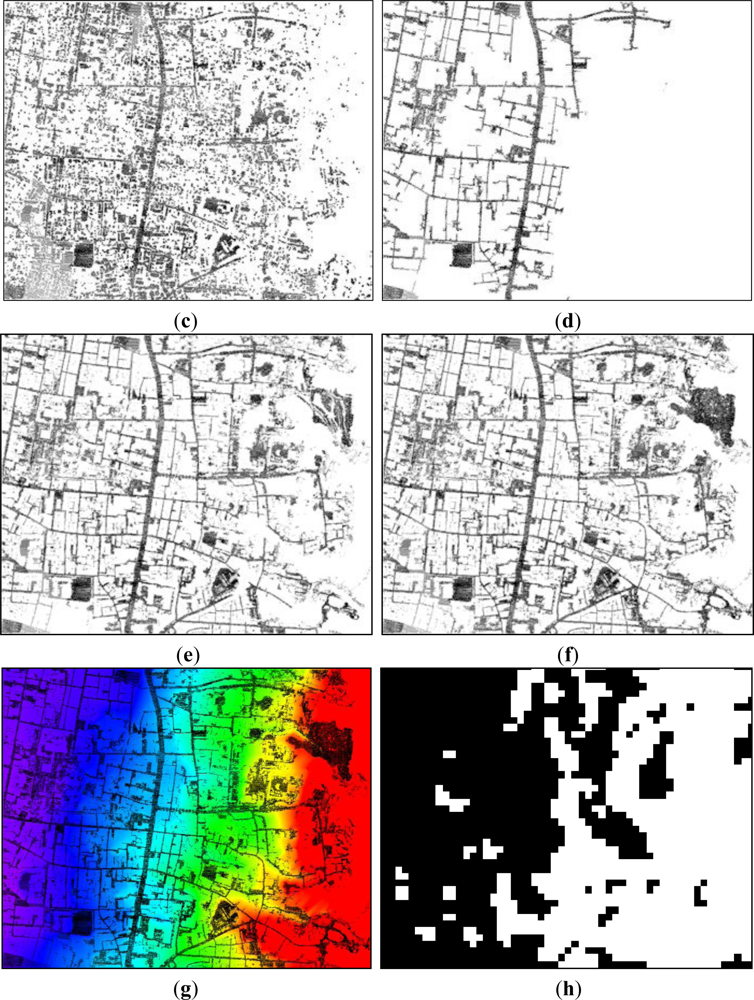
4.1. Results
4.2. Validation
4.2.1. Validation Using ISPRS Benchmark Data
4.2.2. Comparison with TerraScan Using Study Area Data
5. Discussion
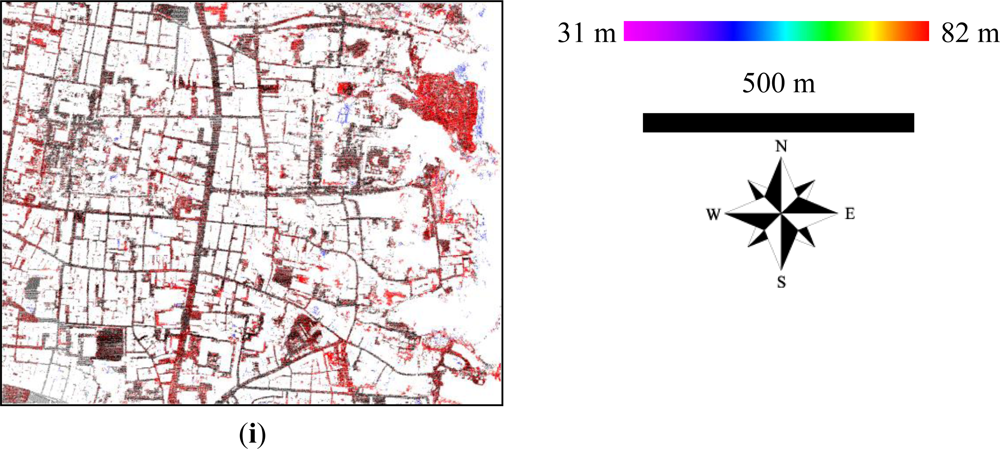
5.1. Qualitative and Quantitative Assessment
5.2. Effect of Updating Slope Parameter
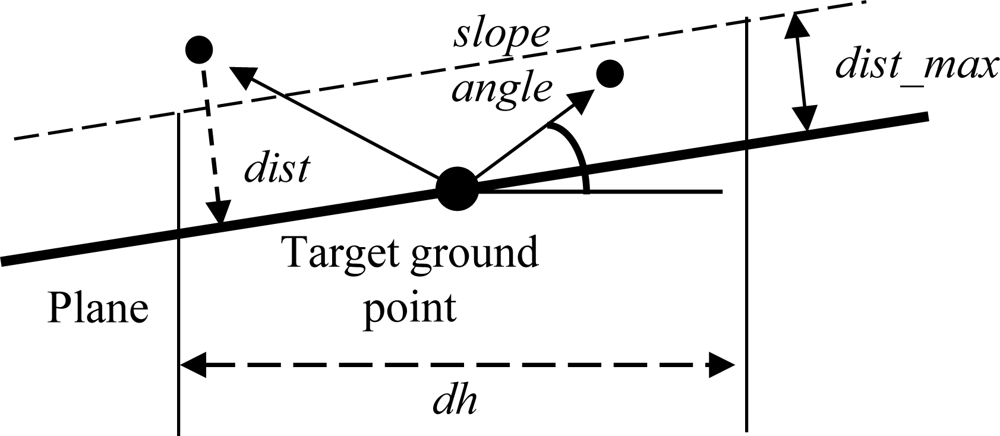
5.3. Definition of Slope Angle
5.4. Effect of Water Body Mask
5.5. Computation Time and Limitations
6. Conclusions
Acknowledgments
References and Notes
- Sithole, G.; Vosselman, G. Experimental comparison of filter algorithms for bare-earth extraction from airborne laser scanning point clouds. ISPRS J. Photogramm 2004, 59, 85–101. [Google Scholar]
- Vosselman, G. Slope based filtering of laser altimetry data. Int. Arch. Photogram. Remote Sens. Spat. Inform. Sci 2000, 33(B4), 935–942. [Google Scholar]
- Sithole, G. Filtering of laser altimetry data using a slope adaptive filter. Int. Arch. Photogram. Remote Sens. Spat. Inform. Sci 2001, 34(Pt. 3/W4), 203–210. [Google Scholar]
- Petzold, B.; Reiss, P.; Stossel, W. Laser scanning-surveying and mapping agencies are using a new technique for the derivation of digital terrain models. ISPRS J. Photogramm 1999, 54, 95–104. [Google Scholar]
- Wack, R.; Wimmer, A. Digital terrain models from airborne laser scanner data—A grid based approach. Int. Arch. Photogram. Remote Sens. Spat. Inform. Sci 2002, 34(Pt. 3B), 293–296. [Google Scholar]
- Sithole, G.; Vosselman, G. Filtering of airborne laser scanner data based on segmented point clouds. Int. Arch. Photogram. Remote Sens. Spat. Inform. Sci 2005, 36(Part 3/W19), 66–71. [Google Scholar]
- Zhang, K.; Chen, S.; Whitman, D.; Shyu, M.; Yan, J.; Zhang, C. A progressive morphological filter for removing non-ground measurements from airborne lidar data. IEEE Trans. Geosci. Remote Sens 2003, 41, 872–882. [Google Scholar]
- Chen, Q.; Gong, P.; Baldocchi, D.; Xie, G. Filtering airborne laser scanning data with morphological methods. Photogramm. Eng. Remote Sensing 2007, 73, 175–185. [Google Scholar]
- Meng, X.; Currit, N.; Zhao, K. Ground filtering algorithms for airborne LiDAR data: A review of critical issues. Remote Sens 2010, 2, 833–860. [Google Scholar]
- Lu, W.; Murphy, K.P.; Little, J.J.; Sheffer, A.; Fu, H. A hybrid conditional random field for estimating the underlying ground surface from airborne LiDAR data. IEEE Trans. Geosci. Remote Sens 2009, 47, 2913–2922. [Google Scholar]
- Yuan, F.; Zhang, J.; Zhang, L.; Gao, J. Urban DEM Generation from Airborne Lidar Data. Proceedings of Joint Urban Remote Sensing Event, Shanghai, China, 20–22 May 2009.
- Axelsson, P. Processing of laser scanner data—Algorithms and applications. ISPRS J. Photogramm. 1999, 54, 138–147. [Google Scholar]
- Axelsson, P. DEM generation from laser scanner data using adaptive TIN models. Int. Arch. Photogram. Remote Sens. Spat. Inform. Sci 2000, 33(Part B4/1), 110–117. [Google Scholar]
- Kobler, A.; Pfeifer, N.; Ogrinc, P.; Todorovski, L.; Oštir, K.; Džeroski, S. Repetitive interpolation: A robust algorithm for DTM generation from aerial laser scanner data in forested terrain. Remote Sens. Environ 2007, 108, 9–23. [Google Scholar]
- Terra Scan User’s Guide. Available online: http://www.terrasolid.fi/system/files/tscan_2.pdf (accessed on 31 August 2011).
- Wang, M.; Tseng, Y.H.; Chou, F.C. DEM Generation Using Adaptive Point Cloud Filtering Algorithm. Proceedings of the 25th Asia Conference on Remote Sensing, Chiang Mai, Thailand, 22–26 November 2004; pp. 55–60.
- Wang, C.K.; Tseng, Y.H. DEM generation from airborne LiDAR data by adaptive dual-directional slope filter. Int. Arch. Photogram. Remote Sens. Spat. Inform. Sci 2010, 38(Part 7B), 628–632. [Google Scholar]
- Mongus, D.; Žalik, B. Parameter-free ground filtering of LiDAR data for automatic DTM generation. ISPRS J. Photogramm 2012, 67, 1–12. [Google Scholar]
- Tóvári, D.; Pfeifer, N. Segmentation based robust interpolation—A new approach to laser data filtering. Int. Arch. Photogram. Remote Sens. Spat. Inform. Sci 2005, 36(Part 3/W19), 79–84. [Google Scholar]
- Bretar, F.; Chehata, N. Terrain modeling from LiDAR range data in natural landscapes: A predictive and Bayesian framework. IEEE Trans. Geosci. Remote Sens 2010, 48, 1568–1578. [Google Scholar]


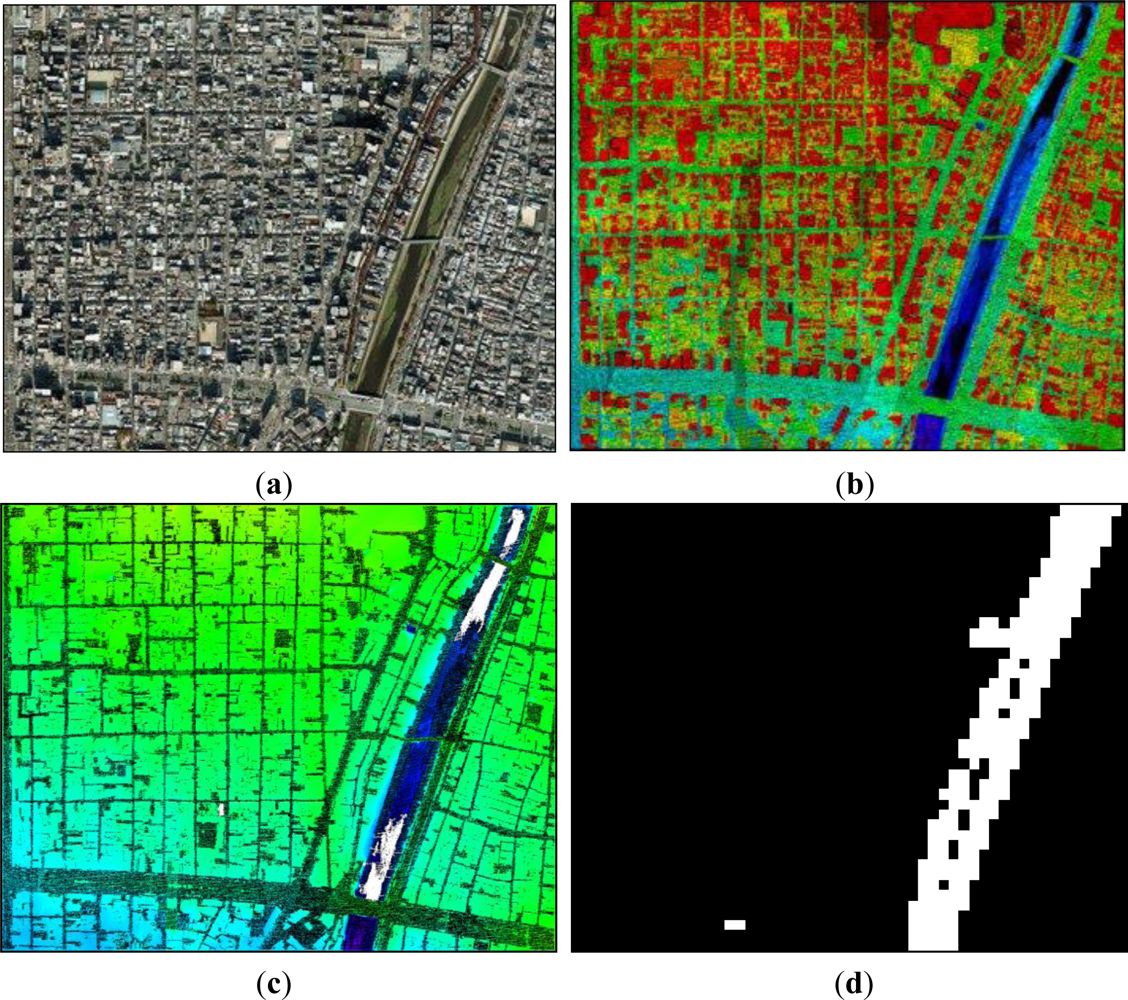
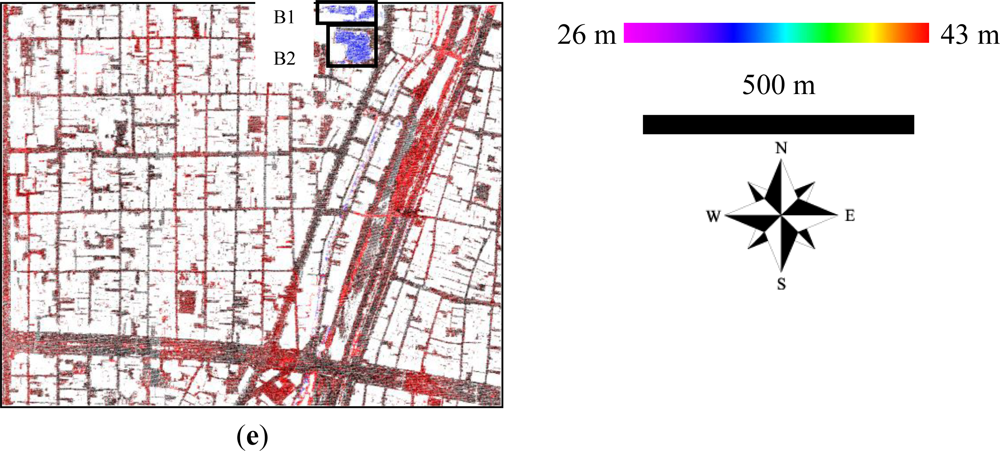
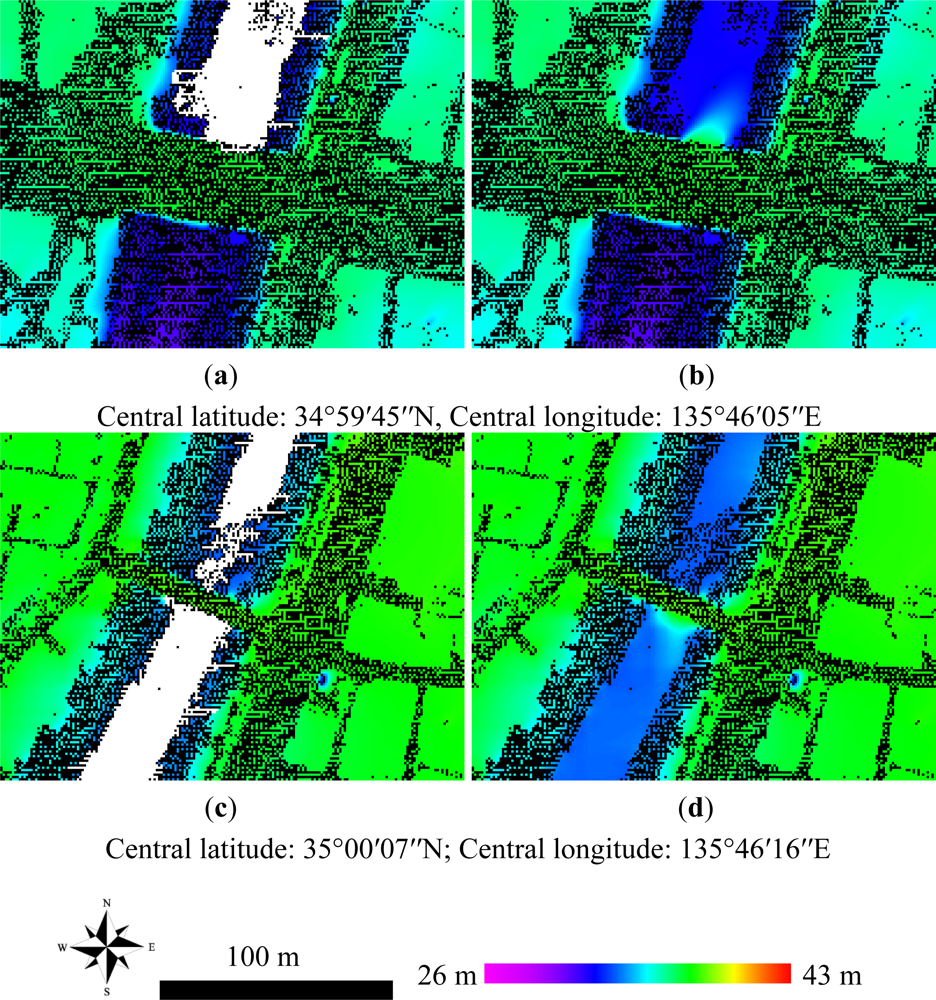
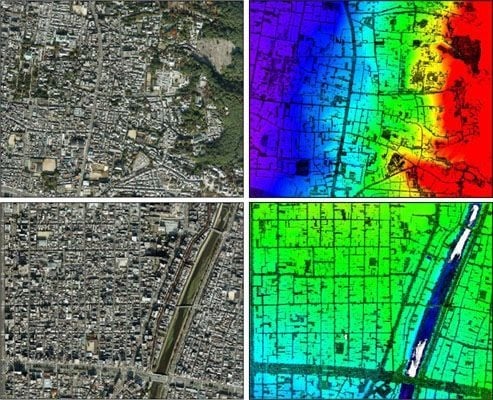
| Measurement date | June 2002 to February 2003 |
| Measurer | Aero Asahi Corporation |
| Density | Approx. 0.68 points/m2 |
| (calculated as valid pixels divided by all pixels of the area) | 0.70 for Higashiyama, and 0.66 for Nakagyo |
| Altitude | 900 to 1,000 m |
| Horizontal accuracy | ±50 cm |
| Vertical accuracy | ±15 cm |
| Process | Parameter | Value Used |
|---|---|---|
| Step (1): River extraction | Window size for initial area detection | 7 m × 7 m |
| Minimum area to accept water body | 100 m2 | |
| Step (2): Finding locally lowest points (LLPs) | Window size | 60 m × 60 m |
| Step (3): Planar surface calculation | Window size (used also in Steps (4) and (5)) | 5 m × 5 m |
| Minimum data number to calculate | 6 points | |
| Maximum root mean square of errors (RMSE) to accept plane | 0.1 m | |
| Maximum distance to plane (used also in Step (5)) | 0.1 m | |
| Minimum vertical component of planar normal | 0.9 | |
| Step (4): GP determination | Maximum slope (used also in Steps (5) and (8)) | 1st loop: 3° 2nd loop: 3° or 4.5°s |
| Maximum height difference to determine as GP (used also in Step (7)) | 0.5 m | |
| Step (6): DTM estimation | Maximum distance of the closest point (same as “Window size” in Step (2)) | 50 m |
| Maximum distance of other points | 100 m | |
| Window size for mean of DTM | 21 m × 21 m | |
| Sample | Algorithm | Total (%) | Type I (%) | Type II (%) |
|---|---|---|---|---|
| 11 | TerraScan | 16.14 | 26.66 | 2.00 |
| Mongus | 11.01 | 7.32 | 15.98 | |
| Proposed | 18.62 | 21.87 | 14.24 | |
| 12 | TerraScan | 11.55 | 21.49 | 1.12 |
| Mongus | 5.17 | 4.23 | 6.15 | |
| Proposed | 7.08 | 8.45 | 5.64 | |
| 21 | TerraScan | 11.56 | 14.30 | 1.95 |
| Mongus | 1.98 | 0.01 | 8.87 | |
| Proposed | 8.50 | 0.60 | 36.17 | |
| 22 | TerraScan | 10.78 | 14.51 | 2.56 |
| Mongus | 6.56 | 4.97 | 10.09 | |
| Proposed | 7.29 | 2.82 | 17.13 | |
| 23 | TerraScan | 8.01 | 12.92 | 2.54 |
| Mongus | 5.83 | 4.38 | 7.45 | |
| Proposed | 8.42 | 11.14 | 5.39 | |
| 24 | TerraScan | 12.97 | 16.38 | 3.98 |
| Mongus | 7.98 | 5.69 | 14.04 | |
| Proposed | 6.71 | 5.24 | 10.59 | |
| 31 | TerraScan | 4.85 | 8.36 | 8.97 |
| Mongus | 3.34 | 0.21 | 7.00 | |
| Proposed | 2.74 | 0.38 | 5.51 | |
| 41 | TerraScan | 13.15 | 25.10 | 0.74 |
| Mongus | 3.71 | 3.39 | 4.03 | |
| Proposed | 3.93 | 2.84 | 5.01 | |
| 42 | TerraScan | 2.55 | 8.00 | 1.39 |
| Mongus | 5.72 | 0.06 | 8.06 | |
| Proposed | 3.26 | 6.97 | 1.72 |
| Process | Parameter | Value Used |
|---|---|---|
| Classify ground | Max building size | 60 m |
| Iteration angle | 3.0° to plane | |
| Iteration distance | 0.5 m | |
| [Option] Reduce iteration angle | Off | |
| [Option] Stop triangulation | Off |
Share and Cite
Susaki, J. Adaptive Slope Filtering of Airborne LiDAR Data in Urban Areas for Digital Terrain Model (DTM) Generation. Remote Sens. 2012, 4, 1804-1819. https://doi.org/10.3390/rs4061804
Susaki J. Adaptive Slope Filtering of Airborne LiDAR Data in Urban Areas for Digital Terrain Model (DTM) Generation. Remote Sensing. 2012; 4(6):1804-1819. https://doi.org/10.3390/rs4061804
Chicago/Turabian StyleSusaki, Junichi. 2012. "Adaptive Slope Filtering of Airborne LiDAR Data in Urban Areas for Digital Terrain Model (DTM) Generation" Remote Sensing 4, no. 6: 1804-1819. https://doi.org/10.3390/rs4061804