A Conceptual Model of Surface Reflectance Estimation for Satellite Remote Sensing Images Using in situ Reference Data
Abstract
:1. Introduction
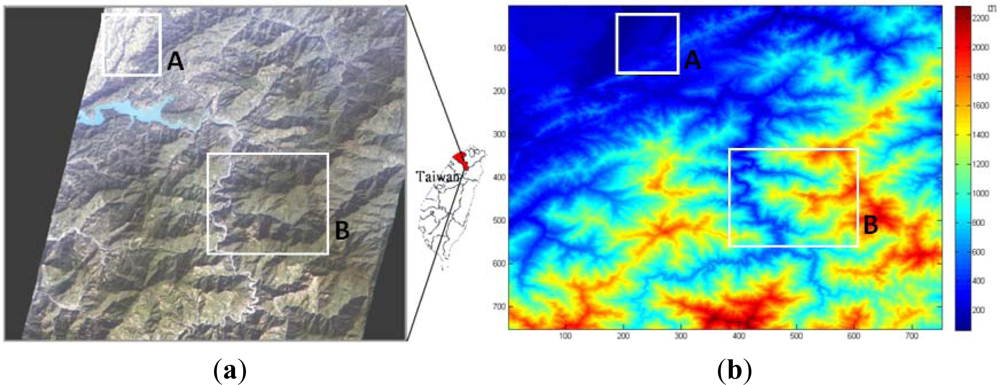
2. Study Area and Data
3. Methodology
3.1. At-Sensor Radiance Modeling
- (θ, ϕ)= the zenith and azimuth angles of the target-sun directions, respectively,
- Lpλ= path radiance,
- Eoλ= exoatmospheric solar irradiance with respect to spectral wavelength λ,
- Edλ= downwelled irradiance,
- rdλ= diffuse reflectance of the Lambertian surface,
- τ1λ= transmittance along the sun-target direction,
- τ2λ= transmittance along the target-sensor direction,
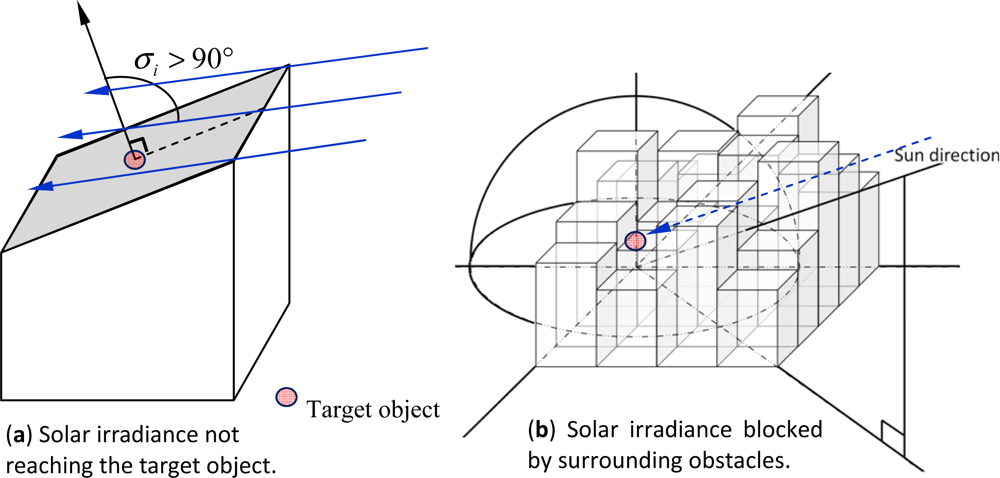
- F = shape factor due to obstruction of terrain slope or adjacent objects,
- σi= incidence angle of the solar irradiance at the target.
3.2. Identification of Shaded Ground Samples
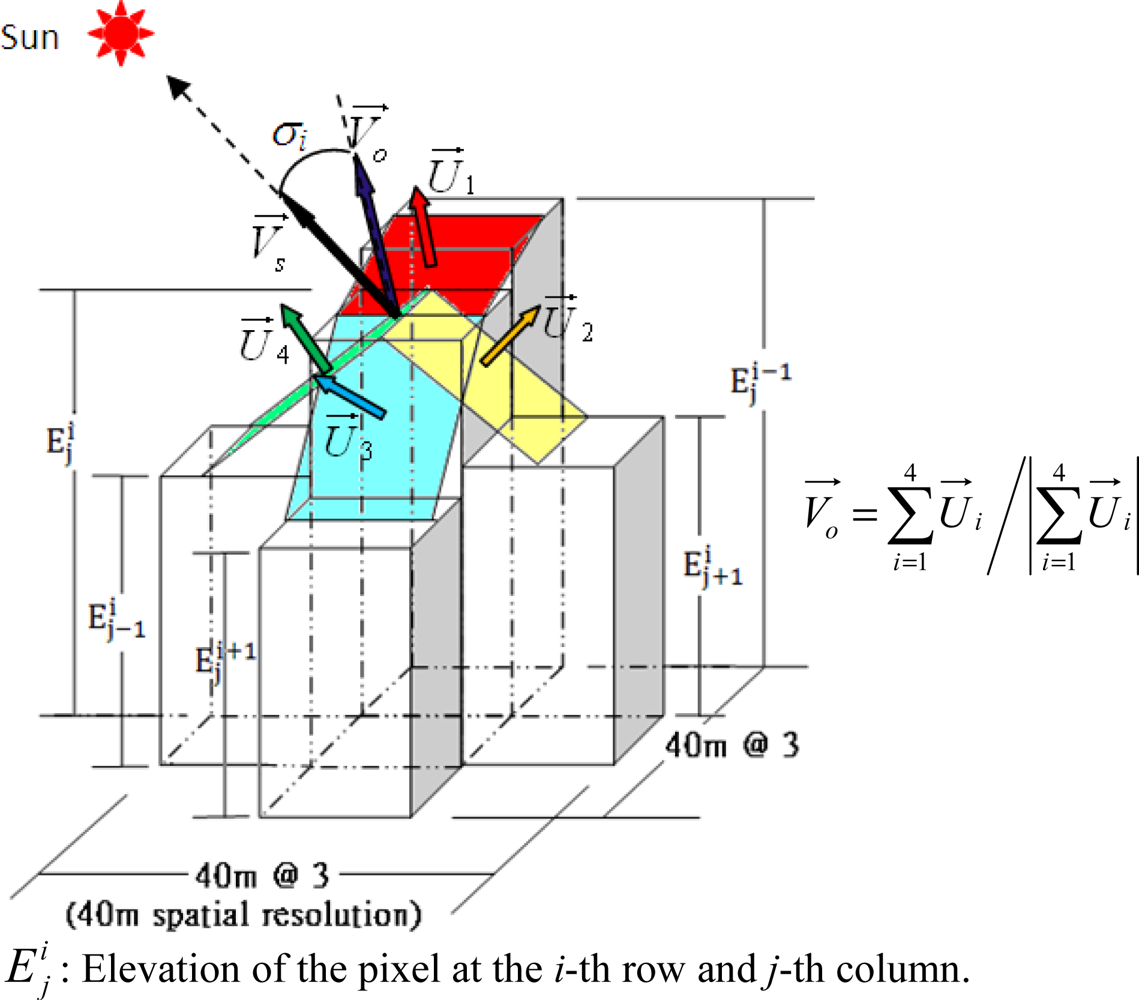
3.3. Modeling of the Shape Factor F
3.4. Estimation of Surface Reflectance Using RCA Samples
4. Results and Discussion
4.1. Calculation of cosσi
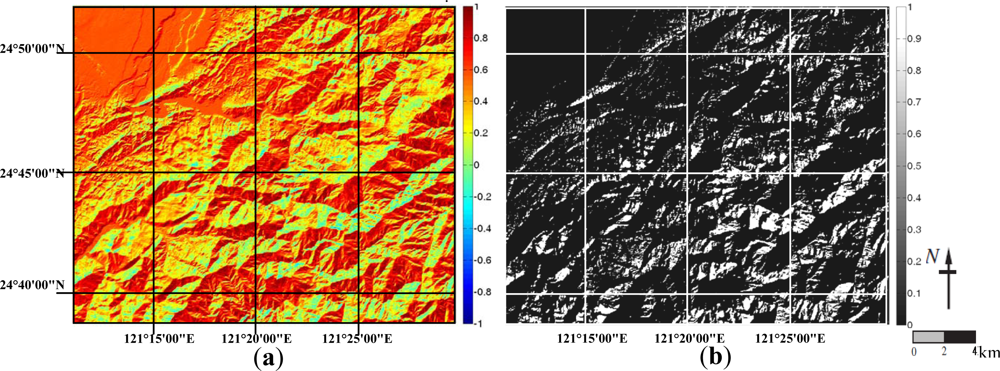
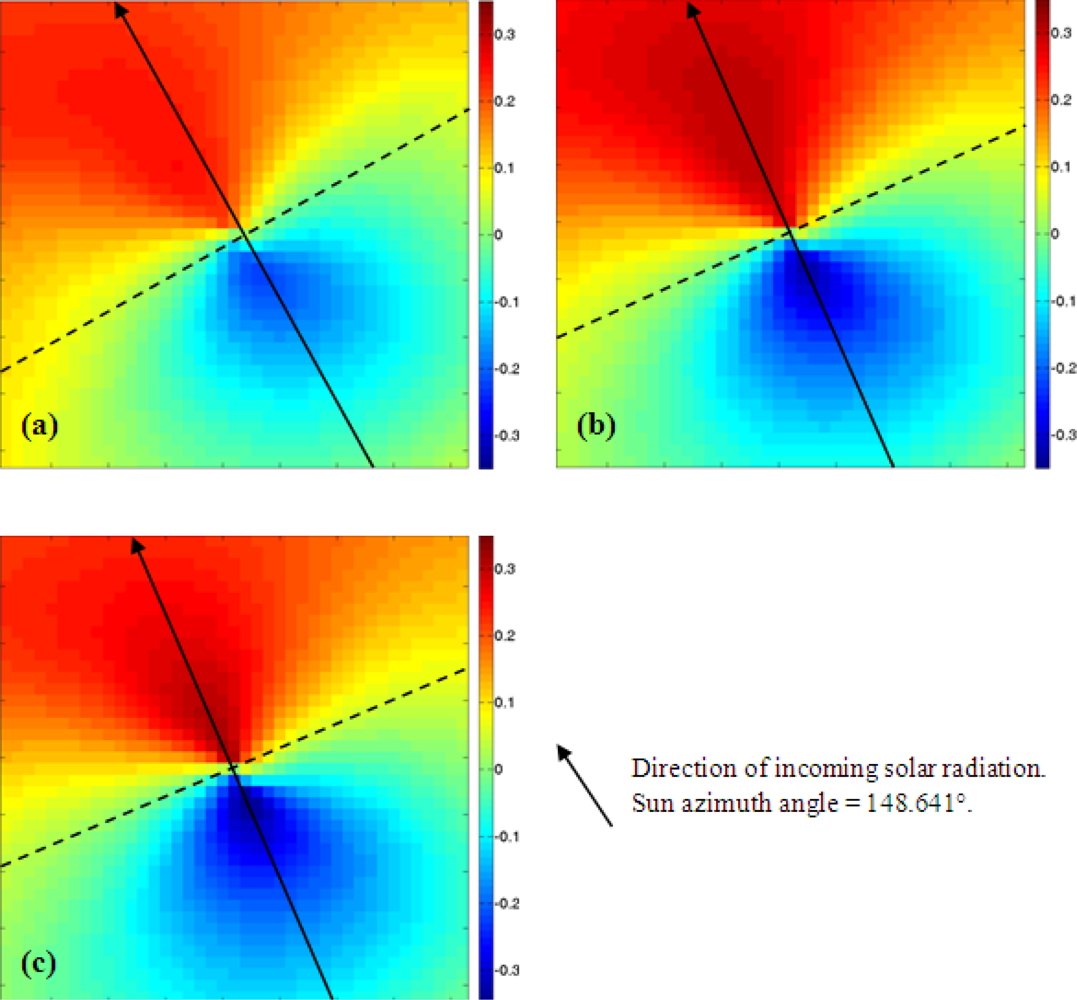
4.2. Correlation Map of Shaded Ground Samples
4.3. Assessing Estimates of Surface Reflectance
5. Conclusions
- A shaded sample identification algorithm using DEM data is proposed in this study.
- The correlation maps demonstrate a pattern that not only is consistent with the atmospheric scattering effect but also characterizes the effect of neighboring samples on radiance received at the target sample. Such result is an indication that the proposed shape factor model (Equation (14)) is physically reasonable.
- The proposed RCA-based surface reflectance estimation method is capable of achieving good reflectance estimates in a region where elevation varies from 0 to approximately 600 m above the mean sea level. Further study on variable size of the elevation matrix with respect to the degree of terrain variation is recommended in order to extend application of the proposed method to areas with substantial terrain variation.
Acknowledgments
References
- Weismiller, R.A.; Kristof, S.J.; Scholtz, D.K.; Anuta, P.E.; Momin, S.A. Change detection in coastal zone environments. Photogramm. Eng. Remote Sensing 1977, 43, 1533–1539. [Google Scholar]
- Vogelmann, J.E. Detection of forest change in the Green Mountains of Vermont using multispectral scanner data. Int. J. Remote Sens 1988, 9, 1187–1200. [Google Scholar]
- Nielsen, A.A.; Conradsen, K.; Simpson, J.J. Multivariate alteration detection (MAD) and MAF postprocessing in multispectral, bitemporal image data: new approaches to change detection studies. Remote Sens. Environ 1998, 64, 1–19. [Google Scholar]
- Teng, S.P.; Chen, Y.K.; Cheng, K.S.; Lo, H.C. Hypothesis-test-based landcover change detection using multi-temporal satellite images. Adv. Space Res 2008, 41, 1744–1754. [Google Scholar]
- Gates, D.M.; Keegan, H.J.; Schleter, J.C.; Weidner, V.R. Spectral qualities of plants. Appl. Opt 1965, 4, 11–20. [Google Scholar]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ 1979, 8, 127–150. [Google Scholar]
- Tucker, C.J.; Holben, B.N.; Elgin, J.H.; Mcmurtrey, J.E. Relation of spectral data to grain yield variation. Photogramm. Eng. Remote Sensing 1980, 46, 657–666. [Google Scholar]
- Asrar, G.; Fuchs, M.; Kanemasu, E.T.; Hatfield, J.L. Estimating absorbed photosynthetic radiation and leaf area index from spectral reflectance in wheat. Agron. J 1984, 76, 300–306. [Google Scholar]
- Slater, P.N. Remote Sensing: Optics and Optical Systems; Addison-Wesley: Reading, MA, USA, 1980; p. 592. [Google Scholar]
- Schott, J.R. Remote Sensing: The Image Chain Approach, 2nd ed.; Oxford University Press: New York, NY, USA, 2007; p. 688. [Google Scholar]
- Liang, S.; Fang, H.; Chen, M. Atmospheric correction of Landsat ETM+ land surface imagery: Part I: Methods. IEEE Trans. Geosci. Remote Sens 2001, 39, 2490–2498. [Google Scholar]
- Forster, B.C. Derivation of atmospheric correction procedures for Landsat MSS with particular reference to unban. Int. J. Remote Sens 1984, 5, 799–817. [Google Scholar]
- Chavez, P.S., Jr. An improved dark-object subtraction technique for atmospheric scattering correction of multispectral data. Remote Sens. Environ 1988, 24, 459–479. [Google Scholar]
- Chavez, P.S., Jr. Radiometric calibration of Landsat Thematic Mapper multispectral images. Photogramm. Eng. Remote Sensing 1989, 55, 1285–1294. [Google Scholar]
- Moran, M.S.; Jackson, P.N.; Slater, P.N.; Teillet, P.M. Evaluation of simplified procedures for retrieval of land surface reflectance factors from satellite sensor output. Remote Sens. Environ 1992, 41, 169–184. [Google Scholar]
- Cheng, K.S.; Su, Y.F.; Yeh, H.C.; Chang, J.H.; Hung, W.C. A path radiance estimation algorithm using reflectance measurements in radiometric control areas. Int. J. Remote Sens 2012, 33, 1543–1566. [Google Scholar]
- Switzer, P.; Kowalik, W.; Lyon, R.J.P. Estimation of atmospheric path-radiance by the covariance matrix method. Photogramm. Eng. Remote Sensing 1981, 47, 1469–1476. [Google Scholar]
- Mueller, R.; Behrendt, T.; Hammer, A.; Kemper, A. A new algorithm for the satellite-based retrieval of solar surface irradiance in spectral bands. Remote Sens 2012, 4, 622–647. [Google Scholar]
- Viggh, H.E.M.; Staelin, D.H. Spatial surface prior information reflectance estimation (SPIRE) algorithms. IEEE Trans. Geosci. Remote Sens 2003, 41, 2424–2435. [Google Scholar]
- Wen, J.; Liu, Q.; Liu, Q.; Xiao, Q.; Li, X. Parametrized BRDF for atmospheric and topographic correction and albedo estimation in Jiangxi rugged terrain, China. Int. J. Remote Sens 2009, 30, 2875–2896. [Google Scholar]
- Yang, S.Z.; Tseng, Y.H. Quality assessment for Digital Elevation Models. Journal of Photogrammetry and Remote Sensing 2008, 13, 195–206, (In Chinese with English abstract). [Google Scholar]
- Mendel, J.M. Lessons in Estimation Theory for Signal Processing, Communications, and Control; Prentice Hall: Upper Saddle River, NJ, USA, 1995; p. 561. [Google Scholar]
- Goodman, L.A. On the exact variance of products. J. Am. Statist. Assoc 1960, 55, 708–713. [Google Scholar]
- Neudecker, H.; Wesselman, A.M. The asymptotic variance matrix of the sample correlation matrix. Linear Algebra Its Appl 1990, 127, 339–599. [Google Scholar]


| Blue Band | Green Band | Red Band | |
|---|---|---|---|
| DNpλ | 59 | 19 | 8 |
| k1λ | 346.011 | 358.119 | 279.024 |
| k2λμ1 | 269.372 | 333.391 | 544.729 |
| k2λK | 47.662 | 36.112 | 28.326 |
| Methods | Blue Band | Green Band | Red Band |
|---|---|---|---|
| This study | 59 | 19 | 8 |
| DOS | 69 | 36 | 26 |
| AERONET | 29 | 19 | 13 |
Share and Cite
Chen, H.-W.; Cheng, K.-S. A Conceptual Model of Surface Reflectance Estimation for Satellite Remote Sensing Images Using in situ Reference Data. Remote Sens. 2012, 4, 934-949. https://doi.org/10.3390/rs4040934
Chen H-W, Cheng K-S. A Conceptual Model of Surface Reflectance Estimation for Satellite Remote Sensing Images Using in situ Reference Data. Remote Sensing. 2012; 4(4):934-949. https://doi.org/10.3390/rs4040934
Chicago/Turabian StyleChen, Hsien-Wei, and Ke-Sheng Cheng. 2012. "A Conceptual Model of Surface Reflectance Estimation for Satellite Remote Sensing Images Using in situ Reference Data" Remote Sensing 4, no. 4: 934-949. https://doi.org/10.3390/rs4040934




