1. Introduction
It can be argued that the wide use of polarimetric SAR data for Earth science applications is hindered by an incomplete understanding of the interactions of radar waves with multi-component landscape elements such as forest and crop structures. Such understanding may be improved by exploring the data through visual interpretation since human vision is particular effective at identifying spatial patterns and correlations. Current visualization strategies for polarimetric radar data can be split into two broad categories. Firstly there are those which examine the full co- and cross-polarized response of individual covariance matrices, or averages of these matrices (e.g., [
1–
3]). Secondly, there are techniques which attempt to apply standardized image processing techniques to polarimetric data sets in the form of grey scale intensity images (e.g., [
4,
5]), RGB composites (e.g., [
6,
7]) or IHS (Intensity, Hue, Saturation) composites (e.g., [
8]). Both of these approaches, however, provide only a partial representation of the data since neither is capable of showing simultaneously both the details of the polarimetric response and the spatial context of such data. Data analysis is therefore always constrained in some way, with the potential for partial or limited understanding of the nature of polarimetric response across a particular target scene.
The exploration of polarimetric response patterns may be improved by visualizing iconic representations of response graphs over large areas. Woodhouse
et al. [
9] describe a technique which combines polarimetric response graphs with the synoptic overview which is characteristic of traditional pixel-based remotely sensed imagery. In the current study a different methodology is described for visualizing fully polarimetric radar data in a synoptic manner by actively employing basic principles of scientific visualization to create graphical icons that convey five variables that can be extracted from the alpha-entropy decomposition [
10]. This icon-based approach allows for the creation of synoptic images that can be used to simultaneously examine five polarimetric variables and the spatial inter-relationships between them within the same image.
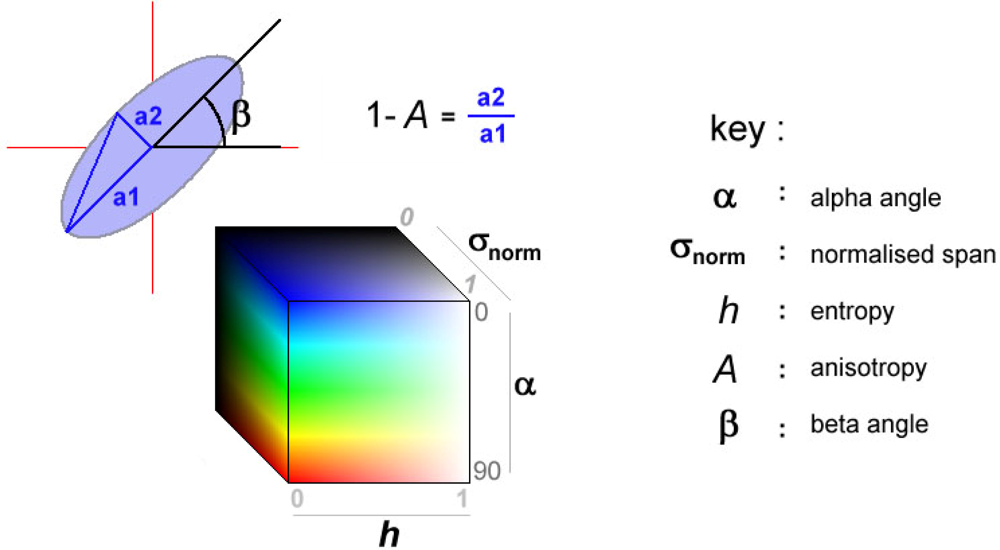
The conceptual basis for the visualization strategy exploits the varying perceptual qualities of visual variables to map total power, entropy, alpha angle, beta angle and anisotropy. As some of these variables have explicit geometric analogues, they can be mapped to the parameters of an ellipse. Even when the variables used do not relate directly to the geometric properties of scatterers, the use of the ellipse as an icon provides a match between the technical language of polarimetry and the graphical language developed by Bertin [
11].
Despite the structural simplicity of the proposed visualization technique, it is notable that the resulting images represent the first time, to the authors’ knowledge, that more than three polarimetric variables have been represented in a single synoptic image. Note, however, that the technique is presented here as an informative methodology for initial data inquiry and not as a substitute for model-based data analysis or classification maps. Instead, it forms an effective first-stage of visualization that is not difficult to implement, but allows a broad appreciation of the information contained within the data. In addition it should be noted that this work presents the methodology but makes no special claim to the efficacy of such a technique—rather it is presented as a novel way of exploring the geographic variation in polarimetric response.
4. Development of the Visualization Methodology
The new visualization technique presented here allows five variables to be mapped to a single location through the use of colored ellipses, in a manner similar to the technique used by Laidlaw
et al. [
20,
21] for visualizing diffusion tensors in a mouse’s spinal column. In
Figure 1, the visual parameterization of the ellipse is illustrated. The construction of images from these ellipses is achieved using the six stages outlined below:
Prior to the creation of each symbol, the pixels are sorted in terms of decreasing entropy, for reasons which are discussed later.
The values for A, α, β, H, and the normalized total power (σnorm) for each pixel are stored in a temporary vector, which is assigned to an image location where the ellipse will be created.
The initial size of the ellipse is found by setting the major axis to a value equal to the normalized total power (σnorm). Although there may be some advantage in mapping the power to the area of the ellipse, this would make narrow ellipses too large.
The anisotropy (A) is then used to define the minor axis, which is equal to (0.1 + 0.9 × (1 − A))σnorm. This means for locations where A= 0, a circular icon is produced, and where A= 1, a thin ellipse is used. The size of the minor axis is restricted to a minimum of 0.1 in order to ensure that the icon remains visible for the highest anisotropy values.
The ellipse is subsequently oriented about its center by β to represent scatterer orientation.
Finally, using the visualization technique proposed by [
8], the color of the ellipse is defined by the alpha angle (α), entropy (
H) and normalized total power (σ
norm), which are ascribed to hue, saturation and intensity values, respectively. The alpha angle is inverted and re-scaled to range between 240° and 0°, and the saturation channel inverted, so that low entropy surface interactions appear as saturated blue ellipses, and low entropy dihedral interactions as saturated red ellipses. Such a scheme therefore maps to the common visual language used for radar imagery.
The images presented in the following section are the result of many iterations, whereby the visualization structure was adapted in order to produce an optimum strategy which allowed the maximum information to be derived from the variables. Such iterations were based on visual analysis of output images, and included alterations to the maximum size of ellipses, and the scaling of intensity values. Preliminary visualizations, for example, placed ellipses in a sequential column-row structure, leading to visual artifacts in the final image caused by pronounced vertical bands of ellipses. In order to remove the banding, the ordering of the ellipses was changed. Instead of using the column/row structure of the data, the ellipses were placed at geographic locations based on the sorting of the entropy channel from high to low values. This produces a ‘jitter’ effect [
21] which acts to apparently randomize the placement of icons.
An additional advantage of this approach is that the high entropy values (from which little information can be derived) are plotted first, and form an underpainting onto which the lower entropy ellipses are placed. This is particularly useful as very low entropy icons are pushed to the front of the image, guiding the viewer to areas where potential information content is highest.
Even after this adjustment, however, the quality of the image was compromised due to the overcrowding of ellipses. In order to overcome this, it was decided that only one in every four data points would be represented on the image. This resulted in a cleaner image where the properties of an individual ellipse could be more easily analyzed. However, this approach runs the risk of ‘missing’ single low entropy targets, such as corner reflectors, which often form the most easily recognizable features in polarimetric datasets. For this reason, the routine was altered so that all ellipses for the final ten percent of the dataset (when sorted in order of decreasing entropy) were always represented.
5. Examples and Analysis
The following examples illustrate the application of the new visualization technique to polarimetric datasets. The first example, shown in
Figure 2, shows L-band quad-pol data collected over San Francisco by the JPL airborne polarimeter (AirSAR). This dataset is commonly used in polarimetric research as a means of testing new techniques, as it contains a variety of well-defined landscape components, including zones of urban development, vegetation, open water and bare rock. Other features of interest include geographical landmarks such as the Golden Gate Bridge, and individual buildings in Golden Gate Park. Examples of the usage of this dataset thus stretch from the first papers to appear on radar polarimetry [
22] up to more recent studies [
23,
24].
The visualization shown in
Figure 2, however, is unique in that it allows for the spatial analysis of five separate variables derived from the Cloude/Pottier decomposition, and reveals a number of interesting relationships and anomalies. In general, there is a clear divide between the three major landscape components. The ocean area, which dominates the majority of the image is characterized by low backscatter values, which decrease with increasing range distance. The dominant blue hue is indicative of low entropy surface scattering, although this is masked in areas of very low backscatter where entropy is high and the black background begins to dominate. The urban areas, in contrast, are characterized by high backscatter values and higher alpha angle values, evident in the yellow/red coloring of the ellipses. The final general regions of the image are the vegetated areas (including Golden Gate Park), which are characterized by high entropy values, and thus contain little color information.
It should be noted that the example images here are purposefully presented without a key to explain the characteristics of the individual ellipses. This is to emphasize the perceptual qualities of the image, rather than concentrate on the information content. The viewer is thus encouraged to ‘look at’ rather than ‘read’ the image, allowing patterns in the data to be established prior to the application of any prior knowledge relating to the nature of polarimetric scattering. If required, however,
Figure 1 acts as a key for all of the images shown here.
A further advantage of the icon-based approach is that it allows for multiple-scale enquiries. While the overview of
Figure 2 allows a quick orientation and assessment of the major scattering properties, a closer inspection allows a more detailed assessment of particular features.
Figure 3 shows a detail of
Figure 2, and allows contemplation of the extra information encoded in the beta angle and anisotropy values. Of particular interest is the difference between the cliffs and the built-up area. It is immediately apparent from the shape of the ellipses that the cliff are characterized by variable anisotropy values, whilst the urban area appears to be dominated by higher values. Both regions, however, have well-defined hues and so are low entropy environments, suggesting the presence of well-defined scattering regimes.
Over the cliffs, the low anisotropy and the low alpha angles support an interpretation of strong single scattering events caused by direct reflection. In the case of the built-up area, there is more variation in the anisotropy, and it is notable that many of the anisotropic ellipses have a yellow/green hue indicating intermediate alpha angle values. Where anisotropy is low, the alpha angle tends to be closer to 180, leading to red, circular icons. This relationship offers support for the assertion that anisotropy is related to the number of scattering mechanisms in a resolution element. In the built-up area, the bright red circular icons are likely to be indicative of pure dihedral scattering, especially as the most obvious example of this phenomena (just below the ‘s’ in buildings in
Figure 3) occurs on the range-ward side of the urban expanse. Deeper into the urban areas, backscatter is more likely to be dominated by a combination of dihedral scattering and direct backscatter, leading to higher anisotropy values, and intermediate alpha angle values.
The proposed visualization technique allows sets of hypotheses similar to those outlined above to be quickly applied to other regions of the image. For example, the presence of low entropy, low anisotropy surface scattering is also evident on the range-ward side of the hills in the upper portion of
Figure 2.
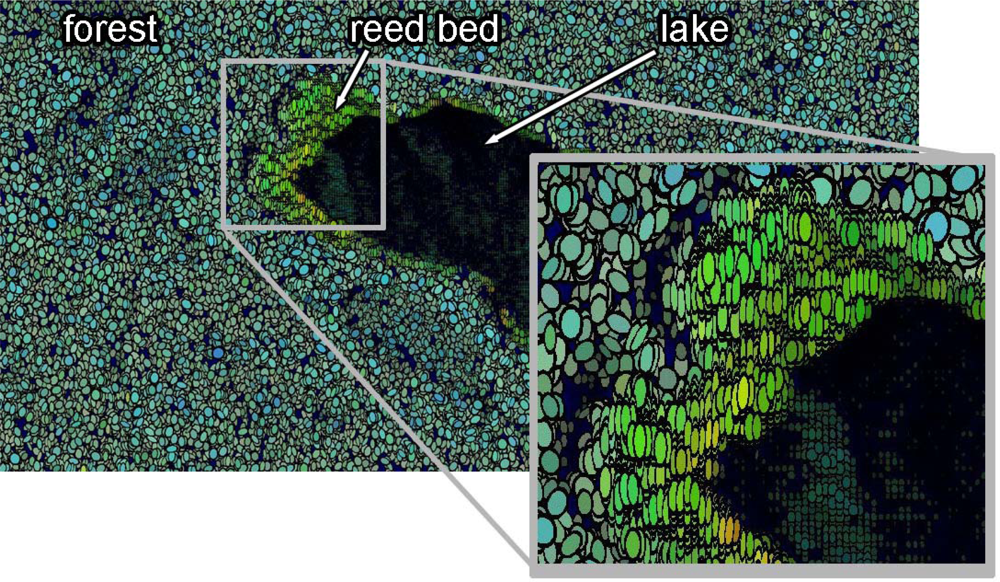
In
Figure 4, a second visualization is presented which shows C-band data collected by the EMISAR airborne polarimeter [
25]. Unlike the previous example, the majority of this dataset is dominated by a single landcover type, namely, managed boreal-type forest. The application of the new visualization technique immediately reveals that little information can be obtained from the anisotropy and beta angle parameters over this region, both of which exhibit apparently random values. The blue/green hue of the ellipses over the forested region suggests a mixture of direct canopy scatter and volume scattering, with stronger blue hues along gaps in the forest corresponding to roads and tracks.
By way of comparison,
Figure 5(a–d) shows the same data represented in some common RGB formats typically used to display polarimetric images.
Figure 5(e) shows not an RGB composite but a Hue-Saturation-Intensity image using the α-H decomposition composed of alpha angle for hue, entropy inversely mapped to saturation, and span to intensity. This is similar to how the color of the ellipses are derived in
Figure 4, but without the information on anisotropy and orientation angle. By definition, all the images in
Figure 5 are only able to show at most three channels of data, whereas
Figure 4 contains five.
What is also immediately apparent, however, is the presence of a region in the image which exhibits spatially continuous values for A and β. This region corresponds with an area of reed beds towards the shore of lake Siggefora, and is shown in the inset of
Figure 4. Note that the continuous beta angle values suggest the presence of vertically oriented scatterers, whilst the high anisotropy values indicate the presence of more than one dominant scattering mechanism. It is also notable that the alpha angle parameter is also continuous over this region, exhibiting an intermediate value. This is particularly interesting, as intermediate alpha angles are more typically associated with volume scattering [
14]. The low entropy angles, however, suggest the presence of a well-defined scattering regime which, on the basis of this visual representation alone, is worthy of further investigation.
The final example in this paper illustrates how the new visualization technique can be applied to a wide variety of polarimetric datasets. In
Figure 6, the technique is applied to a three-dimensional dataset derived from an experiment carried out at the European Microwave Signature Laboratory in 1996 into the application of polarimetric interferometry. The experiment involved placing a 5 m high Balsam Fir tree (
Abies Nordmanniana) in an anechoic chamber and measuring the full scattering matrix using two dual polarized horn antennas [
26].
The images shown in
Figure 6 are constructed using the same technique used for the previous 2D synoptic images. By viewing each of the individual slices, it is possible to examine the scattering properties of vegetation elements such as the tree trunk and major branches. The exploratory nature of these images can be further enhanced by creating animations that illustrate variations in polarimetric properties with respect to canopy depth. On viewing this data as an animation a number of features are readily apparent which can be used to describe the recorded data. The initial images, for example, contain blue, almost circular icons that represent the initial surface backscatter from the major branches in the tree. As the animation proceeds, these ellipses apparently become more anisotropic and migrate towards intermediate alpha angle values. Towards the end of the animation, the lower middle part of the image is dominated by highly anisotropic red ellipses, as a result of dihedral interactions between the chamber floor and the tree trunk. These ellipses also have similar beta angle values, suggesting the presence of vertically oriented scatterers.
6. Discussion
In this paper a visualization technique has been described that allows for the simultaneous visualization of five separate parameters, each of which describes a different aspects of polarimetric scattering. The use of an icon-based approach to visualize variables at specific geographic locations overcomes the three-channel limitation of both RGB and HSV pixel-based images and provides an intuitive link between the jargon of polarimetry and the visual image. This approach thus allows two less well-understood variables (namely, the beta angle and anisotropy) to be compared with three regularly applied variables (the alpha angle, entropy and total power) within their spatial context.
The visualization technique has been applied to a number of different datasets, highlighting areas where the inter-relationships between the five variables may provide further information on how each variable relates to different scattering properties. The value of such images is that the viewer is drawn to areas where strong patterns are apparent, and encouraged to develop hypotheses based on their spatial location and extent. Such an approach can be contrasted with other forms of visualization in remote sensing which rely more heavily on the identification of training areas, or areas of known cover type, and which therefore inherently involve either a priori assumptions or background knowledge of the area in questions.
A further advantage of this visualization strategy is that it is adaptable, and can be simply adjusted to accommodate different variables from those used above. In addition, the structure of the visualization can be adapted to emphasize particular aspects of the dataset. For example, in the above images, decreasing entropy was used to order the sequential layering of the ellipses. A minor adjustment to the IDL procedure would allow this ordering to be based on the total power, or indeed, any of the other variables used. This flexibility encourages an exploratory approach to visualization, whereby hypotheses can be quickly constructed and examined.
In summary, therefore, it can be stated that this new visualization technique allows the synoptic comparison of polarimetric variables which accommodates some of the benefits of both the standard full-image visualization methods with the non-geographic scatterplots. This approach, however, is limited by the fact that, by using a set of derived variables, any interpretation must be weighed against the validity of the chosen set of parameters as adequate indicators of polarimetric properties. The problem of how to most appropriately visualize ‘raw’ polarimetric data for any particular applications, therefore, remains unanswered and is the subject of further study by the authors.