Plant Species Richness is Associated with Canopy Height and Topography in a Neotropical Forest
Abstract
:1. Introduction
2. Materials and Methods
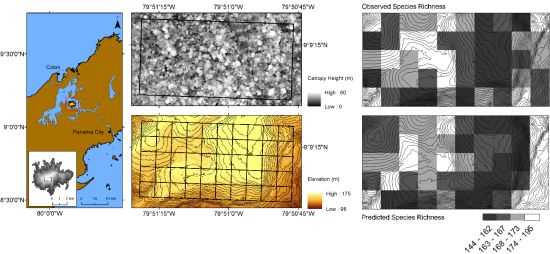
2.1. Study Area
2.2. Computing Species Richness
2.3. Lidar Data
2.3.1. Data Collection
2.3.2. Lidar Measured Variables
2.4. Data Analysis
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
remotesensing-04-04010-s001.pdfAcknowledgments
References
- Hubbell, S.P.; Foster, R.B. The Spatial Context of Regeneration in a Neotropical Forest. In Colonization, Succession and Stability; Crawley, M., Gray, A., Edwards, P.J., Eds.; Blackwell: Oxford, UK, 1987; pp. 395–412. [Google Scholar]
- Harms, K.E.; Condit, R.; Hubbell, S.P.; Foster, R.B. Habitat associations of trees and shrubs in a 50-ha neotropical forest plot. J. Ecol 2001, 89, 947–959. [Google Scholar]
- John, R.; Dalling, J.W.; Harms, K.E.; Yavitt, J.B.; Stallard, R.F.; Mirabello, M.; Hubbell, S.P.; Valencia, R.; Navarrete, H.; Vallejo, M.; Foster, R.B. Soil nutrients influence spatial distributions of tropical tree species. Proc. Natl. Acad. Sci. USA 2007, 104, 864–869. [Google Scholar]
- Engelbrecht, B.M.J.; Comita, L.S.; Condit, R.; Kursar, T.A.; Tyree, M.T.; Turner, B.L.; Hubbell, S.P. Drought sensitivity shapes species distribution patterns in tropical forests. Nature 2007, 447, 80–82. [Google Scholar]
- Comita, L.S.; Engelbrecht, B.M.J. Seasonal and spatial variation in water availability drive habitat associations in a tropical forest. Ecology 2009, 90, 2755–2765. [Google Scholar]
- Asner, G.P.; Mascaro, J.; Muller-Landau, H.C.; Vieilledent, G.; Vaudry, R.; Rasamoelina, M.; Hall, J.S.; van Breugel, M. A universal airborne LiDAR approach for tropical forest carbon mapping. Oecologia 2012, 168, 1147–1160. [Google Scholar]
- Dubayah, R.O.; Drake, J.B. Lidar remote sensing for forestry. J. Forest 2000, 98, 44–46. [Google Scholar]
- Lefsky, M.A.; Cohen, W.B.; Harding, D.J.; Parker, G.G.; Acker, S.A.; Gower, S.T. Lidar remote sensing of above-ground biomass in three biomes. Global Ecol. Biogeogr 2002, 11, 393–399. [Google Scholar]
- Hubbell, S.P.; Foster, R.B.; O’Brien, S.T.; Harms, K.E.; Condit, R.; Wechsler, B.; Wright, S.J.; de Lao, S.L. Light-gap disturbances, recruitment limitation, and tree diversity in a neotropical forest. Science 1999, 283, 554–557. [Google Scholar]
- Condit, R. Tropical Forest Census Plots; Springer-Verlag and R. G. Landes Company: Berlin, Germany, 1998. [Google Scholar]
- Schnitzer, S.A.; Mascaro, J.; Carson, W.P. Treefall Gaps and the Maintenance of Species Diversity in Tropical Forests. In Tropical Forest Community Ecology; Carson, W.P., Schnitzer, S.A., Eds.; Blackwell Publishing: Oxford, UK, 2008; pp. 196–209. [Google Scholar]
- Dalling, J.W.; Schnitzer, S.A.; Baldeck, C.; Harms, K.E.; John, R.; Mangan, S.A.; Lobo, E.; Yavitt, J.B.; Hubbell, S.P. Resource-based habitat associations in a neotropical liana community. J. Ecol 2012, 100, 1174–1182. [Google Scholar]
- Schnitzer, S.A.; Carson, W.P. Treefall gaps and the maintenance of species diversity in a tropical forest. Ecology 2001, 82, 913–919. [Google Scholar]
- Becker, P.; Rabenold, P.E.; Idol, J.R.; Smith, A.P. Water potential gradients for gaps and slopes in a panamanian tropical moist forests dry season. J. Trop. Ecol 1988, 4, 173–184. [Google Scholar]
- Daws, M.I.; Mullins, C.E.; Burslem, D.F.R.P.; Paton, S.R.; Dalling, J.W. Topographic position affects the water regime in a semideciduous tropical forest in Panama. Plant Soil 2002, 238, 79–90. [Google Scholar]
- Gentry, A.H. Changes in plant community diversity and floristic composition on environmental and geographical gradients. Ann. Missouri Bot. Garden 1988, 75, 1–34. [Google Scholar]
- Pyke, C.R.; Condit, R.; Aguilar, S.; Lao, S. Floristic composition across a climatic gradient in a neotropical lowland forest. J. Veg. Sci 2001, 12, 553–566. [Google Scholar]
- Lindzen, R.S.; Choi, Y.S. On the observational determination of climate sensitivity and its implications. Asia Pacific J. Atmos. Sci 2011, 47, 377–390. [Google Scholar]
- Croat, T.B. Flora of Barro Colorado Island; Stanford University Press: Stanford, CA, USA, 1978. [Google Scholar]
- Baillae, I.; Elsenbeer, H.; Barthold, F.; Grimm, R.; Stallard, R. Semi-detailed soil survey of Barro Colorado Island, Panama. Available online: http://biogeodb.stri.si.edu/bioinformatics/bci_soil_map/ (accessed on 6 January 2012).
- Moore, I.D.; Grayson, R.B.; Landson, A.R. Digital terrain modelling: A review of hydrological, geomorphological, and biological applications. Hydrol. Process 1991, 5, 3–30. [Google Scholar]
- Royston, J.P. An extension of Shapiro and Wilk’s W test for normality to large samples. Appl. Statist 1982, 31, 115–124. [Google Scholar]
- Cressie, N. Statistics for Spatial Data; Wiley: New York, NY, USA, 1991. [Google Scholar]
- Beale, C.M.; Lennon, J.J.; Yearsley, J.M.; Brewer, M.J.; Elston, D.A. Regression analysis of spatial data. Ecol. Lett 2010, 13, 246–264. [Google Scholar]
- Pinheiro, J.; Bates, D. Mixed-Effects Models in S and S-PLUS; Springer: New York, NY, USA, 2009. [Google Scholar]
- Pinheiro, J.; Bates, D.; DebRoy, S.; Sarkar, D.; R Development Core Team. nlme: Linear and Non-linear Mixed Effects Models, R package version 3.1–103. 2012.
- R: A language and environment for statistical computing. Available online: http://www.R-project.org (accessed on 1 March 2012).
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Automatic Control 1974, 19, 716–723. [Google Scholar]
- Baltagi, B.H. Econometrics, 5th ed.; Springer: New York, NY, USA, 2011. [Google Scholar]
- Draper, N.R.; Smith, H. Applied Regression Analysis, 3rd ed.; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Arlot, S.; Celisse, A. A survey of cross-validation procedures for model selection. Statistics Surveys 2010, 4, 40–79. [Google Scholar]
- Condit, R.; Hubbell, S.P.; Lafrankie, J.V.; Sukumar, R.; Manokaran, N.; Foster, R.B.; Ashton, P.S. Species-area and species-individual relationships for tropical trees: A comparison of three 50-ha plots. J. Ecol 1996, 84, 549–562. [Google Scholar]
- Asner, G.P.; Hughes, R.F.; Vitousek, P.M.; Knapp, D.E.; Kennedy-Bowdoin, T.; Boardman, J.; Martin, R.E.; Eastwood, M.; Green, R.O. Invasive plants transform the three-dimensional structure of rain forests. Proc. Natl. Acad. Sci. USA 2008, 105, 4519–4523. [Google Scholar]



| Parameter | Estimate | SE | 95 % CI | |
|---|---|---|---|---|
| Upper | Lower | |||
| Standard Deviation Canopy Height (SDCH) | 2.87 | 1.10 | 5.03 | 0.70 |
| Mean Canopy Height (MCH) | −0.97 | 0.38 | −0.23 | −1.71 |
| Mean Elevation | −0.39 | 0.16 | −0.07 | −0.70 |
| Mean Curvature | −31.7 | 10.7 | −10.7 | −52.6 |
| Intercept | 229.3 | 30.4 | 288.7 | 169.8 |
Share and Cite
Wolf, J.A.; Fricker, G.A.; Meyer, V.; Hubbell, S.P.; Gillespie, T.W.; Saatchi, S.S. Plant Species Richness is Associated with Canopy Height and Topography in a Neotropical Forest. Remote Sens. 2012, 4, 4010-4021. https://doi.org/10.3390/rs4124010
Wolf JA, Fricker GA, Meyer V, Hubbell SP, Gillespie TW, Saatchi SS. Plant Species Richness is Associated with Canopy Height and Topography in a Neotropical Forest. Remote Sensing. 2012; 4(12):4010-4021. https://doi.org/10.3390/rs4124010
Chicago/Turabian StyleWolf, Jeffrey A., Geoffrey A. Fricker, Victoria Meyer, Stephen P. Hubbell, Thomas W. Gillespie, and Sassan S. Saatchi. 2012. "Plant Species Richness is Associated with Canopy Height and Topography in a Neotropical Forest" Remote Sensing 4, no. 12: 4010-4021. https://doi.org/10.3390/rs4124010