Estimating the Maximal Light Use Efficiency for Different Vegetation through the CASA Model Combined with Time-Series Remote Sensing Data and Ground Measurements
Abstract
:1. Introduction
2. Material and Methods
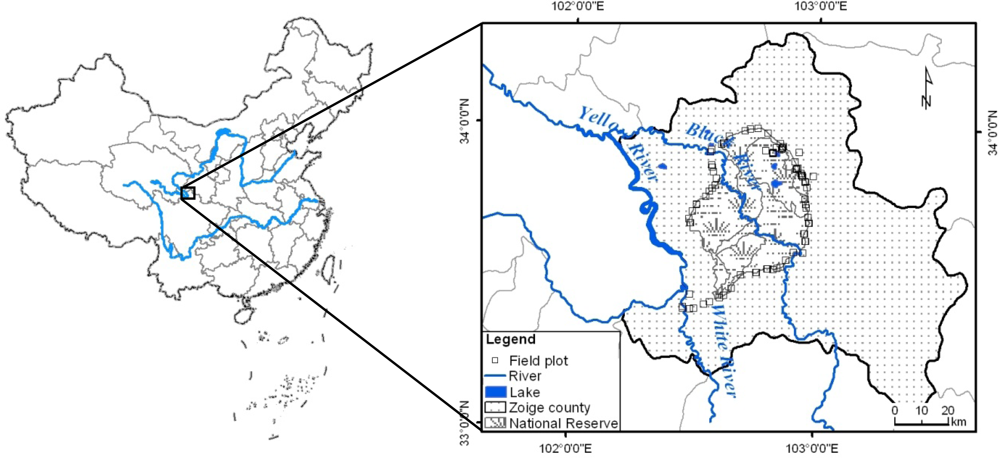
2.1. Study Area
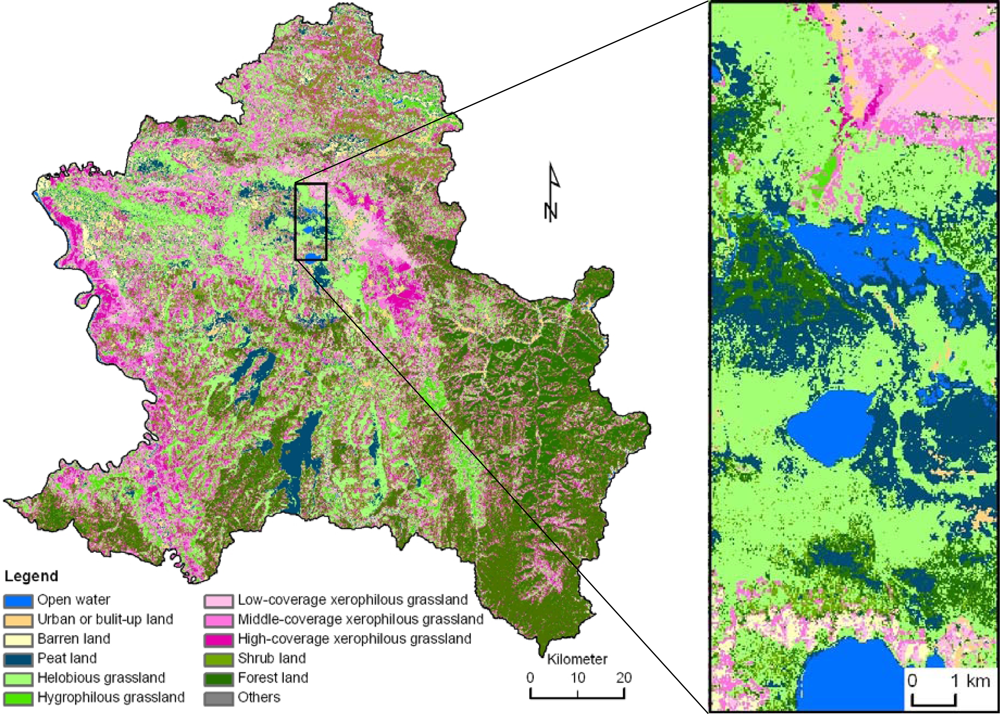
2.2. Data and Processing
2.2.1. Remote Sensing Data
2.2.2. The Meteorological Observations
2.2.3. The Ground Measurements
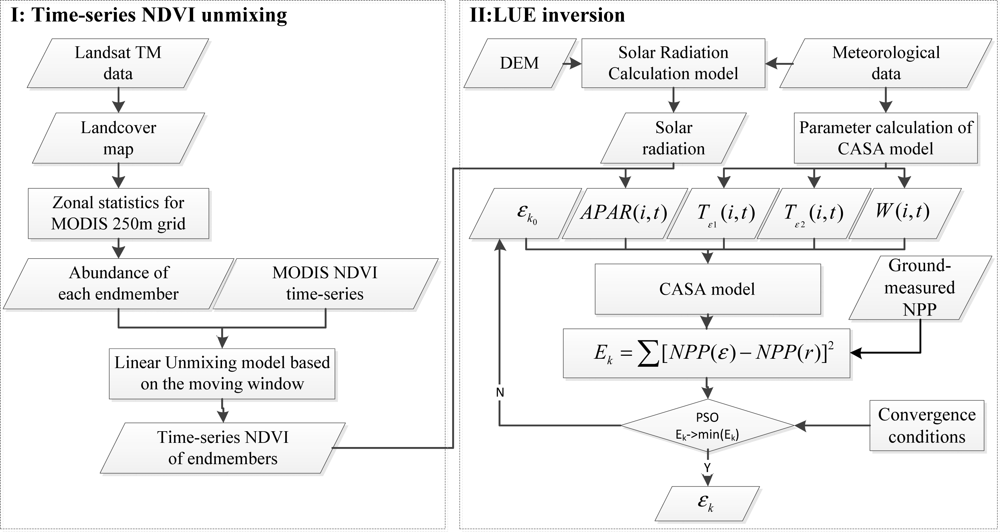
2.3. Model Development
2.3.1. The Time-Series NDVI Unmixing
2.3.2. Derivation of the Input Parameters for the CASA Model
2.3.3. Objective Function of the LUEs Inversion
2.3.4. Model Assessment
3. Results and Analysis
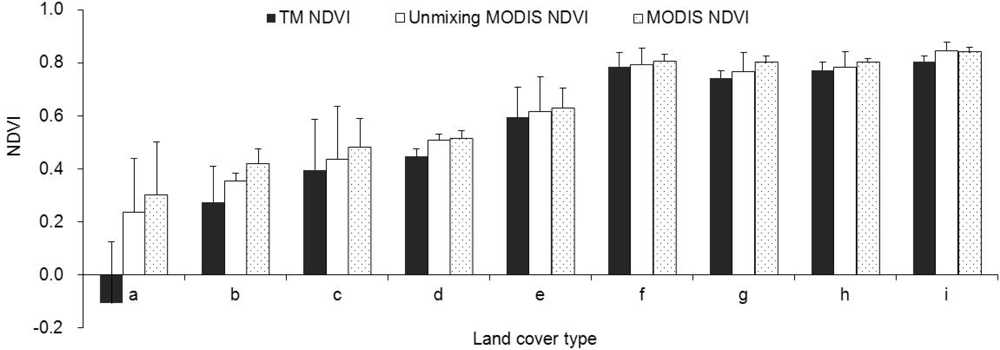
3.1. Unmixing of the Time-Series NDVI
3.2. The Derived Maximal LUEs
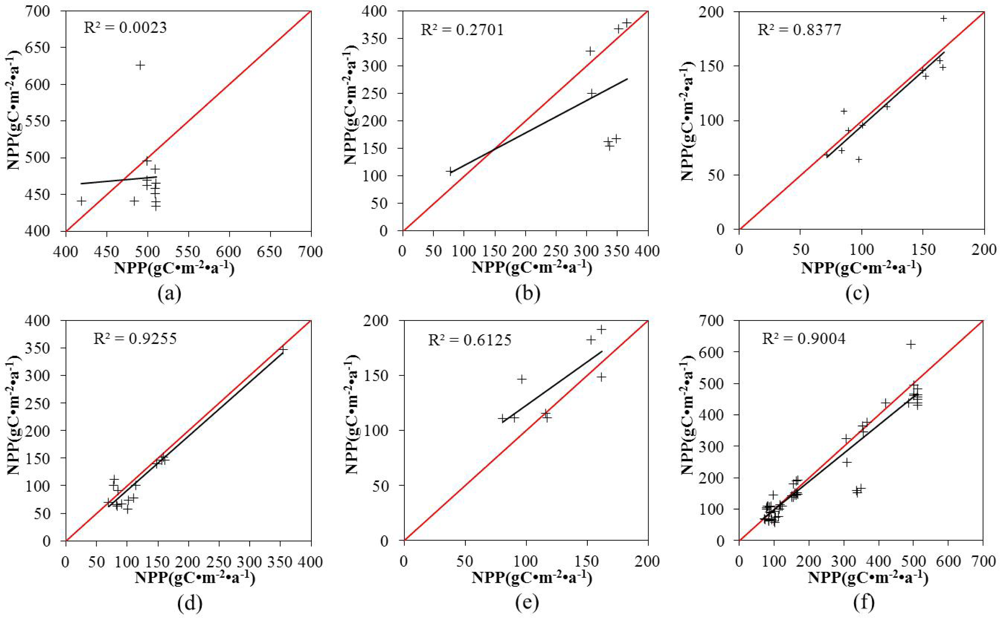
3.3. Accuracy Evaluation
4. Discussion
5. Conclusions
Acknowledgments
References
- Monteith, J.L. Solar radiation and productivity in tropical ecosystems. J. Appl. Ecol. 1972, 9, 747–766. [Google Scholar]
- Wang, H.; Li, X.; Long, H.; Zhu, W. A study of the seasonal dynamics of grassland growth rates in Inner Mongolia based on AVHRR data and a light-use efficiency model. Int. J. Remote Sens. 2009, 30, 3799–3815. [Google Scholar]
- Brogaard, S.; Runnstrom, M.; Seaquist, J.W. Primary production of Inner Mongolia China, between 1982 and 1999 estimated by a satellite data-driven light use efficiency model. Global Planet. Change 2005, 45, 313–332. [Google Scholar]
- As-syakur, A.R.; Osawa, T.; Adnyana, I.W.S. Medium spatial resolution satellite imagery to estimate gross primary production in an urban area. Remote Sens. 2010, 2, 1496–1507. [Google Scholar]
- Propastin, P.; Kappas, M. Modeling Net Ecosystem exchange for grassland in Central Kazakhstan by combining remote sensing and field data. Remote Sens. 2009, 1, 159–183. [Google Scholar]
- Turner, D.P.; Gower, S.T.; Cohen, W.B.; Gregory, M.; Maiersperger, T.K. Effects of spatial variability in light use efficiency on satellite-based NPP monitoring. Remote Sens. Environ. 2002, 80, 397–405. [Google Scholar]
- Bradford, J.B.; Hicke, J.A.; Lauenroth, W.K. The relative importance of light-use efficiency modifications from environmental conditions and cultivation for estimation of large-scale net primary productivity. Remote Sens. Environ. 2005, 96, 246–255. [Google Scholar]
- Zhao, Y.; Niu, S.; Wang, J.; Li, H.; Li, G. Light use efficiency of vegetation: A review. Chin. J. Ecol. 2007, 26, 1471–1477. [Google Scholar]
- Chen, J.; Tang, Y.; Chen, X.; Yang, W. The review of estimating light use efficiency through photochemical reflectance index(PRI). J. Remote Sens. 2008, 12, 331–337. [Google Scholar]
- Ahl, D.E.; Gower, S.T.; Mackay, D.S.; Burrows, S.N.; Norman, J.M.; Diak, G.R.H. Heterogeneity of light use efficiency in a northern Wisconsin forest: Implications for modeling net primary production with remote sensing. Remote Sens. Environ. 2004, 93, 168–178. [Google Scholar]
- Zhu, W.; Pan, Y.; He, J.; Yu, D.; Hu, H. Simulation of maximum light use efficiency for some typical vegetation types in China. Chin. Sci. Bull. 2006, 51, 457–463. [Google Scholar]
- Still, C.J.; Randerson, J.T.; Fung, I.Y. Large-scale plant light use efficiency inferred from the seasonal cycle of atmospheric CO2. Glob. Change Biol. 2004, 10, 1240–1252. [Google Scholar]
- He, D.; Hong, W.; Wu, C.; Lan, B.; Lin, C. Study on light energy utilization percent of phyllostachys pubescens population (In Chinese). J. FuJian College For. 1999, 19, 324–326. [Google Scholar]
- Zhu, Z.; Zhang, F. Solar energy utilization efficiency of the land plants in China (In Chinese). Acta Ecologica Sinica 1985, 5, 343–355. [Google Scholar]
- Xiao, X.; Zhang, Q.; Scott, S. Satellite-based modeling of gross primary production in a seasonally moist tropical evergreen forest. Remote Sens. Environ. 2005, 94, 105–122. [Google Scholar]
- Pei, B.; Yuan, Y.; Jia, Y.; Wang, W.; Josef, E. A study on light utilization of poplar crop intercropping system. Scientia Silvae Sinicae 2000, 36, 13–18. [Google Scholar]
- Jenkins, J.P.; Richardson, A.D.; Braswell, B.H.; Ollinger, S.V.; Hollinger, D.Y.; Smith, M.-L. Refining light-use efficiency calculations for a deciduous forest canopy using simultaneous tower-based carbon flux and radiometric measurements. Agr. Forest Meteorol. 2007, 143, 64–79. [Google Scholar]
- Schwalm, C.R.; Black, T.A.; Amiro, B.D.; Arain, M.A.; Barr, A.G.; Bourque, C.P.-A.; Dunn, A.L.; Flanagan, L.B.; Giasson, M.-A.; Lafleur, P.M.; et al. Photosynthetic light use efficiency of three biomes across an east-west continental-scale transect in Canada. Agr. Forest Meteorol. 2006, 140, 269–286. [Google Scholar]
- Zhang, M.; Yu, G.; Zhuang, J.; Gentry, R.; Fu, Y.; Sun, X.; Zhang, L.; Wen, X.; Wang, Q.; Han, S.; et al. Effects of cloudiness change on net ecosystem exchange, light use efficiency, and water use efficiency in typical ecosystems of China. Agr. Forest Meteorol. 2011, 151, 803–816. [Google Scholar]
- Hilker, T.; Hall, F.G.; Coops, N.C.; Lyapustin, A.; Wang, Y.; Nesic, Z.; Grant, N.; Black, T.A.; Wulder, M.A.; Kljun, N.; et al. Remote sensing of photosynthetic light-use efficiency across two forested biomes: Spatial scaling. Remote Sens. Environ. 2010, 114, 2863–2874. [Google Scholar]
- Hall, F.G.; Hilker, T.; Coops, N.C.; Lyapustin, A.; Huemmrich, K.F.; Middleton, E.; Margolis, H.; Drolet, G.; Black, T.A. Multi-angle remote sensing of forest light use efficiency by observing PRI variation with canopy shadow fraction. Remote Sens. Environ. 2008, 112, 3201–3211. [Google Scholar]
- Drolet, G.G.; Middleton, E.M.; Huemmrich, K.F.; Hall, F.G.; Amiro, B.D.; Barr, A.G.; Black, T.A.; McCaughey, J.H.; Margolis, H.A. Regional mapping of gross light-use efficiency using MODIS spectral indices. Remote Sens. Environ. 2008, 112, 3064–3078. [Google Scholar]
- Goerner, A.; Reichstein, M.; Rambal, S. Tracking seasonal drought effects on ecosystemlight use efficiency with satellite-based PRI in a Mediterranean forest. Remote Sens. Environ. 2009, 113, 1101–1111. [Google Scholar]
- Hilker, T.; Lyapustin, A.; Hall, F.G.; Wang, Y.; Coops, N.C.; Drolet, G.; Black, T.A. An assessment of photosynthetic light use efficiency from space: Modeling the atmospheric and directional impacts on PRI reflectance. Remote Sens. Environ. 2009, 113, 2463–2475. [Google Scholar]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar]
- Potter, C.S.; Randerson, J.T.; Field, C.B.; Matson, P.A.; Vitousek, P.M.; Mooney, H.A.; Klooster, S.A. Terrestrial ecosystem production: A process model based on global satellite and surface data. Global Biogeochem. Cycle. 1993, 7, 811–841. [Google Scholar]
- Running, S.W.; Baldocchi, D.D.; Turner, D.P.; Gower, S.T.; Bakwin, P.S.; Hibbard, K.A. A global terrestrial monitoring network integrating tower fluxes, flask sampling, ecosystem modeling and EOS satellite data. Remote Sens. Environ. 1999, 70, 108–127. [Google Scholar]
- Busetto, L.; Meroni, M.; Colombo, R. Combining medium and coarse spatial resolution satellite data to improve the estimation of sub-pixel NDVI time series. Remote Sens. Environ. 2008, 112, 118–131. [Google Scholar]
- Ichoku, C.; Karnleli. A review of mixture modeling techniques for sub-pixel land cover estimation. Remote Sens. Rev. 1996, 13, 161–186. [Google Scholar]
- Marsh, S.E.; Switzer, P.; Kowalik, W.S.; Lyon, R.J.P. Resolving the percentage of component terrains within single resolution elements. Photogramm. Eng. Remote Sens. 1980, 46, 1079–1086. [Google Scholar]
- Liang, S. Quantitative Remote Sensing of Land Surfaces; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2004. [Google Scholar]
- Chai, X.; Lang, H.; Jin, S. The Swamp of Zoige Plateau; (In Chinese). Science Press: Beijing, China, 1965. [Google Scholar]
- Ma, X.; Niu, H. Marsh of China; (In Chinese). Science Press: Beijing, China, 1991. [Google Scholar]
- Fei, S.; Cui, L.; He, Y.; Chen, X.; Jiang, J. A background study of the wetland ecosystem research station in the Ruoergai plateau. J. Sichuan Forestry Sci. Technol. 2006, 27, 21–29. (In Chinese) [Google Scholar]
- Yong, G.; Shi, C.; Qiu, P. Monitoring on desertification trends of the grassland and shrinking of the wetland in Ruoergai Plateau in North-West Sichuan by means of Remote sensing. J. Mt. Sci. 2003, 21, 758–762. (In Chinese) [Google Scholar]
- Qing, Q.; Hou, M.; Wang, M.; Tian, H. Influences of Meteorological conditions on growing period of Kentucky Bluegrass in Zoige grassland. Chin. J. Agrometeorology 2010, 31, 69–73. (In Chinese) [Google Scholar]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar]
- Bian, J.; Li, A.; Song, M.; Ma, L.; Jiang, J. Reconstructing NDVI time-series data set of MODIS based on the Savitzky-Golay filter. J. Remote Sens. 2010, 14, 725–741. [Google Scholar]
- Li, A.; Deng, W.; Liang, S.; Huang, C. Investigation on the patterns of global vegetation change using a satellite-sensed vegetation index. Remote Sens. 2010, 2, 1530–1548. [Google Scholar]
- Li, A.; Liang, S.; Wang, A.; Huang, C. Investigating the impacts of the North Atlantic Oscillation on global vegetation changes by a remotely sensed vegetation index. Int. J. Remote Sens. 2012, 33, 7222–7239. [Google Scholar]
- Masek, J.G.; Vermote, E.F.; Saleous, N.E.; Wolfe, R.; Hall, F.G.; Huemmrich, K.F.; Gao, F.; Kutler, J.; Lim, T. A land surface reflectance dataset for North America,1990–2000. IEEE Geosci. Remote Sens. Lett. 2006, 3, 68–72. [Google Scholar]
- Li, A.; Jiang, J.; Bian, J.; Deng, W. Combining the matter element model with the associated function of probability transformation for multi-source remote sensing data classification in mountainous regions. ISPRS J. Photogramm. 2012, 67, 80–92. [Google Scholar]
- Tian, Y. The vegetation type and its distribution regularity under different habitats in Zoige Plateau. J. Yangtze Univ. 2005, 2, 1–5. [Google Scholar]
- Zhang, R. Practical Remote Sensing Models and Ground Foundation; (In Chinese). Science Press: Beijing, China, 1996. [Google Scholar]
- Ångström, A. Solar and terrestrial radiation. Quart. J. Roy. Meteorol. Soc. 1924, 50, 121–125. [Google Scholar]
- Prescott, J.A. Evaporation from a water surface in relation to solar radiation. Trans. Roy. Soc. Sci. Austr. 1940, 64, 114–125. [Google Scholar]
- Lohr, S.L. Sampling: Design and Analysis; Duxbury Press: Pacific Grove, CA, USA, 1999. [Google Scholar]
- Raich, J.W.; Rastetter, E.B.; Mellillo, J.M.; Kicklighter, D.W.; Steudler, P.A.; Peterson, B.J.; Grace, A.L.; Moore, B.; Vorosmarty, C.J. Potential net primary productivity in South America: Application of a global model. Ecol. Appl. 1991, 1, 399–429. [Google Scholar]
- Fang, J.; Liu, G.; Xu, S. Biomass and net production of forest vegetation in China. Acta Ecologica Sinica 1996, 16, 497–508. [Google Scholar]
- Oleson, K.W.; Sarlin, S.; Garrison, J.; Smith, S.; Privette, J.L.; Emery, W.J. Unmixing multiple land-cover type reflectances from coarse spatial resolution satellite data. Remote Sens. Environ. 1995, 54, 98–112. [Google Scholar]
- Obata, K.; Miura, T.; Yoshioka, H. Analysis of the scaling effects in the area-averaged fraction of vegetation cover retrieved using an NDVI-isoline-based linearmixture model. Remote Sens. 2012, 4, 2156–2180. [Google Scholar]
- Maselli, F. Definition of spatially variable spectral endmembers by locally calibrated multivariate regression analyses. Remote Sens. Environ. 2001, 75, 29–38. [Google Scholar]
- Ruimy, A.; Saugier, B. Methodology for the estimation of terrestrial net primary production from remotely sensed data. J. Geophy. Res. 1994, 99, 5263–5283. [Google Scholar]
- Piao, S.; Fang, J.; Guo, Q. Application of CASA model to the estimation of Chinese terrestrial net primary productivity. Acta Phytoecologica Sinica 2001, 25, 603–608. [Google Scholar]
- Field, C.B.; Randerson, J.T.; Malmstrom, C.M. Global net primary production: Combining ecology and remote sensing. Remote Sens. Environ. 1995, 51, 74–88. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. Proceedings of the Fourth IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4. pp. 1942–1948.
- Quinlan, J.R. Combining Instance Based and Model-Based Learning. Proceedings of the 10th International Machine Learning Conference, Amherst, MA, USA, 27–29 June 1993; pp. 236–243.
- Li, B. Driving factors of zoige wetland desertification and countermeasures (In Chinese). China Pop. Resour. Environ. 2008, 18, 145–149. [Google Scholar]
- Peng, S.; Guo, Z.; Wang, B. Use of GIS and RS to estimate the light utilization efficiency of the vegetation in Guangdong, China. Acta Ecologica Sinica 2000, 20, 903–909. [Google Scholar]
- Zhu, W.; Pan, Y.; Zhang, J. Estimation of net primary productivity of Chinese terrestrial vegetation based on remote sensing. J. Plant Ecol. 2007, 31, 413–424. [Google Scholar]
- Nakaji, T.; Ide, R.; Oguma, H.; Saigusa, N.; Fujinuma, Y. Utility of spectral vegetation index for estimation of gross CO2 flux under varied sky conditions. Remote Sens. Environ. 2007, 109, 274–284. [Google Scholar]
- Myneni, R.B.; Williams, D.L. On the relationship between fAPAR and NDVI. Remote Sens. Environ. 1994, 49, 200–211. [Google Scholar]
- Kerdiles, H.; Grondona, M.O. NOAA-AVHRR NDVI decomposition and subpixel classification using linear mixing in the Argentinean Pampa. Int. J. Remote Sens. 1995, 16, 1303–1325. [Google Scholar]
- Malenovský, Z.; Bartholomeus, H.M.; Acerbi-Junior, F.W.; Schopfer, J.T.; Painter, T.H.; Epema, G.F.; Bregt, A.K. Scaling dimensions in spectroscopy of soil and vegetation. International J. Appl. Earth Obs. Geoinf. 2007, 9, 137–146. [Google Scholar]
- Marceau, D.J.; Hay, G.J. Remote sensing contributions to the scale issue. Can. J. Remote Sens. 1999, 25, 357–366. [Google Scholar]
- Yu, G.; Wang, Q. Ecophysiology of Plant Photosynthesis, Transpiration, and Water Use; (In Chinese). Science Press: Beijing, China, 2010. [Google Scholar]
- Battaglia, M.; Beadle, C.; Loughhead, S. Photosynthetic temperature response of Eucalyptus globulus and Eucalyptusnitens. Tree Physiol. 1996, 16, 81–89. [Google Scholar]
- Sullivan, N.H.; Bolstad, P.V.; Vose, J.M. Estimates of net photosynthetic parameters for tweleve tree species in mature foests of the southern Appalachina. Tree Physiol. 1996, 16, 397–406. [Google Scholar]
- Goetz, S.J.; Prince, S.N. Modelling terrestrial carbon exchange and storage: Evidence and implications of functional convergence in light-use efficiency. Advan. Ecol. Res. 1999, 28, 57–92. [Google Scholar]



| Vegetation Cover Type | Mean | Std.error | Maximum | Minimum | N |
|---|---|---|---|---|---|
| High-coverage xerophilous grassland | 497.80 | 30.14 | 532.00 | 416.10 | 12 |
| Middle-coverage xerophilous grassland | 314.16 | 48.76 | 378.10 | 220.00 | 8 |
| Low-coverage xerophilous grassland | 87.95 | 41.15 | 134.90 | 23.75 | 12 |
| Hygrophilous grassland | 140.36 | 70.78 | 233.22 | 33.25 | 16 |
| Helobious grassland | 86.62 | 43.17 | 152.00 | 28.50 | 8 |
| Vegetation Cover | Maximal LUE without Unmixing | Maximal LUE with Unmixing | ||||
|---|---|---|---|---|---|---|
| Minimum | Maximum | Optimum | Minimum | Maximum | Optimum | |
| High-coverage xerophilous grassland | 0.652 | 0.696 | 0.669 | 0.951 | 0.988 | 0.982 |
| Middle-coverage xerophilous grassland | 0.440 | 0.452 | 0.450 | 0.502 | 0.654 | 0.615 |
| Low-coverage xerophilous grassland | 0.117 | 0.149 | 0.126 | 0.141 | 0.200 | 0.144 |
| Hygrophilous grassland | 0.170 | 0.223 | 0.192 | 0.235 | 0.304 | 0.267 |
| Helobious grassland | 0.106 | 0.136 | 0.125 | 0.128 | 0.178 | 0.153 |
Share and Cite
Li, A.; Bian, J.; Lei, G.; Huang, C. Estimating the Maximal Light Use Efficiency for Different Vegetation through the CASA Model Combined with Time-Series Remote Sensing Data and Ground Measurements. Remote Sens. 2012, 4, 3857-3876. https://doi.org/10.3390/rs4123857
Li A, Bian J, Lei G, Huang C. Estimating the Maximal Light Use Efficiency for Different Vegetation through the CASA Model Combined with Time-Series Remote Sensing Data and Ground Measurements. Remote Sensing. 2012; 4(12):3857-3876. https://doi.org/10.3390/rs4123857
Chicago/Turabian StyleLi, Ainong, Jinhu Bian, Guangbin Lei, and Chengquan Huang. 2012. "Estimating the Maximal Light Use Efficiency for Different Vegetation through the CASA Model Combined with Time-Series Remote Sensing Data and Ground Measurements" Remote Sensing 4, no. 12: 3857-3876. https://doi.org/10.3390/rs4123857
APA StyleLi, A., Bian, J., Lei, G., & Huang, C. (2012). Estimating the Maximal Light Use Efficiency for Different Vegetation through the CASA Model Combined with Time-Series Remote Sensing Data and Ground Measurements. Remote Sensing, 4(12), 3857-3876. https://doi.org/10.3390/rs4123857






