Estimation of Evapotranspiration from Fields with and without Cover Crops Using Remote Sensing and in situ Methods
Abstract
:1. Introduction
2. Methods and Materials
2.1. METRIC
Land-Use and Elevation Maps
2.2. BREBS
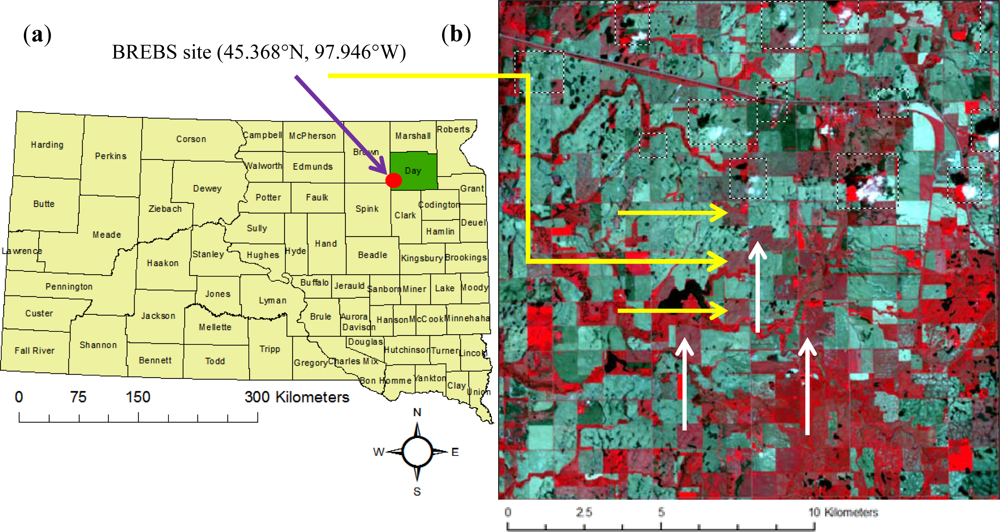
2.2.1. Location of Site
2.2.2. Crop Rotation
2.2.3. Calculation of EToF from BREBS Data
| ETo | = grass based reference evapotranspiration (mm · hr−1); |
| Rn | = net radiation at the grass surface (MJ m−2 · h−1); |
| G | = soil heat flux density (MJ m−2 · h−1); |
| Thr | = mean hourly air temperature (°C); |
| Δ | = saturation slope vapor pressure curve at Thr (kPa° · C−1); |
| γ | = psychrometric constant (kPa° · C−1) |
| e°(Thr) | = saturation vapor pressure at air temperature Thr (kPa); |
| ea | = average hourly actual vapor pressure (kPa); |
| Cd | = diurnal constant (0.24 s · m−1during daytime, 0.96 s · m−1during nighttime); |
| u2 | = average hourly wind speed at 2 m (m · s−1). |
2.3. Preparation of the Images
2.3.1. Cloud Masking
2.3.2. Spline Interpolation
2.3.3. Adjustment for Wet Image
2.3.4. Synthetic Images
2.4. Collation of the Data
3. Results and Discussion
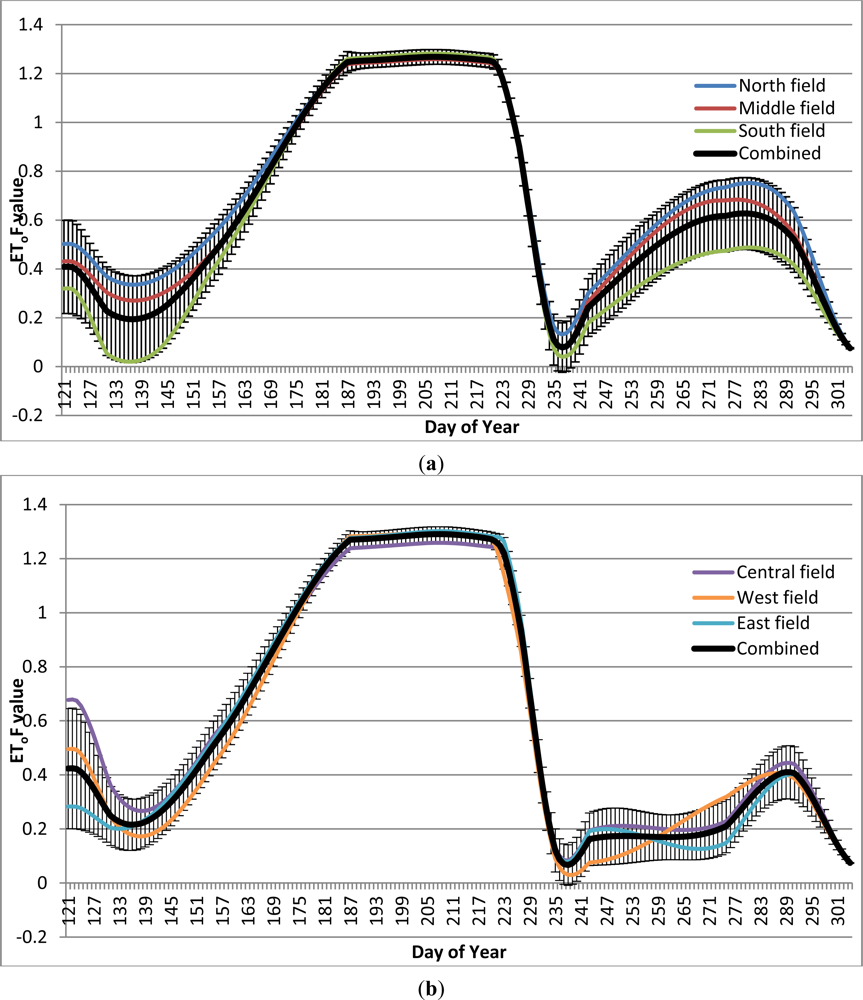
3.1. Analysis of the EToF Curves
3.1.1. Fields with Cover Crops
3.1.2. Fields without Cover Crops
3.2. Cover Crop Season
Statistical Analysis
4. Conclusions
List of Principal Acronyms and Abbreviations
| BREBS | Bowen-Ratio Energy Balance System; |
| ET | Evapotranspiration (mm); |
| ETa | Actual evapotranspiration (mm); |
| ETcc | Estimated actual evapotranspiration of fields planted into cover crop after wheat (mm); |
| ETno cc | Estimated actual evapotranspiration of fields not planted into cover crop after wheat (mm); |
| ETo | Grass-based reference evapotranspiration (mm); |
| EToF | Fraction of grass-based reference crop evapotranspiration (unit-less); |
| ETλE | Estimated actual evapotranspiration using BREBS data (mm); |
| Kc | Ideal crop coefficient (unit-less); |
| METRIC | Mapping Evapotranspiration at high Resolution using Internalized Calibration. |
Acknowledgments
References
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration. Guidelines for Computing Crop Water Requirements. In FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998; p. 300. [Google Scholar]
- ASCE-EWRI. The ASCE Standardized Reference Evapotranspiration Equation. In ASCE-EWRI Standardization of Reference Evapotranspiration Task Committee Report; ASCE: Reston, VA, USA, 2005; p. 216. [Google Scholar]
- Allen, R.G.; Tasumi, M.; Trezza, R. Satellite-based energy balance for Mapping Evapotranspiration with Internalized Calibration (METRIC)—Model. J. Irrig. Drain. Eng 2007, 133, 380–394. [Google Scholar]
- Dabney, S.M.; Delgado, J.A.; Reeves, D.W. Using winter cover crops to improve soil and water quality. Commun. Soil Sci. Plant Anal 2001, 32, 1221–1250. [Google Scholar]
- Keim, B.D. The lasting scientific impact of the Thornthwaite water-balance model. Geol. Rev 2010, 100, 295–300. [Google Scholar]
- Allen, R.G.; Irmak, A.; Trezza, R.; Hendrickx, J.M.H.; Bastiaansseen, W.; Kjaersgaard, J. Satellite-based ET estimation in agriculture using SEBAL and METRIC. Hydrol. Process 2011, 25, 4011–4027. [Google Scholar]
- Prueger, J.H.; Hatfield, J.L.; Sauer, T.J. Surface energy partitioning over rye and oats cover crops in central Iowa. J. Soil Water Cons 1998, 53, 263–268. [Google Scholar]
- Hay, C.H.; Irmak, S. Actual and reference evaporative losses and surface coefficients of a maize field during nongrowing (dormant) periods. J. Irrig. Drain. Eng 2009, 135, 313–322. [Google Scholar]
- Ruhoff, A.; Paz, A.; Collischonn, W.; Aragao, L.; Rocha, H.; Malhi, Y. A MODIS-based energy balance to estimate evapotranspiration for clear-sky bays in Brazilian tropical savannas. Remote Sens 2012, 4, 703–725. [Google Scholar]
- Teixeira, A. Determining regional actual evapotranspiration of irrigated crops and natural vegetation in the São Francisco River Basin (Brazil)—Using remote sensing and Penman-Monteith equation. Remote Sens 2010, 2, 1287–1319. [Google Scholar]
- Chavéz, J.; Gowda, P.; Howell, T.; Garcia, L.; Copeland, K.; Neale, C. ET mapping with high-resolution airborne remote sensing data in an advective semiarid environment. J. Irrig. Eng 2012, 138, 416–423. [Google Scholar]
- Bastiaanssen, W.G.M.; Menenti, M.; Feddes, R.A.; Holtslag, A.M.M. A remote sensing Surface Energy Balance Algorithm for Land (SEBAL): 1. Formulation. J. Hydrol. 1998, 212–213, 198–212. [Google Scholar]
- Tasumi, M.; Trezza, R.; Allen, R.G.; Wright, J.L. Operational aspects of satellite-based energy balance models for irrigated crops in the semi-arid US. J. Irrig. Drain. Eng 2005, 19, 355–376. [Google Scholar]
- Allen, R.G.; Tasumi, M.; Morse, A.T.; Trezza, R.; Kramber, W.; Lorite, I.; Robison, C.W. Satellite-based energy balance for Mapping Evapotranspiration with Internalized Calibration (METRIC)—Applications. J. Irrig. Drain. Eng 2007, 133, 395–406. [Google Scholar]
- Kjaersgaard, J.; Allen, R.G. Remote Sensing Technology to Produce Consumptive Water Use Maps for the Nebraska Panhandle; Kimberly R&E Center-University of Idaho: Aberdeen, ID, USA, 2010; p. 88. [Google Scholar]
- Irmak, A.; Ratcliffe, I.; Ranade, P.; Hubbard, K.; Singh, R.K.; Kamble, B.; Kjaersgaard, J. Estimation of land surface evapotranspiration with a satellite remote sensing procedure. Great Plains Res 2011, 21, 73–88. [Google Scholar]
- Kjaersgaard, J.; Allen, R.G.; Irmak, A. Monthly and growing season ET estimation from moderate-resolution satellites with accounting for precipitation events. Hydrol. Process 2011, 25, 4028–4036. [Google Scholar]
- Bastiaanssen, W.G.M. Regionalization of Surface Flux Densities and Moisture Indicators in Composite Terrain: A Remote Sensing Approach under Clear Skies in Mediterranean Climates. CIP Data Koninklijke Bibliotheek, Den Haag, The Netherlands, 1995; p. 273. [Google Scholar]
- Bowen, I.S. The ratio of heat losses by conduction and by evaporation from any water surface. Phys. Rev. C Nucl. Phys 1926, 27, 779–787. [Google Scholar]
- Kjaersgaard, J.; Trezza, R.; Allen, R.; Robison, C.; Oliveira, A.; Dhungel, R.; Kra, E. Filling Satellite Image Cloud Gaps to Create Complete Images of Evapotranspiration. Proceedings of Remote Sensing and Hydrology 2010 Symposium, Jackson Hole, WY, USA, 27–30 September 2010.


| Doy | Ls # | Clearness Index | Doy | Ls # | Clearness Index | DOY | LS # | Clearness Index |
|---|---|---|---|---|---|---|---|---|
| 123 | 7 | 1 | 187 | 7 | 0.9 | 251* | 7 | 0.95 |
| 131 | 5 | 0.95 | 195 | 5 | 0 | 259 | 5 | 0 |
| 139 | 7 | 0.4 | 203 | 7 | 0.7 | 267 | 7 | 0.8 |
| 147 | 5 | 0 | 211 | 5 | 0.5 | 275 | 5 | 1 |
| 155 | 7 | 0.85 | 219 | 7 | 0.55 | 283 | 7 | 0 |
| 163 | 5 | 0 | 227 | 5 | 1 | 291 | 5 | 1 |
| 171 | 7 | 0 | 235 | 7 | 1 | 299 | 7 | 0.2 |
| 179 | 5 | 0.75 | 243 | 5 | 1 |
| Measurement | Depth (mm) |
|---|---|
| ETo (BREBS) | 266 |
| ETλE (BREBS) | 136 |
| ETcc (METRIC) | 127 |
| ETno cc (METRIC) | 75 |
| Precipitation | 75 |
Share and Cite
Hankerson, B.; Kjaersgaard, J.; Hay, C. Estimation of Evapotranspiration from Fields with and without Cover Crops Using Remote Sensing and in situ Methods. Remote Sens. 2012, 4, 3796-3812. https://doi.org/10.3390/rs4123796
Hankerson B, Kjaersgaard J, Hay C. Estimation of Evapotranspiration from Fields with and without Cover Crops Using Remote Sensing and in situ Methods. Remote Sensing. 2012; 4(12):3796-3812. https://doi.org/10.3390/rs4123796
Chicago/Turabian StyleHankerson, Brett, Jeppe Kjaersgaard, and Christopher Hay. 2012. "Estimation of Evapotranspiration from Fields with and without Cover Crops Using Remote Sensing and in situ Methods" Remote Sensing 4, no. 12: 3796-3812. https://doi.org/10.3390/rs4123796




