3.1. Maize CWSI
Maize dT
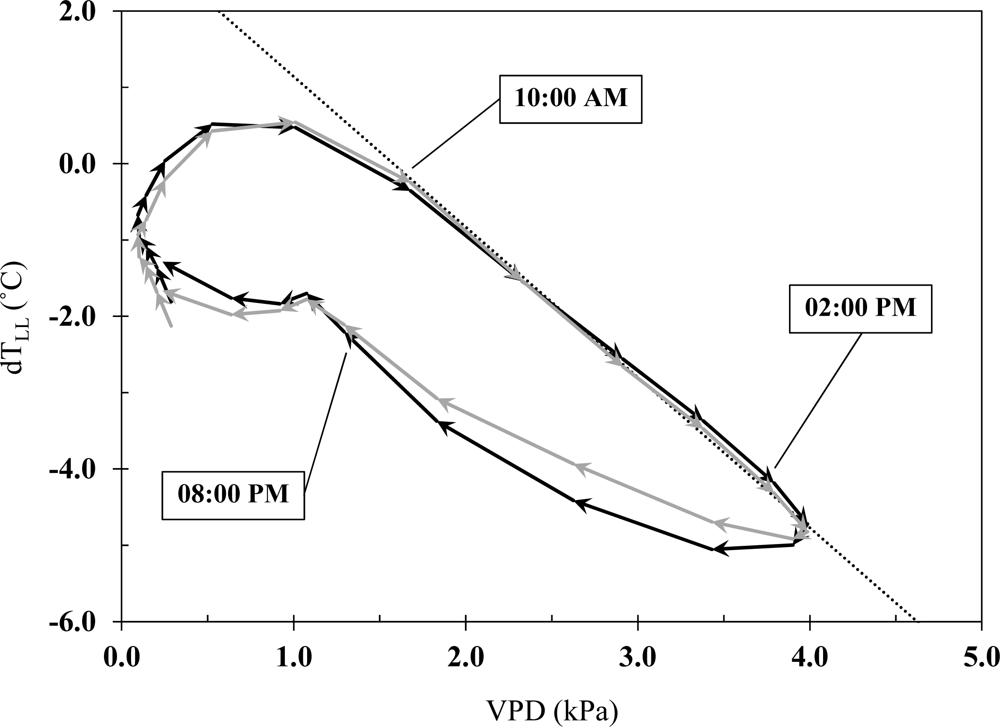
LL, for the semi-arid climate of the study area in Northeastern Colorado, was plotted with VPD for all four experimental plots using data from two dates that each occurred after a significant precipitation. As an example,
Figure 2 shows the resulting graph for plots L-1.1 and L-1.2, using the data collected on 15 August 2011 (R3/R4 stages).
The pattern observed in
Figure 2 is very similar to graphs presented in [
2], where dT
LL increases with increasing VPD for two to three hours after sunrise. At this point in time, incoming shortwave solar irradiance is large enough for stomata to fully open and allow for a transpiration rate equal to the T
c rate (provided sufficient water content is present in the soil root zone). Consequently, dT
LL decreases linearly with increasing VPD until a few hours before sunset, when dT
LL starts behaving differently (
Figure 2). The dotted black line in
Figure 2 presents the non-water-stressed baseline that was developed by Idso [
19] for maize grown in a semi-arid area of Arizona, USA. As it can be seen, the linear section of the dT
LL-
vs.-VPD plot in this study matches closely with this previously developed baseline. This linear section spans over a five-hour period between 10:00 and 15:00 (MST: Mountain Standard Time). However, only the data from two hours before and two hours after solar noon were considered for developing the non-water-stressed baseline and for conducting further analyses. Since solar noon was within a few minutes from 12:00 p.m. during the study, the selected four-hour period was from 10:00 to 14:00 (MST).
Fitting a linear line to the dT
LL-
vs.-VPD data obtained during this four-hour period on the mentioned two dates and over all treatments resulted in the following relationship:
Coefficients of
Equation (5) are close to those developed for maize and presented in [
19] (m = −1.97, b = 3.11) and [
20] (m = −1.97, b = 2.14). This similarity explains the observation of Taghvaeian
et al.[
6] that in comparison with five other previously developed baselines, these two sets of coefficients (from [
19,
20]) had the best performance in accurately defining upper and lower limits of dT
m values measured in this study. During the study period (5 August to 2 September), average dT
LL estimated from
Equation (5) was −1.5, −2.4, −3.1, and −3.8 °C during the 10–11, 11–12, 12–13, and 13–14 h, respectively. The increase in absolute value of dT
LL is due to the increase in VPD from a.m. to p.m. hours. The non-transpiring baseline was also defined using coefficients similar to those of
Equation (5). Average dT
UL over the same period increased from 4.0 °C at 10–11 h to 4.3 °C at 13–14 h, at a constant rate of 0.1 °C·h
−1. These values are similar to the average dT
UL of 4.6 °C, measured from 3 August to 12 September 1995 over a severely stressed maize plot under a Mediterranean semi-arid climate [
7].
Finally, the remote sensing-based CWSI was calculated for each of the one-hour periods between 10:00 and 14:00 (MST). As expected, each time frame resulted in a slightly different CWSI value estimate.
Figure 3 depicts the variation in hourly CWSIs for two plots, L-1.2 and L-2.2, during the four weeks of study. The depth of applied water through either irrigation or precipitation is also showed as vertical bars on a separate ordinate. According to
Figure 3, maize experienced almost no stress during the first week of the study (R2/R3 stages). This is mainly due to the fact that 30.5 mm of rain fell on the field on 4 August 2011. This precipitation event was followed by two more rainfalls during the first week that were not significant in amount, but probably enough to compensate for part of the 4 August rainfall that was evaporated from the soil surface or transpired by maize. CWSI then increased to less than 0.2 before the next precipitation event happened on 14 August 2011. The effect of this precipitation on lowering stress levels is obvious in
Figure 3. After this event, however, CWSI increased steadily until 25 August, which is when the average daily air temperature reached its maximum value of 27.9 °C during the study period. Decreased air temperatures and 21 mm of rainfall on 29 August caused CWSI to remain constant or decrease over the last week of the study (R6 stage). Based on the results, the irrigation that occurred on 21 August for these plots was not able to reverse the trend in CWSI variation, even though it provided 25 mm of water.
Table 3 presents the mean and median hourly CWSI values for all experimental plots during study period.
For each plot, the average CWSI increased from a lower value during the 10–11 h to a maximum value during the 12–13 h and then it decreased slightly during the last hour (13–14). Irmak
et al.[
7] also stated that the period between 12:00 and 13:00 was when CWSI was largest and thus, CWSI-based irrigation scheduling should use the data collected during this period of the day. They also found out that seasonal average of CWSI for maize planted under Mediterranean semiarid climate should stay below 0.22 in order to avoid any yield loss [
7]. This is similar to another previous finding that no significant yield loss occurred under an irrigation scheduling based on CWSI threshold of 0.20 [
20]. Based on the results, irrigation treatments did not have a significant effect on water stress experienced by maize. Average CWSI over all hourly periods was 0.27 and 0.29 for treatments L-1 and L-2, respectively.
3.2. CWSI and Soil Water Content
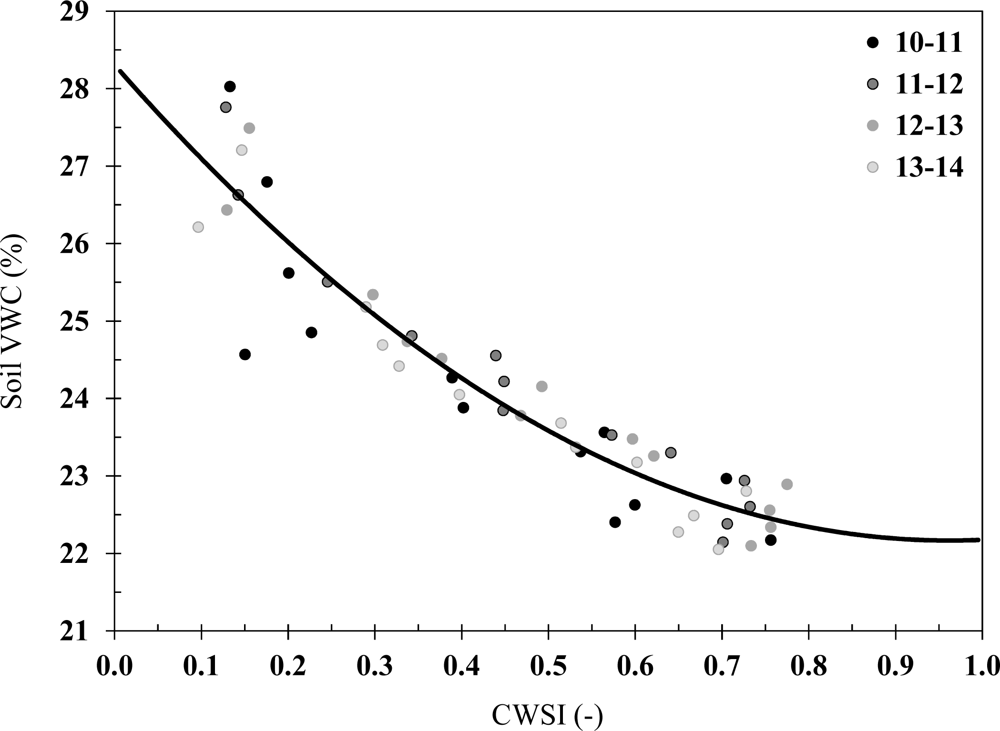
Soil VWC was plotted with CWSI values for each of the four hourly periods. As explained before, VWC data were collected only at plot L-2.1 at a depth of 5.0 cm from the soil surface. Recorded values were then corrected for the effect of soil temperature and were calibrated for the soil texture type using relationships developed in laboratory for the same type of soil [
13]. Plotted data were limited to a 13-day period that occurred during the last two weeks of August (R5/R6 stages) and in between two significant precipitation events (
Figure 4). The topsoil VWC was highly correlated to maize CWSI for all studied hourly periods. When the data from all periods were combined, the relationship between VWC and CWSI was best described by the following second order polynomial:
Based on
Equation (6), VWC would be equal to or greater than 28.31% at no stress and equal to or less than 22.18% at fully stressed conditions. This observation reveals that it only takes about 6% variation in total topsoil VWC to go from maize non-water-stressed to non-transpiring limits for the clay loam soil in Northeastern Colorado.
Several important points should be considered in interpreting and utilizing the CWSI-
vs.-VWC relationship presented in this study. First of all, VWC data that were used in developing
Equation (6) represent soil water content condition in only a thin top layer of the soil, which has larger diurnal temperature variations and it is also more subject to evaporation from the soil surface. As a result, the relationship would be different if the soil water content profile over the entire root zone (e.g., one meter) was included in the analysis. Such a relationship would be truly capable of approximating the amount of irrigation water that needs to be applied at a specific CWSI value and a specific soil type. This approach, however, has faced challenges in the past, as the effective root depth of crop changes during the season [
3]. The authors believe that a feasible solution to this issue is to divide the growing season into shorter growth stages. The CWSI-
vs.-VWC relationships developed over these shorter periods will have higher statistical confidence not only due to the fact that estimates of VWC over the root zone will be improved, but also because crops have different sensitivities to water stress at different growth stages.
Another modification that will considerably increase the utility of CWSI in predicting irrigation requirement is to replace soil VWC with soil matric potential, which would yield a relationship that is universal to all soil types. Then, for a specific soil type, the relationship between soil matric potential and soil water content would be needed,
i.e., the soil water characteristic curve. The second point that should be noted in interpreting
Equation (6) is that the data shown in
Figure 4 were collected during a 13-day period when maize was at R5/R6 (dent and physiological maturity) stage of growth. Since this crop (similar to other crops) has a variable sensitivity to water stress during different growth stages, developed relationships cannot be used to estimate VWC at other growth stages. For example, maize is believed to be more sensitive to water availability during VT (tasseling) and R1 (silking) stages. Thus, a smaller range of VWC values may have been observed if the data in this study were collected during these two stages. Similarly, it is expected that the CWSI-VWC curve would shift toward larger CWSI values after the R6 stage, since transpiration (the main process responsible for cooling the canopy) drops down due to crop senescence.
3.3. Maize Water Use
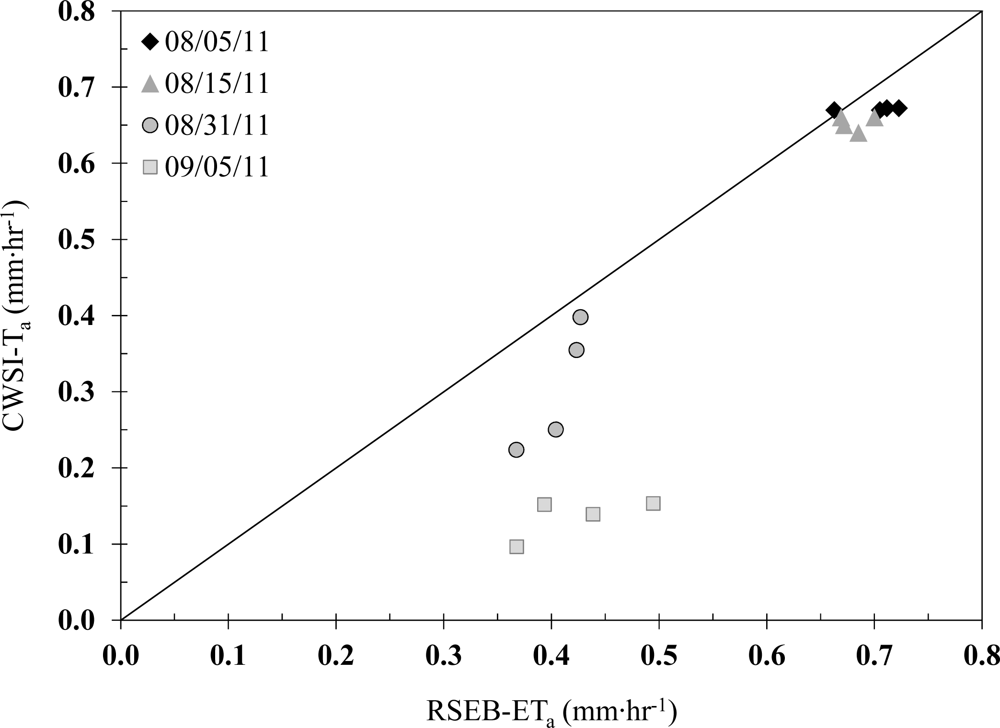
As the first step toward evaluating the performance of the CWSI method in estimating maize water use, hourly CWSI-T
a and RSEB-ET
a were compared on four dates when multispectral radiometer data were collected (
Figure 5). Hourly data were used for comparison in order to exclude any effect that extrapolating from hourly to daily values may have had on water use estimates.
The results showed that the difference between the two estimates increased over time as the crop transitioned from R2 into R6 phases. For the first date (5 August, R2 stage), RSEB-ET
a was 1% smaller than CWSI-T
a for plot L-2.2 and about 6% larger for the other plots. A high Soil Adjusted Vegetation Index (SAVI) of 0.68 indicates that the canopy was at full cover on this date. Thus, it is not surprising that T
a and ET
a estimates are very close to each other, since both nadir-looking radiometer and oblique IRT were viewing only plant leaves. On the second date (15 August, R3/R4 stages) ET
a was from 1% to 7% larger than T
a for all plots. Average SAVI was still rather high (0.63) on this date, meaning that the canopy remained close to full cover, as previous studies show that maize reaches full cover at a SAVI value of 0.64 [
21], which would correspond to a value of leaf area index (LAI) of 3.0 m
2·m
−2 or larger. On the third comparison date (31 August, R5/R6 stages), maize had entered into the maturity/senescence phase, and the growth stage was also more variable among treatments. While Plots L-1.1 and L-2.2 had an average SAVI value of 0.55, Plots L-1.2 and L-2.1 showed more signs of senescence and had an average SAVI of 0.43. So the hand-held multispectral radiometer was viewing both canopy and soil surface. On this date, ET
a estimates were 13% larger than T
a for the former two plots, but they were 63% larger for the latter two plots. It is worth mentioning that this date was preceded by a significant precipitation event (21.1 mm) that occurred two days earlier. The soil surface was still saturated when the field was visited for data collection and thus evaporation from the soil surface was taking place at a relatively high rate. On the last date (5 September R6 stage), all treatments were partially senesced and the average SAVI dropped to 0.37, resulting in ET
a estimates that were from 2.6 to 3.8 times larger than the T
a estimates.
Chávez
et al.[
16] showed that RSEB-ET
a results were in good agreement with estimates of maize ET from eddy-covariance latent heat flux towers, having a small error (mean ± std dev) of −9.2 ± 39.4 W·m
−2. A unit conversion using the average latent heat of vaporization that was estimated during data collection periods showed that this error is equivalent to −0.01 ± 0.06 mm·h
−1. Taking RSEB-ET
a results as a reference, the Mean Absolute Error (MAE) of CWSI-T
a was calculated as 0.03, 0.03, and 0.10 mm·h
−1 on the first three comparison dates, respectively. Limiting the analyses to plots that had larger biomass and therefore less exposed soil (L-1.1 and L-2.2) decreased MAE to 0.02, 0.02, and 0.05 mm·h
−1, respectively. Since these MAE estimates are obtained by comparing CWSI-T
a values to modeled (and not measured) values, they may not be regarded as actual errors of CWSI results. However, it is perhaps safe to conclude that the remote sensing-based CWSI method can yield water use estimates that are as accurate as the RSEB results, since MAE values are all within the accuracy range of the RSEB algorithm. This is a promising finding, as running RSEB models is by far more complicated and time-consuming than the CWSI approach.
Daily maize T
a estimates during the study period showed a pattern similar to what was observed in comparing hourly T
a and ET
a estimates. Plots L-1.1 and L-2.2 that had more biomass and later senescence transpired more water than Plots L-1.2 and L-2.1. T
a rates estimated for the former two plots were also closer to their corresponding ET
a rates compared to the latter two plots.
Figure 6 presents time series of maize water use for all of the studied plots. This figure is succeeded by
Table 4, which summarizes average and cumulative water use estimates for all treatments/plots and based on all implemented methods. Cumulative maize transpiration, averaged over all one-hour periods and the two plots with denser maize canopies (L-1.1 and L-2.2), was 130.9 ± 5.3 mm during the study period. Cumulative maize transpiration for the two plots with sparser maize canopies was 113.6 ± 3.0 mm for the same period. Estimated standard-condition crop transpiration (T
c) was 169.0 mm during the same period, suggesting that maize did experience some water stress, but it was not close to the level that was targeted by applying equal to or less than 114 mm of irrigation water during the growing season. This was due to the fact that limited amounts of irrigation application were accompanied by a higher-than-normal precipitation of 400 mm during the growing season. Such a significant amount of precipitation also masked the effects of different irrigation treatments. As expected, CWSI-T
a estimates were largest and smallest when calculated based on data collected during 10–11 and 12–13 time frames, respectively. Although the magnitude of the difference was not significant (total T
a for 12–13 was from 5% to 10% smaller than 10–11 results among studied plots), these variations should still be considered when selecting a time frame for remote sensing data collection (
i.e., IRT data).
Maize ET
a based on the implemented RSEB model did not have a similar behavior to T
a approximations of the CWSI method. ET
a estimates were much closer among plots, with Plots L-2.1 and L-1.2 having the smallest (156.6 mm) and the largest (161.5 mm) evapotranspiration, respectively. Since comparing hourly CWSI-T
a and RSEB-ET
a showed that both methods generated similar results when only maize leaves were viewed, the different behavior and larger magnitude of total ET
a compared to T
a was most probably due to the effect of water evaporation from the soil surface. As all plots received rather frequent water applications (irrigation or precipitation), lower transpiration at sparser locations was compensated by higher evaporation, resulting in comparable ET
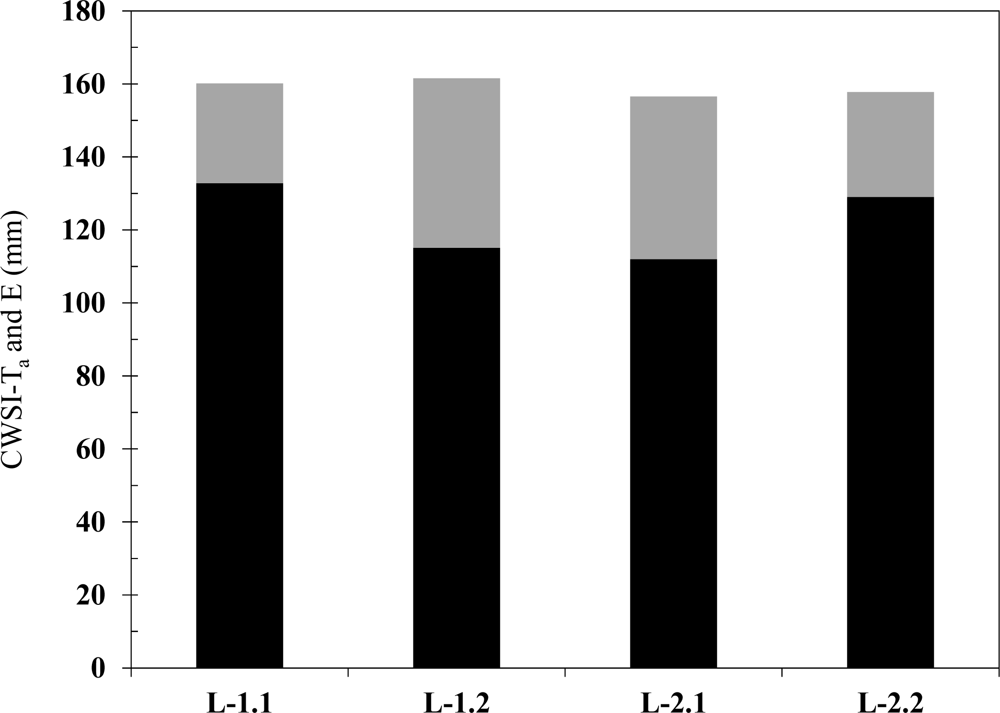
a estimates. During the 29 days of study, maize total transpiration (averaged over all hourly periods) was 132.8, 115.1, 112.0, and 129.1 mm for L-1.1, L-1.2, L-2.1, and L-2.2 plots, respectively (
Figure 7). Maize average RSEB-ET
a for all plots was 159.0 mm, 9% smaller than the standard-condition maize ET
c (173.9 mm) during the same period. Ignoring the inherent error in the results of each method, average water evaporation from the soil surface (E) can be estimated by subtracting CWSI-T
a from RSEB-ET
a. Estimated E was 36.8 mm on average, which accounts for 23% of the total ET
a during the study period.
The ratio of maize ETc to ETa was 1.09, significantly smaller than the ratio of maize Tc to Ta, which varied from 1.33 to 1.43 among the results of hourly periods. In other words, when compared to their corresponding rates under standard (stress-free) conditions, actual transpiration was more reduced than actual evapotranspiration. This difference may imply that evaluating crop Ta can provide more information on the presence and severity of water stress compared to ETa, which also includes water evaporation from the soil surface. Results found in this study are evidence that remote sensing-based maize water stress can be monitored, using infrared thermometry and weather data, to infer on when to irrigate and how much water to apply.