1. Introduction and Background
The magnitude of the surface temperature response of the climate system to an imposed radiative energy imbalance remains just as uncertain today as it was decades ago [
1]. Over 20 coupled ocean-atmosphere climate models tracked by the Intergovernmental Panel on Climate Change (IPCC) produce a wide range of warming estimates in response to the infrared radiative forcing theoretically expected from anthropogenic greenhouse gas emissions [
2].
From a modeling standpoint, this lack of progress is evidence of the complexity of the myriad atmospheric processes that combine to determine the sign and magnitude of feedbacks. It is also due to our inability to quantify feedbacks in the real climate system, a contentious issue with a wide range of published feedback diagnoses [
1] and disagreements over the ability of existing methods to diagnose feedback [
3,
4].
Spencer and Braswell ([
5] hereafter SB10) discussed what they believed to be the primary difficulty in diagnosing feedback from variations in the Earth’s radiative energy balance between absorbed shortwave (SW) solar radiation and thermally emitted longwave (LW) infrared (IR) radiation. SB10 attributed the difficulty to the contamination of the feedback signature by unknown levels of time-varying, internally generated radiative forcing; for example, ‘unforced’ natural variations in cloud cover.
In simple terms, radiative changes resulting from temperature change (feedback) cannot be easily disentangled from those causing a temperature change (forcing).
Much can be learned about the interaction between radiative forcing and feedback through a simple time dependent forcing-feedback model of temperature variations away from a state of energy equilibrium,
Equation (1) states that time-varying sources of non-radiative forcing
S and radiative forcing
N cause a climate system with bulk heat capacity
Cp to undergo a temperature change with time away from its equilibrium state (
dΔT/dt), but with a net radiative feedback ‘restoring force’ (−
λΔT) acting to stabilize the system. For the interannual temperature climate variability we will address here, the heat capacity
Cp in Equation (1) is assumed to represent the oceanic mixed layer. (Note that if
Cp is put inside the time differential term, the equation then becomes one for changes in the heat content of the system with time. While it is possible that feedback can be more accurately diagnosed by analyzing changes in the heat content of the ocean over time [
6], our intent here is to examine the problems inherent in diagnosing feedback based upon surface temperature changes.)
Radiative forcings (
N) of temperature change could arise, for example, from natural fluctuations in cloud cover which are not the direct or indirect result of a temperature change (that is, not due to feedback) [
7]. Examples of non-radiative forcing (
S) would be fluctuations in the heat exchange between the mixed layer and deep ocean, or between the mixed layer and the overlying atmosphere. Importantly, satellite radiative budget instruments measure the combined influence of radiative forcing (
N) and radiative feedback (−
λΔT) in unknown proportions.
Although not usually considered a feedback
per se, the most fundamental component of the net feedback parameter
λ is the direct dependence of the rate of IR emission on temperature, estimated to be about 3.3 W m
−2 K
−1 in the global average [
8]. This ‘Planck’ or ‘Stefan-Boltzmann’ response stabilizes the climate system against runaway temperature changes, and represents a baseline from which feedbacks are traditionally referenced. Positive feedbacks in the climate system reduce the net feedback parameter below 3.3, while negative feedbacks increase it above 3.3. Here we will deal with the net feedback parameter exclusively, as it includes the combined influence of all climate feedbacks, as well as the Planck effect.
The larger the net feedback parameter
λ, the smaller the temperature response to an imposed energy imbalance
N will be; the smaller
λ is, the greater the temperature response will be. A negative value for
λ would indicate a climate system whose temperature is unstable to radiative forcing. The coupled ocean-atmosphere climate models tracked by the IPCC have diagnosed long-term net feedback parameters ranging from
λ = 0.89 for the most sensitive model, MIROC-Hires, to
λ = 1.89 for the least sensitive model, FGOALS [
8]. Since this range is below the Planck response of 3.3 W m
−2 K
−1, all of the IPCC models therefore exhibit net positive feedbacks. Also, since all climate models have net feedback parameters greater than zero, none of the climate models are inherently unstable to perturbations.
It is worth reiterating that satellite radiative budget instruments measure the combined effect of the radiative terms on the RHS of Equation (1), that is, the radiative forcing term
N and the feedback term (−
λΔT). That the presence of
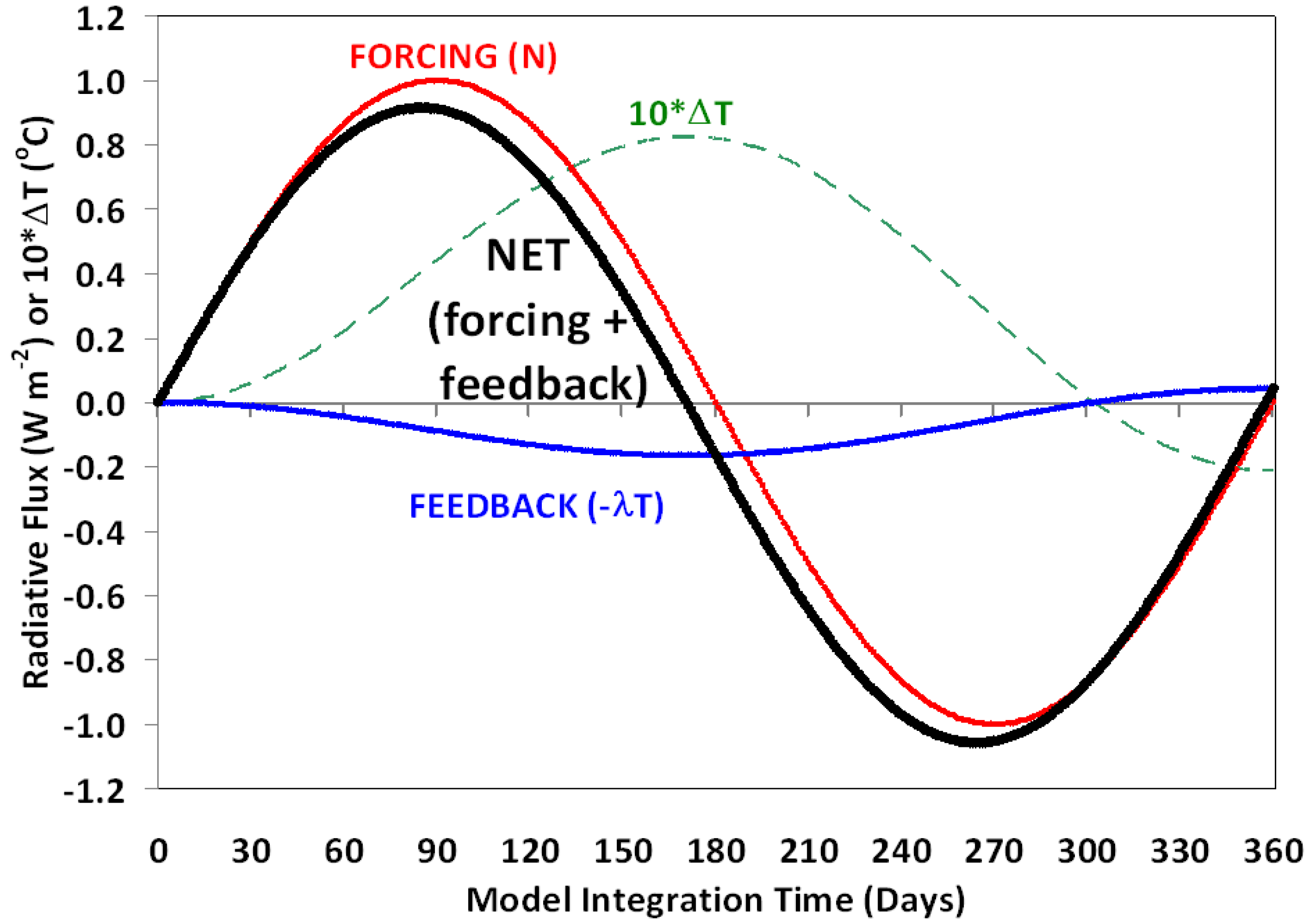
N can have a profound impact on feedback diagnosis is easily demonstrated with a simple time dependent model based upon Equation (1). If we assume
Cp consistent with a 25 m deep oceanic mixed layer, a net feedback parameter
λ = 3, and a sinusoidal forcing with period of one year, the temperature response shown in
Figure 1 will result.
Figure 1.
Simple forcing-feedback model demonstration that satellite radiative budget instrument measurements of Net radiative flux (forcing + feedback) are very different from what is needed to diagnose the net feedback parameter (feedback only).
Figure 1.
Simple forcing-feedback model demonstration that satellite radiative budget instrument measurements of Net radiative flux (forcing + feedback) are very different from what is needed to diagnose the net feedback parameter (feedback only).
In response to radiative forcing, the model ocean warms, which in turn causes a net radiative feedback response. Significant to our goal of diagnosing feedback, the net feedback response to a temperature change is always smaller than the radiative forcing which caused it, owing to the heat capacity of the system, until radiative equilibrium is once again restored. At that point the radiative feedback equals the radiative forcing.
Unfortunately, in the real climate system radiative forcings are continually changing, which means the feedback response will in general be smaller than the radiative forcing. The presence of this radiative forcing tends to confound the accurate determination of feedback. If the only source of radiative variability was feedback, then regression of the time series (−
λΔT) against the temperature time series (
ΔT) in
Figure 1 would yield an accurate feedback diagnosis with the regression slope
λ = 3 W m
−2 K
−1. But the presence of time varying radiative forcing in
Figure 1 has a very different signature than that of feedback, yet it is the sum of the two which the satellite measures.
As shown by SB10, the presence of any time-varying radiative forcing decorrelates the co-variations between radiative flux and temperature. Low correlations lead to regression-diagnosed feedback parameters biased toward zero, which corresponds to a borderline unstable climate system. We believe that the low correlations associated with previous feedback diagnoses with satellite data are themselves prima facie evidence of the presence of radiative forcing in the data.
In the real climate system, it is likely there is almost always a time-varying radiative forcing present, as various internally-generated changes in clouds and water vapor oscillate between positive and negative values faster than the resulting temperature changes can restore the system to radiative equilibrium. This means that feedback diagnosis will, in general, be contaminated by an unknown amount of time-varying internal radiative forcing
N. If those forcings were known, they could have been subtracted from the measured radiative flux variations before diagnosing feedback, e.g., as has been done for the feedback response of the coupled climate models to transient carbon dioxide forcing [
8].
Central to the difficulty of feedback diagnosis is the very different time-dependent relationships which exist between forcing and temperature, versus between feedback and temperature. While there is a substantial time lag between forcing and the temperature response due to the heat capacity of the ocean, the radiative feedback response to temperature is nearly simultaneous with the temperature change. This near-simultaneity is due to a combination of the instantaneous temperature effect on the LW portion of λ (the Planck response of 3.3 W m−2 K−1), and the relatively rapid convective coupling of the surface to the atmosphere, which causes surface temperature-dependent changes in water vapor, clouds, and the vertical profile of temperature.
While SB10 provided evidence that such radiatively-induced temperature changes do exist, and in general lead to an underestimate of the net feedback parameter, this view has been challenged ([
9] hereafter D10) with estimated cloud feedback from satellite observed variations in Earth’s radiative energy balance during 2000–2010. D10 used the usual regression approach. Further, D10 assumed that the temperature changes during 2000–2010 were not radiatively forced by the atmosphere, but non-radiatively forced through changes in ocean circulation associated with the El Niño/Southern Oscillation (ENSO) [
10] phenomenon. If D10 is correct that radiative forcing can be neglected (
N(t) ≈ 0), then satellite observed radiative variations would be dominated by feedback rather than forcing, and one should be able to diagnose feedback through regression of radiative variations against temperature variations.
Here we will provide evidence that those temperature changes instead had a strong component of radiative forcing, with radiative accumulation preceding, and radiative loss following temperature maxima. While SB10 used phase space analysis to demonstrate the presence of radiative forcing, here we will use lag regression analysis. By examining regression coefficients between temperature and radiative flux at a variety of leads and lags, rather than at just zero time lag, we can identify behaviors of the climate system that otherwise cannot be discerned.
First we will demonstrate what these lag relationships look like in the satellite observations and in the coupled climate models. Then, we will explore with a simple forcing-feedback model of the climate system what the relationships mean in terms of forcing and feedback.
3. Simple Model Simulations of Observed Behavior
The effect of radiative (
N)
versus non-radiative (
S) forcing on the lagged regression coefficients can be demonstrated by a simple model based upon Equation (1). This helps to explain the difference between the satellite-measured
versus climate model signatures in
Figure 3. We again ran the simple forcing-feedback model with an assumed net feedback parameter of
λ = 3 W m
−2 K
−1; and an ocean mixed layer depth of 25 m, a choice which requires some discussion.
We found that the assumed mixed layer depth of 25 m is consistent with the average behavior of both the IPCC AR4 coupled climate models and the satellite observations on interannual time scales. Using Equation (1), we estimated Cp from both the coupled climate models and the satellite data by regressing 5-month trends (dΔT/dt) in the global average surface temperature anomalies against the 5-month average radiative imbalances, to get 1/Cp as the regression coefficient. The resulting Cp values from 14 IPCC AR4 models ranged from 11 m to 50 m, with a 14-model average of 27 m, while a similar regression on the 10+ years of satellite data revealed an equivalent mixing depth of 26 m, which supports our use of 25 m. (Note that, since about 30% of Earth is land having comparatively negligible heat capacity, the equivalent mixing depth of 25 m implies an average ocean mixing depth of about (25/0.7=) 35 m for the interannual time scales addressed here. Also, if most of the interannual temperature variability originates in the tropics, our diagnosed mixed layer depth will be biased toward tropical values, which are typically much shallower than at high latitudes.)
For the radiative forcing
N(t) we used a time series of normally-distributed monthly random numbers with box filter smoothing of 9 months to approximate the time scales of variations seen in the climate models and observations in
Figure 3. A separate time series of random numbers without low pass filtering was used for the non-radiative forcing
S(t). This mimics what we believe to be intraseasonal oscillations in the heat flux between the ocean and atmosphere seen in the data [
5,
13]. The model time step was one month, and the model simulations were carried out for 500 years of simulated time.
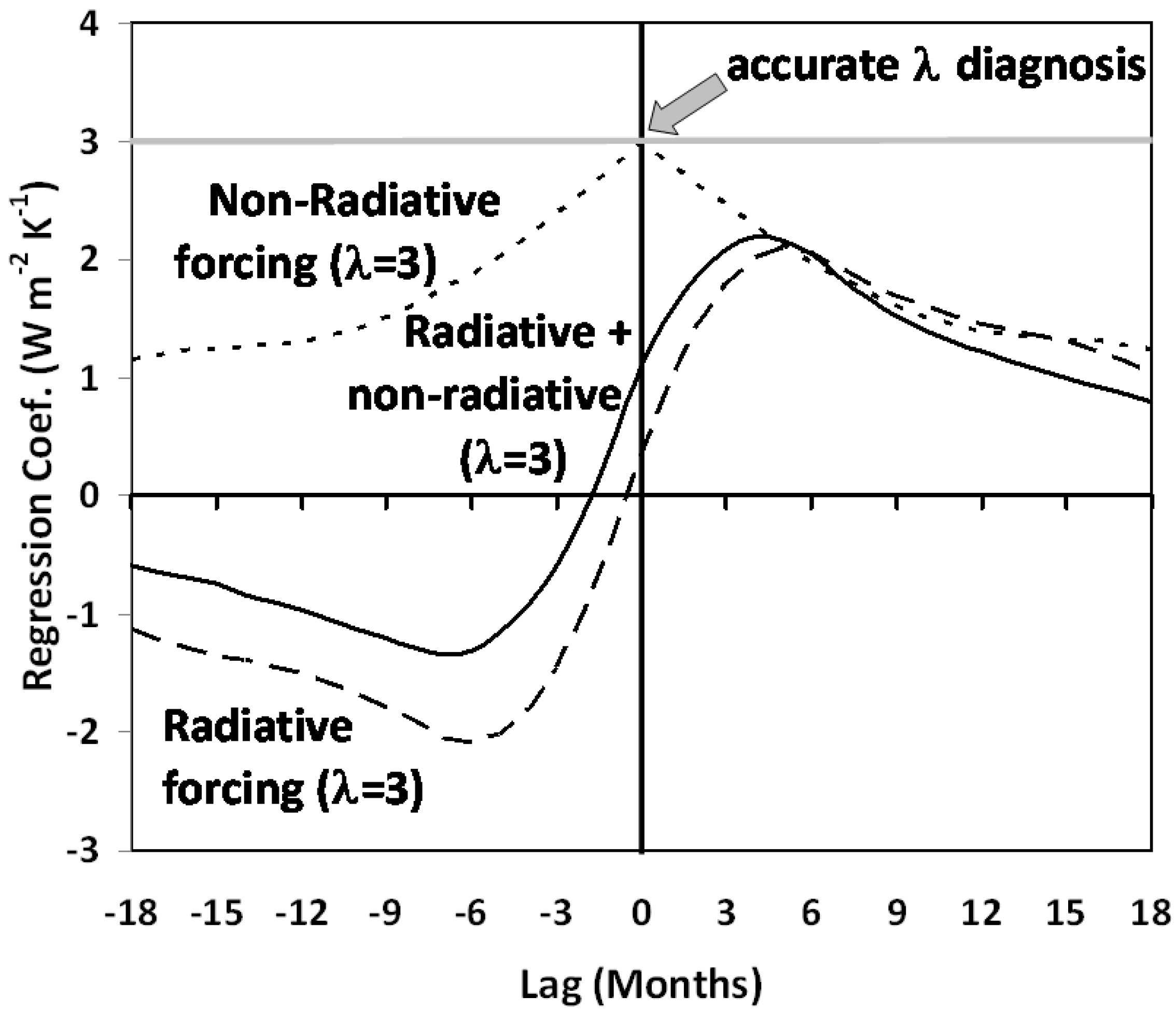
The lag regression results from the simple model are shown in
Figure 4 for (1) pure radiative forcing
N, (2) pure non-radiative forcing
S, and (3) a 70/30% mixture of both. Note that only in the case of pure non-radiative forcing (dotted line), at zero time lag, can accurate diagnosis of the feedback parameter can be made. As discussed above, this is because there is no radiative forcing present to contaminate the radiative feedback signal. Again, this is the only type of forcing D10 assumed was causing the surface temperature variability during 2000–2010, an assumption which allowed neglect of the radiative forcing issues raised here and by SB10.
If the temperature variations are radiatively forced, the lag regression relationships are very different (dashed line in
Figure 4). In this case, radiative gain precedes, and radiative loss follows a temperature maximum, as would be expected based upon conservation of energy considerations. Significantly, the pure radiative forcing curve is most similar to the behavior seen in the coupled climate model output shown in
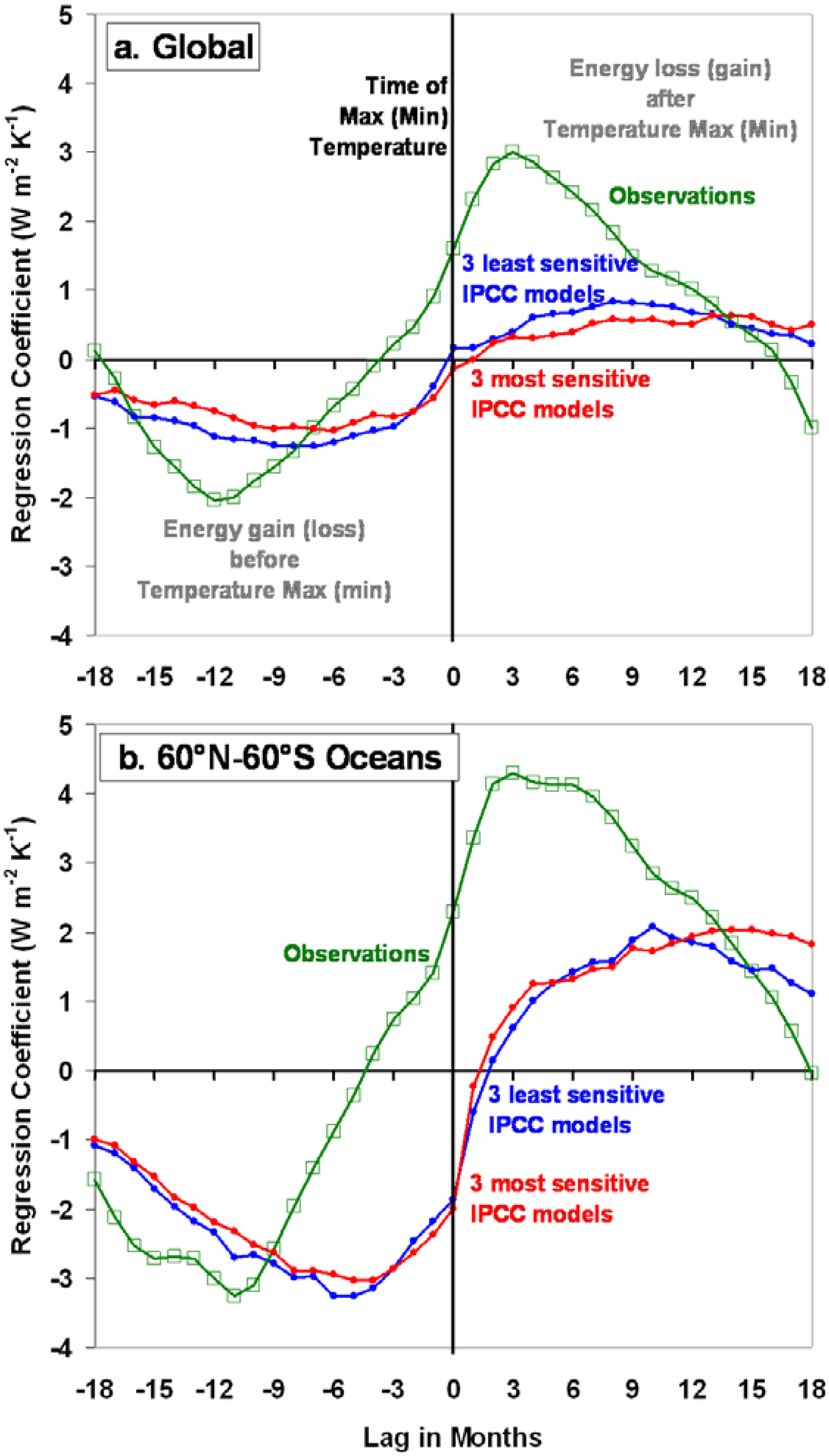
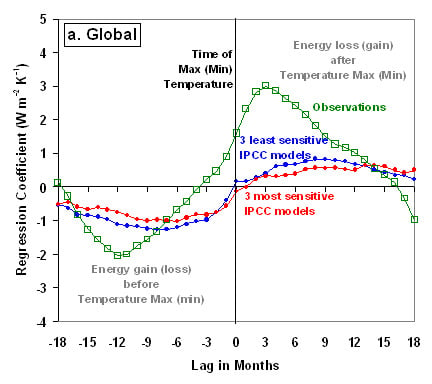
Figure 3, indicating the dominating presence of internal radiative forcing in those models.
Figure 4.
Lag regression coefficients between temperature and radiative flux from the simple forcing-feedback model run for three forcing cases: pure non-radiative forcing (dotted line); pure radiative forcing (dashed line); and a 70% radiative/30% non-radiative forcing mixture. A feedback parameter of 3 W m−2 K−1 and ocean mixing depth of 25 m were specified for all three simulations, which each ran for 500 years of simulated time.
Figure 4.
Lag regression coefficients between temperature and radiative flux from the simple forcing-feedback model run for three forcing cases: pure non-radiative forcing (dotted line); pure radiative forcing (dashed line); and a 70% radiative/30% non-radiative forcing mixture. A feedback parameter of 3 W m−2 K−1 and ocean mixing depth of 25 m were specified for all three simulations, which each ran for 500 years of simulated time.
Finally, a mixture of 70% radiative and 30% non-radiative forcing (solid line in
Figure 3) produces lag regression coefficients that vary in a manner similar to the satellite data in
Figure 3. This suggests that, while the temperature variations during 2000–2010 had a strong radiative forcing component, they were also influenced by more non-radiative forcing than is exhibited by the coupled climate models. In contrast, D10 assumed that non-radiative forcing dominated the climate variability measured by the satellite during 2000–2010.
Thus, we must conclude that time-varying radiative forcing exists in the satellite observations, as evidenced by the radiative gain/loss couplet patterns seen in
Figure 3 and
Figure 4. Diagnosis of feedback cannot easily be made in such situations, because the radiative forcing decorrelates the co-variations between temperature and radiative flux. For example, no matter what feedback is specified when the simple model is only radiatively forced, the regression coefficient at zero time lag for a sufficiently long model simulation is always near-zero. We believe this effect has led to low biases in previously diagnosed feedback parameters from satellite data.
Determination of whether regression coefficients at various non-zero time lags might provide a more accurate estimate of feedback has been recently explored by [
14], but is beyond the scope of this paper. Our preliminary work on this issue suggests no simple answer to the question. We conclude that the fundamental obstacle to feedback diagnosis remains the same, no matter what time lag is addressed: without knowledge of time-varying radiative forcing components in the satellite radiative flux measurements, feedback cannot be accurately diagnosed from the co-variations between radiative flux and temperature.
4. Discussion and Conclusions
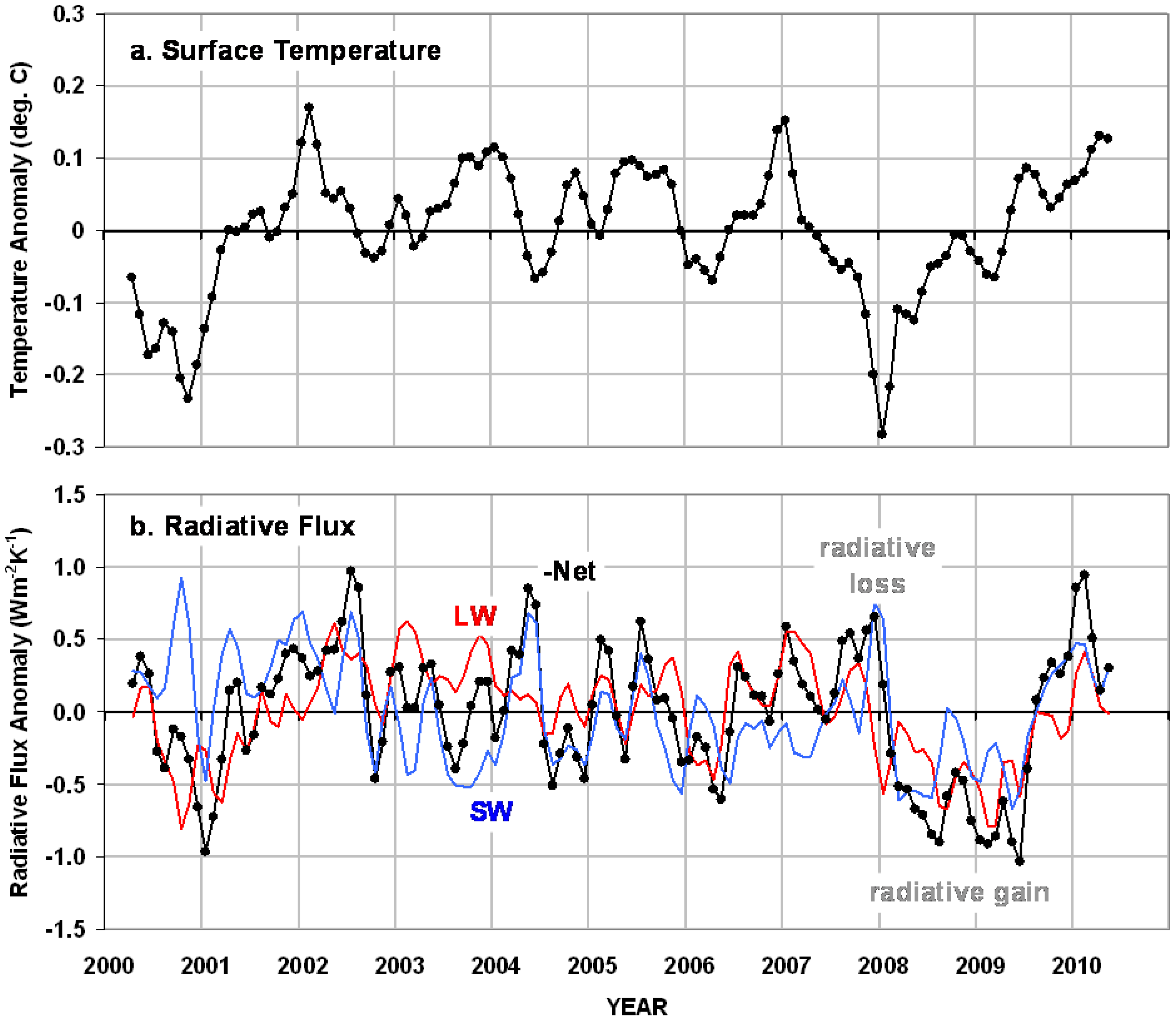
We have shown clear evidence from the CERES instrument that global temperature variations during 2000–2010 were largely radiatively forced. Lag regression analysis supports the interpretation that net radiative gain (loss) precedes, and radiative loss (gain) follows temperature maxima (minima). This behavior is also seen in the IPCC AR4 climate models.
A simple forcing-feedback model shows that this is the behavior expected from radiatively forced temperature changes, and it is consistent with energy conservation considerations. In such cases it is difficult to estimate a feedback parameter through current regression techniques.
In contrast, predominately non-radiatively forced temperature changes would allow a relatively accurate diagnosis of the feedback parameter at zero time lag using regression since most radiative variability would be due to feedback. Unfortunately, this appears not to be the situation in either the satellite observations or the coupled climate models.
Yet, as seen in
Figure 2, we are still faced with a rather large discrepancy in the time-lagged regression coefficients between the radiative signatures displayed by the real climate system in satellite data
versus the climate models. While this discrepancy is nominally in the direction of lower climate sensitivity of the real climate system, there are a variety of parameters other than feedback affecting the lag regression statistics which make accurate feedback diagnosis difficult. These include the amount of non-radiative
versus radiative forcing, how periodic the temperature and radiative balance variations are, the depth of the mixed layer,
etc., all of which preclude any quantitative estimate of how large the feedback difference is. More recent work which attempts to minimize non-feedback influences [
14] might well provide more accurate feedback estimates than previous studies.
Finally, since much of the temperature variability during 2000–2010 was due to ENSO [
9], we conclude that ENSO-related temperature variations are partly radiatively forced. We hypothesize that changes in the coupled ocean-atmosphere circulation during the El Niño and La Niña phases of ENSO cause differing changes in cloud cover, which then modulate the radiative balance of the climate system. As seen in
Figure 3(b) for the ocean-only data, the signature of radiative forcing is stronger over the oceans than in the global average, suggesting a primarily oceanic origin.
What this might (or might not) imply regarding the ultimate causes of the El Niño and La Niña phenomena is not relevant to our central point, though: that the presence of time varying radiative forcing in satellite radiative flux measurements corrupts the diagnosis of radiative feedback.