The Relationship of Time Span and Missing Data on the Noise Model Estimation of GNSS Time Series
Abstract
:1. Introduction
2. Materials and Methods
2.1. Simulation GNSS Time Series
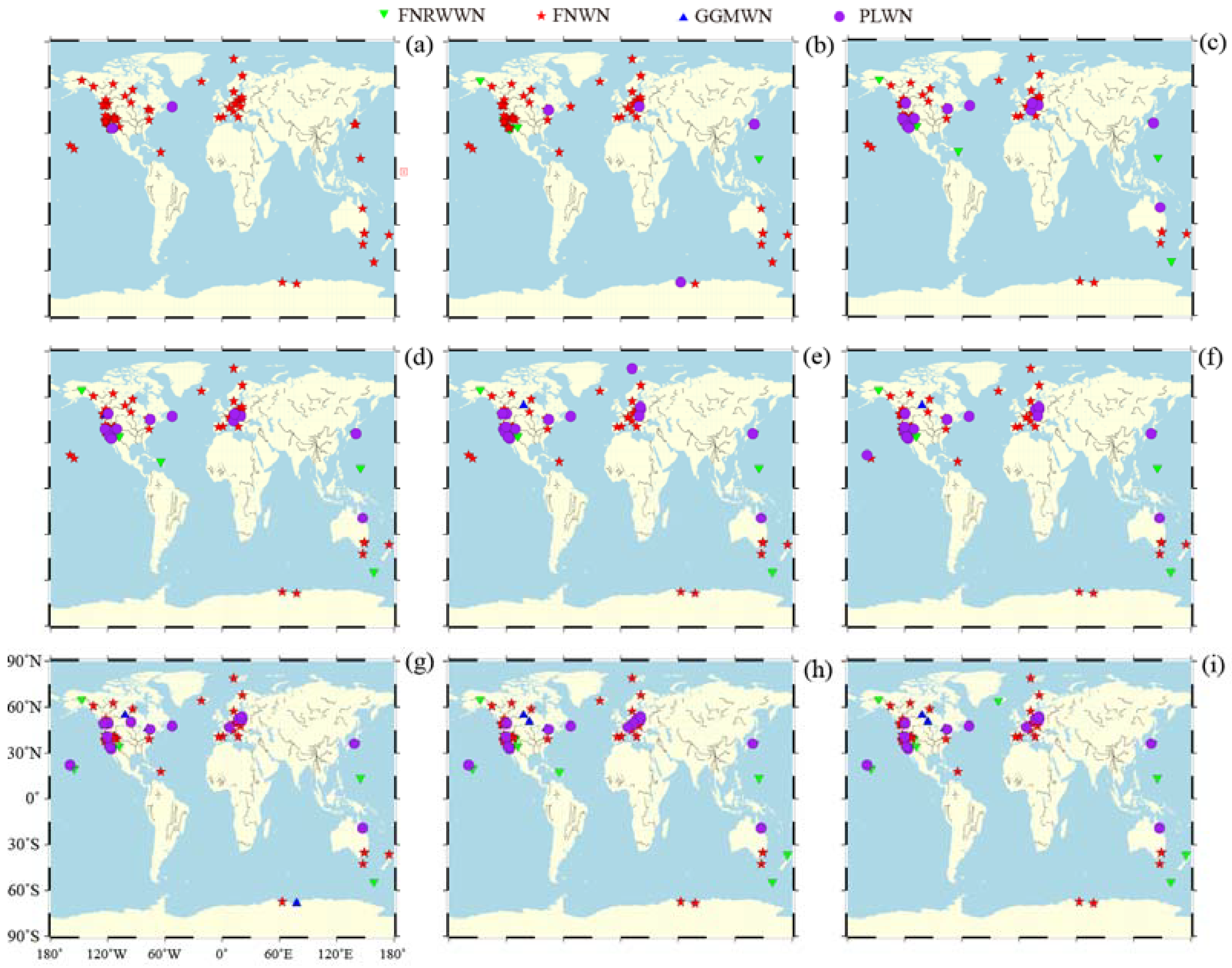
2.2. Real GNSS Time Series
2.3. Stochastic Model Selection Criteria
3. Results
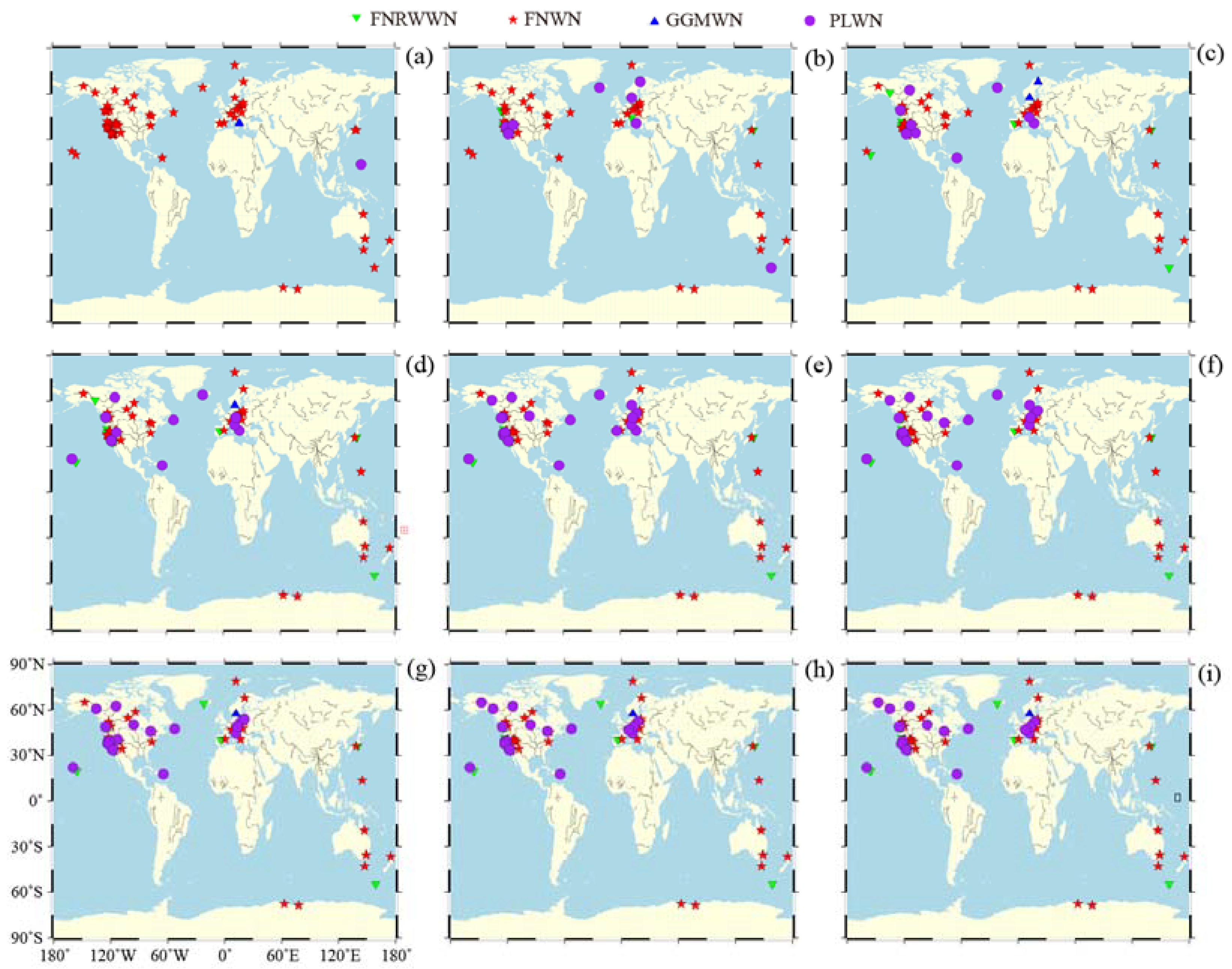
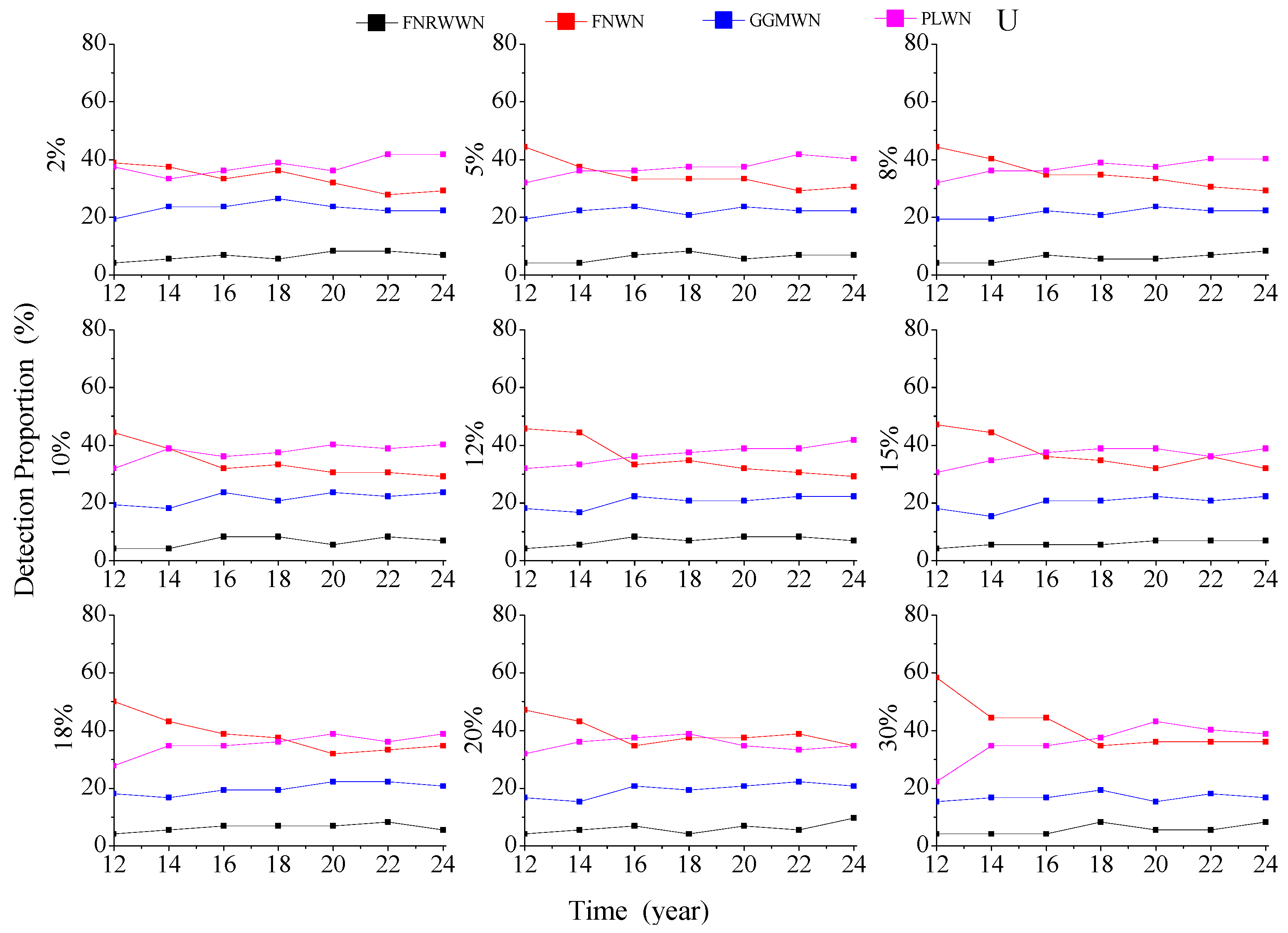
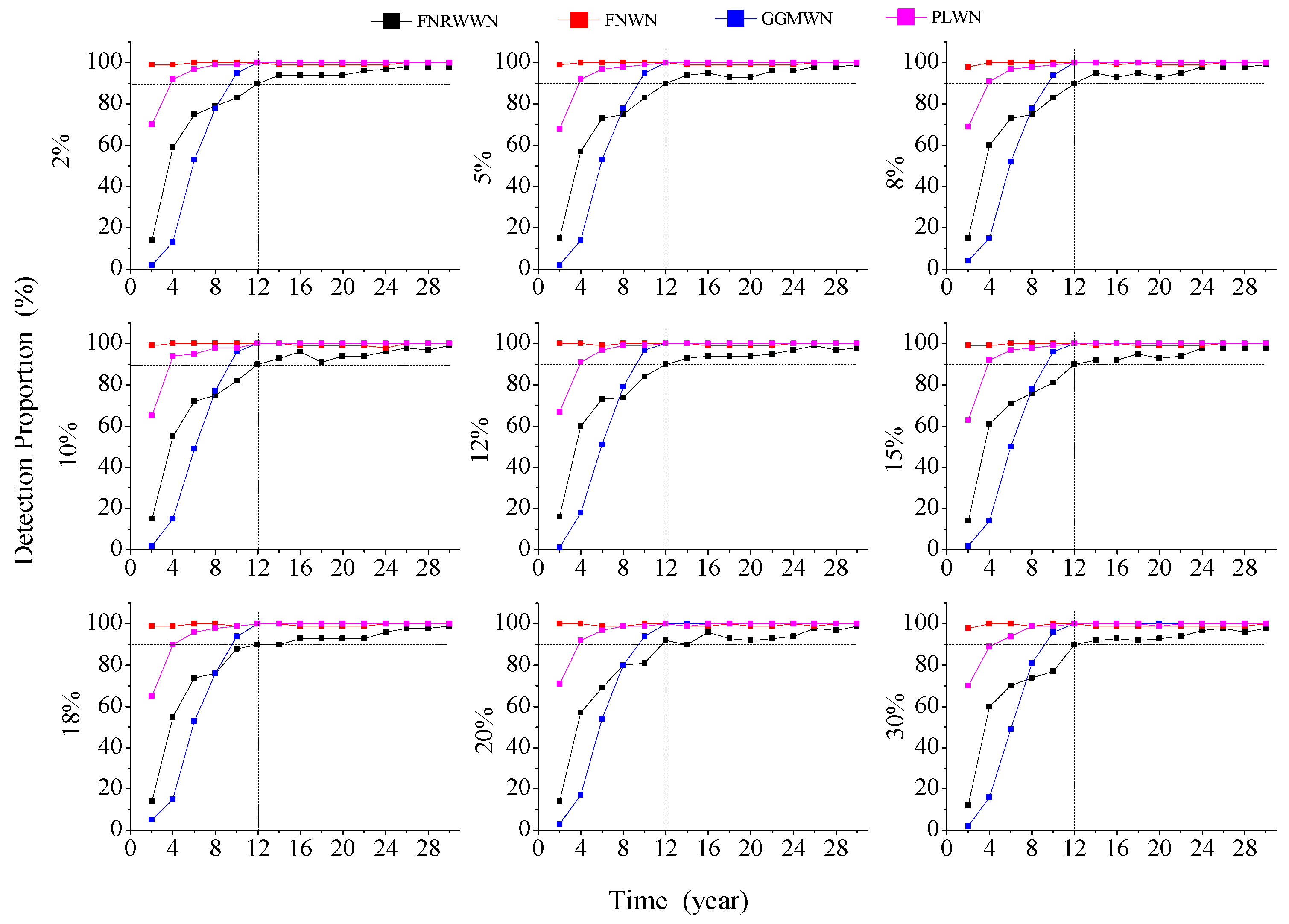
3.1. Impact of Time Span and Missing Data on the Noise Model
3.1.1. Simulations on the Noise Model Estimation
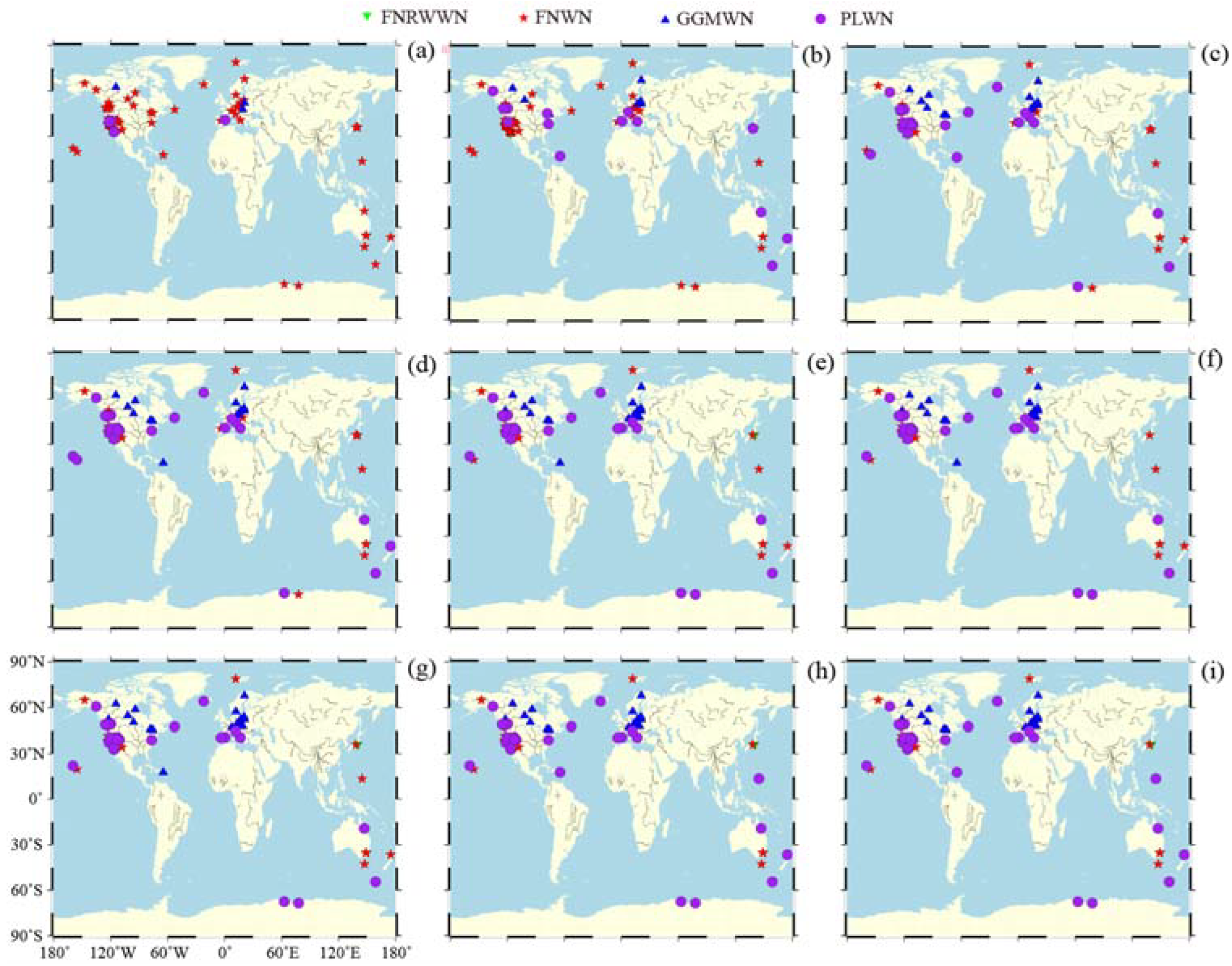
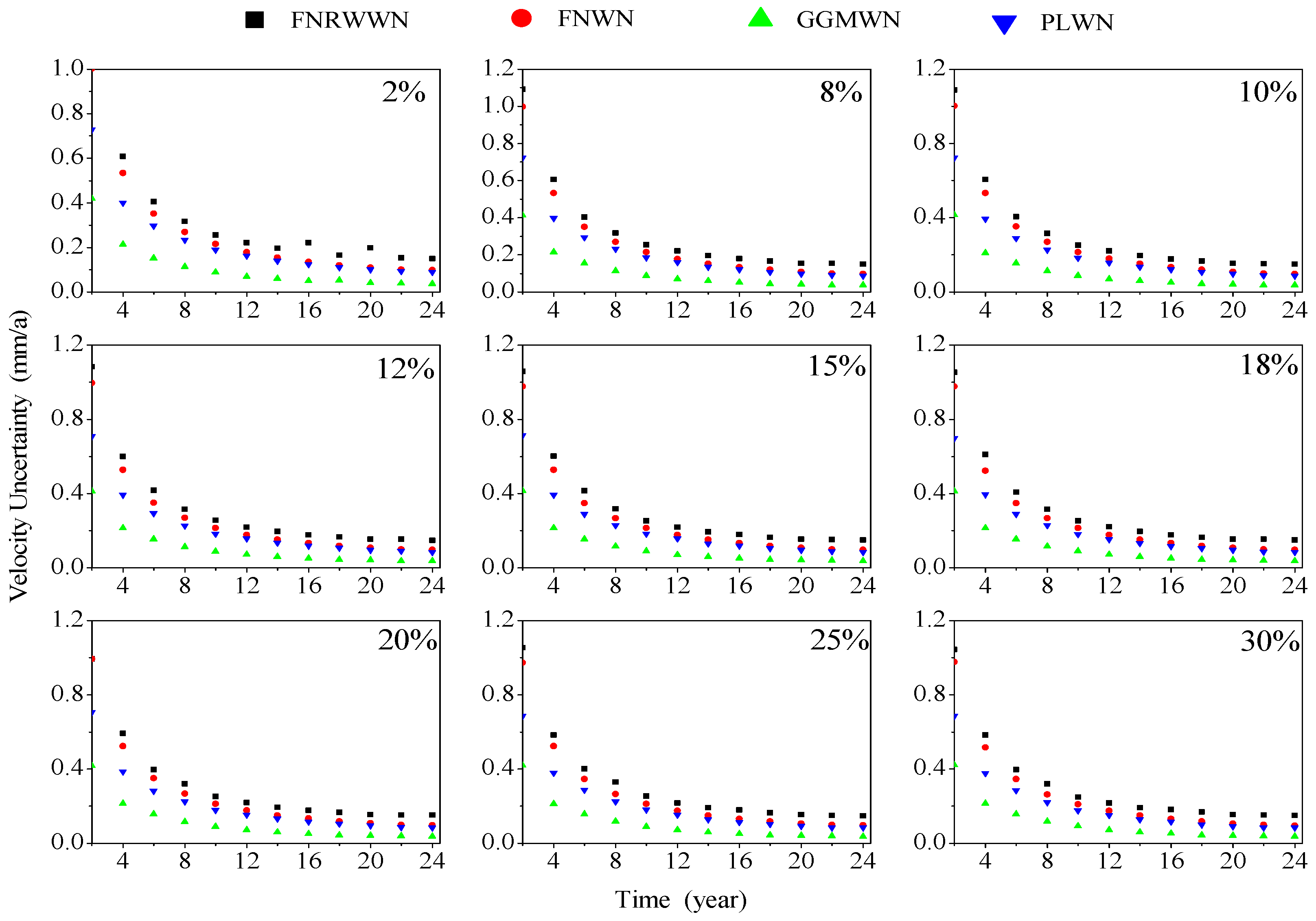
3.1.2. Effect of Missing Data on Noise Model
3.2. Impact of Length and Missing Data on the Noise Model of the GNSS Time Series
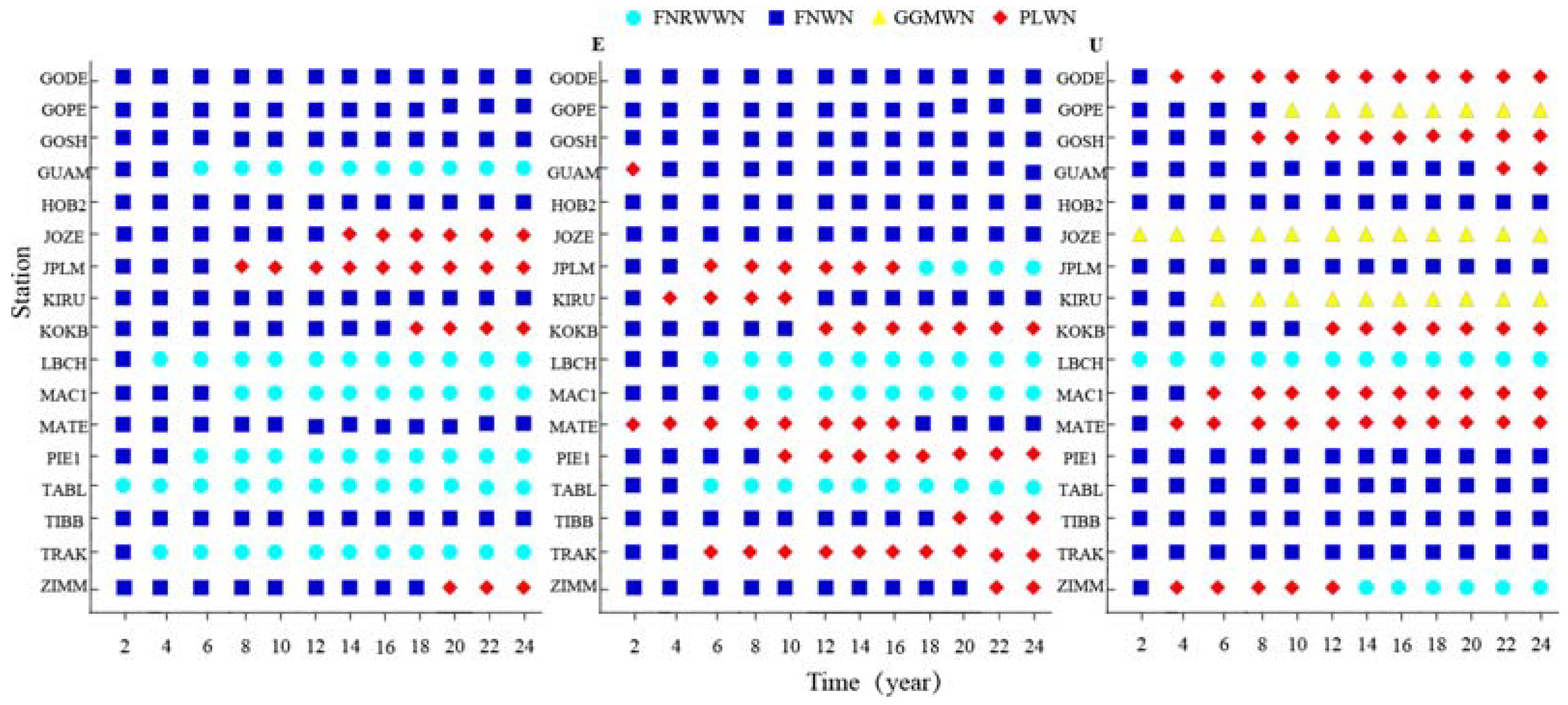
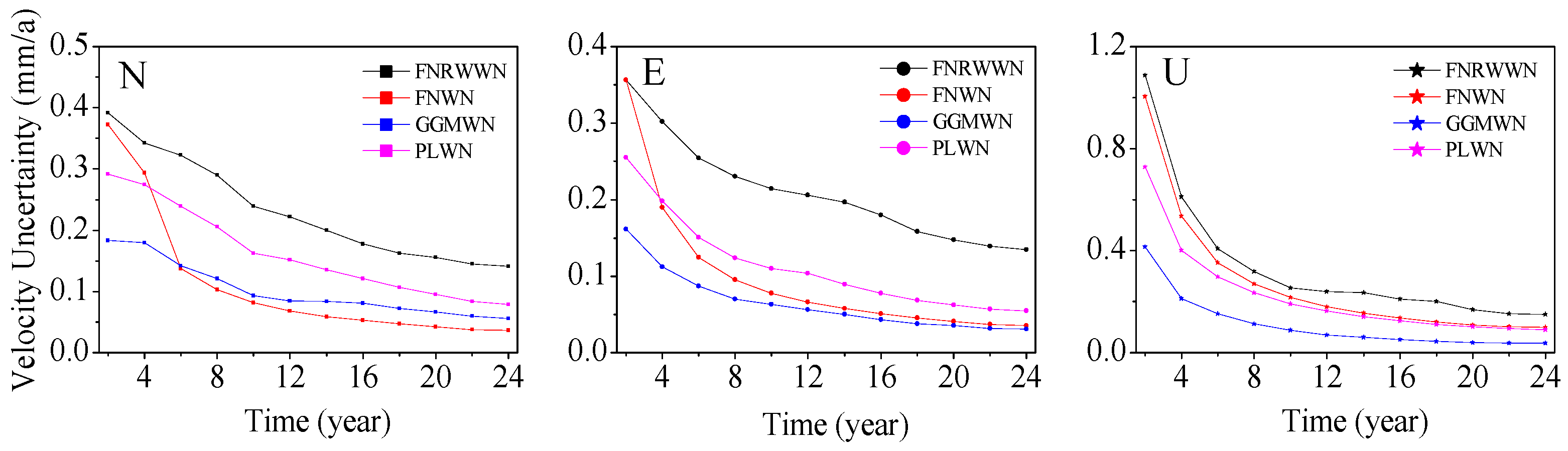
3.2.1. GNSS Time Span on Noise Model Estimation
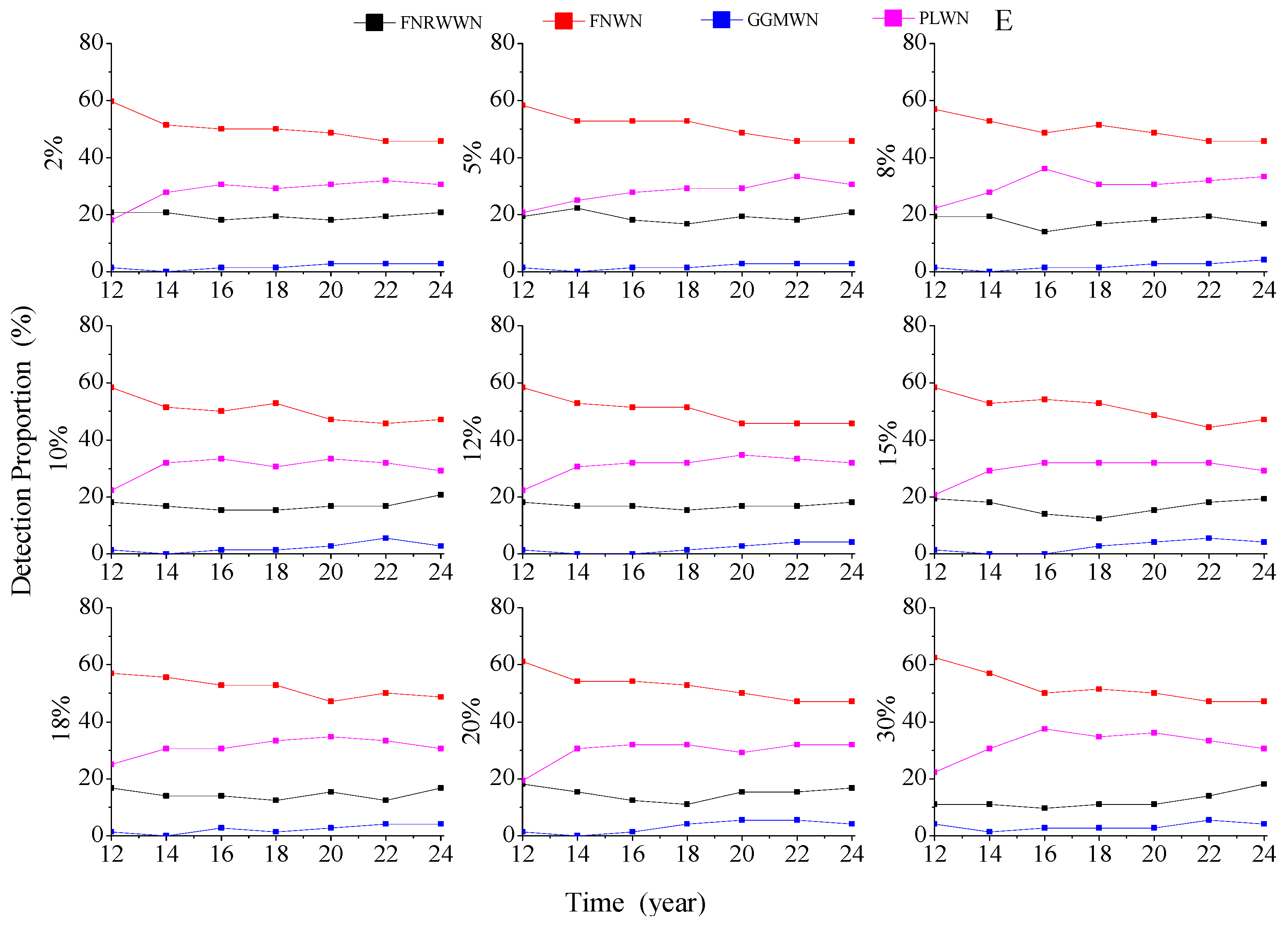
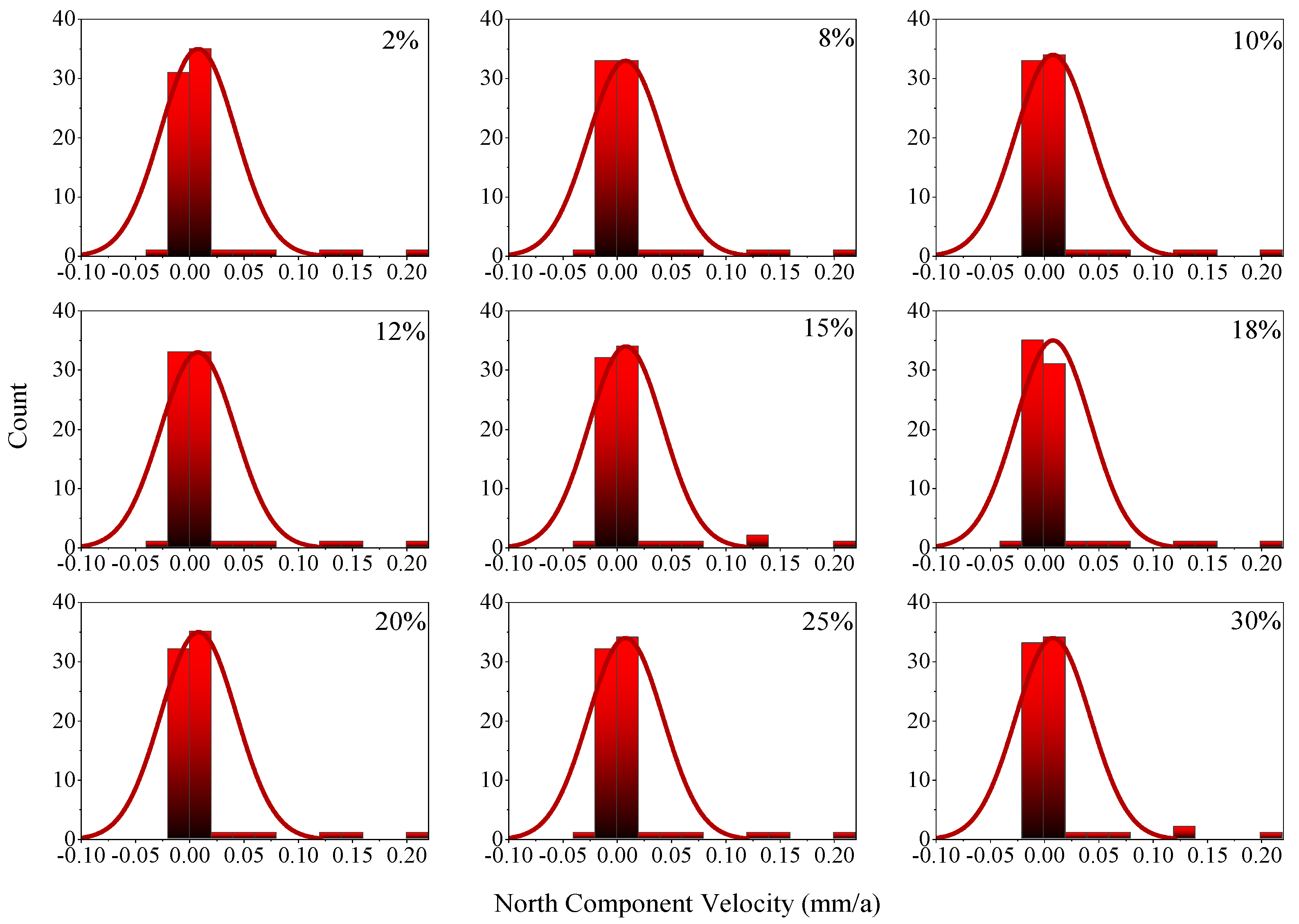
3.2.2. Effect of GNSS Missing Data on Noise Model
4. Discussion
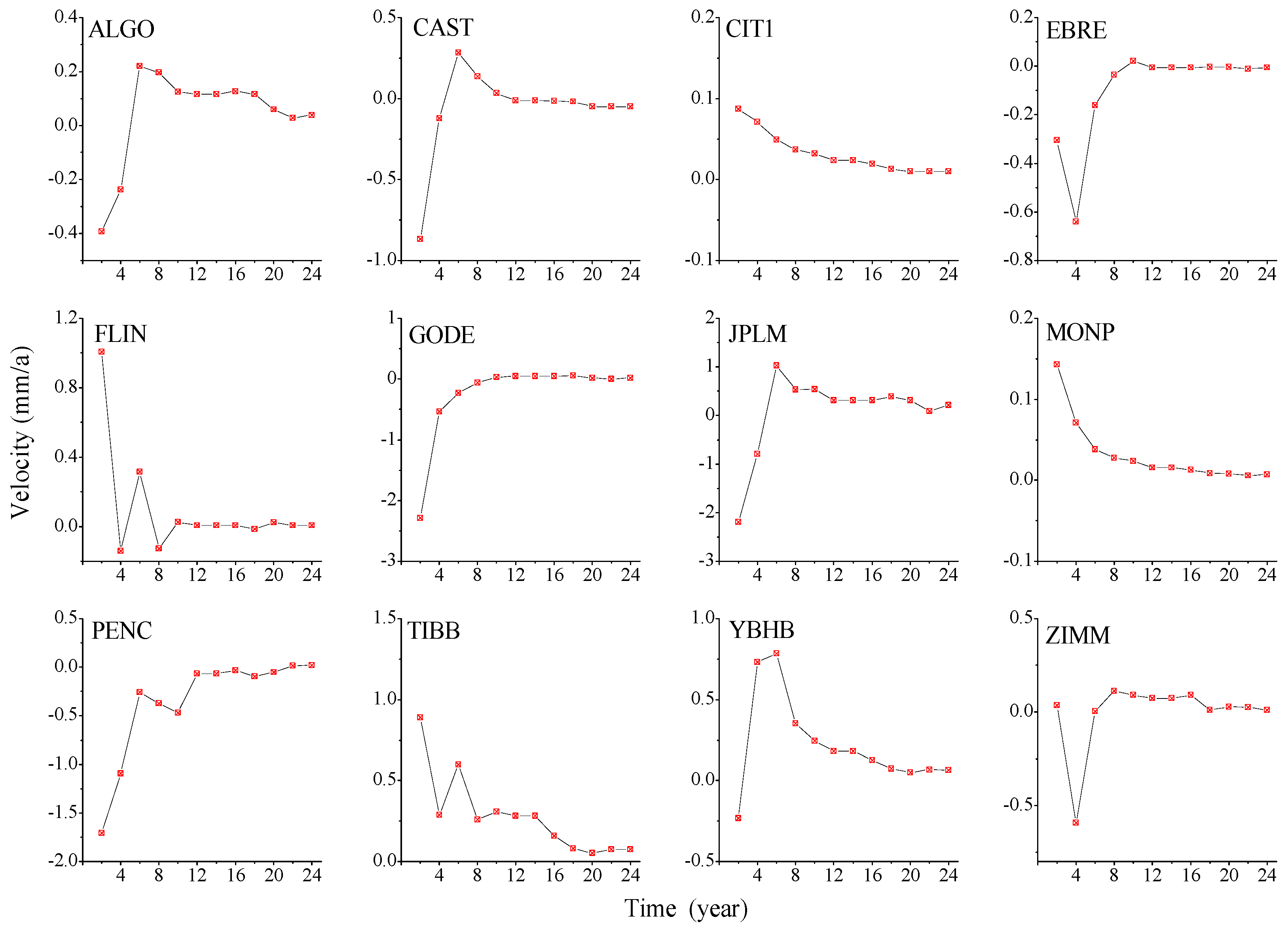
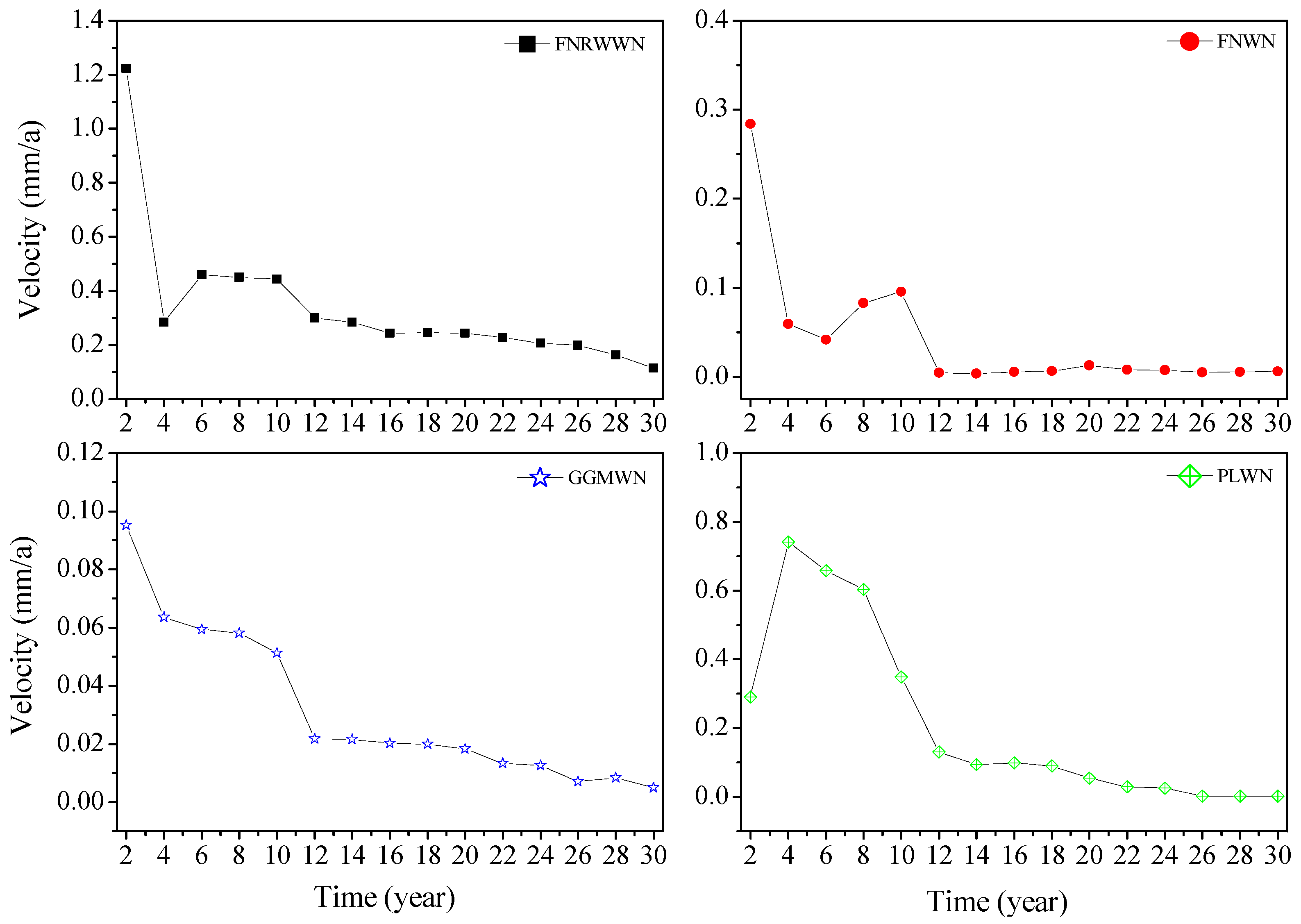
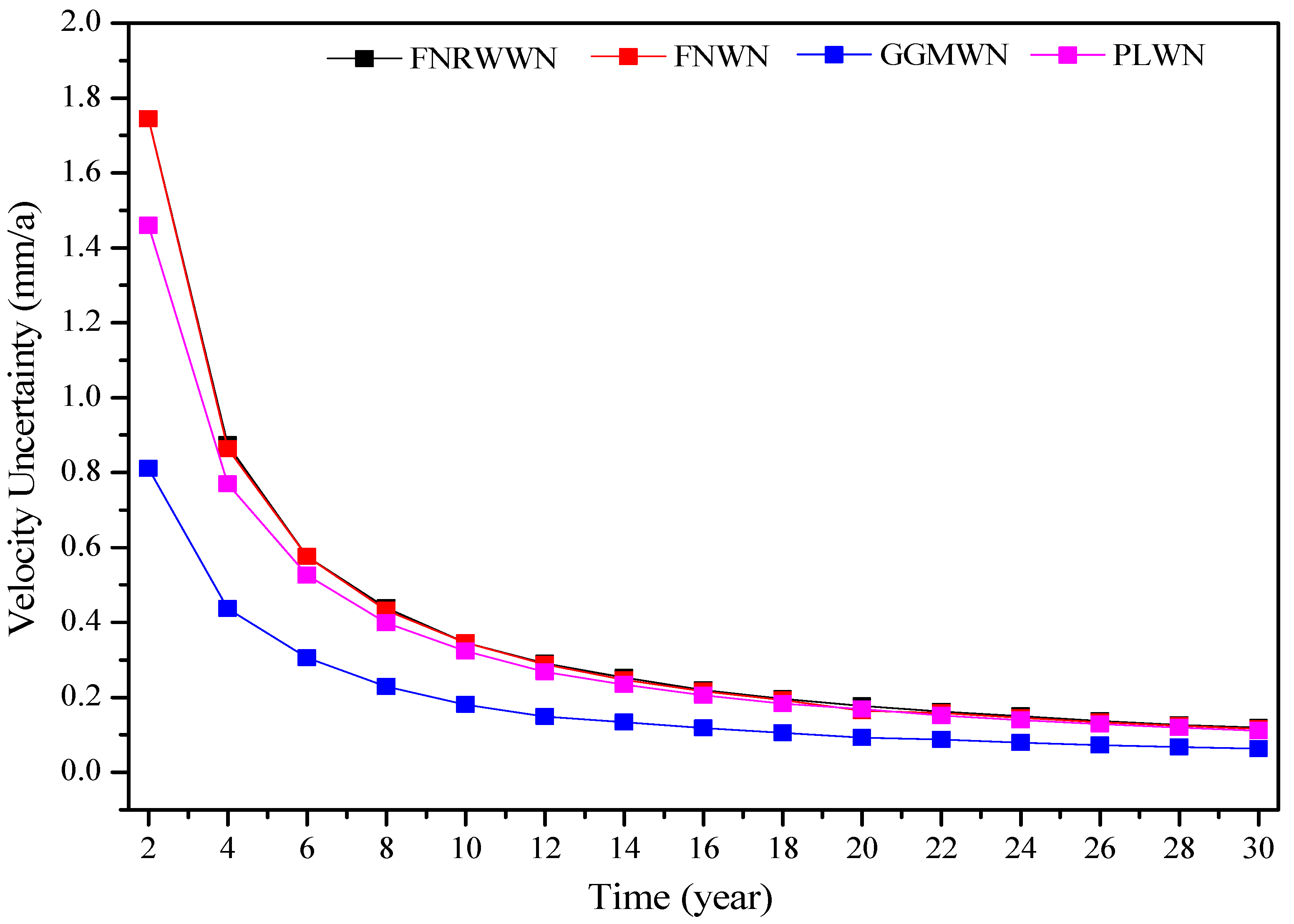
4.1. Impact of Length and Missing Data on the Velocity Estimation of Simulation Time
4.1.1. Simulation Time Span on Velocity Estimation
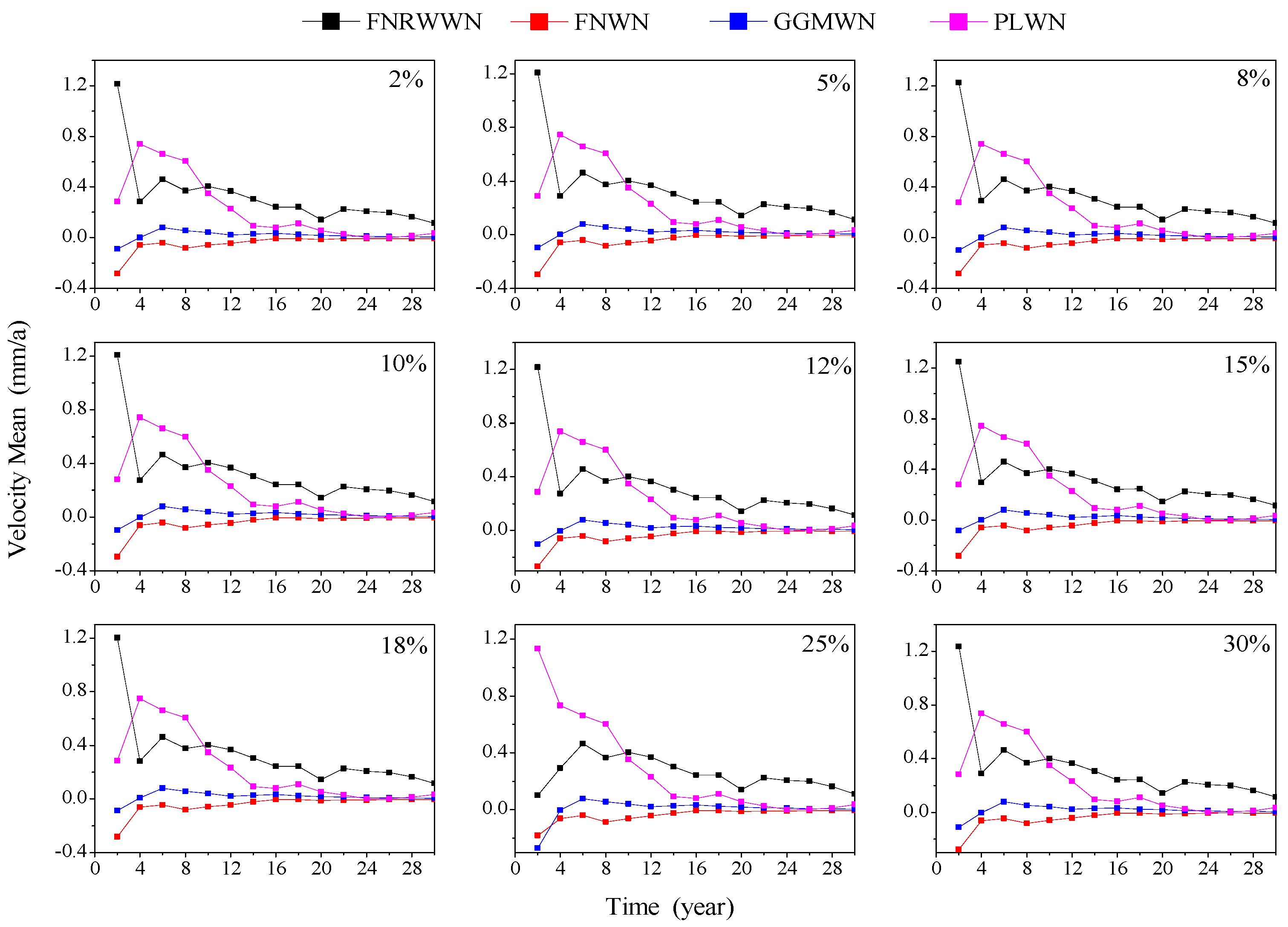
4.1.2. Simulation Missing Data on Velocity Estimation
4.2. Impact of Time Span and Missing Data on the Noise Model of GNSS Time
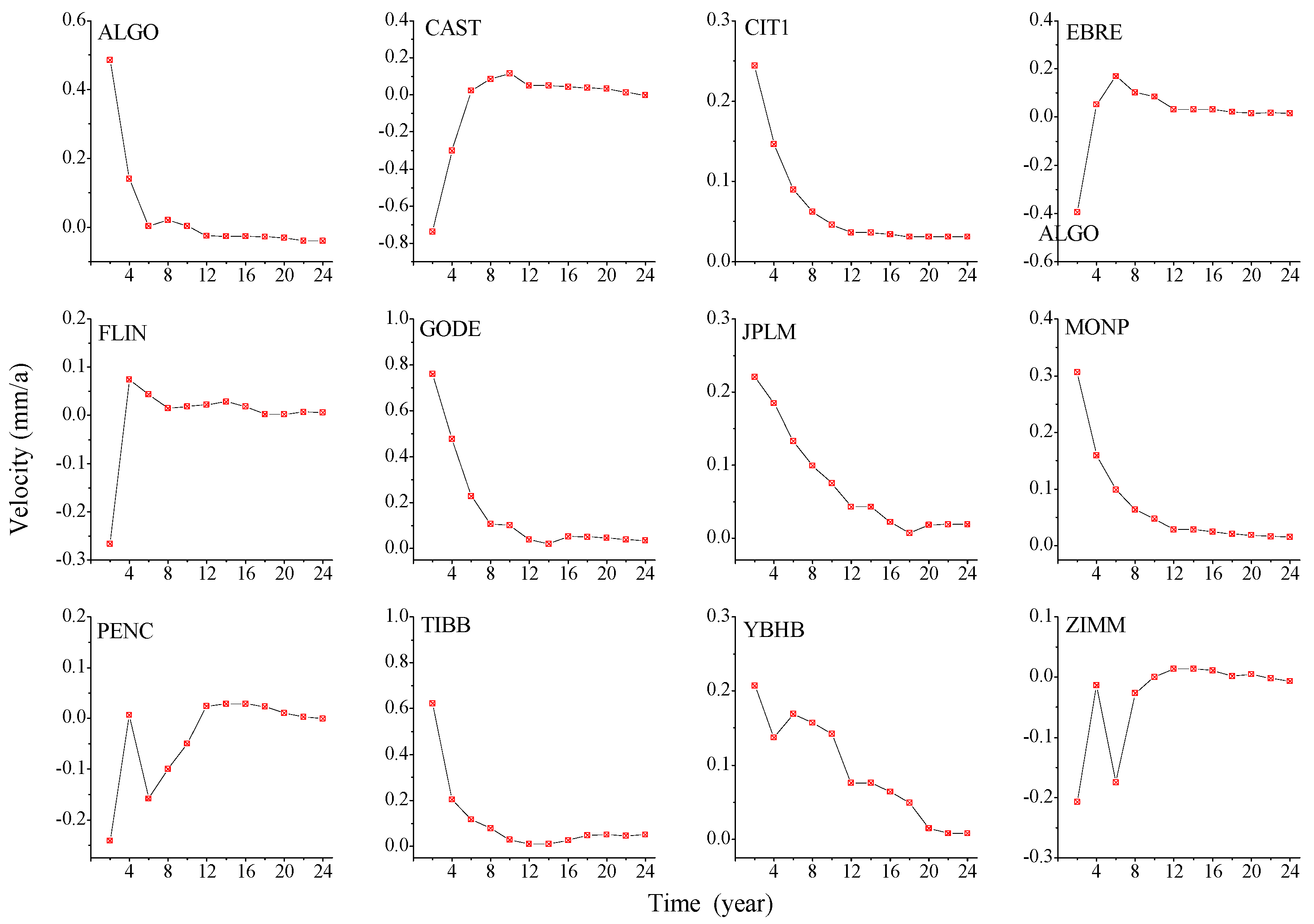
4.2.1. Change in Velocity Estimation Due to Different Time Span in GNSS Time Series
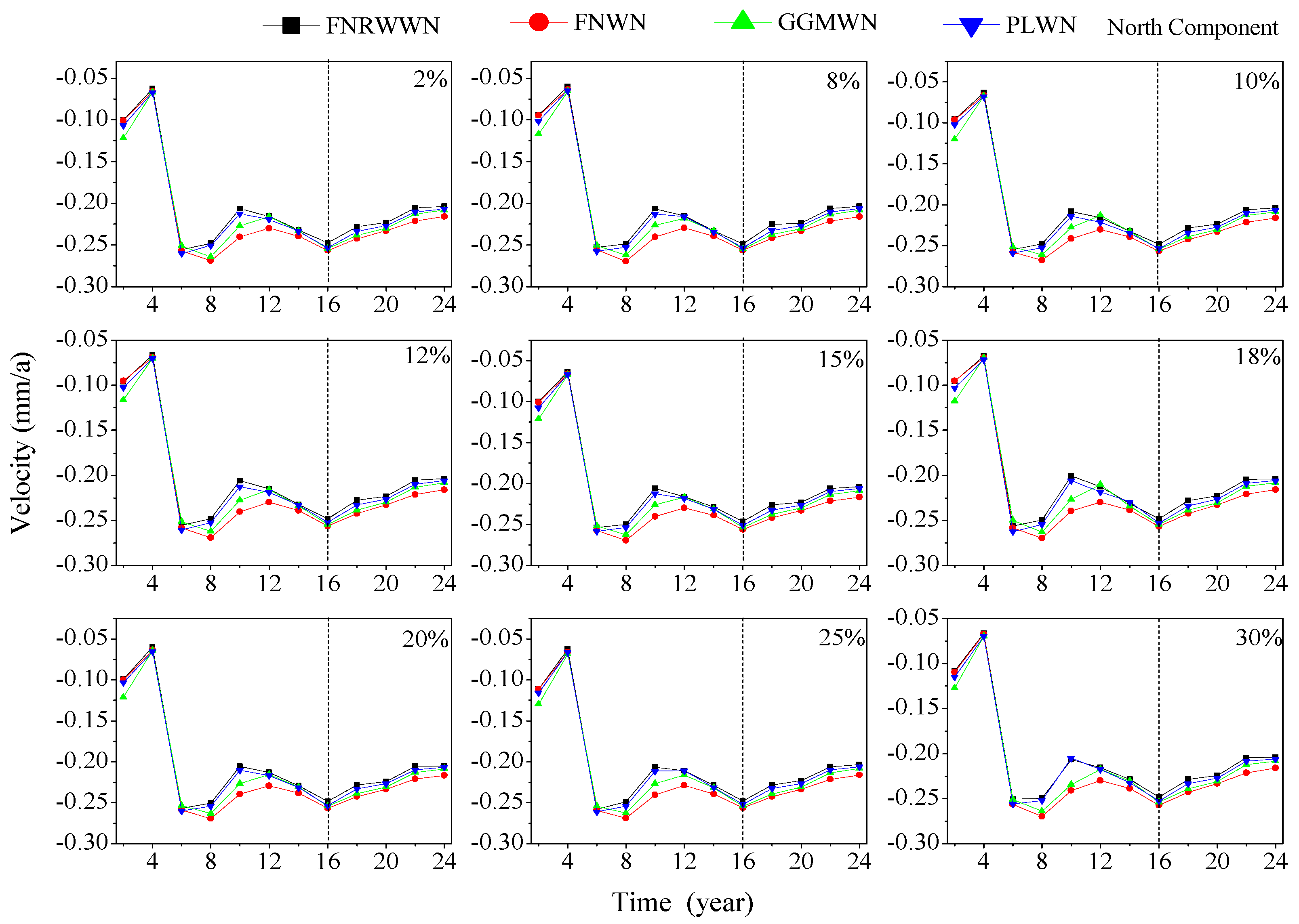
4.2.2. Effect of GNSS Missing Data on Velocity Estimation
5. Conclusions
- (1)
- The BIC_tp model had higher accuracy in estimating colored noise models and is sensitive to RW noise. By analyzing the simulation data and the real GNSS time series noise models, we found that when the time length is greater than 12 years, the detection rate of the simulation data model is close to 1. Considering GNSS observation data, using time series greater than 12 years could obtain more reliable noise model estimation results, proving the accuracy of the BIC_tp model estimation.
- (2)
- The time length had a significant impact on the noise model and station velocity estimation. With increases in the time lengths, the optimal noise model of GNSS time series, the estimated velocity together with associated uncertainty gradually converged (e.g., not much variability), and the percentage of RW noise model increased. We then recommend to use at least 12 years of GNSS data.
- (3)
- Missing data had little effect on different noise models and could be considered as stable when the time series length is greater or equal to 12 years. Missing data did not change the selected noise model. With different data gaps and increasing time length, the velocity uncertainty does not change by approximately 0.2 mm/a at around 12 years.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A

| Site | Longitude | Latitude | Site | Longitude | Latitude |
|---|---|---|---|---|---|
| ALBH | 236.51 | 48.39 | MAW1 | 62.87 | −67.60 |
| ALGO | 281.93 | 45.96 | MEDI | 11.65 | 44.52 |
| AUCK | 174.83 | −36.60 | MHCB | 238.36 | 37.34 |
| BLYT | 245.29 | 33.61 | MKEA | 204.54 | 19.80 |
| BOR1 | 17.07 | 52.28 | MONP | 243.58 | 32.89 |
| CAST | 249.32 | 39.19 | NANO | 235.91 | 49.29 |
| CEDA | 247.14 | 40.68 | NRC1 | 284.38 | 45.45 |
| CHUR | 265.91 | 58.76 | NYAL | 11.87 | 78.93 |
| CIT1 | 241.87 | 34.14 | ONSA | 11.93 | 57.40 |
| CLAR | 242.29 | 34.11 | ORVB | 238.50 | 39.55 |
| CMBB | 239.61 | 38.03 | PENC | 19.28 | 47.79 |
| CRO1 | 295.42 | 17.76 | PIE1 | 251.88 | 34.30 |
| CSN1 | 241.48 | 34.25 | PIN1 | 243.54 | 33.61 |
| DAV1 | 77.97 | −68.58 | PIN2 | 243.54 | 33.61 |
| DHLG | 244.21 | 33.39 | REYK | 338.04 | 64.14 |
| DRAO | 240.38 | 49.32 | SEDR | 237.78 | 48.52 |
| DUBO | 264.13 | 50.26 | SHIN | 239.77 | 40.59 |
| EBRE | 0.49 | 40.82 | SMEL | 247.16 | 39.43 |
| FAIR | 212.50 | 64.98 | STJO | 307.32 | 47.60 |
| FARB | 237.00 | 37.70 | TABL | 242.32 | 34.38 |
| FLIN | 258.02 | 54.73 | TIBB | 237.55 | 37.89 |
| GARL | 240.64 | 40.42 | TID1 | 148.98 | −35.40 |
| GODE | 283.17 | 39.02 | TIDB | 148.98 | −35.40 |
| GOPE | 14.79 | 49.91 | TOW2 | 147.06 | −19.27 |
| GOSH | 245.82 | 40.64 | TRAK | 242.20 | 33.62 |
| GUAM | 144.87 | 13.59 | TSKB | 140.09 | 36.11 |
| HOB2 | 147.44 | −42.80 | UCLU | 234.46 | 48.93 |
| HOPB | 236.93 | 39.00 | USUD | 138.36 | 36.13 |
| JOZE | 21.03 | 52.10 | VILL | 356.05 | 40.44 |
| JPLM | 241.83 | 34.20 | WHC1 | 241.97 | 33.98 |
| KIRU | 20.97 | 67.86 | WHIT | 224.78 | 60.75 |
| KOKB | 200.34 | 22.13 | WILL | 237.83 | 52.24 |
| LAMA | 20.67 | 53.89 | WTZR | 12.88 | 49.14 |
| LBCH | 241.80 | 33.79 | YBHB | 237.29 | 41.73 |
| MAC1 | 158.94 | −54.50 | YELL | 245.52 | 62.48 |
| MATE | 16.70 | 40.65 | ZIMM | 7.47 | 46.88 |
| Model | Driving Noise | Fraction FN | Fraction RW | Fraction WN | Fraction GGM | Fraction PL |
|---|---|---|---|---|---|---|
| FNRWWN | 2.3 | 0.89 | 0.03 | 0.08 | - | - |
| FNWN | 2.3 | 0.9 | - | 0.1 | - | - |
| GGMWN | 2.3 | - | - | 0.1 | 0.9 | - |
| PLWN | 2.3 | - | 0.1 | - | 0.9 |
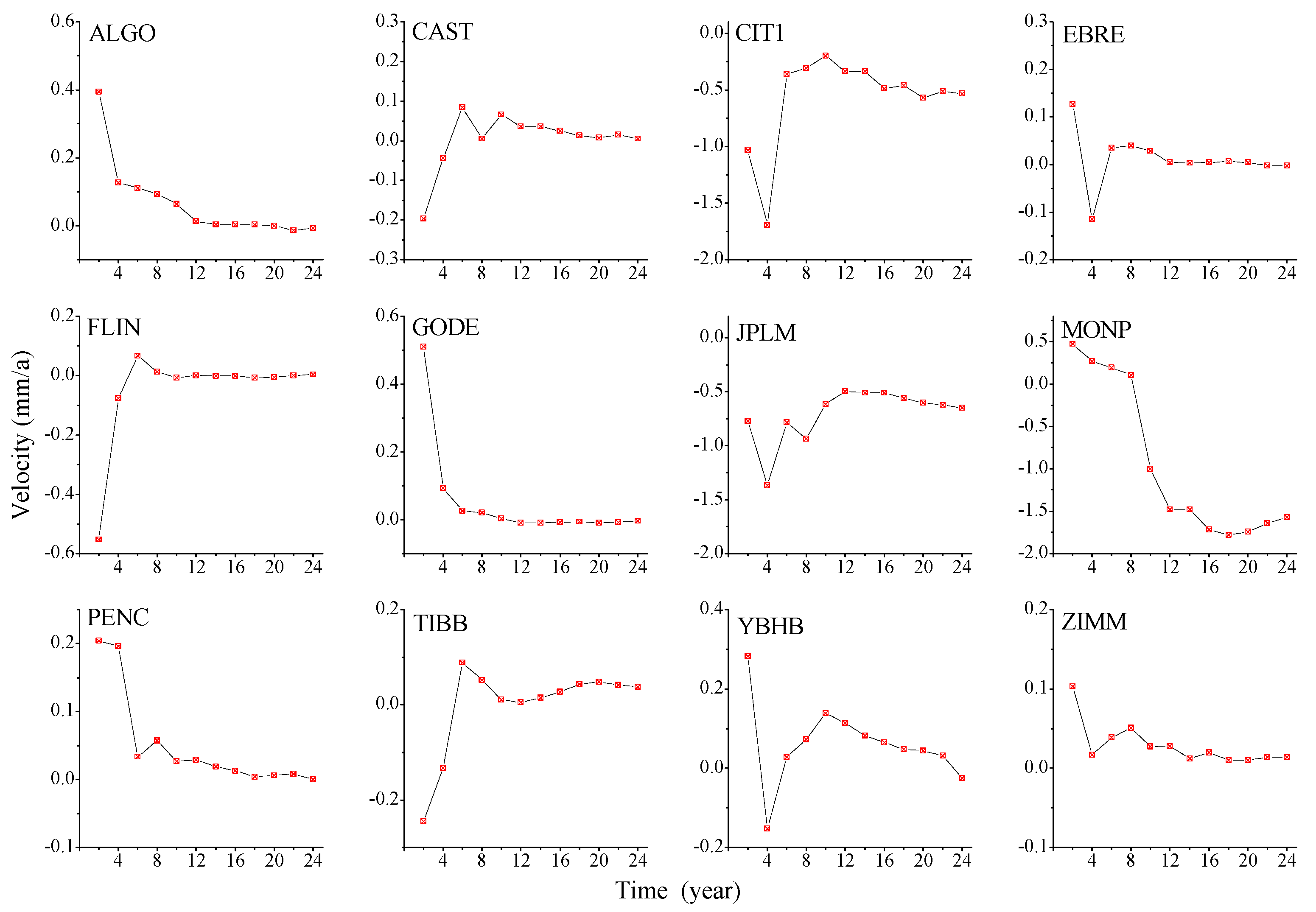
References
- He, X.; Bos, M.S.; Montillet, J.P.; Fernandes, R.; Melbourne, T.; Jiang, W.; Li, W. Spatial variations of stochastic noise properties in GPS time series. Remote Sens. 2021, 13, 4534. [Google Scholar] [CrossRef]
- Fernandes, R.M.S.; Ambrosius, B.A.C.; Noomen, R.; Bastos, L.; Combrinck, L.; Miranda, J.M.; Spakman, W. Angular velocities of Nubia and Somalia from continuous GPS data: Implications on present-day relative kinematics. Earth Planet. Sci. Lett. 2004, 222, 197–208. [Google Scholar] [CrossRef]
- Fernandes, R.M.S.; Bastos, L.; Miranda, J.M.; Lourenço, N.; Ambrosius, B.A.C.; Noomen, R.; Simons, W. Defining the plate boundaries in the Azores region. J. Volcanol. Geotherm. Res. 2006, 156, 1–9. [Google Scholar] [CrossRef]
- Herring, T.A.; Melbourne, T.I.; Murray, M.H.; Floyd, M.A.; Szeliga, W.M.; King, R.W.; Wang, L. Plate Boundary Observatory and related networks: GPS data analysis methods and geodetic products. Rev. Geophys. 2016, 54, 759–808. [Google Scholar] [CrossRef]
- James, T.S.; Morgan, W.J. Horizontal motions due to post-glacial rebound. Geophys. Res. Lett. 1990, 17, 957–960. [Google Scholar] [CrossRef]
- Segall, P.; Davis, J.L. GPS applications for geodynamics and earthquake studies. Annu. Rev. Earth Planet. Sci. 1997, 25, 301–336. [Google Scholar] [CrossRef] [Green Version]
- Troncone, A.; Pugliese, L.; Lamanna, G.; Conte, E. Prediction of rainfall-induced landslide movements in the presence of stabilizing piles. Eng. Geol. 2021, 288, 106143. [Google Scholar] [CrossRef]
- Abatzoglou, J.T.; McEvoy, D.J.; Redmond, K.T. The west wide drought tracker: Drought monitoring at fine spatial scales. Bull. Am. Meteorol. Soc. 2017, 98, 1815–1820. [Google Scholar] [CrossRef]
- Sheorey, P.R.; Loui, J.P.; Singh, K.B.; Singh, S.K. Ground subsidence observations and a modified influence function method for complete subsidence prediction. Int. J. Rock. Mech. Min. 2000, 37, 801–818. [Google Scholar] [CrossRef]
- Sauber, J.; Plafker, G.; Molnia, B.F.; Bryant, M.A. Crustal deformation associated with glacial fluctuations in the eastern Chugach Mountains, Alaska. J. Geophys. Res. Solid Earth 2000, 105, 8055–8077. [Google Scholar] [CrossRef] [Green Version]
- Tregoning, P.; Watson, C.; Ramillien, G.; McQueen, H.; Zhang, J. Detecting hydrologic deformation using GRACE and GPS. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef] [Green Version]
- Husson, L.; Bodin, T.; Spada, G.; Choblet, G.; Kreemer, C. Bayesian surface reconstruction of geodetic uplift rates: Mapping the global fingerprint of Glacial Isostatic Adjustment. J. Geodyn. 2018, 122, 25–40. [Google Scholar] [CrossRef]
- Turner, R.J.; Reading, A.M.; King, M.A. Separation of tectonic and local components of horizontal GPS station velocities: A case study for glacial isostatic adjustment in East Antarctica. Geophys. J. Int. 2020, 222, 1555–1569. [Google Scholar] [CrossRef]
- Jiang, W.; Li, Z.; van Dam, T.; Ding, W. Comparative analysis of different environmental loading methods and their impacts on the GPS height time series. J. Geod. 2013, 87, 687–703. [Google Scholar] [CrossRef]
- He, X.; Montillet, J.P.; Hua, X.; Yu, K.; Jiang, W.; Zhou, F. Noise analysis for environmental loading effect on GPS position time series. Acta Geodyn. Et Geomater. 2017, 14, 131–142. [Google Scholar]
- He, X.; Montillet, J.P.; Fernandes, R.; Bos, M.; Yu, K.; Hua, X.; Jiang, W. Review of current GPS methodologies for producing accurate time series and their error sources. J. Geod. 2017, 106, 12–29. [Google Scholar] [CrossRef]
- Wang, W.; Zhao, B.; Wang, Q.; Yang, S. Noise analysis of continuous GPS coordinate time series for CMONOC. Adv. Space Res. 2012, 49, 943–956. [Google Scholar] [CrossRef]
- Bock, Y.; Melgar, D. Physical applications of GPS geodesy: A review. Rep. Prog. Phys. 2016, 79, 106801. [Google Scholar] [CrossRef]
- Mao, A.; Harrison, C.G.A.; Dixon, T.H. Noise in GPS Coordinate Time Series. J. Geophys. Res. Solid Earth 1999, 104, 2797–2816. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Bock, Y.; Johnson, H.; Fang, P.; Williams, S.; Genrich, J.; Wdowinski, S.; Behr, J. Southern California Permanent GPS Geodetic Array: Error analysis of daily position estimates and site velocities. J. Geophys. Res. Solid Earth 1997, 102, 18035–18055. [Google Scholar] [CrossRef]
- Williams, S.D.; Bock, Y.; Fang, P.; Jamason, P.; Nikolaidis, R.M.; Prawirodirdjo, L.; Miller, M.; Johnson, D.J. Error Analysis of Continuous GPS Position Time Series. J. Geophys. Res. Solid Earth 2004, 109, B03412. [Google Scholar] [CrossRef] [Green Version]
- Langbein, J. Noise in GPS Displacement Measurements from Southern California and Southern Nevada. J. Geophys. Res. Solid Earth 2008, 113, 1–12. [Google Scholar] [CrossRef]
- Li, Z.; Jiang, W.; Liu, H.; Qu, X. Noise model establishment and analysis of IGS reference station coordinate time series inside China. Acta Geod. Cartogr. Sin. 2012, 41, 496–503. [Google Scholar]
- Agnew, D.C. The time-domain behavior of power-law noises. Geophys. Res. Lett. 1992, 19, 333–336. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Van Ness, J.W. Fractional Brownian motions, fractional noises and applications. SIAM Rev. 1968, 10, 422–437. [Google Scholar] [CrossRef] [Green Version]
- Santamaría-Gómez, A.; Bouin, M.N.; Collilieux, X.; Wöppelmann, G. Correlated errors in GPS position time series: Implications for velocity estimates. J. Geophys. Res. Solid Earth 2011, 116. [Google Scholar] [CrossRef]
- He, X.; Bos, M.S.; Montillet, J.P.; Fernandes, R.M.S. Investigation of the noise properties at low frequencies in long GNSS time series. J. Geod. 2019, 93, 1271–1282. [Google Scholar] [CrossRef]
- Bos, M.; Fernandes, R.; Williams, S.; Bastos, L. The noise properties in GPS time series at European stations revisited. In Proceedings of the EGU General Assembly, Vienna, Austria, 7–12 April 2013; p. EGU2013-12825. [Google Scholar]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Bos, M.S.; Fernandes, R.M.S.; Williams, S.D.P.; Bastos, L. Fast Error Analysis of Continuous GNSS Obser-vations with Missing Data. J. Geod. 2013, 87, 351–360. [Google Scholar] [CrossRef] [Green Version]
- Amiri-Simkooei, A.R.; Tiberius, C.C.J.M.; Teunissen, P.J.G. Assessment of noise in GPS coordinate time series: Methodology and results. J. Geophys. Res. Solid Earth 2007, 112. [Google Scholar] [CrossRef] [Green Version]
- Amiri-Simkooei, A.R. Non-negative least-squares variance component estimation with application to GPS time series. J. Geod. 2016, 90, 451–466. [Google Scholar] [CrossRef]
- Xu, C. Reconstruction of gappy GPS coordinate time series using empirical orthogonal functions. J. Geophys. Res. Solid Earth 2016, 121, 9020–9033. [Google Scholar] [CrossRef]
- Bevis, M.; Bedford, J.; Caccamise, D.J., II. The art and science of trajectory modelling. In Geodetic Time Series Analysis in Earth Sciences; Springer: Cham, Switzerland, 2020; pp. 1–27. [Google Scholar]
- He, X.; Hua, X.H.; Lu, T.D.L.; Yu, K.G.; Xuan, W. Analysis of the Impact of Time Span on GPS time series Noise Model and Velocity Estimation. J. Natl. Univ. Def. Sci. Technol. 2017, 6, 12–18. [Google Scholar]
- Montillet, J.P.; Bos, M. Geodetic Time Series Analysis in Earth Sciences; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Bock, Y.; Nikolaidis, R.M.; de Jonge, P.J.; Bevis, M. Instantaneous geodetic positioning at medium distances with the Global Positioning Systems. J. Geophys. Res. 2000, 105, 28223–28253. [Google Scholar] [CrossRef]
- Bock, Y.; Moore, A.W.; Argus, D.; Fang, P.; Golriz, D.; Guns, K.; Jiang, S.; Kedar, S.; Knox, S.A.; Liu, Z.; et al. Extended Solid Earth Science ESDR System (ES3): Algorithm Theoretical Basis Document, NASA MEaSUREs Project, # NNH17ZDA001N. 2021. Available online: http://garner.ucsd.edu/pub/measuresESESES_products/ATBD/ESESES-ATBD.pdf (accessed on 1 January 2022).
- Herring, T.A.; King, R.W.; McClusky, S.C. GAMIT Reference Manual. GPS analysis at MIT; Release 10.4; Massachusetts Institute Technology: Cambridge, MA, USA, 2010. [Google Scholar]
- Herring, T.A.; King, R.W.; McClusky, S.C. GLOBK. Global Kalman Filter VLBI and GPS Analysis Program; Version 10; Massachusetts Institute Technology: Cambridge, MA, USA, 2005. [Google Scholar]
- Lichten, S.M.; Bar-Sever, Y.E.; Bertiger, E.I.; Heflin, M.; Hurst, K.; Muellerschoen, R.J.; Wu, S.C.; Yunck, T.P.; Zumberge, J.F. GIPSY-OASIS II: A high precision GPS data processing system and general orbit analysis tool. Technology 2006, 2, 2–4. [Google Scholar]
- Dong, D.; Herring, T.A.; King, R.W. Estimating regional deformation from a combination of space and terrestrial geodetic data. J. Geod. 1998, 72, 200–214. [Google Scholar] [CrossRef]
- Bos, M.S.; Fernandes, R.M.S.; Williams, S.D.P.; Bastos, L. Fast error analysis of continuous GPS observations. J. Geod. 2008, 82, 157–166. [Google Scholar] [CrossRef] [Green Version]
- Bozdogan, H. Model selection and Akaike’s information criterion (AIC): The general theory and its analytical extensions. Psychometrika 1987, 52, 345–370. [Google Scholar] [CrossRef]
- Wagenmakers, E.J.; Farrell, S. AIC model selection using Akaike weights. Psychon. Bull. Rev. 2014, 11, 192–196. [Google Scholar] [CrossRef]
- Dmitrieva, K.; Segall, P.; Bradley, A.M. Effects of linear trends on estimation of noise in GNSS position time series. Geophys. J. Int. 2016, 208, ggw391. [Google Scholar] [CrossRef] [Green Version]
- Dong, D.; Fang, P.; Bock, Y.; Cheng, M.K.; Miyazaki, S.I. Anatomy of apparent seasonal variations from GPS-derived site position time series. J. Geophys. Res. Solid Earth 2002, 107, ETG 9-1–ETG 9-16. [Google Scholar] [CrossRef] [Green Version]
- Peng, Y.; Dong, D.; Chen, W.; Zhang, C. Stable regional reference frame for reclaimed land subsidence study in East China. Remote Sens. 2022, 14, 3984. [Google Scholar] [CrossRef]
- Montillet, J.P.; Melbourne, T.I.; Szeliga, W.M. GPS vertical land motion corrections to sea-level rise estimates in the Pacific Northwest. J. Geophys. Res. 2018, 123, 1196–1212. [Google Scholar] [CrossRef]
- Benoist, C.; Collilieux, X.; Rebischung, P.; Altamimi, Z.; Jamet, O.; Métivier, L.; Chanard, K.; Bel, L. Accounting for spati-otemporal correlations of GNSS coordinate time series to estimate station velocities. J. Geod. 2020, 135, 101693. [Google Scholar] [CrossRef]
- He, Y.; Nie, G.; Wu, S.; Li, H. Analysis and discussion on the optimal noise model of global GNSS long-term coordinate series considering hydrological loading. Remote Sens. 2021, 13, 431. [Google Scholar] [CrossRef]
- Kall, T.; Oja, T.; Kollo, K.; Liibusk, A. The noise properties and velocities from a time series of Estonian permanent GNSS stations. Geosciences 2019, 9, 233. [Google Scholar] [CrossRef] [Green Version]
- Kaczmarek, A.; Kontny, B. Identification of the noise model in the time series of GNSS stations coordinates using wavelet analysis. Remote Sens. 2018, 10, 1611. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Li, Z.; Jiang, W.; Chen, Q.; Zhu, G.; Wang, J. A New Spatial Filtering Algorithm for Noisy and Missing GNSS Position Time Series Using Weighted Expectation Maximization Principal Component Analysis: A Case Study for Regional GNSS Network in Xinjiang Province. Remote Sens. 2022, 14, 1295. [Google Scholar] [CrossRef]
- Wang, L.; Wu, Q.; Wu, F.; He, X. Noise content assessment in GNSS coordinate time series with autoregres-sive and heteroscedastic random errors. Geophys. J. Int. 2022, 231, 856–876. [Google Scholar] [CrossRef]
- Langbein, J. Estimating rate uncertainty with maximum likelihood: Differences between power-law and flicker–random-walk models. J. Geod. 2012, 86, 775–783. [Google Scholar] [CrossRef] [Green Version]
- Melbourne, T.I.; Webb, F.H. Slow but not quite silent. Science 2003, 300, 1886–1887. [Google Scholar] [CrossRef] [PubMed]
- Klos, A.; Bogusz, J.; Bos, M.S.; Gruszczynska, M. Modelling the GNSS time series: Different approaches to extract seasonal signals. In Geodetic Time Series Analysis in Earth Sciences; Springer: Cham, Switzerland, 2020; pp. 211–237. [Google Scholar]
- Langbein, J.; Svarc, J.L. Evaluation of temporally correlated noise in Global Navigation Satellite System time series: Geodetic monument performance. J. Geophys. Res. Solid Earth 2019, 124, 925–942. [Google Scholar] [CrossRef] [Green Version]
- Langbein, J. Noise in two-color electronic distance meter measurements revisited. J. Geophys. Res. Solid Earth 2004, 109. [Google Scholar] [CrossRef]
- Ren, A.K.; Xr, K.; Shao, Z.H. Establishment and analysis of GPS coordinate time series noise model in GEONET. J. Navig. Position. 2022, 10, 141–151. [Google Scholar]





| Model | FNRWWN | FNWN | |||||||
|---|---|---|---|---|---|---|---|---|---|
| FNRW WN | FN WN | GGM WN | PL WN | FNRW WN | FN WN | GGM WN | PL WN | ||
| Length | |||||||||
| 2a | 14 | 74 | 0 | 12 | 0 | 99 | 1 | 0 | |
| 4a | 58 | 21 | 0 | 21 | 0 | 100 | 0 | 0 | |
| 6a | 74 | 4 | 0 | 22 | 0 | 100 | 0 | 0 | |
| 8a | 79 | 1 | 0 | 20 | 0 | 100 | 0 | 0 | |
| 10a | 84 | 1 | 0 | 15 | 0 | 100 | 0 | 0 | |
| 12a | 95 | 0 | 0 | 5 | 0 | 100 | 0 | 0 | |
| 14a | 94 | 0 | 0 | 6 | 0 | 99 | 0 | 1 | |
| 16a | 95 | 0 | 0 | 5 | 0 | 99 | 0 | 1 | |
| 18a | 94 | 0 | 0 | 6 | 0 | 99 | 0 | 1 | |
| 20a | 94 | 0 | 0 | 6 | 0 | 100 | 0 | 0 | |
| 22a | 97 | 0 | 0 | 3 | 0 | 99 | 0 | 1 | |
| 24a | 97 | 0 | 0 | 3 | 0 | 99 | 0 | 1 | |
| 26a | 98 | 0 | 0 | 2 | 0 | 100 | 0 | 0 | |
| 28a | 98 | 0 | 0 | 2 | 0 | 100 | 0 | 0 | |
| 30a | 99 | 0 | 0 | 1 | 0 | 100 | 0 | 0 | |
| Model | GGMWN | PLWN | |||||||
|---|---|---|---|---|---|---|---|---|---|
| FNRW WN | FN WN | GGM WN | PL WN | FNRW WN | FN WN | GGM WN | PL WN | ||
| Length | |||||||||
| 2a | 5 | 0 | 2 | 93 | 29 | 0 | 2 | 69 | |
| 4a | 0 | 0 | 12 | 88 | 7 | 0 | 0 | 93 | |
| 6a | 0 | 0 | 52 | 48 | 3 | 0 | 0 | 97 | |
| 8a | 0 | 0 | 77 | 23 | 1 | 0 | 1 | 98 | |
| 10a | 0 | 0 | 94 | 6 | 0 | 0 | 1 | 99 | |
| 12a | 0 | 0 | 100 | 0 | 0 | 0 | 0 | 100 | |
| 14a | 0 | 0 | 100 | 0 | 0 | 0 | 0 | 100 | |
| 16a | 0 | 0 | 100 | 0 | 0 | 0 | 0 | 100 | |
| 18a | 0 | 0 | 100 | 0 | 0 | 0 | 0 | 100 | |
| 20a | 0 | 0 | 100 | 0 | 0 | 0 | 0 | 100 | |
| 22a | 0 | 0 | 100 | 0 | 0 | 0 | 0 | 100 | |
| 24a | 0 | 0 | 100 | 0 | 0 | 0 | 0 | 100 | |
| 26a | 0 | 0 | 100 | 0 | 0 | 0 | 0 | 100 | |
| 28a | 0 | 0 | 100 | 0 | 0 | 0 | 0 | 100 | |
| 30a | 0 | 0 | 100 | 0 | 0 | 0 | 0 | 100 | |
| Model | Ratio | Model | Ratio | Model | Ratio | Model | Ratio |
|---|---|---|---|---|---|---|---|
| 5.3 | 1.0 | 0.03 | 0.5 | ||||
| 3.5 | 1.9 | 0.5 | 5.2 | ||||
| 2.5 | 1.1 | 0.1 | 2.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, X.; Lu, T.; Hu, S.; Huang, J.; He, X.; Montillet, J.-P.; Ma, X.; Huang, Z. The Relationship of Time Span and Missing Data on the Noise Model Estimation of GNSS Time Series. Remote Sens. 2023, 15, 3572. https://doi.org/10.3390/rs15143572
Sun X, Lu T, Hu S, Huang J, He X, Montillet J-P, Ma X, Huang Z. The Relationship of Time Span and Missing Data on the Noise Model Estimation of GNSS Time Series. Remote Sensing. 2023; 15(14):3572. https://doi.org/10.3390/rs15143572
Chicago/Turabian StyleSun, Xiwen, Tieding Lu, Shunqiang Hu, Jiahui Huang, Xiaoxing He, Jean-Philippe Montillet, Xiaping Ma, and Zhengkai Huang. 2023. "The Relationship of Time Span and Missing Data on the Noise Model Estimation of GNSS Time Series" Remote Sensing 15, no. 14: 3572. https://doi.org/10.3390/rs15143572









