An Integrated InSAR and GNSS Approach to Monitor Land Subsidence in the Po River Delta (Italy)
Abstract
:1. Introduction
2. The Study Area
3. Materials and Methods
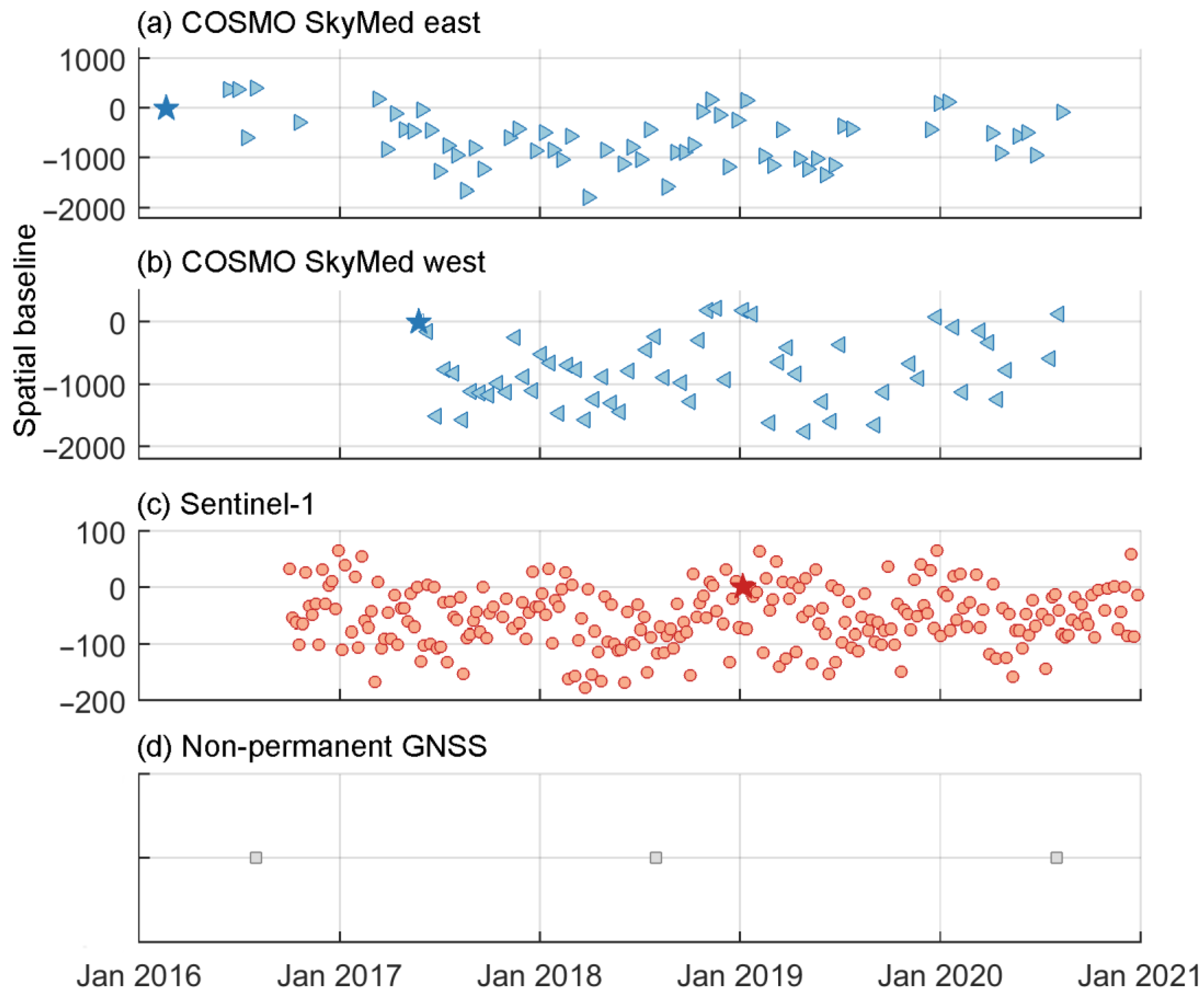
3.1. SAR Data and Processing
3.2. The PODELNET Network
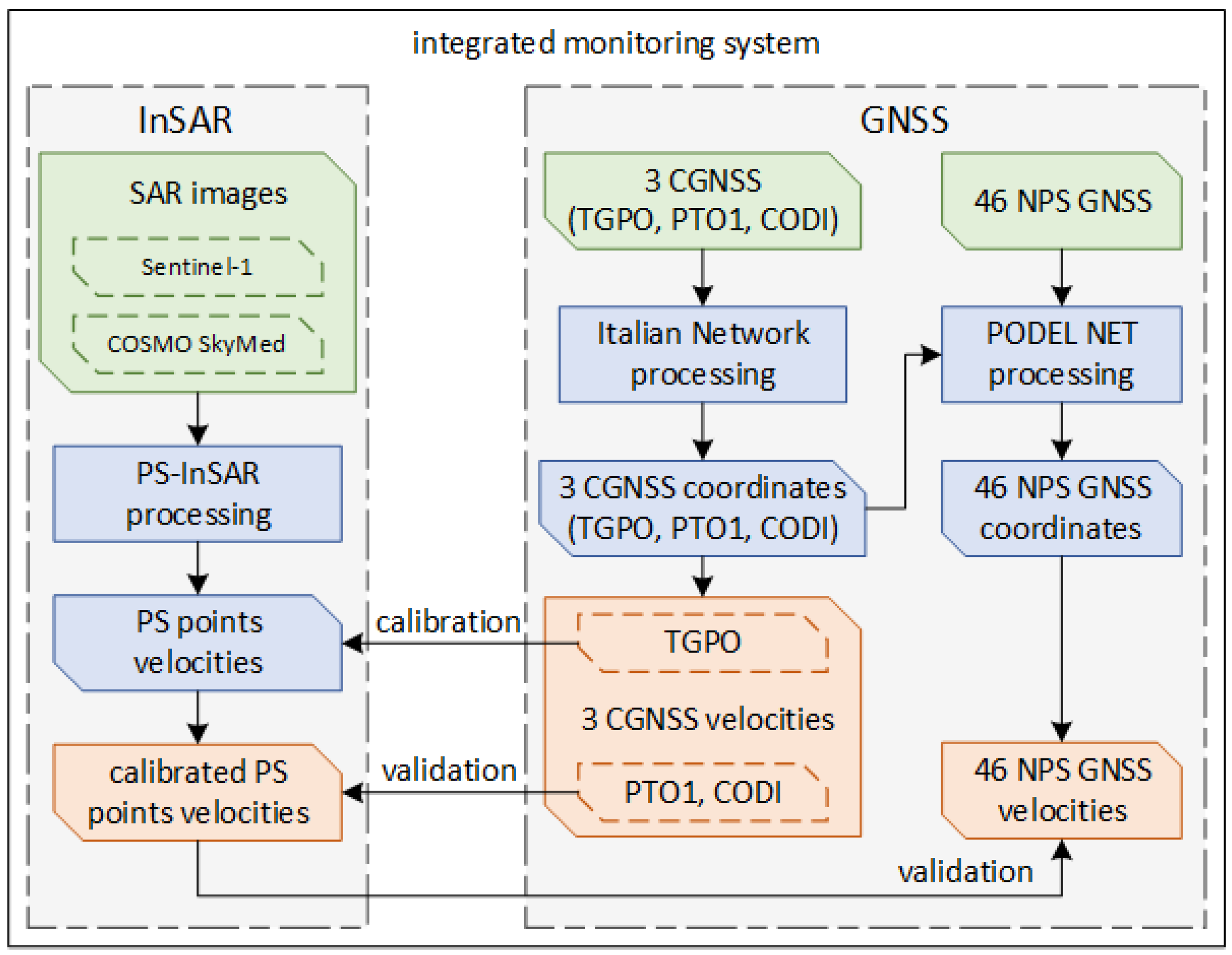
3.3. Integration between InSAR and GNSS Data
4. Results
4.1. Processing of the GNSS Data
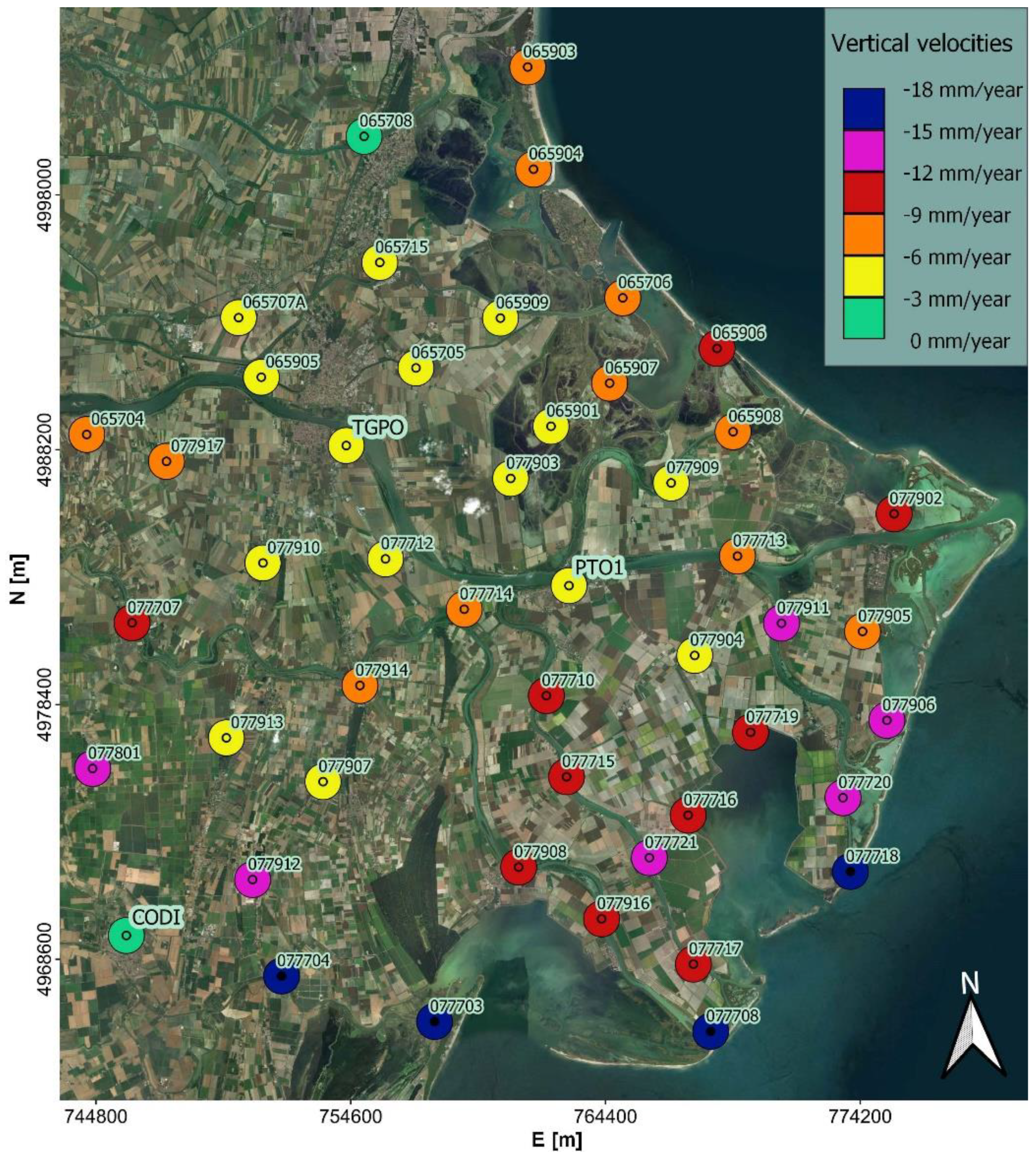
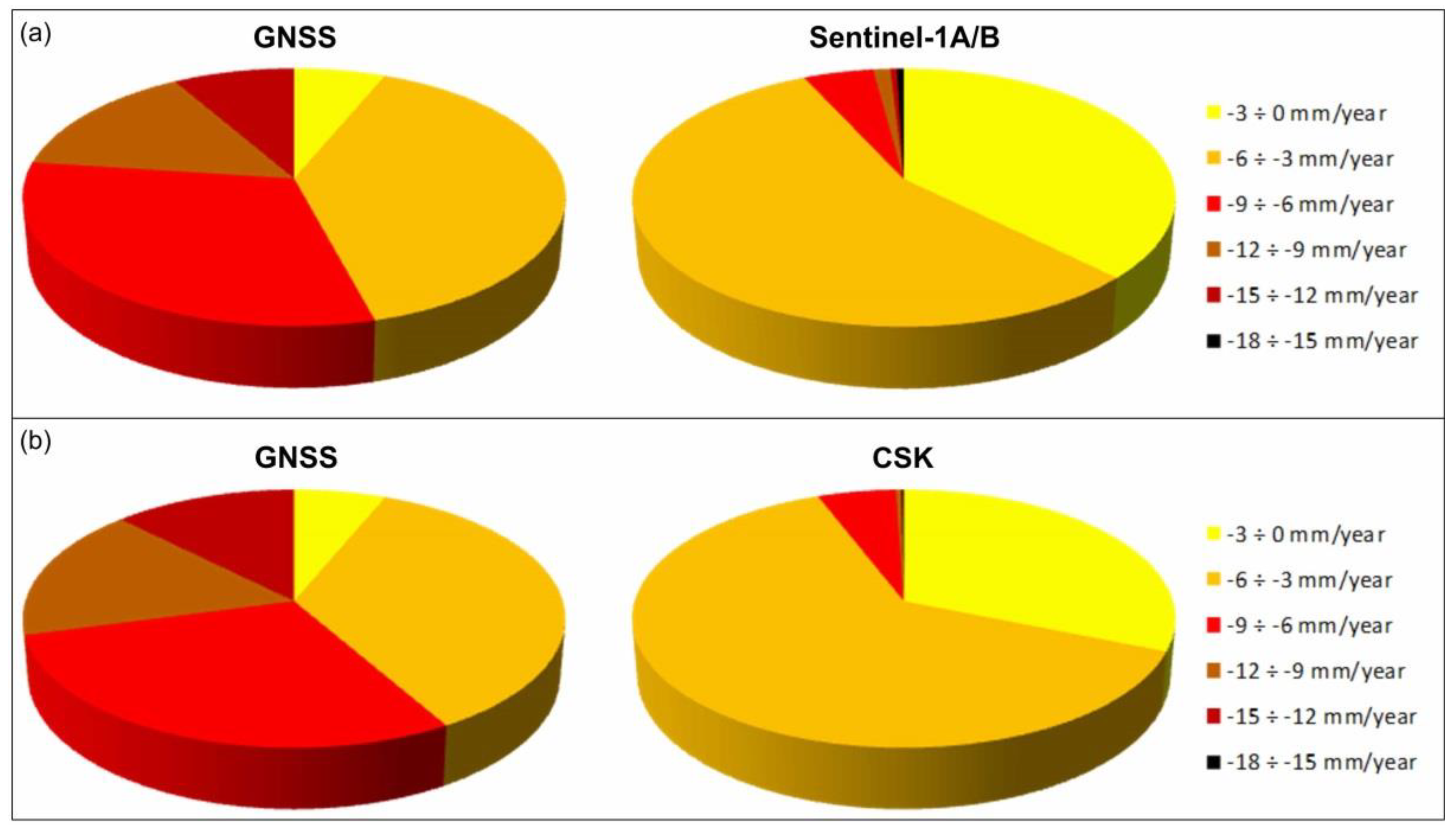
4.2. Comparisons between the GNSS and Interferometric Data
4.3. Integrated Monitoring System
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhou, C.; Gong, H.; Chen, B.; Gao, M.; Cao, Q.; Cao, J.; Duan, L.; Zuo, J.; Shi, M. Land Subsidence Response to Different Land Use Types and Water Resource Utilization in Beijing-Tianjin-Hebei, China. Remote Sens. 2020, 12, 457. [Google Scholar] [CrossRef] [Green Version]
- Ericson, J.P.; Vörösmarty, C.J.; Dingman, S.L.; Ward, L.G.; Meybeck, M. Effective sea-level rise and deltas: Causes of change and human dimension implications. Glob. Planet. Change 2006, 50, 63–82. [Google Scholar] [CrossRef]
- Syvitski, J.; Kettner, A.; Overeem, I.; Hutton, E.; Hannon, M.; Brakenridge, G.; Day, J.; Vörösmarty, C.; Saito, Y.; Giosan, L.; et al. Sinking deltas due to human activities. Nat. Geosci. 2009, 2, 681–686. [Google Scholar] [CrossRef]
- Fiaschi, S.; Fabris, M.; Floris, M.; Achilli, V. Estimation of land subsidence in deltaic areas through differential SAR interferometry: The Po River Delta case study (Northeast Italy). Int. J. Remote Sens. 2018, 39, 8724–8745. [Google Scholar] [CrossRef]
- Fabris, M. Coastline evolution of the Po River Delta (Italy) by archival multi-temporal digital photogrammetry. Geomat. Nat. Hazards Risk 2019, 10, 1007–1027. [Google Scholar] [CrossRef] [Green Version]
- Gido, N.A.A.; Bagherbandi, M.; Nilfouroushan, F. Localized Subsidence Zones in Gävle City Detected by Sentinel-1 PSI and Leveling Data. Remote Sens. 2020, 12, 2629. [Google Scholar] [CrossRef]
- Declercq, P.-Y.; Gérard, P.; Pirard, E.; Walstra, J.; Devleeschouwer, X. Long-Term Subsidence Monitoring of the Alluvial Plain of the Scheldt River in Antwerp (Belgium) Using Radar Interferometry. Remote Sens. 2021, 13, 1160. [Google Scholar] [CrossRef]
- Maltese, A.; Pipitone, C.; Dardanelli, G.; Capodici, F.; Muller, J.-P. Toward a Comprehensive Dam Monitoring: On-Site and Remote-Retrieved Forcing Factors and Resulting Displacements (GNSS and PS–InSAR). Remote Sens. 2021, 13, 1543. [Google Scholar] [CrossRef]
- Chen, X.; Achilli, V.; Cenni, N.; Fabris, M.; Menin, A.; Monego, M.; Floris, M. Monitoring land subsidence and element at risk in the Po Delta area (Northern Italy) through MT-InSAR and GNSS surveys. In Proceedings of the EGU General Assembly Conference Abstracts, Online, 19–30 April 2021; p. EGU21-15859. [Google Scholar]
- Alcaras, E.; Falchi, U.; Parente, C.; Vallario, A. Accuracy evaluation for coastline extraction from Pléiades imagery based on NDWI and IHS pan-sharpening application. Appl. Geomat. 2022. [Google Scholar] [CrossRef]
- Antonioli, F.; Anzidei, M.; Amorosi, A.; Lo Presti, V.; Mastronuzzi, G.; Deiana, G.; De Falco, G.; Fontana, A.; Fontolan, G.; Lisco, S.; et al. Sea-level rise and potential drowning of the Italian coastal plains: Flooding risk scenarios for 2100. Quat. Sci. Rev. 2017, 158, 29–43. [Google Scholar] [CrossRef]
- Kulp, S.A.; Strauss, B.H. New elevation data triple estimates of global vulnerability to sea-level rise and coastal flooding. Nat. Commun. 2019, 10, 4844. [Google Scholar] [CrossRef] [Green Version]
- Fabris, M. Monitoring the Coastal Changes of the Po River Delta (Northern Italy) since 1911 Using Archival Cartography, Multi-Temporal Aerial Photogrammetry and LiDAR Data: Implications for Coastline Changes in 2100 A.D. Remote Sens. 2021, 13, 529. [Google Scholar] [CrossRef]
- Cenni, N.; Fiaschi, S.; Fabris, M. Integrated use of archival aerial photogrammetry, GNSS, and InSAR data for the monitoring of the Patigno landslide (Northern Apennines, Italy). Landslides 2021, 18, 2247–2263. [Google Scholar] [CrossRef]
- Magnússon, E.; Björnsson, H.; Rott, H.; Roberts, M.J.; Pálsson, F.; Guđmundsson, S.; Bennett, R.A.; Geirsson, H.; Sturkell, E. Localized uplift of Vatnajökull, Iceland: Subglacial water accumulation deduced from InSAR and GPS observations. J. Glaciol. 2011, 57, 475–484. [Google Scholar] [CrossRef] [Green Version]
- Cheng, S.; Perissin, D.; Lin, H.; Chen, F. Atmospheric delay analysis from GPS meteorology and InSAR APS. J. Atmos. Sol. -Terr. Phys. 2012, 86, 71–82. [Google Scholar] [CrossRef]
- Bovenga, F.; Nitti, D.O.; Fornaro, G.; Radicioni, F.; Stoppini, A.; Brigante, R. Using C/X-band SAR interferometry and GNSS measurements for the Assisi landslide analysis. Int. J. Remote Sens. 2013, 34, 4083–4104. [Google Scholar] [CrossRef]
- Tapete, D.; Morelli, S.; Fanti, R.; Casagli, N. Localising deformation along the elevation of linear structures: An experiment with space-borne InSAR and RTK GPS on the Roman Aqueducts in Rome, Italy. Appl. Geogr. 2015, 58, 65–83. [Google Scholar] [CrossRef] [Green Version]
- Gudmundsson, M.T.; Jónsdóttir, K.; Hooper, A.; Holohan, E.P.; Halldórsson, S.A.; Ófeigsson, B.G.; Cesca, S.; Vogfjörd, K.S.; Sigmundsson, F.; Högnadóttir, T.; et al. Gradual caldera collapse at Bárdarbunga volcano, Iceland, regulated by lateral magma outflow. Science 2016, 353, aaf8988. [Google Scholar] [CrossRef] [Green Version]
- Wilkinson, M.W.; McCaffrey, K.J.W.; Jones, R.R.; Roberts, G.P.; Holdsworth, R.E.; Gregory, L.C.; Walters, R.J.; Wedmore, L.; Goodall, H.; Iezzi, F. Near-field fault slip of the 2016 Vettore Mw 6.6 earthquake (Central Italy) measured using low-cost GNSS. Sci. Rep. 2017, 7, 4612. [Google Scholar] [CrossRef]
- Saleh, M.; Becker, M. New estimation of Nile Delta subsidence rates from InSAR and GPS analysis. Environ. Earth Sci. 2018, 78, 6. [Google Scholar] [CrossRef]
- Farolfi, G.; Bianchini, S.; Casagli, N. Integration of GNSS and satellite InSAR data: Derivation of fine-scale vertical surface motion maps of Po Plain, Northern Apennines, and Southern Alps, Italy. IEEE Trans. Geosci. Remote Sens. 2019, 57, 319–328. [Google Scholar] [CrossRef]
- Benetatos, C.; Codegone, G.; Ferraro, C.; Mantegazzi, A.; Rocca, V.; Tango, G.; Trillo, F. Multidisciplinary Analysis of Ground Movements: An Underground Gas Storage Case Study. Remote Sens. 2020, 12, 3487. [Google Scholar] [CrossRef]
- Grgić, M.; Bender, J.; Bašić, T. Estimating Vertical Land Motion from Remote Sensing and In-Situ Observations in the Dubrovnik Area (Croatia): A Multi-Method Case Study. Remote Sens. 2020, 12, 3543. [Google Scholar] [CrossRef]
- Chen, X.; Achilli, V.; Fabris, M.; Menin, A.; Monego, M.; Tessari, G.; Floris, M. Combining Sentinel-1 interferometry and ground-based geomatics techniques for monitoring buildings affected by mass movements. Remote Sens. 2021, 13, 452. [Google Scholar] [CrossRef]
- Mancini, F.; Grassi, F.; Cenni, N. A Workflow Based on SNAP–StaMPS Open-Source Tools and GNSS Data for PSI-Based Ground Deformation Using Dual-Orbit Sentinel-1 Data: Accuracy Assessment with Error Propagation Analysis. Remote Sens. 2021, 13, 753. [Google Scholar] [CrossRef]
- Baldi, P.; Casula, G.; Cenni, N.; Loddo, F.; Pesci, A. GPS-based monitoring of land subsidence in the Po Plain (Northern Italy). Earth Planet. Sci. Lett. 2009, 288, 204–212. [Google Scholar] [CrossRef]
- Teatini, P.; Tosi, L.; Strozzi, T. Quantitative evidence that compaction of Holocene sediments drives the present land subsidence of the Po Delta, Italy. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- Caputo, C.; Pieri, M.; Unguendoli, R. Geometric Investigation of the Subsidence in the Po Delta; Consiglio Nazionale delle Ricerche, Laboratorio per lo Studio Della Dinamica Delle Grandi Masse: Roma, Italy, 1970. [Google Scholar]
- Caputo, M. Survey and Geometric Analysis of the Phenomena of Subsidence in the Region of Venice and Its Hinterland; Consiglio Nazionale delle Ricerche, Laboratorio per lo Studio Della Dinamica Delle Grandi Masse: Roma, Italy, 1971. [Google Scholar]
- Borgia, G.C.; Brighenti, G.; Vitali, D. La Coltivazione dei Pozzi Metaniferi del BACINO polesano e Ferrarese: Esame Critico Della Vicenda; Georise International Co., Ltd.: Shanghai, China, 1982. [Google Scholar]
- Carlo, C. Physical Processes and Human Activities in the Evolution of the Po Delta, Italy. J. Coast. Res. 1998, 14, 775–793. [Google Scholar]
- Carminati, E.; Martinelli, G. Subsidence rates in the Po Plain, northern Italy: The relative impact of natural and anthropogenic causation. Eng. Geol. 2002, 66, 241–255. [Google Scholar] [CrossRef]
- Carminati, E.; Martinelli, G.; Severi, P. Influence of glacial cycles and tectonics on natural subsidence in the Po Plain (Northern Italy): Insights from 14C ages. Geochem. Geophys. Geosystems 2003, 4. [Google Scholar] [CrossRef]
- Picotti, V.; Pazzaglia, F.J. A new active tectonic model for the construction of the Northern Apennines mountain front near Bologna (Italy). J. Geophys. Res. Solid Earth 2008, 113. [Google Scholar] [CrossRef]
- Tosi, L.; Da Lio, C.; Strozzi, T.; Teatini, P. Combining L-and X-band SAR interferometry to assess ground displacements in heterogeneous coastal environments: The Po River Delta and Venice Lagoon, Italy. Remote Sens. 2016, 8, 308. [Google Scholar] [CrossRef] [Green Version]
- Martinelli, G.; Chahoud, A.; Dadomo, A.; Fava, A. Isotopic features of Emilia-Romagna region (North Italy) groundwaters: Environmental and climatological implications. J. Hydrol. 2014, 519, 1928–1938. [Google Scholar] [CrossRef]
- Correggiari, A.; Cattaneo, A.; Trincardi, F. The modern Po Delta system: Lobe switching and asymmetric prodelta growth. Mar. Geol. 2005, 222–223, 49–74. [Google Scholar] [CrossRef]
- Simeoni, U.; Corbau, C. A review of the Delta Po evolution (Italy) related to climatic changes and human impacts. Geomorphology 2009, 107, 64–71. [Google Scholar] [CrossRef]
- Corbau, C.; Simeoni, U.; Zoccarato, C.; Mantovani, G.; Teatini, P. Coupling land use evolution and subsidence in the Po Delta, Italy: Revising the past occurrence and prospecting the future management challenges. Sci. Total Environ. 2019, 654, 1196–1208. [Google Scholar] [CrossRef]
- Bondesan, M.; SIMEONI, V. Dinamica e analisi mortologica statistica dei litorali del delta del Po e alle foci dell'Adige e del Brenta. Mem. Degli Ist. Geol. Mineral. Dell'Universita Padova 1983, 36, 1–48. [Google Scholar]
- Cenni, N.; Mantovani, E.; Baldi, P.; Viti, M. Present kinematics of Central and Northern Italy from continuous GPS measurements. J. Geodyn. 2012, 58, 62–72. [Google Scholar] [CrossRef]
- Cenni, N.; Viti, M.; Baldi, P.; Mantovani, E.; Bacchetti, M.; Vannucchi, A. Present vertical movements in Central and Northern Italy from GPS data: Possible role of natural and anthropogenic causes. J. Geodyn. 2013, 71, 74–85. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Nonlinear subsidence rate estimation using permanent scatterers in differential SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2202–2212. [Google Scholar] [CrossRef] [Green Version]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Crosetto, M.; Monserrat, O.; Cuevas-González, M.; Devanthéry, N.; Crippa, B. Persistent scatterer interferometry: A review. ISPRS J. Photogramm. Remote Sens. 2016, 115, 78–89. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Tessari, G.; Fabris, M.; Achilli, V.; Floris, M. Comparison between PS and SBAS InSAR techniques in monitoring shallow landslides. In Understanding and Reducing Landslide Disaster Risk; ICL Contribution to Landslide Disaster Risk Reduction; Springer Nature: Berlin, Germany, 2021; pp. 155–161. [Google Scholar]
- Werner, C.; Wegmüller, U.; Strozzi, T.; Wiesmann, A. Gamma SAR and interferometric processing software. In Proceedings of the ERS-Envisat Symposium, Gothenburg, Sweden, 16–20 October 2000; p. 1620. [Google Scholar]
- Costantini, M. A novel phase unwrapping method based on network programming. IEEE Trans. Geosci. Remote Sens. 1998, 36, 813–821. [Google Scholar] [CrossRef]
- Small, D.; Werner, C.; Nuesch, D. Baseline modelling for ERS-1 SAR interferometry. In Proceedings of the IGARSS'93-IEEE International Geoscience and Remote Sensing Symposium, Tokyo, Japan, 18–21 August 1993; pp. 1204–1206. [Google Scholar]
- Altamimi, Z.; Rebischung, P.; Métivier, L.; Collilieux, X. ITRF2014: A new release of the International Terrestrial Reference Frame modeling nonlinear station motions. J. Geophys. Res. Solid Earth 2016, 121, 6109–6131. [Google Scholar] [CrossRef] [Green Version]
- Cenni, N.; Fiaschi, S.; Fabris, M. Monitoring of Land Subsidence in the Po River Delta (Northern Italy) Using Geodetic Networks. Remote Sens. 2021, 13, 1488. [Google Scholar] [CrossRef]
- Hu, X.; Lu, Z.; Pierson, T.C.; Kramer, R.; George, D.L. Combining InSAR and GPS to Determine Transient Movement and Thickness of a Seasonally Active Low-Gradient Translational Landslide. Geophys. Res. Lett. 2018, 45, 1453–1462. [Google Scholar] [CrossRef]
- Stefani, M.; Vincenzi, S. The interplay of eustasy, climate and human activity in the late Quaternary depositional evolution and sedimentary architecture of the Po Delta system. Mar. Geol. 2005, 222, 19–48. [Google Scholar] [CrossRef]
- Alcaras, E.; Parente, C.; Vallario, A. Comparison of different interpolation methods for DEM production. Int. J. Adv. Trends Comput. Sci. Eng. 2019, 6, 1654–1659. [Google Scholar] [CrossRef]
- Motagh, M.; Djamour, Y.; Walter, T.R.; Wetzel, H.-U.; Zschau, J.; Arabi, S. Land subsidence in Mashhad Valley, northeast Iran: Results from InSAR, levelling and GPS. Geophys. J. Int. 2007, 168, 518–526. [Google Scholar] [CrossRef]
- Meckel, T.A.; ten Brink, U.S.; Williams, S.J. Current subsidence rates due to compaction of Holocene sediments in southern Louisiana. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]


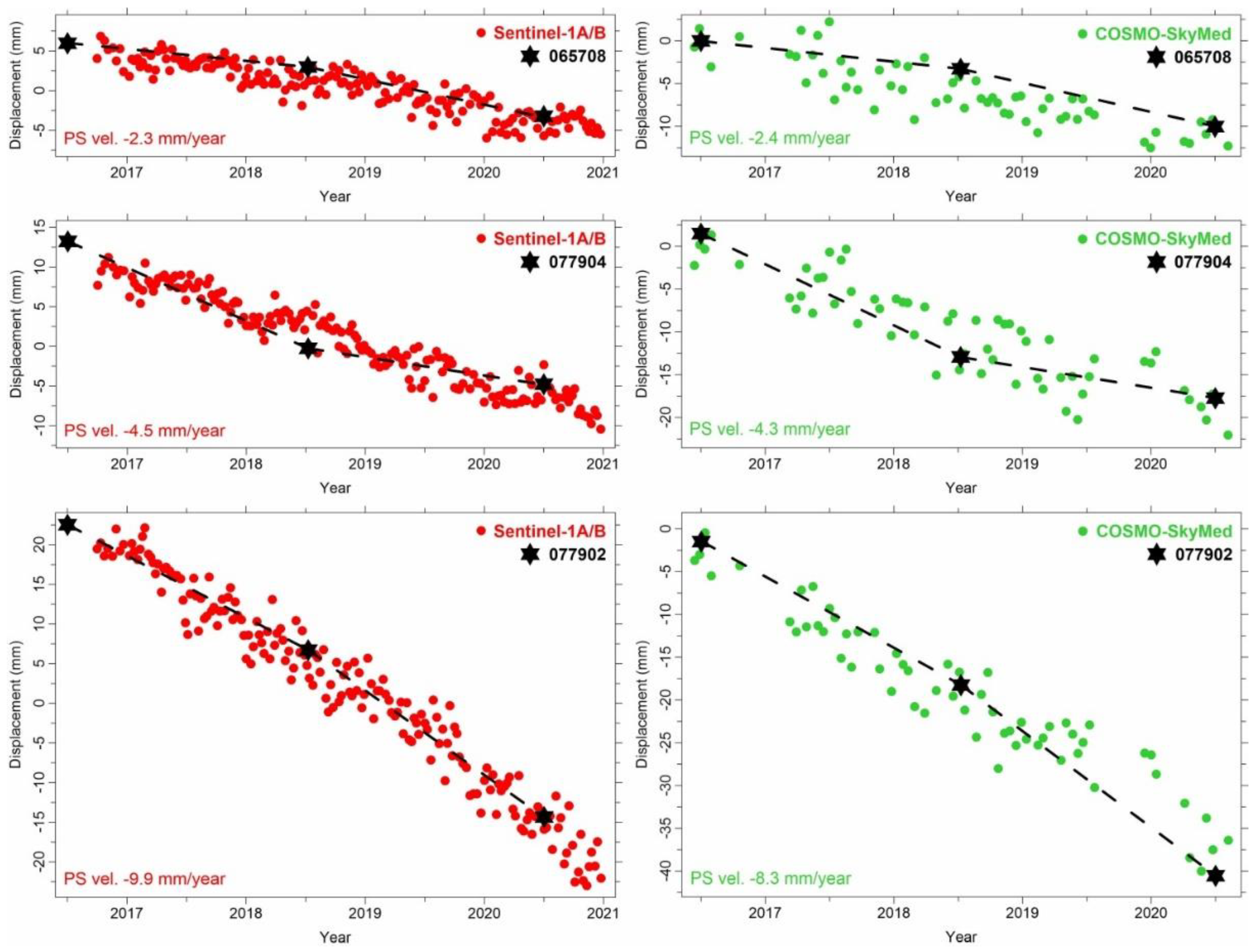
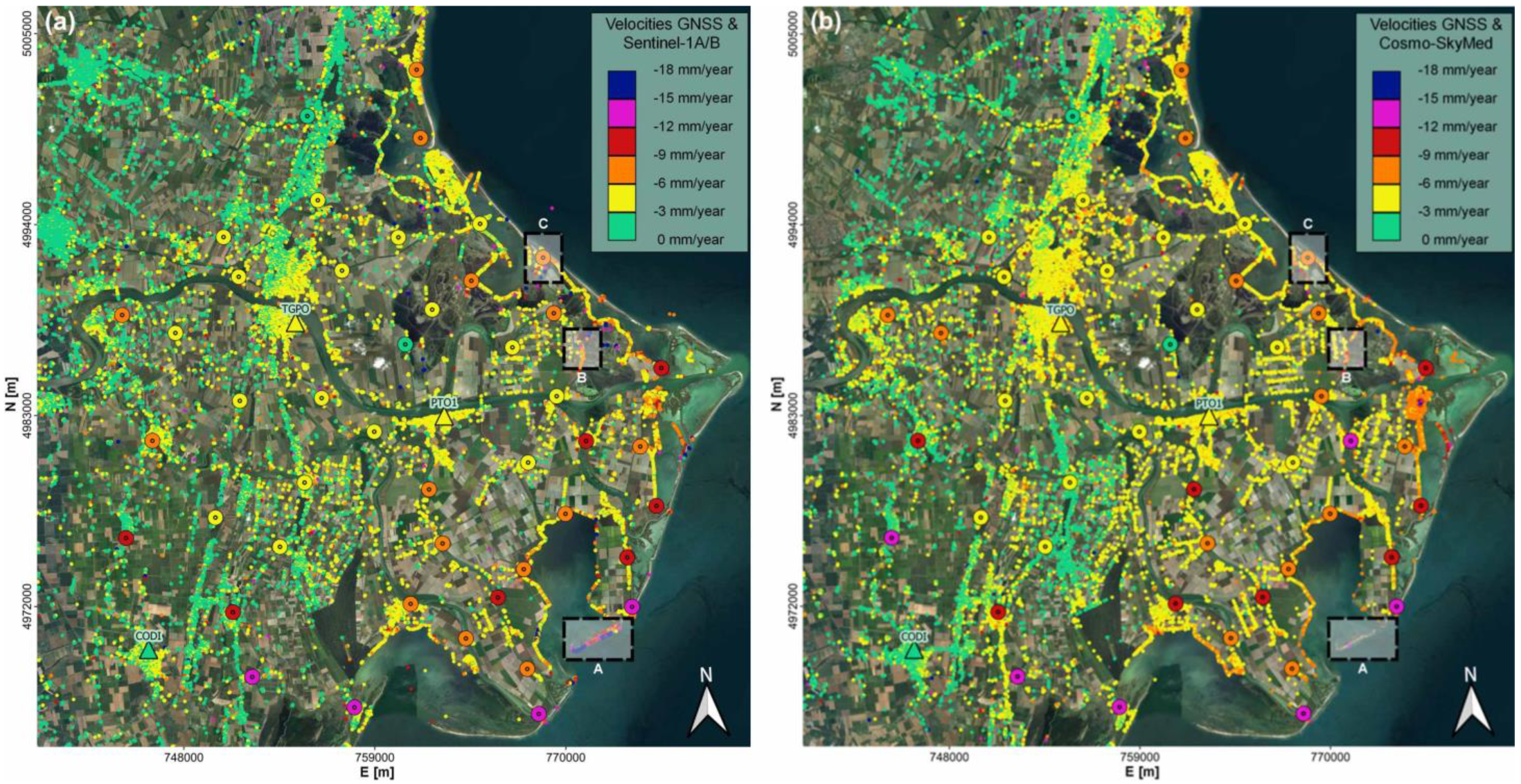
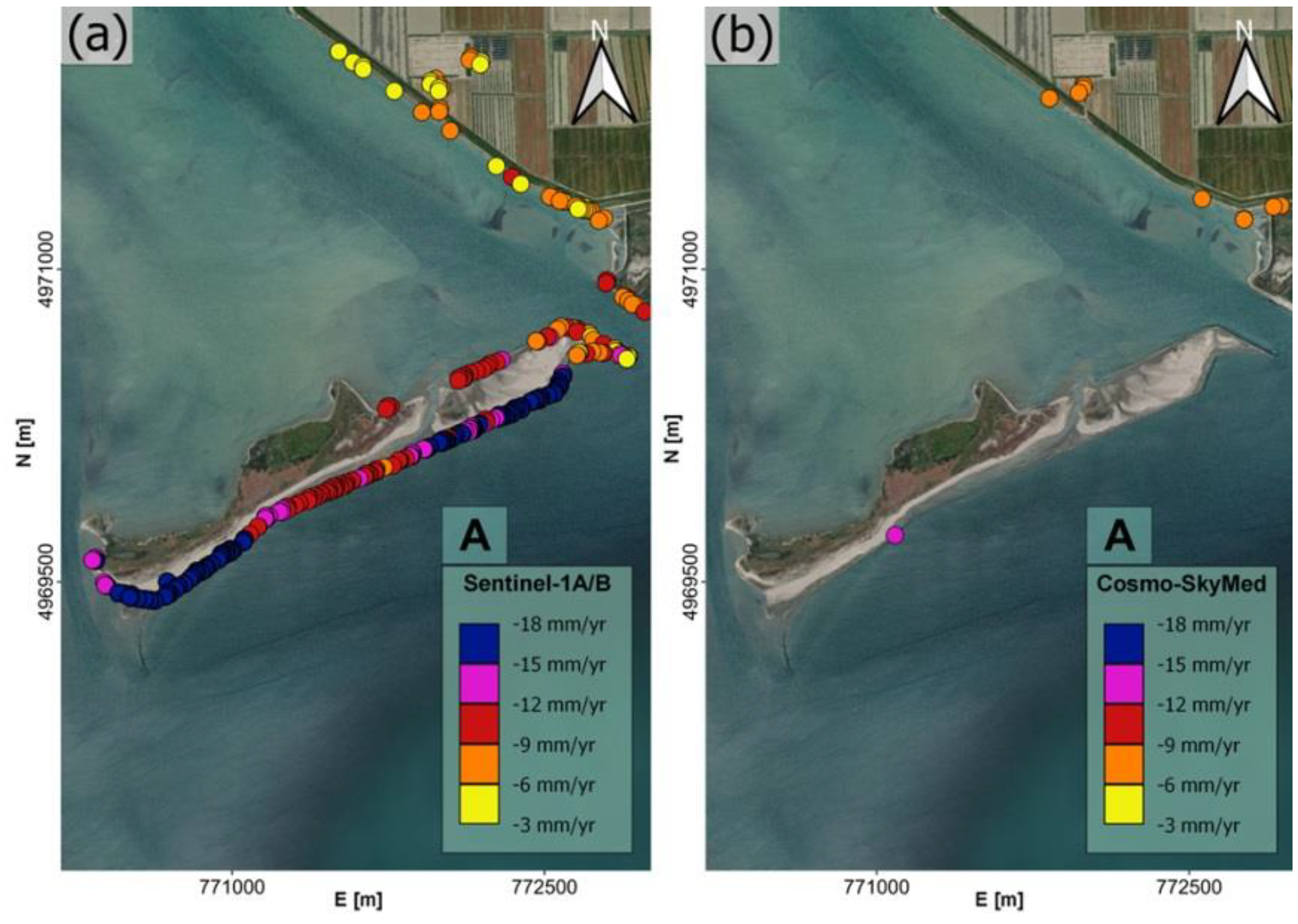



| Code | * Vv (mm/Year) (Period) | * Vv (2016–2018) (mm/Year) | ** Vv (2016–2018) (mm/Year) | ** Vv (2016–2020) (mm/Year) |
|---|---|---|---|---|
| CODI | −3.5 ± 0.7 (2007–2019) | −3.1 ± 0.4 | −2.8 ± 1.7 | −2.8 ± 1.8 |
| PTO1 | −5.8 ± 1.0 (2010–2019) | −5.8 ± 0.4 | −5.1 ± 2.2 | −5.1 ± 2.0 |
| TGPO | −5.6 ± 0.8 (2008–2019) | −6.5 ± 0.4 | −5.0 ± 1.8 | −5.1 ± 1.9 |
| CGNSS Station Code | Distance from the Station (m) | Sentinel-1 | COSMO-SkyMed | |||||
|---|---|---|---|---|---|---|---|---|
| N. of PS | PS Vel. (mm/Year) | CGNSS Vel. (mm/Year) | N. of PS | * PS Vel. (mm/Year) | ** PS Vel. (mm/Year) | CGNSS Vel. (mm/Year) | ||
| CODI | - | 1 | −2.7 | −2.2 ± 0.4 | 1 | −5.0 | −3.0 | −2.5 ± 0.4 |
| - | 2 | −2.6 ± 0.1 | 2 | −4.7 ± 0.3 | −2.7 ± 0.3 | |||
| - | 3 | −2.7 ± 0.2 | 3 | −4.7 ± 0.2 | −2.7 ± 0.2 | |||
| 50 | 4 | −2.7 ± 0.2 | 6 | −4.4 ± 1.1 | −2.4 ± 1.1 | |||
| 100 | 32 | −3.0 ± 0.4 | 44 | −4.5 ± 0.5 | −2.5 ± 0.5 | |||
| 150 | 55 | −3.1 ± 0.4 | 92 | −4.6 ± 0.7 | −2.6 ± 0.7 | |||
| 200 | 71 | −3.2 ± 0.5 | 147 | −4.6 ± 0.7 | −2.6 ± 0.7 | |||
| PTO1 | - | 1 | −4.5 | −4.0 ± 0.5 | 1 | −6.8 | −4.8 | −4.2 ± 0.5 |
| - | 2 | −4.5 ± 0.0 | 2 | −7.3 ± 0.6 | −5.3 ± 0.6 | |||
| - | 3 | −4.5 ± 0.0 | 3 | −7.3 ± 0.5 | −5.3 ± 0.5 | |||
| 50 | 10 | −4.5 ± 0.3 | 31 | −6.9 ± 0.4 | −4.9 ± 0.4 | |||
| 100 | 38 | −4.5 ± 0.3 | 171 | −7.2 ± 0.5 | −5.2 ± 0.5 | |||
| 150 | 62 | −4.4 ± 0.9 | 315 | −7.2 ± 0.5 | −5.2 ± 0.5 | |||
| 200 | 102 | −4.4 ± 0.8 | 461 | −7.2 ± 0.8 | −5.2 ± 0.8 | |||
| TGPO | - | 1 | −4.1 | −4.0 ± 0.5 | 1 | −6.4 | −4.4 | −4.2 ± 0.5 |
| - | 2 | −3.9 ± 0.1 | 2 | −6.5 ± 0.0 | −4.5 ± 0.0 | |||
| - | 3 | −4.0 ± 0.1 | 3 | −6.6 ± 0.2 | −4.6 ± 0.2 | |||
| 50 | 3 | −3.9 ± 0.1 | 16 | −6.4 ± 0.4 | −4.4 ± 0.4 | |||
| 100 | 21 | −3.9 ± 0.4 | 75 | −6.2 ± 0.6 | −4.2 ± 0.6 | |||
| 150 | 42 | −4.0 ± 0.3 | 128 | −6.2 ± 0.6 | −4.2 ± 0.6 | |||
| 200 | 60 | −4.1 ± 1.2 | 199 | −6.2 ± 0.6 | −4.2 ± 0.6 | |||
| NPS Code | Sentinel-1 | COSMO-SkyMed | ||||||
|---|---|---|---|---|---|---|---|---|
| GNSS Velocity (mm/Year) | Number of PS | PS Velocity (mm/Year) | Difference (mm/Year) | GNSS Velocity (mm/Year) | Number of PS | PS Velocity (mm/Year) | Difference (mm/Year) | |
| 065704 | −6.8 | 3 | −3.2 ± 0.1 | −3.6 | −7.9 | 3 | −3.1 ± 0.4 | −4.8 |
| 065705 | −3.9 | 5 | −3.3 ± 0.1 | −0.6 | −4.2 | 6 | −3.5 ± 0.5 | −0.7 |
| 065706 | −5.3 | 49 | −4.1 ± 0.9 | −1.2 | −5.7 | 139 | −5.5 ± 1.6 | −0.2 |
| 065707A | −3.6 | 26 | −3.8 ± 1.6 | 0.2 | −4.2 | 28 | −3.2 ± 1.5 | −1.0 |
| 065708 | −2.3 | 29 | −3.3 ± 1.9 | 1.0 | −2.5 | 166 | −3.2 ± 1.0 | 0.7 |
| 065715 | −3.2 | 18 | −2.7 ± 0.4 | −0.5 | −3.4 | 22 | −3.2 ± 0.6 | −0.2 |
| 065901 | −4.4 | 11 | −5.3 ± 1.4 | 0.9 | −4.7 | 19 | −4.8 ± 1.1 | 0.1 |
| 065903 | −6.8 | 39 | −5.6 ± 1.1 | −1.2 | −7.2 | 172 | −5.7 ± 1.0 | −1.5 |
| 065904 | −6.3 | 3 | −3.2 ± 0.3 | −3.1 | −6.8 | 8 | −3.3 ± 0.2 | −3.5 |
| 065905 | −4.2 | 7 | −4.6 ± 0.8 | 0.4 | −4.8 | 18 | −4.6 ± 0.8 | 0.2 |
| 065906 | −8.3 | 4 | −6.1 ± 1.7 | −2.2 | −8.9 | - | - | - |
| 065907 | −6.4 | 34 | −4.2 ± 1.3 | −2.2 | −6.9 | 65 | −5.3 ± 0.8 | −1.6 |
| 065908 | −6.4 | 10 | −4.8 ± 0.8 | −1.6 | −6.9 | 17 | −4.9 ± 1.4 | −2.0 |
| 065909 | −3.1 | 3 | −1.3 ± 1.3 | −1.8 | −3.3 | 59 | −3.5 ± 0.5 | 0.2 |
| 077703 | −12.6 | 20 | −3.9 ± 1.3 | −8.7 | −13.4 | 161 | −3.8 ± 0.7 | −9.6 |
| 077704 | −12.3 | 2 | −4.7 ± 0.3 | −7.6 | −13.2 | - | - | - |
| 077707 | −7.8 | 60 | −3.1 ± 0.6 | −4.7 | −9.0 | 125 | −2.6 ± 0.6 | −6.4 |
| 077708 | −13.4 | - | - | - | −14.3 | - | - | - |
| 077710 | −8.5 | 3 | −3.9 ± 1.0 | −4.6 | −9.1 | 8 | −4.8 ± 0.3 | −4.3 |
| 077712 | −3.5 | 17 | −3.3 ± 0.6 | −0.2 | −3.7 | 72 | −3.3 ± 0.9 | −0.4 |
| 077713 | −5.6 | - | - | - | −6.0 | - | - | - |
| 077714 | −5.2 | 11 | −3.4 ± 0.2 | −1.8 | −5.6 | 39 | −4.2 ± 0.4 | −1.4 |
| 077715 | −7.2 | - | - | - | −7.6 | - | - | - |
| 077716 | −7.5 | 12 | −4.9 ± 1.2 | −2.6 | −8.0 | 27 | −5.1 ± 1.5 | −2.9 |
| 077717 | −7.2 | 5 | −4.3 ± 0.5 | −2.9 | −7.7 | 8 | −5.1 ± 0.7 | −2.6 |
| 077718 | −11.6 | 8 | −6.7 ± 2.7 | −4.9 | −12.9 | 1 | −6.7 ± 0.0 | −6.2 |
| 077719 | −8.1 | 15 | −4.5 ± 0.7 | −3.6 | −8.6 | 33 | −5.7 ± 0.7 | −2.9 |
| 077720 | −9.2 | 7 | −4.3 ± 1.0 | −4.9 | −10.1 | 24 | −5.8 ± 0.7 | −4.3 |
| 077721 | −10.9 | 11 | −3.8 ± 0.3 | −7.1 | −11.6 | 21 | −4.6 ± 0.4 | −7.0 |
| 077801 | −11.4 | 36 | −2.7 ± 1.3 | −8.7 | −13.2 | 93 | −2.6 ± 0.9 | −10.6 |
| 077902 | −9.2 | 4 | −5.6 ± 2.5 | −3.6 | −9.8 | 2 | −8.4 ± 0.8 | −1.4 |
| 077903 | −2.7 | 11 | −3.6 ± 1.3 | 0.9 | −2.8 | 24 | −3.4 ± 0.6 | 0.6 |
| 077904 | −4.5 | 18 | −4.7 ± 1.8 | 0.2 | −4.8 | 61 | −4.6 ± 0.6 | −0.2 |
| 077905 | −6.2 | 8 | −5.5 ± 1.8 | −0.7 | −6.6 | 45 | −6.2 ± 1.9 | −0.4 |
| 077906 | −9.5 | 8 | −5.0 ± 0.6 | −4.5 | −10.2 | 9 | −5.2 ± 0.8 | −5.0 |
| 077907 | −3.6 | 30 | −2.4 ± 0.5 | −1.2 | −3.9 | 133 | −2.6 ± 0.5 | −1.3 |
| 077908 | −8.5 | 57 | −4.0 ± 1.0 | −4.5 | −9.1 | 378 | −4.2 ± 0.7 | −4.9 |
| 077909 | −3.7 | 2 | −4.2 ± 0.2 | 0.5 | −4.0 | 9 | −5.0 ± 1.3 | 1.0 |
| 077910 | −3.7 | 7 | −2.3 ± 0.8 | −1.4 | −4.2 | 7 | −2.1 ± 1.9 | −2.1 |
| 077911 | −11.5 | 23 | −3.4 ± 1.0 | −8.1 | −12.3 | 142 | −4.8 ± 0.8 | −7.5 |
| 077912 | −9.7 | 55 | −2.9 ± 1.6 | −6.8 | −10.4 | 188 | −1.9 ± 0.7 | −8.5 |
| 077913 | −3.4 | 2 | −1.9 ± 0.1 | −1.5 | −3.9 | 10 | −3.5 ± 1.1 | −0.4 |
| 077914 | −5.5 | 71 | −3.2 ± 0.8 | −2.3 | −5.9 | 319 | −4.5 ± 0.7 | −1.4 |
| 077916 | −7.9 | - | - | - | −8.4 | 4 | −6.9 ± 0.6 | −1.5 |
| 077917 | −5.6 | - | - | - | −6.5 | - | - | - |
| 065704 | −6.8 | 3 | −3.2 ± 0.1 | −3.6 | −7.9 | 3 | −3.1 ± 0.4 | −4.8 |
| 065705 | −3.9 | 5 | −3.3 ± 0.1 | −0.6 | −4.2 | 6 | −3.5 ± 0.5 | −0.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fabris, M.; Battaglia, M.; Chen, X.; Menin, A.; Monego, M.; Floris, M. An Integrated InSAR and GNSS Approach to Monitor Land Subsidence in the Po River Delta (Italy). Remote Sens. 2022, 14, 5578. https://doi.org/10.3390/rs14215578
Fabris M, Battaglia M, Chen X, Menin A, Monego M, Floris M. An Integrated InSAR and GNSS Approach to Monitor Land Subsidence in the Po River Delta (Italy). Remote Sensing. 2022; 14(21):5578. https://doi.org/10.3390/rs14215578
Chicago/Turabian StyleFabris, Massimo, Mattia Battaglia, Xue Chen, Andrea Menin, Michele Monego, and Mario Floris. 2022. "An Integrated InSAR and GNSS Approach to Monitor Land Subsidence in the Po River Delta (Italy)" Remote Sensing 14, no. 21: 5578. https://doi.org/10.3390/rs14215578






