Evaluation of Three Gridded Precipitation Products in Characterizing Extreme Precipitation over the Hengduan Mountains Region in China
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data
2.2.1. Ground Observations of Precipitation
2.2.2. Gridded Precipitation Datasets
2.3. Methodology
2.3.1. Statistical Analysis
2.3.2. Extreme Precipitation Analysis
3. Results
3.1. Comparison of the Applicability of the Three Products in the Study Area
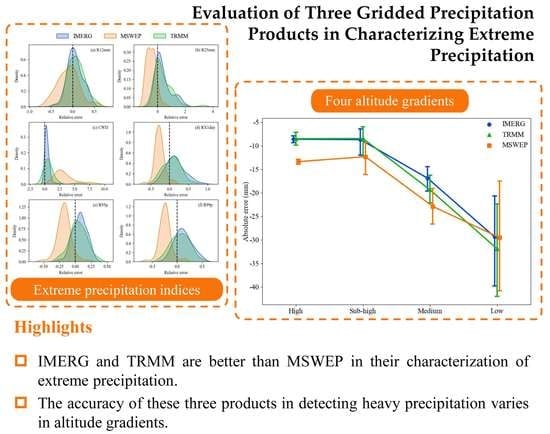
3.2. Comparison of Extreme Precipitation Indices
3.3. Comparison of Three Products for Heavy Rainfall Identification
4. Discussion
4.1. Effect of Elevation
4.2. Benefits and Limitations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bell, J.L.; Sloan, L.C.; Snyder, M.A. Regional changes in extreme climatic events: A future climate scenario. J. Clim. 2004, 17, 81–87. [Google Scholar] [CrossRef]
- You, Q.L.; Kang, S.C.; Aguilar, E.; Pepin, N.; Flugel, W.A.; Yan, Y.P.; Xu, Y.W.; Zhang, Y.J.; Huang, J. Changes in daily climate extremes in China and their connection to the large scale atmospheric circulation during 1961–2003. Clim. Dyn. 2011, 36, 2399–2417. [Google Scholar] [CrossRef]
- Zhang, Y.; Xia, J.; She, D.X. Spatiotemporal variation and statistical characteristic of extreme precipitation in the middle reaches of the Yellow River Basin during 1960–2013. Theor. Appl. Climatol. 2019, 135, 391–408. [Google Scholar] [CrossRef]
- Westra, S.; Alexander, L.V.; Zwiers, F.W. Global Increasing Trends in Annual Maximum Daily Precipitation. J. Clim. 2013, 26, 3904–3918. [Google Scholar] [CrossRef]
- Fang, W.; Huang, S.Z.; Ren, K.; Huang, Q.; Huang, G.H.; Cheng, G.H.; Li, K.L. Examining the applicability of different sampling techniques in the development of decomposition-based streamflow forecasting models. J. Hydrol. 2019, 568, 534–550. [Google Scholar] [CrossRef]
- Zolina, O.; Simmer, C.; Gulev, S.K.; Kollet, S. Changing structure of European precipitation: Longer wet periods leading to more abundant rainfalls. Geophys. Res. Lett. 2010, 37, 460–472. [Google Scholar] [CrossRef]
- Zhang, Q.; Xu, C.Y.; Becker, S.; Zhang, Z.X.; Chen, Y.D.; Coulibaly, M. Trends and abrupt changes of precipitation maxima in the Pearl River basin, China. Atmos. Sci. Lett. 2009, 10, 132–144. [Google Scholar] [CrossRef]
- Kumar, A.; Gupta, A.K.; Bhambri, R.; Verma, A.; Tiwari, S.K.; Asthana, A.K.L. Assessment and review of hydrometeorological aspects for cloudburst and flash flood events in the third pole region (Indian Himalaya). Polar Sci. 2018, 18, 5–20. [Google Scholar] [CrossRef]
- Easterling, D.R.; Evans, J.L.; Groisman, P.Y.; Karl, T.R.; Kunkel, K.E.; Ambenje, P. Observed variability and trends in extreme climate events: A brief review. Bull. Am. Meteorol. Soc. 2000, 81, 417–425. [Google Scholar] [CrossRef]
- Sun, X.; Zhang, G.; Wang, J.; Li, C.; Li, Y. Spatiotemporal Variation of Flash Floods in the Hengduan Mountains Region Affected by Rainfall Properties and Land-use. Nat. Hazards 2021, 111, 465–488. [Google Scholar] [CrossRef]
- Segoni, S.; Piciullo, L.; Gariano, S.L. A review of the recent literature on rainfall thresholds for landslide occurrence. Landslides 2018, 15, 1483–1501. [Google Scholar] [CrossRef]
- Shi, P.J.; Sun, S.; Wang, M.; Li, N.; Wang, J.A.; Jin, Y.Y.; Gu, X.T.; Yin, W.X. Climate change regionalization in China (1961–2010). Sci. China-Earth Sci. 2014, 57, 2676–2689. [Google Scholar] [CrossRef]
- Zhang, K.X.; Pan, S.M.; Cao, L.G.; Wang, Y.; Zhao, Y.F.; Zhang, W. Spatial distribution and temporal trends in precipitation extremes over the Hengduan Mountains region, China, from 1961 to 2012. Quat. Int. 2014, 349, 346–356. [Google Scholar] [CrossRef]
- Yu, H.; Wang, L.; Yang, R.; Yang, M.L.; Gao, R. Temporal and Spatial Distribution of Maximum Daily Precipitation in Hengduan Mountainous Region of China and Its Probability Characteristics. J. Hydrol. Eng. 2020, 25, 05020039. [Google Scholar] [CrossRef]
- Nir, K.; Soni, P.; Tarendra, L.; Ajay, J. Evaluating Satellite Products for Precipitation Estimation in Mountain Regions: A Case Study for Nepal. Remote Sens. 2013, 5, 4107–4123. [Google Scholar] [CrossRef]
- Shimelis, G.; Tena, A.; Broder, M.; Assefa, M. Performance of High Resolution Satellite Rainfall Products over Data Scarce Parts of Eastern Ethiopia. Remote Sens. 2015, 7, 11639–11663. [Google Scholar] [CrossRef]
- Duan, Z.; Liu, J.Z.; Tuo, Y.; Chiogna, G.; Disse, M. Evaluation of eight high spatial resolution gridded precipitation products in Adige Basin (Italy) at multiple temporal and spatial scales. Sci. Total Environ. 2016, 573, 1536–1553. [Google Scholar] [CrossRef] [PubMed]
- Goswami, B.B.; Mukhopadhyay, P.; Mahanta, R.; Goswami, B.N. Multiscale interaction with topography and extreme rainfall events in the northeast Indian region. J. Geophys. Res. Atmos. 2010, 115, 12. [Google Scholar] [CrossRef]
- Prat, O.P.; Barros, A.P. Ground observations to characterize the spatial gradients and vertical structure of orographic precipitation—Experiments in the inner region of the Great Smoky Mountains. J. Hydrol. 2010, 391, 143–158. [Google Scholar] [CrossRef]
- Zeng, W.; Yu, Z.; Wu, S.H.; Qin, J.B. Changes in annual, seasonal and monthly precipitation events and their link with elevation in Sichuan province, China. Int. J. Climatol. 2016, 36, 2303–2322. [Google Scholar] [CrossRef]
- Xu, F.; Jia, Y.W.; Peng, H.; Niu, C.W.; Liu, J.J. Temperature and precipitation trends and their links with elevation in the Hengduan Mountain region, China. Clim. Res. 2018, 75, 163–180. [Google Scholar] [CrossRef]
- Li, G.P.; Yu, Z.B.; Wang, W.G.; Ju, Q.; Chen, X. Analysis of the spatial Distribution of precipitation and topography with GPM data in the Tibetan Plateau. Atmos. Res. 2021, 247, 15. [Google Scholar] [CrossRef]
- Tucker, D. Orographic Precipitation. In Encyclopedia of World Climatology; Oliver, J.E., Ed.; Springer: Dordrecht, The Netherlands, 2005; pp. 552–555. [Google Scholar]
- Guo, Q.K.; Cheng, S.Y.; Qin, W.; Ning, D.H.; Shan, Z.J.; Yin, Z. Vertical variation and temporal trends of extreme precipitation indices in a complex topographical watershed in the Hengduan Mountain Region, China. Int. J. Climatol. 2020, 40, 3250–3267. [Google Scholar] [CrossRef]
- Chu, H.J. Assessing the relationships between elevation and extreme precipitation with various durations in southern Taiwan using spatial regression models. Hydrol. Processes 2012, 26, 3174–3181. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef]
- Beck, H.E.; Wood, E.F.; Pan, M.; Fisher, C.K.; Miralles, D.G.; van Dijk, A.I.J.M.; McVicar, T.R.; Adler, R.F. MSWEP V2 Global 3-Hourly 0.1 degrees Precipitation: Methodology and Quantitative Assessment. Bull. Am. Meteorol. Soc. 2019, 100, 473–502. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Bolvin, D.T.; Nelkin, E.J. The TRMM Multi-Satellite Precipitation Analysis (TMPA). In Satellite Rainfall Applications for Surface Hydrology; Gebremichael, M., Hossain, F., Eds.; Springer: Dordrecht, The Netherlands, 2010; pp. 3–22. [Google Scholar]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The Global Precipitation Measurement Mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Tang, G.; Clark, M.P.; Papalexiou, S.M.; Ma, Z.; Hong, Y. Have satellite precipitation products improved over last two decades? A comprehensive comparison of GPM IMERG with nine satellite and reanalysis datasets. Remote Sens. Environ. 2020, 240, 111697. [Google Scholar] [CrossRef]
- Lakew, H.B. Investigating the effectiveness of bias correction and merging MSWEP with gauged rainfall for the hydrological simulation of the upper Blue Nile basin. J. Hydrol. Reg. Stud. 2020, 32, 100741. [Google Scholar] [CrossRef]
- Hu, Q.F.; Yang, D.W.; Wang, Y.T.; Yang, H.B. Accuracy and spatio-temporal variation of high resolution satellite rainfall estimate over the Ganjiang River Basin. Sci. China-Technol. Sci. 2013, 56, 853–865. [Google Scholar] [CrossRef]
- Manz, B.; Páez-Bimos, S.; Horna, N.; Buytaert, W.; Ochoa-Tocachi, B.; Lavado-Casimiro, W.; Willems, B. Comparative Ground Validation of IMERG and TMPA at Variable Spatiotemporal Scales in the Tropical Andes. J. Hydrometeorol. 2017, 18, 2469–2489. [Google Scholar] [CrossRef]
- Yang, Y.F.; Wu, J.; Bai, L.; Wang, B. Reliability of Gridded Precipitation Products in the Yellow River Basin, China. Remote Sens. 2020, 12, 374. [Google Scholar] [CrossRef]
- Xu, Z.G.; Wu, Z.Y.; He, H.; Wu, X.T.; Zhou, J.H.; Zhang, Y.L.; Guo, X. Evaluating the accuracy of MSWEP V2.1 and its performance for drought monitoring over mainland China. Atmos. Res. 2019, 226, 17–31. [Google Scholar] [CrossRef]
- Zhang, L.P.; Lan, P.; Qin, G.H.; Mello, C.R.; Boyer, E.W.; Luo, P.P.; Guo, L. Evaluation of Three Gridded Precipitation Products to Quantify Water Inputs over Complex Mountainous Terrain of Western China. Remote Sens. 2021, 13, 3795. [Google Scholar] [CrossRef]
- Alijanian, M.; Rakhshandehroo, G.R.; Dehghani, M.; Mishra, A. Probabilistic drought forecasting using copula and satellite rainfall based PERSIANN-CDR and MSWEP datasets. Int. J. Climatol. 2022, 1–18. [Google Scholar] [CrossRef]
- Tang, G.; Ma, Y.; Di, L.; Zhong, L.; Yang, H. Evaluation of GPM Day-1 IMERG and TMPA Version-7 legacy products over Mainland China at multiple spatiotemporal scales. J. Hydrol. 2015, 533, 152–167. [Google Scholar] [CrossRef]
- Ebrahimi, S.; Chen, C.; Chen, Q.W.; Zhang, Y.S.; Ma, N.; Zaman, Q. Effects of temporal scales and space mismatches on the TRMM 3B42 v7 precipitation product in a remote mountainous area. Hydrol. Processes 2017, 31, 4315–4327. [Google Scholar] [CrossRef]
- de Moraes, R.B.F.; Goncalves, F.V. Validation of TRMM data in the geographical regions of Brazil. RBRH-Rev. Bras. Recur. Hidr. 2021, 26, 14. [Google Scholar] [CrossRef]
- Luo, Z.; Shao, Q.; Wan, W.; Li, H.; Chen, X.; Zhu, S.; Ding, X. A new method for assessing satellite-based hydrological data products using water budget closure. J. Hydrol. 2021, 594, 125927. [Google Scholar] [CrossRef]
- Pombo, S.; de Oliveira, R.P. Evaluation of extreme precipitation estimates from TRMM in Angola. J. Hydrol. 2015, 523, 663–679. [Google Scholar] [CrossRef]
- Huang, X.R.Z.; Wang, D.S.; Liu, Y.; Feng, Z.Z.; Wang, D.G. Evaluation of extreme precipitation based on satellite retrievals over China. Front. Earth Sci. 2018, 12, 846–861. [Google Scholar] [CrossRef]
- Liu, J.Y.; Du, J.; Yang, Y.M.; Wang, Y.N. Evaluating extreme precipitation estimations based on the GPM IMERG products over the Yangtze River Basin, China. Geomat. Nat. Hazards Risk 2020, 11, 601–618. [Google Scholar] [CrossRef]
- Ning, B.Y.; Yang, X.M.; Chang, L. Changes of Temperature and Precipitation Extremes in Hengduan Mountains, Qinghai-Tibet Plateau in 1961–2008. Chin. Geogr. Sci. 2012, 22, 422–436. [Google Scholar] [CrossRef]
- Li, Z.; He, Y.; Wang, C.; Wang, X.; Cao, W. Spatial and temporal trends of temperature and precipitation during 1960–2008 at the Hengduan Mountains, China. Quat. Int. 2011, 236, 127–142. [Google Scholar] [CrossRef]
- Yu, C.; Hu, D.Y.; Liu, M.Q.; Wang, S.S.; Di, Y.F. Spatio-temporal accuracy evaluation of three high-resolution satellite precipitation products in China area. Atmos. Res. 2020, 241, 12. [Google Scholar] [CrossRef]
- Tan, X.; Ma, Z.Q.; He, K.; Han, X.Z.; Ji, Q.W.; He, Y. Evaluations on gridded precipitation products spanning more than half a century over the Tibetan Plateau and its surroundings. J. Hydrol. 2020, 582, 17. [Google Scholar] [CrossRef]
- Shi, Z.Q.; Deng, W.; Zhang, S.Y. Spatio-temporal pattern changes of land space in Hengduan Mountains during 1990–2015. J. Geogr. Sci. 2018, 28, 529–542. [Google Scholar] [CrossRef]
- Yu, H.; Wang, L.; Yang, R.; Yang, M.L.; Gao, R. Temporal and spatial variation of precipitation in the Hengduan Mountains region in China and its relationship with elevation and latitude. Atmos. Res. 2018, 213, 1–16. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Bolvin, D.T.; Gu, G.J.; Nelkin, E.J.; Bowman, K.P.; Hong, Y.; Stocker, E.F.; Wolff, D.B. The TRMM multisatellite precipitation analysis (TMPA): Quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Prakash, S.; Mitra, A.K.; AghaKouchak, A.; Liu, Z.; Norouzi, H.; Pai, D.S. A preliminary assessment of GPM-based multi-satellite precipitation estimates over a monsoon dominated region. J. Hydrol. 2018, 556, 865–876. [Google Scholar] [CrossRef] [Green Version]
- Maghsood, F.F.; Hashemi, H.; Hosseini, S.H.; Berndtsson, R. Ground Validation of GPM IMERG Precipitation Products over Iran. Remote Sens. 2019, 12, 48. [Google Scholar] [CrossRef]
- Cma, B.; Xmab, C.; Slab, C.; Shi, H.A. Extensive evaluation of IMERG precipitation for both liquid and solid in Yellow River source region. Atmos. Res. 2021, 256, 105570. [Google Scholar] [CrossRef]
- Li, Z.; Tang, G.Q.; Hong, Z.; Chen, M.Y.; Gao, S.; Kirstetter, P.; Gourley, J.J.; Wen, Y.X.; Yami, T.; Nabih, S.; et al. Two-decades of GPM IMERG early and final run products intercomparison: Similarity and difference in climatology, rates, and extremes. J. Hydrol. 2021, 594, 11. [Google Scholar] [CrossRef]
- Schober, P.; Boer, C.; Schwarte, L.A. Correlation Coefficients: Appropriate Use and Interpretation. Anesth. Analg. 2018, 126, 1763–1768. [Google Scholar] [CrossRef] [PubMed]
- Bharti, V.; Singh, C. Evaluation of error in TRMM 3B42V7 precipitation estimates over the Himalayan region. J. Geophys. Res. Atmos. 2015, 120, 12458–12473. [Google Scholar] [CrossRef]
- Tian, Y.D.; Peters-Lidard, C.D.; Eylander, J.B.; Joyce, R.J.; Huffman, G.J.; Adler, R.F.; Hsu, K.L.; Turk, F.J.; Garcia, M.; Zeng, J. Component analysis of errors in satellite-based precipitation estimates. J. Geophys. Res. Atmos. 2009, 114, 15. [Google Scholar] [CrossRef]
- Xu, R.; Tian, F.Q.; Yang, L.; Hu, H.C.; Lu, H.; Hou, A.Z. Ground validation of GPM IMERG and TRMM 3B42V7 rainfall products over southern Tibetan Plateau based on a high-density rain gauge network. J. Geophys. Res. Atmos. 2017, 122, 910–924. [Google Scholar] [CrossRef]
- Mashingia, F.; Mtalo, F.; Bruen, M. Validation of remotely sensed rainfall over major climatic regions in Northeast Tanzania. Phys. Chem. Earth 2014, 67–69, 55–63. [Google Scholar] [CrossRef]
- Lian, L.; Xu, S.; Li, Z.; Sun, X. Spatial-temporal Variation of Extreme Precipitation Events in Northwest China during 1961–2010. Meteorol. Environ. Res. 2014, 5, 12. [Google Scholar]
- Easterling, D.R.; Alexander, L.V.; Mokssit, A.; Detemmerman, V. CCI/CLIVAR workshop to develop priority climate indices. Bull. Am. Meteorol. Soc. 2003, 84, 1403–1407. [Google Scholar]
- Liu, B.J.; Chen, J.F.; Chen, X.H.; Lian, Y.Q.; Wu, L.L. Uncertainty in determining extreme precipitation thresholds. J. Hydrol. 2013, 503, 233–245. [Google Scholar] [CrossRef]
- Sun, H. China Encyclopedia of Resources Science; China University of Petroleum Press: Beijing, China, 2000. (In Chinese) [Google Scholar]
- Anagnostopoulou, C.; Tolika, K. Extreme precipitation in Europe: Statistical threshold selection based on climatological criteria. Theor. Appl. Climatol. 2012, 107, 479–489. [Google Scholar] [CrossRef]
- Chen, Z. On the principle, contents and methods used to compile the Chinese Geomorphological Maps: Taking the 1:4,000,000 Chinese Geomorphological map as an example. Acta Geogr. Sin. 1993, 48, 105–113. [Google Scholar]
- Mahmoud, M.T.; Mohammed, S.A.; Hamouda, M.A.; Mohamed, M.M. Impact of Topography and Rainfall Intensity on the Accuracy of IMERG Precipitation Estimates in an Arid Region. Remote Sens. 2020, 13, 13. [Google Scholar] [CrossRef]
- Harrison, L.; Funk, C.; Peterson, P. Identifying changing precipitation extremes in Sub-Saharan Africa with gauge and satellite products. Environ. Res. Lett. 2019, 14, 12. [Google Scholar] [CrossRef]
- Gebregiorgis, A.S.; Hossain, F. Understanding the Dependence of Satellite Rainfall Uncertainty on Topography and Climate for Hydrologic Model Simulation. IEEE Trans. Geosci. Remote Sens. 2013, 51, 704–718. [Google Scholar] [CrossRef]
- Satge, F.; Ruelland, D.; Bonnet, M.P.; Molina, J.; Pillco, R. Consistency of satellite-based precipitation products in space and over time compared with gauge observations and snow-hydrological modelling in the Lake Titicaca region. Hydrol. Earth Syst. Sci. 2019, 23, 595–619. [Google Scholar] [CrossRef]
- Morris, C.J.G.; Simmonds, I.; Plummer, N. Quantification of the influences of wind and cloud on the nocturnal urban heat island of a large city. J. Appl. Meteorol. 2001, 40, 169–182. [Google Scholar] [CrossRef]
- Hu, L.; Deng, D.F.; Gao, S.T.; Xu, X.D. The seasonal variation of Tibetan Convective Systems: Satellite observation. J. Geophys. Res. Atmos. 2016, 121, 5512–5525. [Google Scholar] [CrossRef]
- Derin, Y.; Yilmaz, K.K. Evaluation of Multiple Satellite-Based Precipitation Products over Complex Topography. J. Hydrometeorol. 2014, 15, 1498–1516. [Google Scholar] [CrossRef]
- Ebert, E.E.; Janowiak, J.E.; Kidd, C. Comparison of near-real-time precipitation estimates from satellite observations and numerical models. Bull. Am. Meteorol. Soc. 2007, 88, 47–64. [Google Scholar] [CrossRef]
- Tan, M.L.; Duan, Z. Assessment of GPM and TRMM Precipitation Products over Singapore. Remote Sens. 2017, 9, 720. [Google Scholar] [CrossRef]
- Zhang, Y.; Hanati, G.; Danierhan, S.; Liu, Q.Q.; Xu, Z.Y. Evaluation and Comparison of Daily GPM/TRMM Precipitation Products over the Tianshan Mountains in China. Water 2020, 12, 3088. [Google Scholar] [CrossRef]
- Fang, J.; Yang, W.T.; Luan, Y.B.; Du, J.; Lin, A.W.; Zhao, L. Evaluation of the TRMM 3B42 and GPM IMERG products for extreme precipitation analysis over China. Atmos. Res. 2019, 223, 24–38. [Google Scholar] [CrossRef]
- Cheng, C.; Qiuwen, C.; Zheng, D.; Jianyun, Z.; Kangle, M.; Zhe, L.; Guoqiang, T. Multiscale Comparative Evaluation of the GPM IMERG v5 and TRMM 3B42 v7 Precipitation Products from 2015 to 2017 over a Climate Transition Area of China. Remote Sens. 2018, 10, 944. [Google Scholar] [CrossRef]
- Mou, T.; Ab, I.; Zheng, D.; Arthur, C.; Vincent, C. Evaluation of Six High-Resolution Satellite and Ground-Based Precipitation Products over Malaysia. Remote Sens. 2015, 7, 1504–1528. [Google Scholar] [CrossRef]
- Yang, M.X.; Liu, G.D.; Chen, T.; Chen, Y.; Xia, C.C. Evaluation of GPM IMERG precipitation products with the point rain gauge records over Sichuan, China. Atmos. Res. 2020, 246, 12. [Google Scholar] [CrossRef]
- Li, Z.X.; He, Y.Q.; Theakstone, W.H.; Wang, X.F.; Zhang, W.; Cao, W.H.; Du, J.K.; Xin, H.J.; Chang, L. Altitude dependency of trends of daily climate extremes in southwestern China, 1961–2008. J. Geogr. Sci. 2012, 22, 416–430. [Google Scholar] [CrossRef]
- Nair, A.S.; Indu, J. Performance Assessment of Multi-Source Weighted-Ensemble Precipitation (MSWEP) Product over India. Climate 2017, 5, 20. [Google Scholar] [CrossRef]
- Chen, F.R.; Li, X. Evaluation of IMERG and TRMM 3B43 Monthly Precipitation Products over Mainland China. Remote Sens. 2016, 8, 472. [Google Scholar] [CrossRef]
- Gao, J.Y.; Tang, G.Q.; Hong, Y. Similarities and Improvements of GPM Dual-Frequency Precipitation Radar (DPR) upon TRMM Precipitation Radar (PR) in Global Precipitation Rate Estimation, Type Classification and Vertical Profiling. Remote Sens. 2017, 9, 1142. [Google Scholar] [CrossRef]
- Ma, Y.Z.; Tang, G.Q.; Long, D.; Yong, B.; Zhong, L.Z.; Wan, W.; Hong, Y. Similarity and Error Intercomparison of the GPM and Its Predecessor-TRMM Multisatellite Precipitation Analysis Using the Best Available Hourly Gauge Network over the Tibetan Plateau. Remote Sens. 2016, 8, 569. [Google Scholar] [CrossRef]
- Draper, D.W.; Newell, D.A.; McKague, D.S.; Piepmeier, J.R. Assessing Calibration Stability Using the Global Precipitation Measurement (GPM) Microwave Imager (GMI) Noise Diodes. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2015, 8, 4239–4247. [Google Scholar] [CrossRef]
- Sunilkumar, K.; Yatagai, A.; Masuda, M. Preliminary Evaluation of GPM-IMERG Rainfall Estimates Over Three Distinct Climate Zones With APHRODITE. Earth Space Sci. 2019, 6, 1321–1335. [Google Scholar] [CrossRef]
- Libertino, A.; Sharma, A.; Lakshmi, V.; Claps, P. A global assessment of the timing of extreme rainfall from TRMM and GPM for improving hydrologic design. Environ. Res. Lett. 2016, 11, 9. [Google Scholar] [CrossRef]
- Mehran, A.; AghaKouchak, A. Capabilities of satellite precipitation datasets to estimate heavy precipitation rates at different temporal accumulations. Hydrol. Processes 2014, 28, 2262–2270. [Google Scholar] [CrossRef]
- Cheema, M.J.M.; Bastiaanssen, W.G.M. Local calibration of remotely sensed rainfall from the TRMM satellite for different periods and spatial scales in the Indus Basin. Int. J. Remote Sens. 2012, 33, 2603–2627. [Google Scholar] [CrossRef]
- Qi, S.; Lv, A. Applicability analysis of multiple precipitation products in the Qaidam Basin, Northwestern China. Environ. Sci. Pollut. Res. Int. 2022, 29, 12557–12573. [Google Scholar] [CrossRef]
- Moazami, S.; Najafi, M.R. A comprehensive evaluation of GPM-IMERG V06 and MRMS with hourly ground-based precipitation observations across Canada. J. Hydrol. 2021, 594, 17. [Google Scholar] [CrossRef]
- Dore, M.H. Climate change and changes in global precipitation patterns: What do we know? Environ. Int. 2005, 31, 1167–1181. [Google Scholar] [CrossRef]
- Alexander, L.V.; Zhang, X.; Peterson, T.C.; Caesar, J.; Gleason, B.; Tank, A.M.G.K.; Haylock, M.; Collins, D.; Trewin, B.; Rahimzadeh, F.; et al. Global observed changes in daily climate extremes of temperature and precipitation. J. Geophys. Res. Atmos. 2006, 111, 22. [Google Scholar] [CrossRef] [Green Version]











| Dataset | Period | Coverage | Temporal Resolution | Spatial Resolution |
|---|---|---|---|---|
| GPM-IMERG V6 | 2001–2020 | 60°S–60°N | 0.5 h | 0.1° |
| MSWEP V2.2 | 1979–2017 | Global | 3 h | 0.1° |
| TRMM-3B42 V7 | 1998–2020 | 50°S–50°N | 3 h | 0.25° |
| Index | Descriptive Name | Definition | Units |
|---|---|---|---|
| R0.1mm | Number of precipitation days | Annual count of days when precipitation ≥ 0.1 mm | day |
| R10mm | Number of moderate precipitation days | Annual count of days when precipitation ≥ 10 mm | day |
| R12mm | Number of erosion precipitation days | Annual count of days when precipitation ≥ 12 mm | day |
| R25mm | Number of heavy precipitation days | Annual count of days when precipitation ≥ 25 mm | day |
| PRCPTOT | Wet-day precipitation | Sum of daily precipitation > 1.0 mm | mm |
| SDII | Simple daily intensity index | Annual total precipitation divided by the number of wet days | mm/d |
| RX1day | Maximum 1-day precipitation | Maximum 1-day precipitation total | mm |
| CWD | Consecutive wet days | Maximum number of consecutive wet days | day |
| CDD | Consecutive dry days | Maximum number of consecutive dry days | day |
| R95p | Total annual precipitation from very wet day | Annual sum of daily precipitation > 95th percentile | mm |
| R99p | Total annual precipitation from extremely wet day | Annual sum of daily precipitation > 99th percentile | mm |
| Statistical Indices | CMA | IMERG | MSWEP | TRMM |
|---|---|---|---|---|
| Mean (mm) | 2.19 | 2.18 | 2.31 | 2.28 |
| Median (mm) | 1.307 | 1.233 | 1.613 | 1.370 |
| Upper 95th percentile (mm) | 7.949 | 8.088 | 7.556 | 8.221 |
| Upper quartile (mm) | 3.507 | 3.576 | 3.879 | 3.681 |
| Lower quartile (mm) | 0.280 | 0.163 | 0.471 | 0.270 |
| Lower 95th percentile (mm) | 0.000 | 0.005 | 0.092 | 0.011 |
| Range (mm) | [0, 39.657] | [0, 32.129] | [0, 25.975] | [0, 29.557] |
| Skewness | 2.314 | 1.864 | 1.603 | 1.819 |
| Kurtosis | 9.637 | 4.858 | 3.821 | 4.612 |
| Standard deviation (mm) | 2.849 | 2.849 | 2.587 | 2.830 |
| Coefficient of variation (%) | 1.213 | 1.223 | 1.031 | 1.167 |
| Metric | CMA | IMERG | MSWEP | TRMM |
|---|---|---|---|---|
| R0.1mm (days) | 128 ± 3 | 147 ± 3 | 233 ± 4 | 172 ± 6 |
| R10mm (days) | 25 ± 1 | 25 ± 1 | 24 ± 1 | 26 ± 1 |
| R12mm (days) | 20 ± 1 | 21 ± 1 | 18 ± 1 | 21 ± 1 |
| R25mm (days) | 6 ± 1 | 7 ± 0 | 4 ± 0 | 7 ± 0 |
| PRCPTOT | 832.13 ± 32.55 | 849.93 ± 21.17 | 916.05 ± 28.85 | 885.44 ± 26.09 |
| SDII (mm/day) | 6.54 ± 0.21 | 5.91 ± 0.22 | 3.93 ± 0.10 | 5.55 ± 0.26 |
| RX1day (mm) | 57.10 ± 3.42 | 60.81 ± 2.52 | 40.75 ± 2.31 | 56.35 ± 2.49 |
| CWD (days) | 11 ± 0 | 15 ± 1 | 48 ± 3 | 21 ± 2 |
| CDD (days) | 39 ± 1 | 36 ± 1 | 18 ± 1 | 30 ± 1 |
| R95p (mm) | 457.08 ± 19.46 | 478.42 ± 17.20 | 370.92 ± 14.81 | 463.80 ± 15.86 |
| R99p (mm) | 168.55 ± 8.90 | 180.33 ± 7.09 | 125.60 ± 6.33 | 169.75 ± 6.55 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, W.; Wang, G.; Guo, L.; Sun, J.; Sun, X. Evaluation of Three Gridded Precipitation Products in Characterizing Extreme Precipitation over the Hengduan Mountains Region in China. Remote Sens. 2022, 14, 4408. https://doi.org/10.3390/rs14174408
Dong W, Wang G, Guo L, Sun J, Sun X. Evaluation of Three Gridded Precipitation Products in Characterizing Extreme Precipitation over the Hengduan Mountains Region in China. Remote Sensing. 2022; 14(17):4408. https://doi.org/10.3390/rs14174408
Chicago/Turabian StyleDong, Wenchang, Genxu Wang, Li Guo, Juying Sun, and Xiangyang Sun. 2022. "Evaluation of Three Gridded Precipitation Products in Characterizing Extreme Precipitation over the Hengduan Mountains Region in China" Remote Sensing 14, no. 17: 4408. https://doi.org/10.3390/rs14174408