Upscaling Evapotranspiration from a Single-Site to Satellite Pixel Scale
Abstract
:1. Introduction
2. Study Area and Datasets
2.1. Study Area
2.2. Datasets
2.2.1. Station Observation Data
2.2.2. Remote Sensing and Atmospheric Forcing Data
2.2.3. Flux Source Area Data
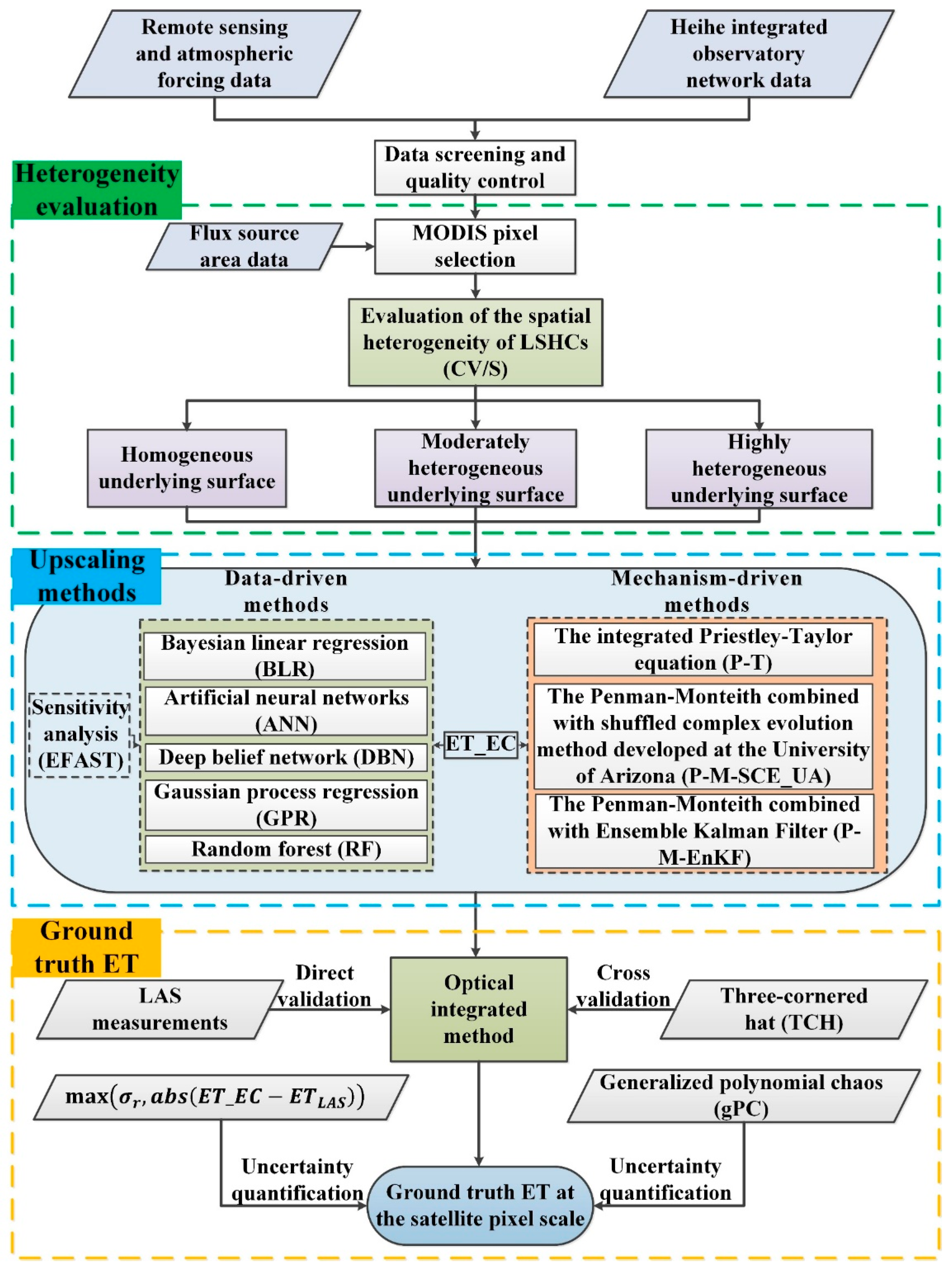
3. Methodology
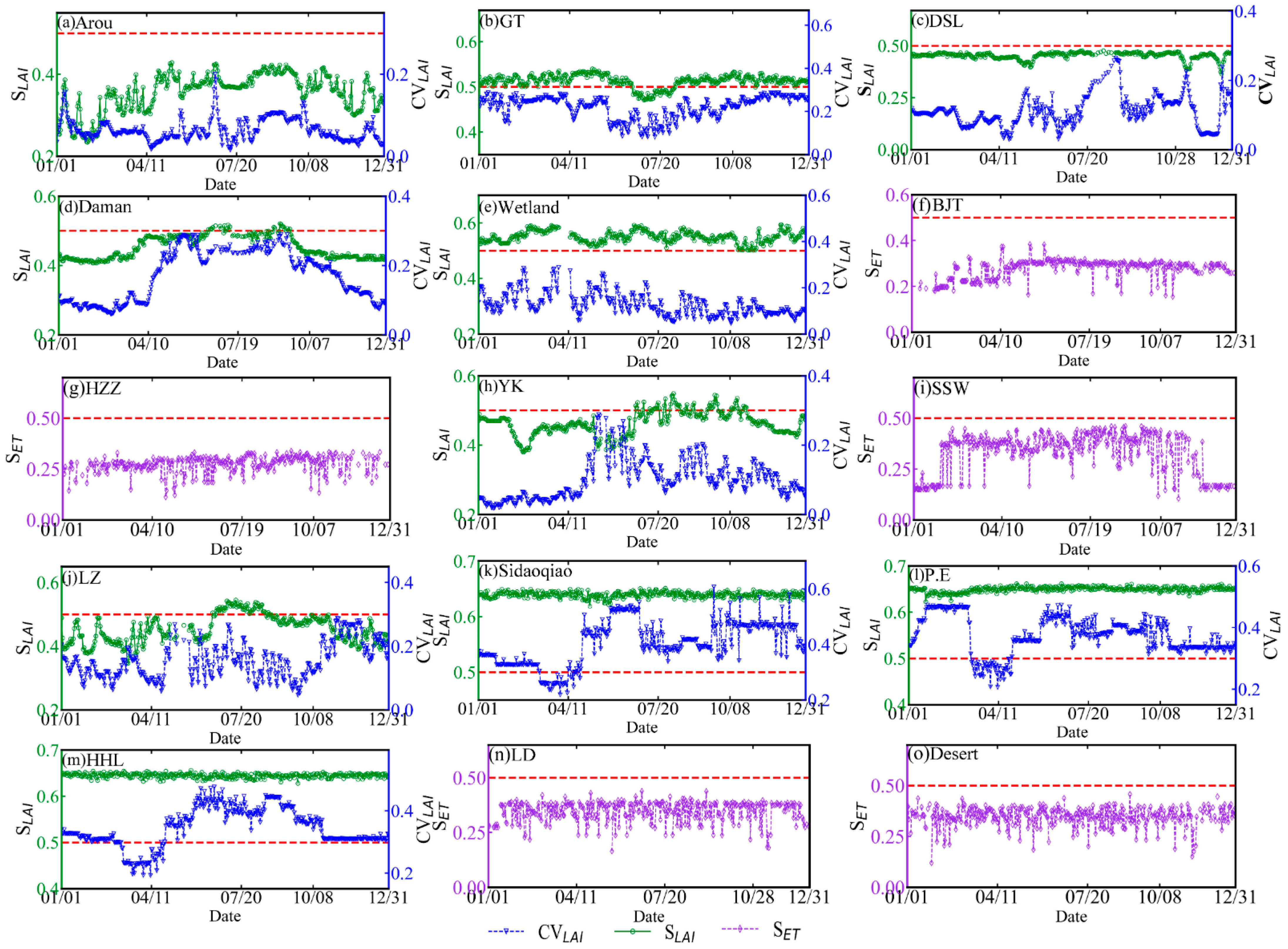
3.1. Evaluation Method of Spatial Heterogeneity
3.2. Upscaling Methods
3.3. Cross-Validation Method
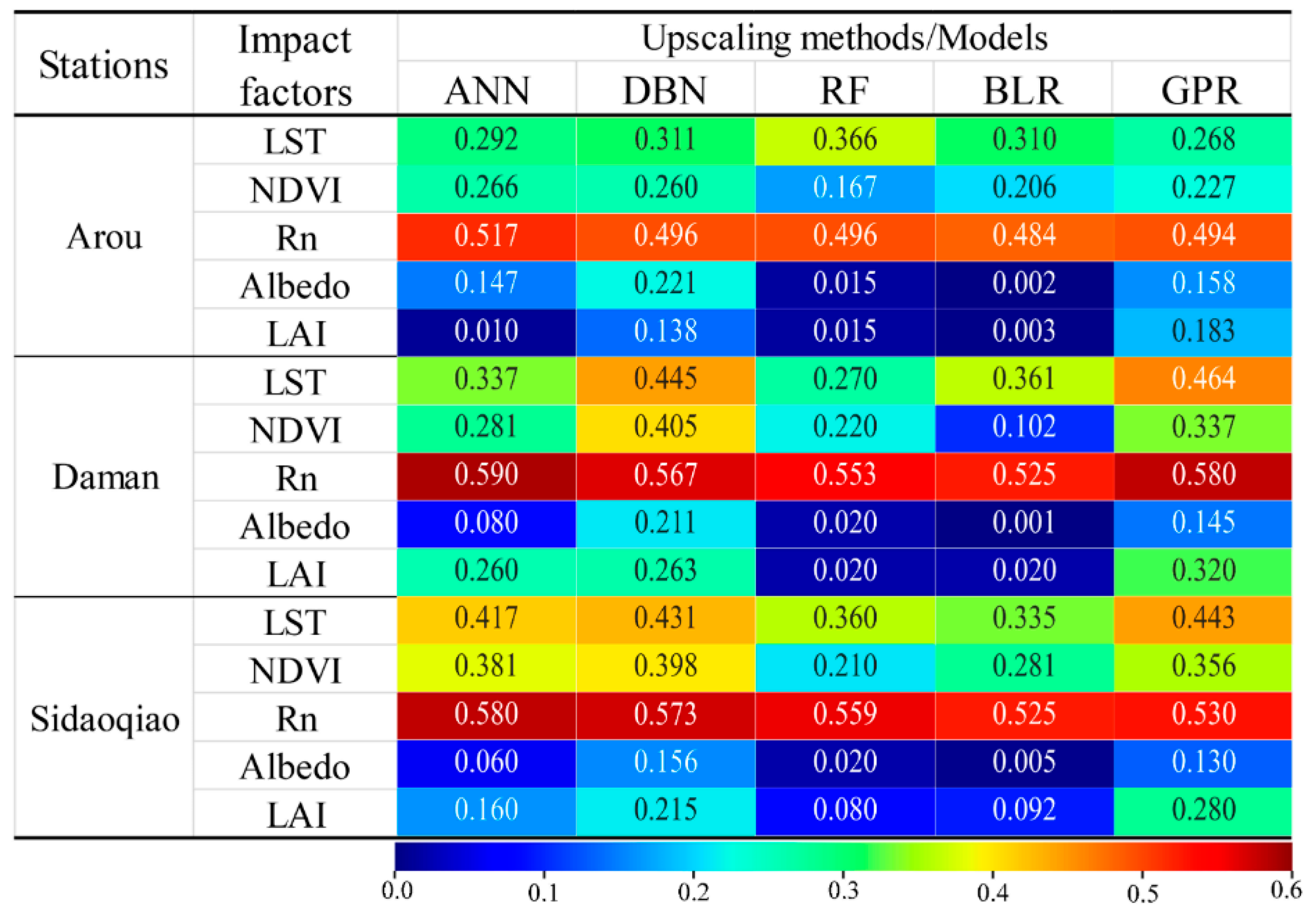
3.4. Sensitivity Analysis Method
3.5. Uncertainty Quantification Method
4. Results and Discussion
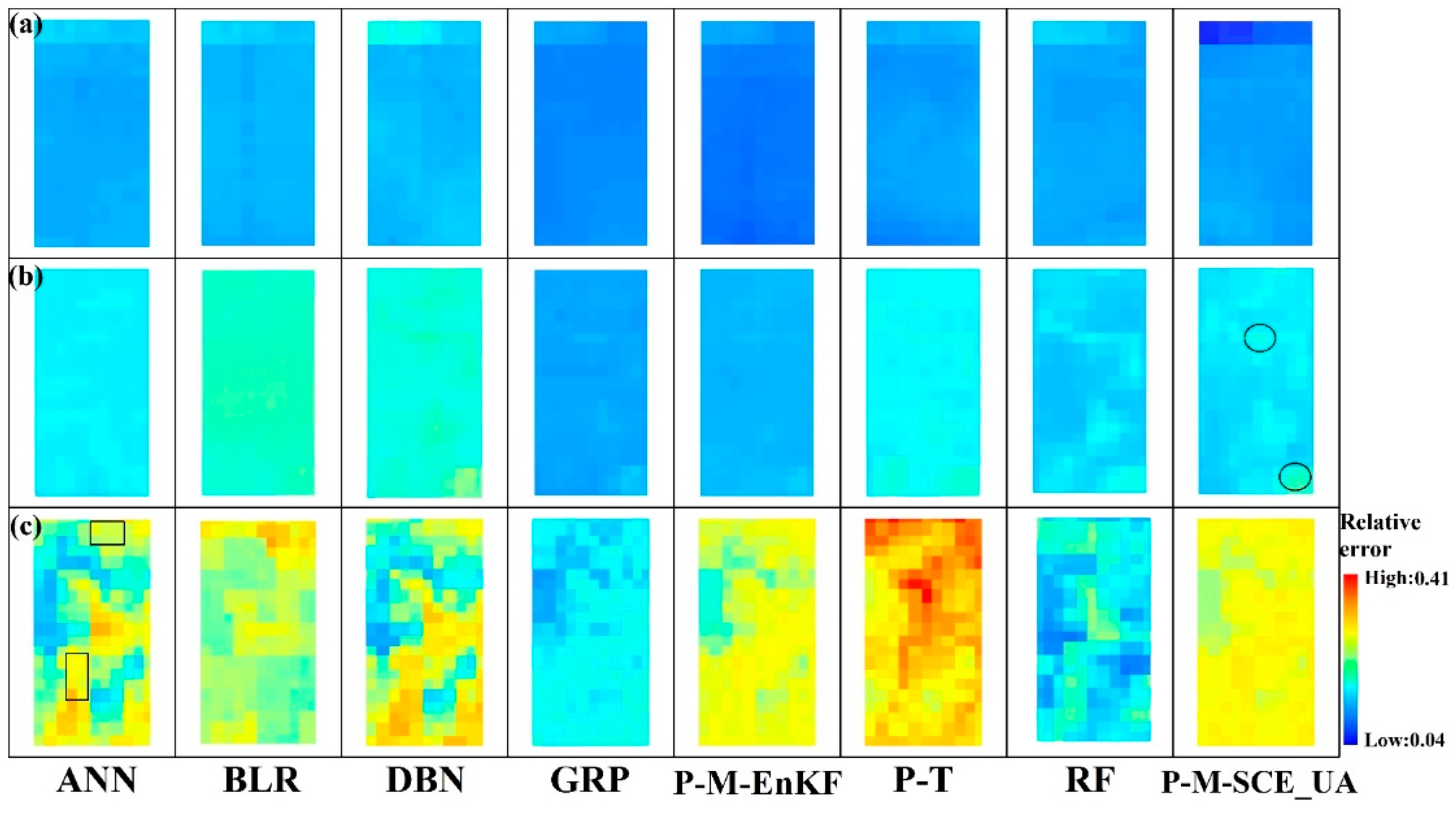
4.1. Analysis of the Spatial Heterogeneity of the LSHCs
4.2. Sensitivity Analysis of Input Variables
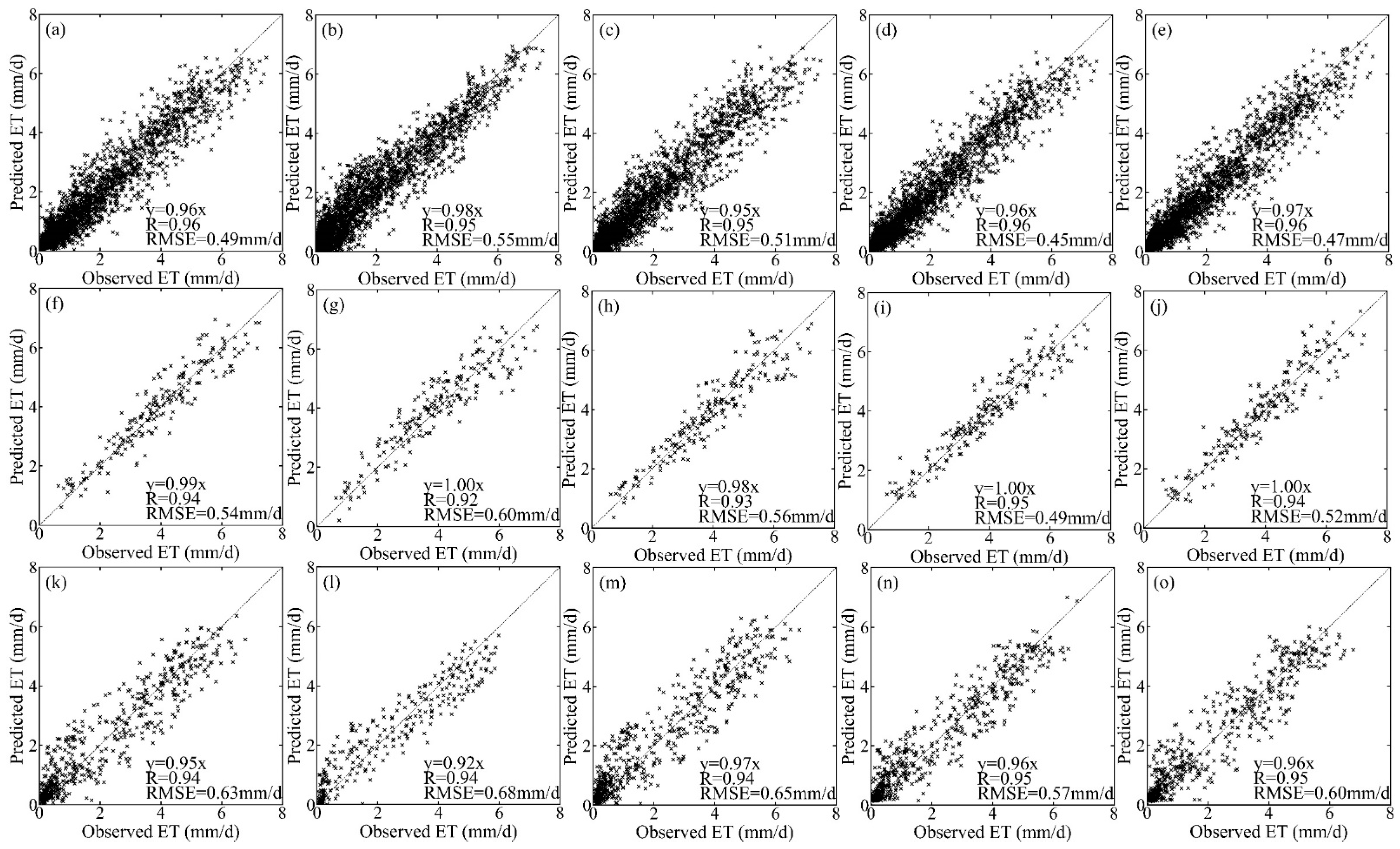
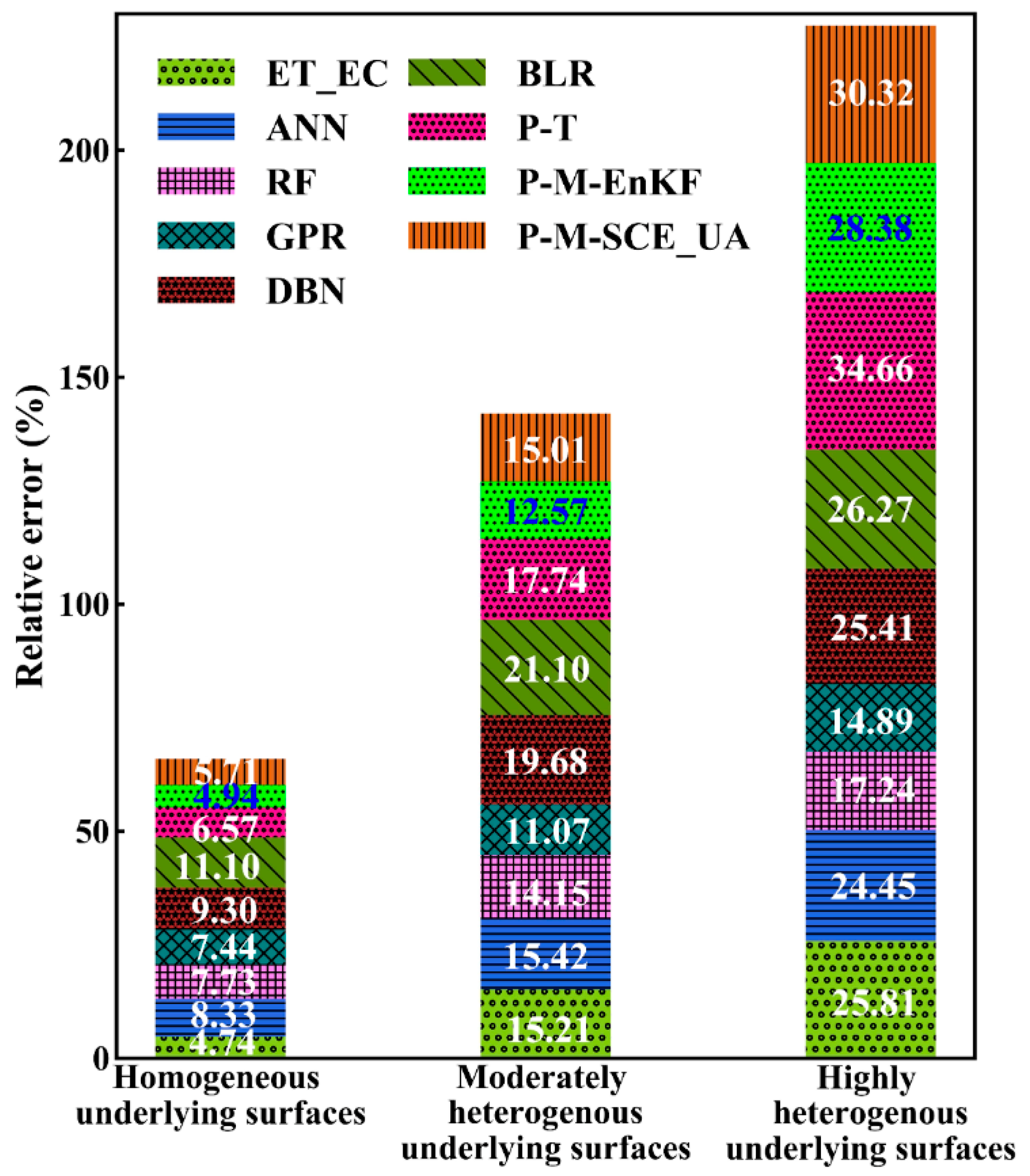
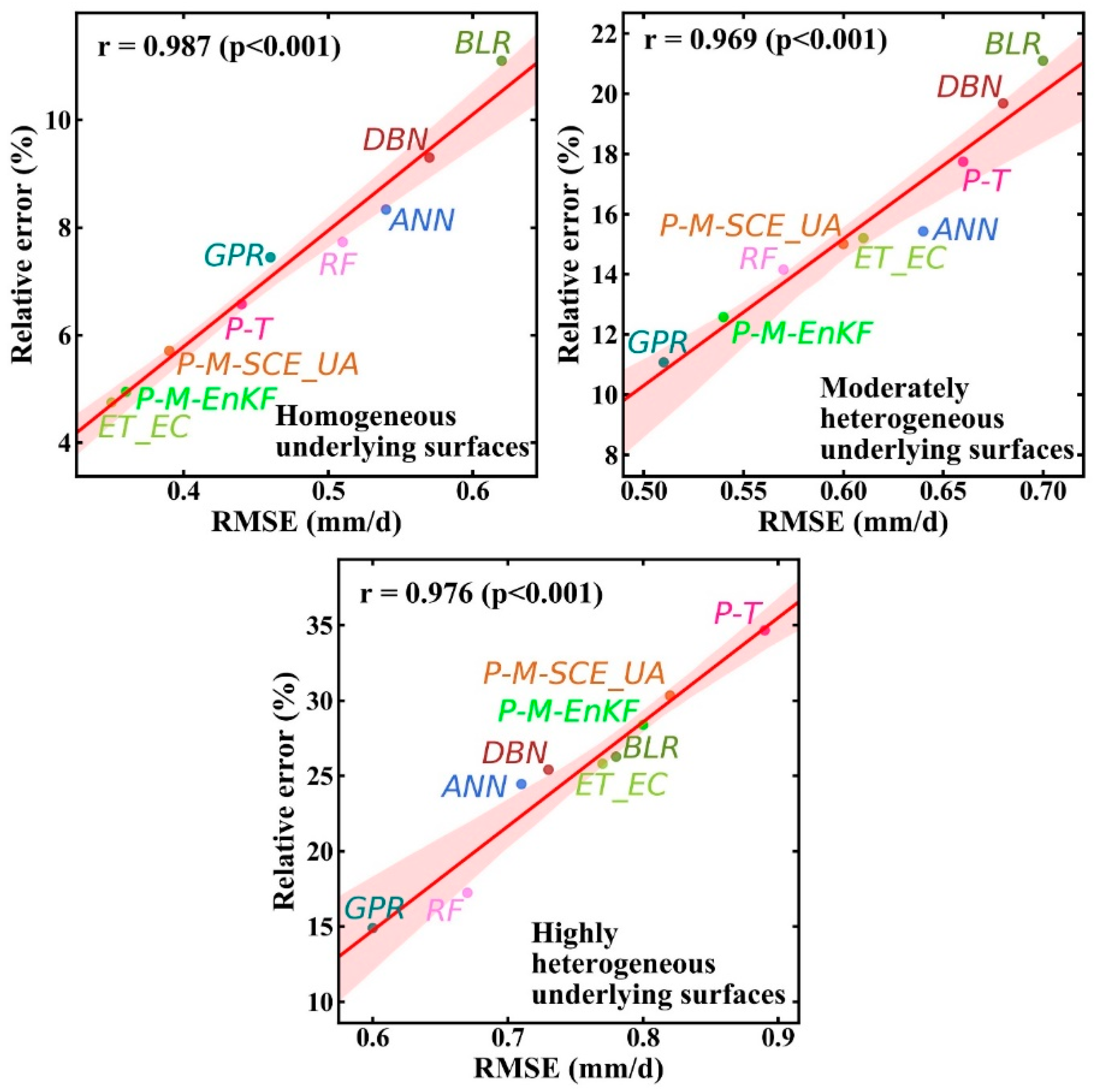
4.3. Optimization of Upscaling Methods
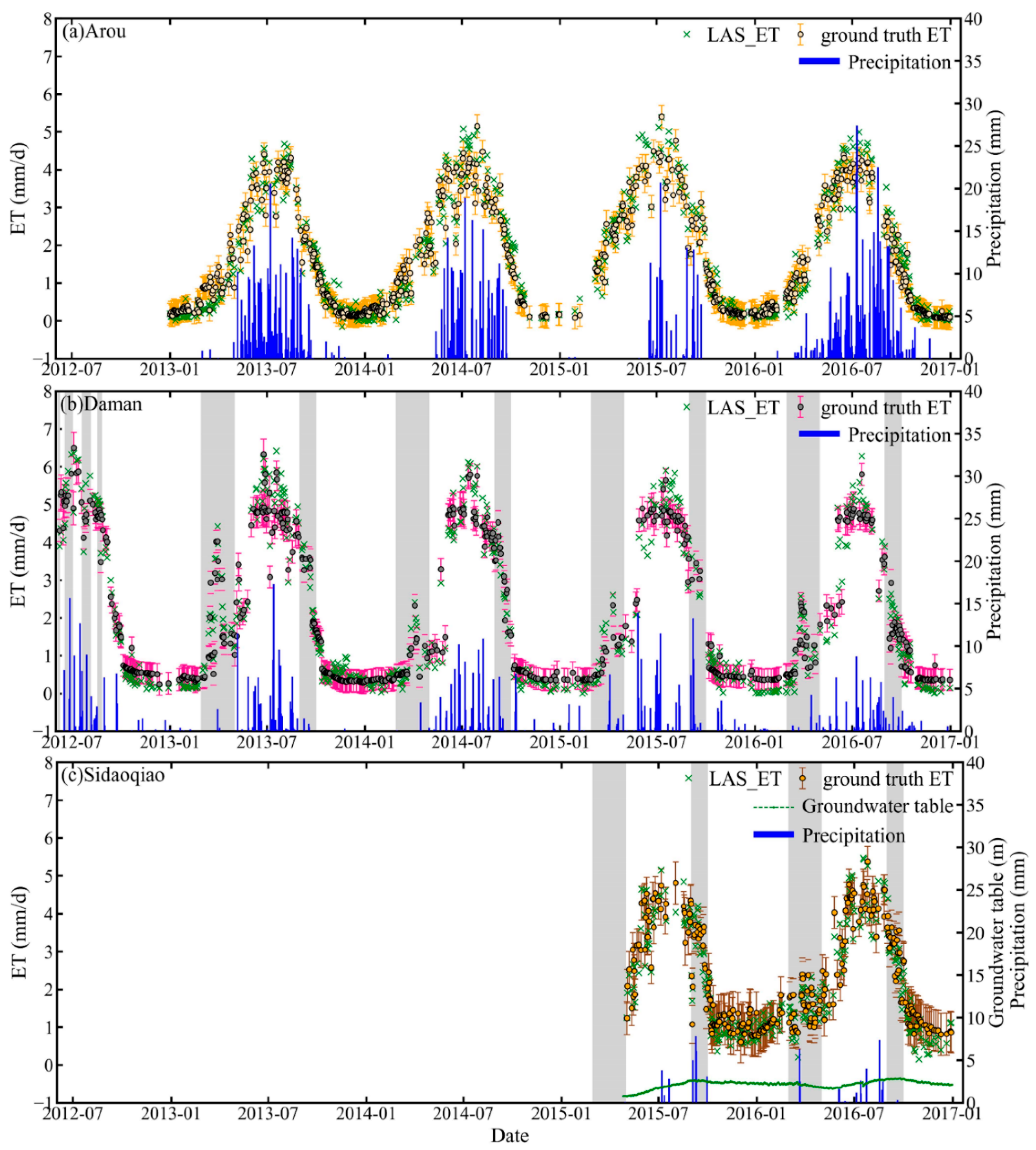
4.3.1. Comparison with LAS Measurements
4.3.2. Cross-Validation with the Three-Cornered Hat Method
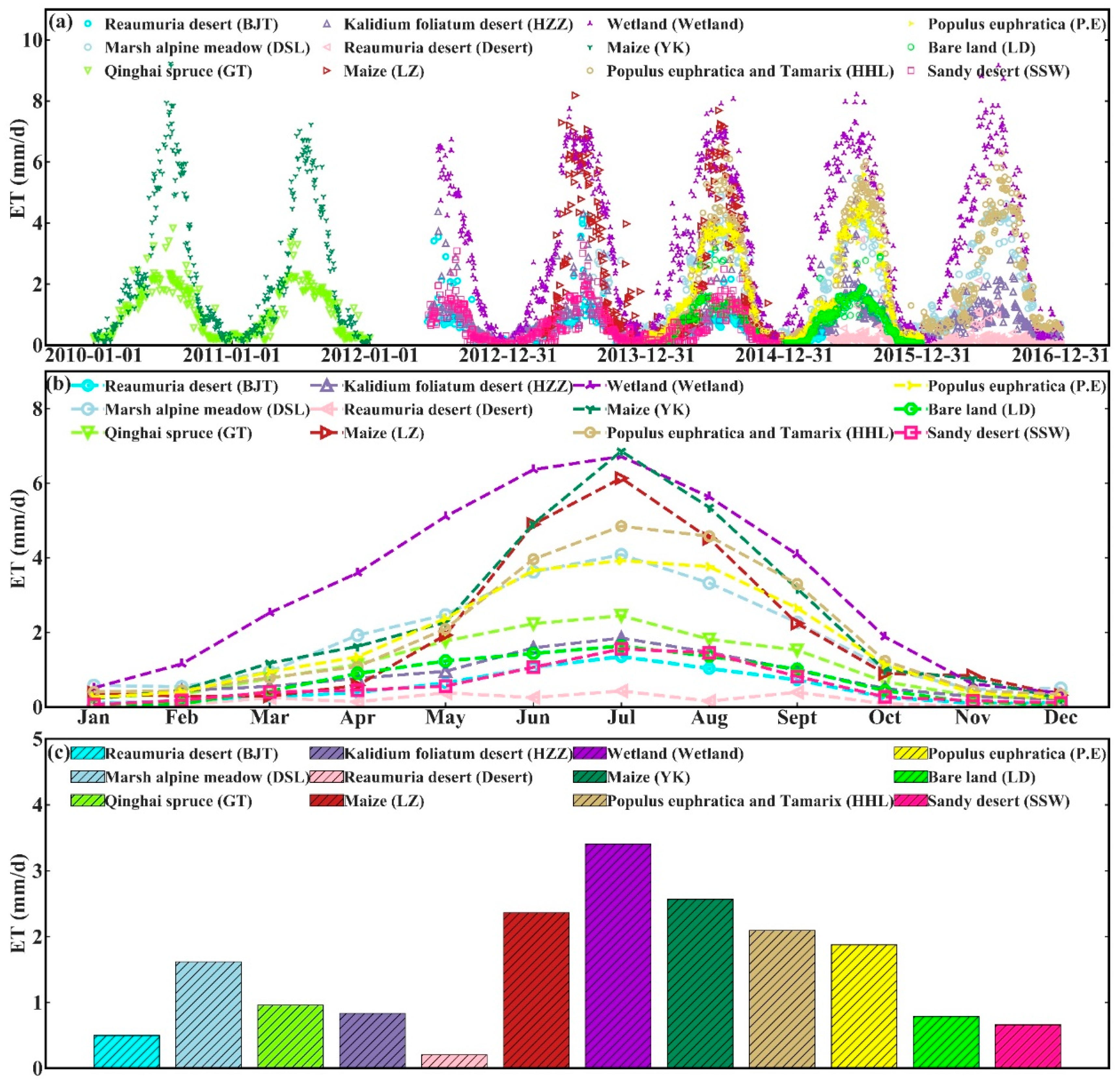
4.4. Acquisition of ET at the Pixel Scale over the Main Surface Types in the HRB
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
Appendix C
Appendix D
References
- Jung, M.; Reichstein, M.; Ciais, P.; Seneviratne, S.I.; Sheffield, J.; Goulden, M.L.; Bonan, G.; Cescatti, A.; Chen, J.; De Jeu, R.; et al. Recent decline in the global land evapotranspiration trend due to limited moisture supply. Nature 2010, 467, 951–954. [Google Scholar] [CrossRef]
- Fisher, J.B.; Melton, F.; Middleton, E.; Hain, C.; Anderson, M.; Allen, R.; McCabe, M.F.; Hook, S.; Baldocchi, D.; Townsend, P.A.; et al. The future of evapotranspiration: Global requirements for ecosystem functioning, carbon and climate feedbacks, agricultural management, and water resources. Water Resour. Res. 2017, 53, 2618–2626. [Google Scholar] [CrossRef]
- Li, Z.L.; Tang, R.; Wan, Z.; Bi, Y.; Zhou, C.; Tang, B.; Yan, G.; Zhang, X. A review of current methodologies for regional Evapotranspiration estimation from remotely sensed data. Sensors 2009, 9, 3801–3853. [Google Scholar] [CrossRef] [Green Version]
- Mu, Q.; Zhao, M.; Running, S.W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Miralles, D.G.; Holmes, T.R.H.; De Jeu, R.A.M.; Gash, J.H.; Meesters, A.G.C.A.; Dolman, A.J. Global land-surface evaporation estimated from satellite-based observations. Hydrol. Earth Syst. Sci. 2011, 15, 453–469. [Google Scholar] [CrossRef] [Green Version]
- Yao, Y.; Liang, S.; Li, X.; Hong, Y.; Fisher, J.B.; Zhang, N.; Chen, J.; Cheng, J.; Zhao, S.; Zhang, X.; et al. Bayesian multimodel estimation of global terrestrial latent heat flux from eddy covariance, meteorological, and satellite observations. J. Geophys. Res. Atmos. 2014, 119, 4521–4545. [Google Scholar] [CrossRef]
- Hu, G.; Jia, L. Monitoring of evapotranspiration in a semi-arid inland river basin by combining microwave and optical remote sensing observations. Remote Sens. 2015, 7, 3056–3087. [Google Scholar] [CrossRef] [Green Version]
- Jiang, C.; Ryu, Y. Multi-scale evaluation of global gross primary productivity and evapotranspiration products derived from Breathing Earth System Simulator (BESS). Remote Sens. Environ. 2016, 186, 528–547. [Google Scholar] [CrossRef]
- Jia, Z.; Liu, S.; Xu, Z.; Chen, Y.; Zhu, M. Validation of remotely sensed evapotranspiration over the Hai River Basin, China. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Nearing, G.S.; Mocko, D.M.; Peters-Lidard, C.D.; Kumar, S.V.; Xia, Y. Benchmarking NLDAS-2 soil moisture and evapotranspiration to separate uncertainty contributions. J. Hydrometeorol. 2016, 17, 745–759. [Google Scholar] [CrossRef]
- Kalma, J.D.; McVicar, T.R.; McCabe, M.F. Estimating land surface evaporation: A review of methods using remotely sensed surface temperature data. Surv. Geophys. 2008, 29, 421–469. [Google Scholar] [CrossRef]
- Ershadi, A.; McCabe, M.F.; Evans, J.P.; Chaney, N.W.; Wood, E.F. Multi-site evaluation of terrestrial evaporation models using FLUXNET data. Agric. For. Meteorol. 2014, 187, 46–61. [Google Scholar] [CrossRef]
- Yao, Y.; Liang, S.; Li, X.; Chen, J.; Wang, K.; Jia, K.; Cheng, J.; Jiang, B.; Fisher, J.B.; Mu, Q.; et al. A satellite-based hybrid algorithm to determine the Priestley-Taylor parameter for global terrestrial latent heat flux estimation across multiple biomes. Remote Sens. Environ. 2015, 165, 216–233. [Google Scholar] [CrossRef] [Green Version]
- Michel, D.; Jiménez, C.; Miralles, D.G.; Jung, M.; Hirschi, M.; Ershadi, A.; Martens, B.; Mccabe, M.F.; Fisher, J.B.; Mu, Q.; et al. The WACMOS-ET project—Part 1: Tower-scale evaluation of four remote-sensing-based evapotranspiration algorithms. Hydrol. Earth Syst. Sci. 2016, 20, 803–822. [Google Scholar] [CrossRef] [Green Version]
- Brunsell, N.A.; Ham, J.M.; Arnold, K.A. Validating remotely sensed land surface fluxes in heterogeneous terrain with large aperture scintillometry. Int. J. Remote Sens. 2011, 32, 6295–6314. [Google Scholar] [CrossRef]
- Senay, G.B.; Friedrichs, M.; Singh, R.K.; Velpuri, N.M. Evaluating Landsat 8 evapotranspiration for water use mapping in the Colorado River Basin. Remote Sens. Environ. 2016, 185, 171–185. [Google Scholar] [CrossRef] [Green Version]
- Ge, Y.; Jin, Y.; Stein, A.; Chen, Y.; Wang, J.; Wang, J.; Cheng, Q.; Bai, H.; Liu, M.; Atkinson, P.M. Principles and methods of scaling geospatial Earth science data. Earth-Sci. Rev. 2019, 197, 102897. [Google Scholar] [CrossRef]
- Liu, S.; Xu, Z.; Song, L.; Zhao, Q.; Ge, Y.; Xu, T.; Ma, Y.; Zhu, Z.; Jia, Z.; Zhang, F. Upscaling evapotranspiration measurements from multi-site to the satellite pixel scale over heterogeneous land surfaces. Agric. For. Meteorol. 2016, 230–231, 97–113. [Google Scholar] [CrossRef]
- Li, X.; Liu, S.; Li, H.; Ma, Y.; Wang, J.; Zhang, Y.; Xu, Z.; Xu, T.; Song, L.; Yang, X.; et al. Intercomparison of Six Upscaling Evapotranspiration Methods: From Site to the Satellite Pixel. J. Geophys. Res. Atmos. 2018, 123, 6777–6803. [Google Scholar] [CrossRef]
- Xu, T.; Guo, Z.; Liu, S.; He, X.; Meng, Y.; Xu, Z.; Xia, Y.; Xiao, J.; Zhang, Y.; Ma, Y.; et al. Evaluating different machine learning methods for upscaling evapotranspiration from flux towers to the regional scale. J. Geophys. Res. Atmos. 2018, 123, 8674–8690. [Google Scholar] [CrossRef]
- Li, X.; Jin, R.; Liu, S.; Ge, Y.; Xiao, Q.; Liu, Q.; Ma, M.; Ran, Y. Upscaling research in HiWATER: Progress and prospects. J. Remote Sens. 2016, 20, 921–932. (In Chinese) [Google Scholar]
- Hao, D.; Xiao, Q.; Wen, J.; You, D.; Wu, X.; Lin, X.; Wu, S. Advances in upscaling methods of quantitative remote sensing. Journal of Remote Sensing. J. Remote Sens. 2018, 22, 408–423. (In Chinese) [Google Scholar]
- Beyrich, F.; Leps, J.P.; Mauder, M.; Bange, J.; Foken, T.; Huneke, S.; Lohse, H.; Lüdi, A.; Meijninger, W.M.L.; Mironov, D.; et al. Area-averaged surface fluxes over the litfass region based on eddy-covariance measurements. Bound. -Layer Meteorol. 2006, 121, 33–65. [Google Scholar] [CrossRef]
- Xu, F.; Wang, W.; Wang, J.; Xu, Z.; Qi, Y.; Wu, Y. Area-averaged evapotranspiration over a heterogeneous land surface: Aggregation of multi-point EC flux measurements with a high-resolution land-cover map and footprint analysis. Hydrol. Earth Syst. Sci. 2017, 21, 4037–4051. [Google Scholar] [CrossRef] [Green Version]
- Xu, F.; Wang, W.; Wang, J.; Huang, C.; Qi, Y.; Li, Y.; Ren, Z. Aggregation of area-averaged evapotranspiration over the Ejina Oasis based on a flux matrix and footprint analysis. J. Hydrol. 2019, 575, 17–30. [Google Scholar] [CrossRef]
- Dold, C.; Heitman, J.; Giese, G.; Howard, A.; Havlin, J.; Sauer, T. Upscaling evapotranspiration with parsimonious models in a North Carolina vineyard. Agronomy 2019, 9, 152. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Yang, J.; Myint, S.W.; Wang, Z.H.; Tong, B. Empirical modeling and spatio-temporal patterns of urban evapotranspiration for the Phoenix metropolitan area, Arizona. GISci. Remote Sens. 2016, 53, 778–792. [Google Scholar] [CrossRef]
- Khoshravesh, M.; Sefidkouhi, M.A.G.; Valipour, M. Estimation of reference evapotranspiration using multivariate fractional polynomial, Bayesian regression, and robust regression models in three arid environments. Appl. Water Sci. 2017, 7, 1911–1922. [Google Scholar] [CrossRef] [Green Version]
- Carter, C.; Liang, S. Evaluation of ten machine learning methods for estimating terrestrial evapotranspiration from remote sensing. Int. J. Appl. Earth Obs. Geoinf. 2019, 78, 86–92. [Google Scholar] [CrossRef]
- Landeras, G.; Ortiz-Barredo, A.; López, J.J. Comparison of artificial neural network models and empirical and semi-empirical equations for daily reference evapotranspiration estimation in the Basque Country (Northern Spain). Agric. Water Manag. 2008, 95, 553–565. [Google Scholar] [CrossRef]
- Rahimikhoob, A. Comparison between M5 model tree and neural networks for estimating reference evapotranspiration in an arid environment. Water Resour. Manag. 2014, 28, 657–669. [Google Scholar] [CrossRef]
- Jung, M.; Reichstein, M.; Margolis, H.A.; Cescatti, A.; Richardson, A.D.; Arain, M.A.; Arneth, A.; Bernhofer, C.; Bonal, D.; Chen, J.; et al. Global patterns of land-atmosphere fluxes of carbon dioxide, latent heat, and sensible heat derived from eddy covariance, satellite, and meteorological observations. J. Geophys. Res. Biogeosci. 2011, 116, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Yang, F.; White, M.A.; Michaelis, A.R.; Ichii, K.; Hashimoto, H.; Votava, P.; Zhu, A.X.; Nemani, R.R. Prediction of continental-scale evapotranspiration by combining MODIS and AmeriFlux data through support vector machine. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3452–3461. [Google Scholar] [CrossRef]
- Bodesheim, P.; Jung, M.; Gans, F.; Mahecha, M.D.; Reichstein, M. Upscaled diurnal cycles of land-Atmosphere fluxes: A new global half-hourly data product. Earth Syst. Sci. Data 2018, 10, 1327–1365. [Google Scholar] [CrossRef] [Green Version]
- Karbasi, M. Forecasting of multi-step ahead reference evapotranspiration using wavelet-Gaussian process regression model. Water Resour. Manag. 2018, 32, 1035–1052. [Google Scholar] [CrossRef]
- Hu, M.; Wang, J.; Ge, Y.; Liu, M.; Liu, S.; Xu, Z.; Xu, T. Scaling flux tower observations of sensible heat flux using weighted area-to-area regression kriging. Atmosphere 2015, 6, 1032–1044. [Google Scholar] [CrossRef] [Green Version]
- Ge, Y.; Liang, Y.; Wang, J.; Zhao, Q.; Liu, S. Upscaling sensible heat fluxes with area-to-area regression kriging. IEEE Geosci. Remote Sens. Lett. 2015, 12, 656–660. [Google Scholar]
- Xu, D.; Agee, E.; Wang, J.; Ivanov, V.Y. Estimation of Evapotranspiration of Amazon Rainforest Using the Maximum Entropy Production Method. Geophys. Res. Lett. 2019, 46, 1402–1412. [Google Scholar] [CrossRef]
- Hajji, I.; Nadeau, D.F.; Music, B.; Anctil, F.; Wang, J. Application of the maximum entropy production model of evapotranspiration over partially vegetated water-limited land surfaces. J. Hydrometeorol. 2018, 19, 989–1005. [Google Scholar] [CrossRef]
- Heinemann, G.; Kerschgens, M. Comparison of methods for area-averaging surface energy fluxes over heterogenous land surfaces using high-resolution non-hydrostatic simulations. Int. J. Climatol. 2005, 25, 379–403. [Google Scholar] [CrossRef]
- Ruehr, S.; Lee, X.; Smith, R.; Li, X.; Xu, Z.; Liu, S.; Yang, X.; Zhou, Y. A mechanistic investigation of the oasis effect in the Zhangye cropland in semiarid western China. J. Arid Environ. 2020, 176, 104120. [Google Scholar] [CrossRef]
- He, X.; Xu, T.; Bateni, S.M.; Ek, M.; Liu, S.; Chen, F. Mapping regional evapotranspiration in cloudy skies via variational assimilation of all-weather land surface temperature observations. J. Hydrol. 2020, 585, 124790. [Google Scholar] [CrossRef]
- Wu, X.; Xiao, Q.; Wen, J.; You, D.; Hueni, A. Advances in quantitative remote sensing product validation: Overview and current status. Earth-Sci. Rev. 2019, 196, 102875. [Google Scholar] [CrossRef]
- Zhang, Y.; Jia, Z.; Liu, S.; Xu, Z.; Xu, T.; Yao, Y.; Ma, Y.; Song, L.; Li, X.; Hu, X.; et al. Advances in validation of remotely sensed land surface evapotranspiration. J. Remote Sens. 2020, 24, 975–999. (In Chinese) [Google Scholar]
- Wu, X.; Xiao, Q.; Wen, J.; You, D. Direct comparison and triple collocation: Which is more reliable in the validation of coarse-scale satellite surface albedo products. J. Geophys. Res. Atmos. 2019, 124, 5198–5213. [Google Scholar] [CrossRef]
- Liu, S.; Li, X.; Xu, Z.; Che, T.; Xiao, Q.; Liu, Q.; Jin, R.; Guo, J.; Wang, L.; Wang, W.; et al. The Heihe Integrated Observatory Network: A basin-scale land surface processes observatory in China. Vadose Zone J. 2018, 17, 1–21. [Google Scholar] [CrossRef]
- Xu, Z.; Liu, S.; Zhu, Z.; Zhou, J.; Shi, W.; Xu, T.; Yang, X.; Zhang, Y.; He, X. Exploring evapotranspiration changes in a typical endorheic basin through the integrated observatory network. Agric. For. Meteorol. 2020, 290, 108010. [Google Scholar] [CrossRef]
- Li, X.; Li, X.; Li, Z.; Ma, M.; Wang, J.; Xiao, Q.; Liu, Q.; Che, T.; Chen, E.; Yan, G.; et al. Watershed allied telemetry experimental research. J. Geophys. Res. Atmos. 2009, 114, D22103. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Cheng, G.; Liu, S.; Xiao, Q.; Ma, M.; Jin, R.; Che, T.; Liu, Q.; Wang, W.; Qi, Y.; et al. Heihe watershed allied telemetry experimental research (HiWater) scientific objectives and experimental design. Bull. Am. Meteorol. Soc. 2013, 94, 1145–1160. [Google Scholar] [CrossRef]
- Liu, S.; Xu, Z.; Wang, W.; Jia, Z.; Zhu, M.; Bai, J.; Wang, J. A comparison of eddy-covariance and large aperture scintillometer measurements with respect to the energy balance closure problem. Hydrol. Earth Syst. Sci. 2011, 15, 1291–1306. [Google Scholar] [CrossRef] [Green Version]
- Liu, S.; Xu, Z. Micrometeorological methods to determine evapotranspiration. In Observation and Measurement of Ecohydrological Processes; Li, X., Vereecken, H., Eds.; Springer: Berlin/Heidelberg, Germeny, 2018; pp. 201–239. [Google Scholar]
- Ji, X.; Zhao, W.; Kang, E.; Zhang, Z.; Jin, B.; Zhao, L. Carbon dioxide exchange in an irrigated agricultural field within an oasis, Northwest China. J. Appl. Meteorol. Climatol. 2011, 50, 2298–2308. [Google Scholar] [CrossRef]
- Xu, Z.; Liu, S.; Li, X.; Shi, S.; Wang, J.; Zhu, Z.; Xu, T.; Wang, W.; Ma, M. Intercomparison of surface energy flux measurement systems used during the HiWATER-MUSOEXE. J. Geophys. Res. Atmos. 2013, 118, 13140–13157. [Google Scholar] [CrossRef]
- Mu, X.; Hu, R.; Huang, S.; Chen, Y. HiWATER: Dataset of emissivity in the middle reaches of the Heihe River Basin in 2012. Beijing normal university; cold and arid regions environmental and engineering research institute. Chinese Acad. Sci. 2012. [Google Scholar]
- Zhu, X.; Chen, J.; Gao, F.; Chen, X.; Masek, J.G. An enhanced spatial and temporal adaptive reflectance fusion model for complex heterogeneous regions. Remote Sens. Environ. 2010, 114, 2610–2623. [Google Scholar] [CrossRef]
- Ma, Y.; Liu, S.; Song, L.; Xu, Z.; Liu, Y.; Xu, T.; Zhu, Z. Estimation of daily evapotranspiration and irrigation water efficiency at a Landsat-like scale for an arid irrigation area using multi-source remote sensing data. Remote Sens. Environ. 2018, 216, 715–734. [Google Scholar] [CrossRef]
- Zhong, B.; Ma, P.; Nie, A.H.; Yang, A.X.; Yao, Y.J.; Lü, W.B.; Zhang, H.; Liu, Q.H. Land cover mapping using time series HJ-1/CCD data. Sci. China Earth Sci. 2014, 57, 1790–1799. [Google Scholar] [CrossRef]
- Guillevic, P.C.; Biard, J.C.; Hulley, G.C.; Privette, J.L.; Hook, S.J.; Olioso, A.; Göttsche, F.M.; Radocinski, R.; Román, M.O.; Yu, Y.; et al. Validation of Land Surface Temperature products derived from the Visible Infrared Imaging Radiometer Suite (VIIRS) using ground-based and heritage satellite measurements. Remote Sens. Environ. 2014, 154, 19–37. [Google Scholar] [CrossRef]
- Huang, G.; Li, X.; Ma, M.; Li, H.; Huang, C. High resolution surface radiation products for studies of regional energy, hydrologic and ecological processes over Heihe river basin, northwest China. Agric. For. Meteorol. 2016, 230–231, 67–78. [Google Scholar] [CrossRef]
- Kormann, R.; Meixner, F.X. An analytical footprint model for non-neutral stratification. Bound. -Layer Meteorol. 2001, 99, 207–224. [Google Scholar] [CrossRef]
- Meijninger, W.M.L.; Hartogensis, O.K.; Kohsiek, W.; Hoedjes, J.C.B.; Zuurbier, R.M.; De Bruin, H.A.R. Determination of area-averaged sensible heat fluxes with a large aperture scintillometer over a heterogeneous surface–Flevoland field experiment. Bound. -Layer Meteorol. 2002, 105, 37–62. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, S.; Hu, X.; Wang, J.; Li, X.; Xu, Z.; Ma, Y.; Liu, R.; Xu, T.; Yang, X. Evaluating Spatial Heterogeneity of Land Surface Hydrothermal Conditions in the Heihe River Basin. Chin. Geogr. Sci. 2020, 30, 855–875. [Google Scholar] [CrossRef]
- Huang, C.; Li, X.; Lu, L. Retrieving soil temperature profile by assimilating MODIS LST products with ensemble Kalman filter. Remote Sens. Environ. 2008, 112, 1320–1336. [Google Scholar] [CrossRef]
- Monteith, J.L. Evaporation and environment. Symp. Soc. Exp. Biol. 1965, 19, 205–234. [Google Scholar] [PubMed]
- Leuning, R.; Zhang, Y.Q.; Rajaud, A.; Cleugh, H.; Tu, K. A simple surface conductance model to estimate regional evaporation using MODIS leaf area index and the Penman-Monteith equation. Water Resour. Res. 2008, 44, W10419. [Google Scholar] [CrossRef]
- Duan, Q.; Gupta, V. Effective and efficient global optimization for conceptual rainfall-runoff models. Water Resour. Res. 1992, 28, 1015–1031. [Google Scholar] [CrossRef]
- Kumar, M.; Raghuwanshi, N.S.; Singh, R. Artificial neural networks approach in evapotranspiration modeling: A review. Irrig. Sci. 2011, 29, 11–25. [Google Scholar] [CrossRef]
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef] [PubMed]
- Williams, C.K.; Rasmussen, C.E. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Tyralis, H.; Papacharalampous, G.; Langousis, A. A brief review of random forests for water scientists and practitioners and their recent history in water resources. Water 2019, 11, 910. [Google Scholar] [CrossRef] [Green Version]
- Ilangakoon, N.T.; Gorsevski, P.V.; Simic Milas, A. Estimating leaf area index by bayesian linear regression using terrestrial Lidar, LAI-2200 plant canopy analyzer, and landsat tm spectral indices. Can. J. Remote Sens. 2015, 41, 315–333. [Google Scholar] [CrossRef]
- Xu, T.; Guo, Z.; Xia, Y.; Ferreira, V.G.; Liu, S.; Wang, K.; Yao, Y.; Zhang, X.; Zhao, C. Evaluation of twelve evapotranspiration products from machine learning, remote sensing and land surface models over conterminous United States. J. Hydrol. 2019, 578, 124105. [Google Scholar] [CrossRef]
- Saltelli, A.; Tarantola, S.; Chan, K.S.P.S.; Saltelli, A.; Tarantoal, S.; Chan, K.S.P.S. A quantitative model-independent method for global sensitivity analysis of model output. Technometrics 1999, 41, 39–56. [Google Scholar] [CrossRef]
- Xiu, D.; Karniadakis, G.E. Modeling uncertainty in flow simulations via generalized polynomial chaos. J. Comput. Phys. 2003, 187, 137–167. [Google Scholar] [CrossRef]
- Najm, H.N. Uncertainty quantification and polynomial chaos techniques in computational fluid dynamics. Annu. Rev. Fluid Mech. 2009, 41, 35–52. [Google Scholar] [CrossRef]
- Yao, Y.; Liang, S.; Fisher, J.B.; Zhang, Y.; Cheng, J.; Chen, J.; Jia, K.; Zhang, X.; Bei, X.; Shang, K.; et al. A Novel NIR-Red Spectral Domain Evapotranspiration Model from the Chinese GF-1 Satellite: Application to the Huailai Agricultural Region of China. IEEE Trans. Geosci. Remote Sens. 2020, 59, 4105–4119. [Google Scholar] [CrossRef]
- Zhang, T.; Jin, S. Evapotranspiration Variations in the Mississippi River Basin Estimated from GPS Observations. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4694–4701. [Google Scholar] [CrossRef]
- Song, L.; Liu, S.; Kustas, W.P.; Nieto, H.; Sun, L.; Xu, Z.; Skaggs, T.H.; Yang, Y.; Ma, M.; Xu, T.; et al. Monitoring and validating spatially and temporally continuous daily evaporation and transpiration at river basin scale. Remote Sens. Environ. 2018, 219, 72–88. [Google Scholar] [CrossRef]
- Velpuri, N.M.; Senay, G.B.; Singh, R.K.; Bohms, S.; Verdin, J.P. A comprehensive evaluation of two MODIS evapotranspiration products over the conterminous United States: Using point and gridded FLUXNET and water balance ET. Remote Sens. Environ. 2013, 139, 35–49. [Google Scholar] [CrossRef]
- Evensen, G. The ensemble Kalman filter: Theoretical formulation and practical implementation. Ocean Dyn. 2003, 53, 343–367. [Google Scholar] [CrossRef]
- Priestley, C.H.B.; Taylor, R.J. On the assessment of surface heat flux and evaporation using large-scale parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Yin, Y.; Wu, S.; Zheng, D.; Yang, Q. Radiation calibration of FAO56 Penman–Monteith model to estimate reference crop evapotranspiration in China. Agric. Water Manag. 2008, 95, 77–84. [Google Scholar] [CrossRef]
- Lindroth, A.; Halldin, S. Numerical analysis of pine forest evaporation and surface resistance. Agric. For. Meteorol. 1986, 38, 59–79. [Google Scholar] [CrossRef]
- Beven, K. A sensitivity analysis of the Penman-Monteith actual evapotranspiration estimates. J. Hydrol. 1979, 44, 169–190. [Google Scholar] [CrossRef]



| Region | No. | Station | Longitude (°) | Latitude (°) | Elevation (m) | Landscape | The Corresponding MODIS Pixels | Time Period of Data Used |
|---|---|---|---|---|---|---|---|---|
| Upstream | 1 | Arou superstation | 100.4643 | 38.0473 | 3033 | Subalpine meadow | 2 × 1 | 2013.1–2016.12 |
| 2 | Guantan (GT) | 100.2503 | 38.5336 | 2835 | Qinghai spruce | 2 × 1 | 2010.1–2011.12 | |
| 3 | Dashalong (DSL) | 98.9406 | 38.8399 | 3739 | Marsh alpine meadow | 1 × 1 | 2013.8–2016.12 | |
| Midstream | 4 | Daman superstation | 100.3722 | 38.8555 | 1556 | Maize | 2 × 1 | 2012.6–2016.12 |
| 5 | Zhangye wetland (Wetland) | 100.4464 | 38.9751 | 1460 | Wetland | 1 × 1 | 2012.6–2016.12 | |
| 6 | Bajitan Gobi (BJT) | 100.3042 | 38.915 | 1562 | Reaumuria desert | 1 × 1 | 2012.5–2015.4 | |
| 7 | Huazhaizi Desert steppe (HZZ) | 100.3186 | 38.7652 | 1731 | Kalidium foliatum desert | 2 × 1 | 2012.6–2016.12 | |
| 8 | Yingke (YK) | 100.4103 | 38.8571 | 1519 | Maize | 1 × 1 | 2010.1–2011.12 | |
| 9 | Shenshawo (SSW) | 100.4933 | 38.7892 | 1594 | Sandy desert | 1 × 1 | 2012.6–2015.4 | |
| 10 | Linze (LZ) | 100.1408 | 39.3281 | 1252 | Maize | 1 × 1 | 2013.1–2014.12 | |
| Downstream | 11 | Sidaoqiao superstation | 101.1374 | 42.0012 | 873 | Tamarix | 2 × 1 | 2015.4–2016.12 |
| 12 | Populus euphratica (P.E) | 101.1239 | 41.9932 | 876 | Populus euphratica | 1 × 1 | 2013.7–2016.4 | |
| 13 | Mixed Forest (HHL) | 101.1335 | 41.9903 | 874 | Populus euphratica and Tamarix | 1 × 1 | 2013.7–2016.12 | |
| 14 | Barren Land (LD) | 101.1326 | 41.9993 | 878 | Bare land | 1 × 1 | 2013.7–2016.3 | |
| 15 | Desert | 100.9872 | 42.1137 | 1054 | Reaumuria desert | 1 × 1 | 2015.4–2016.12 |
| Methods/Observation | Homogeneous Underlying Surfaces (N = 1116) | Moderately Heterogeneous Underlying Surfaces (N = 168) | Highly Heterogeneous Underlying Surfaces (N = 281) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| R | RMSE (mm d−1) | MRE (%) | R | RMSE (mm d−1) | MRE (%) | R | RMSE (mm d−1) | MRE (%) | |
| ET_EC | 0.98 | 0.34 | 1.57 | 0.96 | 0.61 | 10.29 | 0.84 | 0.77 | −13.26 |
| ANN | 0.95 | 0.54 | 9.07 | 0.96 | 0.64 | 10.95 | 0.85 | 0.71 | −11.74 |
| RF | 0.96 | 0.51 | 2.81 | 0.96 | 0.57 | 3.42 | 0.87 | 0.67 | −4.94 |
| GPR | 0.96 | 0.46 | 2.59 | 0.97 | 0.51 | 3.23 | 0.91 | 0.60 | 4.59 |
| DBN | 0.95 | 0.57 | −10.97 | 0.95 | 0.68 | 11.86 | 0.88 | 0.73 | 12.76 |
| BLR | 0.94 | 0.62 | 12.45 | 0.95 | 0.70 | −13.44 | 0.87 | 0.78 | 13.86 |
| P-T | 0.97 | 0.44 | 2.24 | 0.96 | 0.66 | −11.03 | 0.87 | 0.89 | −20.13 |
| P-M-EnKF | 0.98 | 0.36 | −1.68 | 0.97 | 0.54 | 3.37 | 0.86 | 0.80 | −14.73 |
| P-M-SCE_UA | 0.98 | 0.39 | 1.87 | 0.96 | 0.60 | −4.39 | 0.90 | 0.82 | −15.17 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Liu, S.; Yang, X.; Ma, Y.; He, X.; Xu, Z.; Xu, T.; Song, L.; Zhang, Y.; Hu, X.; et al. Upscaling Evapotranspiration from a Single-Site to Satellite Pixel Scale. Remote Sens. 2021, 13, 4072. https://doi.org/10.3390/rs13204072
Li X, Liu S, Yang X, Ma Y, He X, Xu Z, Xu T, Song L, Zhang Y, Hu X, et al. Upscaling Evapotranspiration from a Single-Site to Satellite Pixel Scale. Remote Sensing. 2021; 13(20):4072. https://doi.org/10.3390/rs13204072
Chicago/Turabian StyleLi, Xiang, Shaomin Liu, Xiaofan Yang, Yanfei Ma, Xinlei He, Ziwei Xu, Tongren Xu, Lisheng Song, Yuan Zhang, Xiao Hu, and et al. 2021. "Upscaling Evapotranspiration from a Single-Site to Satellite Pixel Scale" Remote Sensing 13, no. 20: 4072. https://doi.org/10.3390/rs13204072
APA StyleLi, X., Liu, S., Yang, X., Ma, Y., He, X., Xu, Z., Xu, T., Song, L., Zhang, Y., Hu, X., Ju, Q., & Zhang, X. (2021). Upscaling Evapotranspiration from a Single-Site to Satellite Pixel Scale. Remote Sensing, 13(20), 4072. https://doi.org/10.3390/rs13204072







