Remote Sensing-Based Quantification of the Summer Maize Yield Gap Induced by Suboptimum Sowing Dates over North China Plain
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Region
2.2. Data
2.2.1. Remotely Sensed Crop Information
- Quality control: Pixel values with snow or cloud cover in the retrieved data were replaced by linearly interpolating the nearest available pixels in time.
- Time-series filter: TIMESAT3.3 was used to filter the retrieved VI data, with the required parameters were set, as shown in Section 2.3.5.
- Temporal interpolation: Eight-day VI data were linearly interpolated to daily data.
2.2.2. Meteorological Data
- Output cell size = 5 km;
- Power = 2;
- Search radius = variable; and
- Search radius settings: Number of points = 12; maximum distances = 100 km.
2.2.3. Reference Maize Yield
2.3. Methods
2.3.1. Quantifying Yg and the Contribution of SDT to Yg
2.3.2. A Brief Overview of PRYM–Maize
2.3.3. Modifications to PRYM–Maize
2.3.4. Simulating Potential LAI and Yp
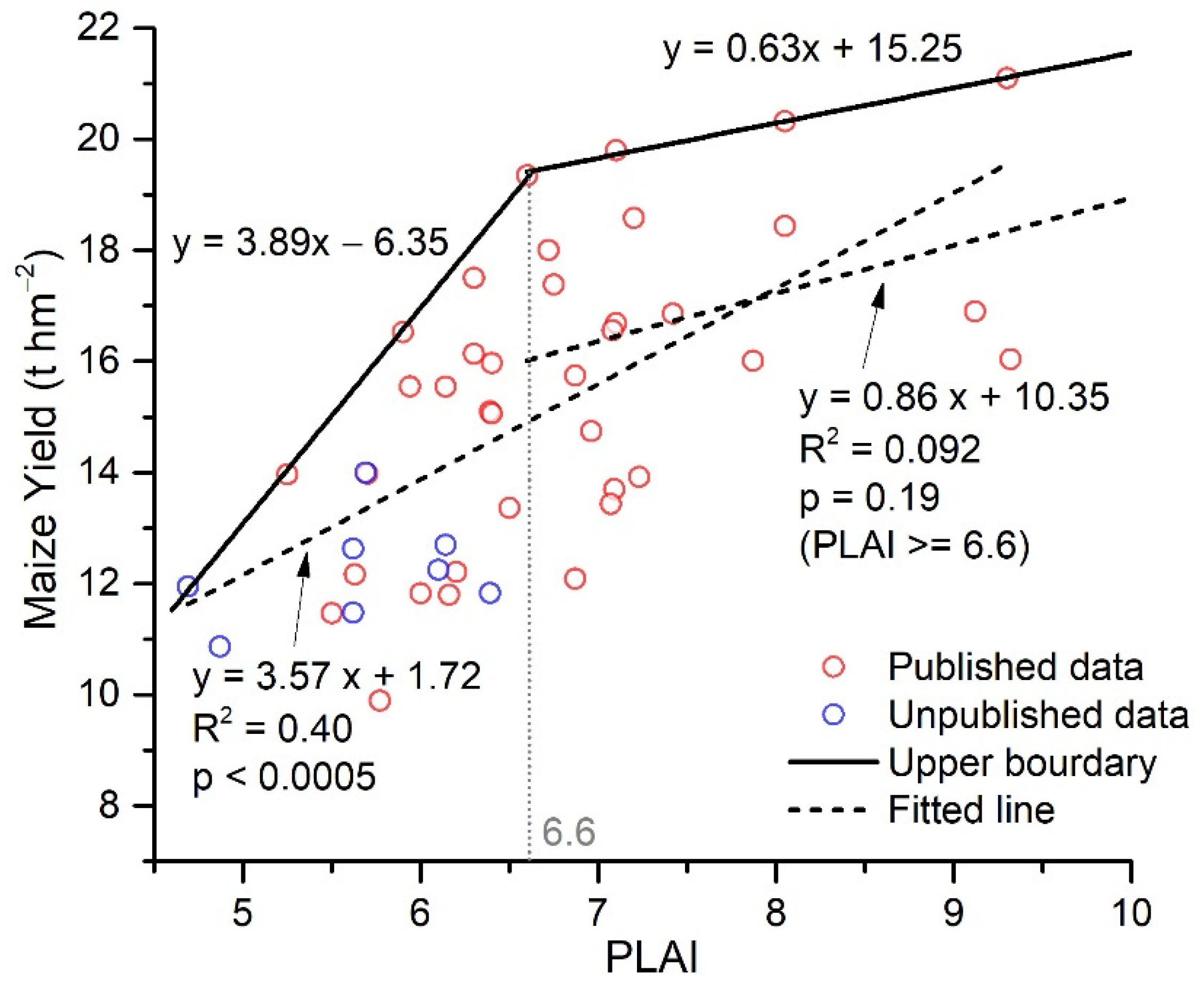
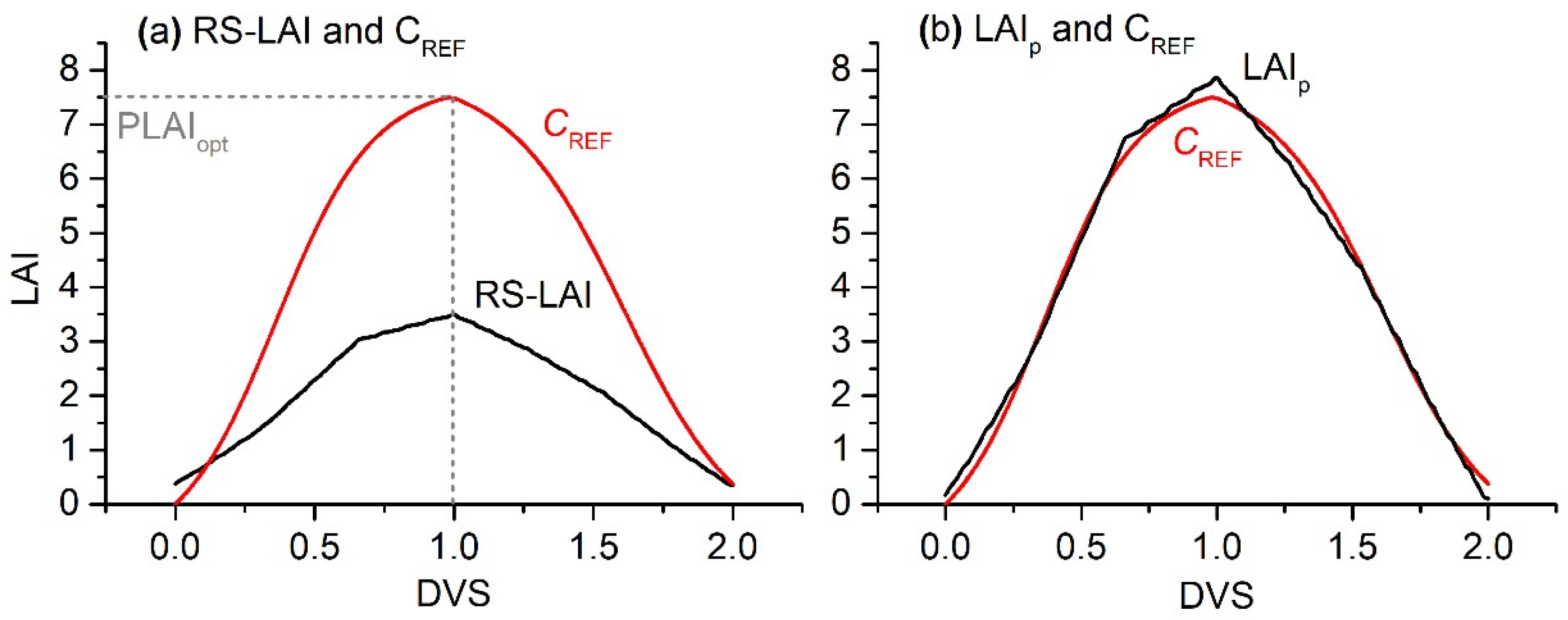
- Derive a reference curve (CRF = ) from the LAI time series within the reference region (Figure 1), where JHV denotes the number of days from EM to HV, LAIRF denotes a reference LAI value of a given day. CRF has a PLAI greater than 6.6, representing the roughly temporal variation in LAIp. We obtain CRF using two procedures: (i) Average the LAI time series of all maize pixels retrieved from MODIS VI-based LAI (Equation (1)) by date in 2010 within the reference region (Figure 2) to obtain an LAI curve (C0 = ) for maize; (ii) calculate CRF from C0 as CRF = PLAIopt, where PLAIopt denotes the optimum PLAI for maize potentially yielding and is expected to be greater than 6.6. In this study, we made a conservative estimate for PLAIopt and set it to 7.5, and this estimate was supported by Liu, Hou, Xie, Ming, Wang, Xu, Liu, Yang and Li [50], who reported PLAI = 7.53 of the maize plants, achieving the highest maize yield (22.5 t hm−2) record in China.
- Derive LAIp for each pixel by fitting the time series of RS-LAI (CRS = ) of the pixel to CRF using linear regression analysis, as shown in Figure 3, where denotes the number of days from EM to HV for a given pixel. In other words, we fitted CRF = for each pixel to obtain k and b and then calculated LAIp as . If , CRF was linearly stretched in the timeline to match the time span of CRS.
- Run the RS process-based crop yield model to simulate Yp0 with input LAI substituted by LAIp, fN(N) = 1, and gsm,2000 = 0.017 m s−1.
- We referred to the method of Lobell [28], which assumed optimal field management (SDT in this study) can be achieved within a given domain with similar climate conditions, to compute Yp at each pixel as the 95th of Yp0 values of surrounding pixels. These surrounding pixels were selected using two criteria: (i) Within a 50 km buffer around the central pixel and (ii) differences in accumulated GDDs and total solar radiation during the growing season (June–September) between the surroundings and the center pixel were less than 50 °C d and 50 MJ, respectively. The buffer size here referred to the size of a zone represented by a meteorological site in Wart, et al. [66].
2.3.5. Extracting Crop Phenology Using RS Data
- Window size = 64 days,
- Start of season method = relative amplitude, and
- Season start/end value = 0.1/0.2,
3. Results
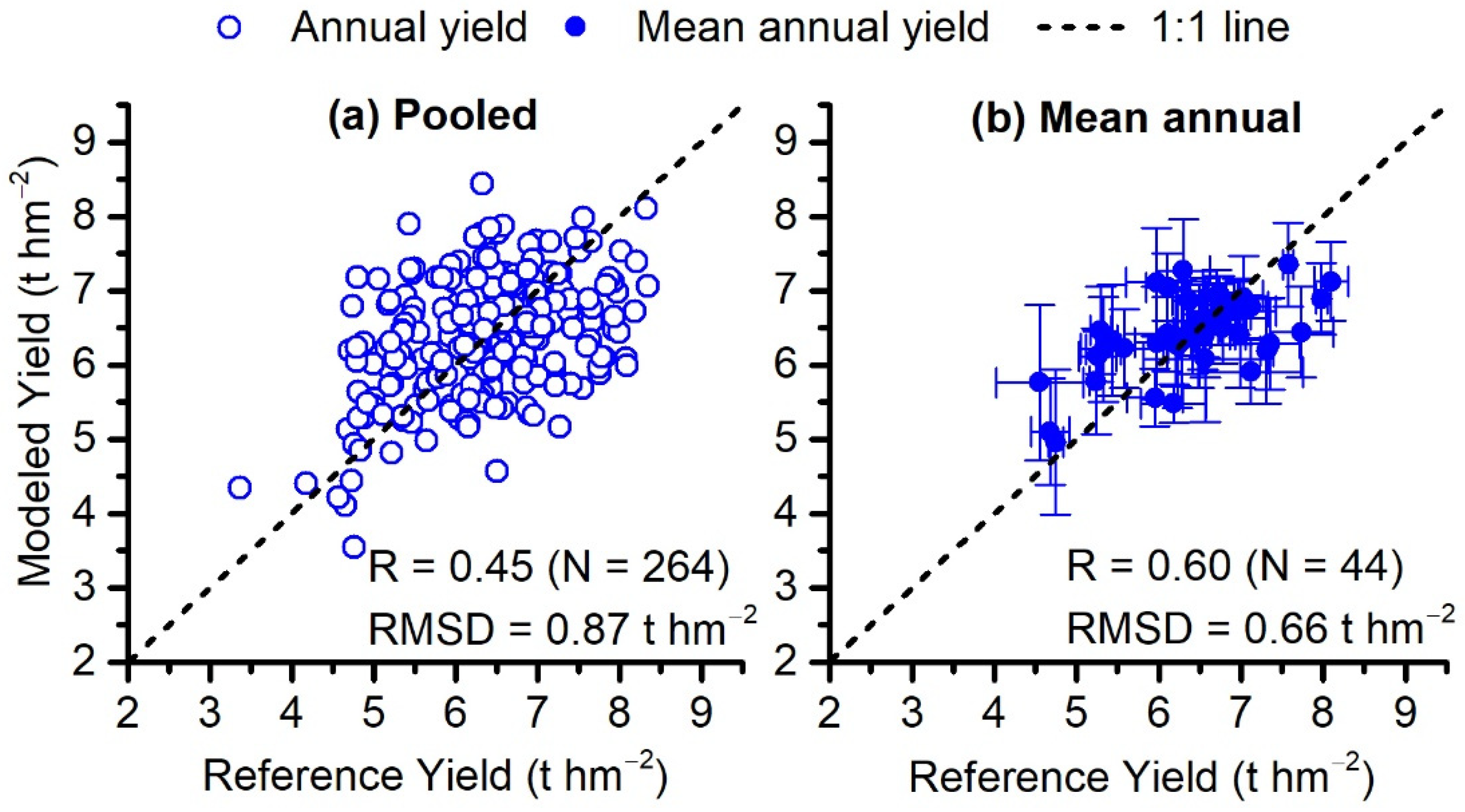
3.1. Modeled Ya
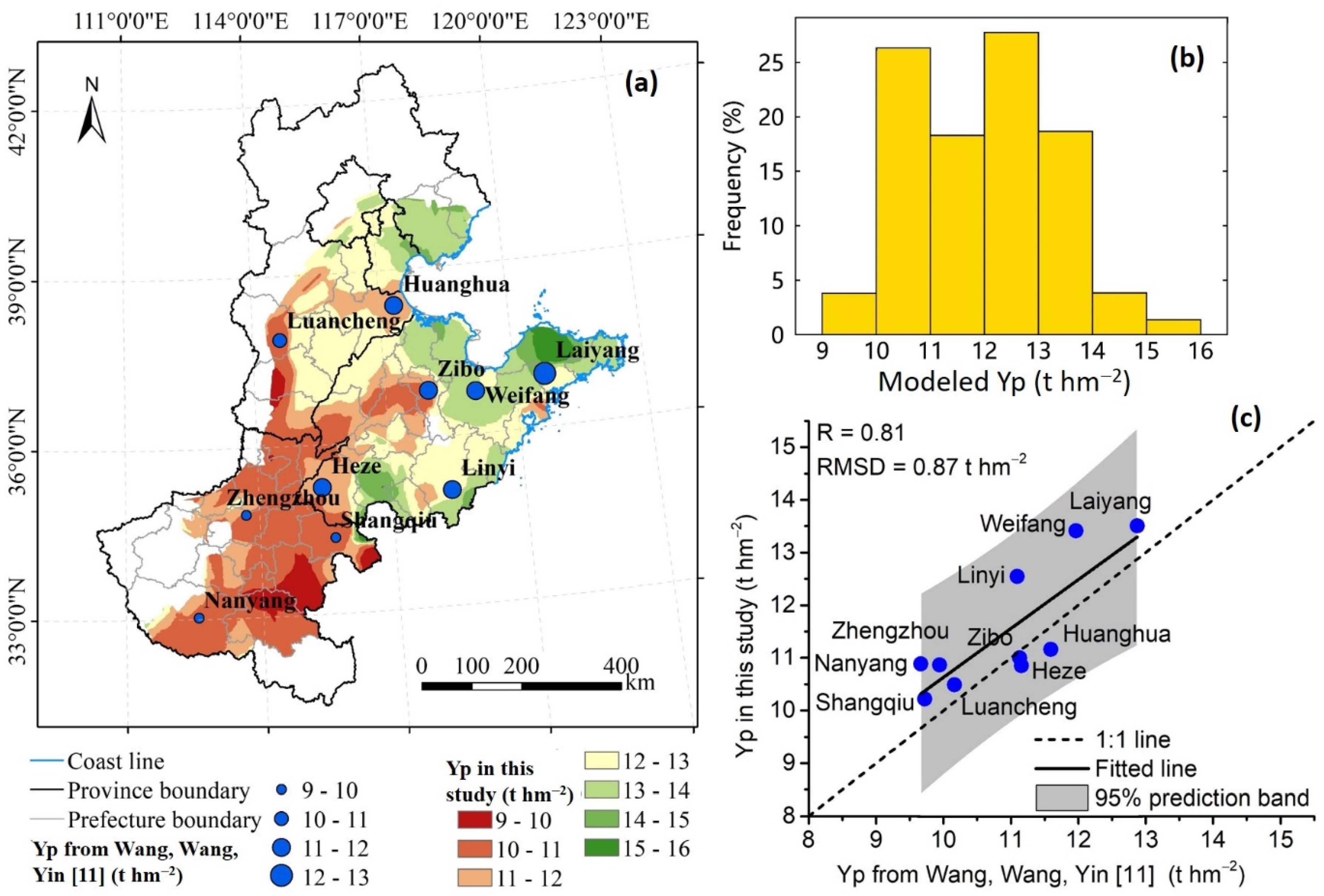
3.2. Modeled Yp
3.3. Yg and the Contribution of Suboptimum SDT to Yg
4. Discussion
4.1. Yg0 Is Partly Persistent
4.2. Yp Derived from Ya and Yp0
4.3. Limits of the Method in This Study
5. Conclusions
- The modified RS crop yield model reasonably estimated the Ya of summer maize over the NCP, but the model’s accuracy was limited by input RS data.
- Modeled Yp showed close relationships with site-level results given by CGMs in previous studies, which demonstrated that the proposed RS-based approach to estimate Yp was effective in modeling Yp over the NCP.
- Large gaps, Ygs, remained between Ya and Yp of summer maize over the NCP and suboptimum SDT, which considerably contributed to Yg; regional Yg over the NCP in the period 2010 to 2015 was 5.0 t hm−2, and the Yg, which accounted for suboptimum SDT (Yg0), was approximately 41% of Yg. However, not all Yg0 could be filled by optimizing SDT because Yg0 was also affected by non-persistent factors. Thus, studies on small regions with higher-resolution RS data are required to decompose the persistent portion from Yg0.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- van Ittersum, M.K.; Cassman, K.G.; Grassini, P.; Wolf, J.; Tittonell, P.; Hochman, Z. Yield gap analysis with local to global relevance—A review. Field Crop Res. 2013, 143, 4–17. [Google Scholar] [CrossRef] [Green Version]
- Farmaha, B.S.; Lobell, D.B.; Boone, K.E.; Cassman, K.G.; Yang, H.S.; Grassini, P. Contribution of persistent factors to yield gaps in high-yield irrigated maize. Field Crop Res. 2016, 186, 124–132. [Google Scholar] [CrossRef]
- Di Mauro, G.; Cipriotti, P.A.; Gallo, S.; Rotundo, J.L. Environmental and management variables explain soybean yield gap variability in Central Argentina. Eur. J. Agron. 2018, 99, 186–194. [Google Scholar] [CrossRef]
- Lobell, D.B.; Ortiz-Monasterio, J.I.; Falcon, W.P. Yield uncertainty at the field scale evaluated with multi-year satellite data. Agric. Syst. 2007, 92, 76–90. [Google Scholar] [CrossRef]
- Gambin, B.L.; Coyos, T.; Di Mauro, G.; Borrás, L.; Garibaldi, L.A. Exploring genotype, management, and environmental variables influencing grain yield of late-sown maize in central Argentina. Agric. Syst. 2016, 146, 11–19. [Google Scholar] [CrossRef]
- Liu, Z.; Yang, X.; Lin, X.; Hubbard, K.G.; Lv, S.; Wang, J. Maize yield gaps caused by non-controllable, agronomic, and socioeconomic factors in a changing climate of Northeast China. Sci. Total Environ. 2016, 541, 756–764. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Y.; Zhang, R.; Li, J.; Zhang, M.; Zhou, S.; Wang, Z. Reduced irrigation increases the water use efficiency and productivity of winter wheat-summer maize rotation on the North China Plain. Sci. Total Environ. 2018, 618, 112–120. [Google Scholar] [CrossRef] [PubMed]
- Cui, X.; Xie, W. Adapting Agriculture to Climate Change through Growing Season Adjustments: Evidence from Corn in China. Am. J. Agric. Econ. 2021, 1–24. [Google Scholar] [CrossRef]
- de Souza Nóia Júnior, R.; Sentelhas, P.C. Soybean-maize succession in Brazil: Impacts of sowing dates on climate variability, yields and economic profitability. Eur. J. Agron. 2019, 103, 140–151. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, S.; Sun, H.; Chen, S.; Shao, L.; Liu, X. Contribution of cultivar, fertilizer and weather to yield variation of winter wheat over three decades: A case study in the North China Plain. Eur. J. Agron. 2013, 50, 52–59. [Google Scholar] [CrossRef]
- Wang, J.; Wang, E.; Yin, H.; Feng, L.; Zhang, J. Declining yield potential and shrinking yield gaps of maize in the North China Plain. Agric. For. Meteorol. 2014, 195–196, 89–101. [Google Scholar] [CrossRef]
- Sun, H.; Zhang, X.; Wang, E.; Chen, S.; Shao, L. Quantifying the impact of irrigation on groundwater reserve and crop production—A case study in the North China Plain. Eur. J. Agron. 2015, 70, 48–56. [Google Scholar] [CrossRef]
- Mohammadi-Ahmadmahmoudi, E.; Deihimfard, R.; Noori, O. Yield gap analysis simulated for sugar beet-growing areas in water-limited environments. Eur. J. Agron. 2020, 113, 125988. [Google Scholar] [CrossRef]
- Lobell, D.B.; Cassman, K.G.; Field, C.B. Crop Yield Gaps: Their Importance, Magnitudes, and Causes. Annu. Rev. Environ. Resour. 2009, 34, 179–204. [Google Scholar] [CrossRef] [Green Version]
- Keating, B.A.; Carberry, P.S.; Hammer, G.L.; Probert, M.E.; Robertson, M.J.; Holzworth, D.; Huth, N.I.; Jng, H.; Meinke, H.; Hochman, Z. An overview of APSIM, a model designed for farming systems simulation. Eur. J. Agron. 2003, 18, 267–288. [Google Scholar] [CrossRef] [Green Version]
- Basso, B.; Liu, L.; Ritchie, J.T. A Comprehensive Review of the CERES-Wheat, -Maize and -Rice Models’ Performances. Adv. Agron. 2016, 136, 27–132. [Google Scholar] [CrossRef]
- Lizaso, J.I.; Boote, K.J.; Jones, J.W.; Porter, C.H.; Echarte, L.; Westgate, M.E.; Sonohat, G. CSM-IXIM: A New Maize Simulation Model for DSSAT Version 4.5. Agron. J. 2011, 103, 766–779. [Google Scholar] [CrossRef]
- Amarasingha, R.P.R.K.; Suriyagoda, L.D.B.; Marambe, B.; Gaydon, D.S.; Galagedara, L.W.; Punyawardena, R.; Silva, G.L.L.P.; Nidumolu, U.; Howden, M. Simulation of crop and water productivity for rice (Oryza sativa L.) using APSIM under diverse agro-climatic conditions and water management techniques in Sri Lanka. Agric. Water Manag. 2015, 160, 132–143. [Google Scholar] [CrossRef]
- Kwesiga, J.; Grotelüschen, K.; Senthilkumar, K.; Neuhoff, D.; Döring, T.F.; Becker, M. Rice Yield Gaps in Smallholder Systems of the Kilombero Floodplain in Tanzania. Agronomy 2020, 10, 1135. [Google Scholar] [CrossRef]
- Devkota, K.P.; McDonald, A.J.; Khadka, A.; Khadka, L.; Paudel, G.; Devkota, M. Decomposing maize yield gaps differentiates entry points for intensification in the rainfed mid-hills of Nepal. Field Crop. Res. 2015, 179, 81–94. [Google Scholar] [CrossRef]
- Gilardelli, C.; Stella, T.; Confalonieri, R.; Ranghetti, L.; Campos-Taberner, M.; García-Haro, F.J.; Boschetti, M. Downscaling rice yield simulation at sub-field scale using remotely sensed LAI data. Eur. J. Agron. 2019, 103, 108–116. [Google Scholar] [CrossRef]
- Huang, J.; Tian, L.; Liang, S.; Ma, H.; Becker-Reshef, I.; Huang, Y.; Su, W.; Zhang, X.; Zhu, D.; Wu, W. Improving winter wheat yield estimation by assimilation of the leaf area index from Landsat TM and MODIS data into the WOFOST model. Agric. For. Meteorol. 2015, 204, 106–121. [Google Scholar] [CrossRef] [Green Version]
- Wang, P.; Sun, R.; Zhang, J.; Zhou, Y.; Xie, D.; Zhu, Q. Yield estimation of winter wheat in the North China Plain using the remote-sensing–photosynthesis–yield estimation for crops (RS–P–YEC) model. Int. J. Remote Sens. 2011, 32, 6335–6348. [Google Scholar] [CrossRef]
- Huang, Y.; Ryu, Y.; Jiang, C.; Kimm, H.; Kim, S.; Kang, M.; Shim, K. BESS-Rice: A remote sensing derived and biophysical process-based rice productivity simulation model. Agric. For. Meteorol. 2018, 256–257, 253–269. [Google Scholar] [CrossRef]
- Chang, Q.; Zhang, J.; Jiao, W.; Yao, F. A Comparative Analysis of the NDVIg and NDVI3g in Monitoring Vegetation Phenology Changes in the Northern Hemisphere. Geocart. Internat. 2016, 33, 1–20. [Google Scholar] [CrossRef]
- Lobell, D.B.; Ortiz-Monasterio, J.I.; Sibley, A.M.; Sohu, V.S. Satellite detection of earlier wheat sowing in India and implications for yield trends. Agric. Syst. 2013, 115, 137–143. [Google Scholar] [CrossRef]
- Ji, Z.; Pan, Y.; Zhu, X.; Wang, J.; Li, Q. Prediction of Crop Yield Using Phenological Information Extracted from Remote Sensing Vegetation Index. Sensors 2021, 21, 1406. [Google Scholar] [CrossRef]
- Lobell, D.B. The use of satellite data for crop yield gap analysis. Field Crop Res. 2013, 143, 56–64. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Chen, X.; Cui, Z.; Lobell, D.B. Using satellite remote sensing to understand maize yield gaps in the North China Plain. Field Crop Res. 2015, 183, 31–42. [Google Scholar] [CrossRef]
- Lobell, D.B.; Ortiz-Monasterio, J.I.; Lee Addams, C.; Asner, G.P. Soil, climate, and management impacts on regional wheat productivity in Mexico from remote sensing. Agric. For. Meteorol. 2002, 114, 31–43. [Google Scholar] [CrossRef]
- Lobell, D.B.; Thau, D.; Seifert, C.; Engle, E.; Little, B. A scalable satellite-based crop yield mapper. Remote Sens. Environ. 2015, 164, 324–333. [Google Scholar] [CrossRef]
- Dehkordi, P.A.; Nehbandani, A.; Hassanpour-bourkheili, S.; Kamkar, B. Yield Gap Analysis Using Remote Sensing and Modelling Approaches: Wheat in the Northwest of Iran. Int. J. Plant Prod. 2020, 14, 443–452. [Google Scholar] [CrossRef]
- Deines, J.M.; Patel, R.; Liang, S.-Z.; Dado, W.; Lobell, D.B. A million kernels of truth: Insights into scalable satellite maize yield mapping and yield gap analysis from an extensive ground dataset in the US Corn Belt. Remote Sens. Environ. 2021, 253, 112174. [Google Scholar] [CrossRef]
- He, L.; Mostovoy, G. Cotton Yield Estimate Using Sentinel-2 Data and an Ecosystem Model over the Southern US. Remote Sens. 2019, 11, 2000. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Bai, Y.; Zhang, J.-H.; Shahzad, A. Developing a process–based and remote sensing driven crop yield model for maize (PRYM–Maize) and its validation over the Northeast China Plain. J. Integr. Agric. 2020, 20, 408–423. [Google Scholar] [CrossRef]
- Liu, Z. The Yield Gaps and Constraint Factors of Spring Maize in Northeast China; China Agricultural University: Beijing, China, 2013. [Google Scholar]
- Xun, L.; Wang, P.; Li, L.; Wang, L.; Kong, Q. Identifying crop planting areas using Fourier-transformed feature of time series MODIS leaf area index and sparse-representation-based classification in the North China Plain. Int. J. Remote Sens. 2019, 40, 2034–2052. [Google Scholar] [CrossRef]
- Bai, Y.; Zhang, J.; Zhang, S.; Yao, F.; Magliulo, V. A remote sensing-based two-leaf canopy conductance model: Global optimization and applications in modeling gross primary productivity and evapotranspiration of crops. Remote Sens. Environ. 2018, 215, 411–437. [Google Scholar] [CrossRef]
- Chen, R.; Ersi, K.; Yang, J.; Lu, S.; Zhao, W. Validation of five global radiation models with measured daily data in China. Energy Convers. Manag. 2004, 45, 1759–1769. [Google Scholar] [CrossRef]
- Bai, Y.; Zhang, J.; Zhang, S.; Koju, U.A.; Yao, F.; Igbawua, T. Using precipitation, vertical root distribution and satellite-retrieved vegetation information to parameterize water stress in a Penman-Monteith approach to evapotranspiration modelling under Mediterranean climate. J. Adv. Model. Earth Syst. 2017, 9, 168–192. [Google Scholar] [CrossRef]
- Supit, I.; Hooijer, A.A.; Van Diepen, C.A. System Description of the WOFOST 6.0 Crop Simulation Model Implemente in CGMS.; Volume 1: Theory and Algorithms; Joint Research Centre, European Commission: Luxembourg, 1994. [Google Scholar]
- Peng, B.; Guan, K.; Chen, M.; Lawrence, D.M.; Pokhrel, Y.; Suyker, A.; Arkebauer, T.; Lu, Y. Improving maize growth processes in the community land model: Implementation and evaluation. Agric. For. Meteorol. 2018, 250–251, 64–89. [Google Scholar] [CrossRef]
- Shawon, A.R.; Ko, J.; Ha, B.; Jeong, S.; Kim, D.K.; Kim, H.-Y. Assessment of a Proximal Sensing-integrated Crop Model for Simulation of Soybean Growth and Yield. Remote Sens. 2020, 12, 410. [Google Scholar] [CrossRef] [Green Version]
- Osborne, T.; Gornall, J.; Hooker, J.; Williams, K.; Wiltshire, A.; Betts, R.; Wheeler, T. JULES-crop: A parametrisation of crops in the Joint UK Land Environment Simulator. Geosci. Model Dev. 2015, 8, 1139–1155. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y. Study on Population Quality and Individual Physiology Function of Super High-yielding Maize (Zea mays L.); Shandong Agricultural University: Tai’an, China, 2008. [Google Scholar]
- Yang, G.; Xin, L.; Chenglian, W.; Xiangning, L. Study on Effects of Plant Densities on the Yield and the Related Characters of Maize Hybrids. Acta Agric. Boreali-Occident. Sin. 2006, 15, 57–60. [Google Scholar]
- Jing, L. Study on Population Quality Indices for High or Super High-Yield of Maize; Yangzhou University: Yangzhou, China, 2011. [Google Scholar]
- Chu, G.; Zhang, J. Effects of Nitrogen Application on Photosynthetic Characteristics, Yield and Nitrogen Use Efficiency in Drip Irrigation of Super High-yield Spring Maize. J. Maize Sci. 2016, 24, 130–136. [Google Scholar] [CrossRef]
- Huang, Z. Studies on Photosynthetic and Nutrient Physiological Characteristics of Super-High Yield Summer Maize Hybrids; Shandong Agricultural University: Tai’an, China, 2007. [Google Scholar]
- Liu, G.; Hou, P.; Xie, R.; Ming, B.; Wang, K.; Xu, W.; Liu, W.; Yang, Y.; Li, S. Canopy characteristics of high-yield maize with yield potential of 22.5 Mg ha−1. Field Crop Res. 2017, 213, 221–230. [Google Scholar] [CrossRef]
- Wang, J. Characteristics on Canopy Vertical Structures and Agronomic Regulation of Super-High Yield of Spring Maize; Inner Mongolia Agricultural University: Huhehot, China, 2009. [Google Scholar]
- Liu, W.; Lv, P.; Su, K.; Yang, J.; Zhang, J.; Dong, S.; Liu, P.; Sun, Q. Effects of planting density on the grain yield and source-sink characteristics of summer maize. Chin. J. Appl. Ecol. 2010, 21, 1737–1743. [Google Scholar]
- Hu, W. A Study on Characteristics of Radiation and Photosynthesis in Canopy of Super High-Yield Summer Maize; Henan Agricultural University: Zhengzhou, China, 2012. [Google Scholar]
- Cao, Y. Study on the Activity of Photosynthesis Enzymes and Protective Enzymes in Super High Yield Corns and Common Corns; Jilin Agricultural University: Changchun, China, 2008. [Google Scholar]
- Jin, X.; Du, X.; Liu, J.; Cheng, F.; Cui, Y. Physiological Characters of the Summer Maize Population with High Yield in the North Areas of the Yellow River, Huai and Hai Rivers Plain. J. Maize Sci. 2012, 20, 79–83. [Google Scholar] [CrossRef]
- Wang, Z. Structural and Functional Properties of Canopy and Root of Super High Yield Spring Maize & Agronomic Water Saving Compensatory Mechanism; Inner Mongolia Agricultural University: Huhehot, China, 2009. [Google Scholar]
- Chang, J.; Zhang, G.; Li, Y.; Yan, L.; Li, C. Study on Growth of Super-high-yield Summer Maize in the Ecological Area of the Yellow River, Huai and Hai Rivers. J. Maize Sci. 2011, 19, 75–79. [Google Scholar] [CrossRef]
- Yang, D.; Zhao, W.; Qin, D.; Liu, F.; Zhang, Q.; Guan, Y.; Yang, K. Yield and Canopy Structure of Maize under the Condition of High Yield Cultivation. J. Maize Sci. 2016, 24, 129–135. [Google Scholar] [CrossRef]
- Bao, Y. Study on Canopy Structure and Photosynthesis Character of Super-High-Yield Maize; Jilin Agricultural University: Changchun, China, 2006. [Google Scholar]
- Zhang, S.; Wang, Y.; Qi, T.; Cheng, L.; Xu, G.; Su, Y.; Qin, Y.; Li, Y. Study on Cultivated Technology for Super High Yield of Summer Maize in Huanghuaihai Region. Chin. Agric. Sci. Bull. 2009, 25, 130–133. [Google Scholar]
- Zhang, Y.; Yang, H.; Gao, J.; Zhang, R.; Wang, Z.; Xu, S.; Fan, X.; Yang, S. Study on Canopy Structure and Physiological Characteristics of Super-High Yield Spring Maize. Sci. Agric. Sin. 2011, 44, 4367–4376. [Google Scholar] [CrossRef]
- Ma, X.; Wang, Q.; Qian, C.; Ke, F.; Wang, C. Canopy Characteris tics of Super-high Yielding Maize Under Different Nitrogen Application. J. Maize Sci. 2008, 16, 158–162. [Google Scholar] [CrossRef]
- Li, X.; Tang, Q.; Li, D.; Li, W.; Li, H.; Cai, Q. Effects of Different Plant Densities on the Photosynthetic-Physiological Characters and Yield Traits in Spring Maize Grown on Super-High Yielding Paddy Field. Acta Agric. Boreali-Sin. 2011, 26, 174–180. [Google Scholar]
- Yang, J.; Gao, H.; Liu, P.; Li, G.; Dong, S.; Zhang, J.; Wang, J. Effects of Planting Density and Row Spacing on Canopy Apparent Photosynthesis of High-Yield Summer Corn. Acta Agron. Sin. 2010, 36, 1226–1233. [Google Scholar] [CrossRef]
- Wu, Z. Creation High-Yield Maize Canopy Structure and Micro-Environmental Factors; Jilin Agricultural University: Changchun, China, 2002. [Google Scholar]
- Wart, J.V.; Kersebaum, K.C.; Peng, S.; Milner, M.; Cassman, K.G. Estimating crop yield potential at regional to national scales. Field Crop Res. 2013, 143, 34–43. [Google Scholar] [CrossRef] [Green Version]
- Meng, Q.; Hou, P.; Wu, L.; Chen, X.; Cui, Z.; Zhang, F. Understanding production potentials and yield gaps in intensive maize production in China. Field Crop Res. 2013, 143, 91–97. [Google Scholar] [CrossRef] [Green Version]
- Li, K. Yield Gap Analysis Focused on Winter Wheat and Summer Maize Rotation in the North China Plain; China Agricultural University: Beijing, China, 2014. [Google Scholar]
- Jin, Z.; Azzari, G.; Lobell, D.B. Improving the accuracy of satellite-based high-resolution yield estimation: A test of multiple scalable approaches. Agric. For. Meteorol. 2017, 247, 207–220. [Google Scholar] [CrossRef]
- Yang, D.; Chen, J.; Zhou, Y.; Chen, X.; Chen, X.; Cao, X. Mapping plastic greenhouse with medium spatial resolution satellite data: Development of a new spectral index. Int. J. Photogramm. Remote Sens. 2017, 128, 47–60. [Google Scholar] [CrossRef]
- Li, J.; Luo, J.; Ming, D.; Shen, Z. A new method for merging IKONOS panchromatic and multispectral image data. In Proceedings of the International Geoscience and Remote Sensing Symposium, Seoul, Korea, 29 July 2005; pp. 3916–3919. [Google Scholar]
- Hilker, T.; Wulder, M.A.; Coops, N.C.; Seitz, N.; White, J.C.; Gao, F.; Masek, J.G.; Stenhouse, G. Generation of dense time series synthetic Landsat data through data blending with MODIS using a spatial and temporal adaptive reflectance fusion model. Remote Sens. Environ. 2009, 113, 1988–1999. [Google Scholar] [CrossRef]
- Celestre, R.; Rosenberger, M.; Notni, G. A novel algorithm for bad pixel detection and correction to improve quality and stability of geometric measurements. J. Phys. Conf. Ser. 2016, 772, 012002. [Google Scholar] [CrossRef] [Green Version]
- Lobell, D.B.; Burke, M.B. On the use of statistical models to predict crop yield responses to climate change. Agric. For. Meteorol. 2010, 150, 1443–1452. [Google Scholar] [CrossRef]
- Challinor, A.J.; Watson, J.; Lobell, D.B.; Howden, S.M.; Smith, D.R.; Chhetri, N. A meta-analysis of crop yield under climate change and adaptation. Nat. Clim. Chang. 2014, 4, 287–291. [Google Scholar] [CrossRef]
- Wang, Y.; Song, Q.; Du, Y.; Wang, J.; Zhou, J.; Du, Z.; Li, T. A random forest model to predict heatstroke occurrence for heatwave in China. Sci. Total Environ. 2019, 650, 3048–3053. [Google Scholar] [CrossRef] [PubMed]
- Han, X.; Wu, J.; Zhou, H.; Liu, L.; Yang, J.; Shen, Q.; Wu, J. Intensification of historical drought over China based on a multi-model drought index. Int. J. Climatol. 2020, 40, 5407–5419. [Google Scholar] [CrossRef]

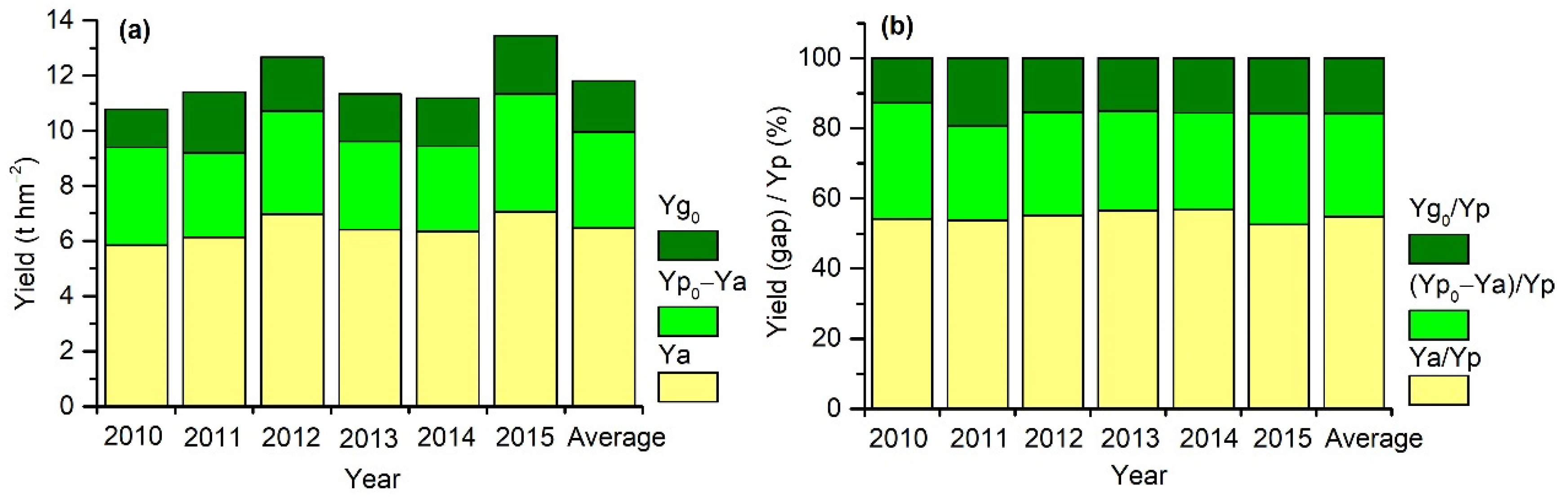

| Year | Ya | Yp | Yg | Yg/Yp | Ya/Yp | Yp0 | Yg0 | CYg0 |
|---|---|---|---|---|---|---|---|---|
| 2010 | 5.8 | 10.8 | 4.9 | 45% | 55% | 9.4 | 1.4 | 29% |
| 2011 | 6.1 | 11.4 | 5.3 | 46% | 54% | 9.2 | 2.2 | 42% |
| 2012 | 7.0 | 12.7 | 5.7 | 45% | 55% | 10.7 | 2.0 | 35% |
| 2013 | 6.4 | 11.3 | 4.9 | 43% | 57% | 9.6 | 1.7 | 35% |
| 2014 | 6.3 | 11.2 | 4.8 | 43% | 57% | 9.4 | 1.8 | 38% |
| 2015 | 7.1 | 13.4 | 6.4 | 48% | 52% | 11.3 | 2.1 | 33% |
| Average | 6.5 | 11.8 | 5.4 | 45% | 55% | 9.9 | 1.9 | 35% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Bai, Y.; Zhang, J. Remote Sensing-Based Quantification of the Summer Maize Yield Gap Induced by Suboptimum Sowing Dates over North China Plain. Remote Sens. 2021, 13, 3582. https://doi.org/10.3390/rs13183582
Zhang S, Bai Y, Zhang J. Remote Sensing-Based Quantification of the Summer Maize Yield Gap Induced by Suboptimum Sowing Dates over North China Plain. Remote Sensing. 2021; 13(18):3582. https://doi.org/10.3390/rs13183582
Chicago/Turabian StyleZhang, Sha, Yun Bai, and Jiahua Zhang. 2021. "Remote Sensing-Based Quantification of the Summer Maize Yield Gap Induced by Suboptimum Sowing Dates over North China Plain" Remote Sensing 13, no. 18: 3582. https://doi.org/10.3390/rs13183582







