Preliminary Evaluation of the Error Budgets in the TALIS Measurements and Their Impact on the Retrievals
Abstract
:1. Introduction
2. Description of TALIS
3. Error Characterization and Simulation Method
3.1. Errors Description
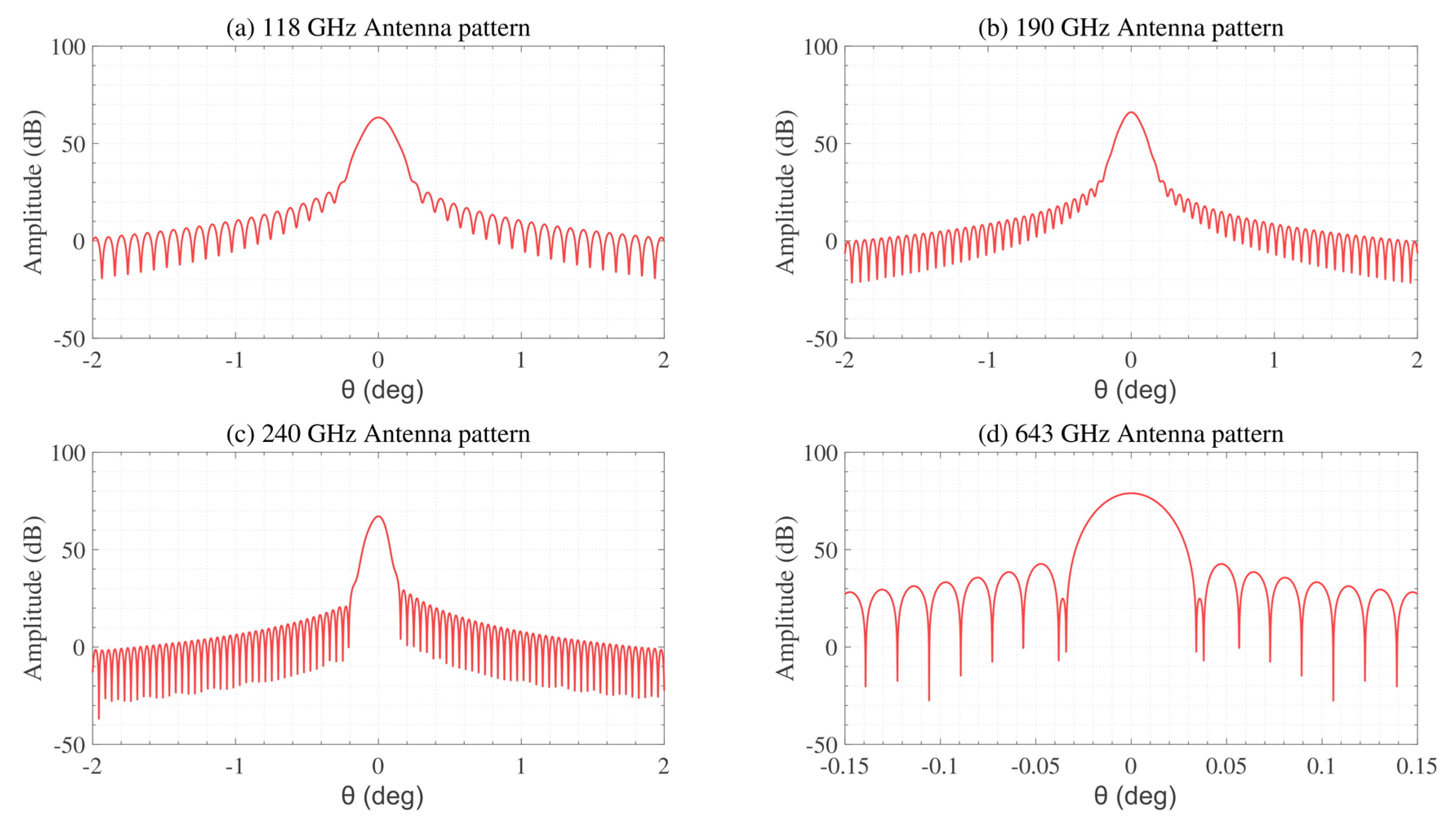
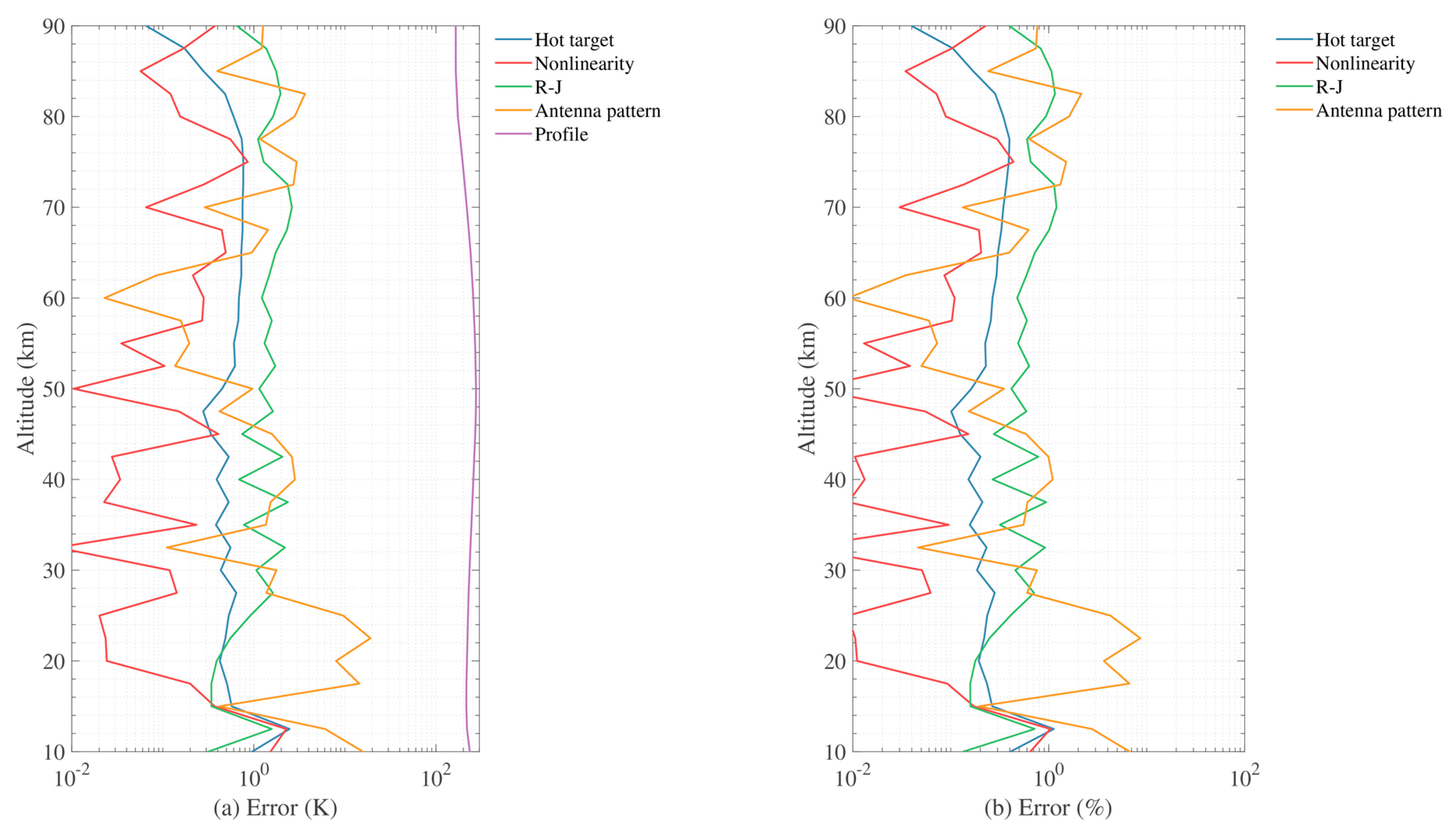
3.1.1. Instrument Uncertainties
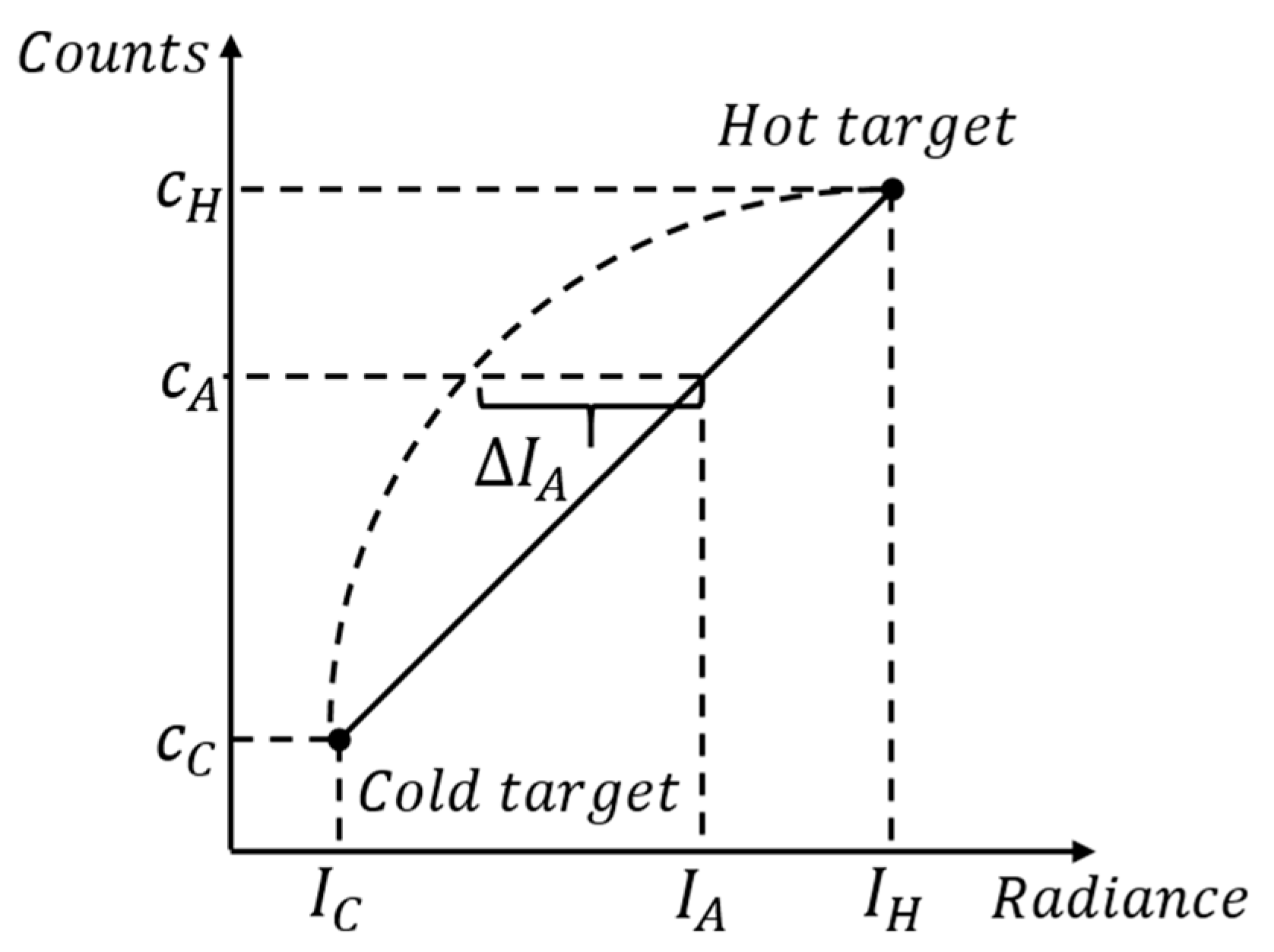
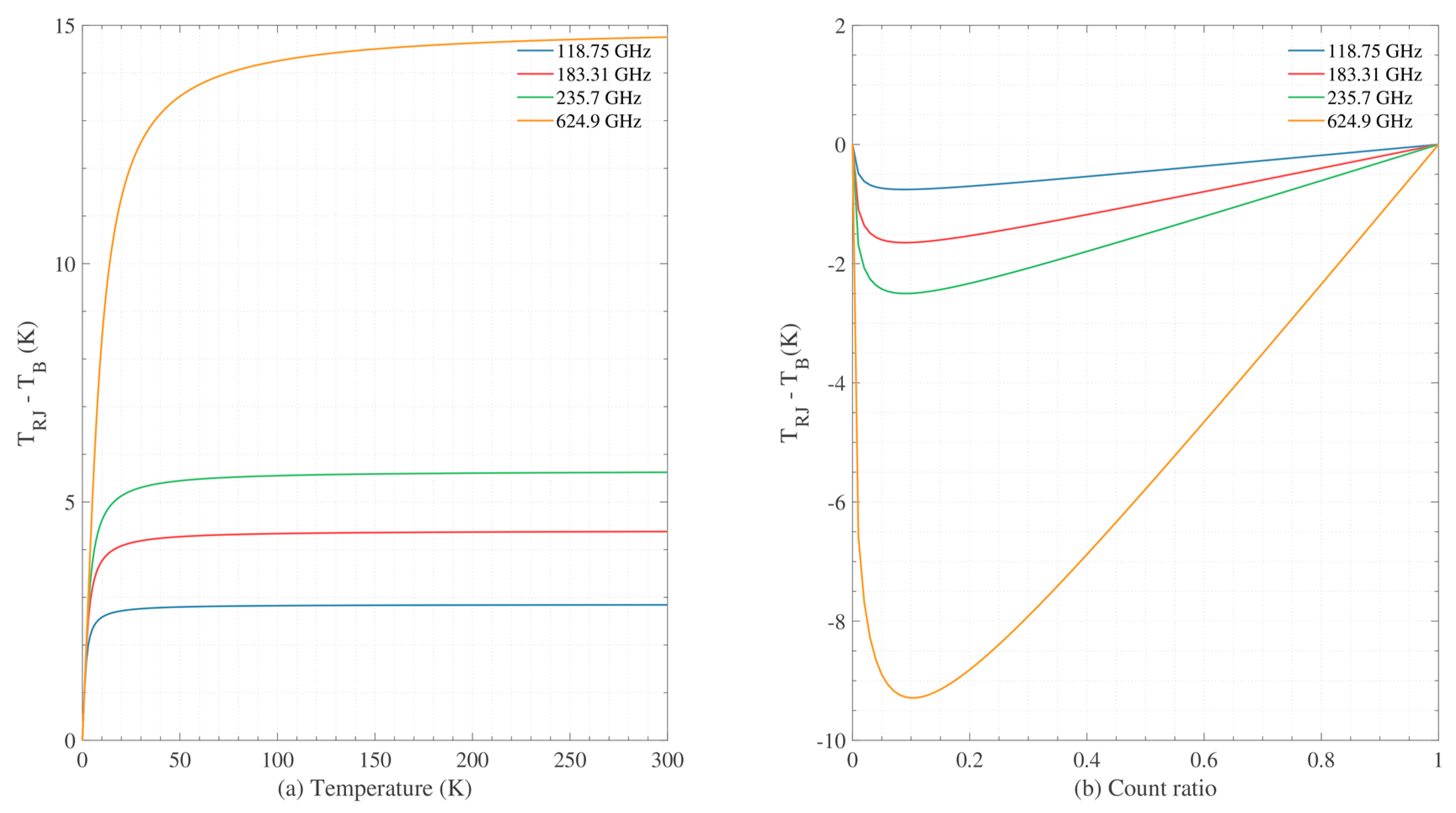
3.1.2. Calibration Errors
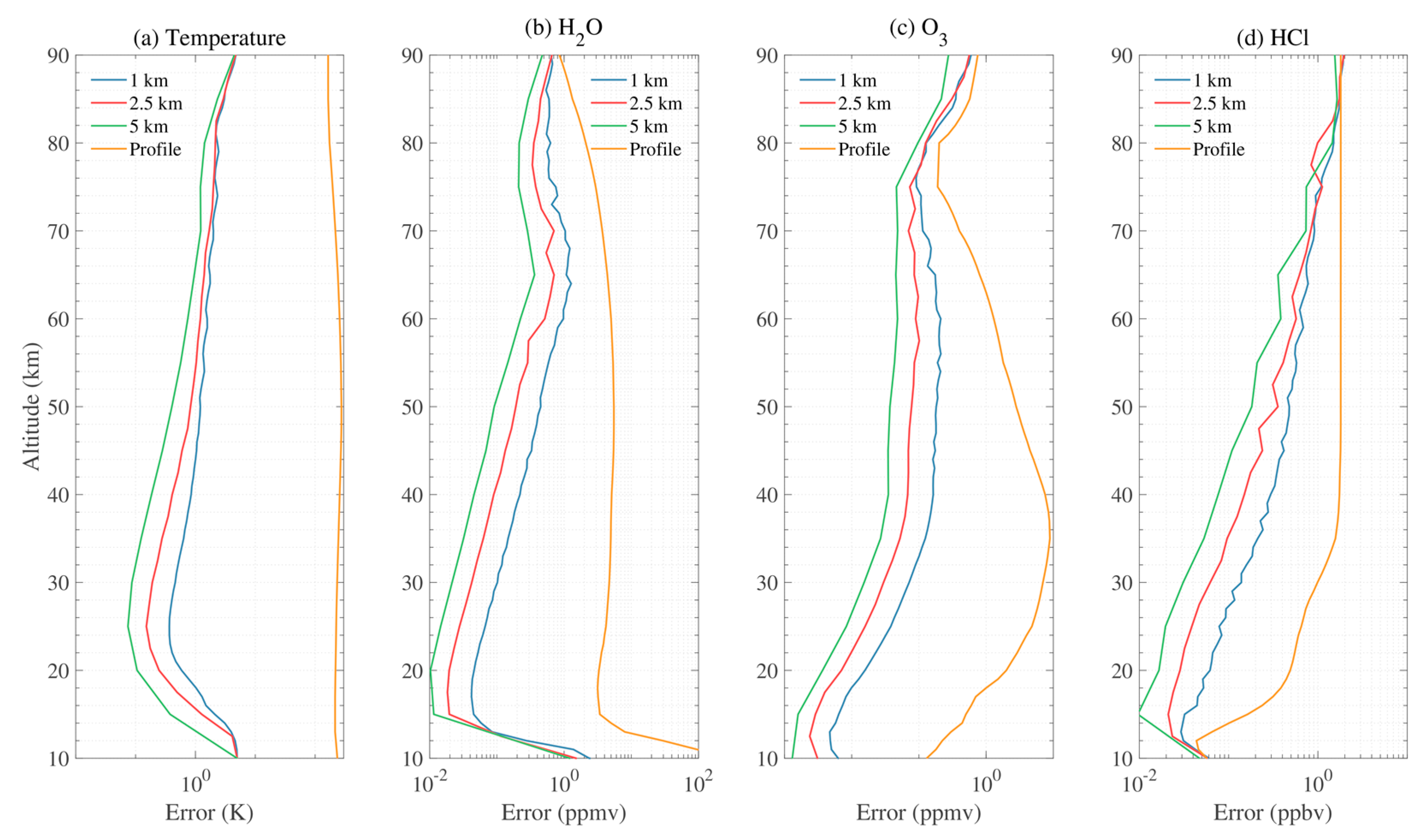
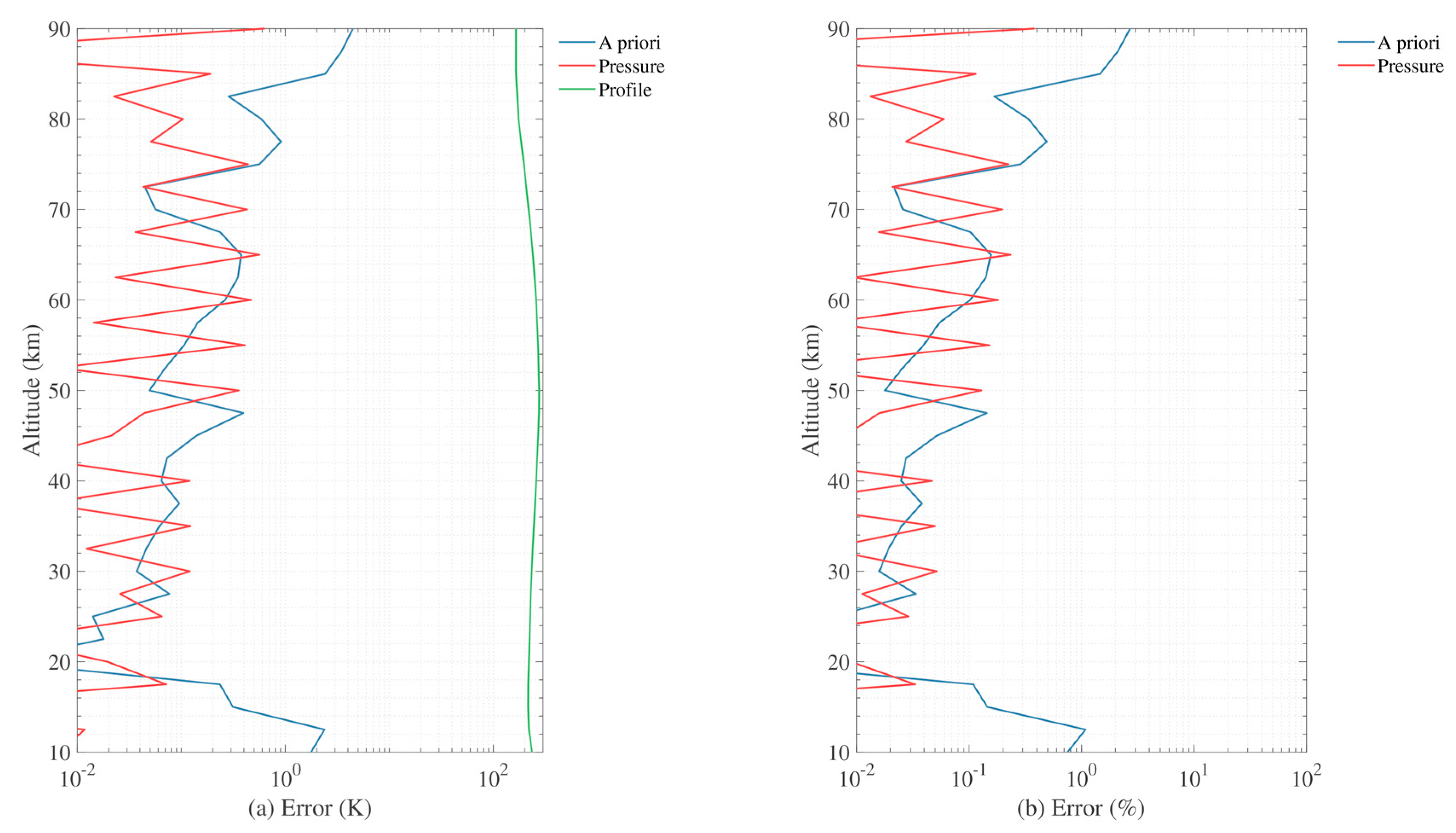
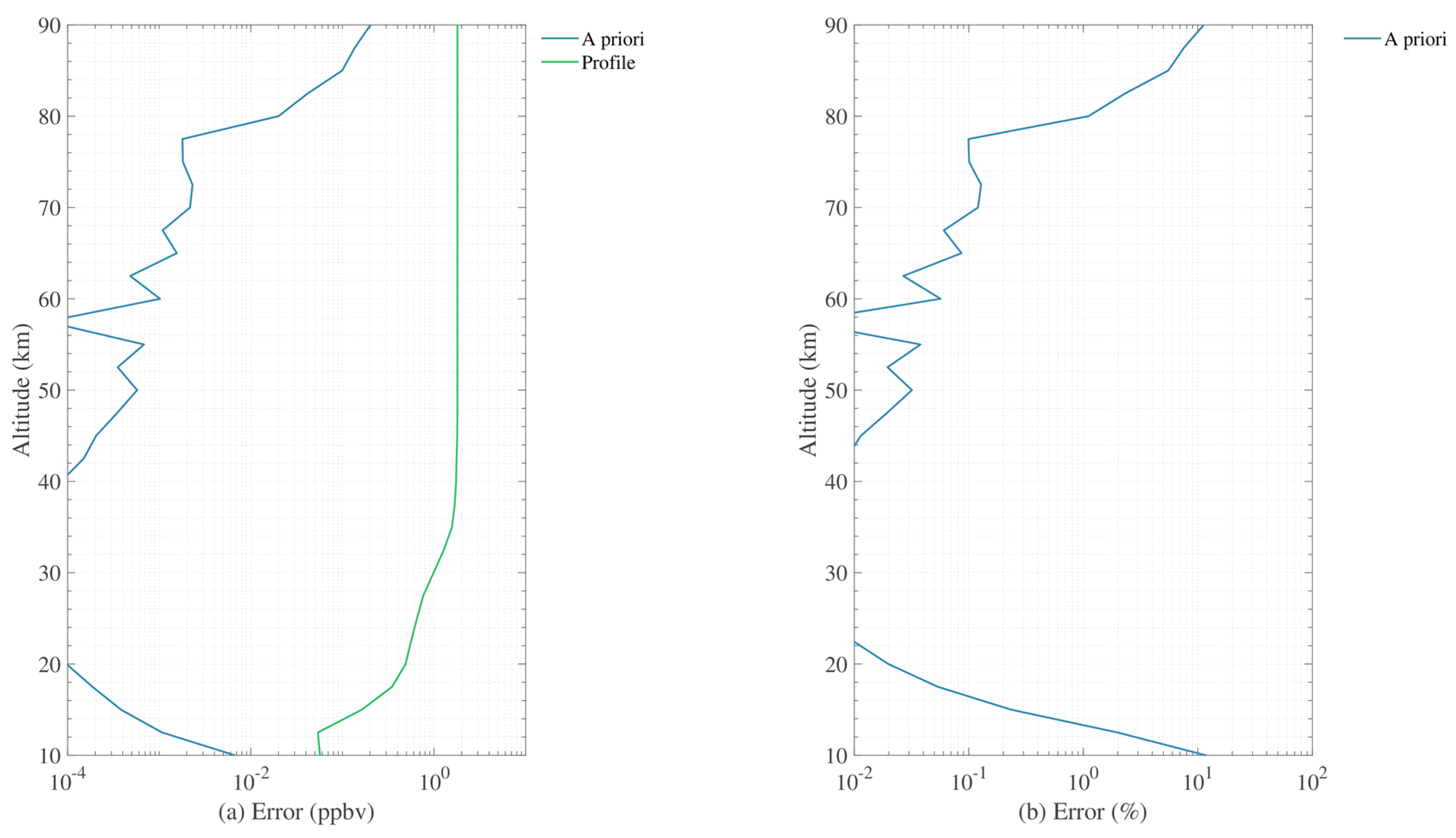
3.1.3. A Priori Errors
3.2. Model and Retrieval Method
4. Results
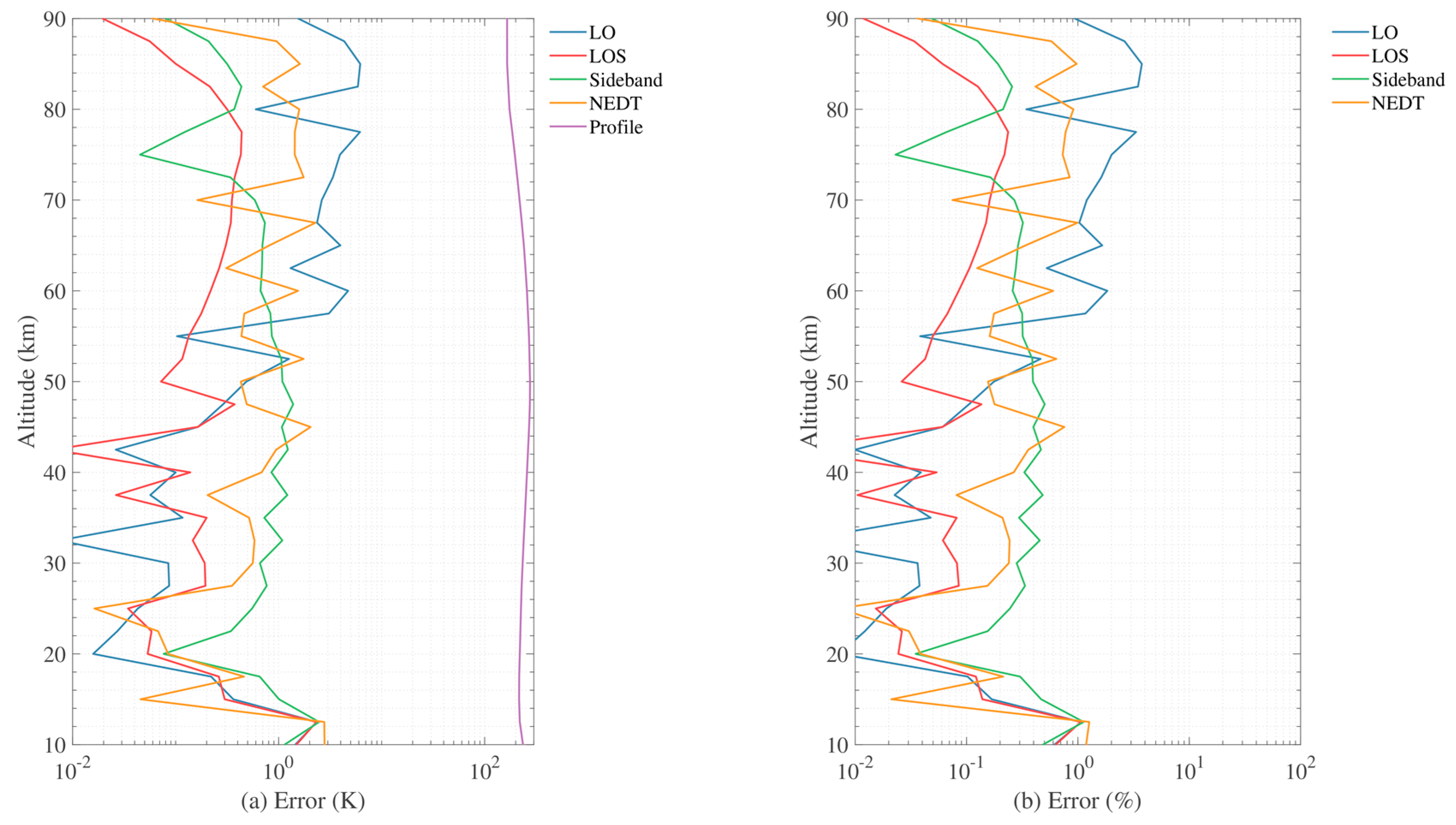
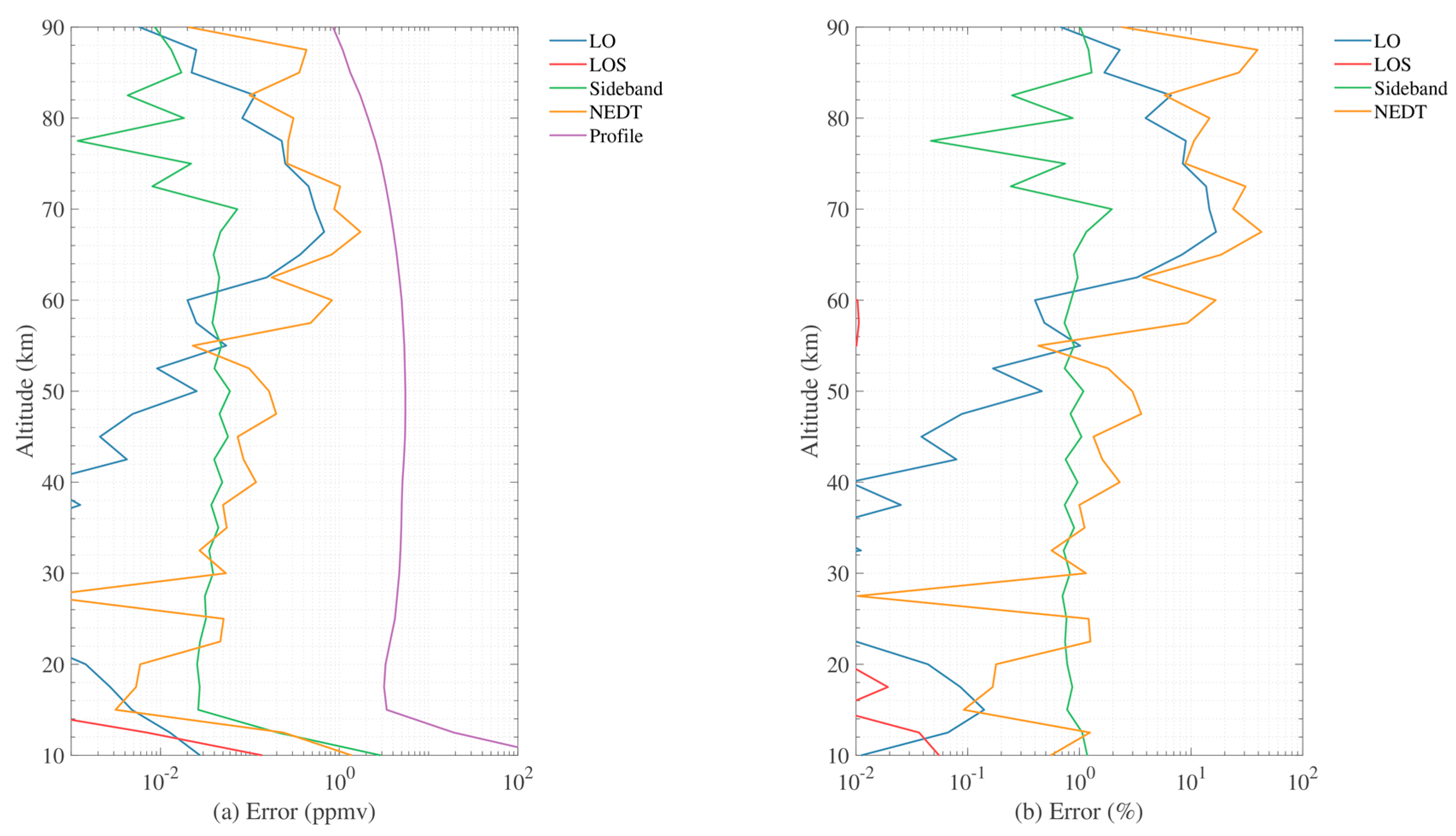
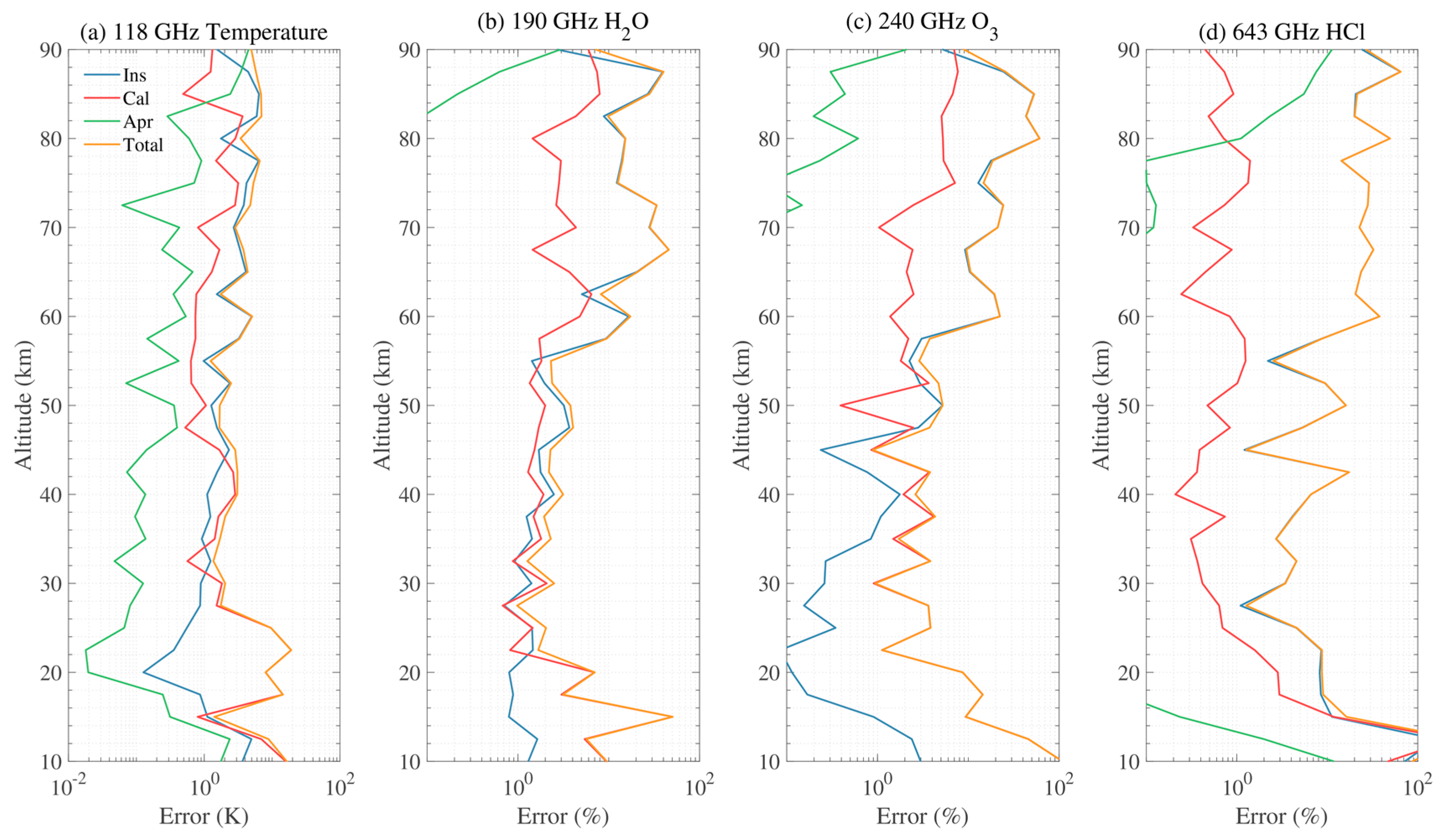
4.1. 118 GHz
4.2. 190 GHz
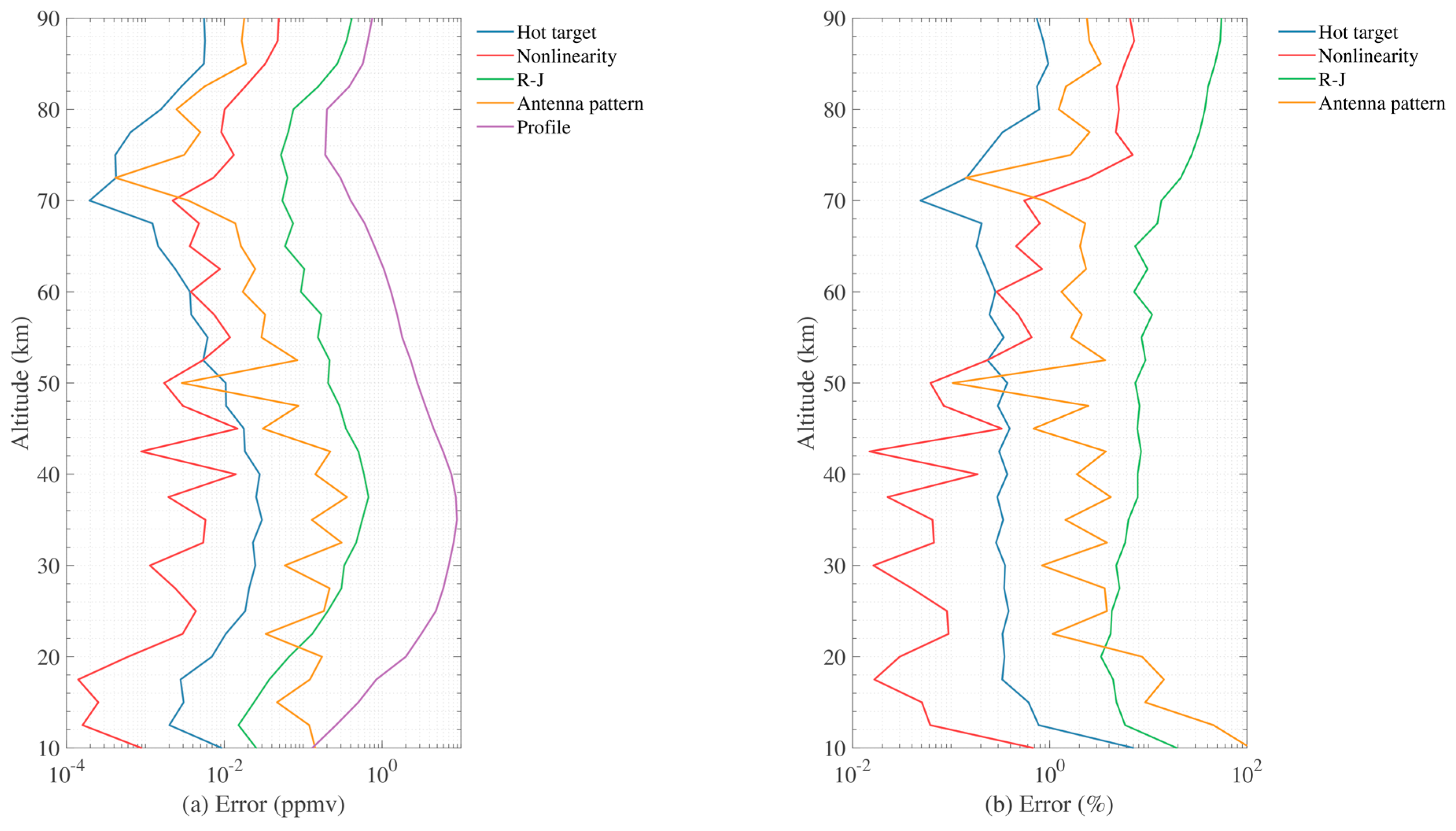
4.3. 240 GHz
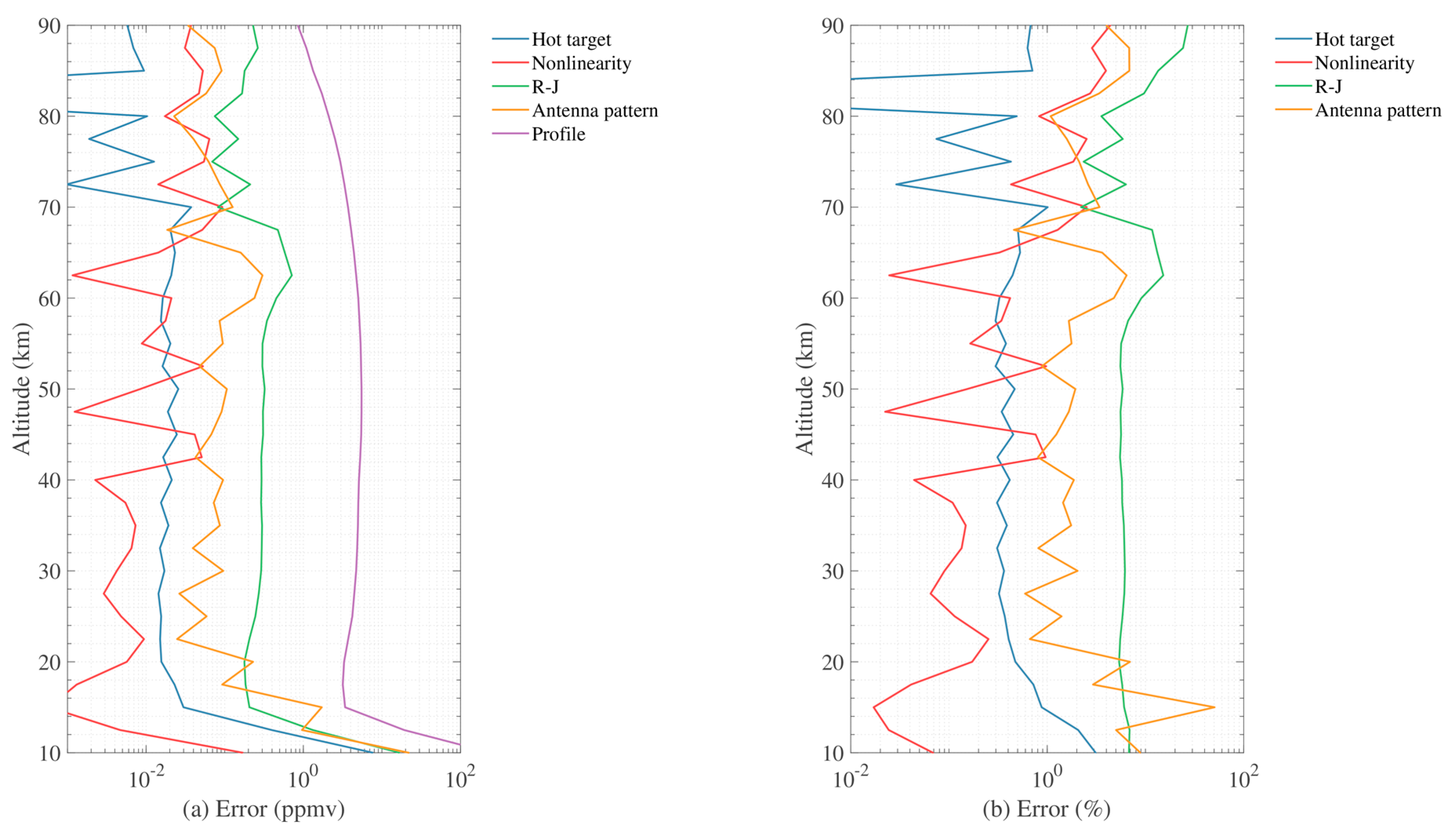
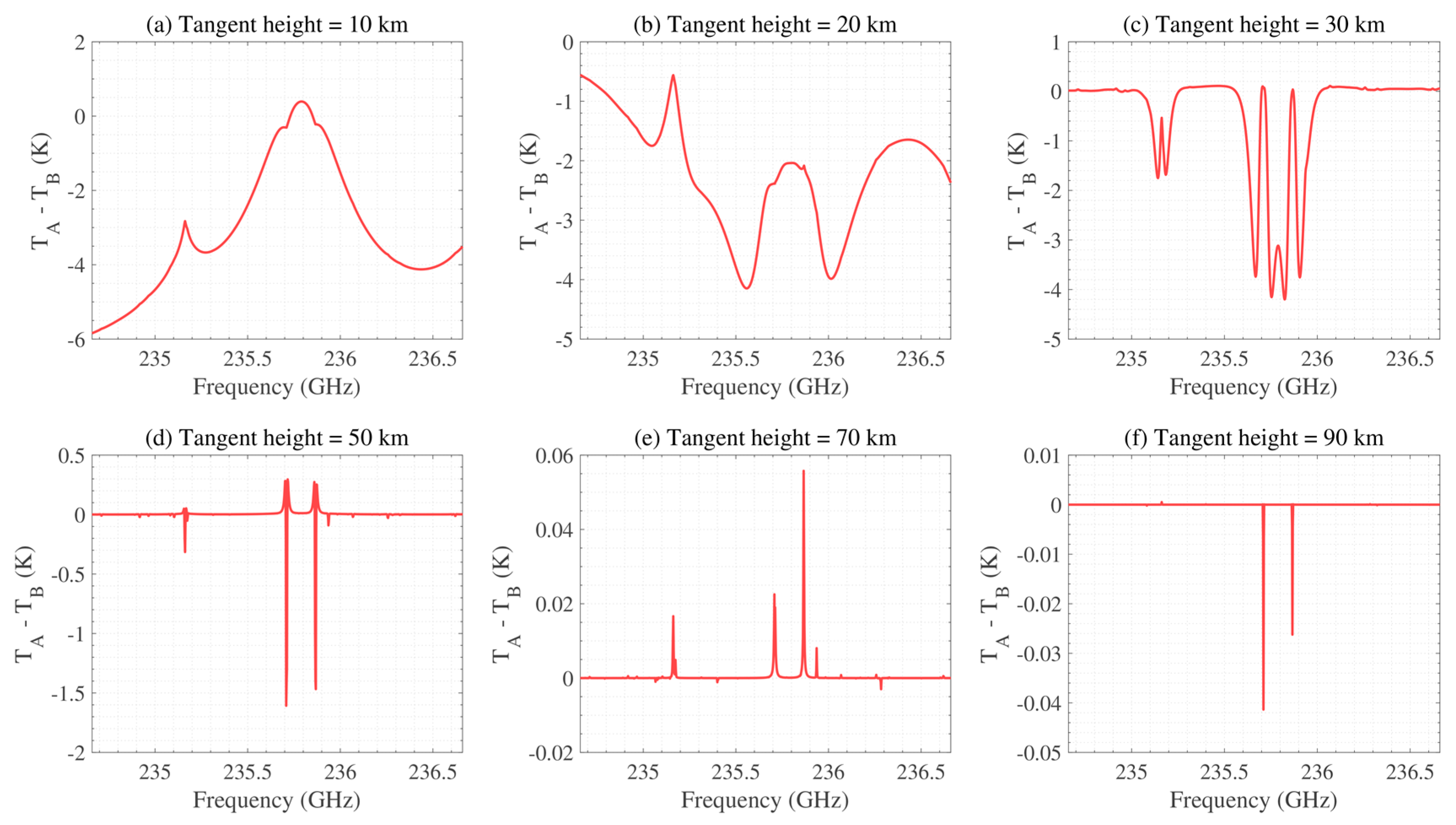
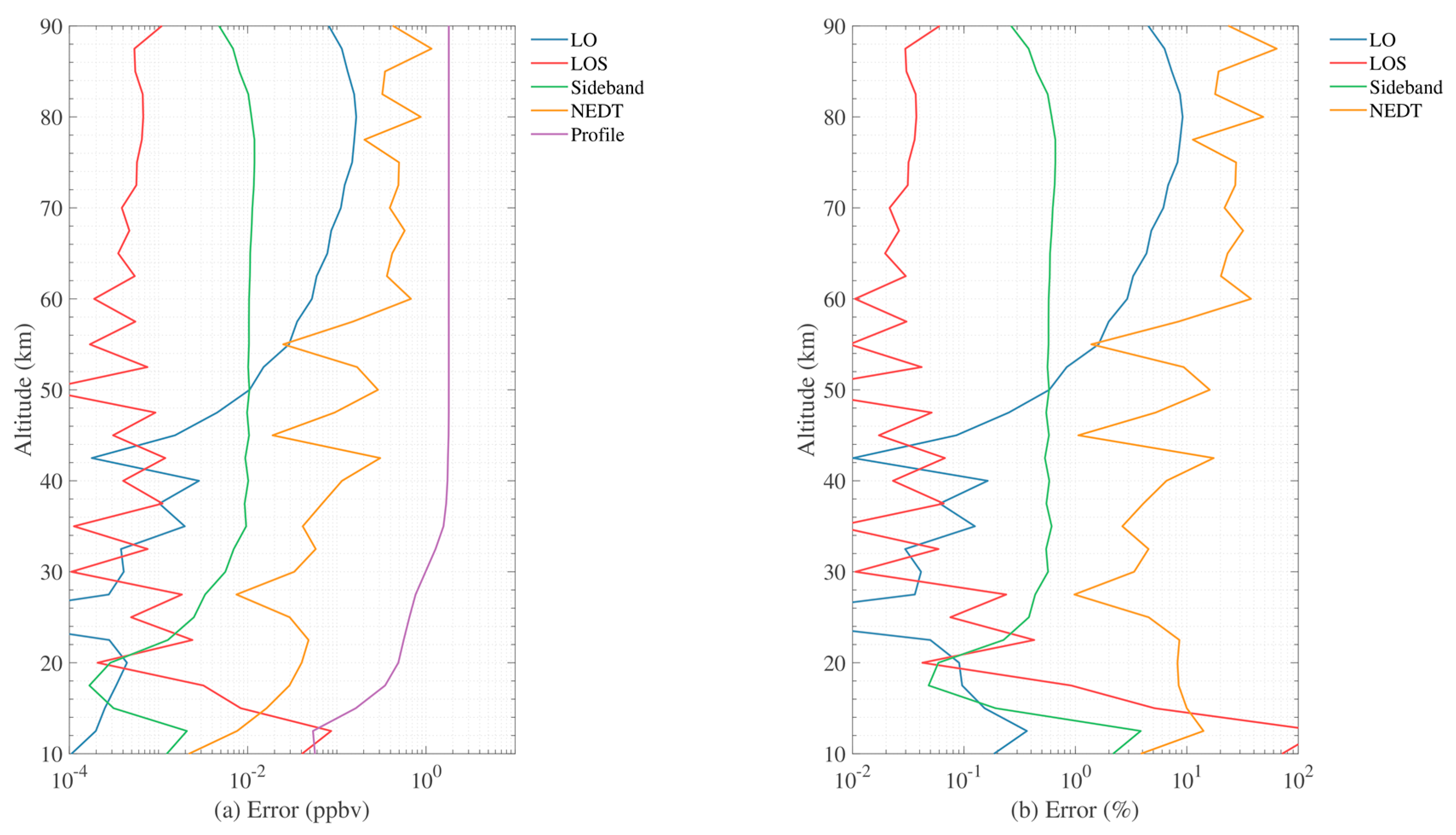
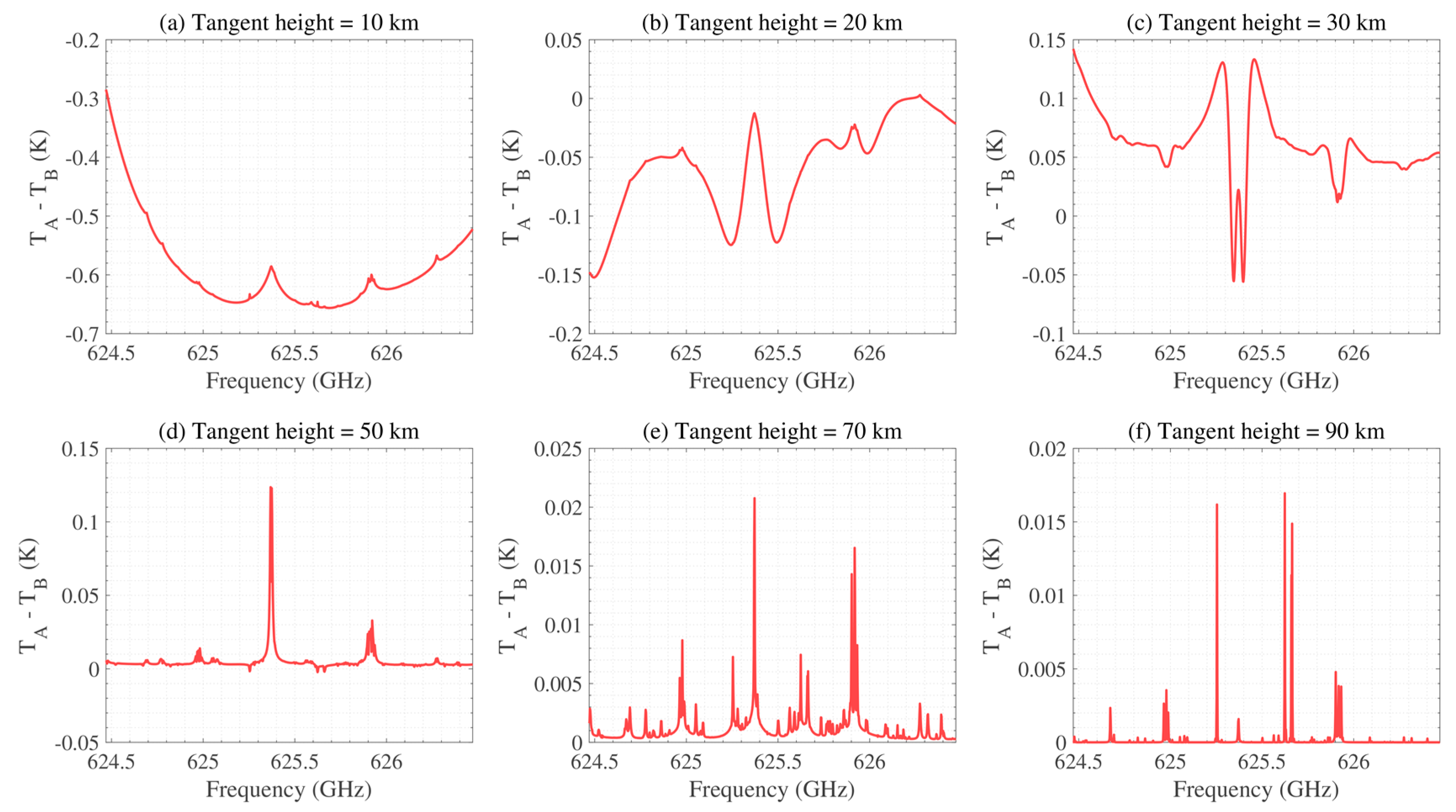
4.4. 643 GHz
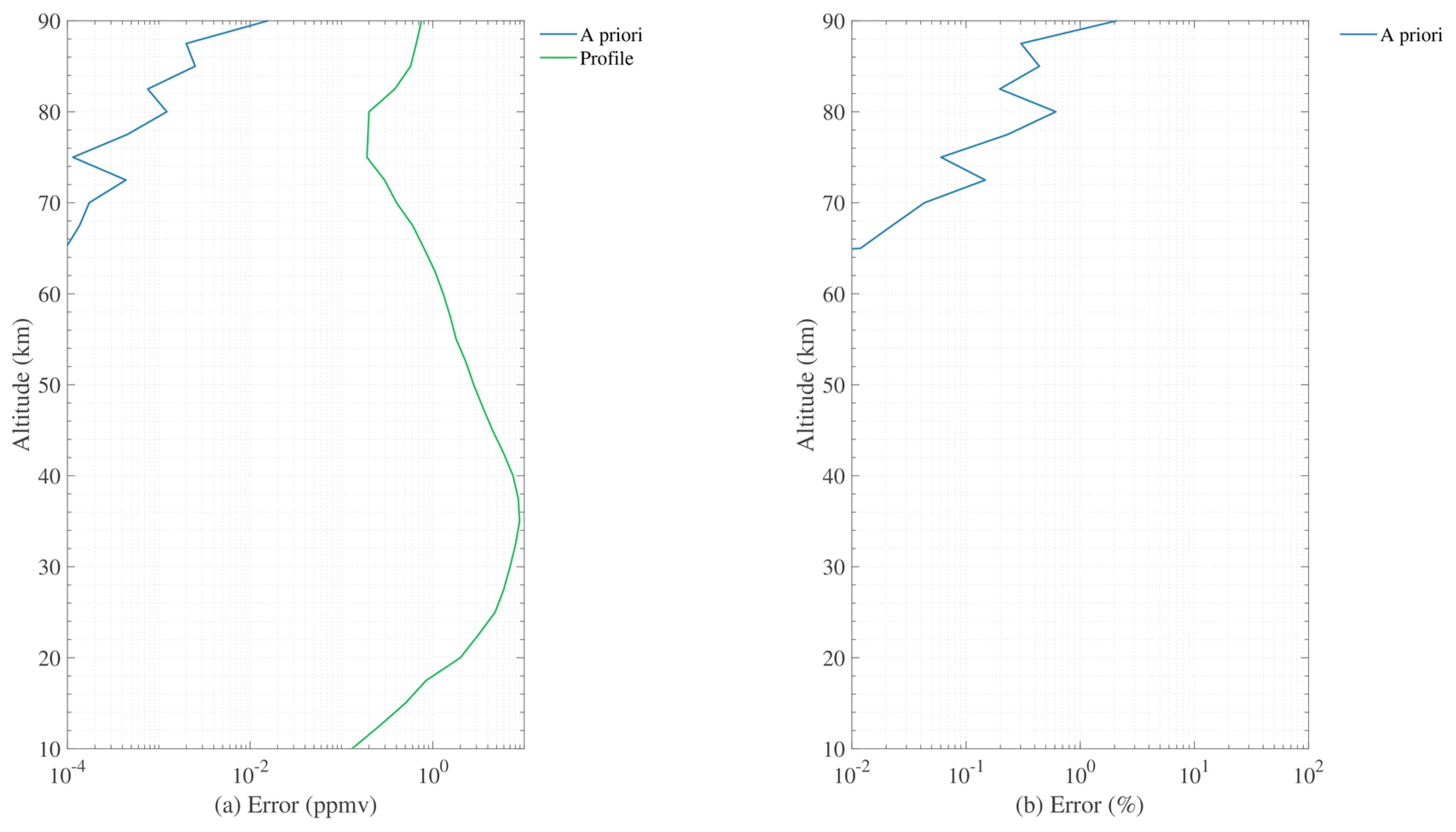
4.5. Overall Error Estimation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Schwartz, M.J.; Lambert, A.; Manney, G.L.; Read, W.G.; Livesey, N.J.; Froidevaux, L.; Ao, C.O.; Bernath, P.F.; Boone, C.D.; Cofield, R.E.; et al. Validation of the Aura Microwave Limb Sounder temperature and geopotential height measurements. J. Geophys. Res. Atmos 2008, 113, D15S11. [Google Scholar] [CrossRef] [Green Version]
- Waters, J.W.; Froidevaux, L.; Read, W.G.; Manney, G.L.; Elson, L.S.; Flower, D.A.; Jarnot, R.F.; Harwood, R.S. Stratospheric ClO and ozone from the Microwave Limb Sounder on the Upper Atmosphere Research Satellite. Nature 1993, 362, 597–602. [Google Scholar] [CrossRef]
- Barath, F.T.; Chavez, M.C.; Cofield, R.E.; Flower, D.A.; Frerking, M.A.; Gram, M.B.; Harris, W.M.; Holden, J.R.; Jarnot, R.F.; Kloezeman, W.G.; et al. The Upper Atmosphere Research Satellite microwave limb sounder instrument. J. Geophys. Res. Atmos. 1993, 98, 10751–10762. [Google Scholar] [CrossRef]
- Waters, J.W.; Read, W.G.; Froidevaux, L.; Jarnot, R.F.; Cofield, R.E.; Flower, D.A.; Lau, G.K.; Pickett, H.M.; Santee, M.L.; Wu, D.L.; et al. The UARS and EOS microwave limb sounder experiments. J. Atmos. Sci. 1999, 56, 194–218. [Google Scholar] [CrossRef] [Green Version]
- Murtagh, D.; Frisk, U.; Merino, F.; Ridal, M.; Jonsson, A.; Stegman, J.; Witt, G.; Eriksson, P.; Jimenez, C.; Mégie, G.; et al. An overview of the Odin atmospheric mission. Can. J. Phys. 2002, 80, 309–319. [Google Scholar] [CrossRef]
- Urban, J.; Lautié, N.; Le Flochmoën, E.; Jiménez, C.; Eriksson, P.; de la Nöe, J.; Dupuy, E.; Ekström, M.; El Amraoui, L.; Frisk, U.; et al. Odin/SMR limb observations of stratospheric trace gases: Level 2 processing of ClO, N2O, HNO3, and O3. J. Geophys. Res. Atmos. 2005, 110, D14307. [Google Scholar] [CrossRef]
- Eriksson, P.; Ekström, M.; Rydberg, B.; Murtagh, D.P. First Odin sub-mm retrievals in the tropical upper troposphere: Ice cloud properties. Atmos. Chem. Phys. 2007, 7, 471–483. [Google Scholar] [CrossRef] [Green Version]
- Frisk, U.; Hagström, M.; Ala-Laurinaho, J.; Andersson, S.; Berges, J.-C.; Chabaud, J.-P.; Dahlgren, M.; Emrich, A.; Florén, H.-G.; Florin, G.; et al. The Odin satellite - I. Radiometer design and test. Astron. Astrophys. 2003, 402, L27–L34. [Google Scholar] [CrossRef] [Green Version]
- Schoeberl, M.R.; Douglass, A.R.; Hilsenrath, E.; Bhartia, P.K.; Beer, R.; Waters, J.W.; Gunson, M.R.; Froidevaux, L.; Gille, J.C.; Barnett, J.J.; et al. Overview of the EOS Aura Mission. IEEE Trans. Geosci. Remote Sens. 2006, 4, 1066–1074. [Google Scholar] [CrossRef] [Green Version]
- Waters, J.W.; Froidevaux, L.; Jarnot, R.F.; Read, W.G.; Pickett, H.M.; Harwood, R.S.; Cofield, R.E.; Filipiak, M.J.; Flower, D.A.; Livesey, N.J.; et al. An Overview of the EOS MLS Experiment, Version 2.0; JPL D-15745/CL# 04-2323; Jet Propulsion Laboratory, California Institute of Technology: Pasadena, CA, USA, 2004. [Google Scholar]
- Waters, J.W.; Froidevaux, L.; Harwood, R.S.; Jarnot, R.F.; Pickett, H.M.; Read, W.G.; Siegel, P.H.; Cofield, R.E.; Filipiak, M.J.; Flower, D.A.; et al. The Earth Observing System Microwave Limb Sounder (EOS MLS) on the Aura Satellite. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1075–1092. [Google Scholar] [CrossRef]
- Wu, D.L.; Schwartz, M.J.; Waters, J.W.; Limpasuvan, V.; Wu, Q.; Killeen, T.L. Mesospheric doppler wind measurements from Aura Microwave Limb Sounder (MLS). Adv. Space Res. 2008, 42, 1246–1252. [Google Scholar] [CrossRef]
- Livesey, N.J.; Logan, J.A.; Santee, M.L.; Waters, J.W.; Doherty, R.M.; Read, W.G.; Froidevaux, L.; Jiang, J.H. Interrelated variations of O3, CO and deep convection in the tropical/subtropical upper troposphere observed by the Aura Microwave Limb Sounder (MLS) during 2004–2011. Atmos. Chem. Phys. 2013, 13, 579–598. [Google Scholar] [CrossRef] [Green Version]
- Wu, D.L.; Jiang, J.H.; Davis, C.P. EOS MLS cloud ice measurements and cloudy-sky radiative transfer model. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1156–1165. [Google Scholar] [CrossRef]
- Kikuchi, K.; Nishibori, T.; Ochiai, S.; Ozeki, H.; Irimajiri, Y.; Kasai, Y.; Koike, M.; Manabe, T.; Mizukoshi, K.; Murayama, Y.; et al. Overview and early results of the Superconducting Submillimeter-Wave Limb-Emission Sounder (SMILES). J. Geophys. Res. Atmos. 2010, 115, D23306. [Google Scholar] [CrossRef]
- Takahashi, C.; Ochiai, S.; Suzuki, M. Operational retrieval algorithms for JEM/SMILES level 2 data processing system. J. Quant. Spectrosc. Ra. 2010, 111, 160–173. [Google Scholar] [CrossRef]
- Baron, P.; Urban, J.; Sagawa, H.; Möller, J.; Murtagh, D.P.; Mendrok, J.; Dupuy, E.; Sato, T.O.; Ochiai, S.; Suzuki, K.; et al. The Level 2 research product algorithms for the Superconducting Submillimeter-Wave Limb-Emission Sounder (SMILES). Atmos. Meas. Tech. 2011, 4, 2105–2124. [Google Scholar] [CrossRef] [Green Version]
- Takahashi, C.; Suzuki, M.; Mitsuda, C.; Ochiai, S.; Manago, N.; Hayashi, H.; Iwata, Y.; Imai, K.; Sano, T.; Takayanagi, M.; et al. Capability for ozone high-precision retrieval on JEM/SMILES observation. Adv. Space Res. 2011, 48, 1076–1085. [Google Scholar] [CrossRef]
- Baron, P.; Murtagh, D.P.; Urban, J.; Sagawa, H.; Ochiai, S.; Kasai, Y.; Kikuchi, K.; Khosrawi, F.; Körnich, H.; Mizobuchi, S.; et al. Observation of horizontal winds in the middle-atmosphere between 30°S and 55°N during the northern winter 2009–2010. Atmos. Chem. Phys. 2013, 13, 6049–6064. [Google Scholar] [CrossRef] [Green Version]
- Jiang, J.H.; Su, H.; Zhai, C.X.; Shen, T.J.; Wu, T.W.; Zhang, J.; Cole, J.N.S.; Salzen, K.V.; Donner, L.J.; Seman, C.; et al. Evaluating the Diurnal Cycle of Upper-Tropospheric Ice Clouds in Climate Models Using SMILES Observations. J. Atmos. Sci. 2015, 72, 1022–1044. [Google Scholar] [CrossRef] [Green Version]
- Baron, P.; Murtagh, D.; Eriksson, P.; Mendrok, J.; Ochiai, S.; Pérot, K.; Sagawa, H.; Suzuki, M. Simulation study for the Stratospheric Inferred Winds (SIW) sub-millimeter limb sounder. Atmos. Meas. Tech. 2018, 11, 4545–4566. [Google Scholar] [CrossRef] [Green Version]
- Ochiai, S.; Baron, P.; Nishibori, T.; Irimajiri, Y.; Uzawa, Y.; Manabe, T.; Maezawa, H.; Mizuno, A.; Nagahama, T.; Sagawa, H.; et al. SMILES-2 Mission for Temperature, Wind, and Composition in the Whole Atmosphere. SOLA 2017, 13A, 13–18. [Google Scholar] [CrossRef] [Green Version]
- Baron, P.; Ochiai, S.; Dupuy, E.; Larsson, R.; Liu, H.X.; Manago, N.; Murtagh, D.; Oyama, S.; Sagawa, H.; Saito, A.; et al. Potential for the measurement of MLT wind, temperature, density and geomagnetic field with Superconducting Submillimeter-Wave Limb-Emission Sounder-2 (SMILES-2). Atmos. Meas. Tech. Discuss. 2019. in review. [Google Scholar]
- Wang, W.Y.; Wang, Z.Z. Performance Evaluation of THz Atmospheric Limb Sounder (TALIS) of China. Atmos. Meas. Technol. 2020, 13, 13–38. [Google Scholar] [CrossRef] [Green Version]
- Verdes, C.; Bühler, S.; von Engeln, A.; Kuhn, T.; Künzi, K.; Eriksson, P.; Sinnhuber, B.M. Pointing and temperature retrieval from millimeter-submillimeter limb soundings. J. Geophys. Res. Atmos. 2002, 107, ACH 10-1–ACH 10-24. [Google Scholar] [CrossRef]
- Eriksson, P.; Ekström, M.; Melsheimer, C.; Buehler, S.A. Efficient forward modelling by matrix representation of sensor responses. Int. J. Remote Sens. 2006, 27, 1793–1808. [Google Scholar] [CrossRef]
- Jarnot, R.F.; Perun, V.S.; Schwartz, M.J. Radiometric and Spectral Performance and Calibration of the GHz Bands of EOS MLS. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1131–1143. [Google Scholar] [CrossRef]
- Ochiai, S.; Kikuchi, K.; Nishibori, T.; Manabe, T. Gain Nonlinearity Calibration of Submillimeter Radiometer for JEM/SMILES. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2012, 5, 962–969. [Google Scholar] [CrossRef]
- Wang, Z.Z.; Li, J.Y.; He, J.Y.; Zhang, S.W.; Gu, S.Y.; Li, Y.; Guo, Y.; He, B.Y. Performance Analysis of Microwave Humidity and Temperature Sounder Onboard the FY-3D Satellite from Prelaunch Multiangle Calibration Data in Thermal/Vacuum Test. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1664–1683. [Google Scholar] [CrossRef]
- Weng, F.Z.; Zou, X.L. Errors from Rayleigh–Jeans approximation in satellite microwave radiometer calibration systems. Appl. Optics 2013, 52, 505–508. [Google Scholar] [CrossRef]
- Jarnot, R.F.; Cofield, R.E.; Waters, W.G.; Flower, D.A. Calibration of the Microwave Limb Sounder on the Upper Atmosphere Research Satellite. J. Geophys. Res. Atmos. 1996, 101, 9957–9982. [Google Scholar] [CrossRef]
- Cofield, R.E.; Stek, P.C. Design and Field-of-View Calibration of 114–660-GHz Optics of the Earth Observing System Microwave Limb Sounder. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1166–1181. [Google Scholar] [CrossRef]
- Rydberg, B.; Eriksson, P.; Kiviranta, J.; Ringsby, J.; Skyman, A.; Murtagh, D. Odin/SMR Algorithm Theoretical Basis Document: Level 1 Processing. Tech.; Department of Space, Earth and Environment, Chalmers University of Technology: Goteborg, Sweden, 2017. [Google Scholar]
- Rodgers, C.D. Inverse Methods for Atmospheric Sounding: Theory and Practice. World Scientific: Singapore, 2000; pp. 81–99. Available online: https://books.google.com.hk/books?hl=en&lr=&id=FjxqDQAAQBAJ&oi=fnd&pg=PR7&dq=Inverse+Methods+for+Atmospheric+Sounding:+Theory+and+Practice&ots=ARbv5T9AWl&sig=dHFruTHfErcOkyZChZL7PbGHfgU&redir_esc=y&hl=zh-CN&sourceid=cndr#v=onepage&q=Inverse%20Methods%20for%20Atmospheric%20Sounding%3A%20Theory%20and%20Practice&f=false (accessed on 10 December 2019).
- Livesey, N.J.; Snyder, W.V.; Read, W.G.; Wagner, P.A. Retrieval Algorithms for the EOS Microwave Limb Sounder (MLS). IEEE Trans. Geosci. Remote Sens. 2006, 44, 1144–1155. [Google Scholar] [CrossRef]
- Erikson, P.; Chen, D. Statistical parameters derived from ozonesonde data of importance for passive remote sensing observations of ozone. Int. J. Remote. Sens. 2002, 23, 4945–4963. [Google Scholar] [CrossRef]
- Rodgers, C.D. Characterization and error analysis of profilesretrieved from remote sounding measurements. J. Geophys. Res. 1990, 95, 5587–5595. [Google Scholar] [CrossRef]
- Eriksson, P.; Buehler, S.A.; Davis, C.P.; Emde, C.; Lemke, O. ARTS, the atmospheric radiative transfer simulator, Version 2. J. Quant. Spectrosc. Ra. 2011, 112, 1551–1558. [Google Scholar] [CrossRef] [Green Version]
- Eriksson, P.; Jiménez, C.; Buehler, S.A. Qpack, a general tool for instrument simulation and retrieval work. J. Quant. Spectrosc. Ra. 2005, 91, 47–64. [Google Scholar] [CrossRef] [Green Version]





| Characteristics | Value |
|---|---|
| Satellite altitude | 600 km |
| Scan altitude | 0–100 km |
| Spectrum integration time | 0.1 s (1 km) |
| Antenna vertical FOV | 5.5 km, 3.8 km, 3.3 km, 0.96 km |
| Spectrometer bandwidth | 2 GHz |
| Spectrometer resolution | 2 MHz |
| Local oscillator frequency | 117.55, 190.1, 239.66, 642.87 GHz |
| Radiometer (GHz) | Spectral Bands (GHz) | System Temperature (K) |
|---|---|---|
| 118 | 115.35–117.35, 117.75–119.75 | 1000 K, DSB |
| 190 | 175.5–177.5, 202.7–204.7; 178.9–180.9, 199.3–201.3; 183.0–185.0, 195.2–197.2 | 1000 K, DSB |
| 240 | 229.66–231.66, 247.66–249.66; 232.16–234.16, 245.16–247.16; 234.66–236.66, 242.66–244.66 | 1000 K, DSB |
| 643 | 624.47–626.47, 659.27–661.27; 627.37–629.37, 656.37–658.37; 632.37–634.37, 651.37–653.37; 634.87–636.87, 648.87–650.87 | 2300 K, DSB |
| Source | Value |
|---|---|
| Sideband weight | 0.2% |
| Local oscillator | 0.5 MHz |
| Pointing offset (LOS) | 0.021° |
| Measurement noise (NEDT) | 2.2 K, 2.2 K, 2.2 K, 5.1 K |
| Source | Value |
|---|---|
| Hot target offset | −0.5 K |
| Nonlinearity | 0.3 K |
| R–J approximation | / |
| Antenna pattern used | 3 dB FWHM |
| Source | Value |
|---|---|
| Temperature a priori | 5 K |
| Pressure a priori | 5% |
| Species a priori | 20% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Wang, Z.; Duan, Y. Preliminary Evaluation of the Error Budgets in the TALIS Measurements and Their Impact on the Retrievals. Remote Sens. 2020, 12, 468. https://doi.org/10.3390/rs12030468
Wang W, Wang Z, Duan Y. Preliminary Evaluation of the Error Budgets in the TALIS Measurements and Their Impact on the Retrievals. Remote Sensing. 2020; 12(3):468. https://doi.org/10.3390/rs12030468
Chicago/Turabian StyleWang, Wenyu, Zhenzhan Wang, and Yongqiang Duan. 2020. "Preliminary Evaluation of the Error Budgets in the TALIS Measurements and Their Impact on the Retrievals" Remote Sensing 12, no. 3: 468. https://doi.org/10.3390/rs12030468





