Adaptive Distance-Weighted Voronoi Tessellation for Remote Sensing Image Segmentation
Abstract
:1. Introduction
- (1)
- We design a monotone decreasing function as the adaptive weight coefficient to control the influence intensity of spatial information. The farther the spatial distance is, the more important the spectral information is. Therefore, both the spectral homogeneity and spatial connectivity of sub-regions can be ensured greatly.
- (2)
- Integrating the adaptive distance-weighted Voronoi tessellation into the fuzzy clustering framework can describe the segmentation uncertainty more effectively and better balance the noise immunity and effective characteristic retention.
2. Methods
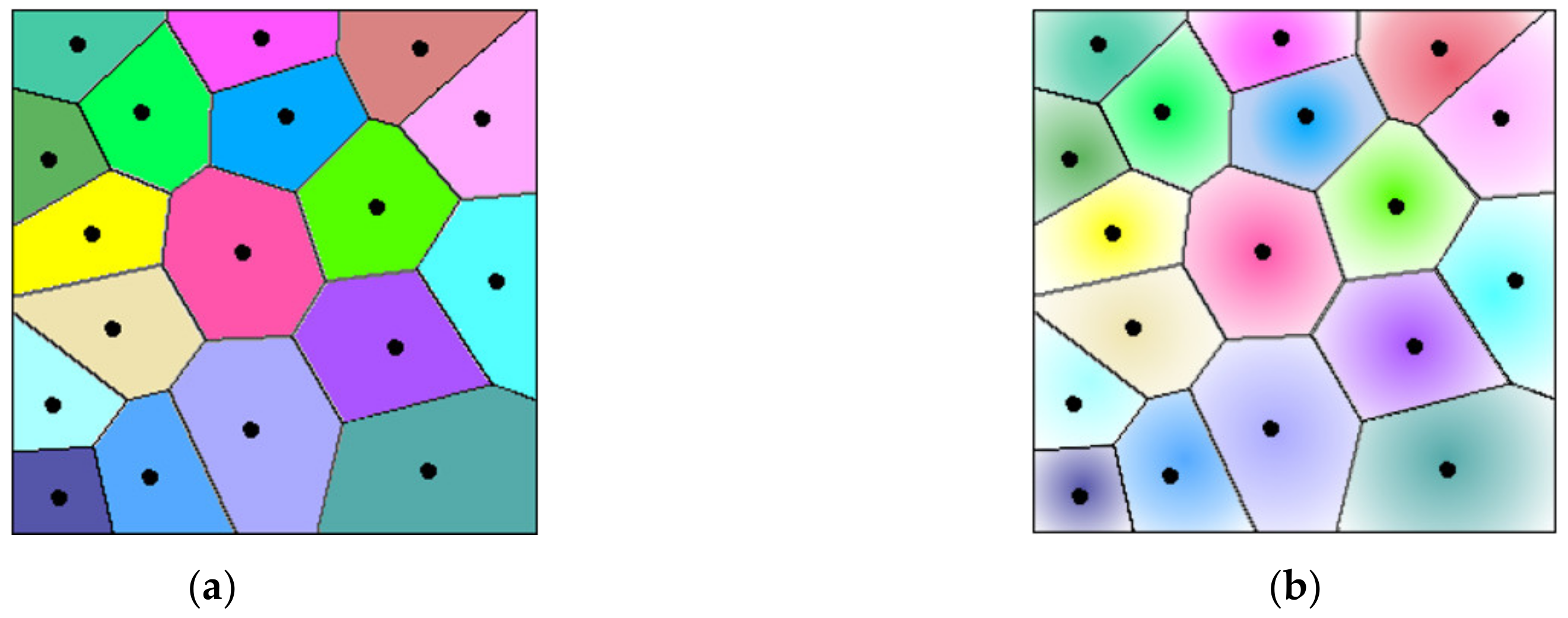
2.1. Adaptive Distance-Weighted Voronoi Tessellation
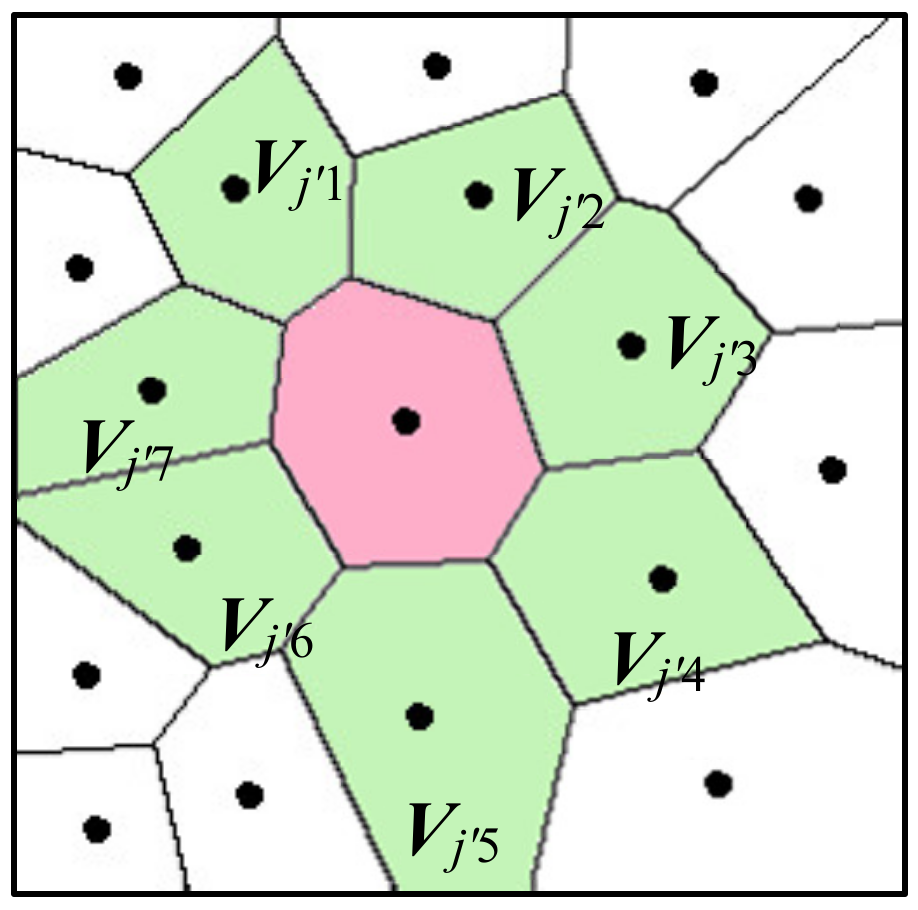
2.2. Segmentation Model
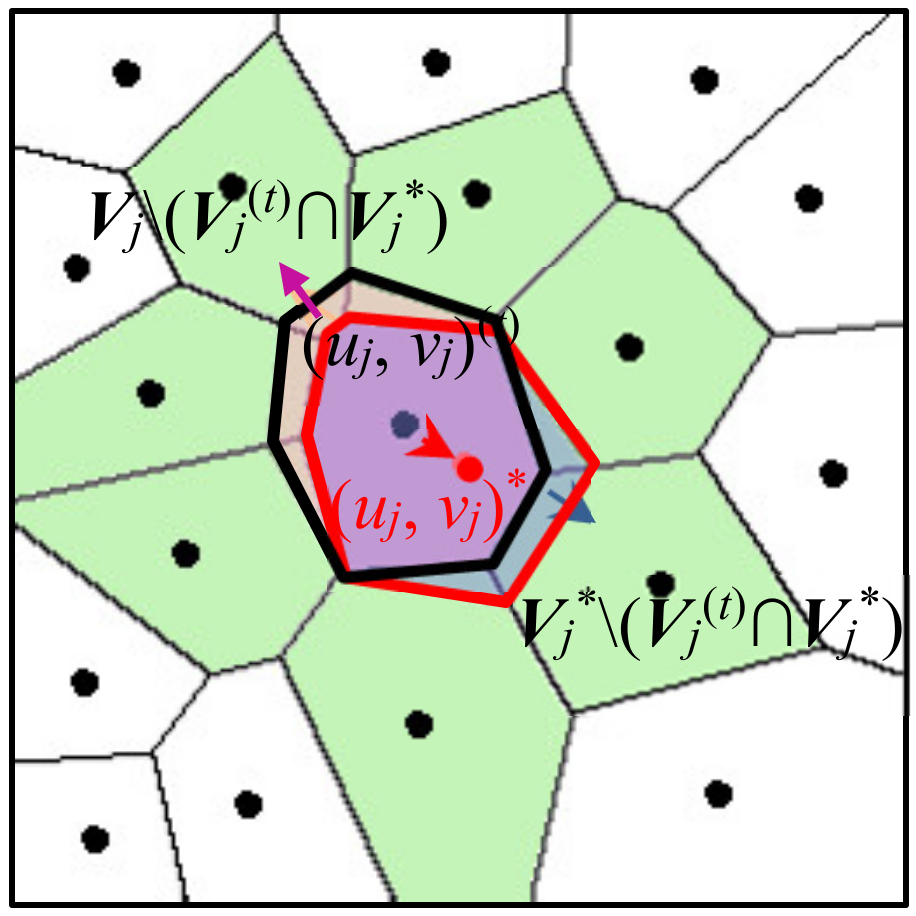
2.3. Parameter Estimation
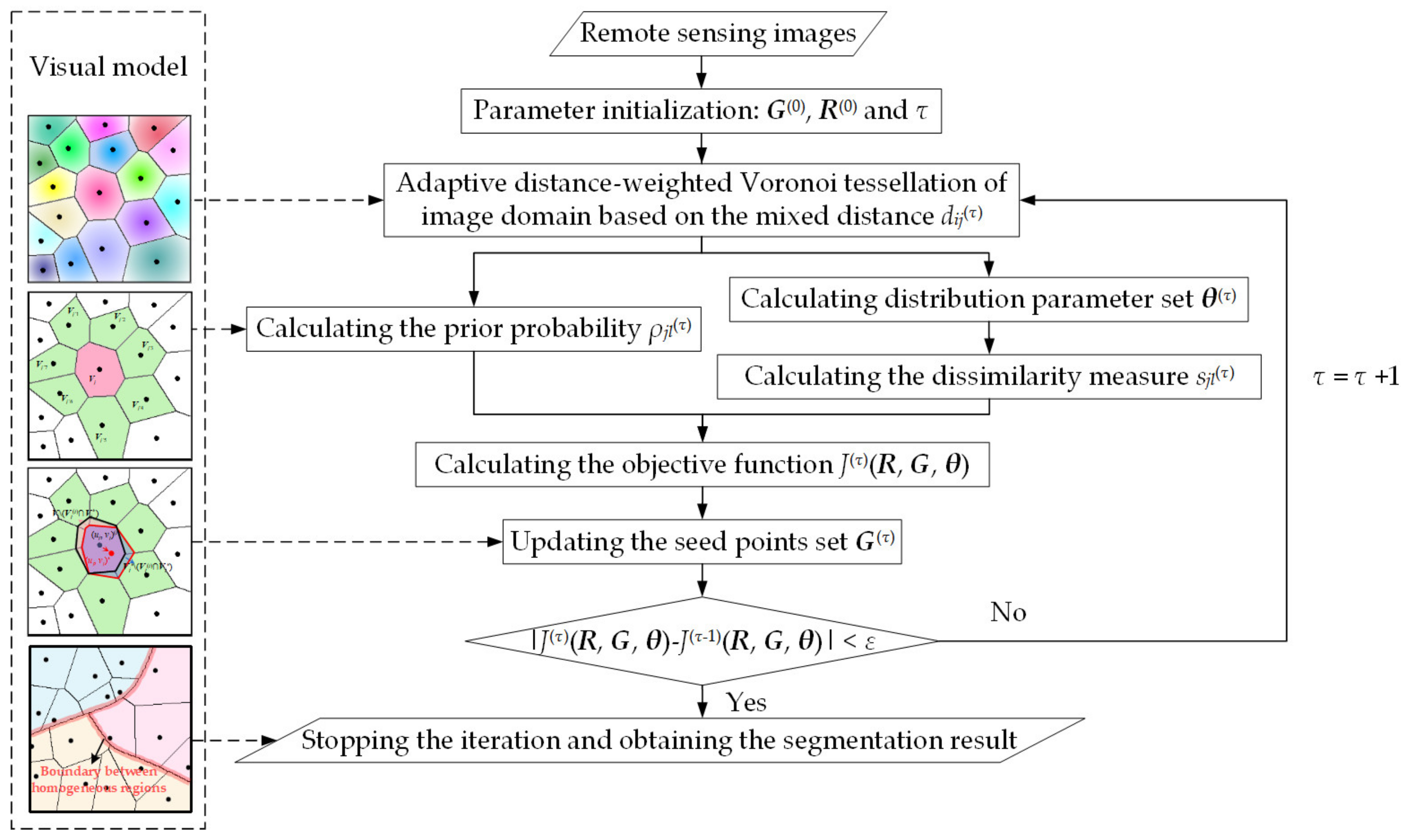
2.4. Summary of the Proposed Algorithm
3. Experimental Results
3.1. Simulated Image
3.2. Remote Sensing Image Segmentation
4. Discussion
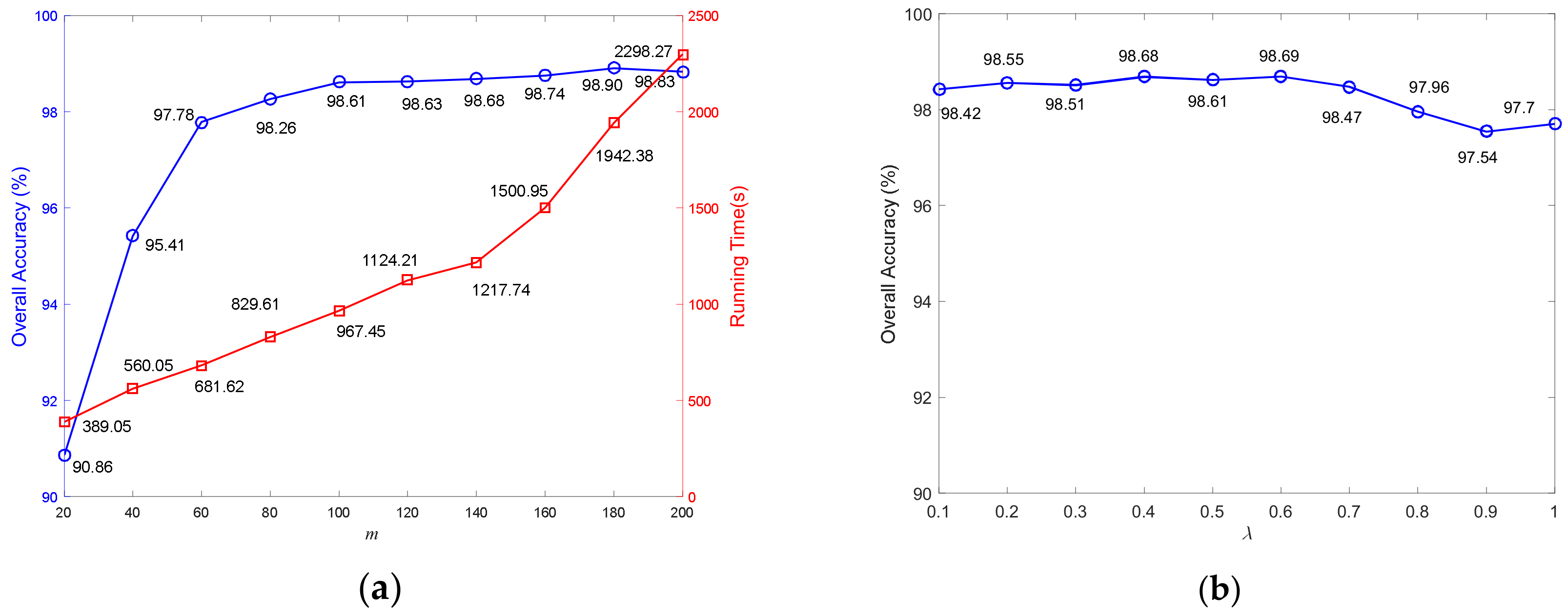
4.1. Parameter Influence Analysis
4.2. Comprehensive Performance Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Troyagalvis, A.; Gancarski, P.; Passat, N.; Bertiequille, L. Unsupervised quantification of under- and over-segmentation for object-based remote sensing image analysis. IEEE J. Sel. Topics Appl. Earth Obs. Remote Sens. 2015, 8, 1936–1945. [Google Scholar] [CrossRef] [Green Version]
- Peng, B.; Zhang, L.; Zhang, D. Automatic image segmentation by dynamic region merging. IEEE Trans. Image Process. 2011, 20, 3592–3605. [Google Scholar] [CrossRef]
- Zhao, J.; Zhong, Y.; Shu, H.; Zhang, L. High-resolution image classification integrating spectral-spatial-location cues by conditional random fields. IEEE Trans. Image Process. 2016, 25, 4033–4045. [Google Scholar] [CrossRef]
- Chen, B.; Qiu, F.; Wu, B.; Du, H. Image segmentation based on constrained spectral variance difference and edge penalty. Remote Sens. 2015, 7, 5980–6004. [Google Scholar] [CrossRef] [Green Version]
- Ciecholewski, M. River channel segmentation in polarimetric SAR images: Watershed transform combined with average contrast maximisation. Expert Syst. Appl. 2017, 82, 196–215. [Google Scholar] [CrossRef]
- Cousty, J.; Bertrand, G.; Najman, L.; Couprie, M. Watershed cuts: Thinnings, shortest path forests, and topological watersheds. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 925–939. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Braga, A.M.; Marques, R.C.P.; Rodrigues, F.A.A.; Medeiros, F.N.S. A median regularized level set for hierarchical segmentation of SAR images. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1171–1175. [Google Scholar] [CrossRef]
- Jin, R.; Yin, J.; Zhou, W.; Yang, J. Level set segmentation algorithm for high-resolution polarimetric SAR images based on a heterogeneous clutter model. IEEE J. Sel. Topics Appl. Earth Obs. Remote Sens. 2017, 10, 4565–4579. [Google Scholar] [CrossRef]
- Mao, T.; Tang, H.; Huang, W. Unsupervised classification of multispectral images embedded with a segmentation of panchromatic images using localized clusters. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8732–8744. [Google Scholar] [CrossRef]
- Fan, J.; Wang, J. A two-phase fuzzy clustering algorithm based on neurodynamic optimization with its application for PolSAR image segmentation. IEEE Trans. Fuzzy Syst. 2018, 26, 72–83. [Google Scholar] [CrossRef]
- Gu, H.; Han, Y.; Yang, Y.; Li, H.; Liu, Z.; Soergel, U.; Blaschke, T.; Cui, S. An efficient parallel multi-scale segmentation method for remote sensing imagery. Remote Sens. 2018, 10, 590. [Google Scholar] [CrossRef] [Green Version]
- Yuan, J.; Wang, D.; Li, R. Remote sensing image segmentation by combining spectral and texture features. IEEE Trans. Geosci. Remote Sens. 2014, 52, 16–24. [Google Scholar] [CrossRef]
- Arisoy, S.; Kayabol, K. Mixture-based superpixel segmentation and classification of SAR images. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1721–1725. [Google Scholar] [CrossRef]
- Qin, X.; Zou, H.; Zhou, S.; Ji, K. Region-based classification of SAR images using Kullback–Leibler distance between generalized Gamma distributions. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1655–1659. [Google Scholar]
- Toro, C.; Martín, C.; Pedrero, A.; Ruiz, E. Superpixel-based roughness measure for multispectral satellite image segmentation. Remote Sens. 2015, 7, 14620–14645. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, M.N.; Yamany, S.M.; Mohamed, N.A.; Farag, A.A.; Moriarty, T.M. A modified fuzzy c-means algorithm for bias field estimation and segmentation of MRI data. IEEE Trans. Med. Imag. 2002, 21, 193–199. [Google Scholar] [CrossRef]
- Szilagyi, L.; Benyo, Z.; Szilagyi, S.M.; Adam, H.S. MR brain image segmentation using an enhanced fuzzy C-means algorithm. In Proceedings of the 25th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Cancun, Mexico, 17–21 September 2003; pp. 724–726. [Google Scholar]
- Cai, W.; Chen, S.; Zhang, D. Fast and robust fuzzy c-means clustering algorithms incorporating local information for image segmentation. Pattern Recognit. 2007, 40, 825–838. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Bruzzone, L.; Shi, W.; Hao, M.; Wang, Y. Enhanced spatially constrained remotely sensed imagery classification using a fuzzy local double neighborhood information C-means clustering algorithm. IEEE J. Sel. Topics Appl. Earth Obs. Remote Sens. 2018, 11, 2896–2910. [Google Scholar] [CrossRef]
- Krinidis, S.; Chatzis, V. A robust fuzzy local information C-means clustering algorithm. IEEE Trans. Image Process. 2010, 19, 1328–1337. [Google Scholar] [CrossRef]
- Gong, M.; Zhou, Z.; Ma, J. Change detection in synthetic aperture radar images based on image fusion and fuzzy clustering. IEEE Trans. Image Process. 2012, 21, 2141–2151. [Google Scholar] [CrossRef]
- Memon, K.H.; Lee, D. Generalised kernel weighted fuzzy C-means clustering algorithm with local information. Fuzzy Sets Syst. 2018, 340, 91–108. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, Q.; Shi, W.; Hao, M. A novel adaptive fuzzy local information C-means clustering algorithm for remotely sensed imagery classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5057–5068. [Google Scholar] [CrossRef]
- Chatzis, S.P.; Varvarigou, T. A fuzzy clustering approach toward hidden Markov random field models for enhanced spatially constrained image segmentation. IEEE Trans. Fuzzy Syst. 2008, 16, 1351–1361. [Google Scholar] [CrossRef]
- Zhao, Q.; Li, X.; Li, Y.; Zhao, X. A fuzzy clustering image segmentation algorithm based on Hidden Markov Random Field models and Voronoi Tessellation. Pattern Recognit. Lett. 2017, 85, 49–55. [Google Scholar] [CrossRef]
- Blaschke, T. Object based image analysis for remote sensing. ISPRS J. Photogramm. Remote Sens. 2010, 65, 2–16. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Xiao, P.; Feng, X. Object-specific optimization of hierarchical multiscale segmentations for high-spatial resolution remote sensing images. ISPRS J. Photogramm. Remote Sens. 2020, 159, 308–321. [Google Scholar] [CrossRef]
- Su, T. Scale-variable region-merging for high resolution remote sensing image segmentation. ISPRS J. Photogramm. Remote Sens. 2019, 147, 319–334. [Google Scholar] [CrossRef]
- Achanta, R.; Shaji, A.; Smith, K.; Lucchi, A.; Fua, P.; Susstrunk, S. SLIC superpixels compared to state-of-the-art superpixel methods. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 2274–2282. [Google Scholar] [CrossRef] [Green Version]
- Pan, X.; Zhou, Y.; Chen, Z.; Zhang, C. Texture relative superpixel generation with adaptive parameters. IEEE Trans. Multimedia. 2019, 21, 1997–2011. [Google Scholar] [CrossRef]
- Lang, F.; Yang, J.; Yan, S.; Qin, F. Superpixel segmentation of polarimetric SAR image using generalized mean shift. Remote Sens. 2018, 10, 1592. [Google Scholar] [CrossRef] [Green Version]
- Stutz, D.; Hermans, A.; Leibe, B. Superpixels: An evaluation of the state-of-the-art. Comput. Vis. Image Und. 2018, 166, 1–27. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Wang, X.; Tan, H.; Xu, C.; Ma, X.; Xu, T. Region merging method for remote sensing spectral image aided by inter-segment and boundary homogeneities. Remote Sens. 2019, 11, 1414. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; He, Y.; Caspersen, J.P. Region merging using local spectral angle thresholds: A more accurate method for hybrid segmentation of remote sensing images. Remote Sens. Environ. 2017, 190, 137–148. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, Y.; Feng, L.; Zhang, X.; Shen, Z.; Zhou, X. Supervised and adaptive feature weighting for object-based classification on satellite images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 3224–3234. [Google Scholar] [CrossRef]
- Lei, T.; Jia, X.; Zhang, Y.; Liu, S.; Meng, H.; Nandi, A.K. Superpixel-based fast fuzzy C-means clustering for color image segmentation. IEEE Trans. Fuzzy Syst. 2019, 27, 1753–1766. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Li, J.; Chapman, M.A. Segmentation of SAR intensity imagery with a Voronoi tessellation, bayesian inference, and reversible jump MCMC algorithm. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1872–1881. [Google Scholar] [CrossRef]







| Algorithms | Key Technology for Segmentation | Typicalness |
|---|---|---|
| FCM_S | A regularization term defined by membership weighted neighborhood pixel dissimilarity measure | playing a guiding role in considering neighborhood constraint |
| HMRF_FCM | Taking Gaussian distribution to describe the dissimilarity and using MRF to model the neighborhood effect | An effective and widely studied pixel-based segmentation method |
| SLIC_FCM | Using SLIC to obtained the sub-regions, and then the segmentation is realized based on FCM | The classical method of generating sub-regions in image processing |
| SF_FCM | Generating sub-regions by multi-scale morphological gradient reconstruction watershed transform | The recent effective method in region-based segmentation algorithms |
| VT_HMRF_FCM | The sub-regions are generated based on Voronoi tessellation according to the spatial information | A region-based algorithm with good noise immunity that tessellation and optimization can be carried out simultaneously |
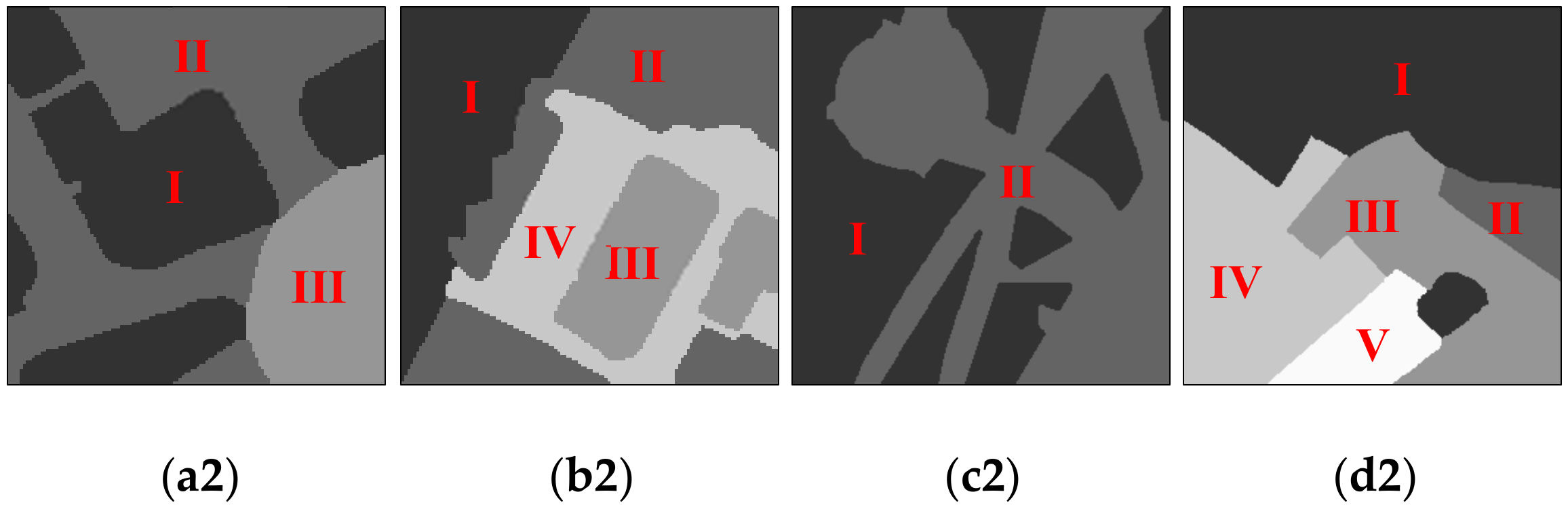
| Parameters | Bands | Homogeneous Regions | ||||
|---|---|---|---|---|---|---|
| I | II | III | IV | V | ||
| Mean | R | 80 | 80 | 20 | 100 | 200 |
| G | 200 | 100 | 150 | 100 | 200 | |
| B | 120 | 200 | 80 | 50 | 250 | |
| Standard deviation | R | 20 | 20 | 10 | 30 | 10 |
| G | 20 | 30 | 20 | 30 | 10 | |
| B | 20 | 20 | 30 | 30 | 8 | |
| Algorithms | Accuracy (%) | Homogeneous Regions | ||||
|---|---|---|---|---|---|---|
| I | II | III | IV | V | ||
| FCM_S | UA | 99.79 | 96.73 | 21.58 | 83.69 | 99.91 |
| PA | 62.96 | 99.58 | 70.64 | 97.82 | 99.96 | |
| OA(%) = 74.48, Kappa = 0.63 | ||||||
| HMRF_FCM | UA | 99.35 | 91.85 | 79.75 | 94.35 | 99.22 |
| PA | 95.14 | 98.83 | 95.24 | 95.60 | 99.56 | |
| OA(%) = 95.85, Kappa = 0.93 | ||||||
| SLIC_FCM | UA | 97.38 | 99.51 | 95.57 | 87.09 | 99.91 |
| PA | 96.07 | 99.24 | 95.17 | 92.86 | 99.04 | |
| OA(%) = 96.02, Kappa = 0.93 | ||||||
| SF_FCM | UA | 96.27 | 97.45 | 99.07 | 96.22 | 97.08 |
| PA | 98.35 | 97.05 | 96.99 | 88.29 | 98.26 | |
| OA(%) = 96.67, Kappa = 0.94 | ||||||
| VT_HMRF_FCM | UA | 99.65 | 96.92 | 99.58 | 84.17 | 99.91 |
| PA | 95.09 | 99.45 | 99.65 | 99.48 | 99.30 | |
| OA(%) = 96.80, Kappa = 0.94 | ||||||
| The proposed algorithm | UA | 99.45 | 98.24 | 99.51 | 96.18 | 99.82 |
| PA | 98.73 | 99.52 | 99.44 | 99.18 | 98.26 | |
| OA(%) = 98.90, Kappa = 0.98 | ||||||
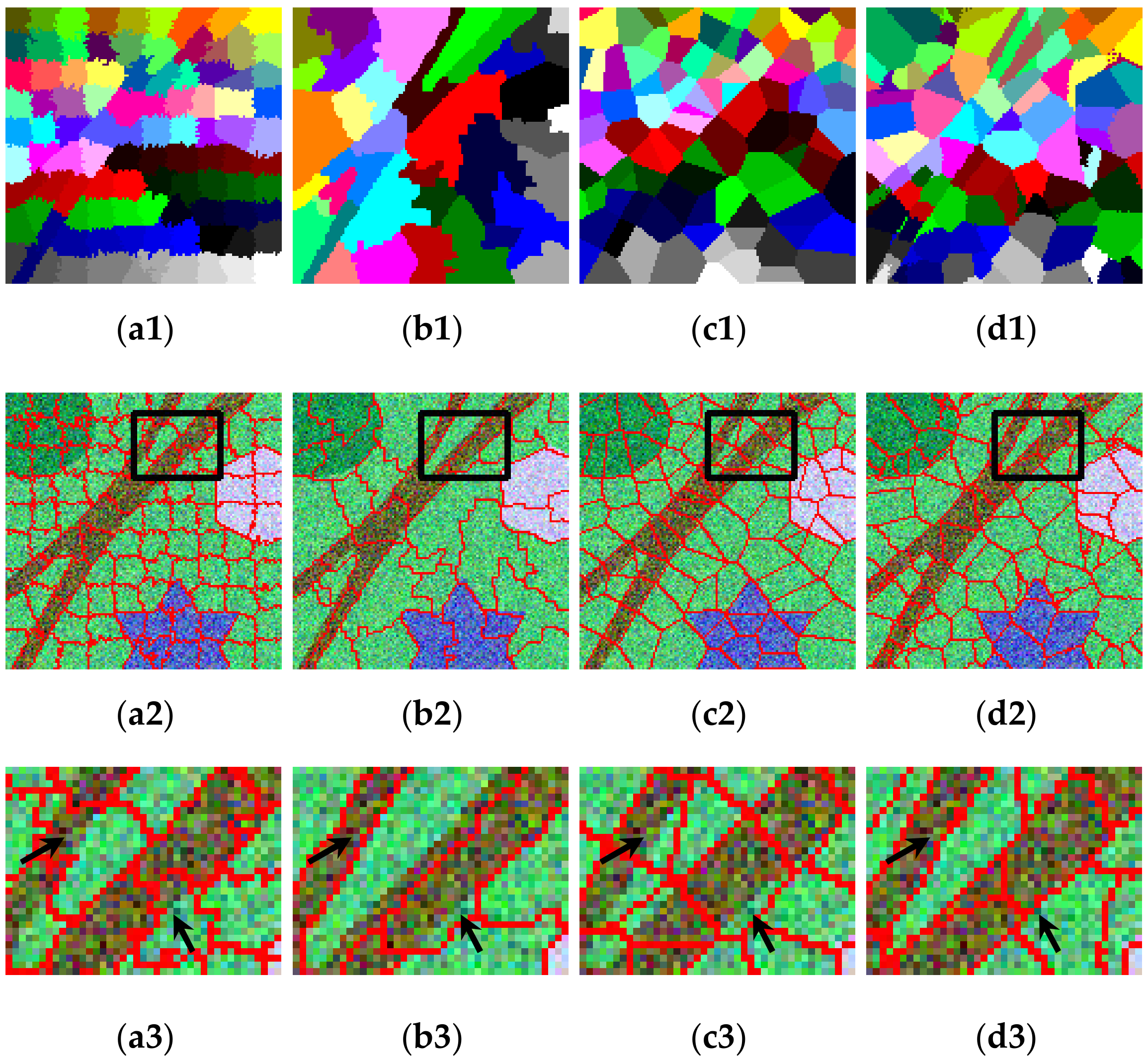
| Algorithms | Figure 9a1 | Figure 9b1 | Figure 9c1 | Figure 9d1 | ||||
|---|---|---|---|---|---|---|---|---|
| OA (%) | Kappa | OA (%) | Kappa | OA (%) | Kappa | OA (%) | Kappa | |
| FCM_S | 72.28 | 0.59 | 82.97 | 0.77 | 83.26 | 0.66 | 48.75 | 0.35 |
| HMRF-FCM | 90.00 | 0.84 | 89.44 | 0.85 | 92.67 | 0.85 | 65.58 | 0.54 |
| SLIC-FCM | 82.18 | 0.72 | 85.46 | 0.80 | 83.64 | 0.67 | 60.02 | 0.47 |
| SF-FCM | 95.92 | 0.93 | 87.28 | 0.82 | 83.34 | 0.66 | 68.56 | 0.58 |
| VT-HMRF-FCM | 95.72 | 0.93 | 93.60 | 0.91 | 90.11 | 0.80 | 93.80 | 0.91 |
| The proposed algorithm | 98.23 | 0.97 | 96.89 | 0.95 | 93.42 | 0.87 | 97.07 | 0.95 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Chen, J.; Zhao, L.; Guo, S.; Sun, L.; Zhao, X. Adaptive Distance-Weighted Voronoi Tessellation for Remote Sensing Image Segmentation. Remote Sens. 2020, 12, 4115. https://doi.org/10.3390/rs12244115
Li X, Chen J, Zhao L, Guo S, Sun L, Zhao X. Adaptive Distance-Weighted Voronoi Tessellation for Remote Sensing Image Segmentation. Remote Sensing. 2020; 12(24):4115. https://doi.org/10.3390/rs12244115
Chicago/Turabian StyleLi, Xiaoli, Jinsong Chen, Longlong Zhao, Shanxin Guo, Luyi Sun, and Xuemei Zhao. 2020. "Adaptive Distance-Weighted Voronoi Tessellation for Remote Sensing Image Segmentation" Remote Sensing 12, no. 24: 4115. https://doi.org/10.3390/rs12244115
APA StyleLi, X., Chen, J., Zhao, L., Guo, S., Sun, L., & Zhao, X. (2020). Adaptive Distance-Weighted Voronoi Tessellation for Remote Sensing Image Segmentation. Remote Sensing, 12(24), 4115. https://doi.org/10.3390/rs12244115







