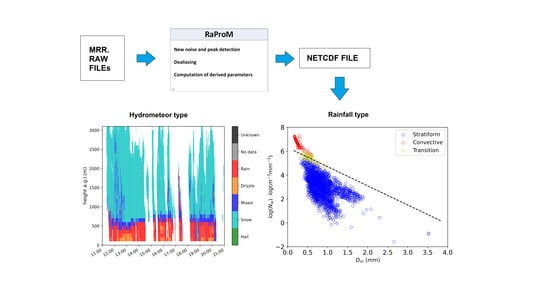
Precipitation Type Classification of Micro Rain Radar Data Using an Improved Doppler Spectral Processing Methodology
Abstract
:1. Introduction
2. Instruments and Site Description
3. New Methodology Proposed
3.1. Spectral Data Processing
3.2. Parameters Calculation
3.2.1. Basic Parameters
3.2.2. Hydrometeor Type Classification
- If vSnow is within the interval ± σ and vRain exceeds + σ, then:
- If the bin height is lower than the BBBottom, the hydrometeor is classified as:Drizzle/Rain—Hail.
- If the bin height is equal or above the BBBottom or BBBottom is not present:Mixed: if Sk > −0.5 and vSnow;Snow: otherwise.
- If vRain and vSnow are within the interval ± σ, then:
- If the bin height is below the BBBottom or BBBottom is not present:Drizzle/Rain—Hail.
- If the bin height is above the BBBottom:Mixed: if the Sk > −0.5 and the vSnow;Snow: otherwise.
- If vRain is within the interval ± σ and vSnow is lower than − σ, then:
- If the bin height is below the BBTop or BBTop is not present:Drizzle/Rain—Hail.
- If the bin height is above the BBTop:Mixed: if the Sk > −0.5 and the vSnow;Snow: otherwise.
- Cases not included in any of the previous categories are labelled as unknown.
3.2.3. Snowfall Rate
3.2.4. Rainfall Parameters from Drizzle/Rain
4. Results
4.1. Case Study
4.1.1. Fall Speed
4.1.2. Equivalent Reflectivity
4.1.3. Hydrometeor Classification
4.1.4. Rain Rate
4.1.5. Stratiform vs. Convective Rain
4.2. Hydrometeor Classification Verification
4.2.1. Verification Data and Methodology
4.2.2. Verification Results
5. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Atlas, D.; Srivastava, R.C.; Sekhon, R.S. Doppler radar characteristics of precipitation at vertical incidence. Rev. Geophys. 1973, 11, 1–35. [Google Scholar] [CrossRef]
- Hauser, D.; Amayenc, P. A new method for deducing hydrometeor-size distributions and vertical air motions from Doppler radar measurements at vertical incidence. J. Appl. Meteorol. 1981, 20, 547–555. [Google Scholar] [CrossRef] [Green Version]
- Battaglia, A.; Kollias, P.; Dhillon, R.; Roy, R.; Tanelli, S.; Lamer, K.; Grecu, M.; Lebsock, M.; Watters, D.; Mroz, K.; et al. Spaceborne Cloud and Precipitation Radars: Status, Challenges, and Ways Forward. Rev. Geophys. 2020, 58, e2019RG000686. [Google Scholar] [CrossRef] [PubMed]
- Kollias, P.; Clothiaux, E.E.; Miller, M.A.; Albrecht, B.A.; Stephens, G.L.; Ackerman, T.P. Millimeter-wavelength radars: New frontier in atmospheric cloud and precipitation research. Bull. Am. Meteorol. Soc. 2007, 88, 1608–1624. [Google Scholar] [CrossRef] [Green Version]
- Ecklund, W.L.; Williams, C.R.; Johnston, P.E.; Gage, K.S. A 3-GHz profiler for precipitating cloud studies. J. Atmos. Ocean. Technol. 1999, 16, 309–322. [Google Scholar] [CrossRef]
- Sheppard, B.E. Measurement of Raindrop Size Distributions Using a Small Doppler Radar. J. Atmos. Ocean. Technol. 1990, 7, 255–268. [Google Scholar] [CrossRef] [Green Version]
- Löffler-Mang, M.; Kunz, M.; Schmid, W. On the performance of a low-cost K-band Doppler radar for quantitative rain measurements. J. Atmos. Ocean. Technol. 1999, 16, 378–387. [Google Scholar] [CrossRef]
- Peters, G.; Fischer, B.; Andersson, T. Rain observations with a vertically looking Micro Rain Radar (MRR). Boreal Environ. Res. 2002, 7, 353–362. [Google Scholar]
- Chandra, A.; Zhang, C.; Kollias, P.; Matrosov, S.; Szyrmer, W. Automated rain rate estimates using the Ka-band ARM zenith radar (KAZR). Atmos. Meas. Tech. Discuss. 2015, 7, 1807–1833. [Google Scholar] [CrossRef]
- Sokol, Z.; Minářová, J.; Novák, P. Classification of hydrometeors using measurements of the ka-band cloud radar installed at the Milešovka Mountain (Central Europe). Remote Sens. 2018, 10, 1674. [Google Scholar] [CrossRef] [Green Version]
- Sokol, Z.; Minářová, J.; Fišer, O. Hydrometeor distribution and linear depolarization ratio in thunderstorms. Remote Sens. 2020, 12, 2144. [Google Scholar] [CrossRef]
- Lolli, S.; D’Adderio, L.; Campbell, J.; Sicard, M.; Welton, E.; Binci, A.; Rea, A.; Tokay, A.; Comerón, A.; Barragan, R.; et al. Vertically Resolved Precipitation Intensity Retrieved through a Synergy between the Ground-Based NASA MPLNET Lidar Network Measurements, Surface Disdrometer Datasets and an Analytical Model Solution. Remote Sens. 2018, 10, 1102. [Google Scholar] [CrossRef] [Green Version]
- Lolli, S.; Vivone, G.; Lewis, J.R.; Sicard, M.; Welton, E.J.; Campbell, J.R.; Comerón, A.; D’Adderio, L.P.; Tokay, A.; Giunta, A.; et al. Overview of the New Version 3 NASA Micro-Pulse Lidar Network (MPLNET) Automatic Precipitation Detection Algorithm. Remote Sens. 2019, 12, 71. [Google Scholar] [CrossRef] [Green Version]
- Adirosi, E.; Baldini, L.; Roberto, N.; Gatlin, P.; Tokay, A. Improvement of vertical profiles of raindrop size distribution from micro rain radar using 2D video disdrometer measurements. Atmos. Res. 2016, 169, 404–415. [Google Scholar] [CrossRef]
- Adirosi, E.; Baldini, L.; Tokay, A.L.I. Rainfall and DSD parameters comparison between micro rain radar, two-dimensional video and parsivel2 disdrometers, and S-band dual-polarization radar. J. Atmos. Ocean. Technol. 2020, 37, 621–640. [Google Scholar] [CrossRef]
- Chang, W.Y.; Lee, G.W.; Jou, B.J.D.; Lee, W.C.; Lin, P.L.; Yu, C.K. Uncertainty in measured raindrop size distributions from four types of collocated instruments. Remote Sens. 2020, 12, 1167. [Google Scholar] [CrossRef] [Green Version]
- Gonzalez, S.; Bech, J.; Udina, M.; Codina, B.; Paci, A.; Trapero, L. Decoupling between precipitation processes and mountain wave induced circulations observed with a vertically pointing K-band doppler radar. Remote Sens. 2019, 11, 1034. [Google Scholar] [CrossRef] [Green Version]
- Jash, D.; Resmi, E.A.; Unnikrishnan, C.K.; Sumesh, R.K.; Sreekanth, T.S.; Sukumar, N.; Ramachandran, K.K. Variation in rain drop size distribution and rain integral parameters during southwest monsoon over a tropical station: An inter-comparison of disdrometer and Micro Rain Radar. Atmos. Res. 2019, 217, 24–36. [Google Scholar] [CrossRef]
- Luo, L.; Xiao, H.; Yang, H.; Chen, H.; Guo, J.; Sun, Y.; Feng, L. Raindrop size distribution and microphysical characteristics of a great rainstorm in 2016 in Beijing, China. Atmos. Res. 2020, 239, 104895. [Google Scholar] [CrossRef]
- Tokay, A.; Hartmann, P.; Battaglia, A.; Gage, K.S.; Clark, W.L.; Williams, C.R. A field study of reflectivity and Z-R relations using vertically pointing radars and disdrometers. J. Atmos. Ocean. Technol. 2009, 26, 1120–1134. [Google Scholar] [CrossRef]
- Bendix, J.; Rollenbeck, R.; Reudenbach, C. Diurnal patterns of rainfall in a tropical Andean valley of southern Ecuador as seen by a vertically pointing K-band Doppler radar. Int. J. Climatol. 2006, 26, 829–846. [Google Scholar] [CrossRef]
- Seidel, J.; Trachte, K.; Orellana-Alvear, J.; Figueroa, R.; Célleri, R.; Bendix, J.; Fernandez, C.; Huggel, C. Precipitation Characteristics at Two Locations in the Tropical Andes by Means of Vertically Pointing Micro-Rain Radar Observations. Remote Sens. 2019, 11, 2985. [Google Scholar] [CrossRef] [Green Version]
- Arulraj, M.; Barros, A.P. Improving quantitative precipitation estimates in mountainous regions by modelling low-level seeder-feeder interactions constrained by Global Precipitation Measurement Dual-frequency Precipitation Radar measurements. Remote Sens. Environ. 2019, 231, 111213. [Google Scholar] [CrossRef]
- Cha, J.-W.; Chang, K.-H.; Yum, S.S.; Choi, Y.-J. Comparison of the bright band characteristics measured by Micro Rain Radar (MRR) at a mountain and a coastal site in South Korea. Adv. Atmos. Sci. 2009, 26, 211–221. [Google Scholar] [CrossRef]
- Brast, M.; Markmann, P. Detecting the Melting Layer with a Micro Rain Radar Using a Neural Network Approach. Atmos. Meas. Tech. Discuss. 2019. [Google Scholar] [CrossRef] [Green Version]
- Frech, M.; Hagen, M.; Mammen, T. Monitoring the Absolute Calibration of a Polarimetric Weather Radar. J. Atmos. Ocean. Technol. 2017, 34, 599–615. [Google Scholar] [CrossRef]
- Fabry, F.; Zawadzki, I. Long-Term Radar Observations of the Melting Layer of Precipitation and Their Interpretation. J. Atmos. Sci. 1995, 52, 838–851. [Google Scholar] [CrossRef]
- Sánchez-Diezma, R.; Zawadzki, I.; Sempere-Torres, D. Identification of the bright band through the analysis of volumetric radar data. J. Geophys. Res. Atmos. 2000, 105, 2225–2236. [Google Scholar] [CrossRef]
- Bordoy, R.; Bech, J.; Rigo, T.; Pineda, N. Analysis of a method for radar rainfall estimation considering the freezing level height. J. Mediterr. Meteorol. Climatol. 2010, 7, 25–39. [Google Scholar] [CrossRef]
- Makino, K.; Shiina, T.; Ota, M. A Precipitation Classification System Using Vertical Doppler Radar Based on Neural Networks. Radio Sci. 2019, 54, 20–33. [Google Scholar] [CrossRef] [Green Version]
- Ryzhkov, A.V.; Schuur, T.J.; Burgess, D.W.; Heinselman, P.L.; Giangrande, S.E.; Zrnic, D.S. The Joint Polarization Experiment: Polarimetric Rainfall Measurements and Hydrometeor Classification. Bull. Am. Meteorol. Soc. 2005, 86, 809–824. [Google Scholar] [CrossRef] [Green Version]
- Park, H.S.; Ryzhkov, A.V.; Zrnić, D.S.; Kim, K.E. The hydrometeor classification algorithm for the polarimetric WSR-88D: Description and application to an MCS. Weather Forecast. 2009, 24, 730–748. [Google Scholar] [CrossRef]
- Schuur, T.J.; Park, H.S.; Ryzhkov, A.V.; Reeves, H.D. Classification of precipitation types during transitional winter weather using the RUC model and polarimetric radar retrievals. J. Appl. Meteorol. Climatol. 2012, 51, 763–779. [Google Scholar] [CrossRef]
- Dolan, B.; Rutledge, S.A.; Lim, S.; Chandrasekar, V.; Thurai, M. A robust C-band hydrometeor identification algorithm and application to a long-term polarimetric radar dataset. J. Appl. Meteorol. Climatol. 2013, 52, 2162–2189. [Google Scholar] [CrossRef]
- Chandrasekar, V.; Keränen, R.; Lim, S.; Moisseev, D. Recent advances in classification of observations from dual polarization weather radars. Atmos. Res. 2013, 119, 97–111. [Google Scholar] [CrossRef]
- Besic, N.; Figueras i Ventura, J.; Grazioli, J.; Gabella, M.; Germann, U.; Berne, A. Hydrometeor classification through statistical clustering of polarimetric radar measurements: A semi-supervised approach. Atmos. Meas. Tech. 2016, 9, 4425–4445. [Google Scholar] [CrossRef] [Green Version]
- METEK. MRR Physical Basics Valid for MRR Service Version ≥ 5.2.0.9; Technical Manual; METEK: Elmshorn, Germany, 2015. [Google Scholar]
- Maahn, M.; Kollias, P. Improved Micro Rain Radar snow measurements using Doppler spectra post-processing. Atmos. Meas. Tech. 2012, 5, 2661–2673. [Google Scholar] [CrossRef] [Green Version]
- Prohom, M.; Puig, O. 18. Weather Observation Network and Climate Change Monitoring in Catalonia, Spain. In Planning to Cope with Tropical and Subtropical Climate Change; De Gruyter Open Poland: Berlin, Germany; Boston, MA, USA, 2016; pp. 322–335. ISBN 9783110480795. [Google Scholar]
- Bech, J.; Codina, B.; Lorente, J.; Bebbington, D. The Sensitivity of Single Polarization Weather Radar Beam Blockage Correction to Variability in the Vertical Refractivity Gradient. J. Atmos. Ocean. Technol. 2003, 20, 845–855. [Google Scholar] [CrossRef] [Green Version]
- Trapero, L.; Bech, J.; Rigo, T.; Pineda, N.; Forcadell, D. Uncertainty of precipitation estimates in convective events by the Meteorological Service of Catalonia radar network. Atmos. Res. 2009, 93, 408–418. [Google Scholar] [CrossRef]
- Udina, M.; Bech, J.; Gonzalez, S.; Soler, M.R.; Paci, A.; Miró, J.R.; Trapero, L.; Donier, J.M.; Douffet, T.; Codina, B.; et al. Multi-sensor observations of an elevated rotor during a mountain wave event in the Eastern Pyrenees. Atmos. Res. 2020, 234, 104698. [Google Scholar] [CrossRef]
- Hildebrand, P.H.; Sekhon, R.S. Objective Determination of the Noise Level in Doppler Spectra. J. Appl. Meteorol. 1974, 13, 808–811. [Google Scholar] [CrossRef] [Green Version]
- Kneifel, S.; Kulie, M.S.; Bennartz, R. A triple-frequency approach to retrieve microphysical snowfall parameters. J. Geophys. Res. Atmos. 2011, 16, 116. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Lei, H.; Yang, J. Microphysical processes of a stratiform precipitation event over eastern China: Analysis using micro rain radar data. Adv. Atmos. Sci. 2017, 34, 1472–1482. [Google Scholar] [CrossRef]
- American Meteorological Society, Cited 2020 Drizzle. Glossary of Meteorology. Available online: https://glossary.ametsoc.org/wiki/Drizzle (accessed on 8 September 2020).
- American Meteorological Society, Cited 2020 Rain. Glossary of Meteorology. Available online: https://glossary.ametsoc.org/wiki/Rain (accessed on 8 September 2020).
- Acquistapace, C.; Löhnert, U.; Maahn, M.; Kollias, P. A new criterion to improve operational drizzle detection with ground-based remote sensing. J. Atmos. Ocean. Technol. 2019, 36, 781–801. [Google Scholar] [CrossRef]
- Kalesse, H.; Szyrmer, W.; Kneifel, S.; Kollias, P.; Luke, E. Fingerprints of a riming event on cloud radar Doppler spectra: Observations and modeling. Atmos. Chem. Phys. 2016. [Google Scholar] [CrossRef] [Green Version]
- Matrosov, S.Y.; Heymsfield, A.J. Empirical relations between size parameters of ice hydrometeor populations and radar reflectivity. J. Appl. Meteorol. Climatol. 2017, 56, 2479–2488. [Google Scholar] [CrossRef]
- Souverijns, N.; Gossart, A.; Lhermitte, S.; Gorodetskaya, I.V.; Kneifel, S.; Maahn, M.; Bliven, F.L.; van Lipzig, N.P.M. Estimating radar reflectivity—Snowfall rate relationships and their uncertainties over Antarctica by combining disdrometer and radar observations. Atmos. Res. 2017, 196, 211–223. [Google Scholar] [CrossRef]
- Gunn, R.; Kinzer, G.D. The terminal velocity of fall for water droplets in stagnant air. J. Meteorol. 1949, 6, 243–248. [Google Scholar] [CrossRef] [Green Version]
- Foote, G.B.; Du Toit, P.S. Terminal Velocity of Raindrops Aloft. J. Appl. Meteorol. 1969, 8, 249–253. [Google Scholar] [CrossRef] [Green Version]
- Thurai, M.; Gatlin, P.N.; Bringi, V.N. Separating stratiform and convective rain types based on the drop size distribution characteristics using 2D video disdrometer data. Atmos. Res. 2016, 169, 416–423. [Google Scholar] [CrossRef]
- Gonzalez, S.; Bech, J. Extreme point rainfall temporal scaling: A long term (1805–2014) regional and seasonal analysis in Spain. Int. J. Climatol. 2017, 37, 5068–5079. [Google Scholar] [CrossRef] [Green Version]
- Friedrich, K.; Kalina, E.A.; Masters, F.J.; Lopez, C.R. Drop-size distributions in thunderstorms measured by optical disdrometers during VORTEX2. Mon. Weather Rev. 2013, 141, 1182–1203. [Google Scholar] [CrossRef]
- Ebert, E.E. Fuzzy verification of high-resolution gridded forecasts: A review and proposed framework. Meteorol. Appl. 2008, 15, 51–64. [Google Scholar] [CrossRef]
- Trapero, L.; Bech, J.; Duffourg, F.; Esteban, P.; Lorente, J. Mesoscale numerical analysis of the historical November 1982 heavy precipitation event over Andorra (Eastern Pyrenees). Nat. Hazards Earth Syst. Sci. 2013, 13, 2969–2990. [Google Scholar] [CrossRef] [Green Version]
- Collier, C.G. The impact of wind drift on the utility of very high spatial resolution radar data over urban areas. Phys. Chem. Earth Part B Hydrol. Ocean. Atmos. 1999, 24, 889–893. [Google Scholar] [CrossRef]
- Sandford, C. Correcting for wind drift in high resolution radar rainfall products: A feasibility study. J. Hydrol. 2015, 531, 284–295. [Google Scholar] [CrossRef]
- Thériault, J.M.; Stewart, R.E.; Henson, W. Impacts of terminal velocity on the trajectory of winter precipitation types. Atmos. Res. 2012, 116, 116–129. [Google Scholar] [CrossRef]















| Frequency (GHz) | 24.23 |
| Radar Type | FMCW |
| Number of range gates | 32 |
| Number of spectral bins | 64 |
| Range resolution (m) | 10–200 |
| Frequency sampling (kHz) | 125 |
| (m/s) | Rain | Drizzle | Mixed | Snow |
|---|---|---|---|---|
| 1142 | 88 | 1057 | 7441 | |
| 0 | 0 | 0 | 4 | |
| 0 | 0 | 2 | 1 | |
| ME | −0.01 | −0.02 | 0.00 | 0.01 |
| RMSE | 0.06 | 0.03 | 0.16 | 0.08 |
| (dBZ) | Rain | Drizzle | Mixed | Snow |
|---|---|---|---|---|
| 1003 | 88 | 1023 | 6518 | |
| 135 | 0 | 32 | 914 | |
| 4 | 0 | 4 | 14 | |
| ME | −0.38 | −0.01 | −0.14 | −0.45 |
| RMSE | 1.28 | 0.04 | 0.75 | 0.80 |
| Class | POD | FAR | ORSS | Method3 (min) | Method3 (%) | Disdrometer (min) | Disdrometer (%) |
|---|---|---|---|---|---|---|---|
| Rain | 0.99 | 0.29 | 0.99 | 7095 | 15.6 | 7173 | 15.8 |
| Drizzle | 0.69 | 0.26 | 0.72 | 3502 | 7.7 | 3108 | 6.8 |
| Hail | 0.55 | 0.01 | 0.98 | 49 | 0.1 | 88 | 0.2 |
| Snow | 0.97 | 0.14 | 0.99 | 3700 | 8.2 | 3897 | 8.6 |
| Mixed | 0.79 | 0.17 | 0.89 | 1001 | 2.2 | 933 | 2.1 |
| No precipitation | 0.94 | 0.05 | 0.99 | 30,037 | 66.2 | 30,185 | 66.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garcia-Benadi, A.; Bech, J.; Gonzalez, S.; Udina, M.; Codina, B.; Georgis, J.-F. Precipitation Type Classification of Micro Rain Radar Data Using an Improved Doppler Spectral Processing Methodology. Remote Sens. 2020, 12, 4113. https://doi.org/10.3390/rs12244113
Garcia-Benadi A, Bech J, Gonzalez S, Udina M, Codina B, Georgis J-F. Precipitation Type Classification of Micro Rain Radar Data Using an Improved Doppler Spectral Processing Methodology. Remote Sensing. 2020; 12(24):4113. https://doi.org/10.3390/rs12244113
Chicago/Turabian StyleGarcia-Benadi, Albert, Joan Bech, Sergi Gonzalez, Mireia Udina, Bernat Codina, and Jean-François Georgis. 2020. "Precipitation Type Classification of Micro Rain Radar Data Using an Improved Doppler Spectral Processing Methodology" Remote Sensing 12, no. 24: 4113. https://doi.org/10.3390/rs12244113