An Efficient Parallel Multi-Scale Segmentation Method for Remote Sensing Imagery

Abstract

Remote sensing (RS) image segmentation is an essential step in geographic object-based image analysis (GEOBIA) to ultimately derive “meaningful objects”. While many segmentation methods exist, most of them are not efficient for large data sets. Thus, the goal of this research is to develop an efficient parallel multi-scale segmentation method for RS imagery by combining graph theory and the fractal net evolution approach (FNEA). Specifically, a minimum spanning tree (MST) algorithm in graph theory is proposed to be combined with a minimum heterogeneity rule (MHR) algorithm that is used in FNEA. The MST algorithm is used for the initial segmentation while the MHR algorithm is used for object merging. An efficient implementation of the segmentation strategy is presented using data partition and the “reverse searching-forward processing” chain based on message passing interface (MPI) parallel technology. Segmentation results of the proposed method using images from multiple sensors (airborne, SPECIM AISA EAGLE II, WorldView-2, RADARSAT-2) and different selected landscapes (residential/industrial, residential/agriculture) covering four test sites indicated its efficiency in accuracy and speed. We conclude that the proposed method is applicable and efficient for the segmentation of a variety of RS imagery (airborne optical, satellite optical, SAR, high-spectral), while the accuracy is comparable with that of the FNEA method.

1. Introduction

Remote sensing (RS) image segmentation is an essential step to ultimately derive “meaningful objects” in geographic object-based image analysis (GEOBIA) [1,2]. The optimal segmentation of an image should result in a balance of over-segmentation and under-segmentation of the scene. Many segmentation methods for RS imagery exist. They can be grouped into four categories: (a) pixel-based (thresholding, clustering, etc.) [3,4]; (b) edge detection (boundary tracking, curve fitting, etc.) [5]; (c) region-based (region growing, watershed, split and merge, level set, etc.) [6]; (d) others (wavelet, neural networks, mean-shift, fuzzy sets, etc.) [7,8]. Region-based segmentation methods are the dominant methods that can be used to create compact regions and identify suitable scales [9]. The fractal net evolution approach (FNEA) and graph method are the two dominant region-based methods. The FNEA, proposed by Baatz and Schäpe in 2000 [10] and commercialized by the software eCognition (http://www.ecognition.com), is a bottom-up region growing and merging technique based on local criteria. The neighboring image objects are merged to form bigger objects based on a minimum heterogeneity rule (MHR) algorithm. Thus, it builds a multi-scale hierarchy structure using a merging technique. In addition, spectral, shape and textural information can be extracted as well, which is helpful for advanced applications [10]. However, this method—as with most local region growing techniques—has some limitations: it is time-consuming to create a large number of initial image objects starting with individual pixels [11]; and it is suboptimal to choose a sequence of starting points in a random sequence, due to the percolation patterns or clusters which increasingly appear, starting at a certain density of points [10]. Graph methods explicitly organize the image elements into mathematically sound structure and make the formulation of the problem more flexible and the computation more efficient [12]. There are four basic algorithms: best merge [13], minimum spanning tree (MST) [14], minimum mean cut [15,16], and normalized cut [17]. The best merge and MST algorithms follow a bottom-up approach: they start from a segmented image, i.e., each pixel constitutes a separate segment; then, these algorithms iteratively merge two adjacent segments. The minimum mean cut and normalized cut algorithms follow a top-down approach: the whole image is one segment initially; then, in each step, one of the segments is split into parts [18]. These graph-based algorithms have been applied to different RS imagery (such as hyperspectral, panchromatic, multispectral, LiDAR, SAR, etc.) [19,20,21,22].

Recently, two obvious trends within RS image segmentation can be observed: (a) new theories are constantly applied, which leads to more and more specific RS image segmentation methods and methodologies; (b) different segmentation algorithms have been combined to overcome the disadvantages of each individual segmentation algorithm [1]. The key problem here is how to combine these algorithms to fully employ the advantages of various algorithms and complement their shortcomings. For instance, Li et al. proposed an efficient multi-scale segmentation method by combining a statistical region merging algorithm and a MHR algorithm, whereby the results showed that the combined algorithm is able to capture the main structural components of imagery by a simple but effective statistical analysis, and it is able to cope with significant noise corruption and handle occlusions with a sort function [23]. Wang presented a multiresolution RS image segmentation method by combining a rainfall watershed algorithm and a fast region merging method, yielding a stable performance for high spatial resolution RS imagery, [24].

Our goal in this research is to develop an efficient segmentation method by combining MST and MHR, which should have the following properties: (a) be suitable for a variety of RS imagery, such as hyperspectral, multispectral, SAR, etc.; (b) be applicable to complex scenes (residential/industrial, residential/agriculture); (c) be efficient for large datasets; (d) the image objects should represent the sub-objects of geo-objects, whereby in an ideal situation, image objects are representations of geo-objects. The initial research was published in the 2015 International Workshop on Image and Data conference [25]. In this paper, we extend the 2015 work significantly by presenting the method in detail and performing a comprehensive evaluation. The main parts of this study are as follows: (a) the MST algorithm for initial segmentation is proposed to be combined with the MHR algorithm for object merging which is adopted in FNEA; (b) an efficient implementation of the segmentation strategy is presented using data partition and a “reverse searching-forward processing” chain based on message passing interface (MPI) parallel technology; (c) high-resolution optical images, a hyperspectral image and a SAR image from four test sites are used to assess the proposed method.

2. Multi-Scale Segmentation Method Based on MST and MHR

The flowchart of our multi-scale segmentation method is shown in Figure 1. It consists of two main procedures: an initial segmentation using the MST algorithm based on the graph theory described in Section 2.1, and an object merging step using the MHR algorithm based on the FNEA method, detailed in Section 2.2.

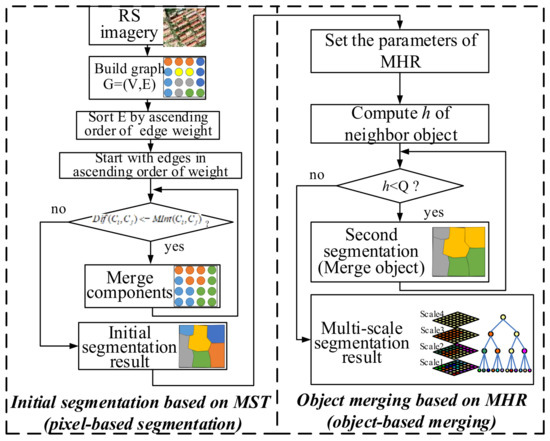
Figure 1. Flowchart of the multi-scale segmentation method based on MST and MHR.

2.1. Initial Segmentation Based on MST

Graph-based image segmentation techniques generally represent the problem in terms of a graph $G=(V,E)$, where each node $v_i\in V$ corresponds to a pixel in the image, and each edge $(v_i,v_j)\in E$ connects a pair of neighboring pixels. Each edge is associated with a corresponding weight $w((v_i,v_j))$, which is a non-negative measure of the dissimilarity (e.g., the difference in intensity, color, motion, location or some other local attribute) between neighboring elements $v_i$ and $v_j$ [14]. A segmentation S is a partition of V into components such that each component (or region) $C\in V$ corresponds to a connected component in a graph $G^{\prime }=(V,E^{\prime })$, where $E^{\prime }\subseteq E$. The pixel-based image is shown as a graph in Figure 2.

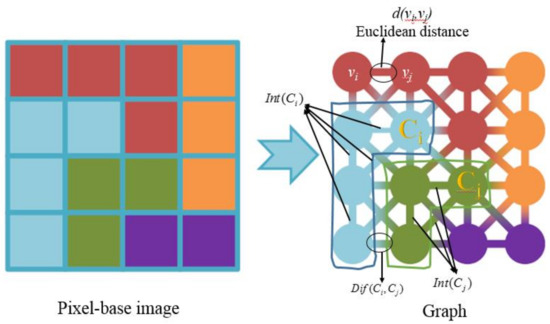
Figure 2. Illustration of a graph-based image segmentation.

The merging criterion D presented by Felzenszwalb and Huttenlocher [14] based on the MST algorithm is used to merge neighboring components, and is,

$$D(C_i,C_j)=\{\begin{array}{cc}true,\hspace{1em}& if\hspace{1em}Dif(C_i,C_j)>MInt(C_i,C_j)\\ false,\hspace{1em}& otherwise\hfill \end{array}$$

(1)

The difference between two components $C_i,C_j$ ($C_i,C_j\in V$), $Dif(C_i,C_j)$, is the minimum weight edge connecting the two components. That is,

$$Dif(C_i,C_j)={\min }_{v_i\in C_i,v_j\in C_j,(v_i,v_j)\in E}w((v_i,v_j))$$

(2)

If there is no edge connecting C_i and C_j, $Dif(C_i,C_j)=1$.

The internal difference of a component C ($C\in V$), $Int(C)$, is described as the largest weight in the MST of the component, $MST(C,E)$, That is,

$$Int(C)={\max }_{e\in MST(C,E)}w(e)$$

(3)

The minimum internal difference, $MInt(C_i,C_j)$, is defined as,

$$MInt(C_i,C_j)=\min (Int(C_i)+\tau (C_i),Int(C_j)+\tau (C_j))$$

(4)

The threshold function is defined as,

$$\tau (C)=k/\left|C\right|$$

(5)

where $\left|C\right|$ denotes the size of C and k is a constant parameter. The role of this parameter is to avoid small regions as excessive noise and to suppress the generation of a large connected region.

There are four steps in the initial segmentation procedure [14]:

(1)

A graph $G=(V,E)$ with vertices V and edges E is built and the weight of each edge is the Euclidean distance $d(v_i,v_j)$ between neighboring elements $v_i$ and $v_j$ in terms of the intensities of all the bands.

(2)

Sort E by non-decreasing edge weight.

(3)

Start with an initial segmentation S⁰, where each vertex $v_i$ is in its own component. Compute a threshold function $\tau (C_i)$ for each component using Formula (5). Then Compute $Dif(C_i,C_j)$ and $MInt(C_i,C_j)$ for each component using Formulas (2) and (4). Subsequently we decide whether $Dif(C_i,C_j)<=MInt(C_i,C_j)$. If the condition holds, the two components are merged; otherwise nothing would be done. Repeat the above steps until all the components are computed.

(4)

The output is a segmentation of V into components $S=(C_1,...,C_R)$.

2.2. Object Merging Based on MHR

To implement the multi-scale segmentation, the MHR is introduced to merge two adjacent regions from the initial segmentation, which could reduce the disturbance from noise, reduce the fragmentized degree of object boundary, and obtain more regular objects [23]. Not only the color heterogeneity ($h_{color}$) but also shape heterogeneity ($h_{shape}$) is considered. The heterogeneity (h) of MHR is defined as,

$$h=w_{color}{h}_{color}+w_{shape}{h}_{shape}$$

(6)

where,

$$h_{color}={\displaystyle \sum _c{w}_c}(n_{merge}\cdot {\sigma }_{c,merge}-(n_{obj\_A}\cdot {\sigma }_{c,obj\_A}+n_{obj\_B}\cdot {\sigma }_{c,obj\_B}))$$

(7)

$$h_{shape}=w_{compt}{h}_{compt}+w_{smooth}{h}_{smooth}$$

(8)

$$h_{compt}=n_{merge}\cdot \frac{l_{merge}}{\sqrt{n_{merge}}}-(n_{obj\_A}\cdot \frac{l_{obj\_A}}{\sqrt{n_{obj\_A}}}+n_{obj\_B}\cdot \frac{l_{obj\_B}}{\sqrt{n_{obj\_B}}})$$

(9)

$$h_{smooth}=n_{merge}\cdot \frac{l_{merge}}{b_{merge}}-(n_{obj\_A}\cdot \frac{l_{obj\_A}}{\sqrt{b_{obj\_A}}}+n_{obj\_B}\cdot \frac{l_{obj\_B}}{\sqrt{b_{obj\_B}}})$$

(10)

The symbols $w_{color}$, $w_{shape}$, $w_{compt}$, $w_{smooth}$ are weights of color, shape, compact and smooth, respectively, and $w_{color}\in [0,1]$, $w_{shape}\in [0,1]$, $w_{compt}\in [0,1]$, $w_{smooth}\in [0,1]$, $w_{color}+w_{shape}=1$, $w_{compt}+w_{smooth}=1$. The symbols $n_{merge}$, $n_{obj\_A}$, $n_{obj\_B}$ represent the number of objects after merging, the number of object A before merging, and the number of object B before merging. Other symbols $l_{obj\_A}$ and $l_{obj\_B}$ are denoted as the perimeters of object A and object B, respectively, where $b_{obj\_A}$ and $b_{obj\_B}$ are the bounding box perimeters of object A and object B. Lastly, the meaning of $b_{merge}$ is the bounding box perimeter of objects after merging.

There are three steps in the merging procedure:

(1)

Set the parameters of MHR, such as weights of color, shape, compact, and smooth ($w_{color}$, $w_{shape}$, $w_{compt}$, $w_{smooth}$), and the scale parameter Q. Then compute the heterogeneity h of adjacent objects using Formula (6).

(2)

Decide whether h satisfies MHR. If h < (Q)², the adjacent smaller objects are merged into a bigger one. Meanwhile, the average size, standard deviation, and mean of all the objects are calculated. Repeat this process until all the objects are merged.

(3)

Repeat steps 1–2 to accomplish the multi-scale segmentations.

3. Parallel Segmentation Based on MPI

One problem with applying this method is that it is very time-consuming for large datasets. Thus, in this section, we present a parallel implementation which relies on a data partition strategy and a “reverse searching-forward processing” chain strategy to boost the segmentation speed on a cluster platform using MPI parallel technology. The MPI has the advantages of portability, standardization, and efficiency, which could solve the communication problems of parallel processing [26]. The computing resources of the cluster platform are divided into one master node and many slave nodes with the Master/Slave mode, which can handle dynamic load balancing [26].

3.1. Data Partition Strategy

Data partition is a common strategy for parallel processing [27]; the data is divided into rectangular blocks using the expand buffer strategy by the master node. The data partition strategy is shown in Figure 3.

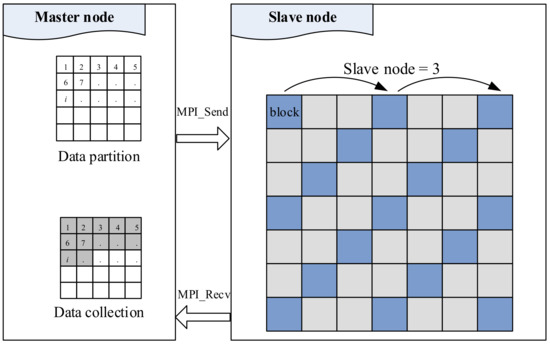
Figure 3. Data partition strategy based on MPI.

It has the following three steps:

(1)

The data is divided into rectangular blocks, and every block is labelled with “1, 2, 3, …, i, …” from left to right, up to down.

(2)

Each block is assigned to a different slave node; the block is labelled as i, that is,

$$i=p+n\times P$$

where, (n, p) is the coordinate of the slave node, which is labeled with index i, and P is the number of slave nodes in the column direction. Here the column and row directions are equivalent to the coordinate in the x and y directions, respectively.

The slave nodes process their blocks according to the label of the blocks and send the result to the master node until all the data has been processed.

3.2. “Reverse Searching-Forward Processing” Chain

The “reverse searching-forward processing” chain is an interconnected system, which describes a series of steps. Each step can be performed simultaneously by different slave nodes [28]. The chain is shown in Figure 4.

Figure 4. “Reverse searching-forward processing” chain based on MPI.

At first, the slave nodes start to search for the relative data and parameters from the result until they find all the data, parameters, and algorithms. Then the slave nodes use the relative data, parameters, and algorithms to process from the source to the result until all the steps are completed.

3.3. Parallel Segmentation Method

The computing resources of the cluster platform are divided into one master node and many slave nodes. The master node is responsible for scheduling tasks and collecting results from the slave nodes. The slave nodes are responsible for processing and submitting the tasks. The source file is a series of images to be processed, and the target file is the segmentation result. The flowchart for the parallel segmentation method based on MPI is shown in Figure 5.

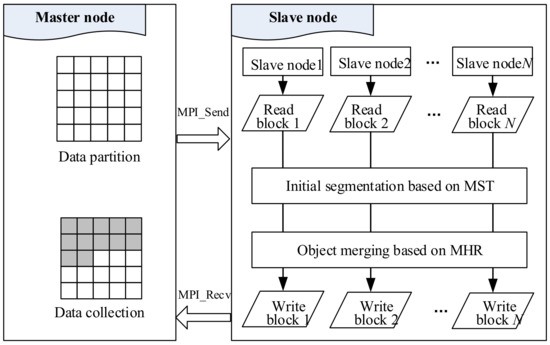
Figure 5. Flowchart for parallel segmentation based on MPI.

The three steps in the parallel segmentation method are:

(1)

The master node is responsible for reading the image and dividing it into blocks using extended buffer strategy. A regular data division is used to divide the original image data into sub-rectangular data blocks, which will be used as the input data and assigned to the slave nodes for parallel computing.

(2)

The slave nodes are responsible for receiving blocks. First, each block is segmented separately, and the data block is segmented to obtain objects initially based on MST. Then, the objects are merged based on MHR to obtain the results. In the end, all the segmentation results are sent to the master node.

(3)

The master node collects the results from each slave node, and outputs the segmentation image.

We apply two strategies to deal with the objects adjacent to borders. One is to use an extended buffer strategy to extend the size of the block under consideration to obtain an extended block. The extended block is processed, and the normal size of the block is output (Figure 6). The other strategy is to remove the boundary of the vectorized segmentation results by the mean feature of the neighboring objects (Figure 7); the mean is calculated using statistical methods. These two strategies do not deal with the boundary problem exhaustively. To solve this problem entirely would be a research question in itself and the subject of another study. Our two-fold solution can deal with the vast majority of specific problems and can be a trade-off between perfection and effort.

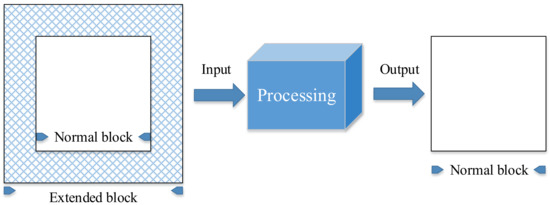
Figure 6. Extended buffer strategy.

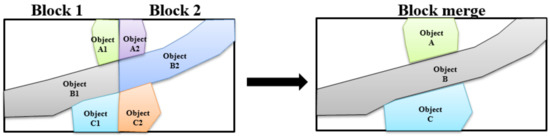
Figure 7. Remove the boundary.

4. Test Sites and Experiments

4.1. Test Sites

We tested the proposed method on a variety of images with different selected landscapes (Table 1). The test images were chosen with diverse scene complexities for exploring the general applicability of the proposed method.

Table 1. Summary of four test sites and imagery types.

Test	Imagery	Spatial Resolution (in m)	Number of Bands	Landscape Characteristics	Location
T1	Airborne true orthophoto	0.05	4	residential/industrial area	Potsdam in Germany
T2	SPECIM AISA EAGLE II image	0.78	10	residential/industrial area	DaFeng, in the Yancheng sub-province of Jiangsu province, in China
T3	WorldView-2 image	0.5	8	residential/agriculture area	Lintong, in the Xi’an sub-province of Shanxi province, in the northwest of China.
T4	RADARSAT-2 image	8	HH, HV, VH, VV	Agriculture area	Genhe, in the Hulunbeier sub-province of Inner Mongolia province, in China

Test data 1 (T1) covering the city of Potsdam in Germany was selected from the ISPRS benchmark project [29], which is an airborne true orthophoto with 0.05 m resolution and four bands (red, green, blue, and infrared). Test data 2 (T2) covering the city of DaFeng in China is a hyperspectral SPECIM AISA EAGLE II data acquired in November 2014 with a spatial resolution of 0.78 m, a spectral resolution of 9.6 nm, and 64 bands with a wavelength from 400 nm to 970 nm. The image was atmospherically corrected using the FLAASH model implemented in the ENVI software (http://www.harrisgeospatial.com/), and then 10 bands were selected using the minimum noise fraction (MNF) method from ENVI. Test data 3 (T3), covering the city of Lintong in the northwest of China, is a panchromatic (Pan) WorldView-2 image with a resolution of 0.5 m and a multispectral (MS) WorldView-2 image acquired in July 2011 with a resolution of 2.0 m (with eight bands, namely coastal, blue, green, yellow, red, red edge, near-infrared 1, and near-infrared 2). The WorldView-2 MS image and the Pan image were then fused using the PanSharp fusion method as implemented within the PCI Geomatica software (http://www.pcigeomatics.com/). Test data 4 (T4) covering the city of Genhe in China is a quad polarization RADARSAT-2 data acquired in September 2012 with a spatial resolution of 8.0 m. It was multi-looked using SARScape (http://www.harrisgeospatial.com/) and filtered using the enhanced Frost method provided by ENVI.

4.2. Results

Our segmentation method was evaluated and compared with the FNEA method, which has the same three parameters, namely, scale, weight of color, and weight of compactness. It is important to set these parameters properly. There are some methods for a fact-based determination of these parameters, such as estimation of scale parameters (ESP) [30], optimized image segmentation [31], segmentation parameter tuner (SPT) [32], plateau objective function (POF) [33] or the work of Stumpf and Kerle (2011), who optimized segmentation through the optimal use of the derived object features in a random forest framework [34]. In FNEA, the color and the shape parameter work contrarily: The larger the weight of the color is, the better the spectral consistency of the resulting objects. The smaller the compactness weight is, the more complex the average shapes of the resulting objects are. In this study, the selection of image segmentation parameters is based on an iterative trial-and-error approach that is often utilized in object-based classification [35,36].

It should be noted that the scale parameter (Q) is the most important factor for segmentation as it controls the relative size of the resulting image objects and has a direct effect on the segmentation accuracy. The bigger the scale value is, the larger the object. The weight of color ($w_{color}$) is considered to be bigger than the weight of shape ($w_{shape}$), and the weight of smoothness ($w_{smooth}$) is considered to be similar to the weight of compactness ($w_{compt}$) [37]. We set the same parameters ($w_{color}$, $w_{smooth}$) for different experiments to compare different methods under the same conditions. For all four test data, $w_{color}$ is 0.9, $w_{smooth}$ is 0.5. The Q of the proposed method is the same as for the FNEA method. The segmentation parameters for the four experiments are shown in Table 2.

Table 2. The segmentation parameters for four experiments.

Segmentation Parameters	Airborne	SPECIM AISA EAGLE II	WorldView-2	RADARSAT-2
weight of color ($w_{color}$)	0.9	0.9	0.9	0.9
weight of smoothness ($w_{smooth}$)	0.5	0.5	0.5	0.5
scale parameter (Q)	240	360	260	2000

The segmentation results of the proposed method and FNEA with Q of 240 for the first test data are shown in Figure 8. Visually, the image objects partially represent parts or sub-objects of the targeted geo-objects, such as buildings, trees, cars, and roads. The two segmentation methods were compared with manually interpreted buildings and individual trees. The segmentation results of the proposed method and the FNEA with Q of 360 for the second test data are shown in Figure 9. Buildings, waters, roads are well segmented. The two segmentation methods were compared to manually interpreted buildings as well. The third test was conducted in a residential/agriculture area. Figure 10 depicts the proposed method and the FNEA method with Q values of 260. As can be seen, buildings, roads and water bodies are well segmented. The two segmentation methods were also compared to manually interpreted objects. The segmentation results of the proposed method and FNEA with Q values of 2000 for the fourth test data are shown in Figure 11. The image objects partially represent sub-objects of geo-objects, such as water bodies, fields, and trees. The two results were compared to manually interpreted fields. Overall, the segmentation results of the two methods for the four experiments look similarly, but there are some differences such as those highlighted for areas A and B in Figure 8, Figure 9, Figure 10 and Figure 11. For area A, highly detailed segments are found in Figure 9a compared with Figure 9b. The opposite is true for area B. The same holds true for Figure 10a,b and for Figure 11a,b.

Figure 8. Segmentation results of the airborne true orthoimage at Q 240 (yellow outlines) and ground truth (104 buildings and individual trees, blue outlines), for area A, highly detailed segments are found in (a) compared with (b), the opposite is true for area B.

Figure 9. Segmentation results of SPECIM AISA EAGLE II image at Q 360 (yellow outlines) and ground truth (28 big buildings, blue outlines), for area A, highly detailed segments are found in (a) compared with (b), the opposite is true for area B.

Figure 10. Segmentation results of worldview-2 image at Q 260 (yellow outlines) and ground truth (28 fields, blue outlines), for area A and B, highly detailed segments are found in (b) compared with (a).

Figure 11. Segmentation results of RADARSAT-2 image at Q 2000 (yellow outlines) and ground truth (21 fields, blue outlines), for area A, highly detailed segments are found in (a) compared with (b), the opposite is true for area B.

4.3. Analysis

4.3.1. Accuracy Evaluation

The geometries of the image objects are compared through a supervised segmentation evaluation [38]. This includes methods that assess the geometric differences between the generated image objects and the ground truth data [39]. For this study, the SPT tool is used to evaluate the segmentation results with seven metrics, namely Hoover Index (H), Area-Fit-Index (AFI), Shape Index (SI), Rand Index (RI), F-measure (F), Segmentation Covering (C), Reference Bounded Segments Booster (RBSB) [32], as shown in Table 3. The ground truth data for the four experiments are shown in Table 4. The values of the respective metrics for the four experiments are shown in Table 5.

Table 3. The metrics for accuracy evaluation.

Metrics	Formula	Explanations
Hoover Index (H)	$H=1-\frac{CD}{N_{GT}}$	Measures the number of correct detection based on the percentage of overlap between segmentation and reference ground truth (GT) [40]. CD is the number of correct detections and $N_{GT}$ represents the number of segments in the GT image. Range [0,1], “H = 0” stands for perfect segmentation.
Area-Fit-Index (AFI)	$AFI=\frac{1}{N_{GT}}{\displaystyle \sum _{k=1}^{N_{GT}}\frac{A_k-A_{l.i{.}_k}}{A_k}}$	Addresses over-/under-segmentation by analyzing the overlapping area between segmentation and reference GT [41]. where Ak is the area, in pixels, of a reference segment Ck in the GT image, and Al.i.k is the area, in pixels, of the segment in the segmentation outcome S, with the largest intersection with the reference segment Ck. NGT is the number of segments in the GT image. “AFI = 0” stands for perfect overlap.
Shape Index (SI)	$SI=\frac{1}{N_{GT}}{\displaystyle \sum _{j=1}^{N_{GT}}(\frac{{\rho }_j}{4\sqrt{A_j}}-\frac{{\rho }_i}{4\sqrt{A_i}})}$	Addresses the shape conformity between segmentation and reference GT [42]. where NGT is the number of segments in the GT image, ρi and ρj are the perimeters of the segments Ci and Cj, and Ai and Aj are their respective areas. Range [0,1], “SI = 0” stands for perfect segmentation.
Rand Index (RI)	$RI=1-\frac{\left|p_{00}\right|+\left|p_{11}\right|}{\left|p\right|}$	Measures the ratio between pairs of pixels that were correctly classified and the total pairs of pixels [43]. Let I = {𝑝1,…,𝑝N} be the set of pixels of the original image and consider the set of all pairs of pixels $𝒫$ = {(𝑝i,𝑝j) I × I|i < j}. Moreover, Ci, a segment in the segmentation S, and Cj, a segment in the GT image, are considered as partitions of the image I. Then, $𝒫$ is divided into four different sets depending on where a pair (𝑝i,𝑝j) of pixels falls: $𝒫$11: in the same segment both in Ci and Cj. $𝒫$10: in the same segment in Ci but different in Cj. $𝒫$01: in the same segment in Cj but different in Ci. $𝒫$00: in different segments both Ci and Cj. Range [0,1], “RI = 0” stands for perfect segmentation.
Precision-Recall (F)	$F=1-\frac{2PR}{P+R}$, $P=\frac{\mathrm{tp}}{\mathrm{tp}+\mathrm{fp}},R=\frac{\mathrm{tp}}{\mathrm{tp}+\mathrm{fn}}$	Measures the trade-off between Precision and Recall considering segmentation as a classification process [44]. Given a segment from the segmentation outcome S and a segment from its GT, four different regions can easily be differentiated: True positives (tp): pixels that belong to both S and GT. False positives (fp): pixels that belong to S but not to GT. False negatives (fn): pixels that belong to GT but not to S. True negatives (tn): pixels that do not belong to S or GT. Range [0,1], “F = 0” stands for perfect segmentation.
Segmentation Covering (C)	$\begin{array}{l}C(S\to GT)=1-\\ \frac{1}{{\displaystyle \sum N_{GT}}}{\displaystyle \sum _{C_{\mathrm{t}}\in GT}\left|C_{\mathrm{t}}\right|}.{\max }_{C_i\in S}O(C_i,C_t)\end{array}$	Measures the number of pixels of the intersection of two segments [44]. where ΣNGT is the total number of pixels in the original image. The overlap between two segments, Ci in a segmentation S and Cj in its GT, is defined as $O(C_i,C_j)=\frac{|C_i\cap C_j|}{|C_i\cup C_j|}$ Range [0,1], “C = 0” stands for perfect segmentation.
Reference Bounded Segments Booster (RBSB)	$RBSB=\frac{1}{N_{GT}}{\displaystyle \sum _{t=1}^{N_{GT}}(\frac{f{n}_t+f{p}_t}{f{n}_t+t{p}_t})}$	Measures the ratio between the number of pixels outside the intersection of two segments with the area of the reference GT [45]. where t represents a segment from GT and NGT is the number of segments in the GT image. fn, fp, tp is the same as Precision-Recall (F). Range [0,1], “RBSB = 0” stands for perfect segmentation.

Table 4. The ground truth data for the four experiments.

Ground Truth Data	Airborne	SPECIM AISA EAGLE II	WorldView-2	RADARSAT-2
Classes, numbers of polygons	buildings and individual trees, 104	big buildings, 28	fields, 28	fields, 21

Table 5. The values of fitness functions for four experiments.

	Airborne		SPECIM AISA EAGLE II		WorldView-2		RADARSAT-2
Metrics	The Proposed Method	FNEA	The Proposed Method	FNEA	The Proposed Method	FNEA	The Proposed Method	FNEA
Hoover Index (H)	0.88	0.84	0.64	0.68	0.68	0.61	0.58	0.57
Area-Fit-Index (AFI)	2.18	2.5	1.33	1.19	2.03	1.48	122.46	310.56
Shape Index (SI)	0.03	0.02	0.05	0.05	0.05	0.04	0.03	0.03
Rand Index (RI)	0.35	0.38	0.26	0.26	0.3	0.26	0.98	0.99
Precision-Recall (F)	0.25	0.28	0.17	0.17	0.21	0.18	0.96	0.98
Segmentation Covering (C)	0.49	0.49	0.45	0.45	0.43	0.35	0.99	0.99
Reference Bounded Segments Booster (RBSB)	0.73	0.75	0.64	0.6	0.6	0.53	0.99	0.99

The values of metrics for Airborne, SPECIM AISA EAGLE II, WorldView-2, RADARSAT-2 image segmentation are shown in Figure 12.

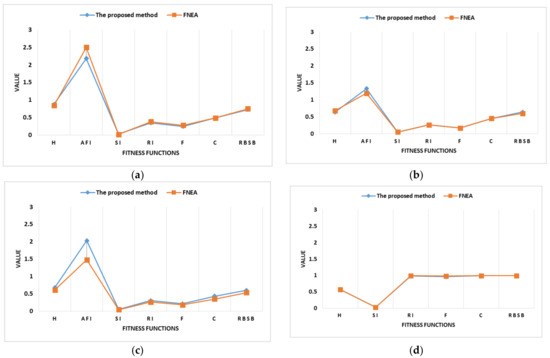
Figure 12. Values of metrics for different sensors using the two segmentation methods described in Section 2. (a). Airborne image segmentation. (b) SPECIM AISA EAGLE II image segmentation. (c) WorldView-2 image segmentation. (d) RADARSAT-2 image segmentation.

All the values except AFI for the airborne image, SPECIM AISA EAGLE II image, and WorldView-2 image were relatively low. The lower the value, the better the result. The results shown in Table 4 demonstrate that the image objects do not over-estimate the ground truth polygons too much, which is desirable. However, the relatively high values suggest that the ground truth polygons are usually far larger in size compared to the evaluated image objects. For the RADARSAT-2 image, all the values are high except H and SI, but the ground truth polygons seem to match the image objects. We segmented the RADARSAT-2 image with different scale parameters and evaluated the segmentation results with the seven metrics. The object boundaries are not clear due to the speckle noise of SAR images, resulting in segments with rough boundaries compared to other images, so the values of RI, F, C, RBSB are close to 1, the AFI is very high, and the overlap is not good between segmentation and reference ground truth. Still, this radar specific phenomenon does not affect the comparative analysis as we use the same evaluation metrics and ground truth.

The curve of the proposed method for the airborne image is the lowest, as shown in Figure 12a. The values of four metrics (AFI, RI, F, RBSB) of the proposed method are the lowest, which shows that the proposed method is better than the FNEA method for airborne images. There is a slight difference between the proposed method and the FNEA for the SPECIM AISA EAGLE II image, as shown in Figure 12b. The values of four metrics (SI, RI, F, C) of the proposed method are the same as the FNEA method, which indicates that the two methods perform similarly on the SPECIM AISA EAGLE II image. The curve of the proposed method is slightly higher than the FNEA method for the WorldView-2 image as shown in Figure 12c, while there is a little difference for the RADARSAT-2 image as shown in Figure 12d. The values of three metrics (AFI, RI, F) are slightly smaller using the proposed method compared to the FNEA, which indicates that the proposed method is better than the FNEA method for RADARSAT-2 image. In summary, the proposed method is generally applicable to different RS imagery and is at least comparable with the FNEA method in accuracy, or even slightly better.

4.3.2. Speed Evaluation

In this section, we analyze the segmentation speed using three metrics: speed-up, efficiency, and effectiveness. The speed evaluation metrics for image segmentation are shown in Table 6.

Table 6. Speed evaluation metrics for image segmentation.

Metrics	Formula	Remarks
Speed-up	$S_P=\frac{T_S}{T_P}$	$T_S$ is the processing time of single computing node. $T_P$ is the processing time of P computing node.
Efficiency	$E_P=\frac{S{}_P}{P}$	$S_P$ is the speed-up of P computing node.
Effectiveness	${\mathrm{F}}_{\mathrm{P}}=\frac{{\mathrm{S}}_{\mathrm{P}}}{\mathrm{P}\times {\mathrm{T}}_{\mathrm{P}}}=\frac{{\mathrm{E}}_{\mathrm{P}}}{{\mathrm{T}}_{\mathrm{P}}}$	$E_P$ is the efficiency of P computing node.

We use two WorldView-2 images with a volume of 1.1 GB and 4.3 GB to test the speed of our segmentation method. The segmentation efficiency is related to the segmentation parameters. The larger the block is, the faster the segmentation. The larger the scale is, the faster the segmentation. In the two tests, the block size is 1024 pixels, and the segmentation parameters are 200, 0.9, 0.5, respectively. The experimental processor is Intel(R) Xeon (R), CPU E5-2640, 24 CPU@2.50 GHz with 16 GB of DDR3. The speed evaluation of parallel segmentation is shown in Figure 13.

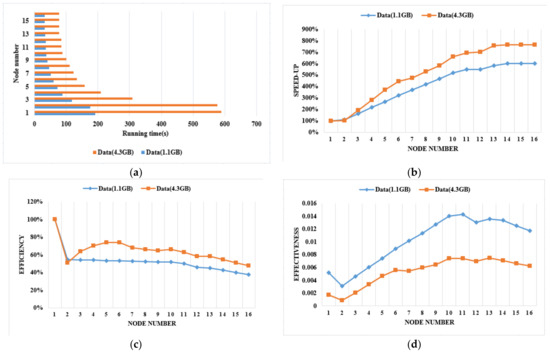
Figure 13. Speed evaluation of parallel segmentation. (a) Running time. (b) Speed-up. (c) Efficiency. (d) Effectiveness.

For the two test data sets, the running time (shown in Figure 13a) tends to decrease with the number of CPUs until it reaches 14, then it becomes stable and shows little variation because of the I/O (Input/Output) reaches a bottleneck. The speed-up (shown in Figure 13b) tends to increase with the number of CPUs until it reaches 14, at which point the maximum is 6 for 1.1 GB data, and 7.65 for 4.3 GB data, then it becomes stable. The efficiency (shown in Figure 13c) tends to decrease as the number of CPUs increases. The effectiveness (shown in Figure 13d) tends to increase with the number of CPUs until it reaches 11, after which it tends to decrease. In summary, when 14 CPUs are used for parallel computing, it is able to achieve the maximum speed-up for the two test data, when 11 CPUs are used for 1.1 GB data and 13 CPUs are used for 4.3 GB data, it is able to achieve the maximum effectiveness, and the parallel computing strategy is more efficient than stand-alone computing. The larger the dataset, the higher the speed-up is, and the higher the efficiency is.

5. Conclusions

This study proposes an efficient parallel multi-scale segmentation method for RS imagery based on graph theory and FNEA, which fully exploits the advantages of both the graph theory and the FNEA method. There are two main contributions: (a) the MST algorithm for initial segmentation is combined with the MHR algorithm which is used for object merging in FNEA; (b) an efficient implementation of the segmentation strategy is presented using data partition and the “reverse searching-forward processing” chain based on MPI parallel technology. Segmentation results using images from different sensors (Airborne, SPECIM AISA EAGLE II, WorldView-2, RADARSAT-2) and complex scenes (residential/industrial, residential/agriculture) covering four sites indicated a general applicability to different RS imagery (airborne optical, satellite optical, SAR, high-spectral) in accuracy using seven different metrics, namely Hoover Index, Area-Fit-Index, F-measure, Shape Index, Reference Bounded Segments Booster, Rand Index, Segmentation Covering. Segmentation results of the WorldView-2 large datasets demonstrate a high efficiency in speed in terms of three metrics: speed-up, efficiency, and effectiveness.

The proposed method has the following advantages: (a) it is an effective method using a fast graph segmentation algorithm to create the initial objects, yielding a linear complexity for the number of image pixels; (b) it is a multi-scale segmentation method for RS imagery using the MHR algorithm to merge the initial object, and it is suitable for a variety of landscapes (residential/industrial, residential/agriculture); (c) it is efficient for large datasets using data partition and the “reverse searching-forward processing” chain based on MPI parallel technology. We conclude that the proposed method has a general applicability and high efficiency for a variety of RS imagery (airborne optical, satellite optical, SAR, high-spectral) with a variety of landscapes (residential/industrial, residential/agriculture), and is at least comparable to the FNEA method in terms of accuracy, in some respects it even performs slightly better.

Nevertheless, as segmentation itself is a problem without a perfect solution—some scholars even claim it is an ill-posed problem—it is hard to find optimal segmentation parameters and there is no optimal solution across a variety of landscapes. Different landscapes may contain inherent features at different scales, thus requiring multi-scale consideration, but recent developments allow for the use of more objective comparisons between the various parameters and thresholds. We referred to the popular ESP tool [30] and to the work of Stumpf and Kerle who determined multiple optimal scales objectively and subsequently linked them to landscape fragments for image-based identification of landslides [34]. Ma et al. [46] extensively analyzed feature selection methods for OBIA classifiers. These and other recent efforts pave the way for future workflows. The currently prevailing strategy of selecting segmentation parameters by an iterative trial-and-error approach still requires a lot of effort. Thus, automated methods need to be investigated for a variety of landscapes. In addition, the boundary problem of parallel segmentation could be tackled in this study satisfactorily but not perfectly. A full exploitation of this problem will be worth a study on its own. In fact, future work needs to integrate concepts from the OBIA community as laid out in [2] and concepts from computer vision, and the segmentation method will be implemented in an open source and made available to the whole RS community.