A New Perspective on Formation of Haze-Fog: The Fuzzy Cognitive Map and Its Approaches to Data Mining
Abstract
:1. Introduction
2. Previous Research on the Formation of Haze-Fog
2.1. Physical Chemistry Mechanism in the Formation of Haze-Fog
2.2. Statistical Analysis of the Formation of Haze-Fog
2.3. Data Mining Methods for the Formation of Haze-Fog
2.4. Proposed Problems
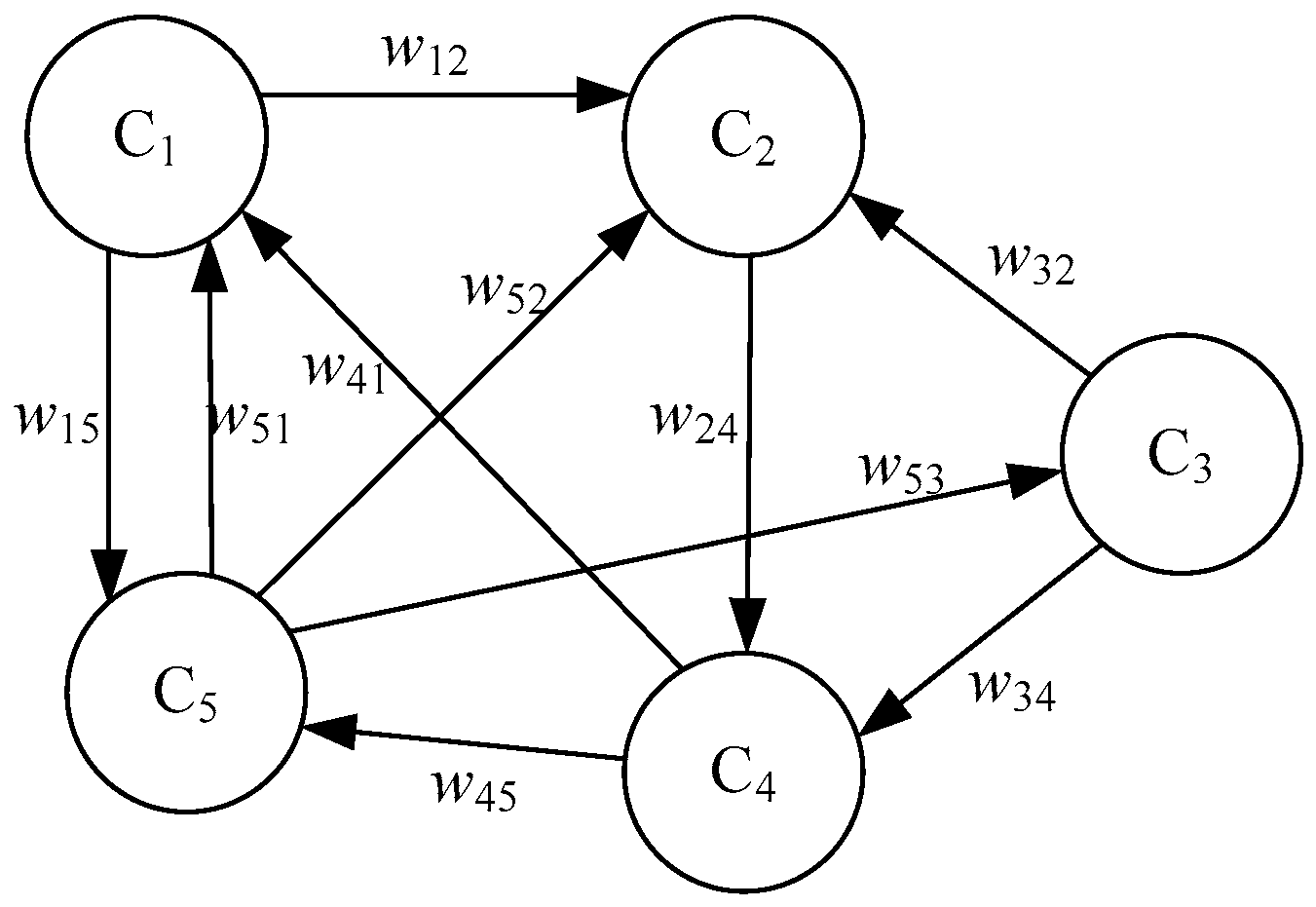
- C = {C1, C2, …, Cn} is the set of n nodes of a graph, which represents a set of concepts of a system, in general.
- W: (Ci, Cj) → wij is a function of n × n to a pair of concepts (Ci, Cj) taking value in the range −1 to 1, with wij denoting a weight of directed edge from Ci to Cj, if i ≠ j, and wij equal to zero if i = j. Thus, W (n × n) = (wij) is a connection matrix.
- A(t) = {A1(t), A2(t), …, An(t)} is a sequence of concepts activation degrees at the moment t. A(0) indicates the initial vector and specifies initial values of all concept nodes and A(t) is a state vector at certain iteration t.
- f is a transformation function, which includes recurring relationship on t ≥ 0 between A(t + 1) and A(t).where is the state of cause concept j at t iteration and is the state of effect concept i at t + 1 iteration, is a cause-effect relationship weight from Cj to Ci. The transformation function is used to confine the weighted sum to a certain range, which is usually set to [0, 1]. The three most commonly used transformation functions are shown in Equations (1)–(3).
- bivalent
- trivalent
- logistic
3. A New Perspective: The Fuzzy Cognitive Map for Haze-Fog Formation
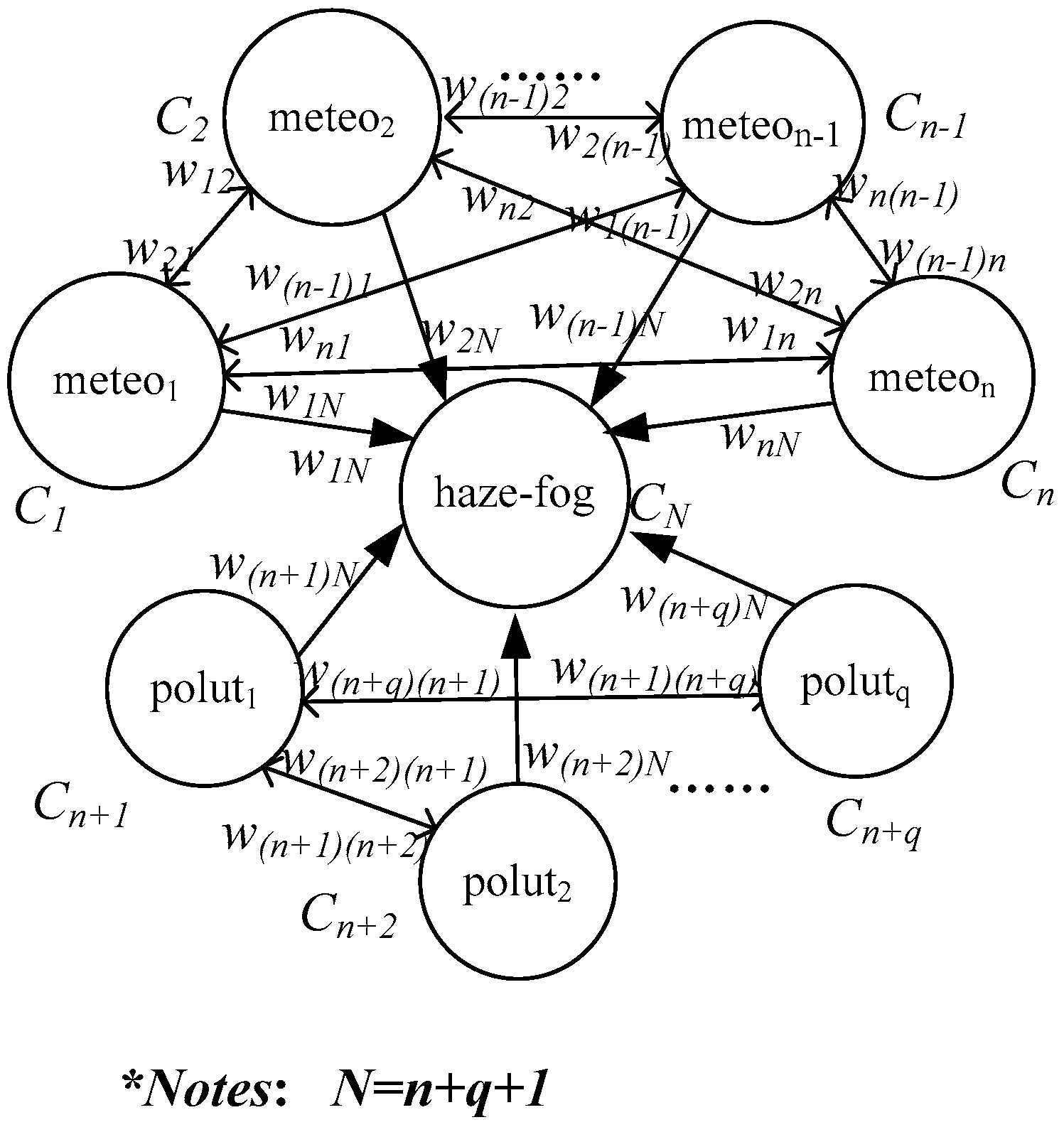
3.1. The Construction of the Fuzzy Cognitive Map for Haze-Fog Formation
3.2. The Evolution Mechanism of the Fuzzy Cognitive Map to Haze-Fog Formation
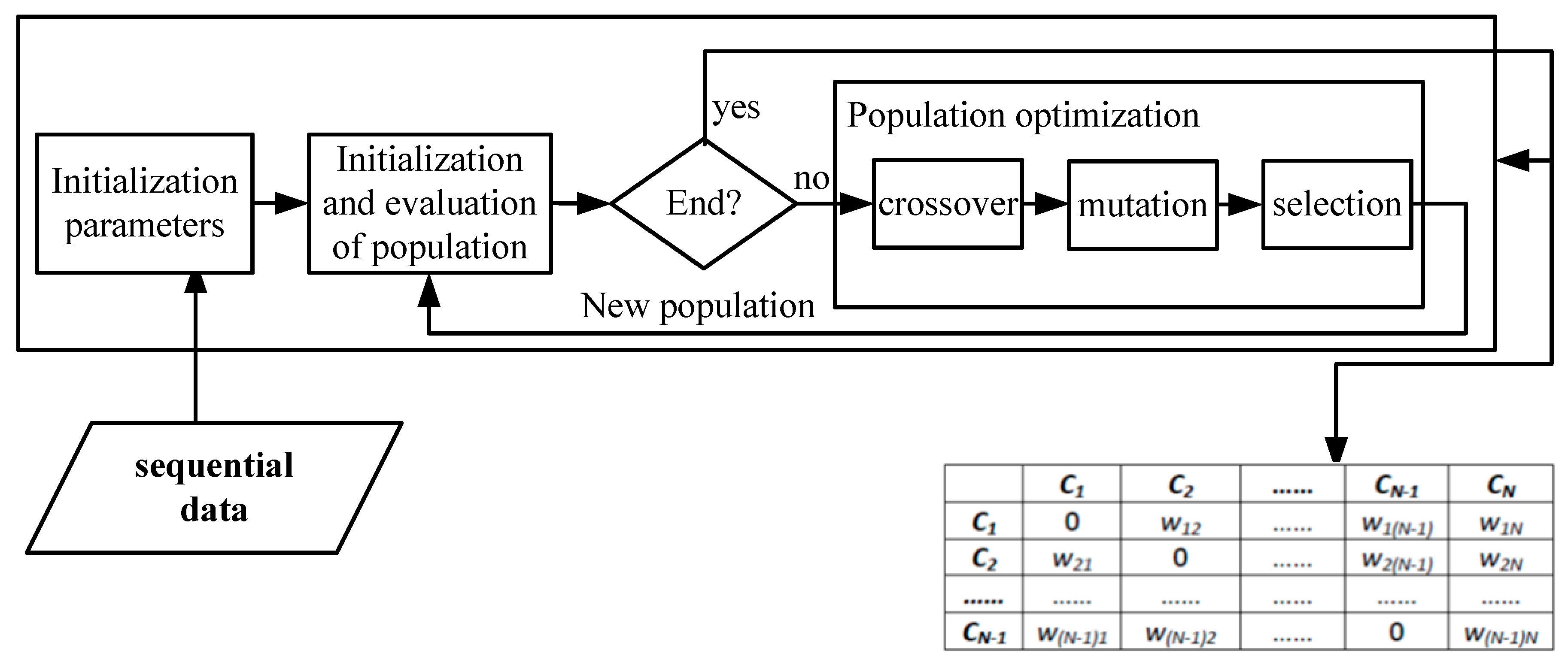
4. The Approach to Data Mining of the Fuzzy Cognitive Map for Haze-Fog Formation
5. Experiments and Results
- recombination method—single-point crossover;
- mutation method—random mutation;
- selection method—roulette wheel;
- probability of recombination: 0.8;
- probability of mutation: 0.5;
- population_size: 200 chromosomes;
- max_generation: 500,000;
- max_fitness: 0.9; and
- the parameters of the FCM:
| if (the forecast value is in the interval of corresponding actual intensity) |
| the number of valid forecast in the right interval plus one; |
| else |
| the invalid number in a wrong interval plus one. |
6. Conclusions
- (1)
- Physical chemistry methods model the actual physics and chemical reactions of pollutants under the influence of the meteorological conditions. However, with more complex nature of reactions, the methods fail to describe and simulate the nonlinear processes involved in the haze-fog formation.
- (2)
- Statistical analysis methods incorporate the factors that are involved in the formation of haze-fog by using the measurements from equipment and the linear analysis of the contributing factors for the formation of haze-fog. They are important cognitive bases for the formation of the haze-fog. However, statistical analysis cannot describe the nonlinear dynamic process responsible for the formation of haze-fog.
- (3)
- Data mining methods can be used to discover the nonlinear relationships in the formation of haze-fog. However, at present, because of the limitation of the model such as in Meng et al. [43], not considering the correlations among the contributing factors and the dynamic changes in data, the results in existing data mining methods are unsatisfactory.
- (1)
- Quantitatively dynamic models need to be further developed for the formation of haze-fog under increasingly complex scenarios.
- (2)
- The relationships among the factor concepts in the formation of haze-fog need to be well recognized and modeled.
- (3)
- The dynamic and nonlinear changes need to be further simulated for forecasting the formation of haze-fog.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Huang, R.J.; Zhang, Y.; Bozzetti, C.; Ho, K.F.; Cao, J.J.; Han, Y.; Daellenbach, K.R.; Slowik, J.G.; Platt, S.M.; Canonaco, F.; et al. High secondary aerosol contribution to particulate pollution during haze events in China. Nature 2014, 514, 218–222. [Google Scholar] [CrossRef] [PubMed]
- Zhou, C.H. On-Line Numerical Research on Atmospheric Aerosols and Their Interaction with Clouds and Precipitation. Ph.D. Thesis, University of Chinese Academy of Sciences, Beijing, China, 2013. [Google Scholar]
- Zhai, P.M.; Yu, R.; Guo, Y.J.; Li, Q.X.; Ren, X.J.; Wang, Y.Q.; Xu, W.H.; Liu, Y.J.; Ding, Y.H. The strong EI Nino in 2015/2016 and its dominant impacts on global and China’s climate. Acta Meteorol. Sin. 2016, 74, 309–321. [Google Scholar]
- Hexun.com. Available online: http://yxx119.blog.hexun.com/96826207_d.html (accessed on 24 November 2014).
- Wang, W. Studies on Haze Control through Middle Route of South-to-Noah Water Diversion Project in Hebei Province. China Water Resour. 2014, 2, 11–13. [Google Scholar]
- Ganguly, N.D.; Tzanis, C. Study of stratosphere-troposphere exchange events of ozone in India and Greece using ozonesonde ascents. Meteorol. Appl. 2011, 18, 467–474. [Google Scholar] [CrossRef]
- Seinfeld, J.H.; Pandis, S.N.; Noone, K. Atmospheric Chemistry and Physics: From Air Pollution to Climate Change, 2nd ed.; Wiley: Hoboken, NJ, USA, 2006; p. 1595. [Google Scholar]
- Tzanis, C. Ground-based observations of ozone at Athens, Greece during the solar eclipse of 1999. Int. J. Remote Sens. 2005, 26, 3585–3596. [Google Scholar] [CrossRef]
- Chan, C.K.; Yao, X.H. Air pollution in megacities in China. Atmos. Environ. 2008, 42, 1–42. [Google Scholar] [CrossRef]
- Tzanis, C.; Tsivola, E.; Efstathiou, M.; Varotsos, C. Forest fires pollution impact on the solar UV irradiance at the ground. Fresenius Environ. Bull. 2009, 18, 2151–2158. [Google Scholar]
- Zhang, X.Y.; Sun, J.Y.; Wang, Y.Q.; Li, W.J.; Zhang, Q.; Wang, W.G.; Quan, J.N.; Cao, G.L.; Wang, J.Z.; Yang, Y.Q.; et al. Factors contributing to haze and fog in China. Chin. Sci. Bull. 2013, 58, 1178–1187. (In Chinese) [Google Scholar] [CrossRef]
- Kosko, B. Fuzzy cognitive maps. Int. J. Man Mach. Stud. 1986, 24, 65–75. [Google Scholar] [CrossRef]
- Papageorgiou, E.I.; Salmeron, J.L. A review of fuzzy cognitive maps research during the last decade. IEEE Trans. Fuzzy Syst. 2013, 21, 66–79. [Google Scholar] [CrossRef]
- Lorenz, E.N. Deterministic non-periodic flow. J. Atmos. Sci. 1963, 20, 98–101. [Google Scholar] [CrossRef]
- Du, J.; Qian, W.H. Three Revolutions in Weather Forecasting. Adv. Meteorol. Sci. Technol. 2014, 4, 13–27. [Google Scholar]
- Papageorgiou, E.I. Learning algorithms for fuzzy cognitive maps—A review study. IEEE Trans. Syst. Man Cybern. Part C 2012, 42, 150–163. [Google Scholar] [CrossRef]
- Peng, Z.; Wu, L.F.; Chen, Z.G. NHL and RCGA based multi-relational fuzzy cognitive map modeling for complex systems. Appl. Sci. 2015, 5, 1399–1411. [Google Scholar] [CrossRef]
- Acampora, G.; Pedrycz, W.; Vitiello, A. A competent memetic algorithm for learning fuzzy cognitive maps. IEEE Trans. Fuzzy Syst. 2015, 23, 2397–2411. [Google Scholar] [CrossRef]
- Stach, W.; Kurgan, L.A.; Pedrycz, W.; Reformat, M. Genetic learning of fuzzy cognitive maps. Fuzzy Set Syst. 2005, 153, 371–401. [Google Scholar] [CrossRef]
- Peláez, C.E.; Bowles, J.B. Using fuzzy cognitive maps as a system model for failure modes and effects analysis. Inf. Sci. 1996, 88, 177–199. [Google Scholar]
- Subramanian, J.; Karmegam, A.; Papageorgiou, E.; Papandrianos, N.; Vasukie, A. An integrated breast cancer risk assessment and management model based on fuzzy cognitive maps. Comput. Methods Programs Biol. 2015, 118, 280–297. [Google Scholar] [CrossRef] [PubMed]
- Aju kumar, V.N.; Gandhi, M.S.; Gandhi, O.P. Identification and assessment of factors influencing human reliability in maintenance using fuzzy cognitive maps. Qual. Reliab. Eng. Int. 2015, 31, 169–181. [Google Scholar] [CrossRef]
- Buruzs, A.; Hatwágner, M.F.; Kóczy, L.T. Expert-based method of integrated waste management systems for developing fuzzy cognitive map. In Complex System Modelling and Control through Intelligent Soft Computations; Zhu, Q., Azar, A.T., Eds.; Springer: Berlin, German, 2015; Volume 319, pp. 111–137. [Google Scholar]
- Mago, V.K.; Morden, H.K.; Fritz, C.; Wu, T.; Namazi, S.; Geranmayeh, P.; Chattopadhyay, R.; Dabbaghian, V. Analyzing the impact of social factors on homelessness: A fuzzy cognitive map approach. BMC Med. Inform. Decis. Mak. 2013, 13, 859–871. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.J.; Zheng, M.; Cai, J. Comparison and Overview of PM2.5 Source Apportionment Methods. Chin. Sci. Bull. 2015, 60, 109–121. [Google Scholar] [CrossRef]
- Tan, C.H.; Chen, X.; Zhao, T.L.; Shan, Y.P. Research Progress on the Development and Application of Air Quality Models. Environ. Monit. Forewarning. 2014, 6, 1–7. [Google Scholar]
- Abdul-Wahab, S.; Sappurd, A.; Al-Damkhi, A. Application of California Puff (CALPUFF) model: A case study for Oman. Clean Technol. Environ. Policy 2010, 23, 177–189. [Google Scholar] [CrossRef]
- Cheng, S.Y.; Liu, L.; Chen, D.S. Pollution abatement for improving air quality of Tangshan municipality, China: A perspective of urban-airshed carrying-capacity concept. Int. J. Environ. Pollut. 2010, 42, 5–31. [Google Scholar] [CrossRef]
- Sickles, J.E.; Shadwick, D.S.; Kilaru, J.V.; Appel, K.W. “Transference ratios” to predict total oxidized sulfur and nitrogen deposition—Part II, modeling results. Atmos. Environ. 2013, 77, 1070–1082. [Google Scholar] [CrossRef]
- Ding, Y.H.; Liu, Y.J. Analysis of long-term variations of fog and haze in China in recent 50 years and their relations with atmospheric humidity. Sci. China Earth Sci. 2014, 57, 36–46. [Google Scholar] [CrossRef]
- Fu, G.Q.; Xu, W.Y.; Yang, R.F.; Li, J.B.; Zhao, C.S. The distribution and trends of fog and haze in the North China Plain over the past 30 year. Atmos. Chem. Phys. 2014, 14, 11949–11958. [Google Scholar] [CrossRef]
- Guo, L.J.; Guo, X.L.; Fang, C.G. Observation analysis on characteristics of formation, evolution and transition of a long-lasting severe fog and haze episode in North China. Sci. China Earth Sci. 2015, 58, 329–344. [Google Scholar] [CrossRef]
- Zhang, R.H.; Li, Q.; Zhang, R.N. Meteorological conditions for the persistent severe fog and haze event over eastern China in January 2013. Sci. China Earth Sci. 2014, 57, 26–35. [Google Scholar]
- Yang, Y.Q.; Wang, J.Z.; Hou, Q. Research on PLAM Index Prediction Method for Air Quality in Beijing during 2008 Olympic Games. In Proceedings of the Conference of Chinese Society for Environmental Sciences, Chengdu, China, 22 August 2014.
- Yang, Y.Q.; Wang, J.Z.; Hou, Q. A PLAM Index Forecast Method for Air Quality of Beijing in Summer. J. Appl. Meteorol. Sci. 2009, 20, 649–655. [Google Scholar]
- Jansen, R.C.; Shi, Y.; Chen, J.M.; Hu, Y.; Xu, C.; Hong, S.; Li, J.; Zhang, M. Using hourly measurements to explore the role of secondary inorganic aerosol in PM2.5 during haze and fog in Hangzhou, China. Adv. Atmos. Sci. 2014, 31, 1427–1434. [Google Scholar] [CrossRef]
- Shen, X.J.; Sun, J.Y.; Zhang, X.Y.; Zhang, Y.M.; Zhang, L.; Che, H.C.; Ma, Q.L.; Yu, X.M.; Yue, Y.; Zhang, Y.W. Characterization of submicron aerosols and effect on visibility during a severe haze-fog episode in Yangtze River Delta, China. Atmos. Environ. 2015, 120, 307–316. [Google Scholar] [CrossRef]
- Zhang, Y.W.; Zhang, X.Y.; Zhang, Y.M. Significant Concentration Changes of Chemical Components of PM1 in the Yangtze River Delta Area of China and the Implications for the Formation Mechanism of Heavy Haze-fog Pollution. Sci. Total Environ. 2015, 538, 7–15. [Google Scholar] [CrossRef] [PubMed]
- Chung, Y.S.; Kim, H.S.; Yoon, M.B. Observations of Visibility and Chemical Compositions Related to fog, Mist and Haze in South Korea. Water Air Soil Pollut. 1999, 111, 139–157. [Google Scholar] [CrossRef]
- Sun, R. Fog-haze Connecting Factors Analysis over the Beijing Region and Advance of the Standard. Master’s Thesis, Nanjing University of Information Science & Technology, Nanjing, China, 2015. [Google Scholar]
- Liu, J. Temporal-Spatial Variation as Well as Evaluation and Prediction Models of Air Pollutants in Beijing. Ph.D. Thesis, University of Science and Technology Beijing, Beijing, China, 2015. [Google Scholar]
- Liu, D.J.; Li, L. Application Study of Comprehensive Forecasting Model Based on Entropy Weighting Method on Trend of PM2.5 Concentration in Guangzhou, China. Int. J. Environ. Res. Public Health 2015, 12, 7085–7099. [Google Scholar] [CrossRef] [PubMed]
- Meng, Z.J.; Yue, X.N.; Wang, D.Z.; Yuan, Z.H. Model of Causes for Urban Fog-Haze Based on Multiple Regression Analysis. J. Shenyang Univ. (Nat. Sci.) 2015, 27, 139–142. [Google Scholar]
- Papakostas, G.A.; Koulouriotis, D.E.; Polydoros, A.S.; Tourassis, V.D. Towards Hebbian learning of Fuzzy Cognitive Maps in pattern classification problems. Expert Syst. Appl. 2012, 39, 10620–10629. [Google Scholar] [CrossRef]
- Papageorgiou, E.I.; Stylios, C.D.; Groumpos, P.P. Active Hebbian learning algorithm to train Fuzzy Cognitive Maps. Int. J. Approx. Reason. 2004, 37, 219–249. [Google Scholar] [CrossRef]
- Wojciech, S.; Lukasz, K.; Witold, P. A divide and conquer method for learning large fuzzy cognitive maps. Fuzzy Sets Syst. 2010, 161, 2515–2532. [Google Scholar]
- Oikonomou, P.; Papageorgiou, E.I. Particle Swarm Optimization Approach for Fuzzy Cognitive Maps Applied to Autism Classification. In Proceedings of the 9th IFIP International Conference on Artificial Intelligence Applications and Innovations, Paphos, Cyprus, 30 September 2013.
- Ncep.Reanalysis.Dailyavgs. Available online: ftp://ftp.cdc.noaa.gov/pub/Datasets/ (accessed on 7 December 2016).

| Inputs: Sample Data from the Process of Haze-Fog Formation |
| Step1. Initialize parameters of genetic algorithm and the FCM within the known range. Step2. Generate initial population based on operator. Step3. Calculate fitness function according to the time series data. Step4. Evolve the population. Step5. Return to Step 3, until the fitness function is maximized (i.e., the end of mining conditions) after finite iterations. |
| Outputs: The Relationship Degrees in the Fuzzy Cognitive Map for Haze-Fog Formation |
| Haze Intensity | [0, 0.25) | [0.25, 0.50) | [0.50, 0.75) | [0.75, 1] | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Forecast Result | FCM | MRM | FCM | MRM | FCM | MRM | FCM | MRM | ||
| Haze Intensity (Actual Number) | ||||||||||
| [0, 0.25) (4) | 4 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| [0.25, 0.50) (2) | 0 | 0 | 2 | 2 | 0 | 0 | 0 | 0 | ||
| [0.50, 0.75) (1) | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | ||
| [0.75, 1] (3) | 0 | 1 | 0 | 0 | 1 | 0 | 2 | 2 | ||
| Haze Intensity | [0, 0.25) | [0.25, 0.50) | [0.50, 0.75) | [0.75, 1] | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Forecast Result | FCM | MRM | FCM | MRM | FCM | MRM | FCM | MRM | ||
| Haze Intensity (Actual Number) | ||||||||||
| [0, 0.25) (6) | 5 | 5 | 1 | 1 | 0 | 0 | 0 | 0 | ||
| [0.25, 0.50) (7) | 0 | 0 | 7 | 7 | 0 | 0 | 0 | 0 | ||
| [0.50, 0.75) (2) | 0 | 0 | 0 | 0 | 2 | 2 | 0 | 0 | ||
| [0.75, 1] (5) | 0 | 1 | 0 | 0 | 1 | 1 | 4 | 3 | ||
| Haze Intensity | [0, 0.25) | [0.25, 0.50) | [0.50, 0.75) | [0.75, 1] | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Forecast Result | FCM | MRM | FCM | MRM | FCM | MRM | FCM | MRM | ||
| Haze Intensity (Actual Number) | ||||||||||
| [0, 0.25) (11) | 10 | 10 | 1 | 1 | 0 | 0 | 0 | 0 | ||
| [0.25, 0.50) (10) | 1 | 1 | 8 | 8 | 1 | 1 | 0 | 0 | ||
| [0.50, 0.75) (3) | 0 | 0 | 0 | 0 | 3 | 2 | 0 | 1 | ||
| [0.75, 1] (6) | 0 | 1 | 0 | 0 | 1 | 1 | 5 | 4 | ||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, Z.; Wu, L. A New Perspective on Formation of Haze-Fog: The Fuzzy Cognitive Map and Its Approaches to Data Mining. Sustainability 2017, 9, 352. https://doi.org/10.3390/su9030352
Peng Z, Wu L. A New Perspective on Formation of Haze-Fog: The Fuzzy Cognitive Map and Its Approaches to Data Mining. Sustainability. 2017; 9(3):352. https://doi.org/10.3390/su9030352
Chicago/Turabian StylePeng, Zhen, and Lifeng Wu. 2017. "A New Perspective on Formation of Haze-Fog: The Fuzzy Cognitive Map and Its Approaches to Data Mining" Sustainability 9, no. 3: 352. https://doi.org/10.3390/su9030352
APA StylePeng, Z., & Wu, L. (2017). A New Perspective on Formation of Haze-Fog: The Fuzzy Cognitive Map and Its Approaches to Data Mining. Sustainability, 9(3), 352. https://doi.org/10.3390/su9030352





