1. Introduction
In the last decade copula modelling has become a frequently used tool in financial economics. Accounts of copula theory are available in [
1,
2]. Hierarchical, copula-based structures have recently been used in some new developments in multivariate modelling; notable among these structures is the pair-copula construction (PCC). Joe (1996) [
3] originally proposed the PCC and further exploration of its properties has been undertaken by Bedford and Cooke [
4,
5] and Kurowicka and Cooke (2006) [
6]. Aas et al., (2009) [
7] provided key inferential insights which have stimulated the use of the PCC in various applications, (see, for example, Schirmacher and Schirmacher (2008) [
8], Chollete et al. [
9], Heinen and Valdesogo [
10], Berg and Aas [
11], Min and Czado [
12] and Smith et al. [
13]. Allen et al., (2013) [
14] provide an illustration of the use of R-Vine copulas in the modelling of the dependences amongst Dow Jones Industrial Average component stocks, and this study is a companion piece.
There have also been some recent applications of copulas in the context of time series models (see the survey by Patton (2009) [
15], and the recently developed COPAR model of Breckmann and Czado [
16], which provides a vector autoregressive VAR model for analysing the non-linear and asymmetric co-dependencies between two series). Nevertheless, in this paper we focus on static modelling of dependencies based on R Vines in the context of modelling the co-dependencies of ten major European markets as captured by ten major indices and one composite European index. We use the British market represented by the FTSE100, the German market as captured by the DAX, the French market via the CAC40, the Netherlands, via the AEX index, the Spanish market represented by the IBEX35, the Danish market by means of the OMX Copenhagen 20, the Swedish market represented by the OMX Stockholm PI Index, the Finnish market using the OMXHPI, the Portuguese market using the PSI General Index (BVLG) and the Belgian market via the Belgian market via the Bell 20 Index (BFX). We also use the EURO STOXX 50 Index, Europe’s leading Blue-chip index for the Eurozone, which consists of 50 major stocks from 12 Eurozone countries: Austria, Belgium, Finland, France, Germany, Greece, Ireland, Italy, Luxembourg, The Netherlands, Portugal and Spain. We undertake our analysis in three different sample periods which include the GFC; pre-GFC (Jan 2005–July 2007), GFC (July 2007–September 2009), and post-GFC periods (September 2009–December 2013). To further show the capabilities of this flexible modelling technique, we also use R-Vine Copulas to quantify Value at Risk for an equally weighted portfolio of our eleven European indices, as an empirical example. The main aim of the paper is to demonstrate the useful application of both C-Vine and R-Vine measures of co-dependency at at time of extreme financial stress and its effectiveness in teasing out changes in co-dependency.
The paper is divided into five sections: the next section provides a review of the background theory and models applied,
Section 3 introduces the sample,
Section 4 and
Section 5 present the results for our analyses featuring C-Vine and R-Vines,
Section 6 provides an example of the use of R-Vines to forecast the Value-at-Risk (VaR) and a brief conclusion follows in
Section 7.
2. Background and Models
Sklar (1959) [
17] provides the basic theorem describing the role of copulas for describing dependence in statistics, providing the link between multivariate distribution functions and their univariate margins. We can speak generally of the copula of continuous random variables
. The problem in practical applications is the identification of the appropriate copula.
Standard multivariate copulas, such as the multivariate Gaussian or Student-t, as well as exchangeable Archimedean copulas, lack the exibility of accurately modelling the dependence among larger numbers of variables. Generalizations of these offer some improvement, but typically become rather intricate in their structure, and hence exhibit other limitations such as parameter restrictions. Vine copulas do not suffer from any of these problems.
Initially proposed by Joe [
3] and developed in greater detail in Bedford and Cooke [
4,
5] and in Kurowicka and Cooke [
6], vines are a flexible graphical model for describing multivariate copulas built up using a cascade of bivariate copulas, so-called pair-copulas. Their statistical breakthrough was due to Aas, Czado, Frigessi, and Bakken [
7] who described statistical inference techniques for the two classes of canonical C-vines and D-vines. These belong to a general class of Regular Vines, or R-vines which can be depicted in a graphical theoretic model to determine which pairs are included in a pair-copula decomposition. Therefore a vine is a graphical tool for labelling constraints in high-dimensional distributions.
This area of the literature has expanded rapidly. Joe et al., (2010) [
18] explore the tail dependence and conditional tail dependence functions of vine copulas of lower-dimensional margins. In addition, the effect of tail dependence of bivariate linking copulas on that of a vine copula is investigated. Geidosch and Fisher (2016) [
19] show the superiority of vine copulas over conventional copulas when modeling the dependence structure of a credit portfolio. Fischer et al. [
20] use vine copula based quantile regression to stress testing German industry sectors.
One drawback in the application of vine copulas is that even for a moderate number of variables, the number of alternative vine decompositions is very large and there is also a large set of candidate bivariate copula families that can be used as building blocks in any given decomposition. Pangiotelis et al. [
21] address this issue via the consideration of two greedy algorithms which automatically select vine structures and component pair-copula building blocks, so as to reduce computional demands, and report positive results from simulations and applications to data drawn from the retail sector. In a similar vein, Bedford et al. [
22] demonstrate how the application of vines can approximate any density as closely as required. They operationalize their result by showing that minimum information copulas can be used to provide parametric classes of copulas that have required levels of approximation. Scheffer and Weiÿ [
23] use nonparametric Bernstein vine copulas as bivariate pair-copulas to model VaR in a GARCH context. Aas (2016) [
24] provides a review of both inference methods and goodness-of-fit tests for pair-copula constructions for financial applications, plus empirical applications of these models in finance and economics, whilst Fermanian [
25] similarly reviews recent developments in copula models.
A regular vine is a special case for which all constraints are two-dimensional or conditional two-dimensional. Regular vines generalize trees, and are themselves specializations of Cantor trees. Combined with copulas, regular vines have proven to be a flexible tool in high-dimensional dependence modelling. Copulas are multivariate distributions with uniform univariate margins. Representing a joint distribution as univariate margins plus copulas allows the separation of the problems of estimating univariate distributions from problems of estimating dependence.
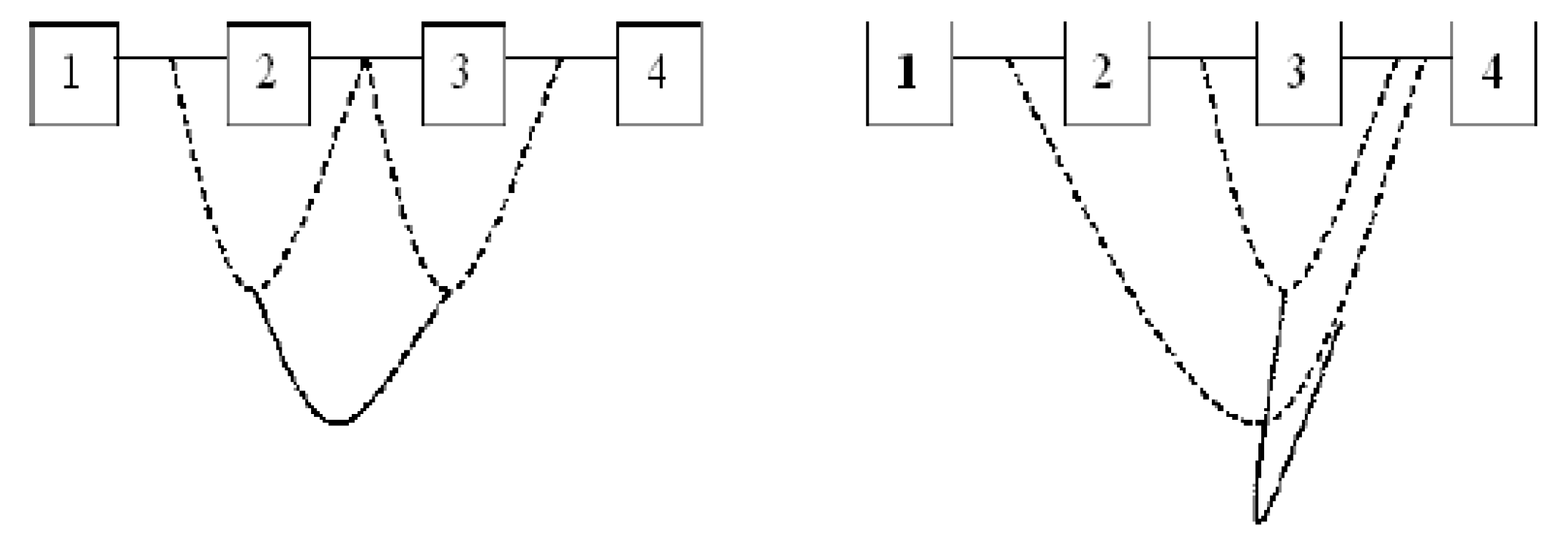
Figure 1 provides an example of two different vine structures, with a regular vine on the left and a non-regular vine on the right, both for four variables.
A vine V on n variables is a nested set of connected trees
where the edges of tree
j are the nodes of tree
. A regular vine on
n variables is a vine in which two edges in tree
j are joined by an edge in tree
only if these edges share a common node,
. Kurowicka and Cook [
26] provide the following definition of a Regular vine.
Definition 1. (Regular vine)
V is a regular vine on n elements with denoting the set of edges of V if
is a connected tree with nodes , plus edges ; for is a tree with nodes ,
(proximity) for , where ∩ denotes the symmetric difference operator and # denotes the cardinality of a set.
An edge in a tree is an unordered pair of nodes of or equivalently, an unordered pair of edges of . By definition, the order of an edge in tree is . The degree of a node is determined by the number of edges attached to that node. A regular vine is called a , or C-vine, if each tree has a unique node of degree and therefore, has the maximum degree. A regular vine is termed a D-vine if all the nodes in have degrees no higher than 2.
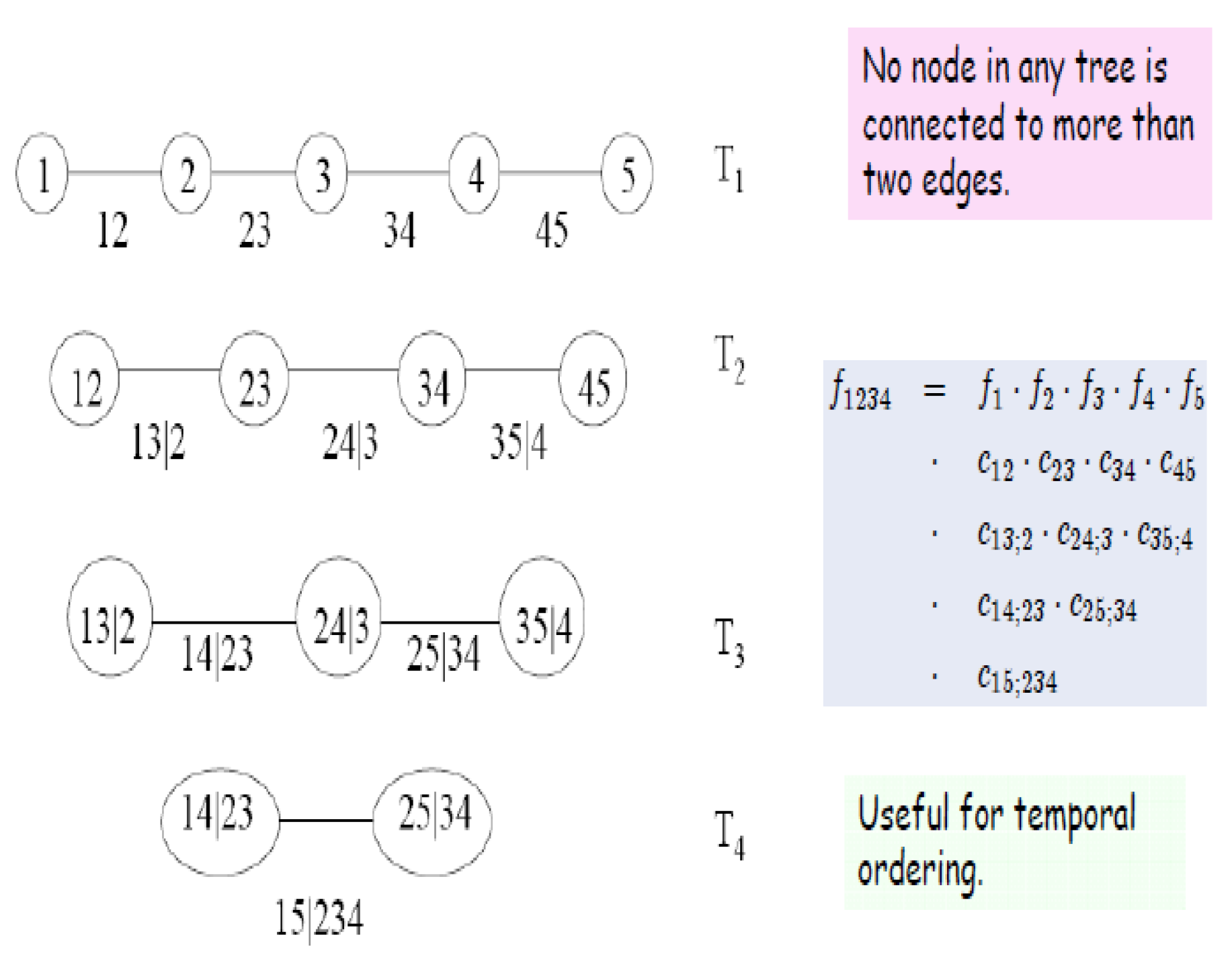
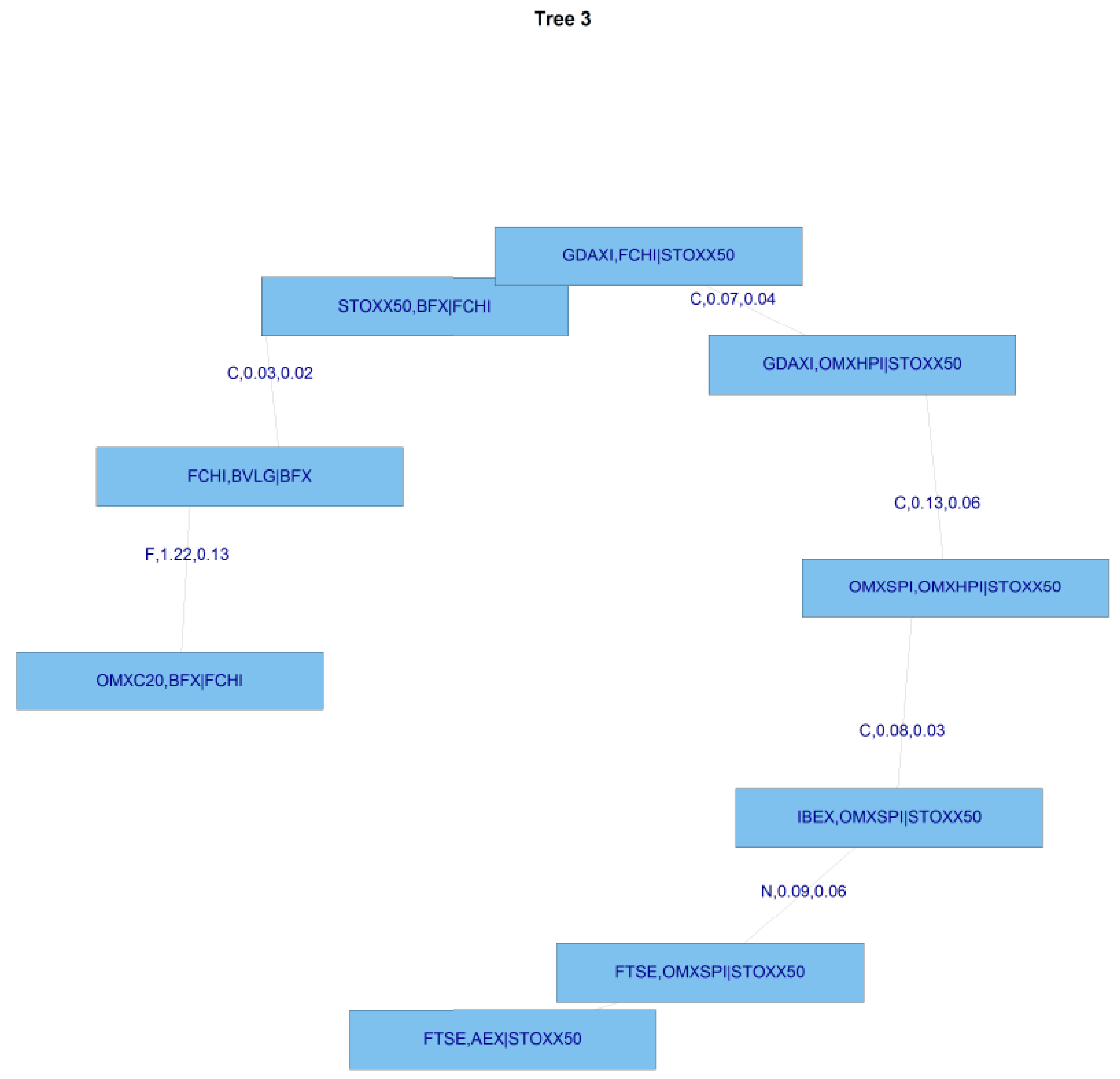
Definition 2. (The following definition is taken from Cook et al., (2011) [27]). For the constraint set associated with e is the complete union of of e, which is the subset of reachable from e by the membership relation. For if , then the conditioning set associated with e isand the conditioned set associated with e isFigure 2 below shows a D-Vine with 5 dimensions. Figure 3 shows an R-Vine on 4 variables, and is sourced from Dissman (2010) [28]. The node names appear in the circles in the trees and the edge names appear below the edges in the trees. Given that an edge is a set of two nodes, an edge in the third tree is a set of a set. The proximity condition can be seen in tree , where the first edge connects the nodes and , and both share node 2 in tree . 2.1. Modelling Vines
Vine structures are developed from pair-copula constructions, in which
pair-copulas are arranged in
trees (in the form of connected acyclic graphs with nodes and edges). At the start of the first C-vine tree, the first root node models the dependence with respect to one particular variable, using bivariate copulas for each pair. Conditioned on this variable, pairwise dependencies with respect to a second variable are modelled, the second root node. The tree is thus expanded in this manner; a root node is chosen for each tree and all pairwise dependencies with respect to this node are modelled conditioned on all previous root nodes. It follows that C-vine trees have a star structure. Brechmann and Schepsmeier (2012) [
29] use the following decomposition in their account of the routines incorporated in the R Library CDVine, which was used for the empirical work in this paper. The multivariate density, the
C Vine density w.l.o.g. root nodes 1, ...,
d,
where
denote the marginal densities and
bivariate copula densities with parameter(s)
(in general,
). The outer product runs over the
trees and root nodes
i, while the inner product refers to the
pair copulas in each tree
.
D-Vines follow a similar process of construction by choosing a specific order for the variables. The first tree models the dependence of the first and second variables, of the second and third, and so on, ... using pair copulas. If we assume the order is
then first the pairs (1, 2), (2, 3), (3, 4) are modelled. In the second tree, the co-dependence analysis can proceed by modelling the conditional dependence of the first and the third variables, given the second variable; the pair
, and so forth. This process can then be continued in the next tree, in which variables can be conditioned on those lying between entries
in the first tree, for example, the pair
. The D-Vine tree has a path structure which leads to the construction of the
D-vine density, which can be constructed as follows:
The outer product runs over
trees, while the pairs in each tree are determined according to the inner product. The conditional distribution functions
can be obtained for an
vector
. This can be done in a pair copula term in tree
by using the pair-copulas of the previous trees
and by sequentially applying the following relationship:
where
is an arbitrary component of
, and
denotes the
- dimensional vector
excluding
. The bivariate copula function is specified by
with parameters
specified in tree
m.
The model of dependency can be constructed in a very flexible way because a variety of pair copula terms can be fitted between the various pairs of variables. In this manner, asymmetric dependence or strong tail behaviour can be accommodated.
Figure 3 shows the various copulae available in the CDVine library in R.
2.2. Regular Vines
Until recently, the focus had been on modelling using C and D vines. However, Dissmann [
28] has pointed the direction for constructing regular vines using graph theoretical algorithms. This interest in pair-copula constructions/regular vines is doubtlessly linked to their high flexibility as they can model a wide range of complex dependencies.
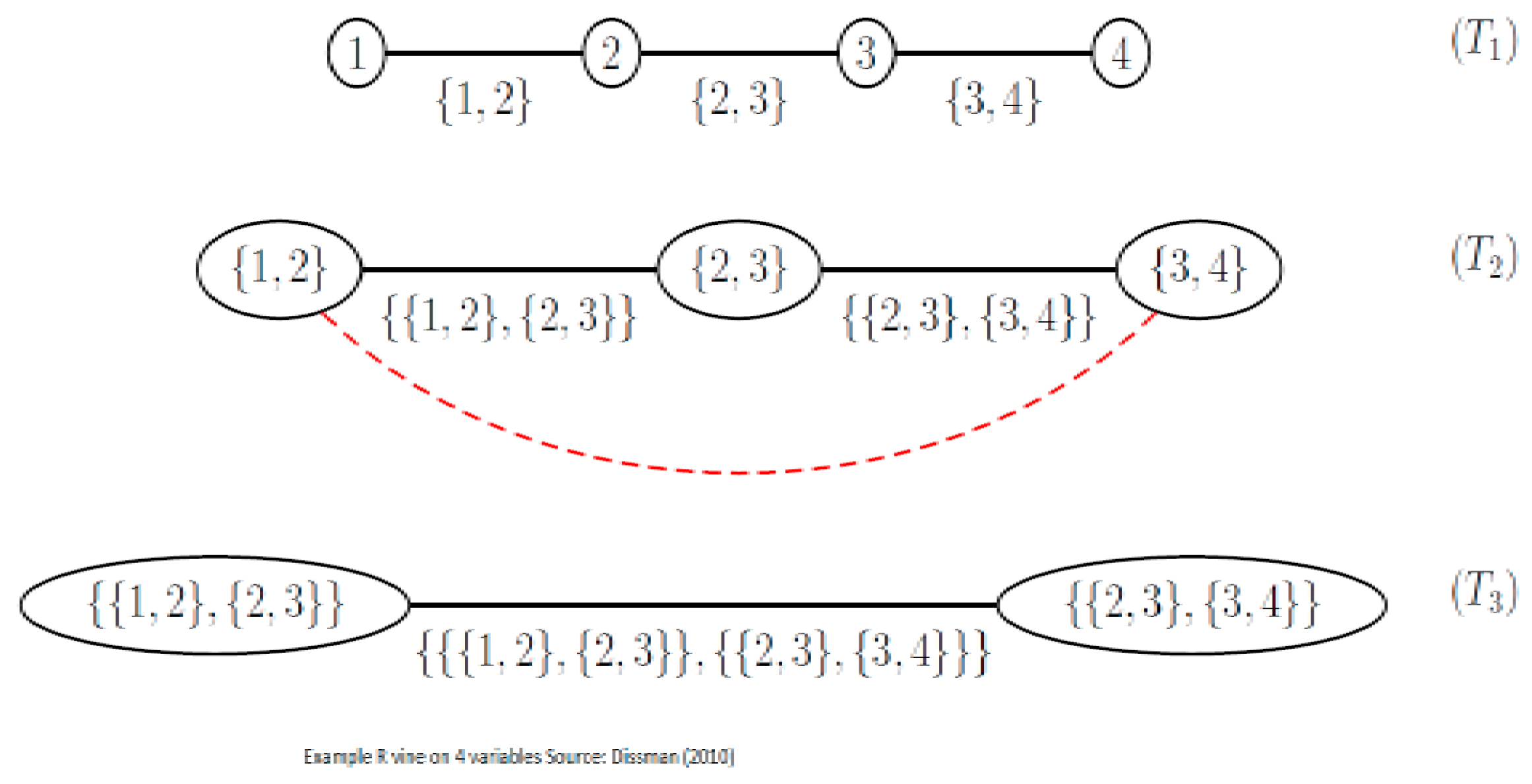
Figure 4 shows an R-Vine on 4 variables, and is sourced from Dissman [
28]. The node names appear in the circles in the trees and the edge names appear below the edges in the trees. Given that an edge is a set of two nodes, an edge in the third tree is a set of a set. The proximity condition can be seen in tree
, where the first edge connects the nodes
and
, plus both share the node 2 in tree
.
The drawback is the curse of dimensionality: the computational effort required to estimate all parameters grows exponentially with the dimension. Morales-N
poles et al. [
30] demonstrate that there are
possible R-Vines on
n nodes. The key to the problem is whether the regular vine can be either truncated or simplified. Brechmann et al. [
28] (p. 2) discuss such simplification methods. They explain that: “by a pairwisely truncated regular vine at level K, we mean a regular vine where all pair-copulas with conditioning set equal to or larger than K are replaced by independence copulas”. They pairwise simplify a regular vine at level K by replacing the same pair-copulas with Gaussian copulas. Gaussian copulas mean a simplification since they are easier to specify than other copulas, easy to interpret in terms of the correlation parameter, and quicker to estimate.
They identify the most appropriate truncation/simplification level by means of statistical model selection methods; specifically, the AIC, BIC and the likelihood-ratio based test proposed by Vuong (1989) [
31]. For R-vines, in general, there are no expressions like Equations (
2) and (
3). This means that an efficient method for storing the indices of the pair copulas required in the joint density function, as depicted in Equation (
4), is required; (4) is a more general case of (
2) and (
3).
Kurowicka [
32] and Dissman [
28] have suggested a method of proceeding which involves specifying a lower triangular matrix
, with
This means that the diagonal entries of
M are the numbers
in descending order. In this matrix, each row proceeding from the bottom represents a tree, the diagonal entry represents the conditioned set and by the corresponding column entry of the row under consideration. The conditioning set is given by the column entries below this row. The corresponding parameters and types of copula can be stored in matrices relating to M. The following example in
Figure 5 is taken from Dissman [
28].
The first section of
Figure 5 provides a key to indicate the 5 different types of copulas used in this example, ranging from Gaussian (1) to Frank (5). The second lower triangular matrix
shows the application of particular types of copulas in the trees,
shows the parameters estimated, and
provides the extra parameters needed when we apply the
t copula.
In
Figure 6 the bottom row of
corresponds to
, the second row to
, and so on. In order to determine the edges in
, we combine the numbers in the bottom row with the diagonal elements in the corresponding columns, for example the edges are (4, 3), (5, 2), (1, 2) and so on. In order to determine the edges in
, we combine the numbers in the second row from the bottom with the diagonal elements in the corresponding columns and condition on the elements in the bottom row. This would give edges
, and so on The final entry is given by the upper entries to the left of the matrix
2.3. Prior Work with R-Vines
The literature was initially mainly concerned with illustrative examples, (see, for example, Aas et al. [
7], Berg and Aas [
11], Min and Czado [
12] and Czado et al. [
33]). Mendes et al., (2010) [
34] use a D-Vine copula model to a six-dimensional data set and consider its use for portfolio management. Dissman [
28] uses R-Vines to analyse dependencies between 16 financial indices covering different European regions and different asset classes, including five equity, nine fixed income (bonds), and two commodity indices. He assesses the relative effectiveness of the use of copulas, based on mixed distributions, t distributions and Gaussian distributions, and explores the loss of information from truncating the R-Vine at earlier stages of the analysis and the substitution of independence copula. He also analyses exchange rates and windspeed data sets with fewer variables.
The research in this paper extends the work of Dissman [
28] applying R-Vines to a European financial data set using a set of eleven European stock indices and features an exploration of how their dependency structures change through periods of extreme stress as represented by the GFC. The paper also features an example of how the dependencies captured by the R-Vine analysis can be used to assess portfolio Value at Risk (VaR) in a manner that closely parallels Breckmann and Czado [
35] who adopted a factor model approach discussed below.
There have been other studies on European stock return series: Heinen and Valdesogo [
10] constructed a CAPM extension using their
Canonical Vine Autoregressive (CAVA) model using marginal GARCH models and a canonical vine copula structure. Breckmann and Czado [
35] develop a regular vine market sector factor model for asset returns that uses GARCH models for margins, and which is similarly developed in a CAPM framework. They explore systematic and unsystematic risk for individual stocks, and consider how vine copula models can be used for active and passive portfolio management and VaR forecasting.
3. Sample
We use a data set of daily returns, which runs from 1 January 2005 to 31 January 2013 for ten European indices and the composite blue chip STOXX50 European index. We use the British FTSE 100 Index, the German DAX Index, the French CAC 40 Index, the Netherlands AEX Amsterdam Index, the Spanish Ibex 35 Index, the Danish OMX Copenhagen 20 Index, the Swedish OMX Stockholm All Share Index, the Finnish OMX Helsinki All Share Index, the Portuguese PSI General Index, and the Belgian Bell 20 Index. As a composite European market index we use the STOXX 50. This index covers 50 stocks from 12 Eurozone countries: Austria, Belgium, Finland, France, Germany, Greece, Ireland, Italy, Luxembourg, the Netherlands, Portugal and Spain. We divide our sample into returns for the pre-GFC (January 2005–July 2007), GFC (July 2007–September 2009) and post-GFC (September 2009–December 2013) periods. The sample is shown in
Table 1.
Table 2 and
Table 3 provide descriptive statistics for the ten European market indices and the composite European STOXX50 index broken down into our three periods; pre-GFC (January 2005–July 2007), GFC (July 2007–September 2009) and post-GFC (September 2009–December 2013). It is apparent that the mean and median returns are uniformly positive in the pre-GFC period, and uniformly negative in the GFC period, whilst the median return is either zero or positive for all but two of the indices during this period. In the post-GFC the mean and median returns for most markets are positive or zero except in the cases of the Spanish and Portuguese markets where there are negative mean returns. The standard deviation is higher in all markets in the GFC period. The Bera-Jarque test significantly rejects normality of the daily return distributions for all indices in all periods. The returns are skewed but in many cases change the direction of the skew from positive to negative in different periods. Only three markets display negative skewness in the GFC period; the Danish, the Portuguese and the Belgian markets. All markets except the Swedish one show greater excess-kurtosis during the GFC period. The GFC period is also characterised by a higher value of the Hurst exponent in all markets, with a value greater than 0.57 in all markets, suggesting the markets display long memory in times of crisis.
The descriptive statistics provided in
Table 2 and
Table 3 suggest that the European index return series in our sample are non-Gaussian and are subject to changes in skewness and kurtosis in the different sample sub-periods. This suggests they should be amenable to analysis by copulas which may capture the effects of fat tails and changes in distributional characteristics.
4. Results
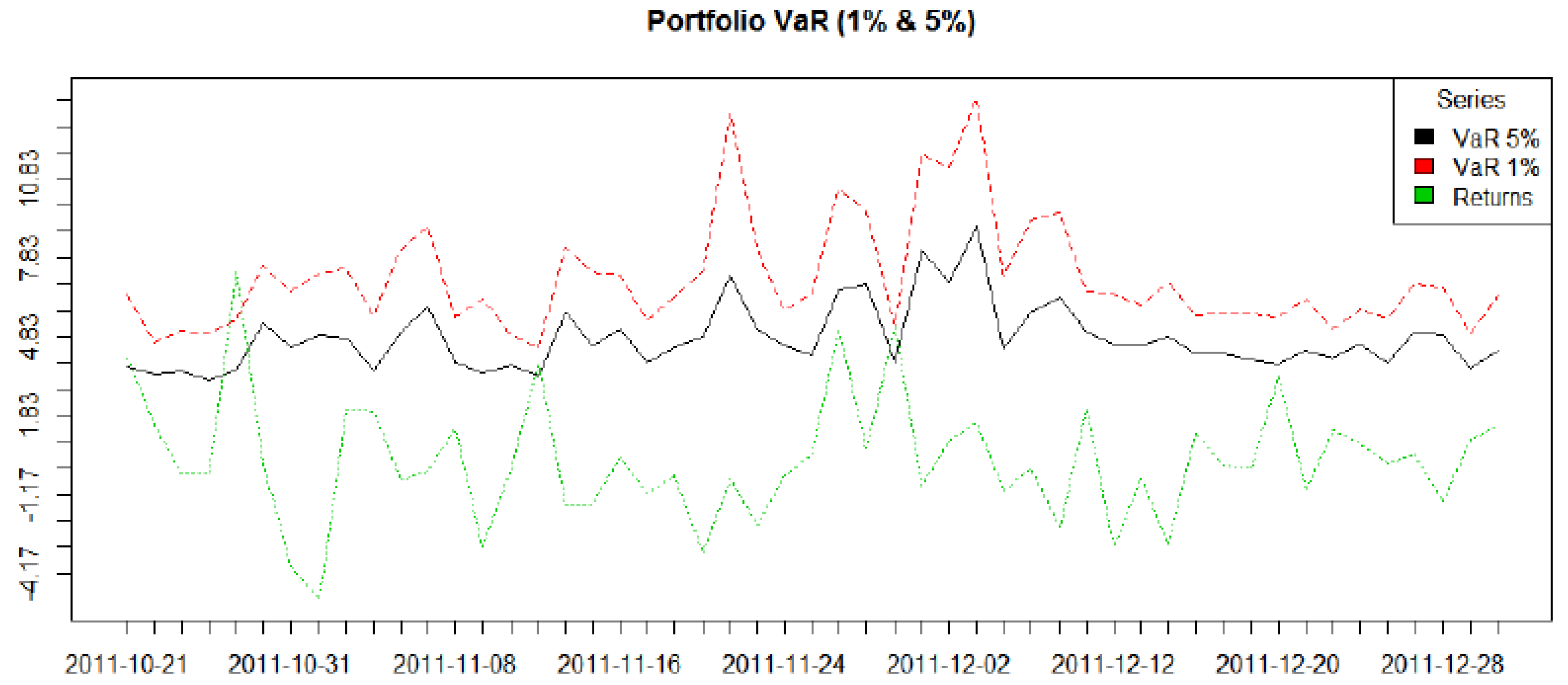
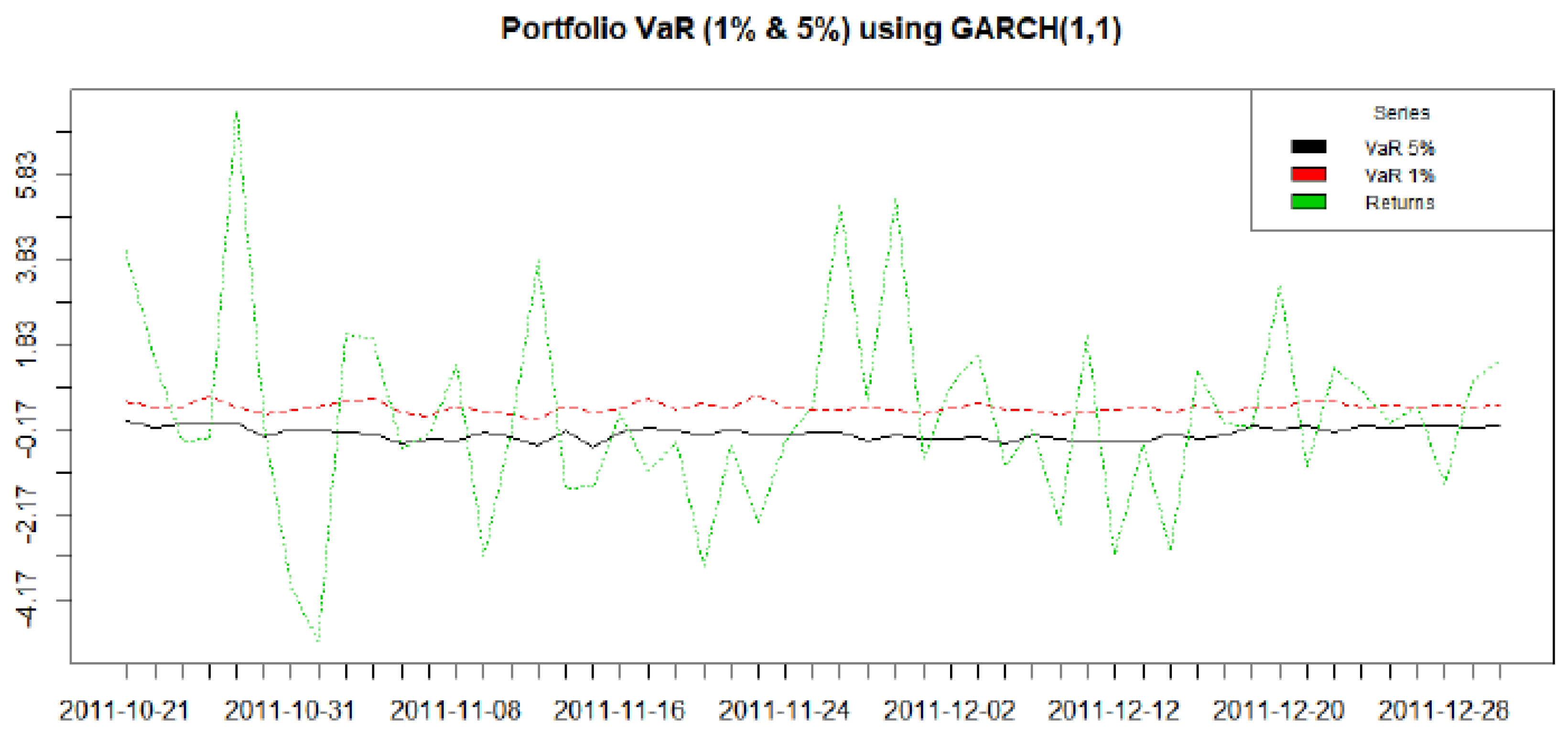
The results are presented here in two parts. In the first subsection below we model the dependence structure of the European set of indices, in three subperiods covering GFC. The second subsection gives results from an empirical exercise modelling VaR using R-Vine Copulas for a 10 asset portfolio and contrasts it with the results of a more traditional Gaussian approach undertaken in a GARCH framework.
4.1. Dependence Modelling Using Vine Copula
We divide the data into three time periods covering the pre-GFC (January 2005–July 2007), GFC (July 2007–September 2009), and post-GFC periods (September 2009–December 2011) to run the C-Vine and R-Vine dependence analysis for the stocks comprising Dow Jones Index. Before we can do this we require appropriately standardised marginal distributions for the basic company return series. These appropriate marginal time series models for the Dow Jones data have to be found in the first step of our two step estimation approach. The following time series models are selected in a stepwise procedure: GARCH (1, 1), ARMA (1, 1), AR(1), GARCH(1, 1), MA(1)-GARCH(1, 1). These are applied to the return data series and we select the model with the highest p-value, so that the residuals can be taken to be i.i.d. The residuals are standardized and the marginals are obtained from the standardized residuals using the Ranks method. These marginals are then used as inputs to the Copula selection routine. The copula are selected using the AIC criterion. We first discuss the results obtained from the pre-GFC period data followed by the GFC and post-GFC periods.
4.2. Pre-GFC
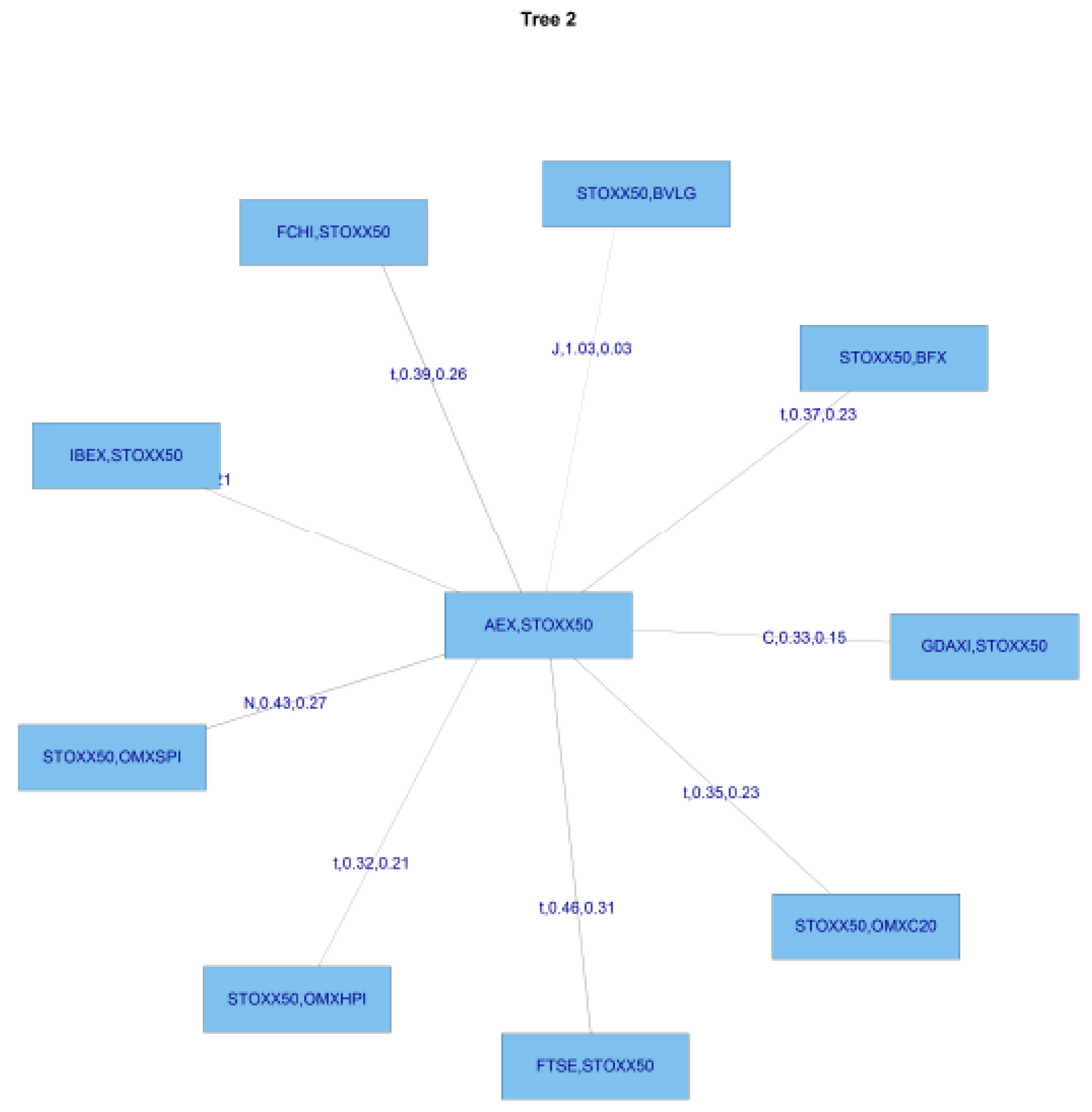
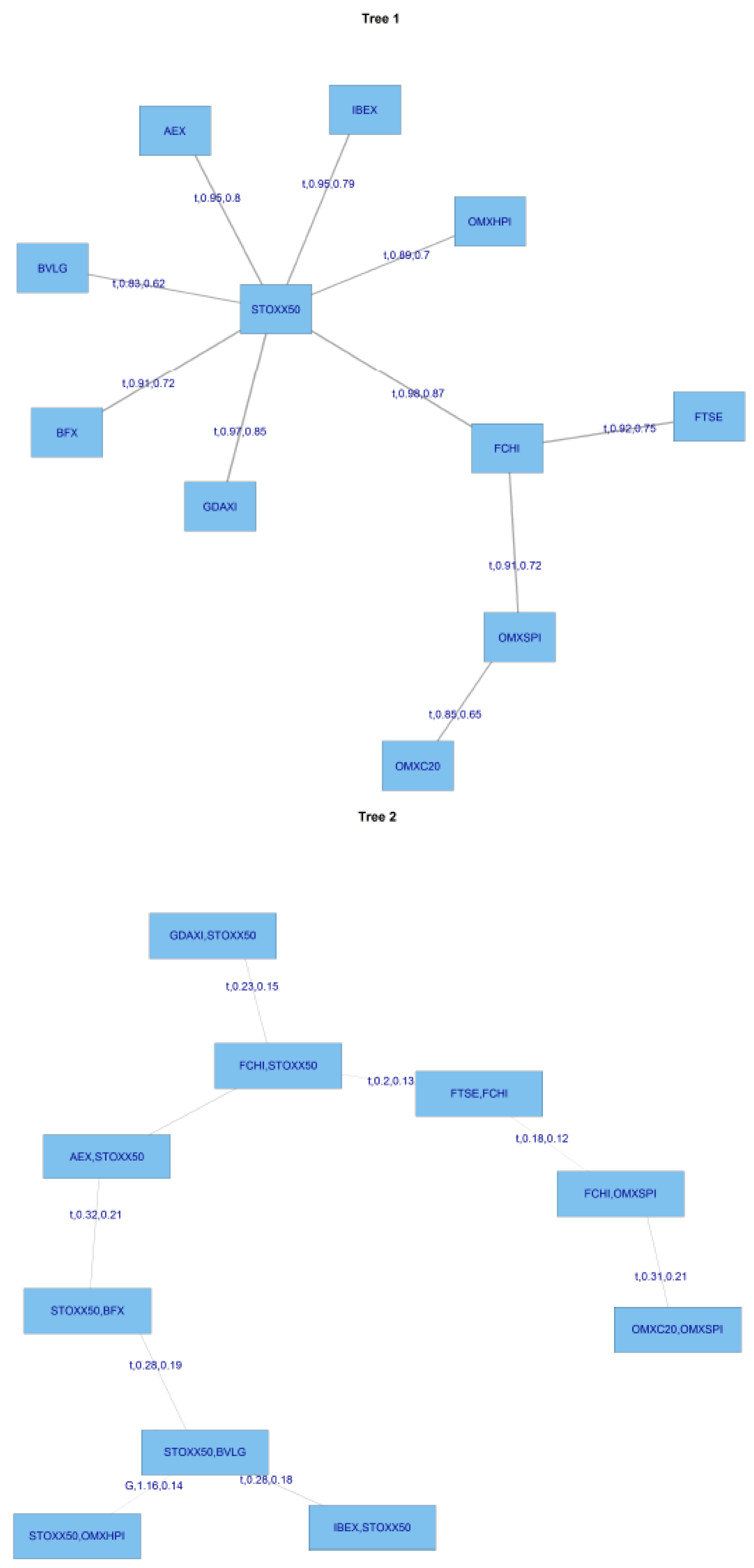
The following
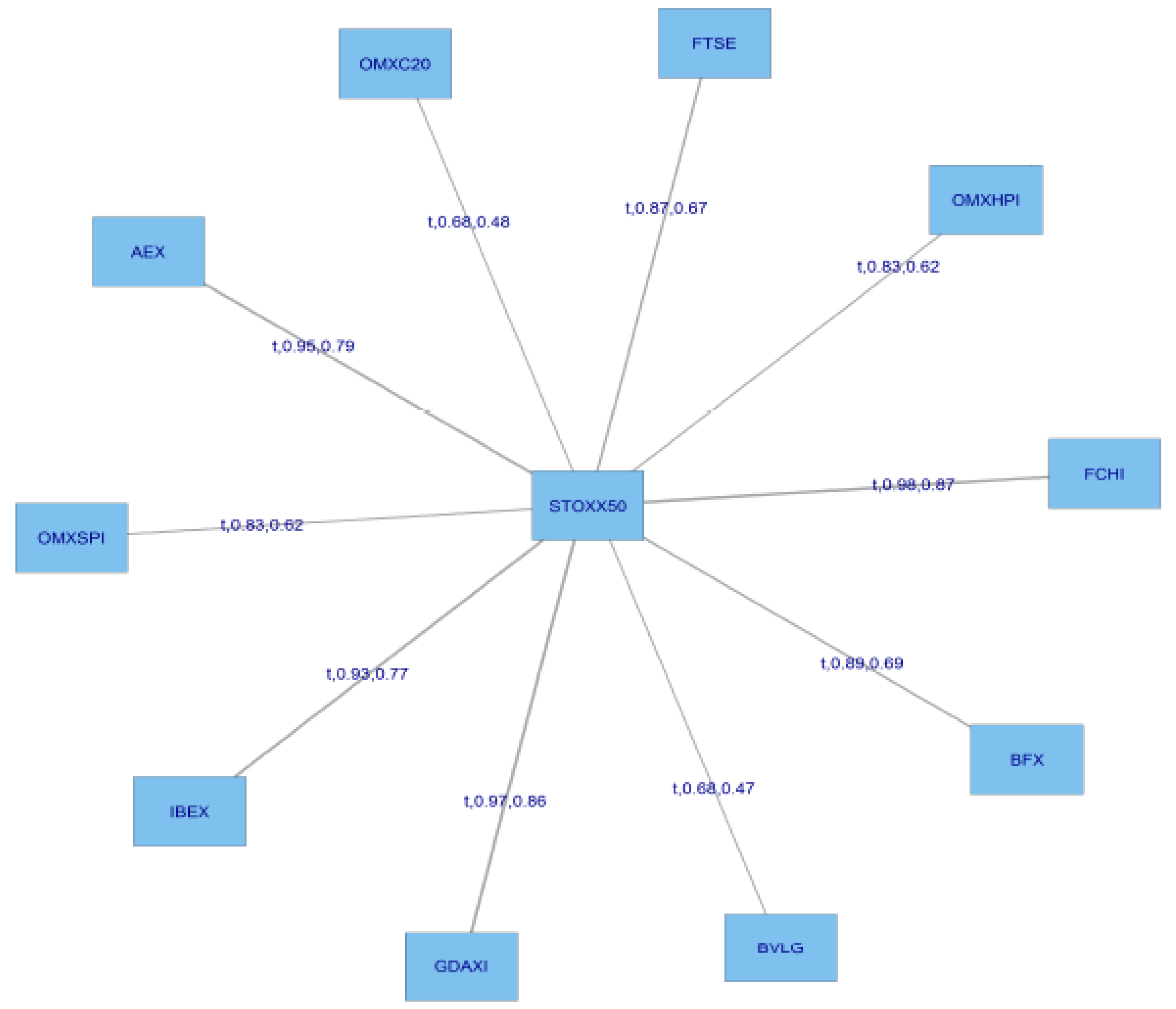
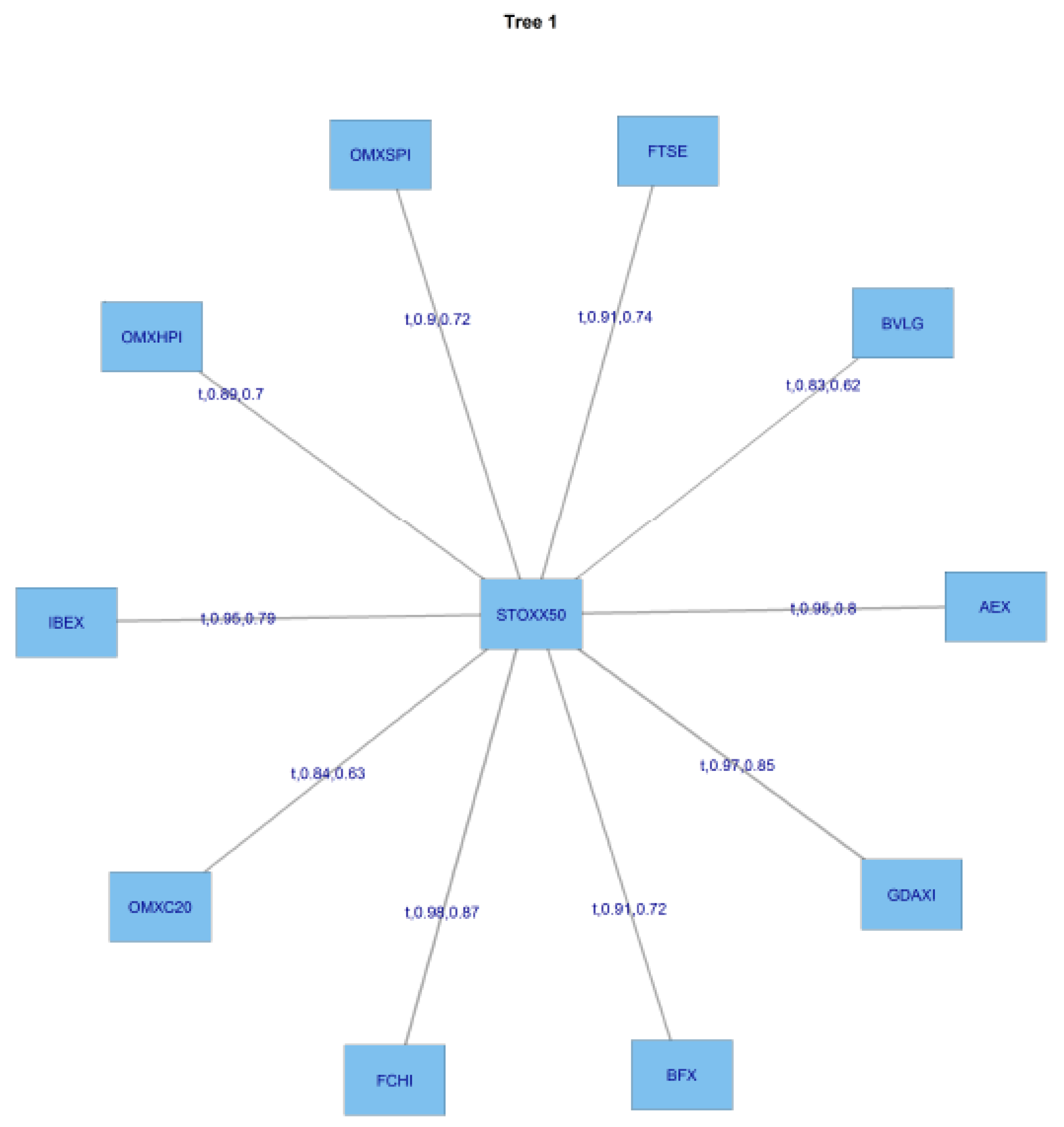
Figure 7 presents the structure of the C-Vines.
For this C Vine selection, we choose as root node the node that maximizes the sum of pairwise dependencies to this node.We commence by linking all the stocks to the STOXX50 index which is at the centre of this diagram. We use a range of Copulas from for selection purposes; the range being (1:6). We apply AIC as the selection criterion to select from the following menu of copulae: 1 = Gaussian copula, 2 = Student t copula (t-copula), 3 = Clayton copula, 4 = Gumbel copula, 5 = Frank copula, 6 = Joe copula.
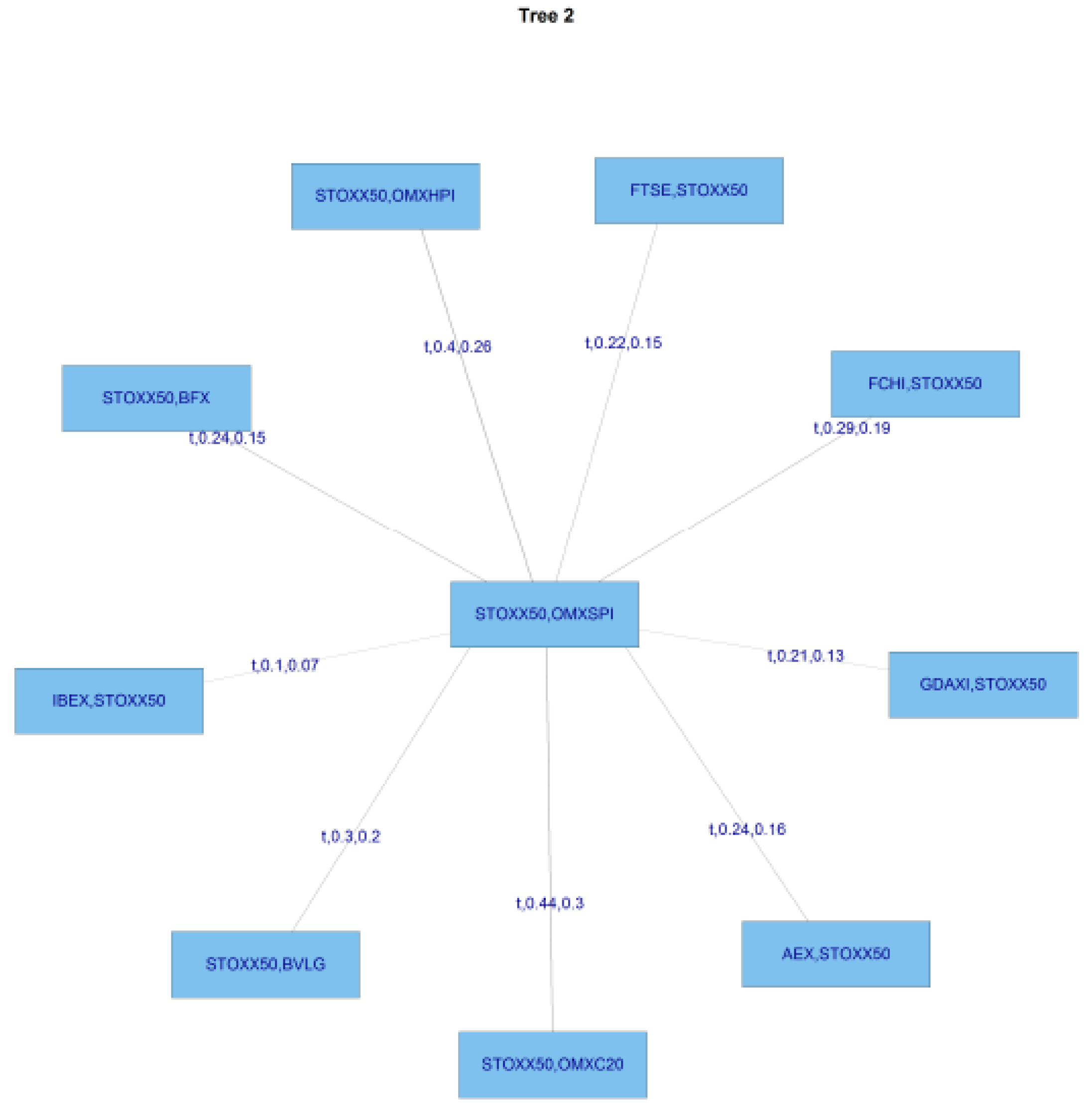
We then compute transformed observations from the estimated pair copulas and these are used as input parameters for the next trees, which are obtained similarly by constructing a graph according to the above C-Vine construction principles (proximity conditions), and finding a maximum dependence tree. The C-Vine tree for period 2 is shown
Figure 8.
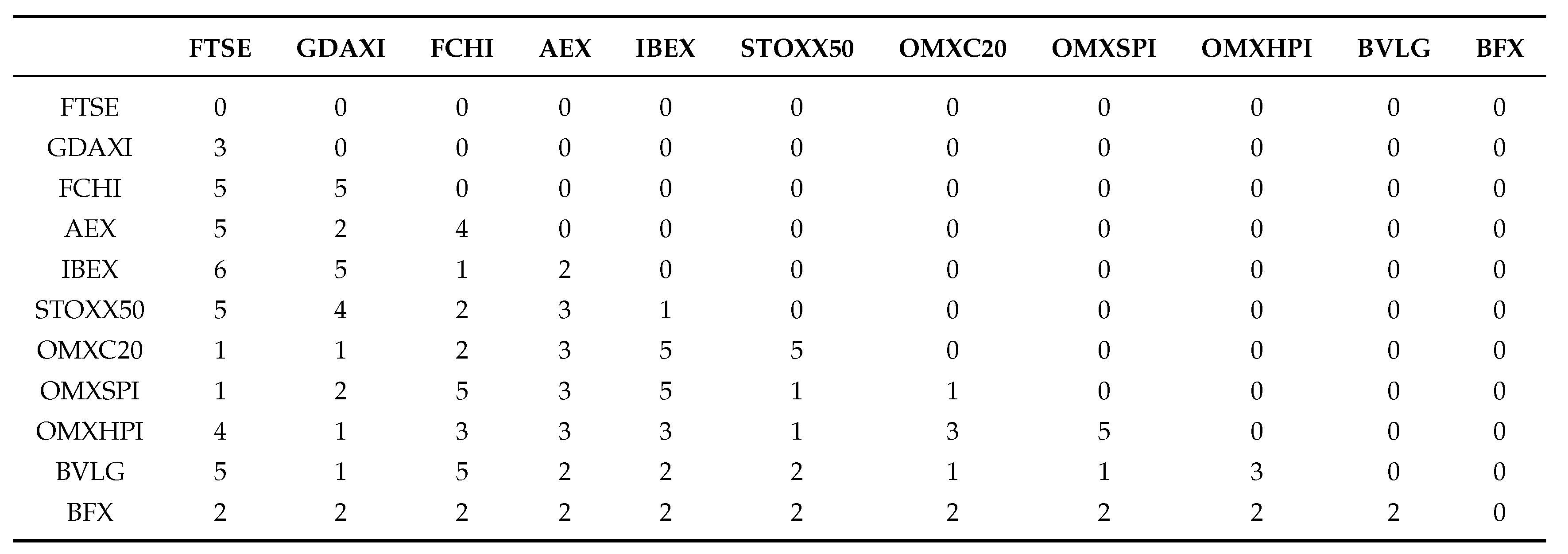
The pre-GFC C-Vine copula specification matrix is displayed in
Table 4 below. It can be seen from the top and bottom of the first column in
Table 4 that in the pre-GFC period the strongest correlations are between the FTSE and Belgian Index BFX. The BFX remains at the bottom across all columns in the last row of
Table 4.
From
Table 4, it can be seen that the strongest individual correlations in the pre-GFC period, are between the FTSE at the top of the first column, BFX in the final row, and the individual diagonal entries starting with the FTSE at the top of the first column, which define the edges. The FTSE is correlated with BVLG (security 11), then conditioned by its relationship with OMXHPI (security 8), the Helsinki exchange index, then OMXSPI (security 5), the Stockholm index, then OMXC20 (security 3), the Copenhagen index, and so on. It can also be seen in
Table 2 that C Vines are less flexible in that the same security number can usually be seen to appear across the rows. This means that it is always appearing in the nodes at that level in the tree. R Vines are more flexible and do not have this requirement. Later in the paper, we will concentrate on the results of the R Vine analysis.
Table 5 shows which copula are fitted to capture dependencies between the various pairs of indices. At the bottom of column 1 in
Table 5 we can see that number 2 copula, the Student t copula is applied, to capture the dependency between FTSE and BFX, and then it is conditioned by the relationship with BVLG but this relationship uses a Frank copula (5), and so forth. All 6 categories of copula are used in
Table 5 but the Student t copula appears most frequently in the table, followed by the Frank copula, the Gaussian copula, the Clayton copula and finally the Joe copula and the Gumbel copula appear once each.
It can be seen in
Table 6 in the entries in the bottom row that there are strong positive dependencies between subsets of the markets concerned. The entry in the bottom of the first column shows the strong positive dependency between the FTSE and BFX. All the entries in the bottom row of
Table 6 are strongly positive. We can see in the first column, that once we have conditioned the FTSE on its relationships with the markets in the bottom half of the column it is strongly positively related to the STOXX50. Not all the dependencies indicated in
Table 6 are positive though, and there are 11 cases of negative co-dependency, once the relationship across other nodes has been taken into account.
Table 7 shows the second set of parameters, in cases where one is needed, for example the Student t copula.
Table 8 shows the tau matrix for the C Vine copulas in the pre-GFC period.
The bottom row of
Table 8 captures the strongest dependencies between the pairs of markets, as represented by their respective indices.
A key concern in this paper is the issue of how dependencies have changed as a result of the GFC?
4.3. GFC Period
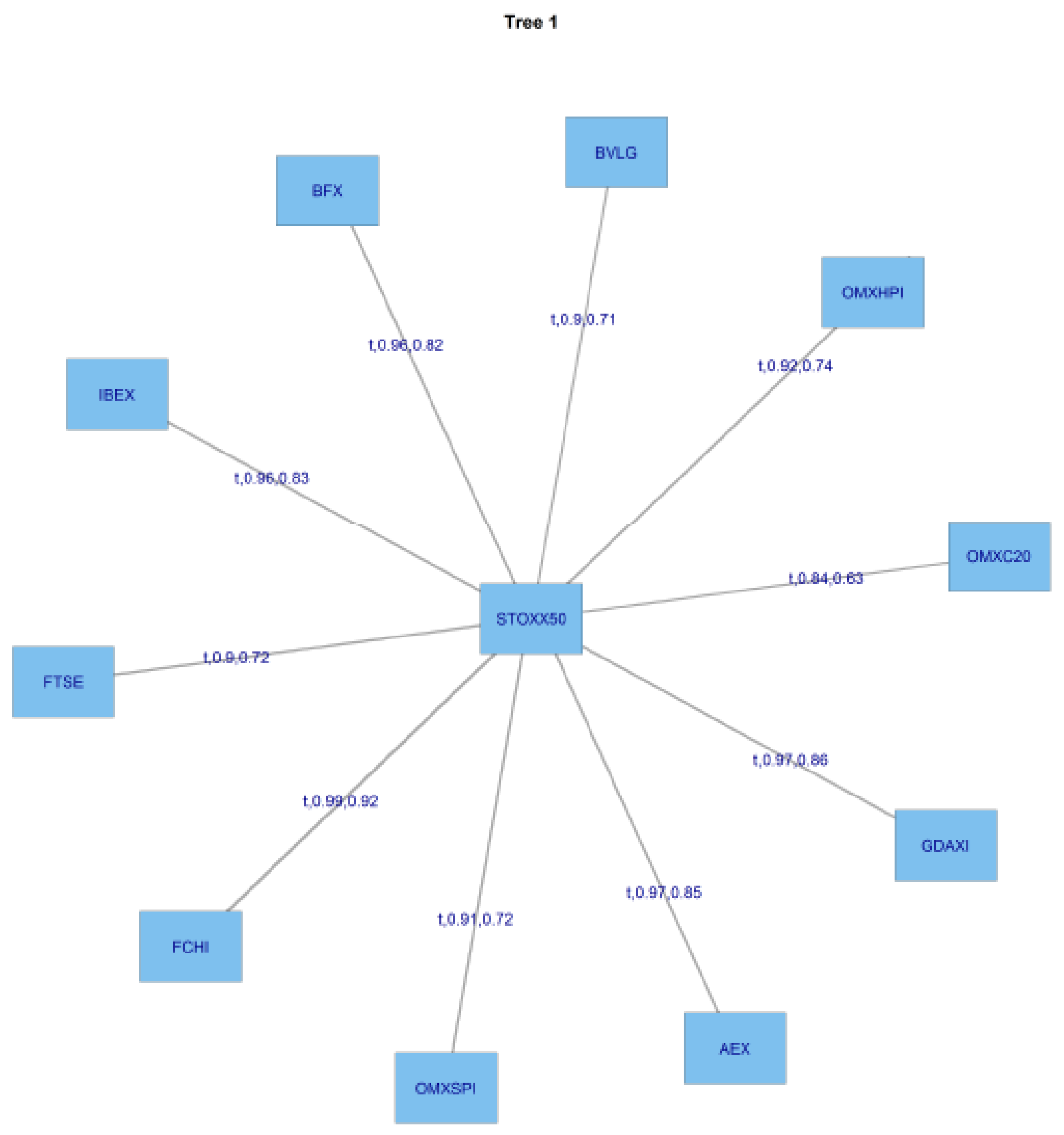
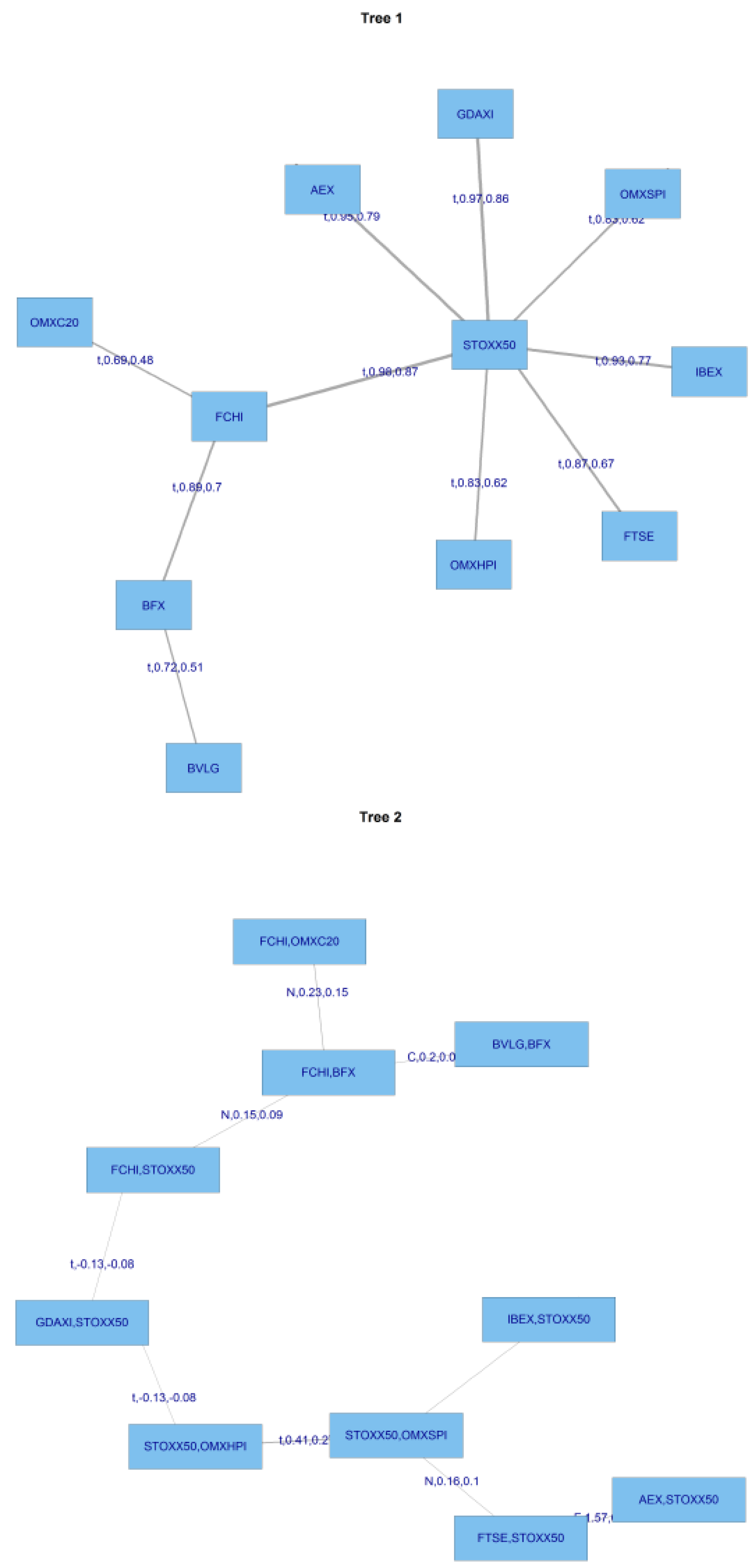
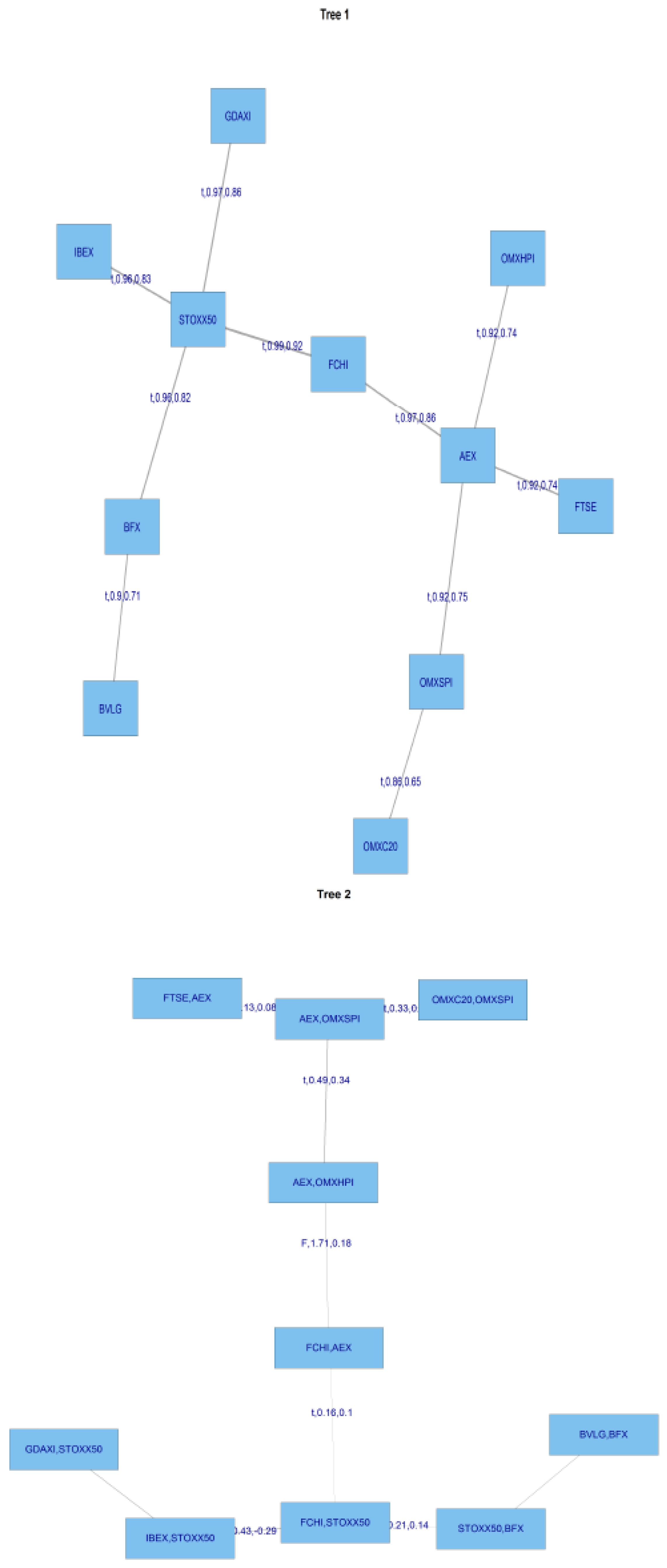
Figure 9 shows tree 1 for C-Vine copula estimates in the GFC period, and
Figure 10 shows tree 2 for the same period.
We are interesting in examing whether the major financial shock which constituted the GFC caused a noticeable change in dependencies?
Table 9 and
Table 10 depicts the copulas chosen to capture dependency relationships during the GFC period.
A comparison of the entries in
Table 10, the copula specification matrix for the GFC, with those in
Table 5, the pre-GFC copula specification matrix, reveals that there is much less us of Gaussian copulas, 3 in
Table 10, compared with 11 in
Table 5. There is now a much greater use made of the Student T copula, on 36 occasions in
Table 10, compared with 18 in
Table 5. The use of the Gumbel copulas has increased from 1 to 4 occasions and the Clayton copula is only used on 2 occasions compared with 5 pre-GFC. The use of the Frank copula has declined from 15 to 6, whilst the Joe copula, now makes 2 appearances compared to 1 pre-GFC. The massive expansion of the use of the Student t copula, together with the other changes mentioned, is consistent with greater weight being placed on the tails of the distribution durng the GFC period.
The dependencies are captured in the Tau matrix shown in
Table 11. A comparison of the values in
Table 11, the tau matrix for the GFC, with those in
Table 8, the tau matrix for the GFC period, reveals that the relationships have become more pronounced. If we look at the dependencies in the bottom row of
Table 11, in 7 from the total of 10 cases the dependencies have increased. It is also true that there has also been a marginal increase in negative dependencies, from 10 pre-GFC to 12 during the GFC, but the values of these are of a low order. The picture that emerges from
Table 11 is one of an increase in dependencies between these major European stock markets during an economic down-turn.
4.4. Post-GFC Period
We will now turn our attention to the post-GFC period. In the case of the European markets, this is likely to be less-clear cut, given that it was characterised by economic turmoil related to the subsequent post-GFC European Sovereign debt crisis.
Figure 11 displays the first tree post-GFC, and
Figure 12 the second tree.
Table 12 shows the post-GFC C-Vine copula structure, and
Table 13 the post-GFC C-Vine Copula Specification Matrix.
It can be seen in
Table 13 that there is a marked change in the type of copula used to capture dependencies in the post-GFC period. The use of the Gaussian copula has risen from 3 during the GFC period to 10 in the post-GFC period, and the application of the Student t copula has dropped from 36 during the GFC to 24 in the post GFC period, whilst the use of the Clayton copula in the post-GFC period rises to 8 from 2 in the GFC period. The Gumbel copula is used on 6 occasions, whilst the Frank copula appears only 5 times, compared with 15 in the pre-GFC period. Finally, the Joe copula, is made use of on 1 occasion. The increase in the use of the Gaussian copula and the reduction in the use of the Student t copula suggests there is much less emphasis on the tails of the distributions in the post-GFC period.
The post-GFC tau matrix is shown in
Table 14. The structure of dependencies that emerges in
Table 14 is quite complex when compared to those of the GFC period. In the bottom row the positive dependencies captured in the tau statistics have increased in 7 of the total of 10 cases. In the GFC period there were 12 negative tau coefficients in the matrix, where as in the post-GFC period this number has reduced to 10. Thus, the broad picture that emerges in the post-GFC period, based on the use of C-Vine copulas, is that overall dependencies increased in the post-GFC period across the major European markets, in association with their experience of the European Sovereign debt crisis. The greater use of Gaussian copulas and the reduction in the use of Student t copulas in this period, suggests that tail behaviour was less important.
We now switch to the more flexible R-Vine framework to compare the two approaches.