Infiltration and Soil Loss Changes during the Growing Season under Ploughing and Conservation Tillage
Abstract
:1. Introduction
2. Materials and Methods
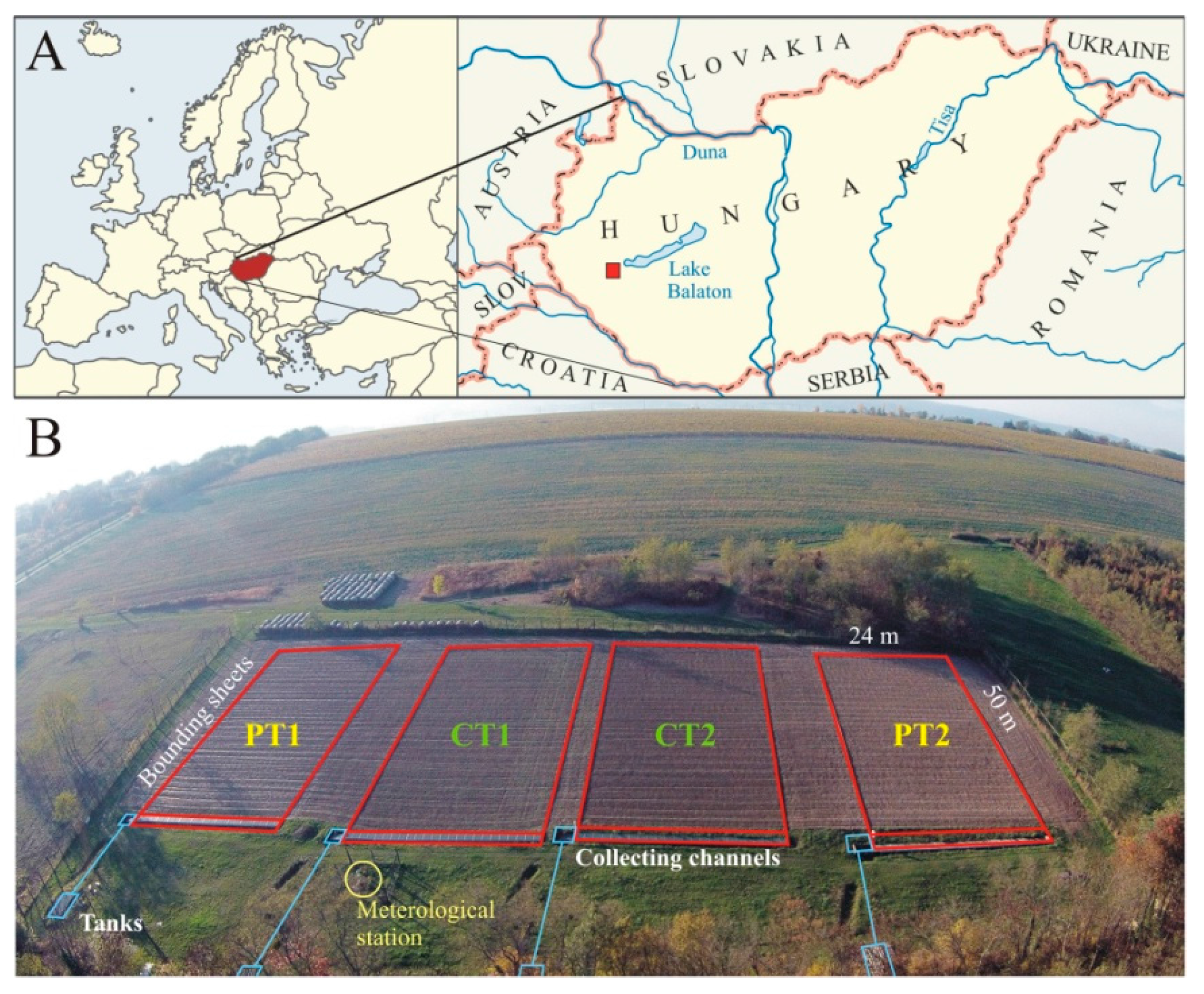
2.1. Study Site
2.2. Rainfall Simulation and Cultivation
2.3. Calculation
2.4. Earthworm Investigation
3. Results and Discussion
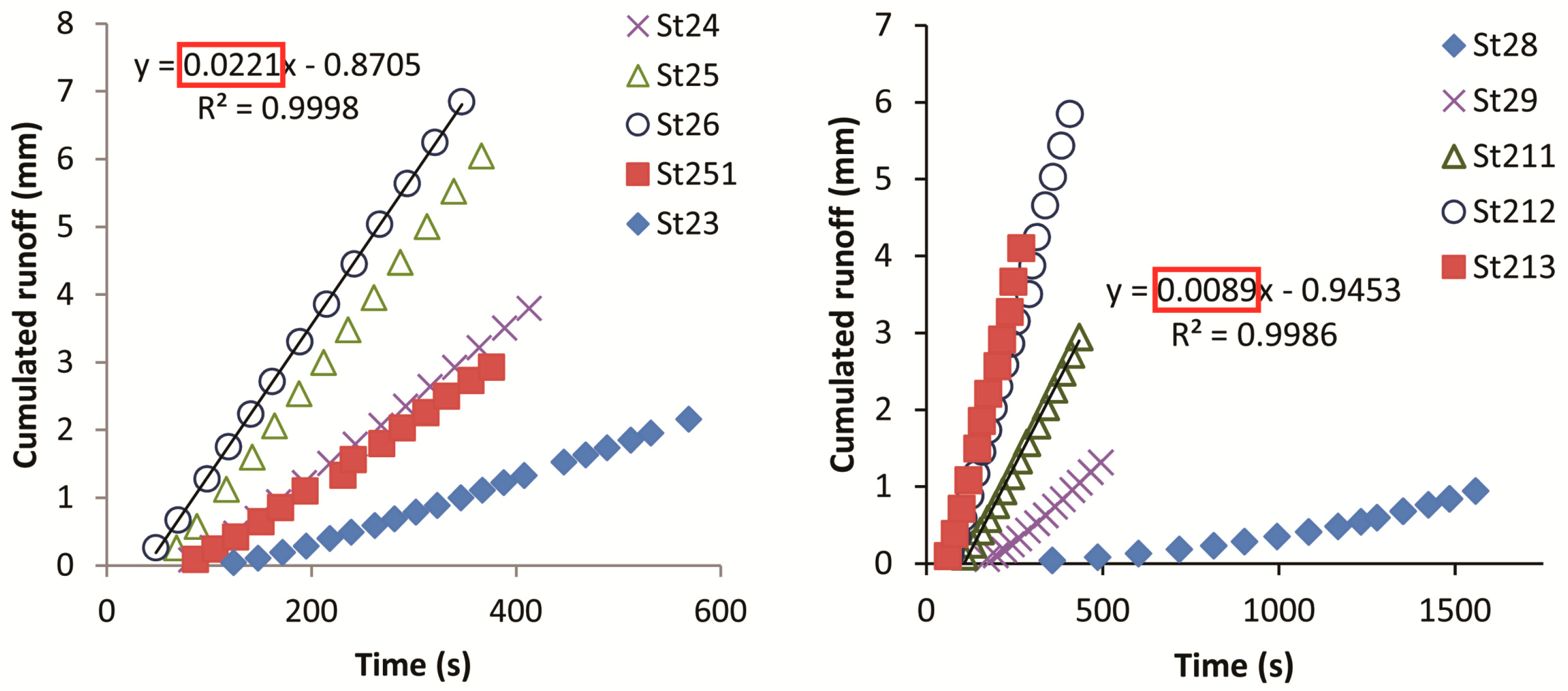
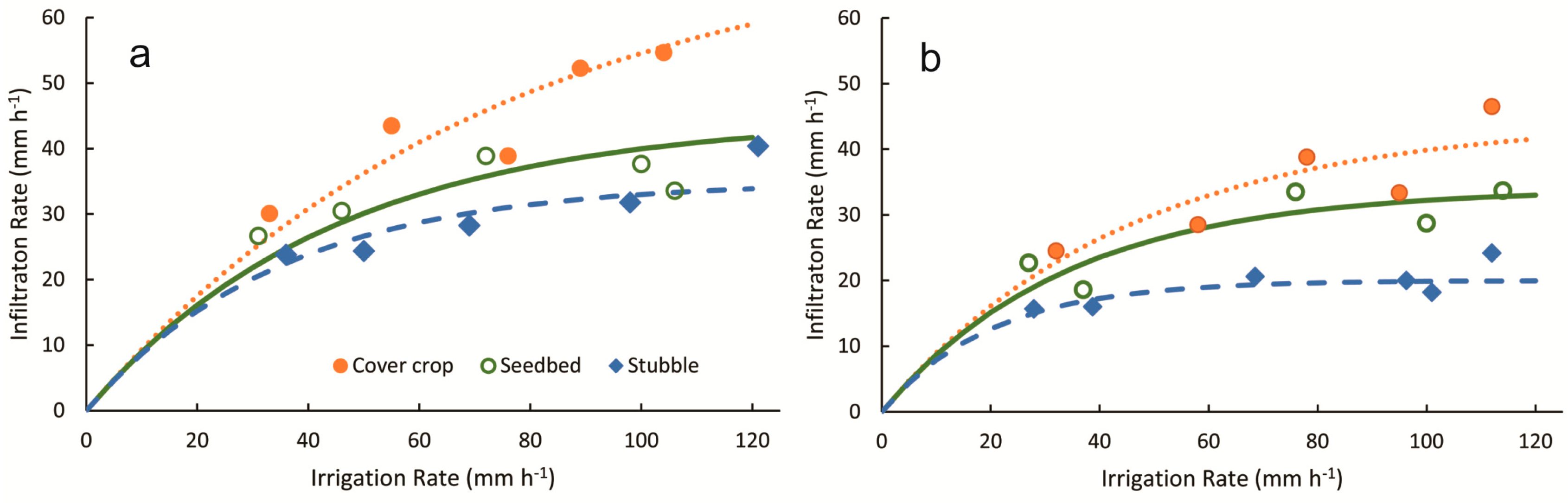
3.1. Hydrological Results for the Small Plots
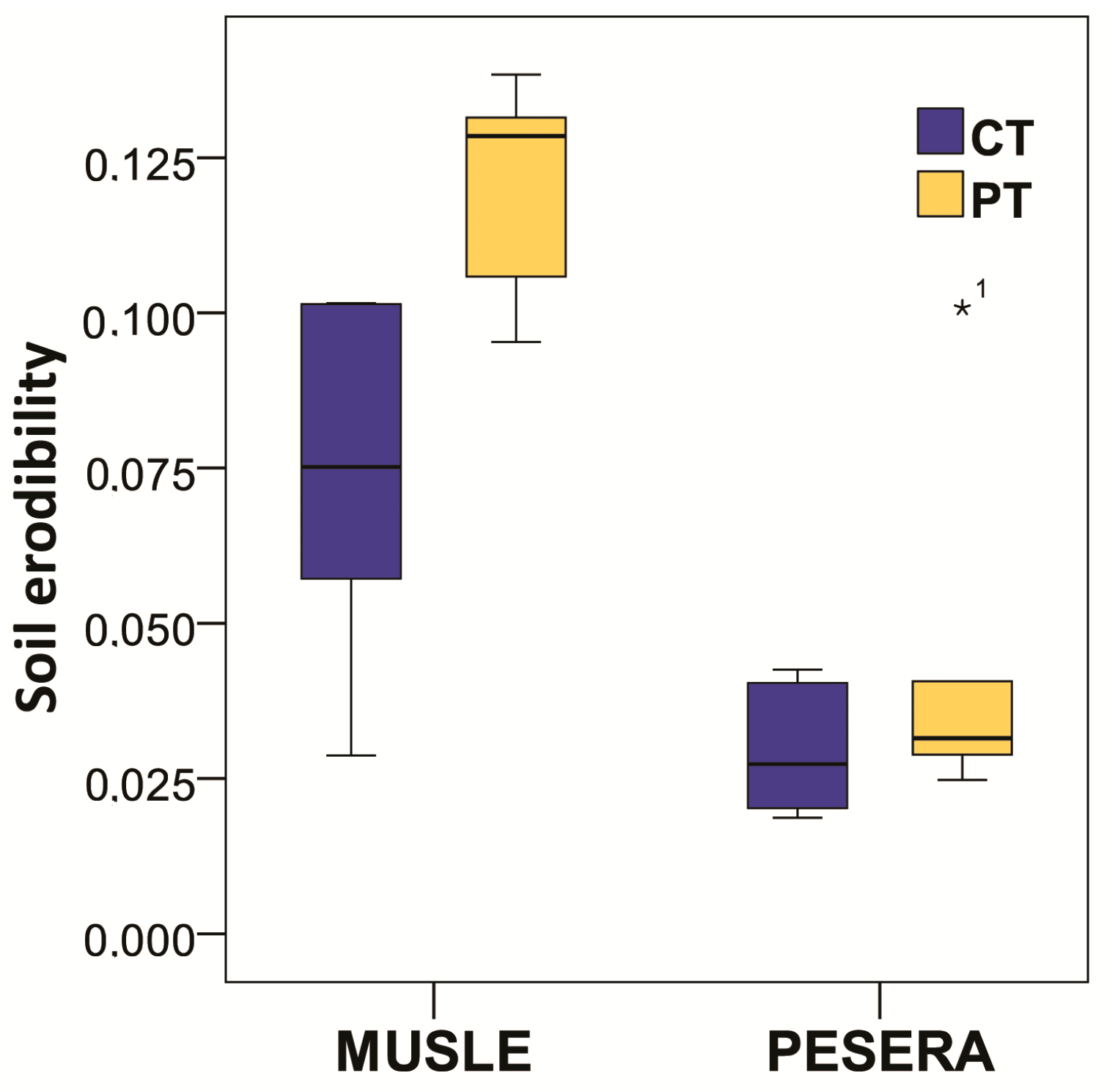
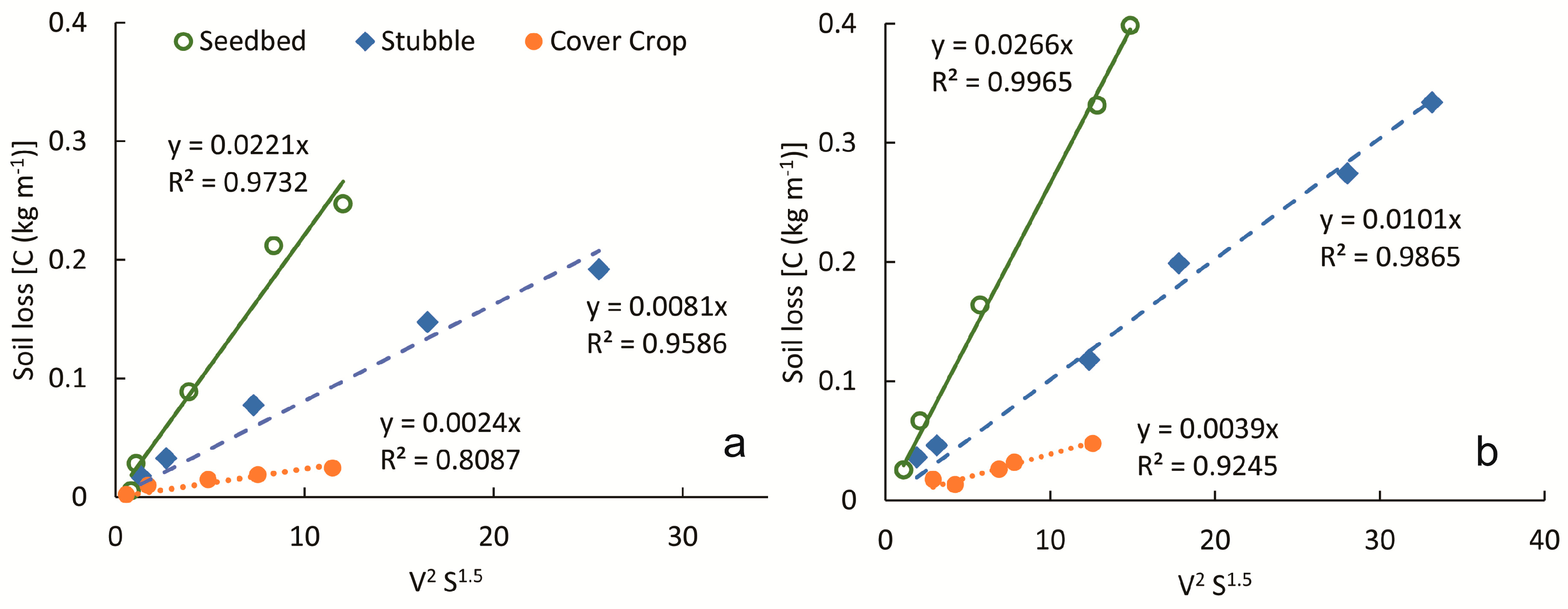
3.2. Soil Loss and Erodibility Results for the Small Plots
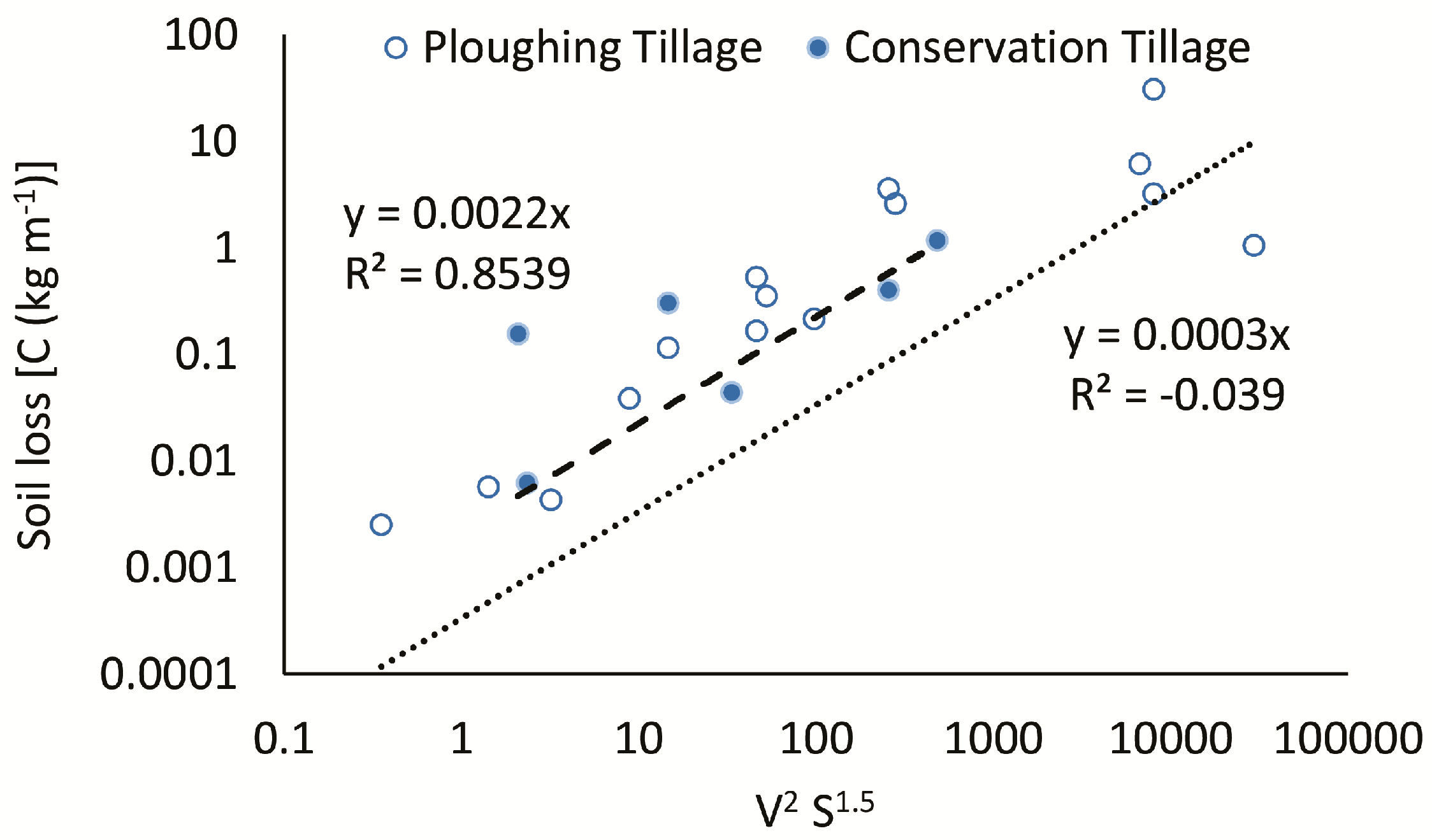
3.3. Field-Scale Results
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Rodrigo-Comino, J.; Wirtz, S.; Brevik, E.C.; Ruiz-Sinoga, J.D.; Ries, J.B. Assessment of agri-spillways as a soil erosion protection measure in Mediterranean sloping vineyards. J. Mt. Sci. 2017, 14, 1009–1022. [Google Scholar] [CrossRef]
- Kassam, A.; Friedrich, T.; Shaxson, F.; Pretty, J. The spread of conservation agriculture: Justification, sustainability, and uptake. Int. J. Agric. Sustain. 2009, 7, 292–320. [Google Scholar] [CrossRef]
- Villatoro-Sánchez, M.; Le Bissonnais, Y.; Moussa, R.; Rapidel, B. Temporal dynamics of runoff and soil loss on a plot scale under a coffee plantation on steep soil (Ultisol), Costa Rica. J. Hydrol. 2015, 523, 409–426. [Google Scholar] [CrossRef]
- Jakab, G.; Németh, T.; Csepinszky, B.; Madarász, B.; Szalai, Z.; Kertész, Á. The influence of short term soil sealing and crusting on hydrology and erosion at Balaton Uplands, Hungary. Carpathian J. Earth Environ. Sci. 2013, 8, 147–155. [Google Scholar]
- Wang, J.; Watts, D.B.; Meng, Q.; Zhang, Q.; Way, T.R. Influence of Surface Crusting on Infiltration of a Loess Plateau Soil. Soil Sci. Soc. Am. J. 2016, 80, 683–692. [Google Scholar] [CrossRef]
- Sang, X.; Wang, D.; Lin, X. Effects of tillage practices on water consumption characteristics and grain yield of winter wheat under different soil moisture conditions. Soil Tillage Res. 2016, 163, 185–194. [Google Scholar] [CrossRef]
- Mallari, K.J.B.; Arguelles, A.C.C.; Kim, H.; Aksoy, H.; Kavvas, M.L.; Yoon, J. Comparative analysis of two infiltration models for application in a physically based overland flow model. Environ. Earth Sci. 2015, 74, 1579–1587. [Google Scholar] [CrossRef]
- Gulick, S.H.; Grimes, D.W.; Goldhamer, D.A.; Munk, D.S. Cover-Crop-Enhanced Water Infiltration of a Slowly Permeable Fine Sandy Loam. Soil Sci. Soc. Am. J. 1994, 58, 1539–1546. [Google Scholar] [CrossRef]
- Mohammadshirazi, F.; Brown, V.K.; Heitman, J.L.; McLaughlin, R.A. Effects of tillage and compost amendment on infiltration in compacted soils. J. Soil Water Conserv. 2016, 71, 443–449. [Google Scholar] [CrossRef]
- Ward, P.R.; Roper, M.M.; Jongepier, R.; Micin, S.F. Impact of crop residue retention and tillage on water infiltration into a water-repellent soil. Biologia 2015, 70, 1480–1484. [Google Scholar] [CrossRef]
- Bogunovic, I.; Bilandzija, D.; Andabaka, Z.; Stupic, D.; Comino, J.R.; Cacic, M.; Brezinscak, L.; Maletic, E.; Pereira, P. Soil compaction under different management practices in a Croatian vineyard. Arab. J. Geosci. 2017, 10, 340. [Google Scholar] [CrossRef]
- Food and Agriculture Organization (FAO). Conservation Agriculture: Case Studies in Latin America and Africa; Food and Agriculture Organization (FAO): Rome, Italy, 2001. [Google Scholar]
- Kassam, A.; Basch, G.; Friedrich, T.; Gonzalez, E.; Trivino, P.; Mkomwa, S. Mobilizing greater crop and land potentials sustainably. Hung. Geogr. Bull. 2017, 66, 3–11. [Google Scholar] [CrossRef]
- Alliaume, F.; Rossing, W.A.H.; Tittonell, P.; Jorge, G.; Dogliotti, S. Reduced tillage and cover crops improve water capture and reduce erosion of fine textured soils in raised bed tomato systems. Agric. Ecosyst. Environ. 2014, 183, 127–137. [Google Scholar] [CrossRef]
- Gomez, J.A. Sustainability using cover crops in Mediterranean tree crops, olives and vines-Challenges and current knowledge. Hung. Geogr. Bull. 2017, 66, 13–28. [Google Scholar] [CrossRef]
- Kramberger, B.; Gselman, A.; Kristl, J.; Lešnik, M.; Šuštar, V.; Muršec, M.; Podvršnik, M. Winter cover crop: The effects of grass–clover mixture proportion and biomass management on maize and the apparent residual N in the soil. Eur. J. Agron. 2014, 55, 63–71. [Google Scholar] [CrossRef]
- Khan, M.N.; Gong, Y.; Hu, T.; Lal, R.; Zheng, J.; Justine, M.F.; Azhar, M.; Che, M.; Zhang, H. Effect of Slope, Rainfall Intensity and Mulch on Erosion and Infiltration under Simulated Rain on Purple Soil of South-Western Sichuan Province, China. Water 2016, 8, 528. [Google Scholar] [CrossRef]
- Rose, C. An Introduction to the Environmental Physics of Soil, Water and Watersheds; Cambridge University Press: Cambridge, UK, 2004; p. 443. [Google Scholar]
- Kuhlman, T.; Reinhard, S.; Gaaff, A. Estimating the costs and benefits of soil conservation in Europe. Land Use Policy 2010, 27, 22–32. [Google Scholar] [CrossRef]
- Szabó, J.; Jakab, G.; Szabó, B. Spatial and temporal heterogeneity of runoff and soil loss dynamics under simulated rainfall. Hung. Geogr. Bull. 2015, 64, 25–34. [Google Scholar] [CrossRef]
- Jirků, V.; Kodešová, R.; Nikodem, A.; Mühlhanselová, M.; Žigová, A. Temporal variability of structure and hydraulic properties of topsoil of three soil types. Geoderma 2013, 204–205, 43–58. [Google Scholar] [CrossRef]
- Stroosnijder, L. Measurement of erosion: Is it possible? Catena 2005, 63, 162–173. [Google Scholar] [CrossRef]
- Martínez-Murillo, J.F.; Nadal-Romero, E.; Regüés, D.; Cerdà, A.; Poesen, J. Soil erosion and hydrology of the western Mediterranean badlands throughout rainfall simulation experiments: A review. Catena 2013, 106, 101–112. [Google Scholar] [CrossRef]
- Rodrigo Comino, J.; Iserloh, T.; Lassu, T.; Cerdà, A.; Keestra, S.D.; Prosdocimi, M.; Brings, C.; Marzen, M.; Ramos, M.C.; Senciales, J.M.; et al. Quantitative comparison of initial soil erosion processes and runoff generation in Spanish and German vineyards. Sci. Total Environ. 2016, 565, 1165–1174. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Hernández, C.; Rodrigo-Comino, J.; Romero-Díaz, A. Impact of lithology and soil properties on abandoned dryland terraces during the early stages of soil erosion by water in south-east Spain. Hydrol. Process. 2017, 31, 3095–3109. [Google Scholar] [CrossRef]
- Madarász, B.; Bádonyi, K.; Csepinszky, B.; Mika, J.; Kertész, Á. Conservation tillage for rational water management and soil conservation. Hung. Geogr. Bull. 2011, 60, 117–133. [Google Scholar]
- Centeri, C.; Jakab, G.; Szabó, S.; Farsang, A.; Barta, K.; Szalai, Z.; Bíró, Z. Comparison of particle-size analyzing laboratory methods. Environ. Eng. Manag. J. 2015, 14, 1125–1135. [Google Scholar]
- Kertész, Á.; Bádonyi, K.; Madarász, B.; Csepinszky, B. Environmental aspects of conventional and conservation tillage. In No-Till Farming Systems; Goddart, T., Zoebish, M., Gan, Y., Ellis, W., Watson, A., Sombatpanit, S., Eds.; Special Publication; World Association of Soiland Water Conservation: Bangkok, Thailand, 2007; pp. 313–329. [Google Scholar]
- Kertész, Á.; Madarász, B.; Csepinszky, B.; Benke, S.Z. The role of conservation agriculture in landscape protection. Hung. Geogr. Bull. 2010, 59, 167–180. [Google Scholar]
- Jakab, G.; Madarász, B.; Szabó, J.; Tóth, A.; Zachary, D.; Szalai, Z.; Dyson, J. Changes to infiltration and soil loss rates during the growing season under conventional and conservation tillage. Geophys. Res. Abstr. 2017, 19. [Google Scholar] [CrossRef]
- Zhang, G.S.; Chan, K.Y.; Oates, A.; Heenan, D.P.; Huang, G.B. Relationship between soil structure and runoff/soil loss after 24 years of conservation tillage. Soil Tillage Res. 2007, 92, 122–128. [Google Scholar] [CrossRef]
- Loch, R.J.; Robotham, B.G.; Zeller, L.; Masterman, N.; Orange, D.N.; Bridge, B.J.; Sheridan, G.; Bourke, J.J. A multi-purpose rainfall simulator for field infiltration and erosion studies. Aust. J. Soil Res. 2001, 39, 599–610. [Google Scholar] [CrossRef]
- Kirkby, M.J.; Irvine, B.J.; Jones, R.J.A.; Govers, G.; The Pesera Team. The PESERA coarse scale erosion model for Europe. I.—Model rationale and implementation. Eur. J. Soil Sci. 2008, 59, 1293–1306. [Google Scholar] [CrossRef] [Green Version]
- Wischmeier, W.H.; Smith, D.D. Predicting Rainfall Erosion Losses: A Guide to Conservation Planning; USDA Agricultural Handbook 537; US Government Printing Office: Washington, DC, USA, 1978.
- Wang, B.; Zheng, F.; Römkens, M.J.M. Comparison of soil erodibility estimate models. Acta Agric. Scand. Sect. B Soil Plant Sci. 2013, 63, 69–79. [Google Scholar] [CrossRef]
- Shabani, F.; Kumar, L.; Esmaeili, A. Improvement to the prediction of the USLE K factor. Geomorphology 2014, 204, 229–234. [Google Scholar] [CrossRef]
- Ostovari, Y.; Ghorbani-Dashtaki, S.; Bahrami, H.A.; Naderi, M.; Dematte, J.A.M.; Kerry, R. Modification of the USLE K factor for soil erodibility assessment on calcareous soils in Iran. Geomorphology 2016, 273, 385–395. [Google Scholar] [CrossRef]
- Williams, J.R. Sediment routing for agricultural watersheds. Water Resour. Bull. 1975, 11, 965–974. [Google Scholar] [CrossRef]
- Harper Adams University College. Earthworm Soil Core Standard Operating Procedure; Crop and Environment Research Centre: Newport, UK, 2003; p. 4. [Google Scholar]
- Blanco-Canqui, H.; Wienhold, B.J.; Jin, V.L.; Schmer, M.R.; Kibet, L.C. Long-term tillage impact on soil hydraulic properties. Soil Tillage Res. 2017, 170, 38–42. [Google Scholar] [CrossRef]
- Lipiec, J.; Kuś, J.; Słowińska-Jurkiewicz, A.; Nosalewicz, A. Soil porosity and water infiltration as influenced by tillage methods. Soil Tillage Res. 2006, 89, 210–220. [Google Scholar] [CrossRef]
- Strudley, M.W.; Green, T.R.; Ascough, J.C. Tillage effects on soil hydraulic properties in space and time: State of the science. Soil Tillage Res. 2008, 99, 4–48. [Google Scholar] [CrossRef]
- Freese, R.C.; Cassel, D.K.; Denton, H.P. Infiltration in a piedmont soil under three tillage systems. J. Soil Water Conserv. 1993, 48, 214–218. [Google Scholar]
- Kis, A.; Pongrácz, R.; Bartholy, J. Projected Trends of precipitation for Hungary: The effects of Bias correction. Légkör 2014, 59, 117–120. [Google Scholar]
- Bartholy, J.; Pongrácz, R.; Kis, A. Projected changes of extreme precipitation using multi-model approach. Q. J. Hung. Meteorol. Serv. 2015, 119, 129–142. [Google Scholar]
- Zicsi, A. Die Auswirkung von Bodenbearbeitungsverfahren auf Zustand und Besatzdichte von Einheimischen Regenwürmern; Graff, B., Satchell, G., Eds.; Progress in Soil Biology; Friedrich Vieweg: Braunschweig, Germany, 1967; pp. 290–298. [Google Scholar]
- Emmerling, C. Response of earthworm communities to different types of soil tillage. Appl. Soil Ecol. 2001, 17, 91–96. [Google Scholar] [CrossRef]
- Birkás, M.; Jolánkai, M.; Gyuricza, C.; Percze, A. Tillage effects on compaction, earthworms and other soil quality indicators in Hungary. Soil Tillage Res. 2004, 78, 185–196. [Google Scholar] [CrossRef]
- Thierfelder, C.; Wall, P.C. Effects of conservation agriculture techniques on infiltration and soil water content in Zambia and Zimbabwe. Soil Tillage Res. 2009, 105, 217–227. [Google Scholar] [CrossRef]
- Mueller, E.N.; Pfister, A. Increasing occurrence of high-intensity rainstorm events relevant for the generation of soil erosion in a temperate lowland region in Central Europe. J. Hydrol. 2011, 411, 266–278. [Google Scholar] [CrossRef]
- Duan, X.; Shi, X.; Li, Y.; Li, R.; Fen, D. A new method to calculate soil loss tolerance for sustainable soil productivity in farmland. Agron. Sustain. Dev. 2017, 37. [Google Scholar] [CrossRef]
- Vaezi, A.R.; Ahmadi, M.; Cerdà, A. Contribution of raindrop impact to the change of soil physical properties and water erosion under semi-arid rainfalls. Sci. Total Environ. 2017, 583, 382–392. [Google Scholar] [CrossRef] [PubMed]
- Vermang, J.; Norton, L.D.; Huang, C.; Cornelis, W.M.; da Silva, A.M.; Gabriels, D. Characterization of Soil Surface Roughness Effects on Runoff and Soil Erosion Rates under Simulated Rainfall. Soil Sci. Soc. Am. J. 2015, 79, 903–916. [Google Scholar] [CrossRef]
- Auerswald, K.; Fiener, P.; Martin, W.; Elhaus, D. Use and misuse of the K factor equation in soil erosion modeling: An alternative equation for determining USLE nomograph soil erodibility values. Catena 2014, 118, 220–225. [Google Scholar] [CrossRef]
- Porto, P.; Walling, D.E.; Capra, A. Using 137Cs and 210Pbex measurements and conventional surveys to investigate the relative contributions of interrill/rill and gully erosion to soil loss from a small cultivated catchment in Sicily. Soil Tillage Res. 2014, 135, 18–27. [Google Scholar] [CrossRef]
- Guo, Q.; Liu, B.; Xie, Y.; Liu, Y.; Yin, S. Estimation of USLE crop and management factor values for crop rotation systems in China. J. Integr. Agric. 2015, 14, 1877–1888. [Google Scholar] [CrossRef]
- Vogel, E.; Deumlich, D.; Kaupenjohann, M. Bioenergy maize and soil erosion—Risk assessment and erosion control concepts. Geoderma 2016, 261, 80–92. [Google Scholar] [CrossRef]
- Panagos, P.; Borrelli, P.; Meusburger, K.; van der Zanden, E.H.; Poesen, J.; Alewell, C. Modelling the effect of support practices (-factor) on the reduction of soil erosion by water at European scale. Environ. Sci. Policy 2015, 51, 23–34. [Google Scholar] [CrossRef] [Green Version]

| Ploughing Tillage | Conservation Tillage |
|---|---|
| In 2015 After Sunflower Harvest | |
| Stubble chopping | Stubble chopping |
| Discing and rolling | Discing and rolling |
| Medium deep subsoiling | Medium deep subsoiling |
| Ploughing | - |
| Leveling | - |
| Sowing (cover crop *) | Sowing (cover crop *) |
| In 2016 | |
| Weed control and chopping | Weed control and chopping |
| Seedbed preparation | Seedbed preparation |
| Sowing (maize **) | Sowing (maize **) |
| Stubble chopping | Stubble chopping |
| Discing | Discing |
| Rain Amount | Rain intensity | Runoff | Final Runoff Intensity | Apparent Infiltration | Soil Loss | MUSLE K | |
|---|---|---|---|---|---|---|---|
| (mm) | (mm h−1) | (mm) | (mm h−1) | (mm h−1) | (t ha−1) | ||
| Cover crop | 14.7 | 32 | 2.6 | 7.56 | 24.44 | 0.06 | 0.040 |
| 10.6 | 78 | 3.7 | 39.24 | 38.76 | 0.09 | 0.019 | |
| 8.2 | 58 | 3.4 | 29.52 | 28.48 | 0.04 | 0.012 | |
| 11.1 | 95 | 6.6 | 61.56 | 33.44 | 0.16 | 0.020 | |
| 9.7 | 112 | 5.5 | 65.52 | 46.48 | 0.11 | 0.014 | |
| 17.5 | 33 | 2.3 | 2.88 | 30.12 | 0.01 | 0.009 | |
| 12.7 | 55 | 1.9 | 11.52 | 43.48 | 0.03 | 0.021 | |
| 13.5 | 89 | 4.2 | 36.72 | 52.28 | 0.06 | 0.013 | |
| 9.2 | 76 | 3.3 | 37.08 | 38.92 | 0.05 | 0.012 | |
| 14.5 | 104 | 5.7 | 49.32 | 54.68 | 0.08 | 0.012 | |
| Seedbed | 13.4 | 27 | 0.9 | 4.32 | 22.68 | 0.09 | 0.138 |
| 5.9 | 37 | 2.4 | 18.36 | 18.64 | 0.22 | 0.095 | |
| 8.7 | 76 | 4.3 | 42.48 | 33.52 | 0.55 | 0.106 | |
| 10.2 | 100 | 6.4 | 71.28 | 28.72 | 1.11 | 0.129 | |
| 11.1 | 114 | 7.5 | 80.28 | 33.72 | 1.33 | 0.131 | |
| 13.4 | 31 | 1.0 | 4.32 | 26.68 | 0.02 | 0.029 | |
| 6.3 | 46 | 1.5 | 15.48 | 30.52 | 0.09 | 0.057 | |
| 8.7 | 72 | 3.4 | 33.12 | 38.88 | 0.30 | 0.075 | |
| 11.3 | 100 | 6.6 | 62.28 | 37.72 | 0.82 | 0.102 | |
| 8.6 | 106 | 4.3 | 72.36 | 33.64 | 0.71 | 0.101 | |
| Stubble | 6.4 | 28 | 2.6 | 12.24 | 15.7 | 0.12 | 0.113 |
| 6.1 | 39 | 2.9 | 22.68 | 16.04 | 0.15 | 0.070 | |
| 10.2 | 68 | 6.03 | 47.88 | 20.57 | 0.39 | 0.062 | |
| 10.8 | 96 | 7.8 | 76.32 | 19.98 | 0.66 | 0.053 | |
| 13.1 | 101 | 10.3 | 82.8 | 18.2 | 0.91 | 0.059 | |
| 6.9 | 36 | 1.6 | 12.24 | 23.76 | 0.06 | 0.066 | |
| 6.5 | 50 | 2.7 | 25.56 | 24.44 | 0.11 | 0.075 | |
| 9.3 | 69 | 5.0 | 40.68 | 28.32 | 0.26 | 0.086 | |
| 12.3 | 98 | 7.8 | 66.24 | 31.76 | 0.49 | 0.040 | |
| 15.4 | 121 | 9.5 | 80.64 | 40.36 | 0.64 | 0.036 |
| Time of Year | Soil Conditions | CT | PT | Rate |
|---|---|---|---|---|
| April | Cover crop | 73 | 44 | 1.62 |
| May | Seedbed | 45 | 35 | 1.29 |
| October | Stubble | 35 | 20 | 1.75 |
| Date | (Day.Month.) | 4.3. | 6. 6. | 16. 6. | 20.6. | 14.7. | 18.7. | 6.8. | 16.8. | 27.10. | Sum. | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Precipi-Tation | amount | mm | 17.2 | 38.8 | 10.0 | 9.4 | 58.6 | 9.8 | 35.0 | 20.0 | 36.4 | |
| I30 | mm h−1 | 2.4 | 28.2 | 8.8 | 4.4 | 22.2 | 9.6 | 12.2 | 12.8 | 6.2 | ||
| duration | h | 14.0 | 6.7 | 5.5 | 7.8 | 11.1 | 0.7 | 8.9 | 2.7 | 7.83 | ||
| Runoff (mm) | CT | plot1 | 1.57 | 0.142 | 0.567 | 0.003 | 2.282 | |||||
| plot2 | 2.16 | 0.375 | 0.150 | 2.685 | ||||||||
| PT | plot1 | 0.058 | 8.02 | 1.571 | 0.292 | 16.796 | 0.117 | 0.375 | 0.292 | 27.521 | ||
| plot2 | 8.77 | 1.642 | 0.967 | 8.767 | 0.667 | 0.713 | 0.667 | 0.175 | 22.368 | |||
| Soil loss (t ha−1) | CT | plot1 | 0.08 | 0.031 | 0.009 | 0.120 | ||||||
| plot2 | 0.23 | 0.061 | 0.001 | 0.292 | ||||||||
| PT | plot1 | 0.001 | 1.23 | 0.720 | 0.008 | 0.208 | 0.001 | 0.023 | 0.008 | 2.199 | ||
| plot2 | 6.08 | 0.512 | 0.043 | 0.637 | 0.106 | 0.069 | 0.033 | 0.001 | 7.481 | |||
| Sediment cc. (g L−1) | CT | plot1 | 5.1 | 21.9 | 1.6 | |||||||
| plot2 | 10.7 | 16.3 | 0.7 | |||||||||
| PT | plot1 | 1.7 | 15.4 | 46.0 | 2.8 | 1.2 | 0.9 | 6.2 | 2.8 | |||
| plot2 | 69.6 | 31.3 | 4.5 | 7.3 | 16.0 | 9.7 | 5.0 | 0.6 | ||||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jakab, G.; Madarász, B.; Szabó, J.A.; Tóth, A.; Zacháry, D.; Szalai, Z.; Kertész, Á.; Dyson, J. Infiltration and Soil Loss Changes during the Growing Season under Ploughing and Conservation Tillage. Sustainability 2017, 9, 1726. https://doi.org/10.3390/su9101726
Jakab G, Madarász B, Szabó JA, Tóth A, Zacháry D, Szalai Z, Kertész Á, Dyson J. Infiltration and Soil Loss Changes during the Growing Season under Ploughing and Conservation Tillage. Sustainability. 2017; 9(10):1726. https://doi.org/10.3390/su9101726
Chicago/Turabian StyleJakab, Gergely, Balázs Madarász, Judit Alexandra Szabó, Adrienn Tóth, Dóra Zacháry, Zoltán Szalai, Ádám Kertész, and Jeremy Dyson. 2017. "Infiltration and Soil Loss Changes during the Growing Season under Ploughing and Conservation Tillage" Sustainability 9, no. 10: 1726. https://doi.org/10.3390/su9101726






