Evaluating Carbon Stock Changes in Forest and Related Uncertainty
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Carbon Stock and Stock Change Estimates and Uncertainty Analysis
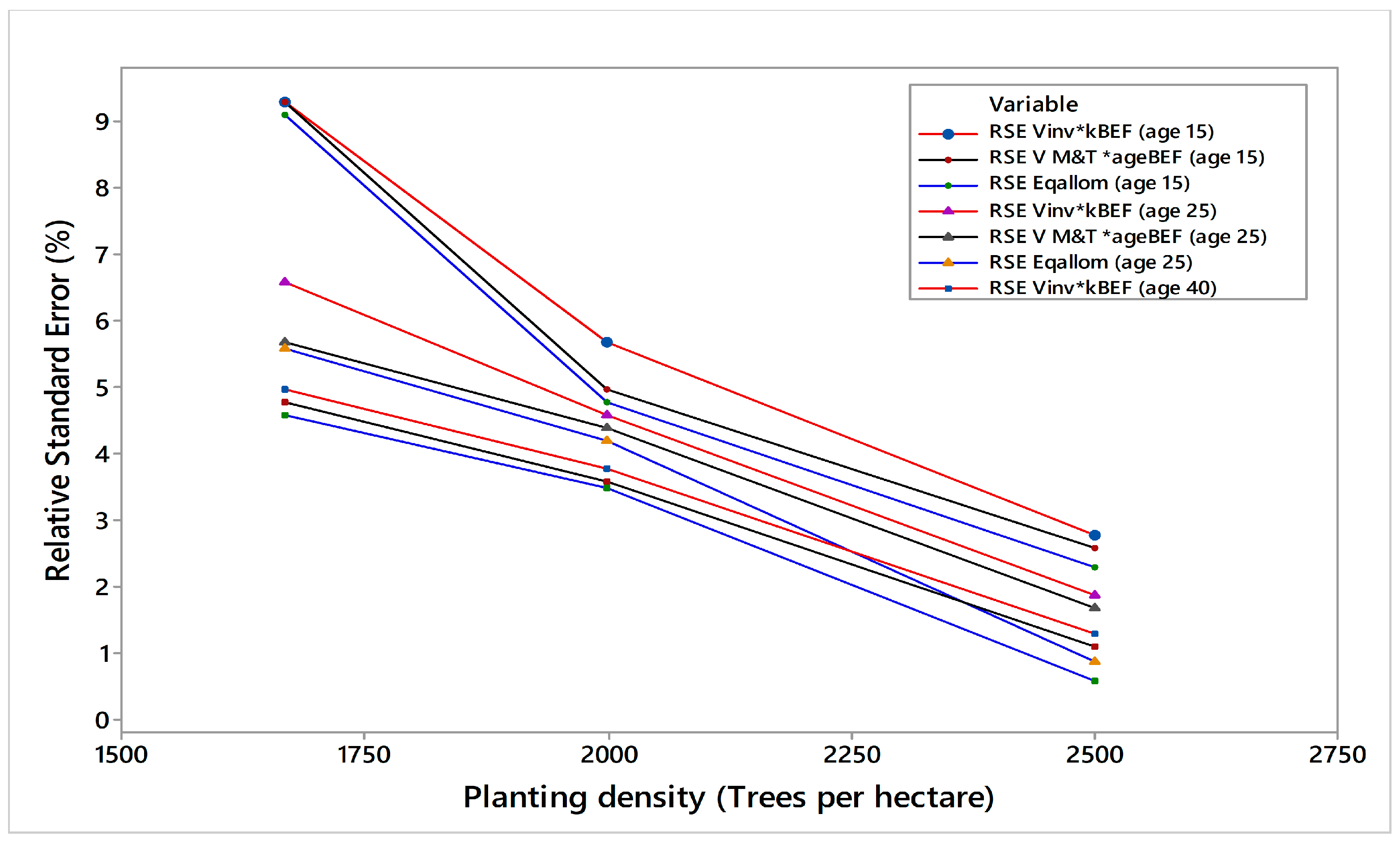
3. Results
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Reichstein, M.; Ciais, P.; Papale, D.; Valentini, R.; Running, S.; Viovy, N.; Cramer, W.; Granier, A.; Ogée, J.; Allard, V.; et al. Reduction of ecosystem productivity and respiration during the European summer 2003 climate anomaly: A joint flux tower, remote sensing and modeling analysis. Glob. Chang. Biol. 2007, 13, 634–651. [Google Scholar] [CrossRef]
- Achard, F.; Eva, H.D.; Stibig, H.; Mayaux, P.; Gallego, J.; Richards, T.; Malingreau, J. Determination of deforestation rates of the world’s humid tropical forests. Science 2002, 297, 999–1002. [Google Scholar] [CrossRef] [PubMed]
- Gullison, R.E.; Frumhoff, P.C.; Canadell, J.G.; Field, C.B.; Nepstad, D.C.; Hayhoe, K.; Avissar, R.; Curran, L.M.; Friedlingstein, P.; Jones, C.D.; et al. Tropical forests and climate policy. Science 2007, 316, 985–986. [Google Scholar] [CrossRef]
- Yu, G.R.; Chen, Z.; Piao, S.L.; Peng, C.H.; Ciais, P.; Wang, Q.F.; Li, X.R.; Zhu, X.J. High carbon dioxide uptake by subtropical forest ecosystems in the East Asian monsoon region. Proc. Natl. Acad. Sci. USA 2014, 111, 4910–4915. [Google Scholar] [CrossRef]
- Sanesi, G.; Lafortezza, R.; Colangelo, G.; Marziliano, P.A.; Davies, C. Root system investigation in sclerophyllous vegetation: An overview. Ital. J. Agron. 2013, 8, 121–126. [Google Scholar] [CrossRef]
- Marziliano, P.A.; Lafortezza, R.; Medicamento, U.; Lorusso, L.; Giannico, V.; Colangelo, C.; Sanesi, G. Estimating belowground biomass and root/shoot ratio of Phillyrea latifolia L. in the Mediterranean forest landscapes. Ann. For. Sci. 2015, 72, 585–593. [Google Scholar] [CrossRef]
- Tobin, B.; Nieuwenhuis, M. Biomass expansion factors for Sitka spruce (Picea sitchensis (Bong) Carr.) in Ireland. Eur. J. For. Res. 2007, 126, 189–196. [Google Scholar] [CrossRef]
- Lehtonen, A.; Mäkipää, R.; Heikkinen, J.; Sievänen, R.; Liski, J. Biomass expansion factors (BEF) for Scots pine, Norway spruce and birch according to stand age for boreal forests. For. Ecol. Manag. 2004, 188, 211–224. [Google Scholar] [CrossRef]
- Petersson, H.; Holm, S.; Ståhl, G.; Alger, D.; Fridman, J.; Lethonen, A.; Lundstrøm, A.; Mäkipää, R. Individual tree biomass functions or biomass expansion factors for assessment of carbon stock changes in living biomass—A comparative study. For. Ecol. Manag. 2012, 270, 78–84. [Google Scholar]
- Pajtik, J.; Konopka, B.; Lukac, M. Biomass functions and expansion factors in young Norway spruce (Picea abies [L.] Karst) trees. For. Ecol. Manag. 2008, 256, 1096–1103. [Google Scholar]
- Intergovernmental Panel on Climate Change. Good Practice Guidance for Land Use, Land-Use Change and Forestry; Penman, J., Gytarsky, M., Hiraishi, T., Kruger, D., Pipatti, R., Buendia, L., Miwa, K., Ngara, T., Tanabe, K., Wagner, F., Eds.; IPCC/IGES: Hayama, Japan, 2003. [Google Scholar]
- (Intergovernmental Panel on Climate Change). 2006 IPCC Guidelines for National Greenhouse Gas Inventories; Eggleston, H.S., Buendia, L., Miwa, K., Ngara, T., Tanabe, K., Eds.; Prepared by the National Greenhouse Gas Inventories Programme; IGES: Hayama, Japan, 2006. [Google Scholar]
- Mund, M.; Kummetz, E.; Hein, M.; Bauer, G.A.; Schulze, E.D. Growth and carbon stocks of a spruce forest chronosequence in central Europe. For. Ecol. Manag. 2002, 171, 275–296. [Google Scholar] [CrossRef]
- Barman, R.; Jain, A.K.; Liang, M.L. Climate-driven uncertainties in modeling terrestrial gross primary production: A site level to global-scale analysis. Glob. Chang. Biol. 2014, 20, 1394–1411. [Google Scholar] [CrossRef] [PubMed]
- Ahlstroem, A.; Schurgers, G.; Arneth, A.; Smith, B. Robustness and uncertainty in terrestrial ecosystem carbon response to CMIP5 climate change projections. Environ. Res. Lett. 2012, 7, 044008. [Google Scholar] [CrossRef]
- Bolker, B. Ecological Models and Data in R; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Phillips, O.L.; Malhi, Y.; Higuchi, N.; Laurance, W.F.; Nunez, P.V.; Vasquez, R.M.; Laurance, S.G.; Ferreira, L.V.; Stern, M.; Brown, S.; et al. Changes in the carbon balance of tropical forests: Evidence from long-term plots. Science 1998, 282, 439–442. [Google Scholar] [CrossRef] [PubMed]
- Chave, J.; Condit, R.; Muller-Landau, H.C.; Thomas, S.C.; Ashton, P.S.; Bunyavejchewin, S.; Co, L.L.; Dattaraja, H.S.; Davies, S.J.; Esufali, S.; et al. Assessing evidence for a pervasive alteration in tropical tree communities. PLoS Biol. 2008, 6, e45. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lewis, S.L.; Lopez-Gonzalez, G.; Sonke, B.; Affum-Baffoe, K.; Baker, T.R.; Ojo, L.O.; Phillips, O.L.; Reitsma, J.M.; White, L.; Comiskey, J.A.; et al. Increasing carbon storage in intact African tropical forests. Nature 2009, 457, 1003–1006. [Google Scholar] [CrossRef] [PubMed]
- Röhling, S.; Dunger, K.; Kändler, G.; Klatt, S.; Riedel, T.; Stümer, W.; Brötz, J. Comparison of calculation methods for estimating annual carbon stock change in German forests under forest management in the German greenhouse gas inventory. Carbon Balance Manag. 2016, 11, 12. [Google Scholar] [CrossRef] [PubMed]
- Pelletier, J.; Kirby, K.R.; Potvin, C. Significance of carbon stock uncertainties on emission reductions from deforestation and forest degradation in developing countries. For. Policy Econ. 2010, 24, 3–11. [Google Scholar] [CrossRef]
- Coletta, V.; Menguzzato, G.; Pellicone, G.; Veltri, A.; Marziliano, P.A. Effect of thinning on above-ground biomass accumulation in a Douglas fir plantation in southern Italy. J. For. Res. 2016, 27, 1313–1320. [Google Scholar] [CrossRef]
- Marziliano, P.A.; Coletta, V.; Menguzzato, G.; Nicolaci, A.; Pellicone, G.; Veltri, A. Effects of planting density on the distribution of biomass in a Douglas fir plantation in southern Italy. iForest 2015, 8, 368–376. [Google Scholar] [CrossRef]
- Tabacchi, G.; Di Cosmo, L.; Gasparini, P. Aboveground tree volume and phytomass prediction equations for forest species in Italy. Eur. J. For. Res. 2011, 130, 911–934. [Google Scholar] [CrossRef]
- Menguzzato, G.; Tabacchi, G. Prove di diradamento su Pseudotsuga menziesii in Calabria, Ambiente tavole di cubatura e della biomassa epigea. Ann. Ist. Sper. Selvic. 1986, 17, 255–293. [Google Scholar]
- Jalkanen, A.; Mäkipää, R.; Stahl, G.; Lehtonen, A.; Peterson, H. Estimation of the biomass stock of trees in Sweden: Comparison of biomass equations and age-dependent biomass expansion factors. Ann. For. Sci. 2005, 62, 845–851. [Google Scholar] [CrossRef]
- Schlesinger, W.H. Biogeochemistry: An Analysis of Global Change; Academic Press Inc.: London, UK; Harcourt Brace Jovanovich Publishers: San Diego, CA, USA, 1991; p. 443. [Google Scholar]
- Mäkipää, R.; Peltoniemi, M.; Monni, S.; Palosuo, T.; Lehtonen, A.; Savolainen, I. Key sources of uncertainty in forest carbon inventories. In Proceedings of the EU Workshop on Uncertainties in Greenhouse Gas Inventories, Helsinki, Finland, 5–6 September 2005. [Google Scholar]
- Zianis, D.; Muukkonen, P.; Mäkipää, R.; Mencuccini, M. Biomass and Stem Volume Equations for Tree Species in Europe. Silva Fennica Monographs 4. 2005. Available online: http://www.metla.fi/silvafennica/full/smf/smf004.pdf (accessed on 20 July 2017).
- Clark, D.B.; Clark, D.A. Landscape-scale variation in forest structure and biomass in a tropical rain forest. For. Ecol. Manag. 2000, 137, 185–198. [Google Scholar] [CrossRef]
- Keller, M.; Palace, M.; Hurtt, G. Biomass estimation in the Tapajos National Forest, Brazil: Examination of sampling and allometric uncertainties. For. Ecol. Manag. 2001, 154, 371–382. [Google Scholar] [CrossRef]
- Chave, J.; Condit, R.; Aguilar, S.; Hernandez, A.; Lao, S.; Perez, R. Error propagation and scaling for tropical forest biomass estimates. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2004, 359, 409–420. [Google Scholar] [CrossRef] [PubMed]
- Chave, J.; Andalo, C.; Brown, S.; Cairns, M.A.; Chambers, J.Q.; Eamus, D.; Folster, H.; Fromard, F.; Higuchi, N.; Kira, T.; et al. Tree allometry and improved estimation of carbon stocks and balance in tropical forests. Oecologia 2005, 145, 87–99. [Google Scholar] [CrossRef] [PubMed]
- Brown, S. Estimating Biomass and Biomass Change of Tropical Forests; Forestry Paper Food and Agriculture Organization: Rome, Italy, 1997; 94p. [Google Scholar]
- Nogueira, E.M.; Fearnside, P.M.; Nelson, B.W.; Barbosa, R.I.; Keizer, E.W.H. Estimates of forest biomass in the Brazilian Amazon: New allometric equations and adjustments to biomass from wood-volume inventories. For. Ecol. Manag. 2008, 256, 1853–1867. [Google Scholar] [CrossRef]
- Fehrmann, L.; Kleinn, C. General considerations about the use of allometric equations for biomass estimation on the example of Norway spruce in central Europe. For. Ecol. Manag. 2006, 236, 412–421. [Google Scholar] [CrossRef]
- Lehtonen, A.; Cienciala, E.; Tatarinov, F.; Makipaa, R. Uncertainty estimation of biomass expansion factors for Norway spruce in the Czech Republic. Ann. For. Sci. 2007, 64, 133–140. [Google Scholar]
- Cienciala, E.; HenÏlík, V.; Zatloukal, V. Assessment of carbon stock change in forests adopting IPCC LULUCF Good Practice Guidance in the Czech Republic. For. J. 2006, 52, 17–28. [Google Scholar]


| Equation Name | Equation Expression | Equation |
|---|---|---|
| Volume equation for Douglas fir from the National Italian Forest Inventory (INFC) | (1) | |
| A constant BEF from the INFC for conifer plantations in Italy | BEF = 1.41 Basic wood density = 0.43 | (2) |
| Volume equation for the Douglas fir plantation in Calabria | (3) | |
| Age-dependent BEF equations elaborated for Douglas fir in Calabria | (4) | |
| Allometric equations for Douglas fir in Calabria | (5) |
| Above-Ground Carbon Estimates | ||||||
|---|---|---|---|---|---|---|
| Age (Years) | Density Classes (Trees ha−1) | W1 (Mg ha−1) | W2 (Mg ha−1) | W3 (Mg ha−1) | Average (Mg ha−1) | ANOVA Planting Density |
| 15 | 2500 | 60.9 | 84.2 | 70.2 | 71.8 A | |
| 2000 | 59.4 | 85.0 | 70.0 | 71.5 A | F = 36.3; p = 0.003 | |
| 1667 | 53.9 | 73.8 | 61.0 | 62.9 B | ||
| ANOVA Models F = 191.2; p ≤ 0.001 | Average | 58.1 | 81.0 | 67.1 | ||
| A | B | C | ||||
| 25 | 2500 | 146.4 | 137.9 | 114.6 | 133.0 A | |
| 2000 | 146.4 | 144.9 | 120.5 | 137.3 A | F = 1.02; p = 0.438 | |
| 1667 | 155.7 | 139.4 | 116.0 | 137.0 A | ||
| ANOVA Models F = 49.2; p = 0.002 | Average | 149.5 | 140.7 | 117.0 | ||
| A | A | B | ||||
| 40 | 2500 | 258.9 | 170.5 | 142.5 | 190.6 A | |
| 2000 | 291.8 | 204.6 | 170.8 | 222.4 B | F = 51.3; p = 0.001 | |
| 1667 | 230.0 | 156.8 | 131.0 | 172.6 C | ||
| ANOVA Models F = 272.9; p ≤ 0.001 | Average | 260.2 | 177.3 | 148.1 | ||
| A | B | C | ||||
| RSE of Biomass Estimates | ||||||
|---|---|---|---|---|---|---|
| Age (Years) | Density Classes (Trees ha−1) | W1 (%) | W2 (%) | W3 (%) | Average | ANOVA Planting Density |
| 15 | 2500 | 2.8 | 2.6 | 2.3 | 2.6 A | |
| 2000 | 5.7 | 5.0 | 4.8 | 5.2 B | F = 791.79; p ≤ 0.0001 | |
| 1667 | 9.3 | 9.3 | 9.1 | 9.2 C | ||
| ANOVA Models F = 5.013; p = 0.081 | Average | 5.9 | 5.6 | 5.4 | ||
| A | A | A | ||||
| 25 | 2500 | 1.9 | 1.7 | 0.9 | 1.5 A | |
| 2000 | 4.6 | 4.4 | 4.2 | 4.4 B | F = 216.67; p ≤ 0.0001 | |
| 1667 | 6.6 | 5.7 | 5.6 | 6.0 C | ||
| ANOVA Models F = 6.766; p = 0.052 | Average | 4.4 | 3.9 | 3.6 | ||
| A | AB | B | ||||
| 40 | 2500 | 1.4 | 1.1 | 0.6 | 1.0 A | |
| 2000 | 3.9 | 3.6 | 3.5 | 3.7 B | F = 379.18; p ≤ 0.0001 | |
| 1667 | 5.9 | 5.1 | 4.9 | 5.3 C | ||
| ANOVA Models F = 11.273; p = 0.023 | Average | 3.7 | 3.3 | 3.0 | ||
| A | AB | B | ||||
| U (%) of biomass estimates (Average by density classes) | ||||||
| 15 | 7.3 | 6.8 | 6.7 | |||
| 25 | 5.8 | 5.0 | 4.7 | |||
| 40 | 4.9 | 4.2 | 3.6 | |||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marziliano, P.A.; Menguzzato, G.; Coletta, V. Evaluating Carbon Stock Changes in Forest and Related Uncertainty. Sustainability 2017, 9, 1702. https://doi.org/10.3390/su9101702
Marziliano PA, Menguzzato G, Coletta V. Evaluating Carbon Stock Changes in Forest and Related Uncertainty. Sustainability. 2017; 9(10):1702. https://doi.org/10.3390/su9101702
Chicago/Turabian StyleMarziliano, Pasquale A., Giuliano Menguzzato, and Vittoria Coletta. 2017. "Evaluating Carbon Stock Changes in Forest and Related Uncertainty" Sustainability 9, no. 10: 1702. https://doi.org/10.3390/su9101702






