Data Quality Assessment of the Uncertainty Analysis Applied to the Greenhouse Gas Emissions of a Dairy Cow System
Abstract
:1. Introduction
2. Materials and Methods
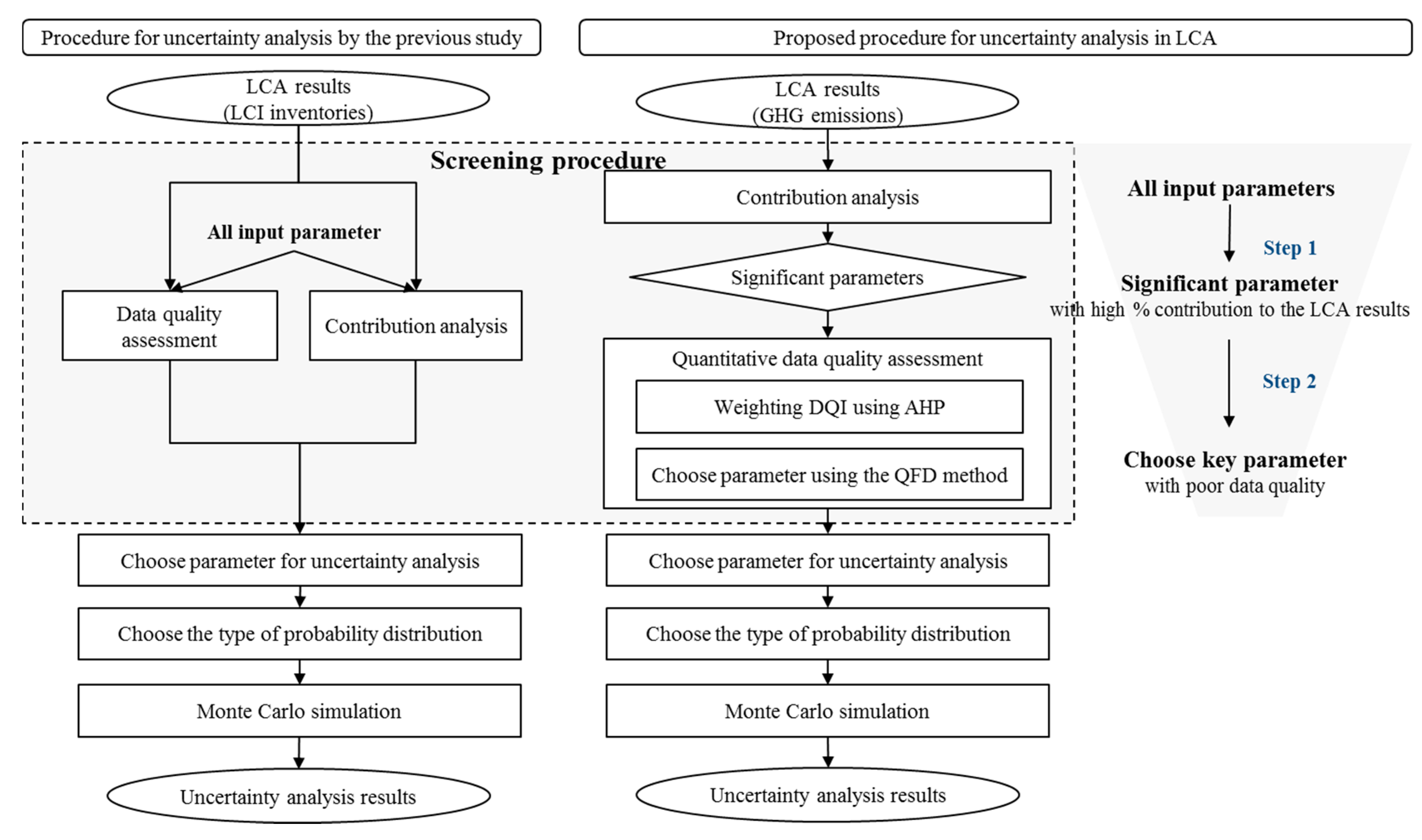
2.1. Simplified Procedure for Selecting Key Parameters
2.2. Overview of the Proposed Method
2.2.1. Step 1: Contribution Analysis and Choice of Significant Parameters
2.2.2. Step 2: Quantitative Data Quality Assessment
Construction of Reciprocal Matrix
Estimation of Relative Importance of the Five DQIs
Choose Input Parameter for Uncertainty Analysis Using the QFD Method
2.2.3. Step 3: Choice of Probability Distribution and Monte Carlo Simulation
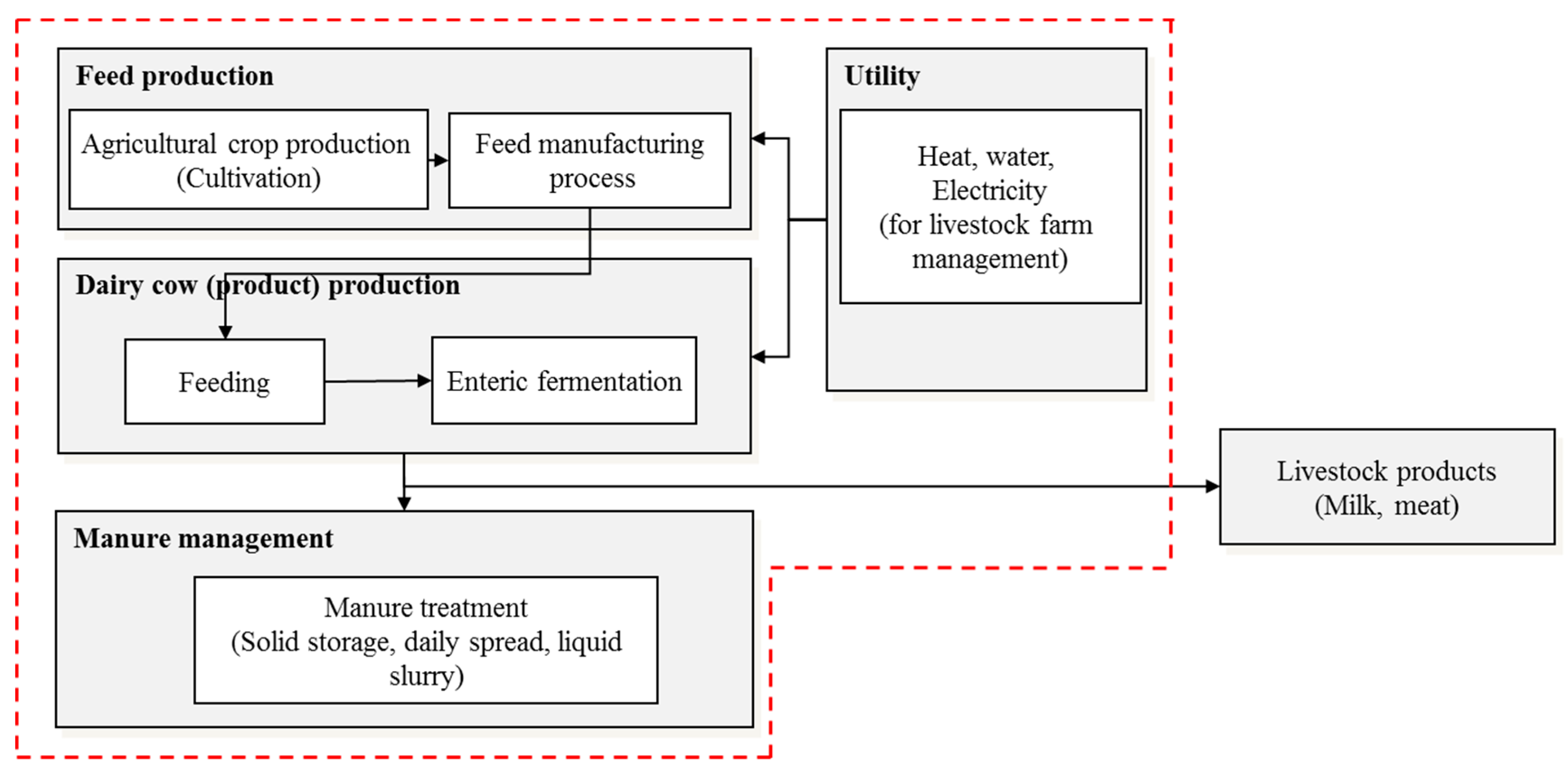
2.3. Case Study
3. Results
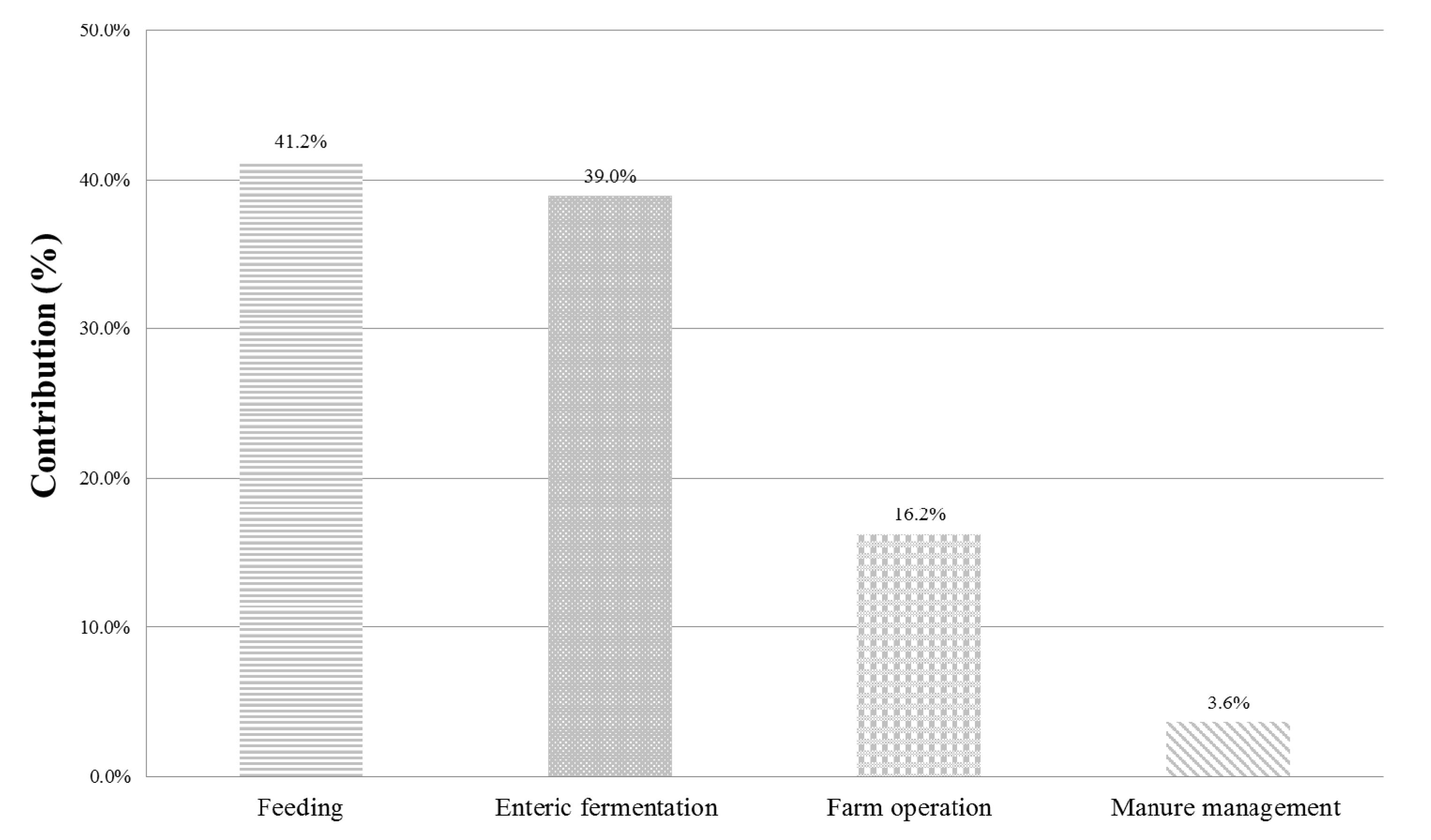
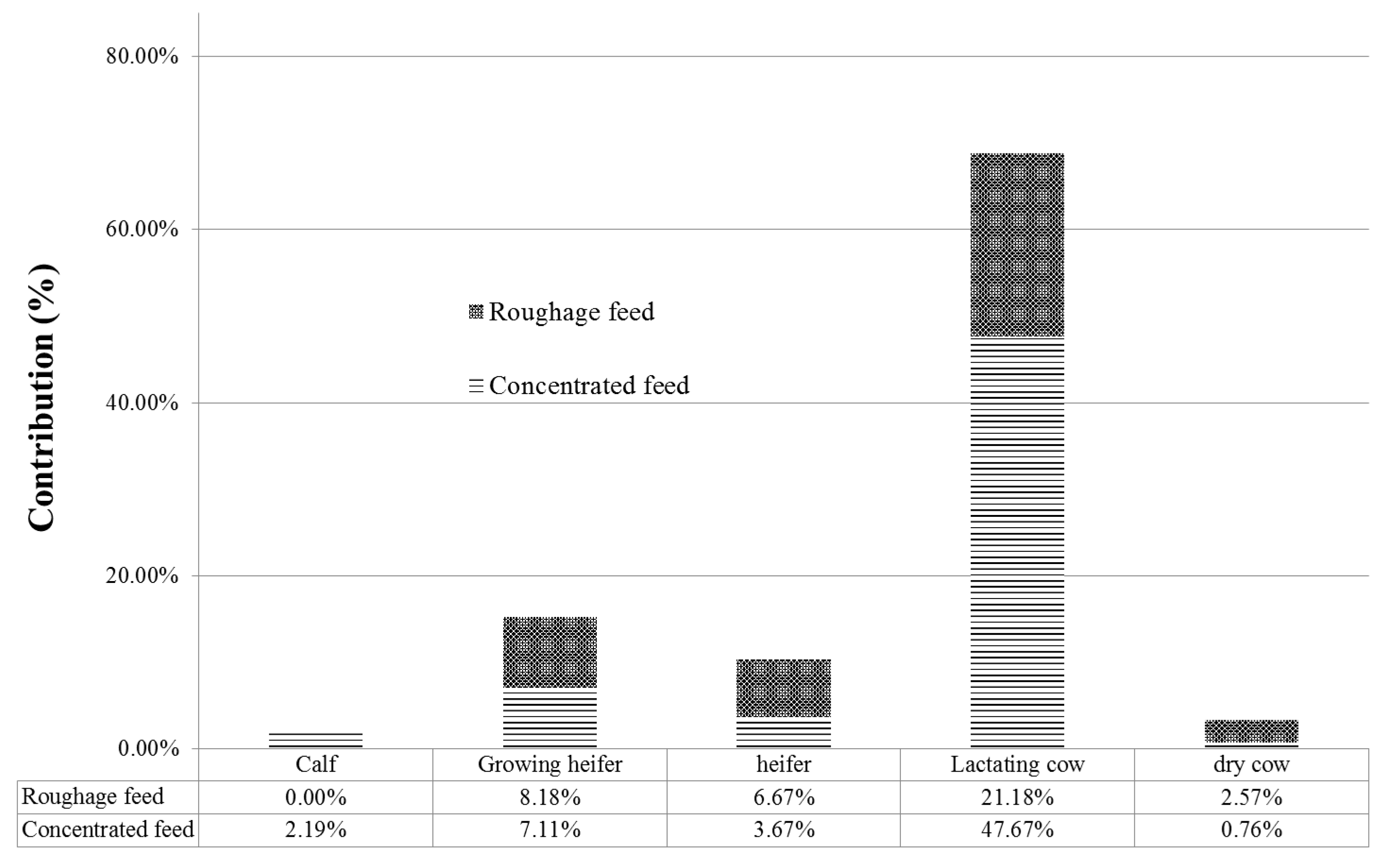
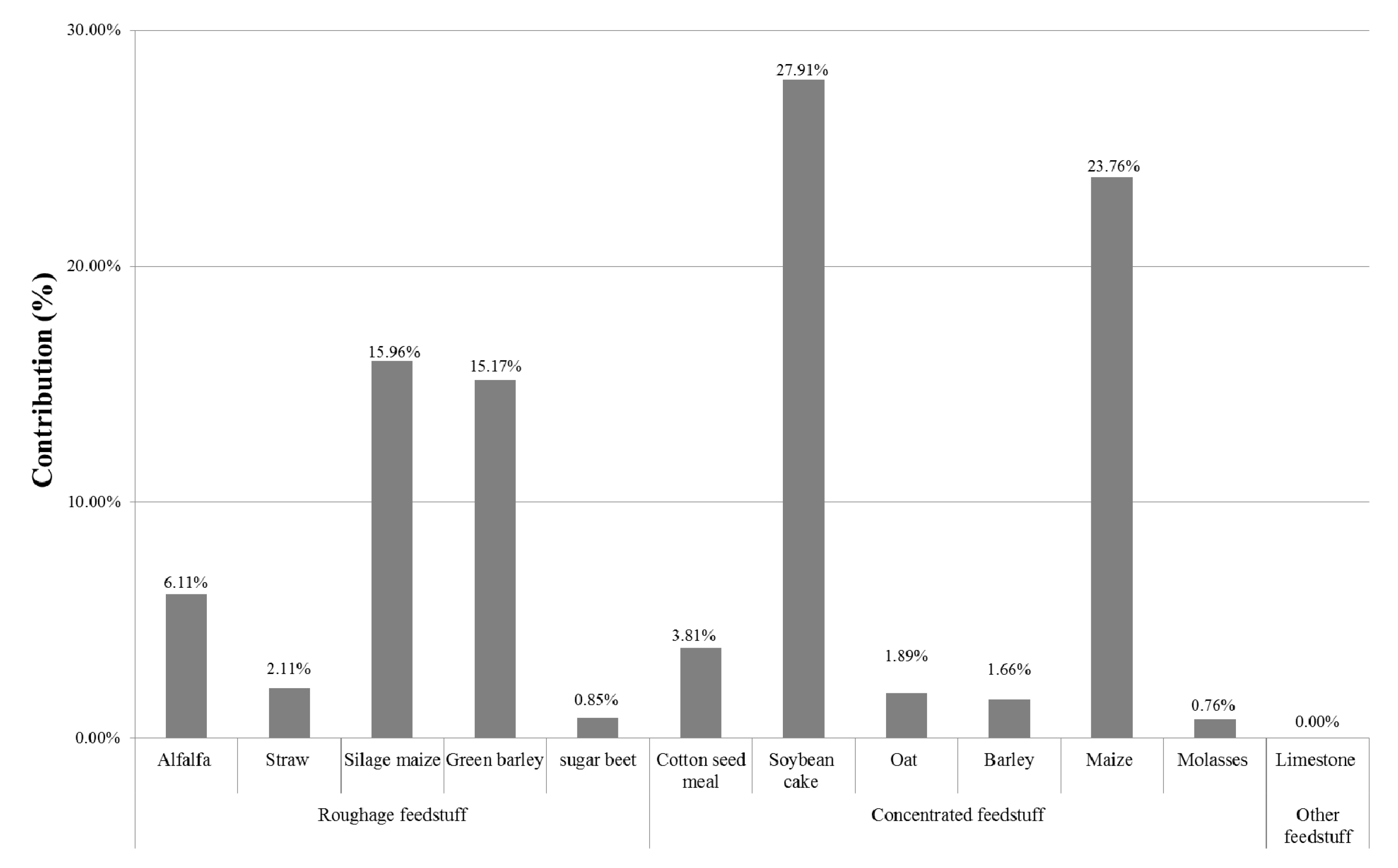
3.1. Step 1: Contribution Analysis and Choice of Significant Parameters
- In the feeding activity: the total number of parameters were 19; they include the number of feed intakes (two feeds such as roughage and concentrated feed), head (five in the growth phase) and the emissions factors (EF) (emission factors for 12 feedstuffs).
- In the enteric fermentation activity: the total number of parameters were 20; they include the number of feed intakes (two feeds), heads (five in the growth phase), methane conversion factors, Ym and the EF and Growth Energy (GE) (12 feedstuffs).
- In the farm operation: the total number of parameters were 14; they include the types of energy (seven types of energy consumption) and EFs of energy (seven types such as coal, diesel, electricity, etc.).
- In the manure management: the total number of parameters were 27; they include the number of heads (five in the growth phase), daily volatile solid excreted in five growth phases, and others (see Baek et al. [9] for further details).
3.2. Step 2: Quantitative Data Quality Assessment
3.3. Step 3: Choice of Probability Distribution and Monte Carlo Simulation
4. Discussion
5. Conclusions
- Parameter uncertainty is the major source of uncertainty of LCA results, but it is difficult to quantify all types of uncertainty in the input parameter.
- The DQI indicators used to generate the aggregated DQI scores were treated with equal weight, or in two types of weight based on an abstract basis.
- (i)
- A simplified procedure based on a contribution analysis followed by a data quality assessment was proposed for selecting input parameters for the uncertainty analysis, and
- (ii)
- A quantitative data quality assessment method based on the modified pedigree method was proposed, which adopted the AHP (analytic hierarchy process) method and QFD (quality function deployment).
Acknowledgements
Author Contributions
Conflicts of Interest
References
- Gerber, P.J.; Steinfeld, H.; Henderson, B.; Mottet, A.; Opio, C.; Dijkman, J.; Tempio, G. Tackling Climate Change through Livestock: A Global Assessment of Emissions and Mitigation Opportunities; Food and Agriculture Organization of the United Nations (FAO): Washington, DC, USA, 2013. [Google Scholar]
- Bailey, R.; Froggatt, A.; Wellesley, L. Livestock—Climate Change’s Forgotten Sector; Global Public Opinion on Meat and Dairy Consumption; The Royal Institute of International Affairs: London, UK, 2014. [Google Scholar]
- Cederberg, C.; Mattsson, B. Life cycle assessment of milk production—A comparison of conventional and organic farming. J. Clean. Prod. 2000, 8, 49–60. [Google Scholar] [CrossRef]
- Haas, G.; Wetterich, F.; Köpke, U. Comparing intensive, extensified and organic grassland farming in southern Germany by process life cycle assessment. Agric. Ecosyst. Environ. 2001, 83, 43–53. [Google Scholar] [CrossRef]
- Ogino, A.; Kaku, K.; Osada, T.; Shimada, K. Environment: Environmental impacts of the Japanese beef-fattening system with different feeding lengths as evaluated by a life-cycle assessment method. J. Anim. Sci. 2004, 82, 2115–2122. [Google Scholar] [CrossRef] [PubMed]
- Halberg, N.; van der Werf, H.M.; Basset-Mens, C.; Dalgaard, R.; de Boer, I.J. Environmental assessment tools for the evaluation and improvement of European livestock production systems. Livest. Prod. Sci. 2005, 96, 33–50. [Google Scholar] [CrossRef]
- International Organization for Standardization (ISO). Technical Committee ISO/TC 207, Environmental Management. Subcommittee SC 5, Life Cycle Assessment. Environmental Management: Life Cycle Assessment: Requirements and Guidelines; International Organization for Standardization (ISO): Geneva, Switzerland, 2006. [Google Scholar]
- Thomassen, M.A.; van Calker, K.J.; Smits, M.C.; Iepema, G.L.; de Boer, I.J. Life cycle assessment of conventional and organic milk production in the Netherlands. Agric. Syst. 2008, 96, 95–107. [Google Scholar] [CrossRef]
- Baek, C.Y.; Lee, K.M.; Park, K.H. Quantification and control of the greenhouse gas emissions from a dairy cow system. J. Clean. Prod. 2014, 70, 50–60. [Google Scholar] [CrossRef]
- Huijbregts, M.A. Application of uncertainty and variability in LCA. Int. J. Life Cycle Assess. 1998, 3, 273–280. [Google Scholar] [CrossRef]
- Heijungs, R.; Huijbregts, M.A. A review of approaches to treat uncertainty in LCA. In Proceedings of the IEMSS Conference, Osnabrück, Germany, 14–17 June 2004. [Google Scholar]
- Funtowicz, S.O.; Ravetz, J.R. Uncertainty and Quality in Science for Policy; Springer Science & Business Media: Berlin, Germany, 1990; Volume 15. [Google Scholar]
- Firestone, M.; Fenner-Crisp, P.; Barry, T.; Bennett, D.; Chang, S.; Callahan, M.; Barnes, D. Guiding Principles for Monte Carlo Analysis; US Environmental Protection Agency: Washington, DC, USA, 1997. [Google Scholar]
- Lloyd, S.M.; Ries, R. Characterizing, Propagating, and Analyzing Uncertainty in Life-Cycle Assessment: A Survey of Quantitative Approaches. J. Ind. Ecol. 2007, 11, 161–179. [Google Scholar] [CrossRef]
- Huijbregts, M.A.; Gilijamse, W.; Ragas, A.M.J.; Reijnders, L. Evaluating Uncertainty in Environmental Life-Cycle Assessment. A Case Study Comparing Two Insulation Options for a Dutch One-Family Dwelling. Environ. Sci. Technol. 2003, 37, 2600–2608. [Google Scholar] [CrossRef] [PubMed]
- Basset-Mens, C.; Kelliher, F.M.; Ledgard, S.; Cox, N. Uncertainty of global warming potential for milk production on a New Zealand farm and implications for decision making. Int. J. Life Cycle Assess. 2009, 14, 630–638. [Google Scholar] [CrossRef]
- Chen, X.; Corson, M.S. Influence of emission-factor uncertainty and farm-characteristic variability in LCA estimates of environmental impacts of French dairy farms. J. Clean. Prod. 2014, 81, 150–157. [Google Scholar] [CrossRef]
- Flysjö, A.; Henriksson, M.; Cederberg, C.; Ledgard, S.; Englund, J.-E. The impact of various parameters on the carbon footprint of milk production in New Zealand and Sweden. Agric. Syst. 2011, 104, 459–469. [Google Scholar] [CrossRef]
- Groen, E.A.; Bokkers, E.A.; Heijungs, R.; de Boer, I.J. Methods for global sensitivity analysis in life cycle assessment. Int. J. Life Cycle Assess. 2017, 22, 1125–1137. [Google Scholar] [CrossRef]
- Mutel, C.L.; de Baan, L.; Hellweg, S. Two-step sensitivity testing of parametrized and regionalized life cycle assessments: Methodology and case study. Environ. Sci. Technol. 2013, 47, 5660–5667. [Google Scholar] [CrossRef] [PubMed]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis: The Primer; John Wiley & Sons: Hoboken, NJ, USA, 2008; pp. 157–158. [Google Scholar]
- Maurice, B.; Frischknecht, R.; Coelho-Schwirtz, V.; Hungerbühler, K. Uncertainty analysis in life cycle inventory. Application to the production of electricity with French coal power plants. J. Clean. Prod. 2000, 8, 95–108. [Google Scholar] [CrossRef]
- Weidema, B.P.; Wesnæs, M.S. Data quality management for life cycle inventories—An example of using data quality indicators. J. Clean. Prod. 1996, 4, 167–174. [Google Scholar] [CrossRef]
- Wang, E.; Shen, Z.; Neal, J.; Shi, J.; Berryman, C.; Schwer, A. An AHP-weighted aggregated data quality indicator (AWADQI) approach for estimating embodied energy of building materials. Int. J. Life Cycle Assess. 2012, 17, 764–773. [Google Scholar] [CrossRef]
- Canter, K.G.; Kennedy, D.J.; Montgomery, D.C.; Keats, J.B.; Carlyle, W.M. Screening stochastic life cycle assessment inventory models. Int. J. Life Cycle Assess. 2002, 7, 18–26. [Google Scholar] [CrossRef]
- Kennedy, D.J.; Montgomery, D.C.; Quay, B.H. Data quality. Int. J. Life Cycle Assess. 1996, 1, 199–207. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytic Hierarchy Process; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Saaty, L.T. How to make a decision: Analytic hierarchy process. Eur. J. Oper. Res. 1994, 48, 9–26. [Google Scholar] [CrossRef]
- Chuang, P.T. Combining the analytic hierarchy process and quality function deployment for a location decision from a requirement perspective. Int. J. Adv. Manuf. Technol. 2001, 18, 842–849. [Google Scholar] [CrossRef]
- Saaty, L.T. Decision making with the analytic hierarchy process. Int. J. Serv. Sci. 2008, 1, 83–98. [Google Scholar] [CrossRef]
- Macharis, C.; Springael, J.; De Brucker, K.; Verbeke, A. PROMETHEE and AHP: The design of operational synergies in multicriteria analysis: Strengthening PROMETHEE with ideas of AHP. Eur. J. Oper. Res. 2004, 153, 307–317. [Google Scholar] [CrossRef]
- Vose, D. Quantitative Risk Analysis—A Guide to Monte Carlo Simulation Modeling; Wiley: Hoboken, NJ, USA, 1996; pp. 103–117. [Google Scholar]
- Mon, J.P.; Korea Dairy Committee and Ministry of Agriculture; Food and Rural Affairs. Dairy Statistical Yearbook 2010, 121–128. Available online: http://ebook.dairy.or.kr/autoalbum/view.html (accessed on 20 September 2017).
- Anderson, T.W.; Darling, D.A. Asymptotic theory of certain goodness-of-fit criteria based on stochastic processes. Ann. Math. Stat. 1952, 25, 193–212. [Google Scholar] [CrossRef]
- Oracle. Crystal Ball 11.1.2 User's Guide; Oracle: Redwood, CA, USA, 2012. [Google Scholar]
- Aull-Hyde, R.; Erdogan, S.; Duke, J.M. An experiment on the consistency of aggregated comparison matrices in AHP. Eur. J. Oper. Res. 2006, 171, 290–295. [Google Scholar] [CrossRef]
- Lee, K.M.; Park, K.H. Development of carbon tracing system for livestock agriculture. In Development of LCI DB and Estimation of Greenhouse Gas from Feedstuff; Research Report; National Institute of Animal Science of the Republic of Korea: Jeonju, Korea, 2012. [Google Scholar]
- Intergovernmental Panel on Climate Change (IPCC). IPCC Climate Change Fourth Assessment Report: Climate Change; Intergovernmental Panel on Climate Change (IPCC): Geneva, Switzerland, 2007. [Google Scholar]
- Park, B.H. Food, Agriculture, Forestry and Fisheries Statistical Yearbook; Ministry of Agriculture, Food and Rural Affairs: Guelph, ON, Canada, 2011; pp. 128–129.
- Lee, S.J. Korean Feeding Standard for Dairy Cattle; National Institute of Animal Science: Jeonju, Korea, 2007; pp. 250–255, 374–429. [Google Scholar]
- Heijungs, R. Identification of key issues for further investigation in improving the reliability of life-cycle assessments. J. Clean. Prod. 1996, 4, 159–166. [Google Scholar] [CrossRef]
- Wang, E.; Shen, Z. A hybrid Data Quality Indicator and statistical method for improving uncertainty analysis in LCA of complex system—Application to the whole-building embodied energy analysis. J. Clean. Prod. 2013, 43, 166–173. [Google Scholar] [CrossRef]
| Category | Contents |
|---|---|
| Number of cow heads | 90 |
| Head per growth phase | Calf: 10, growing heifers: 27, heifers: 14, lactating cows: 36, dry cows: 3 |
| Farm size | Large-scale (>80) |
| Manure treatment system | Solid storage (composting settled solids) |
| Milk production | 1450 kg/day |
| Functional unit | 1 kg raw milk FPCM (fat and protein corrected milk) (fat content = 4%, protein contents = 3.3%) |
| Reciprocal Matrix | |||||||
| DQI | Reliability | Completeness | Temporal | Geographical | Technological | Sum | CR: 0.073 |
| Reliability | 1 | 4.400 | 3.667 | 4.333 | 5.100 | ||
| Completeness | 0.227 | 1 | 3.073 | 3.320 | 4.220 | ||
| Temporal | 0.273 | 0.325 | 1 | 2.745 | 2.833 | ||
| Geographical | 0.231 | 0.301 | 0.364 | 1 | 0.983 | ||
| Technological | 0.196 | 0.237 | 0.353 | 1.02 | 1 | ||
| Sum | 1.927 | 6.264 | 8.457 | 12.415 | 14.137 | 43.200 | |
| Normalization Matrix | |||||||
| DQI | Reliability | Completeness | Temporal | Geographical | Technological | Sum | Relative importance (wi) |
| Reliability | 0.519 | 0.702 | 0.434 | 0.349 | 0.361 | 2.365 | 0.473 |
| Completeness | 0.118 | 0.160 | 0.363 | 0.267 | 0.299 | 1.207 | 0.241 |
| Temporal | 0.142 | 0.052 | 0.118 | 0.221 | 0.200 | 0.733 | 0.147 |
| Geographical | 0.120 | 0.048 | 0.043 | 0.081 | 0.070 | 0.361 | 0.072 |
| Technological | 0.102 | 0.038 | 0.042 | 0.082 | 0.071 | 0.334 | 0.067 |
| DQI | Significant Parameters | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Feeding Activity | Enteric Fermentation Activity | |||||||||||||
| Relative Importance (wi) | EF(i) | Ym | GE | |||||||||||
| Alfalfa | Silage Maize | Green Barley | Cotton Seed Meal | Soybean Cake | Maize | Alfalfa | Silage Maize | Green Barley | Cotton Seed Meal | Soybean Cake | Maize | |||
| Reliability | 0.473 | 3 | 3 | 2 | 2 | 3 | 3 | 4 | 4 | 3 | 3 | 3 | 4 | 4 |
| Completeness | 0.241 | 3 | 3 | 2 | 3 | 3 | 3 | 4 | 4 | 3 | 2 | 3 | 3 | 3 |
| Temporal | 0.147 | 3 | 3 | 2 | 3 | 3 | 3 | 3 | 3 | 4 | 2 | 3 | 4 | 4 |
| Geographical | 0.072 | 4 | 4 | 2 | 4 | 4 | 4 | 5 | 5 | 5 | 4 | 4 | 4 | 4 |
| Technological | 0.067 | 4 | 4 | 3 | 3 | 4 | 4 | 3 | 3 | 5 | 3 | 3 | 3 | 3 |
| raw score (wij) | 3.14 | 3.14 | 2.07 | 2.60 | 3.14 | 3.14 | 3.86 | 3.86 | 3.42 | 2.68 | 3.07 | 3.69 | 3.69 | |
| relative weight | 0.08 | 0.08 | 0.05 | 0.06 | 0.08 | 0.08 | 0.09 | 0.09 | 0.08 | 0.06 | 0.07 | 0.09 | 0.09 | |
| Significant Parameter | Stochastic Assumption | Probability Distribution | ||
|---|---|---|---|---|
| Input Parameter (Random Variable) | ||||
| Feeding | EF(i) (kg CO2 eq/kg) | Soybean cake | Mean: 0.712, Std. Dev.: 0.090 | Normal distribution |
| Maize | Mean: 0.744, Std. Dev.: 0.084 | Normal distribution | ||
| Alfalfa | Mean: 0.326, Std. Dev.: 0.029 | Normal distribution | ||
| Silage Maize | Mean: 0.224, Std. Dev.: 0.071 | Normal distribution | ||
| Feeding(j, lactating cow) (kg DM/yr head) | Concentrated feed | Likeliest: 4803, Scale: 493 | Maximum Extreme distribution | |
| Enteric fermentation | Roughage feed | Likeliest: 6226, Scale: 639 | Maximum Extreme distribution | |
| GE(i) (Mcal/kg DM) | Soybean cake | Mean: 4.713, Std. Dev.: 0.519 | Normal distribution | |
| Maize | Mean: 4.447, Std. Dev.: 0.441 | Normal distribution | ||
| Alfalfa | Mean: 4.08, Std. Dev.: 0.410 | Normal distribution | ||
| Silage Maize | Mean: 4.14, Std. Dev.: 0.401 | Normal distribution | ||
| Methane conversion factor Ym (%) | Minimum: 5.5%, Likeliest: 6.5%, Maximum: 7.5% | Triangular distribution | ||
| The GHG Emissions (kg CO2-eq/1 kg of FPCM) | ||||
|---|---|---|---|---|
| Parameter | The Proposed Method | The Existing Method | ||
| Feeding | Enteric Fermentation | Feeding | Enteric Fermentation | |
| Point estimate | 0.43 | 0.41 | 0.43 | 0.41 |
| Mean | 0.44 | 0.42 | 0.43 | 0.41 |
| Standard Deviation | 0.04 | 0.02 | 0.04 | 0.03 |
| Coefficient of Variation (%) | 6.67 | 4.17 | 8.64 | 7.83 |
| 95% confidence interval | <0.38, 0.49> | <0.38, 0.44> | <0.36, 0.51> | <0.35, 0.48> |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baek, C.-Y.; Park, K.-H.; Tahara, K.; Chun, Y.-Y. Data Quality Assessment of the Uncertainty Analysis Applied to the Greenhouse Gas Emissions of a Dairy Cow System. Sustainability 2017, 9, 1676. https://doi.org/10.3390/su9101676
Baek C-Y, Park K-H, Tahara K, Chun Y-Y. Data Quality Assessment of the Uncertainty Analysis Applied to the Greenhouse Gas Emissions of a Dairy Cow System. Sustainability. 2017; 9(10):1676. https://doi.org/10.3390/su9101676
Chicago/Turabian StyleBaek, Chun-Youl, Kyu-Hyun Park, Kiyotaka Tahara, and Yoon-Young Chun. 2017. "Data Quality Assessment of the Uncertainty Analysis Applied to the Greenhouse Gas Emissions of a Dairy Cow System" Sustainability 9, no. 10: 1676. https://doi.org/10.3390/su9101676





