1. Introduction
Solar car races are well-known as universities and college competitions with the aim of of promoting alternative energies and energy efficiency. Nevertheless, major engineering developments are required to have a competitive vehicle and several developments that have emerged in these races are now applied in different industrial sectors. High efficiency electric motors and drivers [
1], low consumption tires, solar panel Maximum Power Point Trackers (MPPTs), solar panel encapsulations and telemetry systems are some of the technological products raised on racing solar cars [
2].
The Bridgestone World Solar Challenge (WSC) is one of the most popular solar vehicle races where recognized universities and industries from all over the world join forces to compete every two years. The main objective is to cross Australia from Darwin to Adelaide (3022 km) using only solar energy. The success on this challenge demands both an efficient vehicle and an adequate control strategy during the entire race [
3].
The vehicle must be designed, built and raced with the purpose of being energy efficient. The main features of the car are based on two properties: reliable and autonomous. For the autonomy, the car should capture as much as possible energy from the sun and spend the lowest possible energy when traveling. The design and manufacture processes take into account: reliability, safety, solar panel efficiency, aerodynamics, weight reduction, among other important considerations (see [
4,
5,
6,
7,
8]).
With the vehicle conceived, the final step is to define the race strategy in order to obtain the best performance and take advantage of its capabilities. The narrow gap between the energy input from the solar panel and the consumption of the motor creates the necessity of optimizing the driver decisions seeking a good energy management. The race plan must define the speed on the entire path, taking into account the vehicle properties, the road characteristics, the weather conditions, and all the factors that can affect the vehicle or the race development. The solar car racing strategy problem has been narrowly disclosed academically due to the competitive nature of cars racing. Since the early 90’s, less than 10 studies about this topic have been formally published. On the contrary, train optimal control has been widely studied and disclosed for decades. Although several differences are remarkable, the energy efficiency operation is the main objective of both applications and different approaches can be applied on solar cars.
In this work, the racing strategy of the EPM-EAFIT solar car for WSC 2015 is presented. A literary revision of solar car strategy and an overview on train speed optimization is exposed in
Section 2.
Section 3 describes the race model in order to simulate the vehicle performance for a given conditions. Once the race model is complete, an optimization process is linked to this model and the best driving parameters are found in order to minimize the objective function, i.e. racing time (See
Section 4). Three different optimization methods are tested and results are exposed on
Section 5.
2. Solar Car Racing Strategy
Defining a solar car racing strategy can be treated as a control optimization problem where, in the most general case, a velocity pattern for the vehicle must be found in order to minimize the time to complete a defined distance considering race, energy and environmental conditions. The route planning and selection [
9] is excluded from the race strategy considering that solar car races have a strictly defined path.
Regarding solar cars in general, the most relevant publications are “Speed of Light” [
10] and “The Leading Edge” [
11], these two books include some basic information and a general description about racing strategy. On 1998, Shimizu et al. [
12] described the racing strategy of the “Honda Dream” solar car during the 1990, 1993 and 1996 WSC races. They divided the racing strategy on three principal topics: a “Supervision support system”, a “Cruising simulation program” and a “Power/Speed optimizing control algorithm”.
The aim of this work is on the optimization algorithm, including by nature, the simulation program. The supervising support system that is mainly related to telemetry hardware and software is not included.
From the point of view of the optimization problem solution, two main approaches can be clearly defined: mathematical optimization and heuristic methods, specially evolutionary algorithms. Mathematical optimization of solar car strategies has been mainly studied by Peter Pudney and Phil Howlett and disclosed in a series of evolving publications [
13,
14,
15]. A complete discussion of speedholding and other racing strategies is supported on mathematical validations. Other mathematical optimization approaches based on optimal control are done by Guerrero-Merino and Duarte-Mermoud [
16] with a power input prediction and pseudospectral methods to find an optimal velocity.
On the other hand, heuristic approaches for solar cars racing strategies propose to create a detailed race simulation model, including complex mathematical definitions and random variables, and then find the optimal velocity of the vehicle using any heuristic optimization. The evolutionary algorithms are widely used on other optimization cases such as structural design [
17] or multiobjective problems [
18] with outstanding results. For solar cars, on 2013, Yesil et al. [
19] proposed an heuristic optimization using Big Bang-Big Crunch for the 2013 WSC, they do not compare the results with other methods and experimental validation is missing. Nevertheless they reported a satisfactory outcome with their implementation.
For other electric vehicles, the optimal driving strategy and velocity profile has been widely studied on train operation control. These optimization techniques and approaches can be extrapolated to solar cars due to its similarity, mainly on the energy consumption calculation. The optimization objective in these cases is to minimize the energy consumption of a train that travels between two points and subject to a defined trip time and some other driving conditions [
20]. Howlett and Pudney [
21,
22,
23] have applied optimal control techniques to mathematically find optimal driving patterns that minimize the energy spent. On 1997, Chang and Sim [
24] firstly proposed the use of Genetic Algorithms (GA) for the train coasting segments between two stations with a multiobjective optimization to include the spent energy, the punctuality and the passengers comfort on the objective function. From there on, On the last two decades, several applications of GA and other heuristic methods to minimize the train energy consumption on different cases have reported successful results [
25,
26,
27].
Using heuristic methods, it is possible to actively include variations and nonlinear functions to the race model while the optimization algorithm will still find a solution. Besides, the growing computational capacity, including parallel computing, opens field for the application of these methods. In this work, a heuristic optimization approach is proposed and the optimization results are compared with previous ones.
3. The Race Model
The first step for optimizing a solar car performance is to model the vehicle behavior on the race. With this race model, the consequences of different strategy inputs on the race performance is obtained.
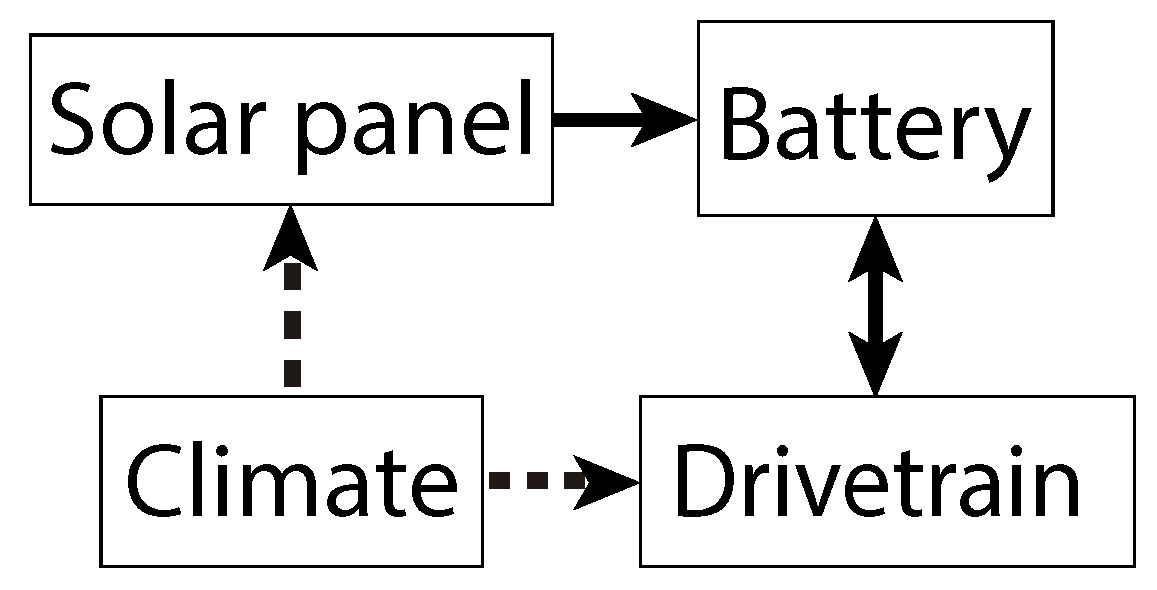
For a solar car simulation, three main models should be coupled together: battery, motion equations (energy consumption) and solar panel (input). The environmental conditions affect the energy input via radiation and temperature and the energy output mainly because of the wind that influence the drag force. Then, they are considered into an independent module of the race model.
Figure 1 illustrates the interactions between modules on the model.
In order to accurately estimate the vehicle performance in the race, the model should include all the car characteristics such as weight, roll coefficient, aerodynamic properties among others. Also external information like road slope, sun position, sun irradiation, wind and others should be considered. This model must be tuned up and validated with experimental tests of the vehicle before expecting valid results.
One of the main inputs of the race model is the velocity set point of the vehicle for the whole race. This is a user (driver) input that affects the outcome on the competition. The velocity set point is a curve that indicates the speed of the car during the race. According to the practical limitations in the race, this velocity is defined to be an integer number in kilometers per hour (km/h) and bounded by the speed limits of the road. Moreover, although the velocity set point can change every instant, it is practical to keep it constant for certain periods of time, generating this way a vector containing the velocity set point for defined segments of the race. Then, the size of this velocity vector is the same number of divisions of the race made for the optimization process.
3.1. Drivetrain
The energy consumption of the vehicle is simulated using the drivetrain model. The main forces that directly oppose the vehicle movement are: aerodynamic drag, tyre rolling resistance and gravity component due to the road slope. The instantaneous power needed on the drive wheels can be calculated as defined in Equation (
1) where
stands for the instantaneous power,
v for the instantaneous velocity,
m for the vehicle mass,
a for the acceleration,
is the vehicle drag area coefficient,
the air density,
the wind velocity component on the vehicle forward direction,
the tyre roll coefficient,
g the gravity acceleration and
the road slope.
For road sections with constant slope and velocity, the wheel power remains constant and the consumed energy (
) can be calculated according to the time (
) on the respective section and the drivetrain efficiency under these conditions (
). Equation (
2) defines the consumed energy estimation for constant speed sections.
In the case of Csiro motors, the instantaneous drivetrain efficiency is estimated according to the study reported on [
28].
3.2. Solar Panel
The photovoltaic solar panel energy generation is simulated taking into account the sun elevation angle (
), the estimated solar irradiance at ground level (
) (See
Section 3.4), the panel+MPPTs efficiency (
) and the panel effective area (
) that considers the instantaneous canopy shadows over the cells. The electric power produced by the solar panel (
) is calculated as defined on Equation (
3).
The solar panel efficiency is experimentally determined taking into account the forced convection cooling of the cells due to the vehicle movement as reported in [
8].
3.3. Battery
A battery model is developed according to the specific cells datasheets and duty cycle experiments. Based on the charge and discharge data integration, the input and output energy are calculated and the battery overall efficiency (
) is estimated according to Equation (
4) where
and
represent the total energy obtained from the discharge and charge test cycles. The energy stored in the battery (
) is defined by Equation (
5) where
and
are the instantaneous solar panel power and drivetrain power respectively, the charge and discharge efficiencies are assumed both equal to
.
3.4. Climate
The more relevant climate factors that affect the vehicle simulation are the solar irradiance (See Equation (
3) and the wind velocity vector (See Equation (
1). The stochasticity of these two variables is removed in order to guarantee repeatability of the optimization process. Nevertheless, a clever estimation of both parameters is included in the simulation.
The solar irradiance (
) is calculated according to the air mass factor and the Lambert’s law (also known as Beer–Bouguer–Lambert’s Law) to define the atmospheric transmittance [
29,
30]. Cloudless sky is assumed and the model is validated experimentally. Equation (
6) defines the radiation estimation,
represents the extraterrestrial solar radiation,
the total atmospheric extinction or attenuation coefficient and
the air mass factor (defined on Equation (
7).
On the other hand, the wind velocity vector is estimated and included according to the monthly averages reported online by the Australian Government Bureau of Meteorology [
31].
4. Optimization Process
As stated in
Section 2, a heuristic optimization approach is selected for defining the race strategy. The main purpose is to find the best velocity in order to minimize the solar car racing time. To have an accurate race model, the optimization step is implemented as depicted in
Figure 2. Different velocity vectors are produced by the optimization algorithm and evaluated in the race model.
The number of race divisions for the velocity vector define the search space size. When the velocity is assumed constant all over the race, the optimization variable is a 1-dimensional vector and a global optimum solution can be found with an exhaustive search. On the other hand, with large velocity vectors, a larger search space is created and clever optimization techniques are needed to find a near-optimal solution. Then, different optimization techniques are used depending on the optimization variable size.
4.1. Exhaustive Search
To be sure of finding a global optimum, the first optimization method is the well-known Exhaustive Search (ES), also named brute-force search. The purpose is to test all the possible solutions and choose the best one. In the case of a 1D velocity vector, it is possible to test all the integer numbers between velocity bounds and pick the best, if the optimization variable is greatly larger it results as non-viable to test all the possible combinations.
4.2. Genetic Algorithms
As proposed on 1975 by John Holland [
32], GA is an evolutionary method based on natural populations and genetic studies to mimic a biological evolution process. With a combination between the natural selection process in which “most fit individuals survive” and random events such as coupling and mutating, an evolution towards an optimal solution is guaranteed. Since the 1970s, new implementations, variations and improvements have been developed showing the large capabilities of this method. For the solar car race strategy problem, a GA is implemented following recommendations given by Sastry et al. [
33].
4.3. Big Bang-Big Crunch
An alternative evolutionary optimization method already implemented on solar car strategy by Yesil et al. [
19] is called Big Bang-Big Crunch (BB-BC). It was first developed by Erol and Eksin on 2006 [
34] reporting an efficiency improvement with respect to a general GA method. The general aim of this method is to iteratively generate random individuals around a center of mass (big bang) and recalculate the center of mass according to the weighted average fitness of the population (big crunch). On every iteration, the radius for new individuals generation is reduced in order to progressively diminish the search space. Equation (
8) defines the way to calculate this value, where
is the center of mass,
n is the population size,
is an individual of the population and
its fitness value.
An implementation of the standard BB-BC algorithm is also made and tested for this project.
4.4. Algorithm Hybridization
To improve the optimization performance, a combination of different methods is proposed. In this case, a Local Search (LS) step [
35] is included after the GA and BB-BC processes as reported on [
36]. One-directional variations are made iteratively to the optimal solution given by the evolutionary algorithm, this has the purpose of evaluating the candidate solutions in the vicinity of the evolutionary algorithm result, if the objective function result is improved, this new solution is saved and the process is iteratively repeated.
5. Results
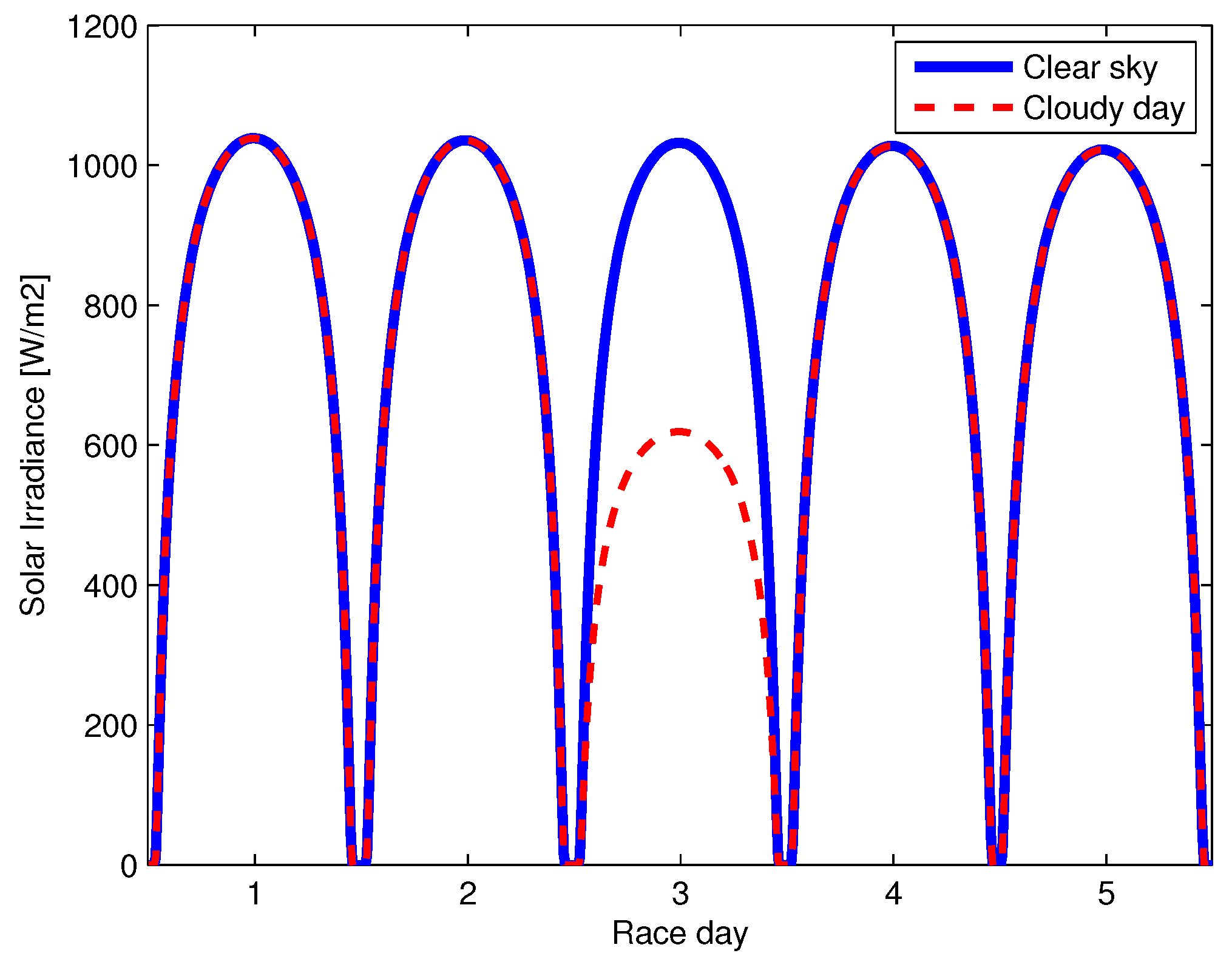
To solve the problem of finding an optimal speed for the EPM-EAFIT Solar Car, for the 2015 WSC, different approaches are implemented and compared. Two environmental cases are proposed: a fully clear sky race (Clear sky case) and a race with one cloudy day that diminishes the entire day irradiance to a 60% of the clear sky one (Cloudy day case).
Figure 3 illustrates the solar irradiance estimation for both cases.
Regarding the optimization method, five main approaches are analyzed for the two environmental cases:
Constant speed during all race (1D optimization variable) with exhaustive search optimization.
Race length divided into halves, two different speeds (2D) and exhaustive search optimization.
Race length divided in three parts, three different speeds (3D) and exhaustive search optimization.
Race divided in 10 segments (10D optimization variable) according to mandatory 30 min control stops defined by the race; GA and BB-BC evolutionary method optimization.
The ES is not implemented with more than 3D vectors due to the large number of possible combinations, in these cases the time required to finish the calculation is considerable. The GA and BB-BC methods are both implemented with 10D vectors and a constant population of 720 candidates. The initial population is created with a random number generator between the minimum velocity and the road speed limit with a uniform distribution.
Every GA iteration involves:
Evaluation of the fitness function (race simulation) for every candidate. The best individual is saved.
Selection of the most fit individuals. The best half of the population is saved for crossover.
Crossover. Random pairs of individuals (parents) are selected from the saved population and four new candidates (sons) are obtained with a linear combination of every pair.
Random mutations are included on the population. An aleatory number from an uniform distribution between and 10 km/h is added to a 10% of the new population.
These steps are repeated until the maximum number of iterations is reached. Also, an early convergence criteria is defined to stop the iterations.
For the BB-BC implementation, the steps 2 and 3 from GA are replaced by the calculation of the center of mass and random generation of new individuals around it as explained on
Section 4.3. The other steps are performed as explained for GA. For both methods 50 iterations are executed. The hybridization proposed on
Section 4.4 is evaluated with the GA+LS and BB-BC+LS algorithms.
The obtained results for a given specific solar car properties, road and the Clear sky weather conditions are shown on
Table 1, the results for the same vehicle properties and road but Cloudy day weather conditions are shown on
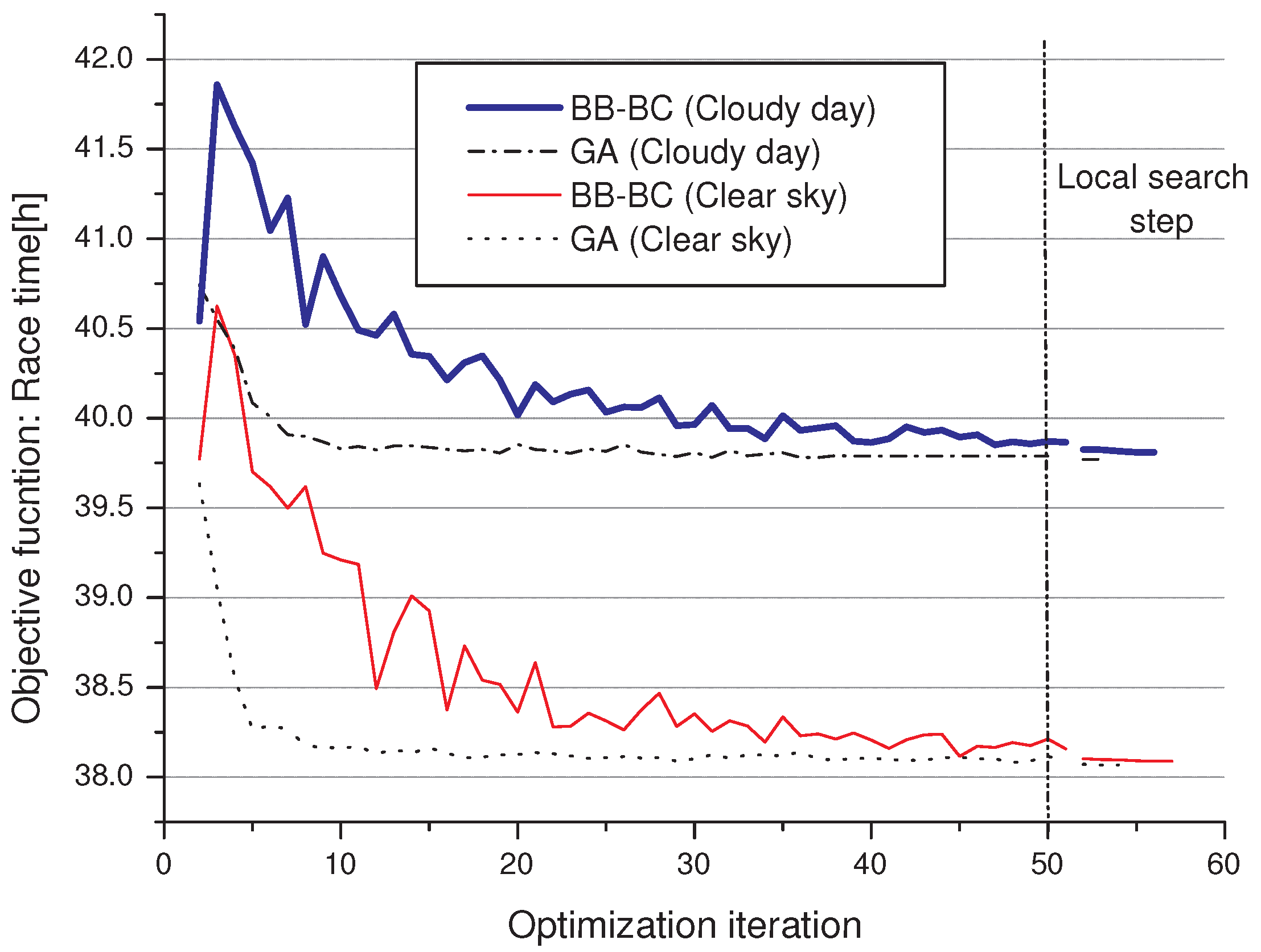
Table 2. The convergence graph for the two different weather cases is presented on
Figure 4. Both the race simulation and the optimization method are programmed in C++ using Microsoft Visual C++ editor and compiler under Windows operative system, then executed serially (not on parallel) on a laptop with Intel Core i7 @ 2.3GHz processor.
6. Case Study
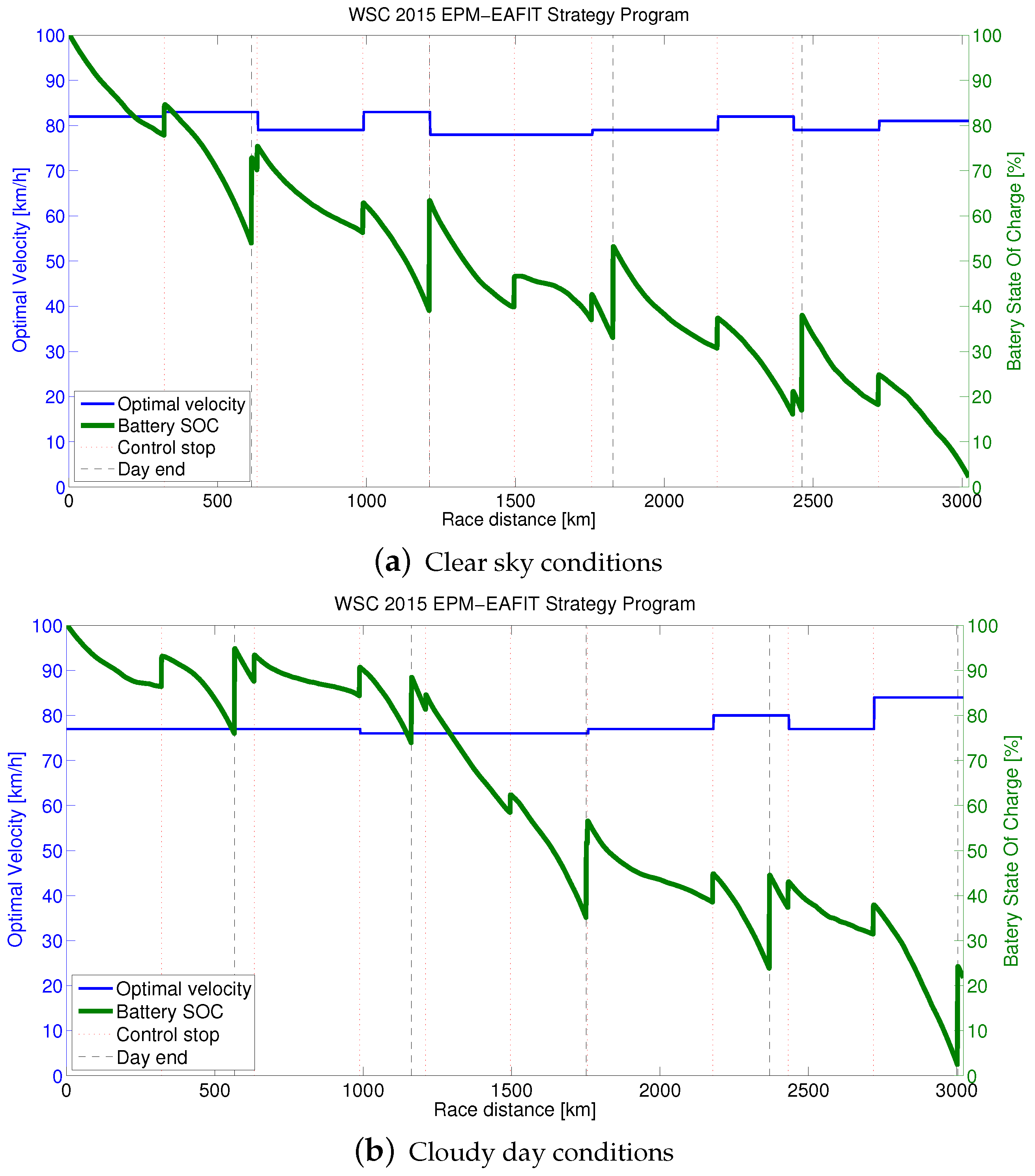
The optimal speed found is only valid for the vehicle properties defined on the race model input. This optimal speed produces a curve that indicates the optimal State Of Charge (SOC) of the battery during the entire race.
Figure 5 illustrates the SOC behavior according to the best solution found using GA+LS and considering the two environmental cases. The optimal velocity vectors are also depicted.
7. Conclusions
The solar car racing strategy planning is the activity to define the best user inputs in order to optimize the energy management and, therefore, minimize an objective function. In this case, the objective function was the time to arrive to the finish line, namely race time, subject to limited energy and other vehicle, road and environmental constraints.
The selected optimization algorithm depended on the size of the search space and the time required to run one single simulation. In this case, one race simulation needed between 4 and 6 milliseconds (ms) of computing time. Then, it was possible to estimate the time needed to execute a defined number of simulations. When an exhaustive search was not practical due to the expensive running time, an evolutionary method was recommended.
In the two cases of study, the GA showed faster convergence and better result than the BB-BC, moreover a monotonic decreasing tendency over the iterations was observed in the graph. Both evolutionary methods tested did not find a global optimum solution, this was verified with the LS step added after, given the small improvements obtained with this hybridization in all the cases.
Enlarging the search space by increasing the number of race divisions produced better solutions than 1, 2 or 3D optimization variables, taking into account that in the case of 10D velocity vectors finding the global optimum solution was not guaranteed with the methods used. No difference was obtained with the change of 1D to 2D, but a (equivalent to 7 min on race) reduction was reached with the 10D vector. The ES method with 3D vectors remarkably exceeded the total race simulations executed (with respect to the other test cases) and, therefore, the total computing time.
The optimal velocity found, was the one that makes the battery SOC end near empty. A 30 min recharging stop was considered if the battery is drained before the finish line but this was evaded in the optimal strategies found. Although a non constant velocity was proved to be better, the 10 optimal velocities for the race kept between 78 and 83 km/h on the Clear sky case and between 75 and 84 km/h on the Cloudy day one. In practical terms if the speed control of the car is manual, this can lead to the same speed all the race.
The 40% solar irradiance reduction on a complete day represented an increase in the race time of almost 2 h, going from a racing time of 38.068 to 39.771 h according to the GA+LS optimization results. The consequences of different environmental cases can also be estimated using this process.
The time efficiency of this optimization method makes it a feasible option to recalculate the strategy during the race after deviations from the predicted behavior or climate prediction changes, a new optimal strategy is obtained in less than 3 min of computing time. This method can be applied to other objective functions and any type of electric vehicle with a given characterization. Other interests can maximize the distance with limited energy or limited time, minimize the external energy used on a given path or optimize the recharging times for a given route.