Assessing Collective Measures in Rural Policy: The Effect of Minimum Participation Rules on the Distribution of Benefits from Irrigation Infrastructure
Abstract
:1. Introduction
2. Methods
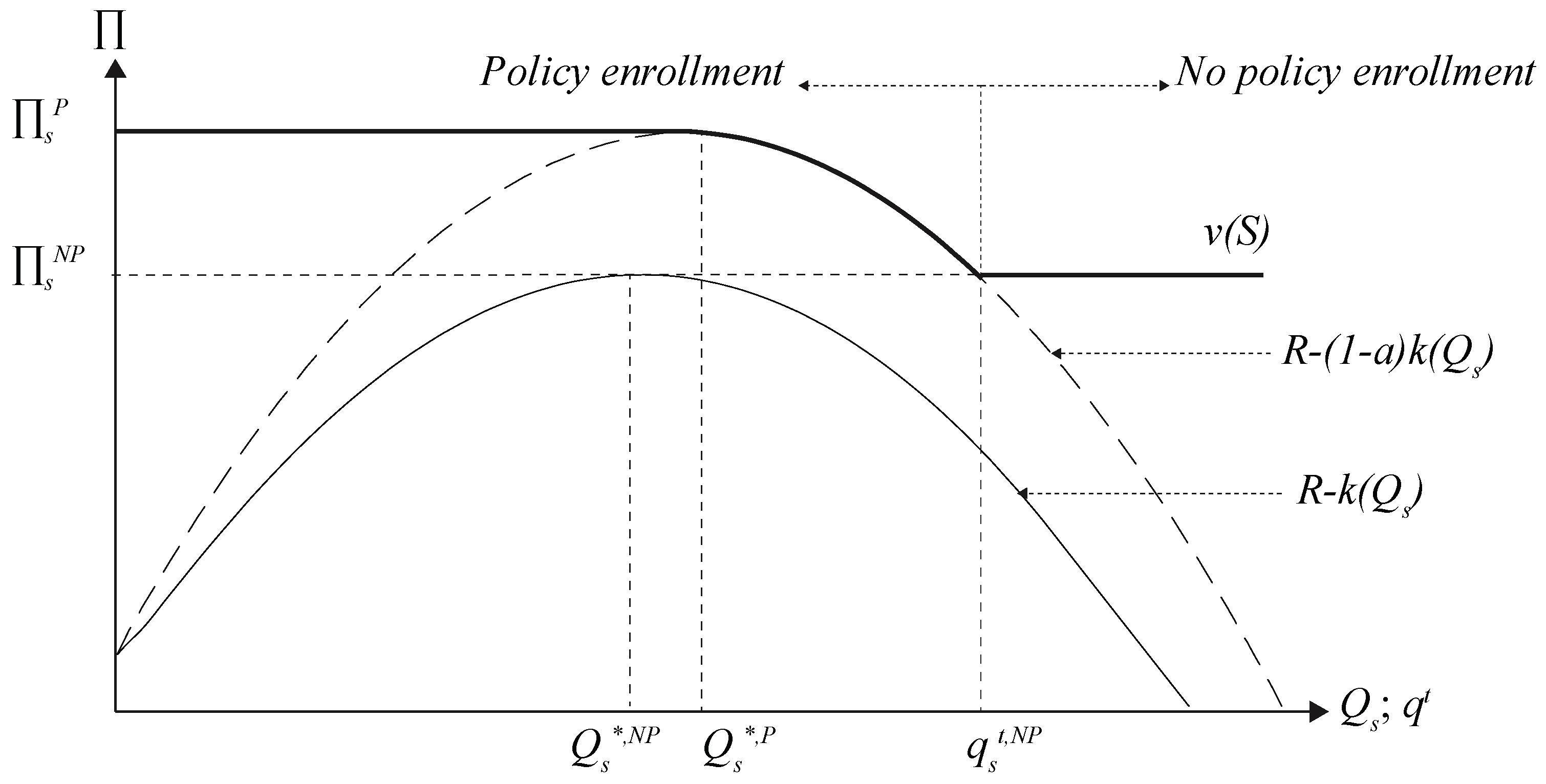
2.1. The Caracteristic Function in a Reservoir Construction Game and the Effect of of the q-Rule and of the n-Rule
2.2. Shapley Value and Nash–Harsanyi Solution
2.3. Numerical Application
3. Results
3.1. Effect of MPR on the Characteristic Function
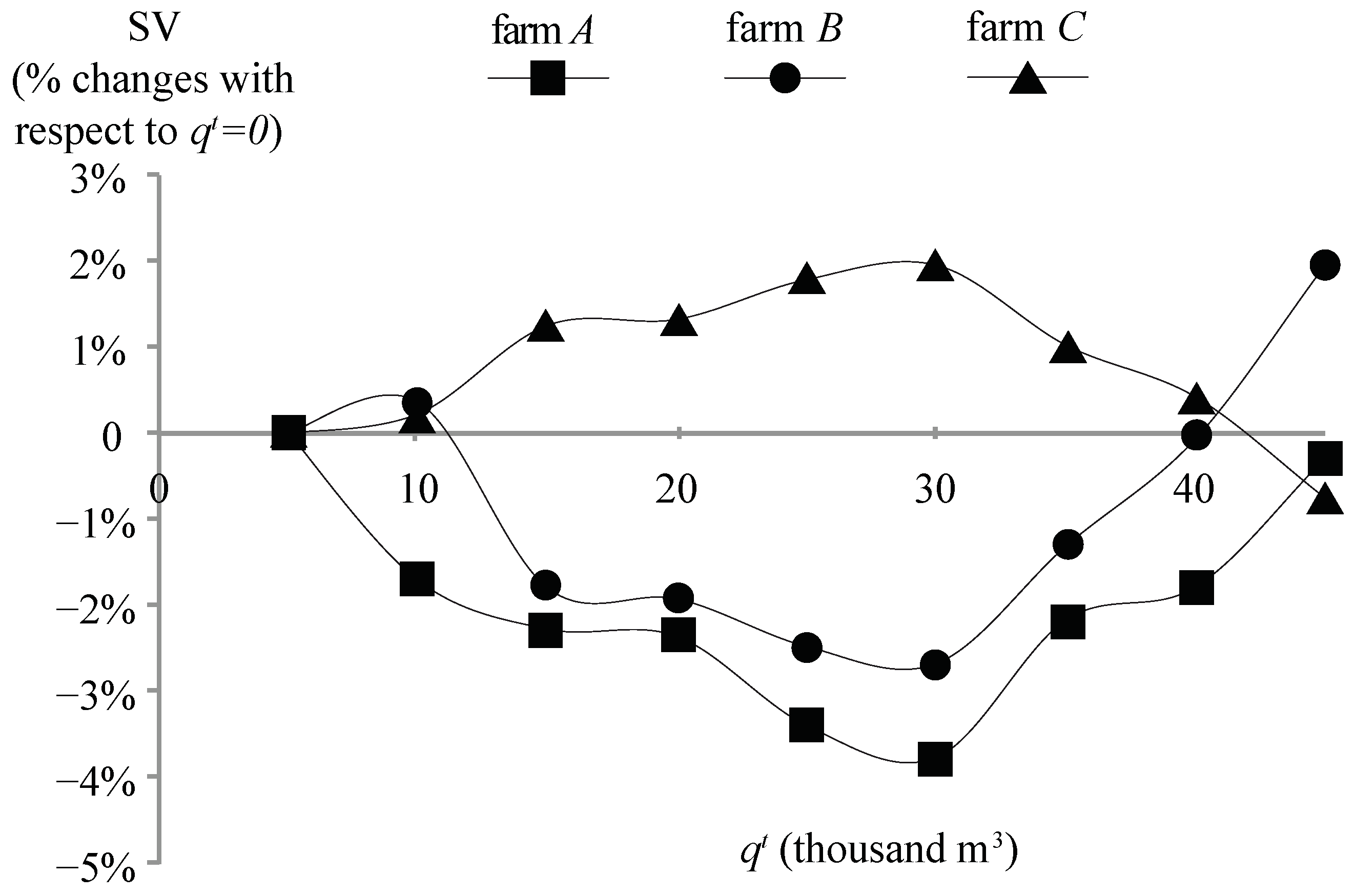
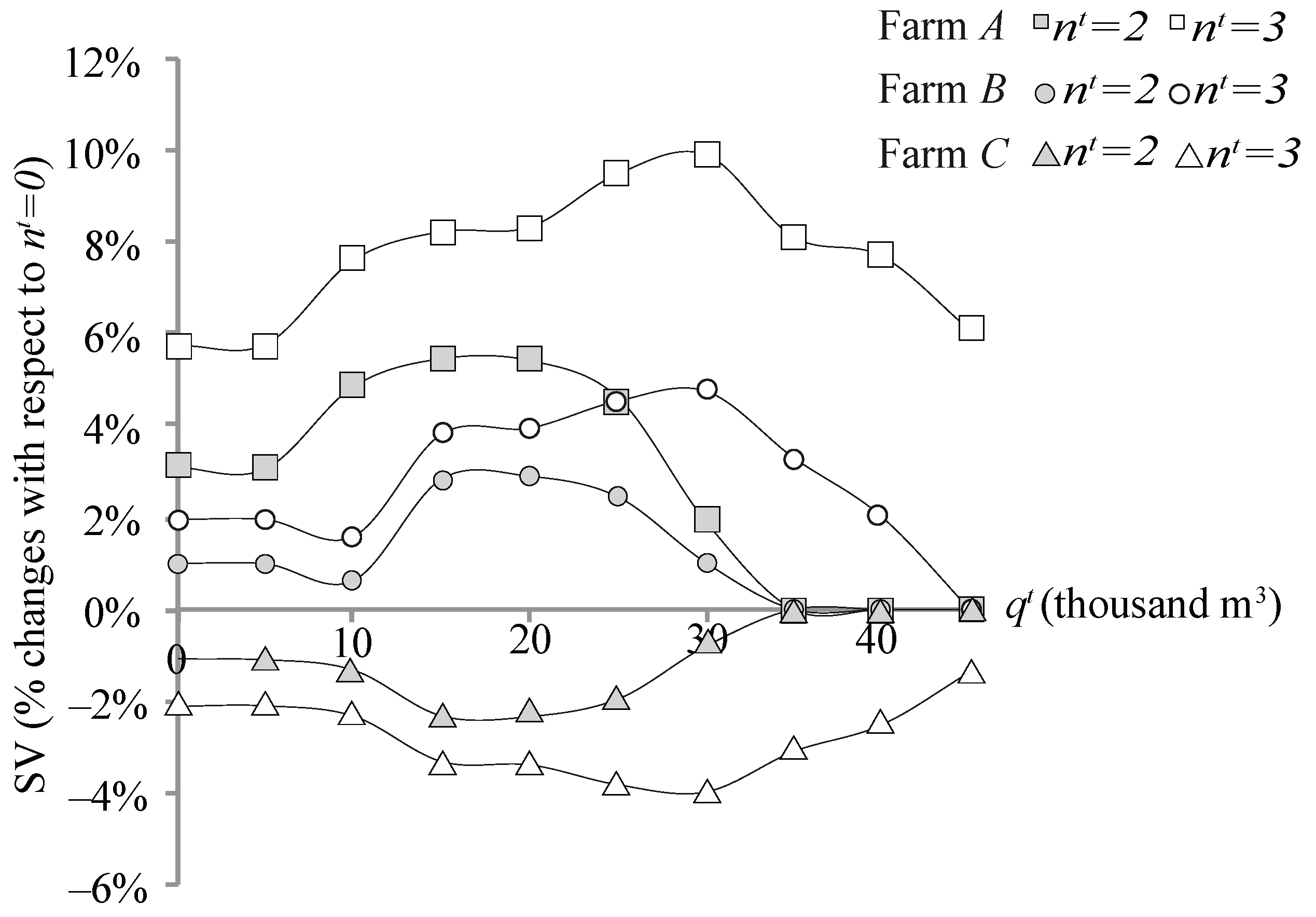
3.2. Shapley Value
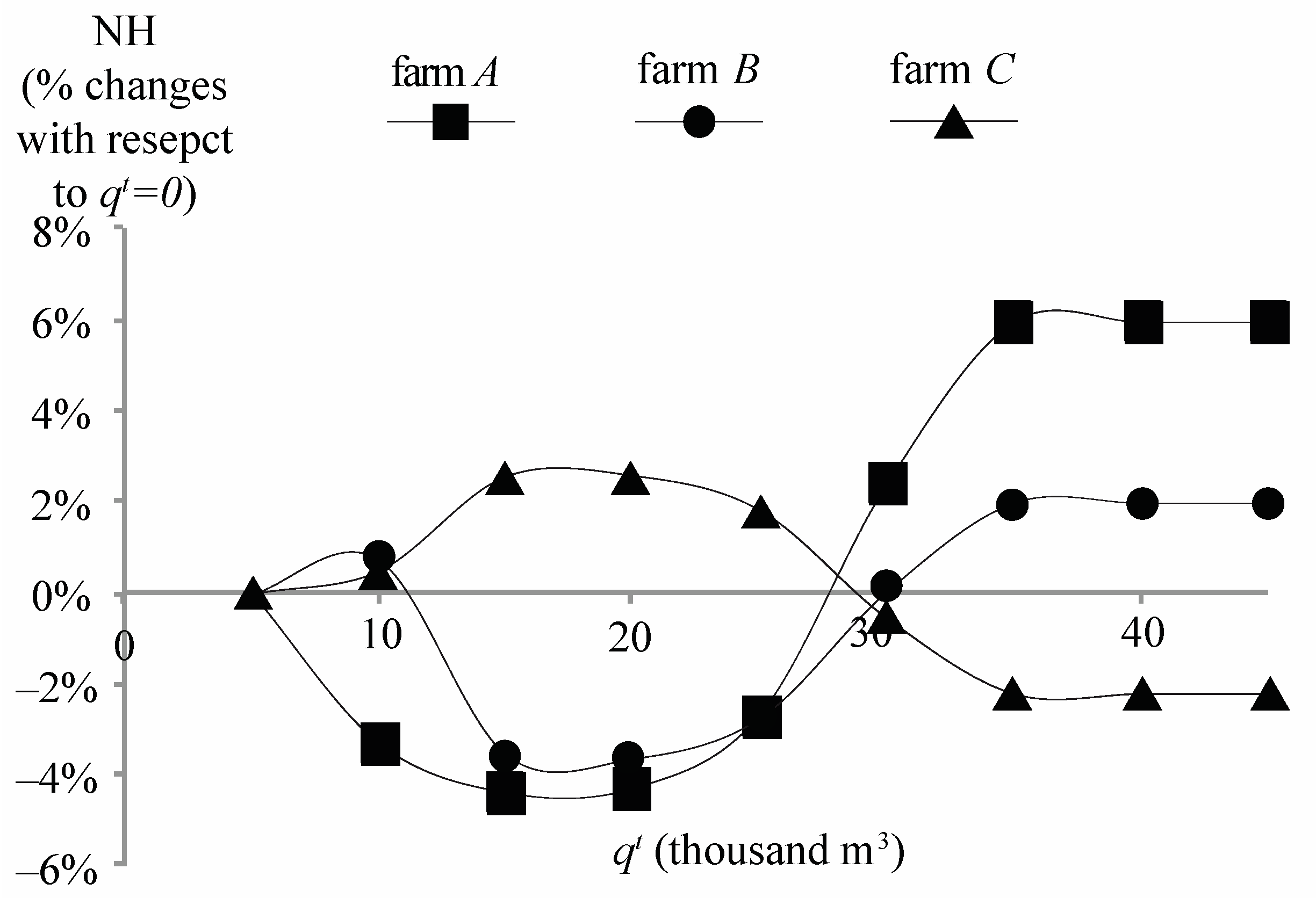
3.3. Nash–Harsanyi Solution
3.4. Comparison of the Solutions
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| nt = 1 | nt = 2 | nt = 3 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Farm | A | B | C | A | B | C | A | B | C |
| qt = 0 | 8490 | 15,824 | 37,991 | 8751 | 15,981 | 37,574 | 8981 | 16,133 | 37,192 |
| qt = 5000 | 8490 | 15,824 | 37,991 | 8751 | 15,981 | 37,574 | 8981 | 16,133 | 37,192 |
| qt = 10,000 | 8346 | 15,881 | 38,079 | 8751 | 15,981 | 37,574 | 8981 | 16,133 | 37,192 |
| qt = 15,000 | 8298 | 15,539 | 38,469 | 8751 | 15,981 | 37,574 | 8981 | 16,133 | 37,192 |
| qt = 20,000 | 8290 | 15,520 | 38,495 | 8740 | 15,970 | 37,596 | 8981 | 16,133 | 37,192 |
| qt = 25,000 | 8202 | 15,432 | 38,671 | 8581 | 15,811 | 37,914 | 8981 | 16,133 | 37,192 |
| qt = 30,000 | 8171 | 15,401 | 38,734 | 8327 | 15,557 | 38,421 | 8981 | 16,133 | 37,192 |
| qt = 35,000 | 8307 | 15617 | 38,382 | 8307 | 15,617 | 38,382 | 8981 | 16,133 | 37,192 |
| qt = 40,000 | 8339 | 15,814 | 38,153 | 8339 | 15,814 | 38,153 | 8981 | 16,133 | 37,192 |
| qt = 45,000 | 8466 | 16,133 | 37,707 | 8466 | 16,133 | 37,707 | 8981 | 16,133 | 37,192 |
| nt = 1 | nt = 2 | nt = 3 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Farm | A | B | C | A | B | C | A | B | C |
| qt = 0 | 8782 | 16,001 | 37,524 | 9303 | 16,315 | 36,688 | 9303 | 16,315 | 36,688 |
| qt = 5000 | 8782 | 16,000 | 37,524 | 9303 | 16,315 | 36,688 | 9303 | 16,315 | 36,688 |
| qt = 10,000 | 8492 | 16,115 | 37,699 | 9303 | 16,315 | 36,688 | 9303 | 16,315 | 36,688 |
| qt = 15,000 | 8396 | 15,431 | 38,479 | 9303 | 16,315 | 36,688 | 9303 | 16,315 | 36,688 |
| qt = 20,000 | 8404 | 15,416 | 38,486 | 9303 | 16,315 | 36,688 | 9303 | 16,315 | 36,688 |
| qt = 25,000 | 8546 | 15,558 | 38,203 | 9303 | 16,315 | 36,688 | 9303 | 16,315 | 36,688 |
| qt = 30,000 | 8990 | 16,002 | 37,314 | 9303 | 16,315 | 36,688 | 9303 | 16,315 | 36,688 |
| qt = 35,000 | 9303 | 16,315 | 36,688 | 9303 | 16,315 | 36,688 | 9303 | 16,315 | 36,688 |
| qt = 40,000 | 9303 | 16,315 | 36,688 | 9303 | 16,315 | 36,688 | 9303 | 16,315 | 36,688 |
| qt = 45,000 | 9303 | 16,315 | 36,688 | 9303 | 16,315 | 36,688 | 9303 | 16,315 | 36,688 |
Appendix B
| nt = 1 | nt = 2 | nt = 3 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Farm | A | B | C | A | B | C | A | B | C |
| qt = 0 | 1.25 | 1.24 | 1.21 | 0.81 | 0.82 | 0.85 | 1.43 | 1.42 | 1.38 |
| qt = 5000 | 1.25 | 1.24 | 1.21 | 0.81 | 0.82 | 0.85 | 1.43 | 1.42 | 1.38 |
| qt = 10,000 | 1.19 | 1.19 | 1.16 | 0.81 | 0.82 | 0.85 | 1.43 | 1.42 | 1.38 |
| qt = 15,000 | 0.99 | 0.99 | 0.99 | 0.81 | 0.82 | 0.85 | 1.43 | 1.42 | 1.38 |
| qt = 20,000 | 0.99 | 0.99 | 0.99 | 0.81 | 0.82 | 0.86 | 1.43 | 1.42 | 1.38 |
| qt = 25,000 | 1.03 | 1.03 | 1.02 | 0.87 | 0.88 | 0.91 | 1.43 | 1.42 | 1.38 |
| qt = 30,000 | 1.04 | 1.04 | 1.03 | 0.97 | 0.97 | 0.98 | 1.43 | 1.42 | 1.38 |
| qt = 35,000 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 1.43 | 1.42 | 1.38 |
| qt = 40,000 | 1.09 | 1.08 | 1.06 | 1.09 | 1.08 | 1.06 | 1.43 | 1.42 | 1.38 |
| qt = 45,000 | 1.27 | 1.24 | 1.19 | 1.27 | 1.24 | 1.19 | 1.43 | 1.42 | 1.38 |
| nt = 1 | nt = 2 | nt = 3 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Farm | A | B | C | A | B | C | A | B | C |
| qt = 0 | 1.08 | 1.14 | 1.48 | 0.64 | 0.71 | 1.14 | 1.3 | 1.35 | 1.59 |
| qt = 5000 | 1.08 | 1.14 | 1.48 | 0.64 | 0.71 | 1.14 | 1.3 | 1.35 | 1.59 |
| qt = 10,000 | 1.11 | 1.06 | 1.37 | 0.64 | 0.71 | 1.14 | 1.3 | 1.35 | 1.59 |
| qt = 15,000 | 0.95 | 1.03 | 0.98 | 0.64 | 0.71 | 1.14 | 1.3 | 1.35 | 1.59 |
| qt = 20,000 | 0.94 | 1.03 | 0.99 | 0.64 | 0.71 | 1.15 | 1.3 | 1.35 | 1.59 |
| qt = 25,000 | 0.89 | 0.97 | 1.22 | 0.64 | 0.71 | 1.32 | 1.3 | 1.35 | 1.59 |
| qt = 30,000 | 0.73 | 0.81 | 1.56 | 0.64 | 0.71 | 1.59 | 1.3 | 1.35 | 1.59 |
| qt = 35,000 | 0.64 | 0.75 | 1.59 | 0.64 | 0.75 | 1.59 | 1.3 | 1.35 | 1.59 |
| qt = 40,000 | 0.73 | 0.9 | 1.59 | 0.73 | 0.9 | 1.59 | 1.3 | 1.35 | 1.59 |
| qt = 45,000 | 0.94 | 1.17 | 1.59 | 0.94 | 1.17 | 1.59 | 1.3 | 1.35 | 1.59 |
References
- Velten, S.; Leventon, J.; Jager, N.; Newig, J. What Is Sustainable Agriculture? A Systematic Review. Sustainability 2015, 7, 7833–7865. [Google Scholar] [CrossRef]
- Lefebvre, M.; Espinosa, M.; Gomez y Paloma, S.; Paracchini, M.L.; Piorr, A.; Zasada, I. Agricultural landscapes as multi-scale public good and the role of the Common Agricultural Policy. J. Environ. Plan. Manag. 2014. [Google Scholar] [CrossRef]
- Baylis, K.; Peplow, S.; Rausser, G.; Simon, L. Agri-environmental policies in the EU and United States: A comparison. Ecol. Econ. 2008, 65, 753–764. [Google Scholar] [CrossRef]
- Organisation for Economic Co-Operation and Development (OECD). Providing Agri-Environmental Public Goods through Collective Action; OECD: Paris, France, 2013. [Google Scholar]
- Dupraz, P.; Latouche, K.; Turpin, N. Threshold effect and co-ordination of agri-environmental efforts. J. Environ. Plan. Manag. 2009, 52, 613–630. [Google Scholar] [CrossRef]
- Parkhurst, G.M.; Shogren, J.F.; Bastian, C.; Kivi, P.; Donner, J.; Smith, R.B.W. Agglomeration bonus: An incentive mechanism to reunite fragmented habitat for biodiversity conservation. Ecol. Econ. 2002, 41, 305–328. [Google Scholar] [CrossRef]
- Wätzold, F.; Drechsler, M. Agglomeration payment, agglomeration bonus or homogeneous payment? Resour. Energy Econ. 2014, 37, 85–101. [Google Scholar] [CrossRef]
- Reeson, A.F.; Rodriguez, L.C.; Whitten, S.M.; Williams, K.; Nolles, K.; Windle, J.; Rolfe, J. Adapting auctions for the provision of ecosystem services at the landscape scale. Ecol. Econ. 2011, 70, 1621–1627. [Google Scholar] [CrossRef]
- Parkhurst, G.M.; Shogren, J.F. Spatial incentives to coordinate contiguous habitat. Ecol. Econ. 2007, 64, 344–355. [Google Scholar] [CrossRef]
- Banerjee, S.; de Vries, F.P.; Hanley, N.; van Soest, D.P. The impact of information provision on agglomeration bonus performance: An experimental study on local networks. Am. J. Agric. Econ. 2014, 96, 1009–1029. [Google Scholar] [CrossRef]
- Banerjee, S.; Kwasnica, A.M.; Shortle, J.S. Agglomeration bonus in small and large local networks: A laboratory examination of spatial coordination. Ecol. Econ. 2012, 84, 142–152. [Google Scholar] [CrossRef]
- Albers, H.J.; Ando, A.W.; Batz, M. Patterns of multi-agent land conservation: Crowding in/out, agglomeration, and policy. Resour. Energy Econ. 2008, 30, 492–508. [Google Scholar] [CrossRef]
- Bamière, L.; David, M.; Vermont, B. Agri-environmental policies for biodiversity when the spatial pattern of the reserve matters. Ecol. Econ. 2013, 85, 97–104. [Google Scholar] [CrossRef]
- Drechsler, M.; Wätzold, F.; Johst, K.; Shogren, J.F. An agglomeration payment for cost-effective biodiversity conservation in spatially structured landscapes. Resour. Energy Econ. 2010, 32, 261–275. [Google Scholar] [CrossRef]
- Romstad, E. Team approaches in reducing nonpoint source pollution. Ecol. Econ. 2003, 47, 71–78. [Google Scholar] [CrossRef]
- Ostrom, E. Governing the Commons: The Evolution of Institutions for Collective Action; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Jeuland, M.; Baker, J.; Bartlett, R.; Lacombe, G. The costs of uncoordinated infrastructure management in multi-reservoir river basins. Environ. Res. Lett. 2014, 9, 105006. [Google Scholar] [CrossRef]
- Ward, F.A. Financing Irrigation Water Management and Infrastructure: A Review. Int. J. Water Resour. Dev. 2010, 26, 321–349. [Google Scholar] [CrossRef]
- Anderies, J.M.; Janssen, M.A. Robustness of Social-Ecological Systems: Implications for Public Policy. Policy Stud. J. 2013, 41, 513–536. [Google Scholar] [CrossRef]
- Segerson, K. Voluntary Approaches to Environmental Protection and Resource Management. Annu. Rev. Resour. Econ. 2013, 5, 161–180. [Google Scholar] [CrossRef]
- Janssen, M.A.; Anderies, J.M.; Joshi, S.R. Coordination and cooperation in asymmetric commons dilemmas. Exp. Econ. 2011, 14, 547–566. [Google Scholar] [CrossRef]
- Marchiori, C. Inequality and rules in the governance of water resources. Ecol. Econ. 2014, 105, 124–129. [Google Scholar] [CrossRef] [Green Version]
- Zavalloni, M.; Raggi, M.; Viaggi, D. Water harvesting reservoirs with internal water reallocation: A case study in Emilia Romagna, Italy. J. Water Supply Res. Technol. 2014, 63, 489–496. [Google Scholar] [CrossRef]
- Parrachino, I.; Dinar, A.; Patrone, F. Cooperative Game Theory and Its Application to Natural, Environmental, and Water Resource Issues: 3. Application to Water Resources; World Bank Policy Research Working Paper; World Bank: Washington, DC, USA, 2006. [Google Scholar]
- Dinar, A.; Albiac, J.; Sánchez-Soriano, J. Game Theory and Policy Making in Natural Resources and the Environment; Routledge: London, UK, 2008; Volume 10. [Google Scholar]
- Dinar, A.; Howitt, R.E. Mechanisms for Allocation of Environmental Control Cost: Empirical Tests of Acceptability and Stability. J. Environ. Manag. 1997, 49, 183–203. [Google Scholar] [CrossRef]
- Jiang, Y.; Hellegers, P. Joint pollution control in the Lake Tai Basin and the stabilities of the cost allocation schemes. J. Environ. Manag. 2016, 184, 504–516. [Google Scholar] [CrossRef] [PubMed]
- Kahil, M.T.; Dinar, A.; Albiac, J. Cooperative water management and ecosystem protection under scarcity and drought in arid and semiarid regions. Water Resour. Econ. 2016, 13, 60–74. [Google Scholar] [CrossRef]
- Madani, K.; Dinar, A. Cooperative institutions for sustainable common pool resource management: Application to groundwater. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Madani, K.; Hooshyar, M. A game theory–reinforcement learning (GT–RL) method to develop optimal operation policies for multi-operator reservoir systems. J. Hydrol. 2014, 519, 732–742. [Google Scholar] [CrossRef]
- Slikker, M.; van den Nouweland, A. Social and Economic Networks in Cooperative Game Theory; Springer: New York, NY, USA, 2012. [Google Scholar]
- Black, J.; Levi, M.D.; de Meza, D. Creating a Good Atmosphere: Minimum Participation for Tackling the “Greenhouse Effect”. Economica 1993, 60, 281–293. [Google Scholar] [CrossRef]
- Carraro, C.; Marchiori, C.; Oreffice, S. Endogenous Minimum Participation in International Environmental Treaties. Environ. Resour. Econ. 2009, 42, 411–425. [Google Scholar] [CrossRef]
- McEvoy, D.; Cherry, T.; Stranlund, J. Endogenous Minimum Participation in International Environmental Agreements: An Experimental Analysis. Environ. Resour. Econ. 2015, 62, 729–744. [Google Scholar] [CrossRef]
- Rutz, S. Minimum Participation Rules and the Effectiveness of Multilateral Environmental Agreements; Swiss Federal Institute of Technology; Center for Economic Research: Zürich, Switzerland, 2001. [Google Scholar]
- Kesternich, M. Minimum participation rules in international environmental agreements: Empirical evidence from a survey among delegates in international climate negotiations. Appl. Econ. 2016, 48, 1047–1065. [Google Scholar] [CrossRef]
- Gillies, D.B. Solutions to general non-zero-sum games. Contrib. Theory Games 1959, 4, 47–85. [Google Scholar]
- Shapley, L.S. Cores of convex games. Int. J. Game Theory 1971, 1, 11–26. [Google Scholar] [CrossRef]
- Shapley, L.S. A value for n-person games. Ann. Math. Stud. 1953, 28, 307–318. [Google Scholar]
- Gately, D. Sharing the Gains from Regional Cooperation: A Game Theoretic Application to Planning Investment in Electric Power. Int. Econ. Rev. 1974, 15, 195–208. [Google Scholar] [CrossRef]
- Viaggi, D.; Raggi, M.; Bartolini, F.; Gallerani, V. Designing contracts for irrigation water under asymmetric information: Are simple pricing mechanisms enough? Agric. Water Manag. 2010, 97, 1326–1332. [Google Scholar] [CrossRef]
- Consorzio di Bonifica della Romagna Occidentale (CBRO). L’utilizzo dei Fondi Europei per la Valorizzazione del Territorio Rurale. Presentazione dei Progetti Realizzati Nell’ambito del PSR 2007–2013; CBRO: Lugo, Italy, 2015. (In Italian) [Google Scholar]
- Young, H.P.; Okada, N.; Hashimoto, T. Cost allocation in water resources development. Water Resour. Res. 1982, 18, 463–475. [Google Scholar] [CrossRef] [Green Version]
- Loehman, E.; Orlando, J.; Tschirhart, J.; Whinston, A. Cost allocation for a regional wastewater treatment system. Water Resour. Res. 1979, 15, 193–202. [Google Scholar] [CrossRef]
- Castro, J.; Gómez, D.; Tejada, J. Polynomial calculation of the Shapley value based on sampling. Comput. Oper. Res. 2009, 36, 1726–1730. [Google Scholar] [CrossRef]
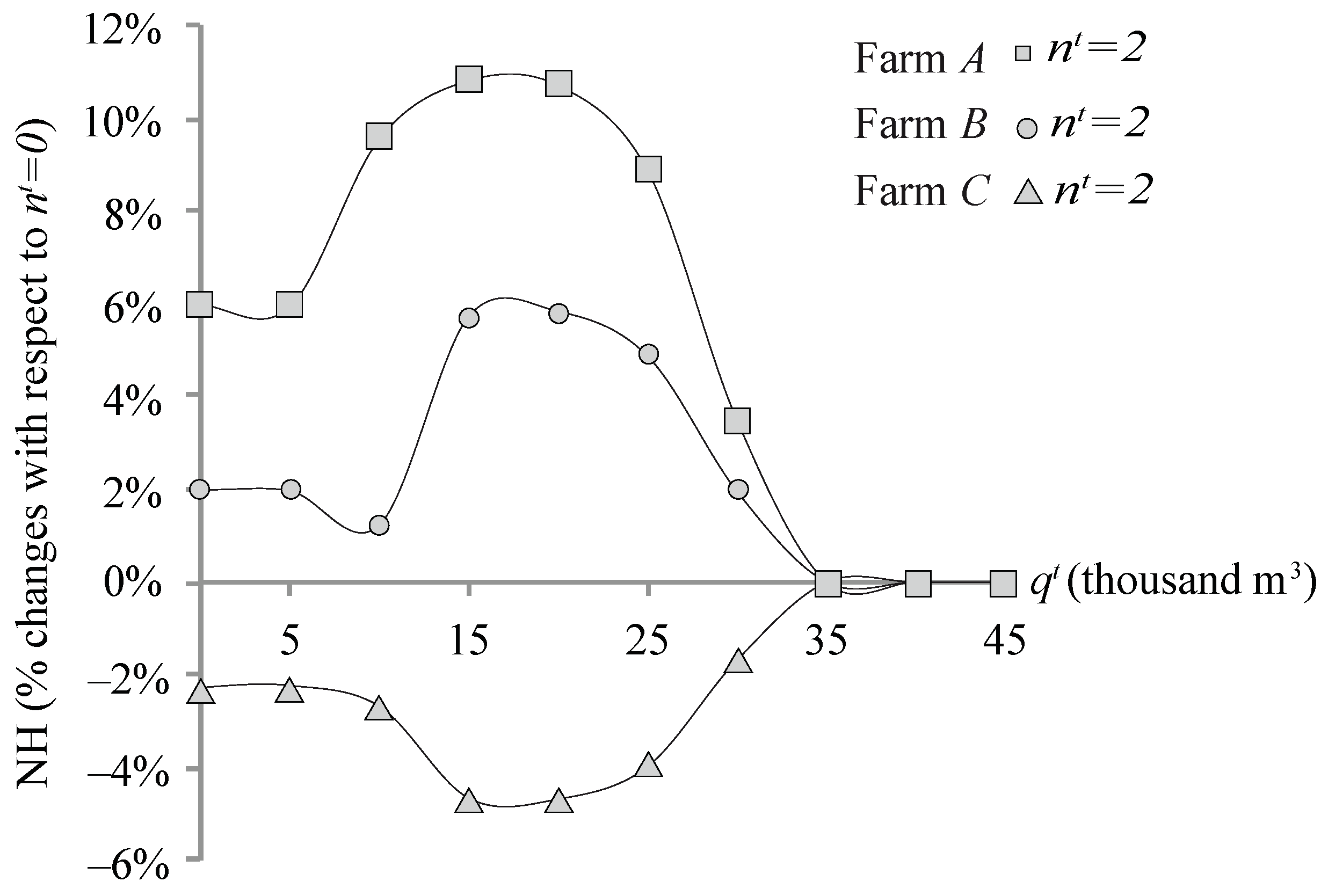
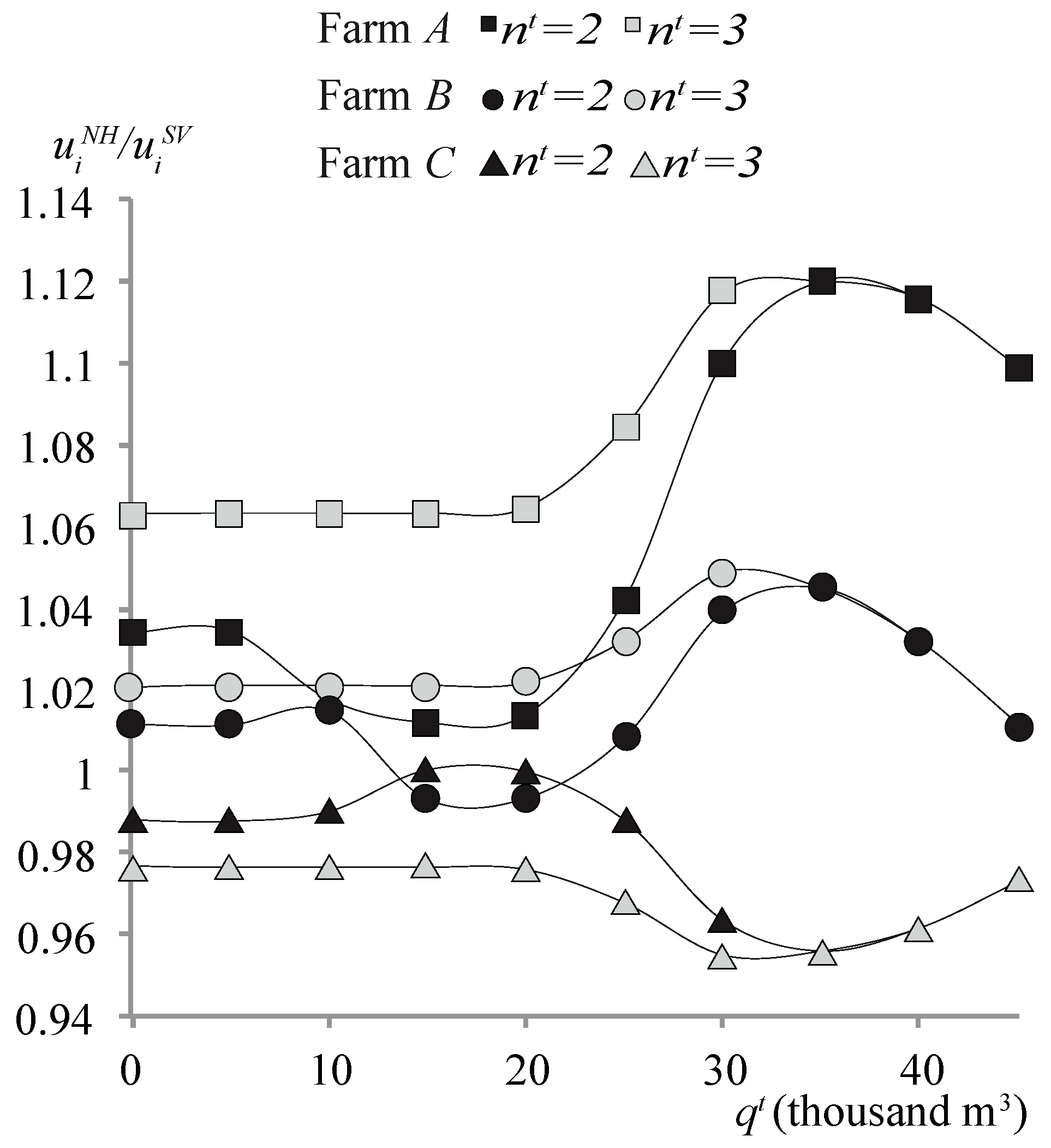
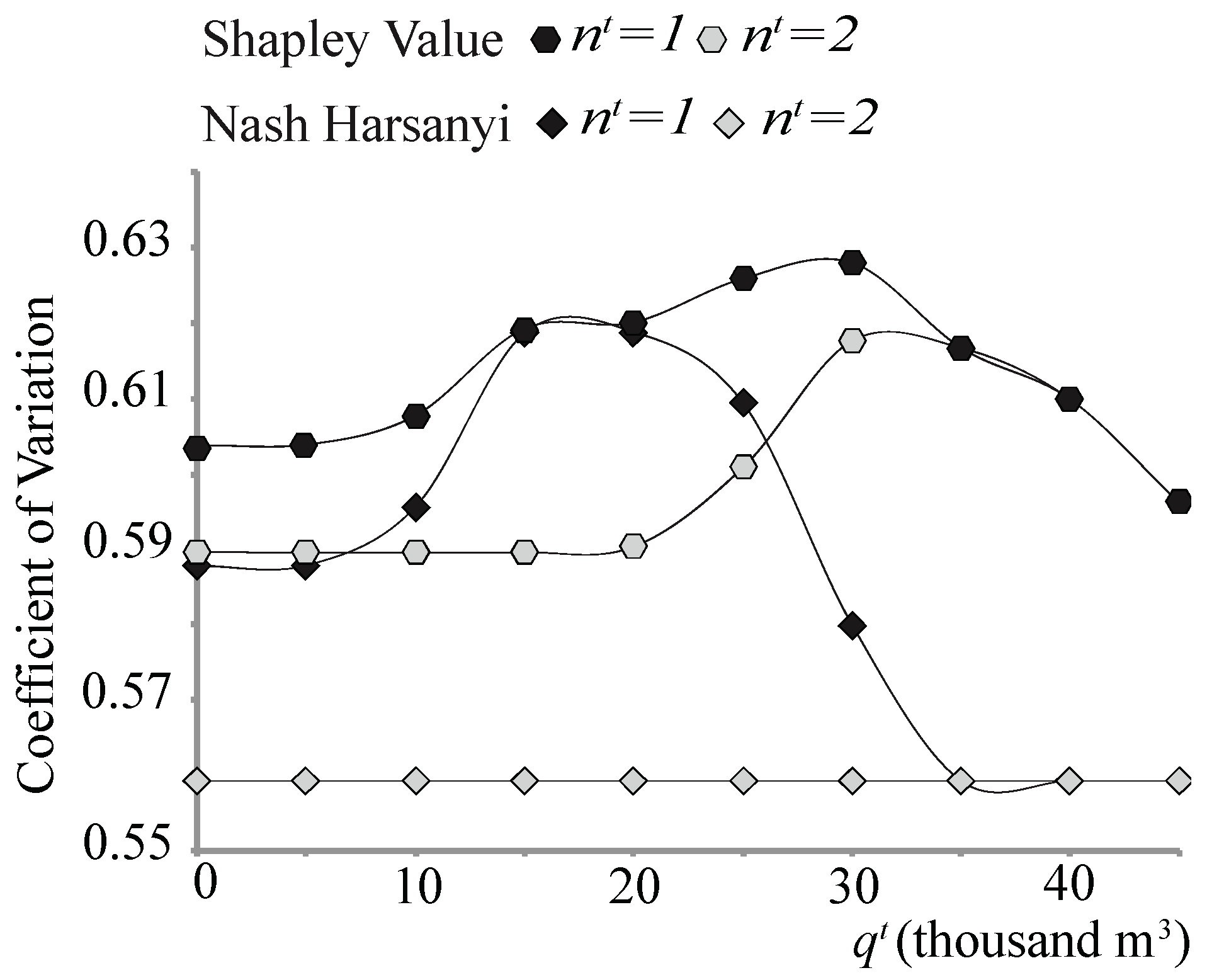
| Revenue Function Parameters | Farm A | Farm B | Farm C |
|---|---|---|---|
| η | −0.0002 | −0.0005 | −0.0006 |
| β | 1.2017 | 1.1498 | 1.1803 |
| γ | 680.22 | 747.05 | 817.76 |
| l | 3.76 ha | 12.54 ha | 32.59 ha |
| Coalition | ΠsP(Qs*,P) (€) | ΠsNP(Qs*,NP) (€) | qst,NP (m3) | Qs*,P (m3) |
|---|---|---|---|---|
| (A) | 4951 | 3610 | 12,082 | 7009 |
| (B) | 12,170 | 10,622 | 15,048 | 8754 |
| (C) | 33,693 | 30,996 | 32,344 | 20,150 |
| (A,B) | 19,126 | 16,585 | 28,893 | 18,261 |
| (A,C) | 41,938 | 38,328 | 47,523 | 31,185 |
| (B,C) | 49,386 | 45,620 | 50,680 | 33,292 |
| (A,B,C) | 62,306 | 57,438 | 70,992 | 49,036 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zavalloni, M.; Raggi, M.; Viaggi, D. Assessing Collective Measures in Rural Policy: The Effect of Minimum Participation Rules on the Distribution of Benefits from Irrigation Infrastructure. Sustainability 2017, 9, 1. https://doi.org/10.3390/su9010001
Zavalloni M, Raggi M, Viaggi D. Assessing Collective Measures in Rural Policy: The Effect of Minimum Participation Rules on the Distribution of Benefits from Irrigation Infrastructure. Sustainability. 2017; 9(1):1. https://doi.org/10.3390/su9010001
Chicago/Turabian StyleZavalloni, Matteo, Meri Raggi, and Davide Viaggi. 2017. "Assessing Collective Measures in Rural Policy: The Effect of Minimum Participation Rules on the Distribution of Benefits from Irrigation Infrastructure" Sustainability 9, no. 1: 1. https://doi.org/10.3390/su9010001
APA StyleZavalloni, M., Raggi, M., & Viaggi, D. (2017). Assessing Collective Measures in Rural Policy: The Effect of Minimum Participation Rules on the Distribution of Benefits from Irrigation Infrastructure. Sustainability, 9(1), 1. https://doi.org/10.3390/su9010001






