The Shortest Path Problems in Battery-Electric Vehicle Dispatching with Battery Renewal
Abstract
:1. Introduction
2. The Shortest Path Problems in Electric Vehicle Dispatching
2.1. The Shortest Path Problem in Electric Transit Bus Scheduling
2.2. The Shortest Path Problem in Electric Truck Routing with Time Windows
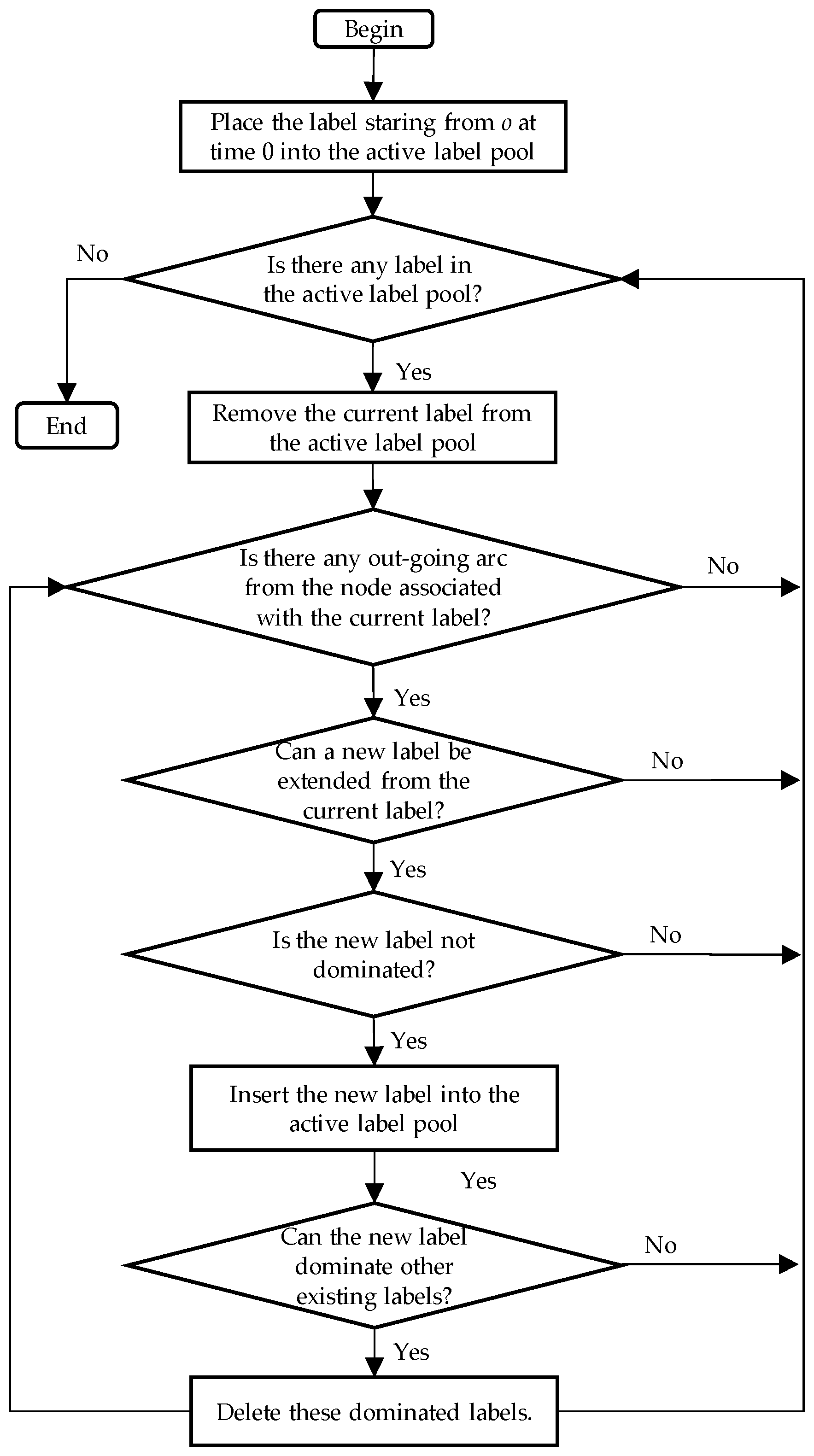
3. The Label-Correcting Algorithm
3.1. The Label Operations for Electric Bus Scheduling
3.2. The Label Operations for Electric Truck Routing
4. Computational Experiments
4.1. The Shortest Path in Electric Bus Scheduling with Battery Renewal
4.2. The Shortest Path in Electric Truck Routing with Battery Renewal
5. Conclusions and Future Research
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Environmentally Friendly Options and UPS Services. Available online: http://www.ups.com/content/us/en/bussol/browse/article/small-business-sustainability.html?srch_pos=2&srch_phr=electric+delivery+trucks (accessed on 10 December 2015).
- United Nations Environment Programme. UNEP Environmental Assessment Expo 2010 Shanghai, China; Tech. Rep. DCP/1209/NA; 2009. Available online: http://www.sepb.gov.cn/platform/UserFiles/File/2009-08-18-16-53-46-884+0800-570148450609847911.pdf (accessed on 23 June 2016).
- Beijing Electric Vehicle Promotion Application Action Plan (2014–2017). Available online: http://www.zhengwu.beijing.gov.cn/ghxx/qtgh/t1359600.htm (accessed on 12 December 2015).
- Desaulniers, G.; Lavigne, J.; Soumis, F. Multi-depot vehicle scheduling problems with time windows and waiting costs. Eur. J. Oper. Res. 1998, 3, 479–494. [Google Scholar] [CrossRef]
- Desrocher, M.; Desrosier, J.; Solomon, M.M. A new optimization algorithm for the vehicle-routing problem with time windows. Oper. Res. 1992, 2, 342–354. [Google Scholar] [CrossRef]
- Desrochers, M.; Soumis, F. A column generation approach to the urban transit crew scheduling problem. Transp. Sci. 1989, 1, 1–13. [Google Scholar] [CrossRef]
- Muter, I.; Birbil, S.I.; Bulbul, K.; Sahin, G.; Yenigun, H.; Tas, D.; Tuzun, D. Solving a robust airline crew pairing problem with column generation. Comput. Oper. Res. 2013, 3, 815–830. [Google Scholar] [CrossRef]
- Beasley, J.E.; Christo, N. An algorithm for the resource-constrained shortest-path problem. Networks 1989, 3, 379–394. [Google Scholar] [CrossRef]
- Desrochers, M.; Soumis, F. A generalized permanent labeling algorithm for the shortest path problem with time windows. INFOR 2014, 3, 191–212. [Google Scholar]
- Dumitrescu, I.; Boland, N. Improved preprocessing, labeling and scaling algorithms for the weight-constrained shortest path problem. Networks 2003, 3, 135–153. [Google Scholar] [CrossRef]
- Handler, G.Y.; Zang, I. A dual algorithm for the constrained shortest path problem. Networks 2006, 4, 293–309. [Google Scholar] [CrossRef]
- Santos, L.; Coutinho-Rodrigues, J.; Current, J.R. An improved solution algorithm for the constrained shortest path problem. Transp. Res. Part B Methodol. 2006, 7, 756–771. [Google Scholar] [CrossRef]
- Xing, T.; Zhou, X. Reformulation and solution algorithms for absolute and percentile robust shortest path problems. IEEE Trans. Intell. Transp. Syst. 2013, 2, 943–954. [Google Scholar] [CrossRef]
- Feillet, D.; Dejax, P.; Gendreau, M.; Gueguen, C. An exact algorithm for the elementary shortest path problem with resource constraints: Application to some vehicle routing problems. Networks 2004, 3, 216–229. [Google Scholar] [CrossRef]
- Righini, G.; Salani, M. Symmetry helps: Bounded bi-directional dynamic progrmamming for the elementary shortest path problem with resource constraints. Discret. Optim. 2006, 3, 255–273. [Google Scholar] [CrossRef]
- Righini, G.; Salani, M. New dynamic programming algorithms for the resource constrained elementary shortest path problem. Networks 2008, 3, 155–170. [Google Scholar] [CrossRef]
- Houck, D.J.; Picard, J.C.; Queyranne, M.; Vemuganti, R.R. The travelling salesman problem as a constrained shortest path problem: Theory and computational experience. Oper. Res. 1980, 2, 93–109. [Google Scholar]
- Irnich, S.; Villeneuve, D. The shortest-path problem with resource constraints and k-cycle elimination for k > 3. INFORMS J. Comput. 2006, 3, 391–406. [Google Scholar] [CrossRef]
- Bode, C.; Irnich, S. The shortest-path problem with resource constraints with (k, 2)-loop elimination and its application to the capacitated arc-routing problem. Eur. J. Oper. Res. 2014, 2, 415–426. [Google Scholar] [CrossRef]
- Garey, M.R.; Johnson, D.S. Computers and Intractability: A Guide to the Theory of NP-Completeness, 1st ed.; W.H. Freeman: New York, NY, USA, 1979. [Google Scholar]
- Wang, Y.W.; Lin, C.C. Locating road-vehicle refueling stations. Transp. Res. Part E Logist. Transp. Rev. 2009, 5, 821–829. [Google Scholar] [CrossRef]
- Yildiz, B.; Arslan, O.; Karasan, O.E. A branch and price approach for routing and refueling station location model. Eur. J. Oper. Res. 2015, 3, 815–826. [Google Scholar]
- Huang, S.; He, L.; Gu, Y.; Wood, K.; Benjaafar, S. Design of a mobile charging service for electric vehicles in an urban environment. IEEE Trans. Intell. Transp. Syst. 2014, 2, 787–798. [Google Scholar] [CrossRef]
- Kang, Q.; Wang, J.; Zhou, M.; Ammari, A.C. Centralized charging strategy and scheduling algorithm for electric vehicles under a battery swapping scenario. IEEE Trans. Intell. Transp. Syst. 2015, 1, 1–11. [Google Scholar] [CrossRef]
- Roberti, R.; Wen, M. The electric traveling salesman problem with time windows. Transp. Res. Part E Logist. Transp. Rev. 2016, 89, 32–52. [Google Scholar] [CrossRef]
- Bruglieri, M.; Pezzella, F.; Pisacane, O.; Suraci, S. A variable neighborhood search branching for the electric vehicle routing problem with time windows. Electron. Notes Discret. Math. 2015, 47, 221–228. [Google Scholar] [CrossRef]
- Yang, J.; Sun, H. Battery swap station location-routing problem with capacitated electric vehicles. Comput. Oper. Res. 2015, 55, 217–232. [Google Scholar] [CrossRef]
- Yagcitekin, B.; Uzunoglu, M. A double-layer smart charging strategy of electric vehicles taking routing and charge scheduling into account. Appl. Energy 2016, 167, 407–419. [Google Scholar] [CrossRef]
- Elkins, J.; Hemby, J.; Rao, V.; Szykman, J.; Fitz-Simons, T.; Doll, D.; Mintz, D.; Rush, A.; Frank, N.; Schmidt, M.; et al. National Air Quality and Emission Trends Report Special Studies Edition; U.S. Environmental Protection Agency: North Carolina, CA, USA, 2003.
- O’brien, W.A. Electric vehicles (EVs): A look behind the scenes. IEEE Aerosp. Electron. Syst. Mag. 1993, 5, 38–41. [Google Scholar] [CrossRef]
- Argonne National Laboratory. Electric Buses Energize Downtown Chattanooga. Available online: http://www.afdc.energy.gov/afdc/pdfs/chatt_cs.pdf (accessed on 12 December 2015).
- Beijing Readies Electric Buses for Summer Olympics. Available online: http://www.evworld.com/news.cfm?newsid=18730 (accessed on 13 December 2015).
- Namsan Electric Bus Cruises into International Limelight. Available online: http://www.cnngo.com/seoul/life/namsan-electric-bus-cruises-limelight-262862 (accessed on 13 December 2015).
- Quick-charge Electric Bus Rolls into L.A. County. Available online: http://www.wired.com/autopia/2010/09/proterra-ecoride-foothill-transit (accessed on 13 December 2015).
- Transi. Bus Technology Feasibility Study. Available online: http://www.advancedenergy.org/transportation/additional_efforts/TransitBusFeasibilityStudy_Final.pdf (accessed on 20 December 2015).
- Final Environmental Review of the 2010 World Exposition. Available online: http://www.unep.org/newscentre/Default.aspx?DocumentID=2659&ArticleID=8964&l=en#sthash.zr7SV1wK.dpuf (accessed on 15 November 2015).
- Shafia, M.A.; Aghaee, M.P.; Sadjadi, S.J.; Jamili, A. Robust train timetabling problem: Mathematical model and branch and bound algorithm. IEEE Trans. Intell. Transp. Syst. 2012, 1, 307–317. [Google Scholar] [CrossRef]
- Li, J.Q. Transit bus scheduling with limited energy. Transp. Sci. 2013, 4, 521–539. [Google Scholar] [CrossRef]
- UPS’ Brown Trucks Get Greener with Electric Power. Available online: http://www.sfgate.com/cgi-bin/article.cgi?f=/c/a/2011/08/25/BU7I1KRF10.DTL (accessed on 12 December 2015).
- Ford Transit Connect Electric Commercial van Helps Customers Go Completely Gas-Free. Available online: http://www.media.ford.com/article_display.cfm?article_id=31991 (accessed on 12 December 2015).
- Boland, N.; Dethridge, J.; Dumitrescu, I. Accelerated label setting algorithms for the elementary resource-constrained shortest path problem. Oper. Res. Lett. 2004, 1, 58–68. [Google Scholar] [CrossRef]
- Christo, N.; Mingozzi, A.; Toth, P. State-space relaxation procedures for the computation of bounds to routing problems. Networks 2006, 2, 145–164. [Google Scholar]
- IBM Cplex. Available online: https://www-01.ibm.com/software/commerce/optimization/cplex-optimizer/ (accessed on 9 June 2016).
- GTFS data. Available online: http://www.gtfs-data-exchange.com/agency/county-connection (accessed on 12 December 2015).
- Energy Information Administration. (2011, Dec). Prices and Factors Affecting Prices. Available online: http://www.eia.gov/energyexplained/index.cfm?page=electricity_factors_affecting_prices (accessed on 12 December 2015).
- Solomon, M.M. Algorithms for the vehicle-routing and scheduling problems with time window constraints. Oper. Res. 1987, 2, 254–265. [Google Scholar] [CrossRef]
- Li, J.Q. Match bus stops to a digital road network by the shortest path model. Transp. Res. Part C Emerg. Technol. 2012, 2, 119–131. [Google Scholar] [CrossRef]
- Ford Working with Best Buy to Offer Focus Electric Charging Station Sales, Installation and Support. Available online: http://www.media.ford.com/article_display.cfm?article_id=33772 (accessed on 12 December 2015).



| Objective Function and Restrictions | Variable Range | Equation No. |
|---|---|---|
| (a1) | ||
| st | ||
| (a2) | ||
| (a3) | ||
| (a4) | ||
| (a5) | ||
| (a6) | ||
| (a7) | ||
| Objective Function and Restrictions | Variable Range | Equation No. |
|---|---|---|
| (b1) | ||
| st | ||
| (a2) − (a7) | (b2) | |
| (b3) | ||
| (b4) | ||
| (b5) | ||
| (b6) | ||
| (b7) |
| Instance | # of Trips | # of Time-Expanded Nodes | Description |
|---|---|---|---|
| S Sa Sb Sc | 242 | 952 951 943 930 | published weekend schedules randomly-generated based S same as above same as above |
| W Wa Wb Wc | 947 | 1132 1136 1136 1130 | published weekday schedules randomly-generated based W same as above same as above |
| W1 W1a W1b W1c | 463 | 1073 1087 1074 1084 | half of W randomly-generated based W1 same as above same as above |
| W2 W2a W2b W2c | 484 | 1132 1131 1124 1126 | the other half of W randomly-generated based W2 same as above same as above |
| Instance | Dual | Max Distance 120 km | Max Distance 150 km | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Optimal Objective Value | CPLEX | Label Correcting | Optimal Objective Value | CPLEX | Label Correcting | ||||
| CPU (s) | Labels | CPU (s) | CPU (s) | Labels | CPU (s) | ||||
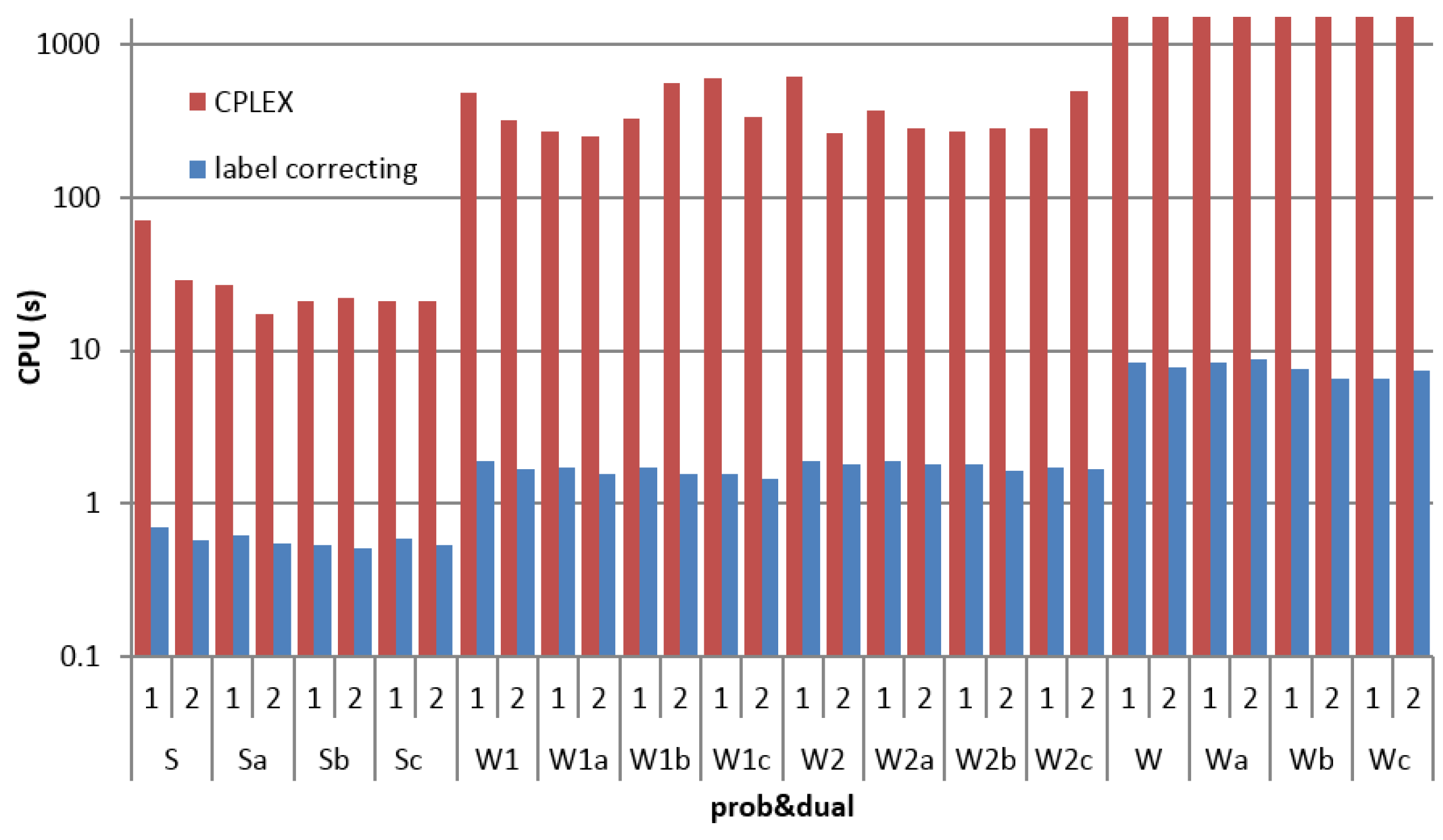
| S Sa Sb Sc | 1 2 1 2 1 2 1 2 | –822,351 –819,804 –707,440 –705,225 –712,234 –724,879 –751,972 –790,796 | 117.94 1167.49 26.77 39.38 45.25 26.09 101.99 33.72 | 2875 2668 1735 2065 1917 2134 2305 2283 | 0.72 0.72 0.53 0.52 0.54 0.54 0.57 0.56 | –824,405 –829,648 –707,440 –705,225 –712,234 –724,879 –755,469 –790,796 | 141.92 61.65 27.79 32.6 38.13 29.23 42.92 40.46 | 2897 2739 1735 2066 1919 2134 2511 2302 | 0.74 0.78 0.55 0.58 0.56 0.6 0.6 0.58 |
| W1 W1a W1b W1c | 1 2 1 2 1 2 1 2 | –1,175,252 –1,185,467 –1,190,403 –1,140,363 –1,180,257 –1,133,505 –1,226,202 –1,160,532 | 2927.46 338.88 262.11 328.97 738.82 249.87 248.59 + | 3239 3012 3123 3075 3431 2702 3116 4126 | 1.64 1.62 1.5 1.46 1.46 1.35 1.69 1.53 | –1,175,252 –1,185,467 –1,190,403 –1,140,363 –1,181,390 –1,133,505 –1,226,202 –1,162,385 | + 273.81 273.04 256.57 298.17 808.2 251.33 1052.89 | 3287 2987 3123 3078 3639 2717 3118 4513 | 1.74 1.71 1.58 1.56 1.69 1.41 1.8 1.65 |
| W2 W2a W2b W2c | 1 2 1 2 1 2 1 2 | –1,241,010 –1,250,571 –1,236,314 –1,293,550 –1,271,817 –1,228,527 –1,321,741 –1,279,684 | 1142.48 339.46 314.43 421.19 3565.16 1645.09 376.29 274.28 | 3060 3133 3492 2899 4166 3831 3967 3681 | 1.69 1.65 1.61 1.62 1.53 1.56 1.81 1.84 | –1,241,010 –1,250,571 –1236,314 –1293,550 –1286,476 –1235,273 –1,321,741 –1,279,684 | + 593.26 481.85 1513.48 505.13 424.58 362.13 311.64 | 3195 3205 3548 2924 4906 4133 3990 3742 | 1.82 1.74 1.66 1.68 1.58 1.67 1.92 1.97 |
| W Wa Wb Wc | 1 2 1 2 1 2 1 2 | –1,614,504 –1,574,276 –1,465,572 –1,513,933 –1,484,716 –1,469,219 –1,490,073 –1,518,417 | * * * * * * * * | 8333 7751 7953 8779 13,329 8644 8952 12,600 | 8.58 8.13 7.47 8.04 8.24 7.99 8.04 8.72 | –1,628,219 –1,590,012 –1,471,389 –1,518,442 –1,495,817 –1,502,780 –1,498,017 –1,526,627 | * * * * * * * * | 9104 8420 8228 9101 16,182 10,332 10,500 14,393 | 9.65 8.96 8.21 9.07 9.42 8.74 9.36 9.74 |
| Instance | # of Customers | # of Time-Expanded Nodes | Instance | # of Customers | # of Time-Expanded Nodes | |||
|---|---|---|---|---|---|---|---|---|
| Time Windows | Time Windows | |||||||
| [5, 20] min | [5, 40] min | [5, 60] min | [5, 20] min | [5, 40] min | ||||
| 50a | 50 | 620 | 665 | 685 | 150a | 150 | 662 | 695 |
| 50b | 50 | 585 | 666 | 687 | 150b | 150 | 636 | 677 |
| 50c | 50 | 623 | 661 | 681 | 150c | 150 | 652 | 716 |
| 50d | 50 | 597 | 641 | 665 | 150d | 150 | 638 | 696 |
| 50e | 50 | 547 | 644 | 653 | 150e | 150 | 665 | 686 |
| 100a | 100 | 644 | 656 | 662 | 200a | 200 | 667 | 678 |
| 100b | 100 | 634 | 639 | 663 | 200b | 200 | 664 | 680 |
| 100c | 100 | 655 | 693 | 696 | 200c | 200 | 633 | 680 |
| 100d | 100 | 645 | 680 | 700 | 200d | 200 | 645 | 660 |
| 100e | 100 | 658 | 683 | 697 | 200e | 200 | 656 | 694 |
| Instance | Dual | Max Distance 100 km | Max Distance 130 km | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Optimal Objective Value | CPLEX | State Relaxation | Optimal Objective Value | CPLEX | State Relaxation | ||||||
| Optimal Gap | CPU (s) | Labels | CPU (s) | Optimal Gap | CPU (s) | Labels | CPU (s) | ||||
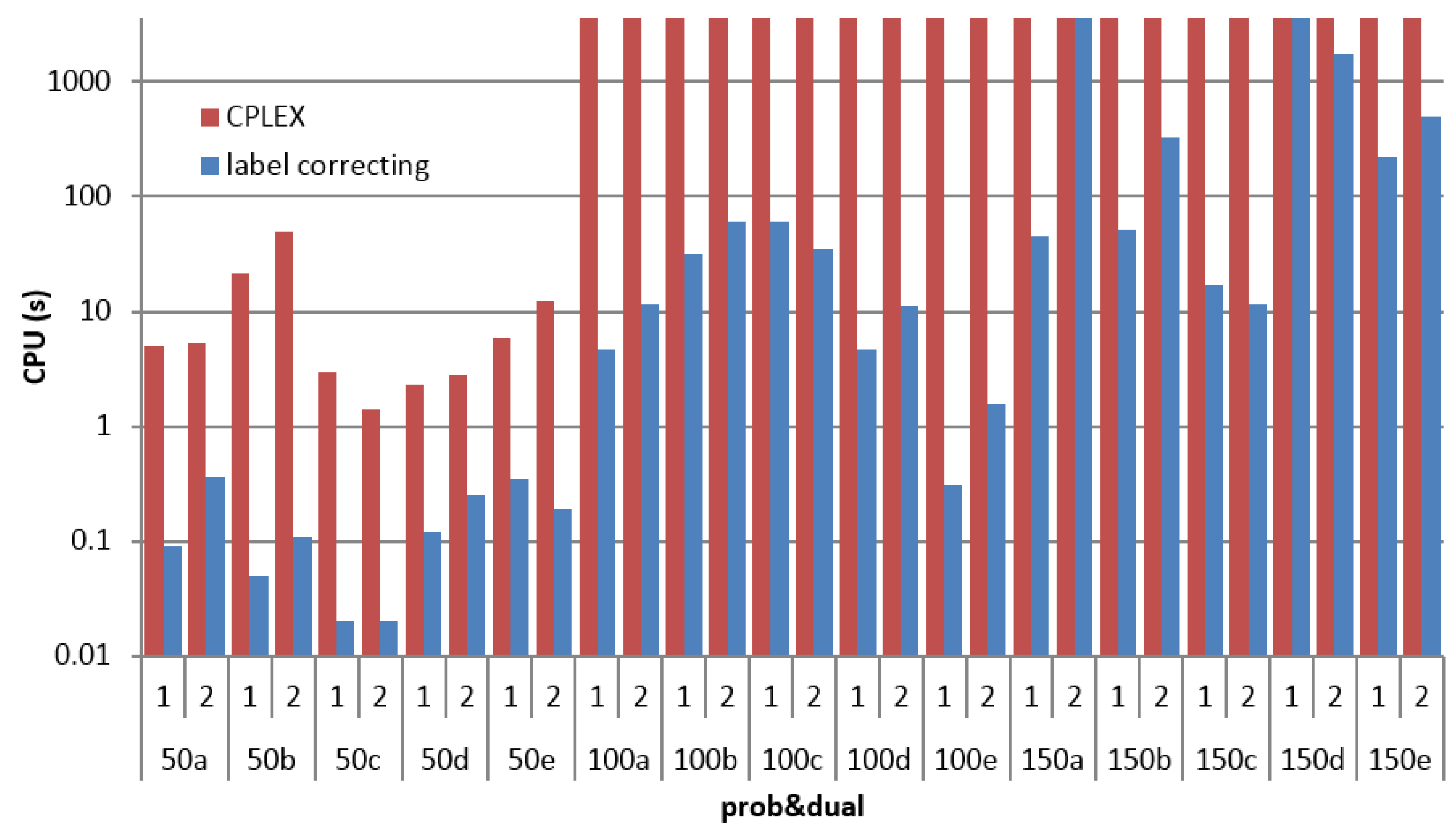
| 50a | 1 | −6220 | 0.00 | 0.63 | 1744 | 0.02 | −6220 | 0.00 | 0.70 | 1780 | 0.02 |
| 2 | −5314 | 0.00 | 0.63 | 1491 | 0.02 | −5314 | 0.00 | 0.61 | 1539 | 0.02 | |
| 50b | 1 | −8742 | 0.00 | 0.57 | 2896 | 0.01 | −8742 | 0.00 | 0.57 | 2904 | 0.01 |
| 2 | −8320 | 0.00 | 0.55 | 3204 | 0.02 | −8320 | 0.00 | 0.57 | 3208 | 0.02 | |
| 50c | 1 | −7195 | 0.00 | 0.50 | 2657 | 0.01 | −7195 | 0.00 | 0.50 | 2771 | 0.02 |
| 2 | −7487 | 0.00 | 0.53 | 2629 | 0.01 | −7487 | 0.00 | 0.49 | 2824 | 0.01 | |
| 50d | 1 | −12,234 | 0.00 | 0.54 | 3412 | 0.02 | −12,234 | 0.00 | 0.54 | 3846 | 0.02 |
| 2 | −11,807 | 0.00 | 0.59 | 4405 | 0.02 | −11,807 | 0.00 | 0.56 | 4841 | 0.02 | |
| 50e | 1 | −7986 | 0.00 | 0.47 | 2163 | 0.01 | −7986 | 0.00 | 0.49 | 2404 | 0.01 |
| 2 | −7962 | 0.00 | 0.48 | 2287 | 0.01 | −7962 | 0.00 | 0.45 | 2536 | 0.01 | |
| 100a | 1 | −11,773 | 0.00 | 1.66 | 5088 | 0.04 | −11,773 | 0.00 | 1.45 | 5483 | 0.04 |
| 2 | −12,385 | 0.00 | 1.37 | 5364 | 0.05 | −12,385 | 0.00 | 1.35 | 5754 | 0.04 | |
| 100b | 1 | −12,292 | 0.00 | 3.84 | 9008 | 0.09 | −13,195 | 0.00 | 1.55 | 9588 | 0.1 |
| 2 | −10,774 | 0.00 | 5.41 | 9615 | 0.10 | −11,494 | 0.00 | 1.59 | 10,277 | 0.11 | |
| 100c | 1 | −11,655 | 0.00 | 1.27 | 6211 | 0.05 | −11,655 | 0.00 | 1.23 | 6446 | 0.06 |
| 2 | −9025 | 0.00 | 1.33 | 5253 | 0.04 | −9025 | 0.00 | 1.38 | 5539 | 0.04 | |
| 100d | 1 | −13,405 | 0.00 | 1.70 | 9543 | 0.08 | −13,405 | 0.00 | 1.55 | 9816 | 0.09 |
| 2 | −12,576 | 0.00 | 1.53 | 10,192 | 0.10 | −12,576 | 0.00 | 1.67 | 10,391 | 0.1 | |
| 100e | 1 | −13,473 | 0.00 | 1.61 | 10,546 | 0.10 | −13,473 | 0.00 | 1.50 | 11,208 | 0.11 |
| 2 | −14,937 | 0.00 | 1.57 | 8134 | 0.08 | −14,937 | 0.00 | 1.53 | 8628 | 0.08 | |
| 150a | 1 | −14,980 | 0.00 | 4.99 | 20,942 | 0.84 | −16,159 | 0.00 | 3.48 | 21,548 | 0.84 |
| 2 | −16,327 | 0.00 | 6.80 | 18,039 | 0.75 | −16,883 | 0.00 | 4.66 | 18,726 | 0.75 | |
| 150b | 1 | −15,493 | 0.00 | 4.56 | 12,588 | 0.14 | −15,493 | 0.00 | 4.54 | 12,913 | 0.15 |
| 2 | −14,026 | 0.00 | 6.85 | 9966 | 0.13 | −14,026 | 0.00 | 5.86 | 10,167 | 0.14 | |
| 150c | 1 | −17,062 | 0.00 | 3.18 | 14,051 | 0.62 | −17,062 | 0.00 | 5.24 | 14,118 | 0.65 |
| 2 | −16,292 | 0.00 | 4.13 | 18,626 | 1.50 | −16,292 | 0.00 | 4.32 | 18,738 | 1.58 | |
| 150d | 1 | −18,158 | 0.00 | 10.70 | 29,828 | 3.36 | −19,656 | 0.00 | 4.61 | 31,441 | 2.34 |
| 2 | −17,744 | 0.00 | 12.90 | 19,941 | 1.48 | −18,587 | 0.00 | 5.99 | 26,233 | 1.87 | |
| 150e | 1 | −17,925 | 0.00 | 43.71 | 23,911 | 0.42 | −19,214 | 0.00 | 11.70 | 26,744 | 0.44 |
| 2 | −19,397 | 0.00 | 24.29 | 23,281 | 0.38 | −21,270 | 0.00 | 6.96 | 25,491 | 0.39 | |
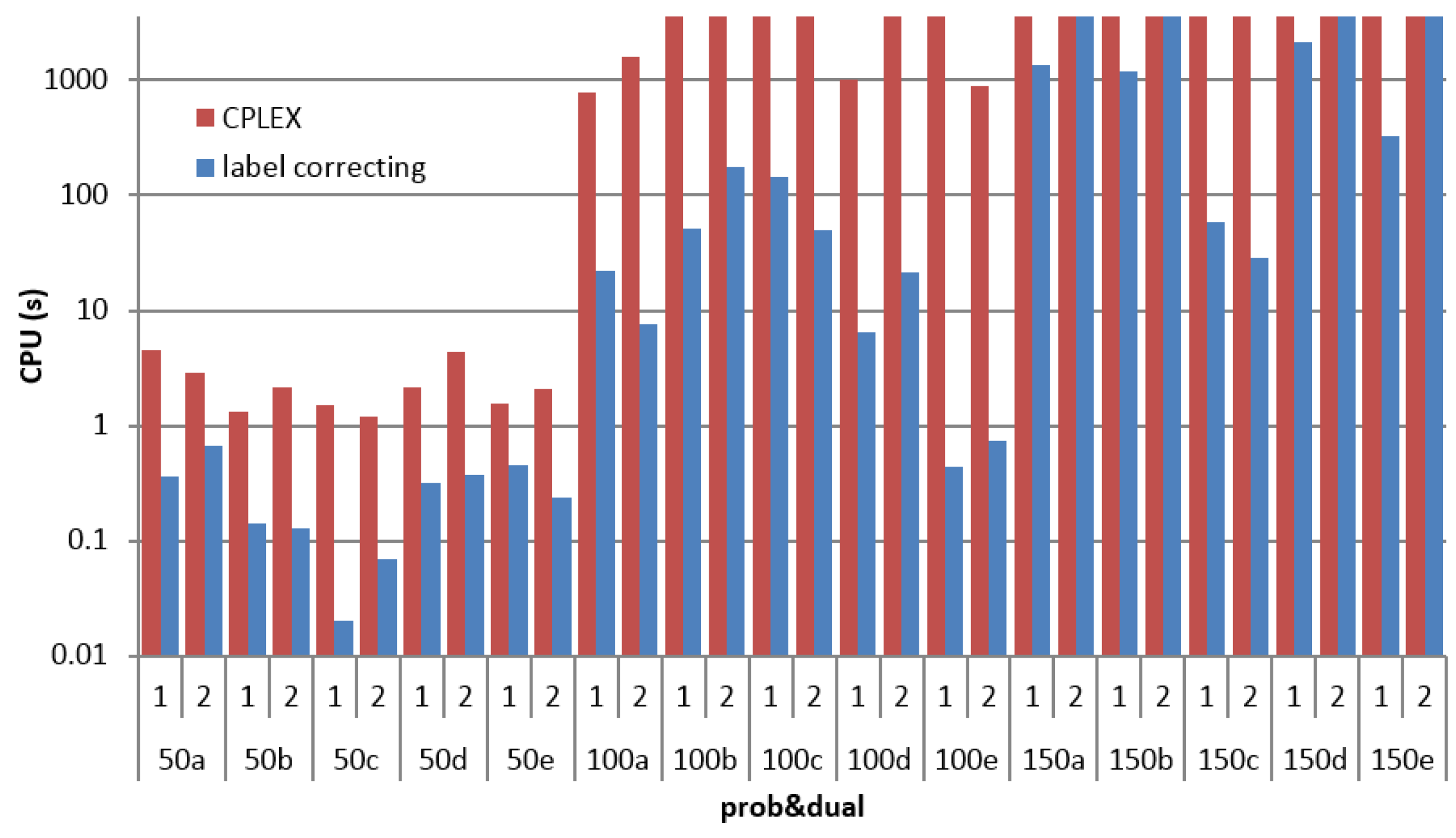
| 200a | 1 | −17,718 | 0.00 | 15.93 | 25,200 | 2.40 | −19,265 | 0.00 | 13.09 | 24,390 | 0.53 |
| 2 | −18,891 | 0.00 | 24.28 | 30,553 | 2.68 | −18,891 | 0.00 | 10.14 | 26,201 | 2.37 | |
| 200b | 1 | −21,300 | 0.00 | 13.07 | 26,969 | 0.53 | −22,216 | 0.00 | 7.18 | 27,031 | 0.54 |
| 2 | −22,300 | 0.00 | 12.21 | 20,303 | 0.36 | −23,112 | 0.00 | 6.95 | 20,396 | 0.38 | |
| 200c | 1 | −18,336 | 0.00 | 14.00 | 23,512 | 1.29 | −19,260 | 0.00 | 6.19 | 25,316 | 1.43 |
| 2 | −17,194 | 0.00 | 14.90 | 25,744 | 2.46 | −18,212 | 0.00 | 6.54 | 26,967 | 2.46 | |
| 200d | 1 | −19,536 | 0.00 | 27.92 | 46,037 | 4.80 | −20,742 | 0.00 | 67.16 | 48,768 | 4.93 |
| 2 | −20,315 | 0.00 | 92.37 | 46,088 | 2.80 | −20,607 | 0.00 | 58.97 | 46,342 | 5.51 | |
| 200e | 1 | −20,541 | 0.00 | 14.92 | 30,201 | 0.62 | −20,541 | 0.00 | 18.21 | 30,808 | 0.65 |
| 2 | −21,171 | 0.00 | 36.28 | 20,917 | 1.00 | −22,303 | 0.00 | 21.47 | 21,413 | 0.98 | |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, M.; Li, J.-Q. The Shortest Path Problems in Battery-Electric Vehicle Dispatching with Battery Renewal. Sustainability 2016, 8, 607. https://doi.org/10.3390/su8070607
Huang M, Li J-Q. The Shortest Path Problems in Battery-Electric Vehicle Dispatching with Battery Renewal. Sustainability. 2016; 8(7):607. https://doi.org/10.3390/su8070607
Chicago/Turabian StyleHuang, Minfang, and Jing-Quan Li. 2016. "The Shortest Path Problems in Battery-Electric Vehicle Dispatching with Battery Renewal" Sustainability 8, no. 7: 607. https://doi.org/10.3390/su8070607
APA StyleHuang, M., & Li, J.-Q. (2016). The Shortest Path Problems in Battery-Electric Vehicle Dispatching with Battery Renewal. Sustainability, 8(7), 607. https://doi.org/10.3390/su8070607





