Analysis of Spatial Disparities and Driving Factors of Energy Consumption Change in China Based on Spatial Statistics
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data
2.2. Methods
2.2.1. Global Spatial Autocorrelation
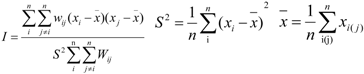
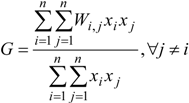
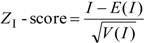
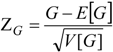
2.2.2. Local Spatial Autocorrelation
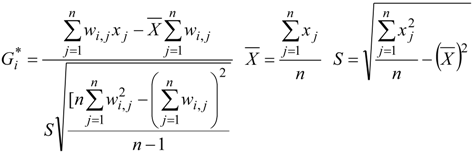
2.2.3. Spatial Autoregressive Model
ε = λw2ε + μ
μ ~ N(0, Ω)
Ωii = hi (Zα), hi > 0
ε = λwε + μ
3. Results and Discussion
3.1. Analysis of Global Spatial Disparities
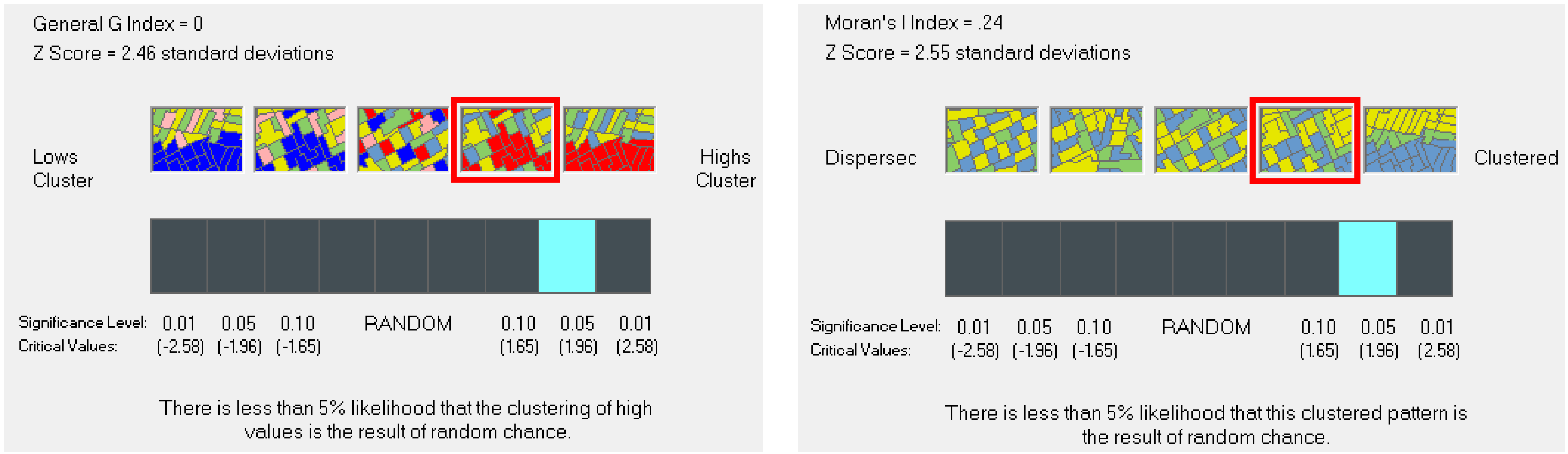
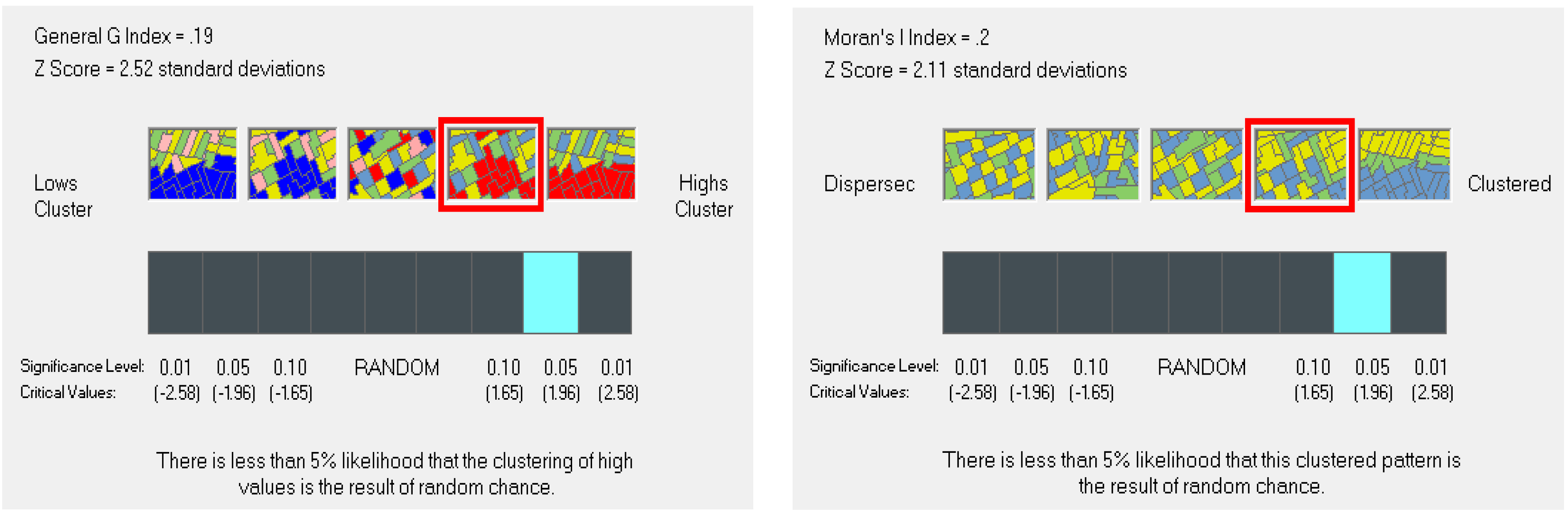
3.2. Analysis of Local Spatial Disparities
3.2.1. Analysis of Local Moran’s Ii
| Time stage | Minimum | Maximum | Mean | Moran’s Ii (+) | Moran’s Ii (−) | Range |
|---|---|---|---|---|---|---|
| 1990–2000 | −1.0771 | 1.9914 | 0.2178 | 74.1935 | 25.8065 | 3.0685 |
| 2000–2010 | −0.4994 | 2.7136 | 0.1822 | 51.6129 | 48.3871 | 3.2130 |
| 1990–2010 | −0.5502 | 2.8206 | 0.2164 | 58.0650 | 41.9350 | 2.2704 |
3.2.2. Analysis of Spatial Association Clustering and Distribution Features Based on Local Moran’s Ii
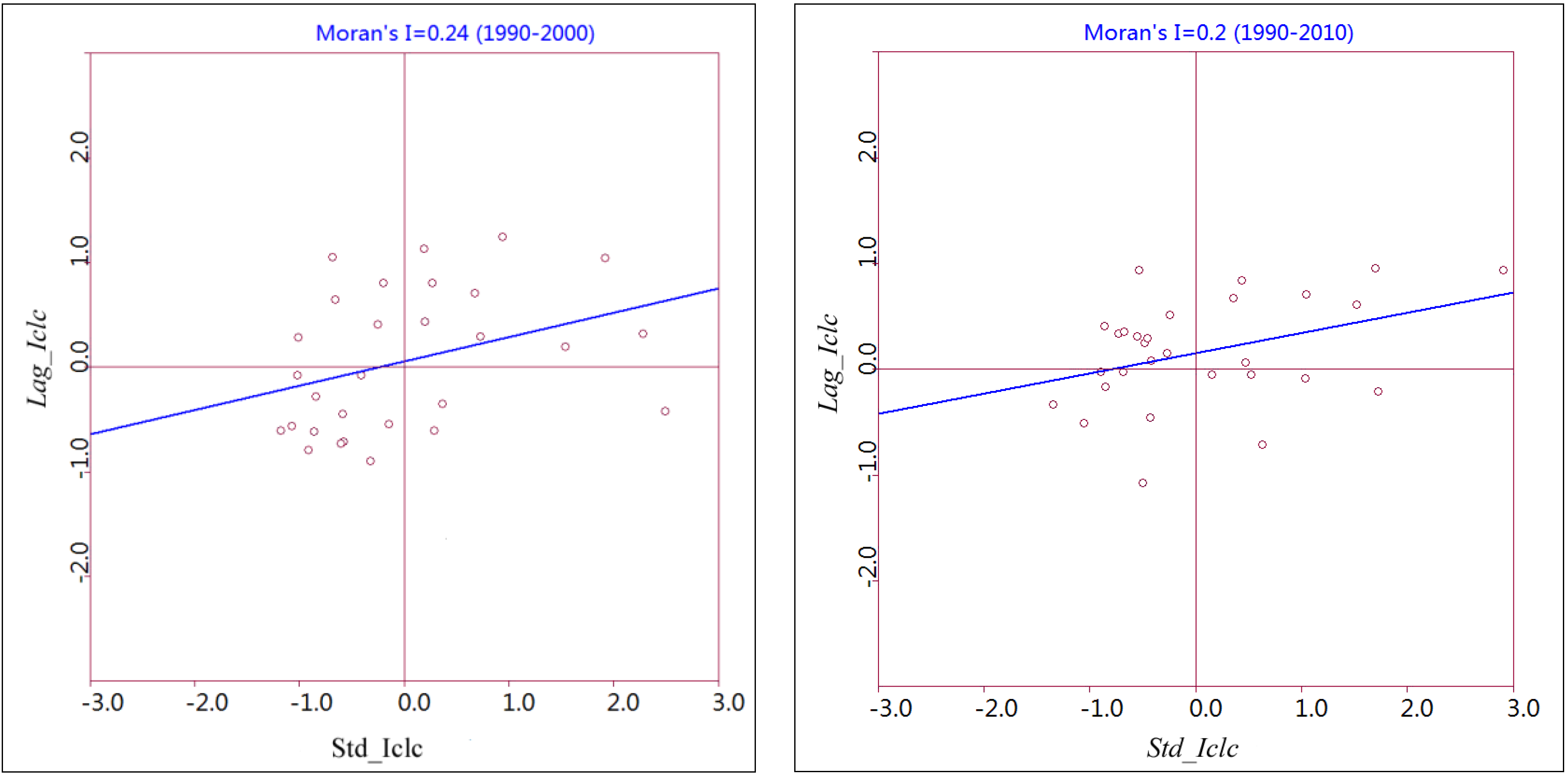
| Time Stage | Std-Iclc > 0 | Std-Iclc < 0 | Lag-Iclc > 0 | Lag-Iclc < 0 | H–H | H–L | L–L | L–H | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ratio | Ratio | Ratio | Ratio | Comparison Ratio | Ratio | Comparison Ratio | Ratio | Comparison Ratio | Ratio | Comparison Ratio | Ratio | |
| 1990–2000 | 40.00 | 60.00 | 50.00 | 50.00 | S+L+ | 30.00 | S+L− | 10.00 | S−L− | 26.67 | S−L+ | 23.33 |
| 2000–2010 | 40.00 | 60.00 | 63.33 | 36.67 | S+L+ | 23.33 | S+L− | 16.67 | S−L− | 16.67 | S−L+ | 33.33 |
| 1990–2010 | 40.00 | 60.00 | 63.33 | 36.67 | S+L+ | 23.33 | S+L− | 16.67 | S−L− | 30.00 | S−L+ | 30.00 |
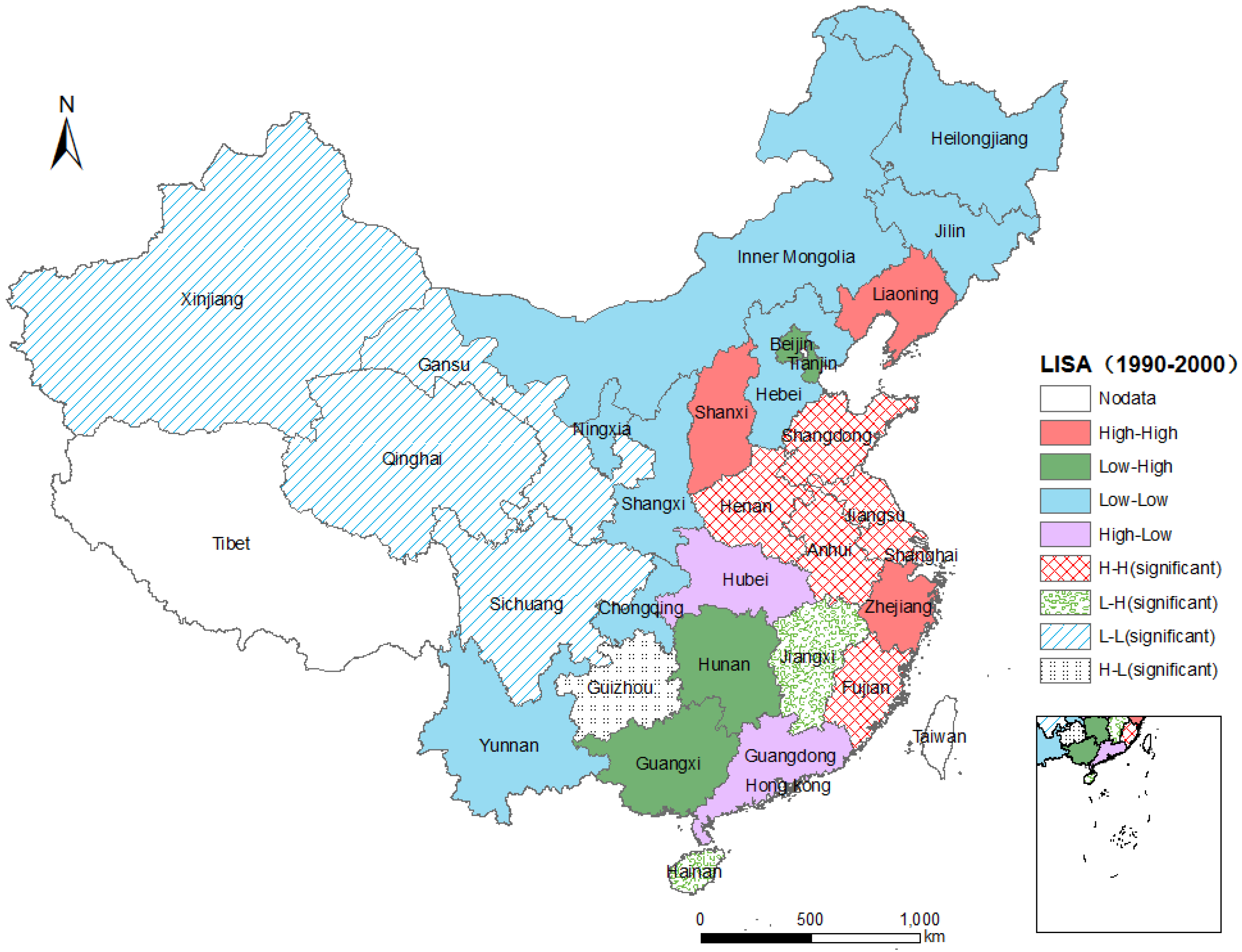
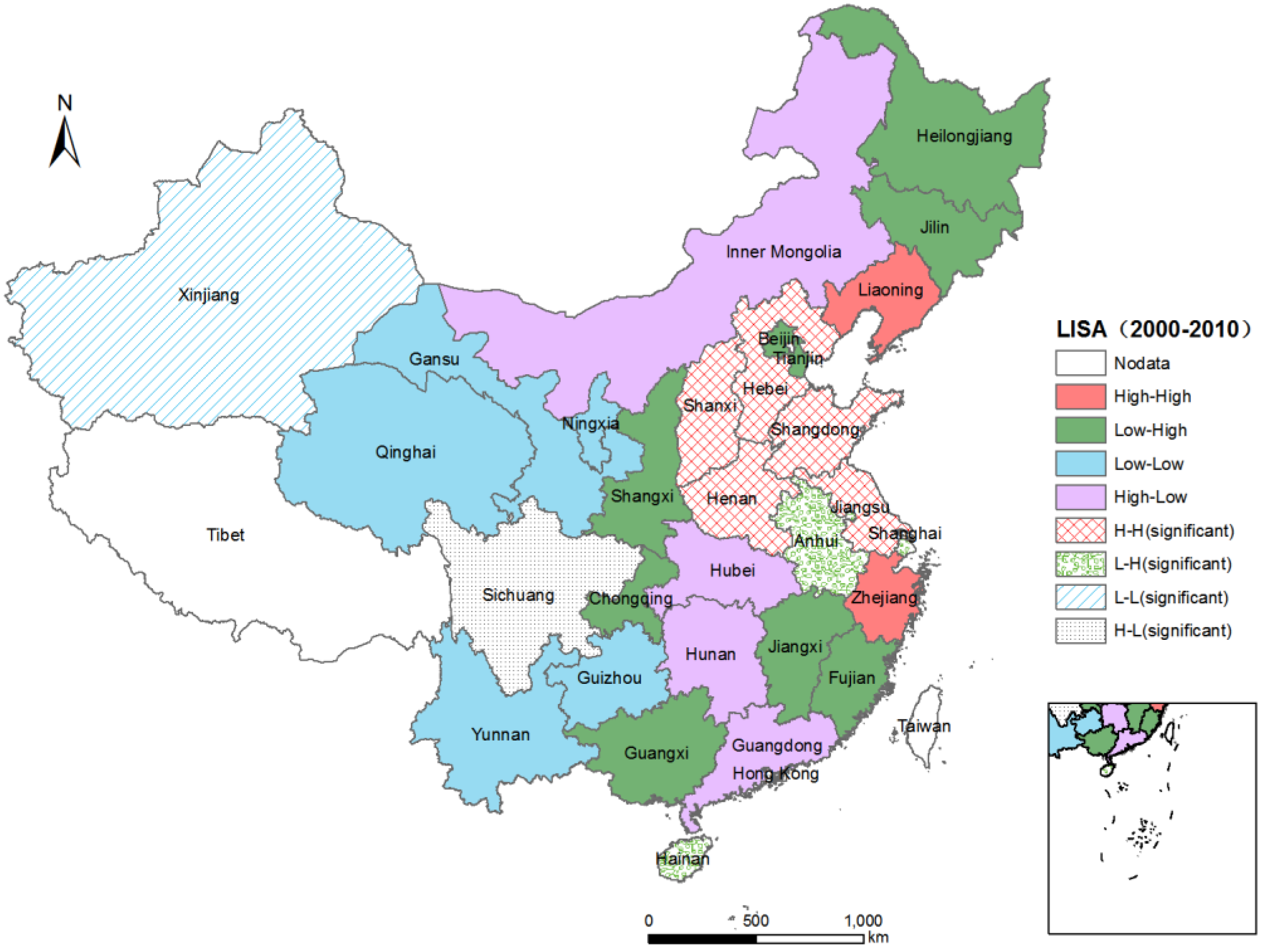
3.3. Influencing Factors of Energy Consumption Change
| Independent Variable | Moran’s I | E (I) | Mean | SD | ZI-score |
|---|---|---|---|---|---|
| Population growth rate | 0.3476 * | −0.0345 | −0.0326 | 0.1127 | 3.3904 |
| GDP growth rate | 0.4580 ** | −0.0345 | −0.0363 | 0.1160 | 4.2456 |
| Urbanization rate | 0.3781 * | −0.0345 | −0.0319 | 0.1145 | 3.6035 |
| Industrialized rate | 0.0022 | −0.0345 | −0.0264 | 0.1133 | 0.3239 |
| Percentage of industry production value change | 0.2073 * | −0.0345 | −0.0302 | 0.0997 | 2.4252 |
| Percentage of transportation industry production value change | 0.4439 ** | −0.0345 | −0.0337 | 0.1135 | 4.2149 |
| Model type | R2 or Pseudo R2 | LIK | AIC | SC |
|---|---|---|---|---|
| Linear regression model | 0.8065 | 3.7631 | 6.4737 | 16.5117 |
| Spatial lag model (SLM) | 0.8425 | 6.5164 | 2.9673 | 14.4392 |
| Spatial error model (SEM) | 0.8075 | 3.7948 | 6.4103 | 16.4482 |
| Variable | Coefficient | Std. Error | t Statistic | Probability |
|---|---|---|---|---|
| (A) Linear regression model R2 = 0.8065 | ||||
| Constant | 0.0251 | 0.2425 | 0.1034 | 0.9185 |
| Population growth rate | 0.3109 | 0.0826 | 3.7640 | 0.0010 |
| GDP growth rate | 0.6732 | 0.2250 | 2.9924 | 0.0063 |
| Urbanization rate | −1.1445 | 0.2193 | −5.2181 | 0.0000 |
| Industrialized rate | 0.3300 | 0.2028 | 1.6269 | 0.1168 |
| Percentage of industry production value change | 0.1439 | 0.0805 | 1.7887 | 0.0863 |
| Percentage of transportation industry production value change | 0.3321 | 0.1804 | 1.8407 | 0.0781 |
| Variable | Coefficient | Std. Error | Z-value | Probability |
| (B) Spatial lag model Pseudo R2 = 0.8425 | ||||
| ρ | −0.3713 | 0.1427 | −2.6011 | 0.0093 |
| Constant | 0.1942 | 0.2002 | 0.9700 | 0.3321 |
| Population growth rate | 0.3268 | 0.0656 | 4.9787 | 0.0000 |
| GDP growth rate | 0.7766 | 0.1814 | 4.2811 | 0.0000 |
| Urbanization rate | −1.2822 | 0.1779 | −7.2057 | 0.0000 |
| Industrialized rate | 0.3868 | 0.1628 | 2.3763 | 0.0175 |
| Percentage of industry production value change | 0.1783 | 0.0654 | 2.7268 | 0.0064 |
| Percentage of transportation industry production value change | 0.4302 | 0.1446 | 2.9745 | 0.0029 |
| Variable | Coefficient | Std. Error | Z-value | Probability |
| (C) Spatial error model Pseudo R2 = 0.8075 | ||||
| λ | −0.1227 | 0.2709 | −0.4529 | 0.6506 |
| Constant | 0.0557 | 0.2122 | 0.2624 | 0.7930 |
| Population growth rate | 0.3094 | 0.0723 | 4.2819 | 0.0000 |
| GDP growth rate | 0.6730 | 0.1960 | 3.4345 | 0.0006 |
| Urbanization rate | −1.1609 | 0.1941 | −5.9822 | 0.0000 |
| Industrialized rate | 0.3287 | 0.1796 | 1.8297 | 0.0673 |
| Percentage of industry production value change | 0.1423 | 0.0701 | 2.0294 | 0.0424 |
| Percentage of transportation industry production value change | 0.3623 | 0.1589 | 2.2793 | 0.0226 |
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Arouri, M.E.; Ben Youssef, A.; M’Henni, H.; Rault, C. Energy consumption, economic growth and CO2 emissions in Middle East and North African countries. Energy Policy 2012, 45, 342–349. [Google Scholar] [CrossRef] [Green Version]
- Payne, J.E. The Causal Dynamics Between US Renewable Energy Consumption, Output, Emissions, and Oil Prices. Energy Sour. Part B—Econ. Plan. Policy 2012, 7, 323–330. [Google Scholar] [CrossRef]
- Deng, S.H.; Zhang, J.; Shen, F.; Guo, H.; Li, Y.W.; Xiao, H. The Relationship Between Industry Structure, Household-number and Energy Consumption in China. Energy Sour. Part B-Econ. Plan. Policy 2014, 9, 325–333. [Google Scholar] [CrossRef]
- Dong, X.B.; Ulgiati, S.; Yan, M.C.; Zhang, X.S.; Gao, W.S. Energy and eMergy evaluation of bioethanol production from wheat in Henan Province, China. Energy Policy 2008, 36, 3882–3892. [Google Scholar] [CrossRef]
- Dong, X.B.; Zhang, Y.F.; Cui, W.J.; Xun, B.; Yu, B.H.; Ulgiati, S.; Zhang, X.S. Emergy-Based Adjustment of the Agricultural Structure in a Low-Carbon Economy in Manas County of China. Energies 2011, 4, 1428–1442. [Google Scholar] [CrossRef]
- Liu, Y.B. Exploring the relationship between urbanization and energy consumption in China using ARDL (autoregressive distributed lag) and FDM (factor decomposition model). Energy 2009, 34, 1846–1854. [Google Scholar] [CrossRef]
- Liu, Y.B.; Xie, Y.C. Asymmetric adjustment of the dynamic relationship between energy intensity and urbanization in China. Energy Econ. 2013, 36, 43–54. [Google Scholar] [CrossRef]
- Lu, W.W.; Chen, C.; Su, M.R.; Chen, B.; Cai, Y.P.; Xing, T. Urban energy consumption and related carbon emission estimation: A study at the sector scale. Front. Earth Sci. 2013, 7, 480–486. [Google Scholar] [CrossRef]
- Yu, H.Y. The influential factors of China’s regional energy intensity and its spatial linkages: 1988–2007. Energy Policy 2012, 45, 583–593. [Google Scholar] [CrossRef]
- Liu, Y.B. Energy Production and Regional Economic Growth in China: A More Comprehensive Analysis Using a Panel Model. Energies 2013, 6, 1409–1420. [Google Scholar] [CrossRef]
- Dietz, T.; Stern, P.C.; Weber, E.U. Reducing Carbon-Based Energy Consumption through Changes in Household Behavior. Daedalus 2013, 142, 78–89. [Google Scholar] [CrossRef]
- Wu, Y. Determinants and Spatial Spillovers Effects of Regional Energy Consumption in China: Positive Study Based on Spatial Panel Data Econometric Models. J. Nanjing Agric. Univ. 2012, 12, 124–132. [Google Scholar]
- Zou, Y.; Lu, Y. Regional characteristics of energy efficiency in China based on spatial auto regression model. Stat. Res. 2005, 10, 67–71. [Google Scholar]
- Wang, H.G.; Shen, L.S. A Spatial Panel Statistical Analysis on Chinese Economic Growth and Energy Consumption. J. Quant. Tech. Econ. 2007, 12, 98–107. [Google Scholar]
- Wu, Y.; Li, J. A local spatial econometric study on relationship between electricity consumption and economic growth of Chinese provinces. Sci. Geogr. Sin. 2009, 29, 30–35. [Google Scholar]
- Guo, L.; Du, S.H.; Haining, R.; Zhang, L.J. Global and local indicators of spatial association between points and polygons: A study of land use change. Int. J. Appl. Earth Obs. 2013, 21, 384–396. [Google Scholar] [CrossRef]
- Ertur, C.; Koch, W. Regional disparities in the European Union and the enlargement process: An exploratory spatial data analysis, 1995–2000. Ann. Reg. Sci. 2006, 40, 723–765. [Google Scholar] [CrossRef]
- Ruiz, A.R.; Pascual, U.; Romero, M. An exploratory spatial analysis of illegal coca cultivation in Colombia using local indicators of spatial association and socioecological variables. Ecol. Indic. 2013, 34, 103–112. [Google Scholar] [CrossRef]
- Anselin, L.; Sridharan, S.; Gholston, S. Using exploratory spatial data analysis to leverage social indicator databases: The discovery of interesting patterns. Soc. Indic. Res. 2007, 82, 287–309. [Google Scholar] [CrossRef]
- Anselin, L. Spatial Econometrics: Methods and Models; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1988. [Google Scholar]
- Xie, H.L.; Liu, Z.F.; Wang, P.; Liu, G.Y.; Lu, F.C. Exploring the Mechanisms of Ecological Land Change Based on the Spatial Autoregressive Model: A Case Study of the Poyang Lake Eco-Economic Zone, China. Int. J. Environ. Res. Public Health 2013, 11, 583–599. [Google Scholar] [CrossRef]
- Anselin, L. Local indicators of spatial association. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]
- Anselin, L. From SpaceStat to CyberGIS: Twenty Years of Spatial Data Analysis Software. Int. Reg. Sci. Rev. 2012, 35, 131–157. [Google Scholar] [CrossRef]
- Getis, A.; Ord, K. The analysis of spatial association by use of distance statistics. Geogr. Anal. 1992, 24, 189–206. [Google Scholar] [CrossRef]
- Poulsen, M.; Johnston, R.; Forrest, J. The intensity of ethnic residential clustering: Exploring scale effects using local indicators of spatial association. Environ. Plan. A 2010, 42, 874–894. [Google Scholar] [CrossRef]
- Gray, D. District House Price Movements in England and Wales 1997–2007: An Exploratory Spatial Data Analysis Approach. Urban Stud. 2012, 49, 1411–1434. [Google Scholar] [CrossRef]
- Gaither, C.J.; Poudyal, N.C.; Goodrick, S.; Bowker, J.M.; Malone, S.; Gan, J.B. Wildland fire risk and social vulnerability in the Southeastern United States: An exploratory spatial data analysis approach. For. Policy Econ. 2011, 13, 24–36. [Google Scholar] [CrossRef]
- Xie, H.L.; Wang, P.; Huang, H.S. Ecological Risk Assessment of Land Use Change in the Poyang Lake Eco-economic Zone, China. Int. J. Environ. Res. Public Health 2013, 10, 328–346. [Google Scholar] [CrossRef]
- Xie, H.L.; Kung, C.C.; Zhao, Y.L. Spatial disparities of regional forest land change based on ESDA and GIS at the county level in Beijing-Tianjin-Hebei area. Front. Earth Sci. 2012, 6, 445–452. [Google Scholar] [CrossRef]
- Menard, S. Applied Logistic Regression Analysis; Sage: Thousand Oaks, CA, USA, 1995. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Xie, H.; Liu, G.; Liu, Q.; Wang, P. Analysis of Spatial Disparities and Driving Factors of Energy Consumption Change in China Based on Spatial Statistics. Sustainability 2014, 6, 2264-2280. https://doi.org/10.3390/su6042264
Xie H, Liu G, Liu Q, Wang P. Analysis of Spatial Disparities and Driving Factors of Energy Consumption Change in China Based on Spatial Statistics. Sustainability. 2014; 6(4):2264-2280. https://doi.org/10.3390/su6042264
Chicago/Turabian StyleXie, Hualin, Guiying Liu, Qu Liu, and Peng Wang. 2014. "Analysis of Spatial Disparities and Driving Factors of Energy Consumption Change in China Based on Spatial Statistics" Sustainability 6, no. 4: 2264-2280. https://doi.org/10.3390/su6042264






