Oil Consumption, CO2 Emission, and Economic Growth: Evidence from the Philippines
Abstract
:1. Introduction
| Countries | Periods | Causality Relationship | Sources |
|---|---|---|---|
| BRICs | 1971–2005 | Short run: C→Y, E→CY | Pao and Tsai [16] |
| Long run: YC→E, CE→Y | |||
| Strong: C→EY, E→CY, Y→E | |||
| Central America (6) | 1971–2004 | short run: E→CY, Y→CE | Apergis and Payne [17] |
| long run: EY→C, YC→E | |||
| China | 1960–2007 | long run: Y→E, E→C | Zhang and Cheng [18] |
| 1981–2006 | long run: Y→CE, C→E, E→YC | Chang [19] | |
| CIS | 1992–2004 | short run: E→CY, Y→CE | Apergis and Payne [20] |
| long run: EY→C, CY→E | |||
| Europe (19) | 1960–2005 | short run: (Denmark) Y→C,E | Acaravci and Ozturk [21] |
| (Greece) Y→E (Italy) E→C, Y→CE | |||
| (Swiss) E→Y, Y→E | |||
| long run: (Denmark) EY→C | |||
| (Greece) EY→C (Iceland) EY→C | |||
| (Italy) EY→C, YC→E (Portugal) EY→C | |||
| (Swiss) EY→C EC→Y | |||
| Greece | 1977–2007 | short run: Y→C, E→C | Hatzigeorgiou et al. [22] |
| long run: Y→EC, E→C, C→E | |||
| strong: Y→EC, E→C | |||
| Iran | 1967–2007 | long run: Y→CE | Lotfalipour et al. [23] |
| Malaysia | 1971–1999 | short run: Y→E | Ang [24] |
| long run: CE→Y, YC→E | |||
| strong: CE→Y, Y→E | |||
| France | 1960–2000 | short run: E→Y | Ang [25] |
| long run: EY→C, CY→E | |||
| South Africa | 1965–2006 | C→Y, E→YC | Menyah and Wolde-Rufael [26] |
| Turkey | 1960–2005 | short run: C→EY, E→C, Y→C | Halicioglu [27] |
| long run: EY→C, EC→Y | |||
| 1968–2005 | long run: CE→Y | Ozturk and Acaravci [28] |
2. Methodology
2.1. Granger-Causality and Stationarity
2.2. Co-Integration
2.3. Error-Correction Model
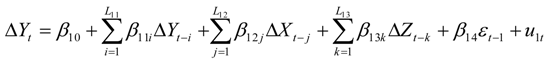
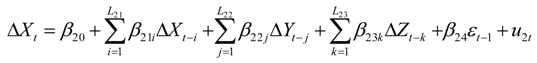
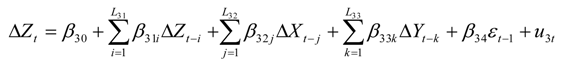
3. Results and Discussion
3.1. Data
3.2. Results of Unit Roots and Co-Integration Tests
| Variables | Levels | First differences | ||
|---|---|---|---|---|
| PP values | p-values | PP values | p-values | |
| Oil consumption (X) | −6.24 [4] | 0.727 | −21.88 [3]** | 0.048 |
| CO2 emissions (Y) | −10.00 [10] | 0.436 | −41.33 [2]** | 0.001 |
| GDP (Z) | −7.31 [8] | 0.639 | −44.19 [2]** | 0.000 |
| Variables | Optimal lags | Break points | Test statistics | Inferences |
|---|---|---|---|---|
| Oil consumption (X) | 6 | 1984 | −2.77 | Non-stationary |
| CO2 emissions (Y) | 10 | 1987 | −2.19 | Non-stationary |
| GDP (Z) | 1 | 1985 | −1.58 | Non-stationary |
| Null hypotheses | Likelihood ratio test statistic | p-values |
|---|---|---|
| The number of co-integrating equations is zero (R = 0) | 36.63 | 0.027 |
| The number of co-integrating equations is at most one (R ≤ 1) | 14.43 | 0.158 |
| The number of co-integrating equations is at most two (R ≤ 2) | 0.04 | 0.620 |
3.3. Results of the Error-Correction Model and Granger-Causality Tests
| Null Hypotheses | Source of Causality (Independent Variables) | ||||||
|---|---|---|---|---|---|---|---|
| Short-Run | Long-Run | Joint (Short/Long-Run) | |||||
| F-values | t-values | F-values | |||||
| ΔZ | ΔX | ΔY | εt-1 | ΔZ, εt-1 | ΔX, εt-1 | ΔY, εt-1 | |
| Oil consumption and/or CO2 emissions do not cause economic growth | 7.244** | 8.515** | −3.890** | 17.777** | 17.601** | ||
| (0.010) | (0.006) | (0.000) | (0.005) | (0.000) | |||
| Economic growth and/or CO2 emissions do not cause oil consumption | 2.996** | 2.490* | −2.118** | 4.762** | 2.713* | ||
| (0.045) | (0.086) | (0.042) | (0.007) | (0.061) | |||
| Oil consumption and/or economic growth do not cause CO2 emissions | 1.825 | 5.320** | 1.439 | 2.793* | 5.590** | ||
| (0.175) | (0.009) | (0.158) | (0.074) | (0.007) | |||
3.4. Discussions

4. Conclusions
Author Contributions
Conflicts of Interest
References and Notes
- BP Statistical Review of World Energy 2012. Available online: http://www.bp.com/assets/bp_internet/globalbp/globalbp_uk_english/reports_and_publications/statistical_energy_review_2011/STAGING/local_assets/pdf/statistical_review_of_world_energy_full_report_2012.pdf (accessed on 10 November 2013).
- Energy Information Administration. Overview Data for Philippines. Available online: http://www.eia.gov/countries/country-data.cfm?fips=RP (accessed on 5 November 2013).
- Yang, H.Y. A note on the causal relationship between energy and GDP in Taiwan. Energy Econ. 2000, 22, 309–317. [Google Scholar] [CrossRef]
- Aqeel, A.; Butt, M.S. The relationship between energy consumption and economic growth in Pakistan. Asia-Pacific Devel. J. 2001, 8, 101–110. [Google Scholar]
- Zou, G.; Chau, K.W. Short- and long-run effects between oil consumption and economic growth in China. Energy Policy 2006, 34, 3644–3655. [Google Scholar] [CrossRef]
- Lee, C.C.; Chang, C.P. Structural breaks, energy consumption, and economic growth revisited: Evidence from Taiwan. Energy Econ. 2005, 27, 857–872. [Google Scholar] [CrossRef]
- Yoo, S.-H. Oil consumption and economic growth: evidence from Korea. Energ. Source. Part B 2006, 1, 235–243. [Google Scholar] [CrossRef]
- Yuan, J.-H.; Kang, J.G.; Zhao, C.H.; Hu, Z.G. Energy consumption and economic growth: Evidence from China at both aggregated and disaggregated levels. Energy Econ. 2008, 30, 3077–3094. [Google Scholar] [CrossRef]
- Ghosh, S. High speed diesel consumption and economic growth in India. Energy 2010, 35, 1794–1798. [Google Scholar] [CrossRef]
- Fatai, K.; Oxley, L.; Scrimgeour, F.G. Modelling the causal relationship between energy consumption and GDP in New Zealand, Australia, India, Indonesia, the Philippines and Thailand. Math. Comput. Simulat. 2004, 64, 431–445. [Google Scholar] [CrossRef]
- Rufael, Y. Disaggregated industrial energy consumption and GDP: the case of Shanghai, 1952–1999. Energy Econ. 2004, 26, 69–75. [Google Scholar] [CrossRef]
- Transport and Traffic Planners INC. A Strategic Approach to Climate Change in the Philippines. Available online: http://siteresources.worldbank.org/INTPHILIPPINES/Resources/PH_Low_Carbon_Transport_and_Power.pdf (accessed on 8 November 2013).
- Bloch, H.; Rafiq, S.; Salim, R. Coal consumption, CO2 emission and economic growth in China: Empirical evidence and policy responses. Energy Econ. 2012, 34, 518–528. [Google Scholar] [CrossRef]
- Usama, A.M. Oil consumption, CO2 emission and economic growth in MENA countries. Energy 2011, 36, 6165–6172. [Google Scholar] [CrossRef]
- Fuinhas, J.A.; Marques, A.C. Energy consumption and economic growth nexus in Portugal, Italy, Greece, Spain and Turkey: An ARDL bounds test approach (1965–2009). Energy Econ. 2012, 34, 511–517. [Google Scholar] [CrossRef]
- Pao, H.T.; Tsai, C.M. CO2 emissions, energy consumption and economic growth in BRIC countries. Energy Policy 2010, 38, 7850–7860. [Google Scholar] [CrossRef]
- Apergis, N.; Payne, J.E. CO2 emissions, energy usage, and output in Central America. Energy Policy 2009, 37, 3282–3286. [Google Scholar] [CrossRef]
- Zhang, X.P.; Cheng, X.M. Energy consumption, carbon emissions and economic growth in China. Ecolog. Econ. 2009, 68, 2706–2712. [Google Scholar] [CrossRef]
- Chang, C.C. A multivariate causality test of carbon dioxide emissions, energy consumption and economic growth in China. Appl. Energy 2010, 87, 3533–3537. [Google Scholar] [CrossRef]
- Apergis, N.; Payne, J.E. The emissions, energy consumption, and growth nexus: Evidence from the commonwealth of independent states. Energy Policy 2010, 38, 650–655. [Google Scholar] [CrossRef]
- Acaravci, A.; Ozturk, I. On the relationship between energy consumption, CO2 emissions and economic growth in Europe. Energy 2010, 35, 5412–5420. [Google Scholar] [CrossRef]
- Hatzigeorgiou, E.; Polatidis, H.; Haralambopoulos, D. CO2 emissions, GDP and energy intensity: A multivariate cointegration and causality analysis for Greece, 1977–2007. Appl. Energy 2011, 88, 1377–1385. [Google Scholar] [CrossRef]
- Lotfalipour, M.R.; Falahi, M.A.; Ashena, M. Economic growth, CO2 emissions, and fossil fuels consumption in Iran. Energy 2010, 35, 5115–5120. [Google Scholar] [CrossRef]
- Ang, J.B. Economic development, pollutant emissions and energy consumption in Malaysia. J. Pol. Modeling 2008, 30, 271–278. [Google Scholar] [CrossRef]
- Ang, J.B. CO2 emissions, energy consumption, and output in France. Energy Policy 2007, 35, 4772–4778. [Google Scholar] [CrossRef]
- Menyah, K.; Wolde-Rufael, Y. Energy consumption, pollutant emissions and economic growth in South Africa. Energy Econ. 2010, 32, 1374–1382. [Google Scholar] [CrossRef]
- Halicioglu, F. An econometric study of CO2 emissions, energy consumption, income and foreign trade in Turkey. Energy Policy 2009, 37, 1156–1164. [Google Scholar] [CrossRef] [Green Version]
- Ozturk, I.; Acaravci, A. CO2 emissions, energy consumption and economic growth in Turkey. Renew. Sust. Energy Rev. 2010, 14, 3220–3225. [Google Scholar] [CrossRef]
- Granger, C.W.J. Investigating causal relation by econometric and cross-sectional method. Econometrica 1969, 37, 424–438. [Google Scholar] [CrossRef]
- Granger, C.W.J. Newbold, and P. Spurious regressions in econometrics. J. Econometrics 1974, 2, 111–120. [Google Scholar] [CrossRef]
- Geweke, J.; Meese, R.; Dent, W. Comparing alternative tests for causality in temporal systems: Analytic results and experimental evidence. J. Econometrics 1983, 21, 161–194. [Google Scholar] [CrossRef]
- Stock, J.H.; Watson, M.W. Interpreting the evidence in money-income causality. J. Econometrics 1989, 40, 161–182. [Google Scholar] [CrossRef]
- Engle, R.F.; Granger, C.W.J. Cointegration and error correction: Representation, estimation and testing. Econometrica 1987, 55, 251–276. [Google Scholar] [CrossRef]
- Phillips, P.C.B.; Perron, P. Testing for a unit root in time series regression. Biometrika 1988, 75, 335–346. [Google Scholar] [CrossRef]
- Toda, H.Y.; Phillips, P.C.B. Vector autoregressions and causality. Econometrica 1993, 61, 1367–1393. [Google Scholar] [CrossRef]
- Johansen, S.; Juselius, K. Maximum likelihood estimation and inference on cointegration with applications to the demand for money. Oxford Bull. Econ. Statist. 1990, 52, 169–210. [Google Scholar] [CrossRef]
- Park, J.Y. Canonical cointegrating regressions. Econometrica 1992, 60, 119–143. [Google Scholar] [CrossRef]
- World Bank. World Development Indicators 2013. Available online: http://databank.worldbank.org (accessed on 10 November 2013).
- Pantula, S.G.; Gonzalez-Farias, G.; Fuller, W.A. A comparison of unit-root test criteria. J. Bus. Econ. Statist. 1994, 12, 449–459. [Google Scholar]
- Lanne, M.; Lutkepohl, H.; Saikkonen, P. Comparison unit root tests for times series with level shifts. J. Time Ser. Anal. 2002, 23, 1467–9892. [Google Scholar]
- Brown, R.; Durbin, J.; Evans, J. Techniques for testing the constancy of regression relationships over time. J. Roy. Stat. Soc. B 1975, 37, 149–172. [Google Scholar]
- An anonymous reviewer indicated this point.
- Rafiq, S.; Salim, R.A. The linkage between energy consumption and income in six emerging economies in Asia: Empirical analysis. Int. J. Emerg. Market. 2006, 6, 50–73. [Google Scholar] [CrossRef]
- Apergis, N.; Tang, C.F. Is the energy-led growth hypothesis valid? New evidence from a sample of 85 countries. Energy Econ. 2013, 38, 24–31. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Lim, K.-M.; Lim, S.-Y.; Yoo, S.-H. Oil Consumption, CO2 Emission, and Economic Growth: Evidence from the Philippines. Sustainability 2014, 6, 967-979. https://doi.org/10.3390/su6020967
Lim K-M, Lim S-Y, Yoo S-H. Oil Consumption, CO2 Emission, and Economic Growth: Evidence from the Philippines. Sustainability. 2014; 6(2):967-979. https://doi.org/10.3390/su6020967
Chicago/Turabian StyleLim, Kyoung-Min, Seul-Ye Lim, and Seung-Hoon Yoo. 2014. "Oil Consumption, CO2 Emission, and Economic Growth: Evidence from the Philippines" Sustainability 6, no. 2: 967-979. https://doi.org/10.3390/su6020967





