Environmental xenobiotics are substances, which did not exist in nature before their synthesis by humans. They are becoming increasingly problematic in medicine and environmental systems, since they are relatively new substances and difficult to categorize, and since it is challenging to assess their effects on human health and the environment.

A xenobiotic is defined as a chemical, which is found in an organism but which is not normally produced or expected to be present in it [1,2]. The term xenobiotic also includes substances, which are present in much higher concentrations than are usual. Drugs and antibiotics are normally specified as xenobiotics in humans. Natural compounds can also become xenobiotics if they are taken in by an organism.

Over the last decades, xenobiotics have been extended to the environment. Many studies [3,4,5,6,7,8] have shown that the term xenobiotic is related to environmental impact, emphasizing that environmental xenobiotics in the context of pollutants are substances foreign to an entire biological system, which did not exist in nature before their synthesis by humans. Examples of environmental xenobiotics include dioxins and polychlorinated biphenyls, plastics, pesticides, and compounds in emissions from fossil fuel-fired devices like power stations and automobiles. The existence of environmental xenobiotics poses potentially dangerous and unstable situations, because the possible harmful effects of anthropogenic xenobiotics on ecosystems in the natural environment. The objective of this paper is to enhance knowledge of the impacts of environmental xenobiotics on humans and other life forms by proposing a pattern depicting mathematically modeled processes of resonant absorption of a xenobiotic harmonic oscillation by an organism modulated as an absorbing oscillator structure.

Over the last decades, several xenobiotics have been found to be toxic to the immune system [1,5,9,10], meaning that xenobiotics have the capacity to suppress the body’s defenses against pathogenic microorganisms. This suppression can cause increased susceptibility to cancer or autoimmune diseases. Immunotoxicology deals with the effects of physical and chemical agents and other toxic substances on the immune system [1,2]. Although immunotoxicology is a relatively new field, important data have been accumulated over the last several years on immunotoxicity of certain environmental xenobiotics [1,2,5,11,12,13].

Many reports in the literature [1,2,5,14,15,16,17] describe the immunotoxic effects of xenobiotics, recognizing that the immune system as a whole can be the target for xenobiotic induced toxicity. Recent reports [3,4,6,7,8,9] suggest that environmental xenobiotics may be associated with endocrine alterations in people, wildlife, and test animals. For instance, pharmacological investigations as well as natural poisoning episodes have identified associations between exogenous chemicals and alterations in multiple hormonal systems.

Furthermore, persistent environmental contaminants such as dioxins and polychlorinated biphenyls (PCBs) have been shown to modulate the activities of several different hormones [5,9,10,15]. Note that dioxins are one of the most toxic human-made compounds and are persistent contaminants in the environment. The term dioxin refers to a family of related chemical compounds that include the chlorinated dibenzo-p-dioxins and chlorinated dibenzofurans, which form a class of compounds called polychlorinated diaromatic hydrocarbons (PCDH). These compounds accumulate in people and wildlife organisms and are considered responsible for causing toxic effects, birth defects, immunotoxicity, tumor production, changes in metabolism and death. By extension, the unborn child or the neonate may be at special risk from environmental xenobiotics, because of its rapid growth and development in addition to its enhanced exposure. Also, the disruption of the reproductive system of male and female animals in the wild [9,15] has been attributed to environmental xenobiotics.

Similarly, problems caused by environmental emissions during the operation of coal-fired power stations, beyond the environmental depletion, are also related to and impact human health [11,12,13]. The combustion of coal leads to emissions of acid gases and greenhouse gases that contribute significantly to acid rain and have been associated with global warming [12,17]. During electrical energy generation, coal-fired power plants emit particulate matter, SO₂, NO_x as well as gases that undergo chemical reactions to form fine particles in the atmosphere [18]. These reactive chemicals (particulate matter, sulfur dioxide and nitrogen oxides) represent environmental xenobiotics, which spread over hundreds to thousands of kilometers downwind of power plants. Consequently, in addition to the environmental harm caused by greenhouse gases and other emissions, the air emissions of coal-fired power stations encompass a certain amount of toxic xenobiotics that result in significant numbers of human deaths and diseases [12,13]. Through exposure to these environmental xenobiotics, people can experience heart diseases, respiratory illness and lung cancer, as well as other health problems such as adverse reproductive outcomes, infant death, chronic bronchitis, asthma, and other lung diseases [11,16,17].

As a consequence, the pollutant load caused by environmental xenobiotics concerns researchers in medical and environmental fields.

A body removes xenobiotics by xenobiotic metabolism [1,2,7], which consists of deactivation (mostly occurring in the liver) and excretion of xenobiotics. Hepatic enzymes are responsible for the metabolism of xenobiotics by first activating them, via the processes of oxidation, reduction, hydrolysis and hydration of the xenobiotics, followed by conjugating the active secondary metabolites with glucuronic or sulphuric acid. These processes are followed by excretion in bile or urine, as well as other excretion routes such as feces, breath and sweat. A sequence of stages can occur in which a xenobiotic basically passes through the phase of biotransformation into metabolic products, each having its own behavior regarding distribution and bio-reactivity.

Studies [1,2,5] have shown that organisms along with ecosystems can evolve to tolerate xenobiotics, but their resistance levels are strongly depending on genetic factors, the routes of administration of the xenobiotic, and the toxin concentration and exposure duration. Still, the evolutionary immunotoxic response of an organism is for now considered somewhat unpredictable, since studies [3,4,5,6,7,8,9,10,11] have identified important human health and wildlife effects even when xenobiotic concentrations were not significantly increased.

A better understanding may be related to the wave shape of a xenobiotic oscillation, if we accept a holistic view of xenobiotic metabolism. Following this idea, we here study a superposition of two oscillations, one corresponding to the biological organism system and the other to the environmental xenobiotic. A myriad of assays could be experimentally run to improve understanding, but such an approach is time and effort consuming and usually yields case-specific information. The more abstract view adopted here seeks an analogy between a living system (an organism) and an electrical system, based on the understanding that any biological organism may be seen as a system oscillating at its own frequency (or having an own wavelength).

Consequently, the processes of absorption, distribution, biotransformation and removal of environmental xenobiotics could be studied through mathematical models and methods. In related research, compartmental analysis has been applied to the body [18,19,20]. Compartmental analysis applies mathematical patterns to develop models for the biological behavior of a system by defining the compartmental concept in a simplified manner in terms of human body locations, for modeling purposes. For instance, the human body input compartment could be defined by the absorption surfaces at lung level. Furthermore, xenobiotic transfer is achieved through the central distribution compartment of a fluid biological space, mainly blood and plasma. Note that the distribution stage can be assessed at the same time with a persistent accumulation stage in blood and in extracellular spaces of tissues and organs. Bio-reactive compartments are defined, including receivers, enzymes, proteins etc. These compartments are involved in both biotransformation and removal.

These ideas [20] led to the emergence of several peripheral and central compartments that play an important role in representing the kinetics of metabolism in a model.

According to the theory of complex systems analysis, one could apply the mathematical pattern method for the assessment of the behavior of an ecosystem or biological organism. A mathematical model represents a transformation of the relations between the system variables in appropriate mathematical structures. The mathematical patterns are usually expressed by algebraic equations, differential or logical, with their form, structure and parameters depending on the real system [18,19,20,21,22]. Furthermore, the mathematical patterns, which depict in an abstract form the behavior of a real system, are the basis of the analysis and synthesis of real systems, as well as the starting point of system simulation (by applying specialized simulation languages).

This study deals with a pattern depicting the mathematical representation of the process of environmental xenobiotic absorption. To fully understand xenobiotic processes, mathematical patterns also need to be established for describing the xenobiotic entrance into the system, circulation and distribution to organs and tissues where metabolism occurs, and subsequent excretion, but that work is beyond the scope of the present undertaking.

By analogy with thermal physics, where the temperature difference gives the sense and magnitude of the transferred energy, the main vector of behavioral analysis in the situation of an environmental xenobiotic “attack” is represented by the xenobiotic concentration c(t).

To create a homogenous framework and problem definition, we address the percentage representation of the xenobiotic concentration through the spatial concentration vector c(t). The mathematic model depicting such a vector can be linear or non-linear, as evidenced by the relation between the system input and output. Note that a linear pattern respects the superposition principle and the homogeneity property.

Consider a mathematical model with the input quantities x_i(t) and the output quantities z_i(t). According to the superposition principle, the mathematical model is linear if the input x(t) = x₁(t) + x₂(t) determines an output z(t) = z₁(t) + z₂(t). Also, one can define the homogeneity property if for an input α · x_i(t) the resulting output is α · z_i(t), with α denoting the transfer coefficient or attenuation factor. Note that if we are dealing with nonlinear models, the pattern linearization through the tangent to the curve at an operation point can be achieved by developing a Taylor series of the function near this point.

We hope to later show that a mathematical model described by a differential equation of order two with concentrated parameters could be accepted for a complex process of an environmental xenobiotic absorption by a linear structure. In line with this idea, we define a hypothetical situation in which, from an environmental xenobiotic source with harmonic behavior, the xenobiotic is absorbed by the biologic organism modeled as a system with a linear structure. The xenobiotic concentration is subsequently denoted by z(t).

Within the structure of a modulated absorption system corresponding to the biological organism (the target of a xenobiotic), one can identify specific elements of xenobiotic compounds that are of a dissipating type or an accumulating type. As stated earlier, a mathematical model depicting a xenobiotic absorption process could be a differential equation of order 2. Consequently, we consider an analogous pattern of physics, namely an electrical structure type RLC series circuit, where the accumulating elements are described by the capacity C and the inductance L, while the dissipating elements are characterized by the resistance R [23,24]. Note that we have considered a simplified hypothesis referring to a concentrated parameters circuit, connected to a harmonic source, with the possibility of defining the elements RLC in various ways.

The differential equation corresponding to this transient regime is:

The solution of the differential Equation (1) is expressed by the relationship:

Here:

δ is the damping factor of the circuit:

ω₀ is the resonant pulsation:

ω_e is the own pulsation of the biologic organism system:

and

If the damping factor has a small value, δ → 0 and Ψ = π / 2. Applying mathematical calculus, the xenobiotic concentration expression results:

This expression emphasizes the superposition of two oscillating components, with the harmonic xenobiotic pulsation ω and the biologic system pulsation ω₀ = ω_e, respectively.

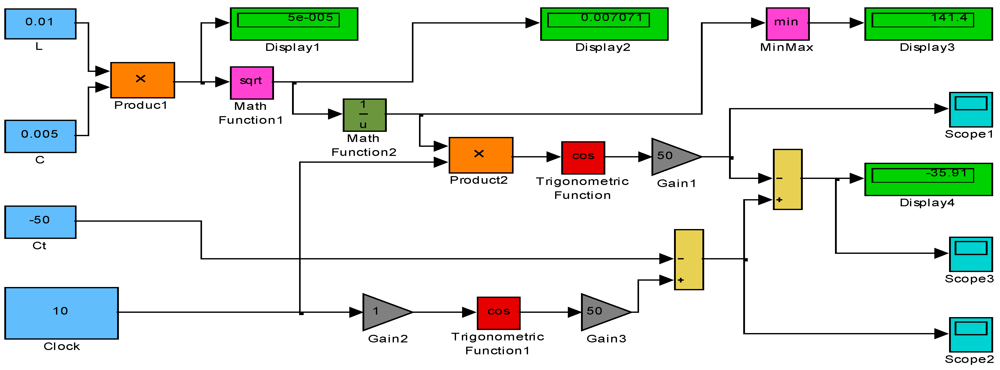
The mathematical modeling stage is followed by the simulation of specific phenomena by using appropriate computer software. For instance, one could use MATLAB software with SIMULINK and SimPowerSystems extensions. For this purpose we developed a SIMULINK model entailing specific blocks generated by the SIMULINK library.

Based on the MATLAB-SIMULINK utility, the explicit function (15) leads to obtaining the simulation model for the spatial vector of concentration z(t), depicted in Figure 1.

Subsequently, based on this simulation pattern, the representations of Figure 2, Figure 3 and Figure 4 have been obtained.

Figure 2 depicts the modulating signal obtained on basis of absorption circuit elements corresponding to the biological system with the resonant pulsation ω₀.

In Figure 3, the xenobiotic harmonic oscillation, with the pulsation ω, is presented.

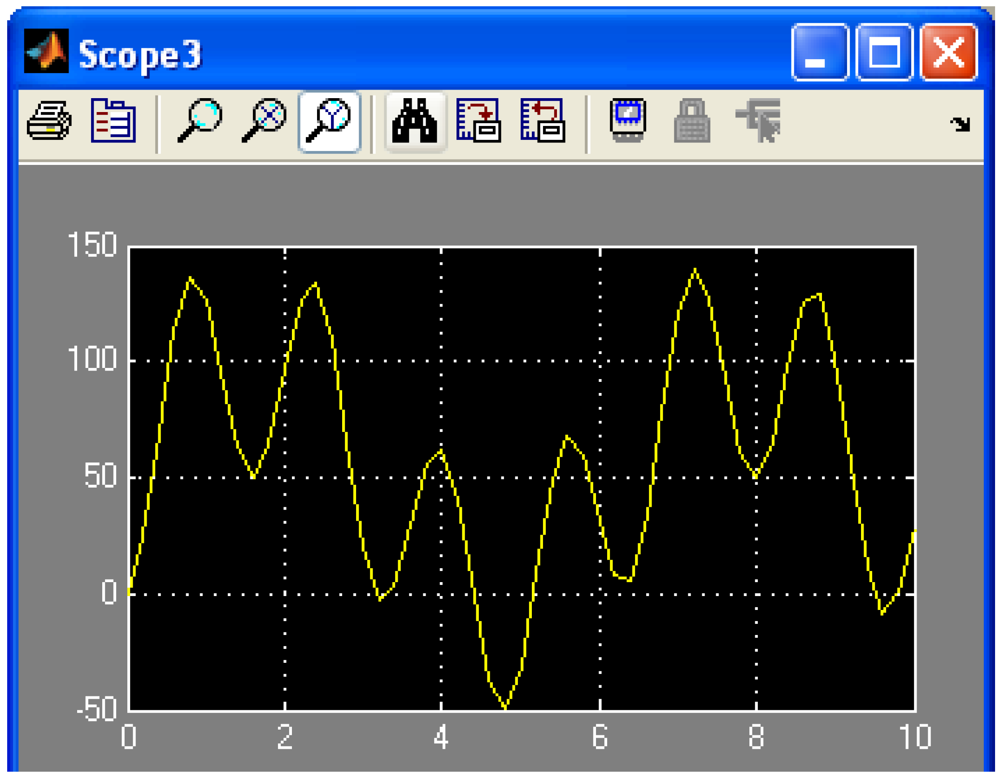
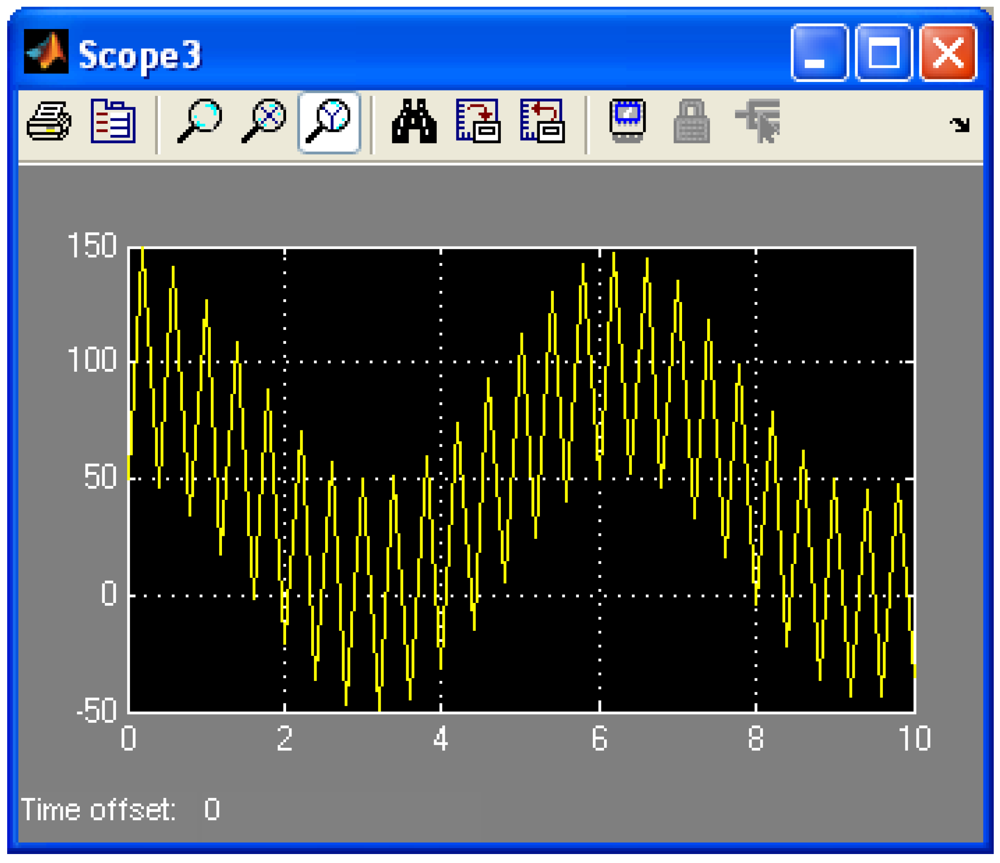
Figure 4 shows the simulation diagram for the spatial vector of concentration z(t) as a resultant oscillation wave depicting by the resonant absorption process of the environmental xenobiotic. This representation shows that in the particular case of the resonant absorption of the harmonic environmental xenobiotic, the output can be three times greater than the input amplitude. Note that to maintain a good degree of generality in this study we use the quantities with relative values.

The majority of research carried out on environmental contaminants has shown that these pollutants, following low level exposure to humans and animals, cause unexplained and irregular concentrations of xenobiotics to be accumulated in biological systems [1,2,3,4,5,6,7,8,9,10]. 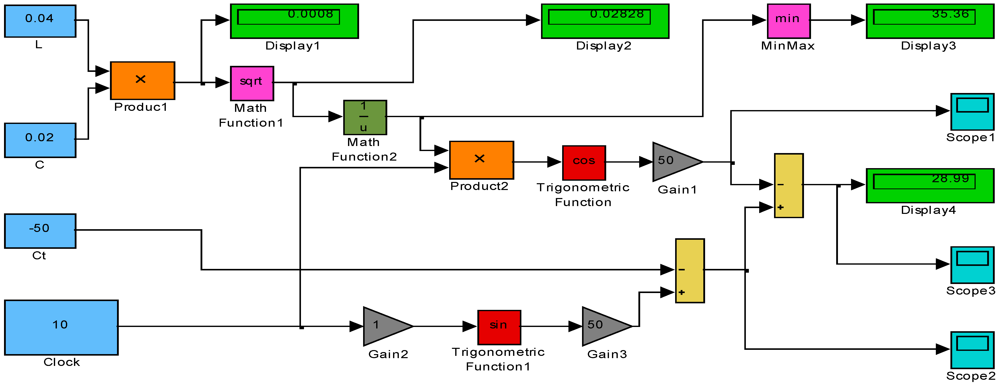In line with this idea and based on the same mathematical model, we further investigate the resonant absorption process considering a lower resonant pulsation ω₀₂ of the biological system. The simulation model for the spatial vector of concentration z(t) is depicted in Figure 5. Based on this simulation pattern, the representations of Figure 6, Figure 7 and Figure 8 are obtained. 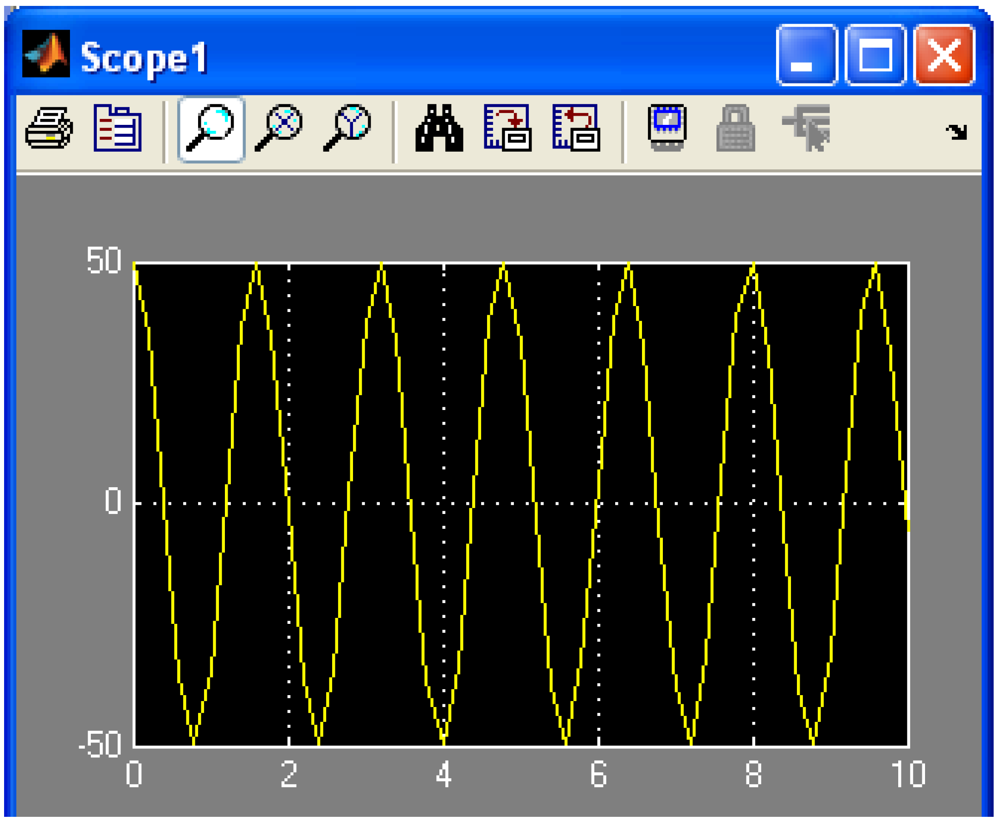Figure 6 depicts the modulating signal obtained on the basis of absorption circuit elements corresponding to the biological system with the resonant pulsation ω₀₂. In Figure 7, the xenobiotic harmonic oscillation, with the pulsation ω, is presented, while Figure 4 shows the simulation diagram for the spatial vector of concentration z(t) in this case, as a resultant oscillation wave depicting the resonant absorption process of the environmental xenobiotic.

Through this second case we seek to ascertain that the natural resonant frequency, as a characteristic parameter of any biologic entity, plays an important role in the evolution law of the absorption process of environmental xenobiotics. Since this could be a plausible explanation for the unpredictable results of experimental tests, it is likely that mathematical modeling and simulation represent a good additional approach in the study of absorption and removal processes for environmental xenobiotics.

The study of any system, including biological systems, usually entails an analysis of inputs and outputs, and system behavior can be assessed on the basis of mathematical modeling and simulation. Here, for an environmental xenobiotic source with an assumed harmonic behavior, the xenobiotic concentration evolution within a biological system is determined, assuming an analogy with a linear structure characterized by xenobiotic compounds of both dissipating and accumulating types.

Based on MATLAB software with SIMULINK and SimPowerSystems extensions, a SIMULINK model is developed entailing specific blocks generated with the SIMULINK library. The results determine the variation in time of the spatial vector of concentration z(t) as periodical, with the wave shape determined by taking into consideration a modulation of the main excitation harmonic provided by the xenobiotic, and the resulting high frequency modulating signal on the basis of elements specific to a xenobiotic absorption circuit. It is observed that the spatial vector of concentration has a temporal variation of a harmonic modulated type, defined by the absorption medium. The curves vary when the input parameters are changed.

This study also aims to ascertain if the natural resonant frequency, as a characteristic parameter of any biologic entity, can provide a plausible explanation of the unpredictable results of experimental tests on the absorption process of environmental xenobiotics. Mathematical modeling and simulation could provide an appropriate additional approach for studying absorption and removal processes of environmental xenobiotics.

Through consideration of hypothetic simulation diagrams for the spatial vector of xenobiotic concentration z(t) in a biological system, this study demonstrates the need for joint efforts by researchers in medicine, environmental engineering and computing for enhancing knowledge of the impacts of environmental xenobiotics on humans and other life forms.