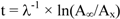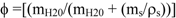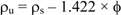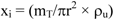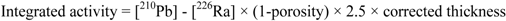1. Introduction
The Apipucos Reservoir is a sub-basin of the Capibaribe River, located in Apipucos, in the western area of the city of Recife, State of Pernambuco, built in order to control the Capibaribe River flooding. However, several districts of the metropolitan area of Recife, such as Casa Amarela, Nova Descoberta, Macaxeira, among others, make this dam a waste and sewage dumping area.
The
210Pb has two natural origins: one source is the
210Pb, originally formed in the atmosphere due to the decay of the
222Rn, usually named “unsupported
210Pb”, while the other, named “supported
210Pb” has its origin in the continuous production of
222Rn arising from the natural
226Ra contained in the sediments [
1]. The third source of
210Pb could be due to an anthropogenic origin, coming from wastes enriched in this radionuclide. The basis for the
210Pb dating technique applicable to sediment records is based on the determination of the
210Pb excess activities (“unsupported
210Pb” activities) in the layers of the cores in sediments uncontaminated with
210Pb [
1]. These excess
210Pb values are calculated by subtracting the estimated “supported
210Pb” value from the
210Pb activities determined in every layer. In this model, it is assumed that the incorporation of unsupported
210Pb to the sediment is produced at a constant flow and that the sedimentation rate is also constant [
2,
3]. It is the so-called Constant Initial Concentration (CIC) model. According to this hypothesis, the
210Pb excess activity in a layer z (cm) deep, A (z) (Bq/kg), is expressed as:
where A
o (Bq/kg) is the
210Pb excess activity in the top layer of the sediment core, λ is the
210Pb decay constant (0.031 year
-1), and ω is the sedimentation rate (cm.year
-1). There is another model for calculating this flux and the sedimentation rate is the Constant Rate of Supply model (CRS), which assumes a constant unsupported lead-210 flux to the sediment, but permits the sediment supply to vary [
4,
5,
6]. According to this model (
Figure 1):
where A∞ is the integrated activity from the surface to Ao, and Ax is the integrated activity from x to Ao.
Figure 1.
Constant Rate of Supply (CRS) model for dating by 210Pb.
Figure 1.
Constant Rate of Supply (CRS) model for dating by 210Pb.
2. Methods
Normally, it is not recommended to use direct methods for measuring alpha and beta radiation for the determination of 210Pb in environmental samples. However, the method becomes accurate when the sample is subjected to a radiochemical separation, stored for 15–30 days (to allow for 210Bi ingrowth) and then counted in a gas flow proportional detector. The efficiency and self-absorption curves are obtained for specific radionuclide and standards.
The sampling locations are shown in
Table 1. A 70-cm long 5-cm internal-diameter wide core was used for sediment sampling. Each core was sectioned into 3 cm intervals from the top (an estimated value, determined
in loco, “theoretical”).
Samples were dried at 105 °C to determine their water content. About 5 g dry material from each sample was dissolved with HNO
3 and HF. The
210Pb and
226Ra contents were separated by the method described in Moreira’s studies [
7]. The samples were placed in a 2 L beaker and the volume was made up to 1 L with water. To the same beaker, we added 1.0 mL (as a spike) of Pb
2+ (20 mg/mL) and Ba
2+ (20 mg/mL) with 5.0 mL of citric acid and 6 drops of methyl red indicator. The solution was stirred in a magnetic stirrer while adding concentrated NH
4OH until the turning of the indicator from pink to yellow (pH = 4.5 – 5.0) and heated in a heating plate. After that, 50 mL of 3M H
2SO
4 was added so that all ions precipitate as sulphates. Then the solution was decanted for 24 h. After that, the supernatant was separated and discarded, and the precipitate was transferred to centrifuge tubes with deionized water. After the centrifugation, the supernatant was discarded. To the precipitate was added 15 mL of tritriplex and heated in heating plate to dissolve all the precipitate. Four drops of methyl red and 1 mL of 1.8N H
2SO
4 were added, as well as glacial acid for pH adjustment. After being centrifuged, the supernatant was taken for the analysis of lead and the precipitate was kept for radio analysis. The supernatant containing the
210Pb was heated in a water bath, then, 2.0 mL of 1M Na
2S was added to precipitate the
210Pb as lead sulfide. The solution was centrifuged, the supernatant discarded and 5 mL of nitric acid (1:2) was added to the precipitate. The precipitate was heated in a water bath, where the elemental sulfur is formed while lead remains in solution. The solution was filtered through Whatman filter paper (blue ribbon) with the addition of 10 mL 40% ammonium acetate. The solution was heater in a heating plate and 2.0 mL of 30% Na
2CrO
4 was added to precipitate the lead as PbCrO
4. The samples were measured after 15 days of precipitation. To the precipitates previously obtained, 2.0 g EDTA and 40 mL of deionized water, 5.0 mL NH
4OH concentrated and three drops of methyl red were added and the solution was heated again in a heating plate to dissolve any precipitate. After total dissolution 5.0 mL (NH
4)
2SO
4 (25 mg/mL) was added and the radio was precipitated with glacial acetic acid. In the next day, the precipitate was filtered. Samples were measured after 21 days of precipitation. The chemical yield was determined by gravimetry and the contents of
210Pb and
226Ra were determined by alpha-beta counting from their daughters with a system Canberra℘ (model S5-XLB). The measurement time for each sample was standardized at 50 minutes, cover with a plastic thin layer for
210Pb analysis.
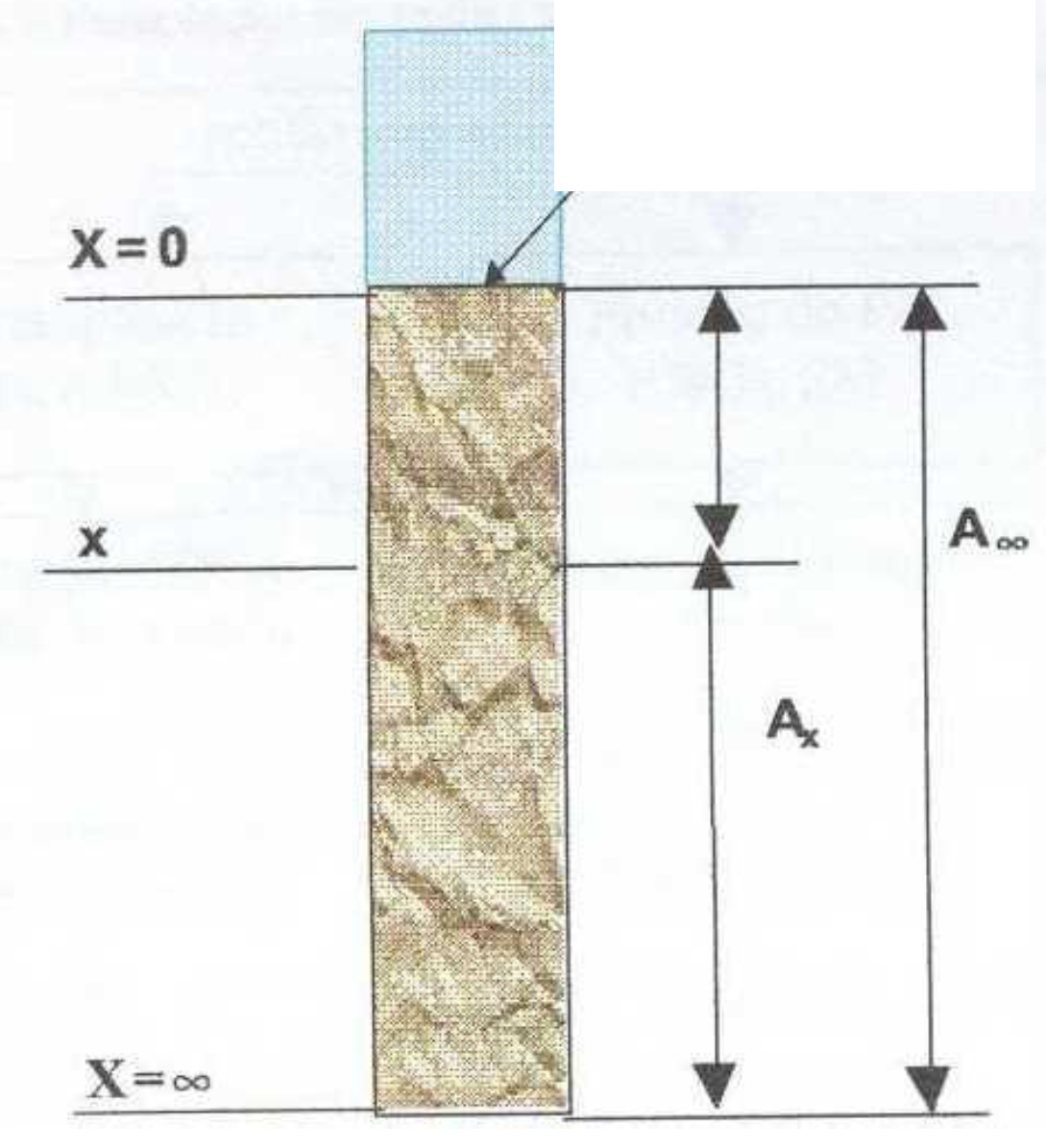
Table 1 shows the geographical coordinates of the sampling points. And
Figure 2 shows the localization of the sampling points.
Table 1.
Sedimentsampling pointsin the Apipucos Reservoir.
Table 1.
Sedimentsampling pointsin the Apipucos Reservoir.
| Sampling | Latitude | Longitude |
|---|
| Point | (S) | (W) |
|---|
| 1 | 8°01230’ | 34°56019’ |
| 2 | 8°01251’ | 34°55985’ |
| 3 | 8°01265’ | 34°55930’ |
| 4 | 8°01273’ | 34°55907’ |
Figure 2.
Points of sediment core sampling.
Figure 2.
Points of sediment core sampling.
3. Results and Discussions
Figure 3 shows the results for grain size analysis for a section from one of the cores. All core sections analyzed showed a predominance of medium sand in their structure [
8].
Figure 3.
Grain size analysis.
Figure 3.
Grain size analysis.
Sedimentation rates in the Apipucos Reservoir were determined by applying the
210Pb CIC model (
Figure 4,
Figure 5,
Figure 6,
Figure 7) and the CRS model (
Figure 10 and
Figure 11) to sediment cores collected at different stations. Sedimentation rate refers to the amount of materials (organic and inorganic) deposited by the action of rain water and water over a given time interval. The transport and deposition of sediments in a lake or river can cause degradation of the body of water, causing changes in the physical and chemical characteristics of water.
There is no standard for the optimum thickness for core sectioning, and the literature shows that thickness between 2 and 7 cm have been used. However, a thickness of 1 cm does not show very accurate results. In this work, we intended to maintain an average value of 3 cm for the thickness of each core section. However, when the values are corrected for compaction thicknesses ranging from 5 to 25 cm were found, considering all the collection points. Therefore, the corrected depth values will be used in the graphs for the sediment age calculation. Some researchers do not consider the top part of the core (first sedimentary layers) for calculating the ages because they consider that a lot of mixture can take place in these layers. A difference from 10 years is admissible for this dating method.
For the first collection point, it was possible to fill the entire length of the sampler with sediment. However, for the other collection points it was only possible to fill only half of the sampler length with sediment, due to the influence of the water column. Given the limited number of data points per core the uncertainty on the sedimentation rates are high. There is no information about the water depth.
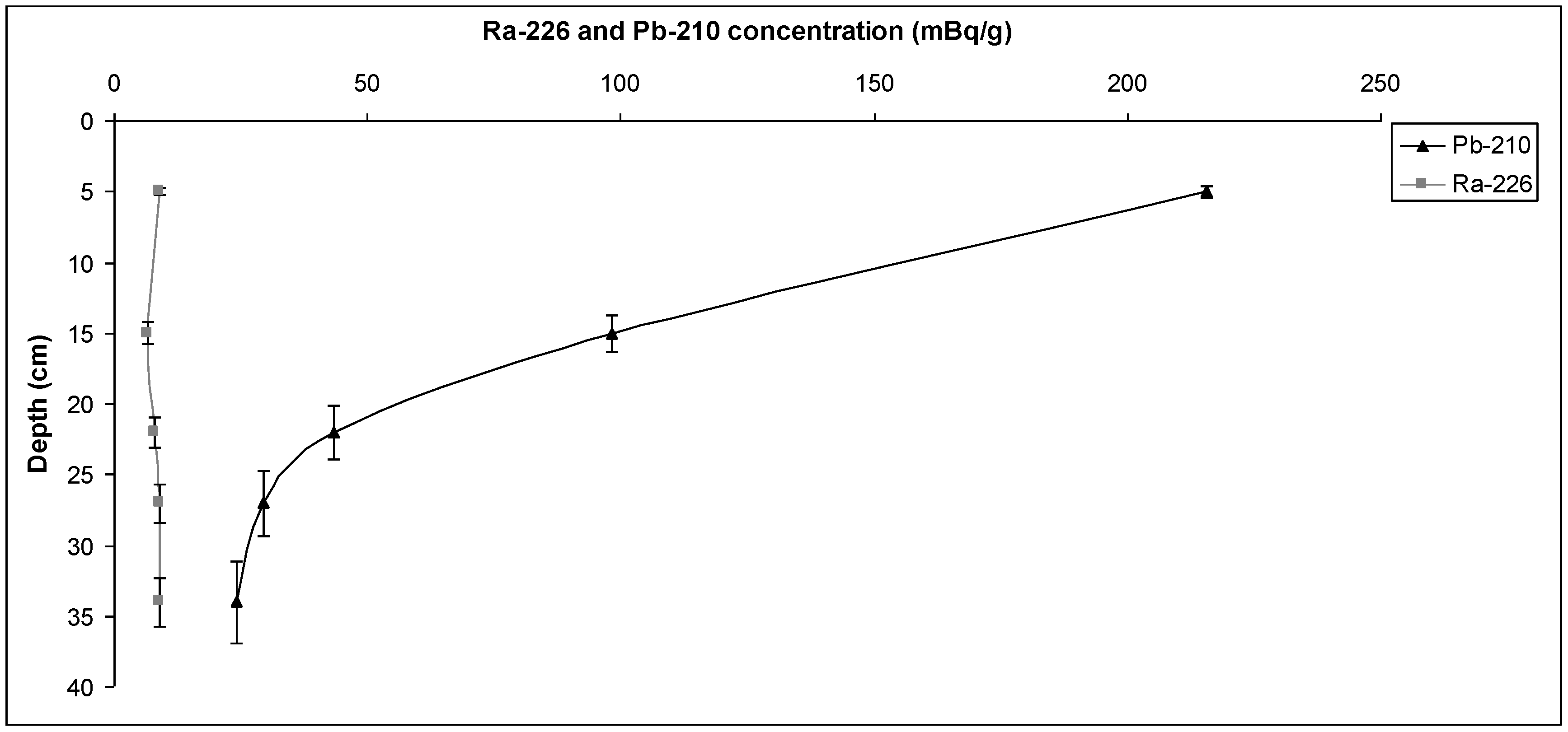
The presence of anthropogenic inputs of
210Pb (from the atmosphere) in the uppermost layers of the sediment cores is the hypothesis on which the lead-210 method is based. In this way, this technique is used to obtain a confident chronology covering the last 100 years. The depth for sediment analysis at each point, however, depends on how long it takes for the equilibrium between
210Pb and
226Ra concentrations to be reached (
Figure 8 and
Figure 9).
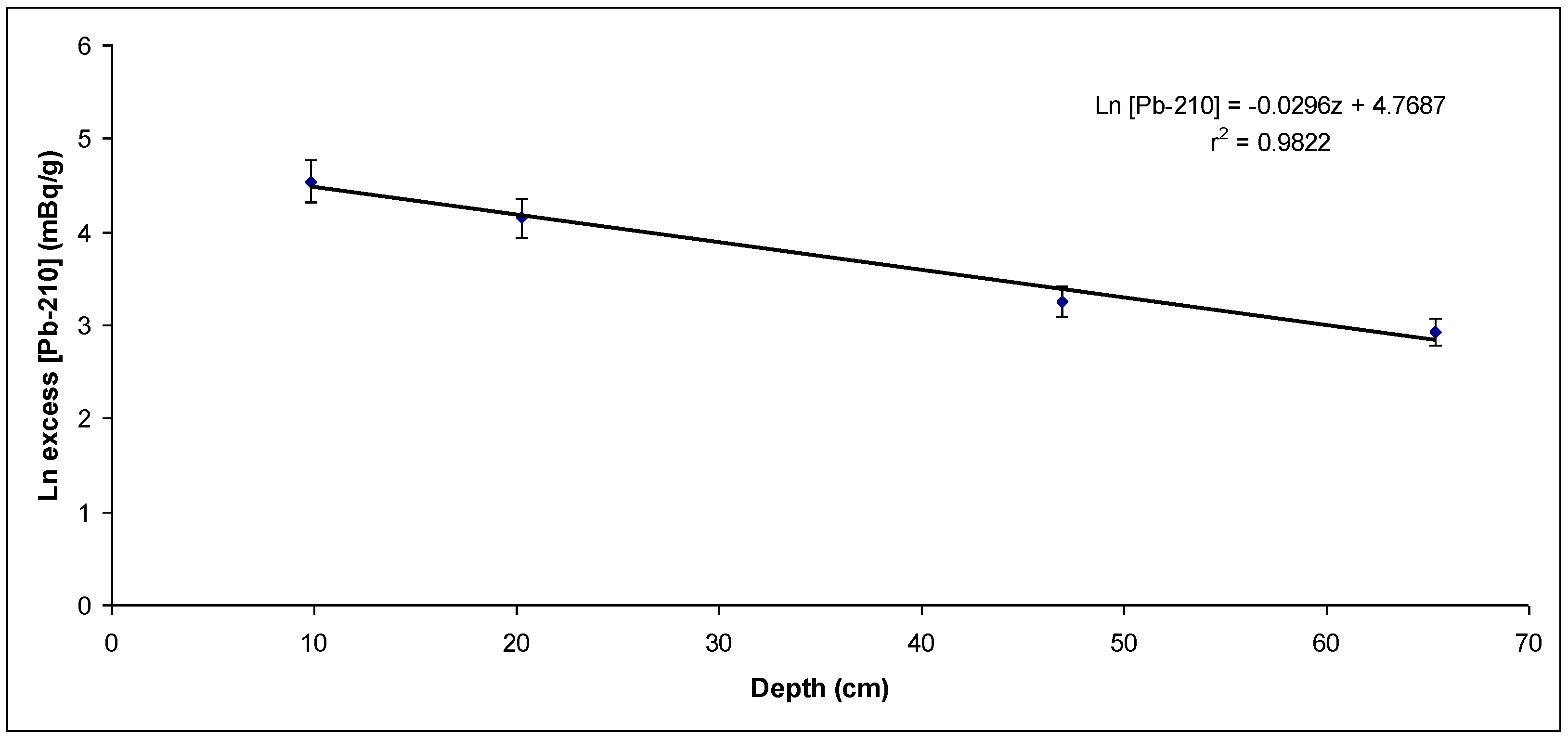
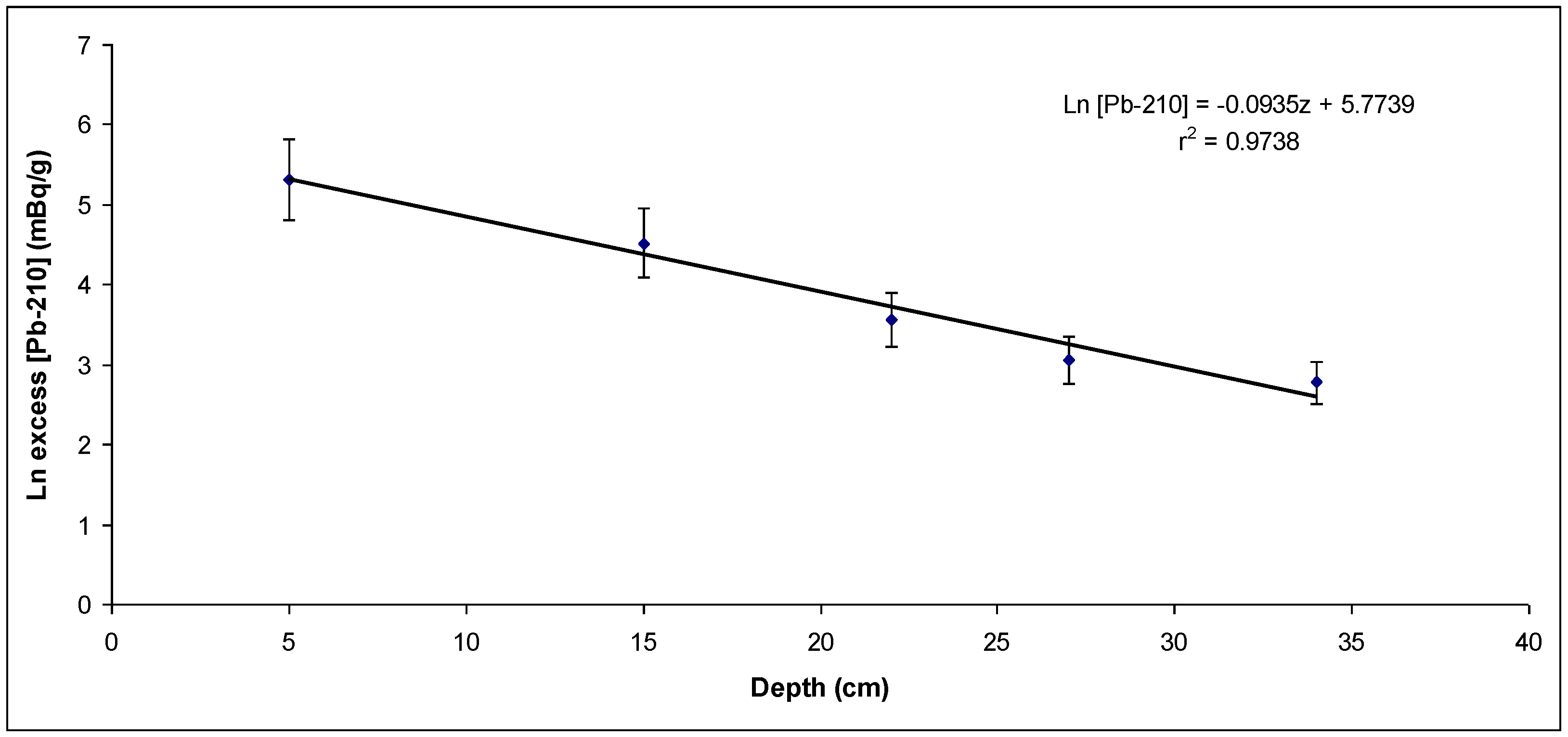
Figure 4.
Unsupported 210Pb activity concentration versus layer depth from the first sampling point (sedimentation rate: 1.05 cm/y).
Figure 4.
Unsupported 210Pb activity concentration versus layer depth from the first sampling point (sedimentation rate: 1.05 cm/y).
Figure 5.
Unsupported 210Pb activity concentration versus layer depth from the second sampling point (sedimentation rate: 0.33 cm/y).
Figure 5.
Unsupported 210Pb activity concentration versus layer depth from the second sampling point (sedimentation rate: 0.33 cm/y).
Figure 6.
Unsupported 210Pb activity concentration versus layer depth from the third sampling point (sedimentation rate: 3.1 cm/y).
Figure 6.
Unsupported 210Pb activity concentration versus layer depth from the third sampling point (sedimentation rate: 3.1 cm/y).
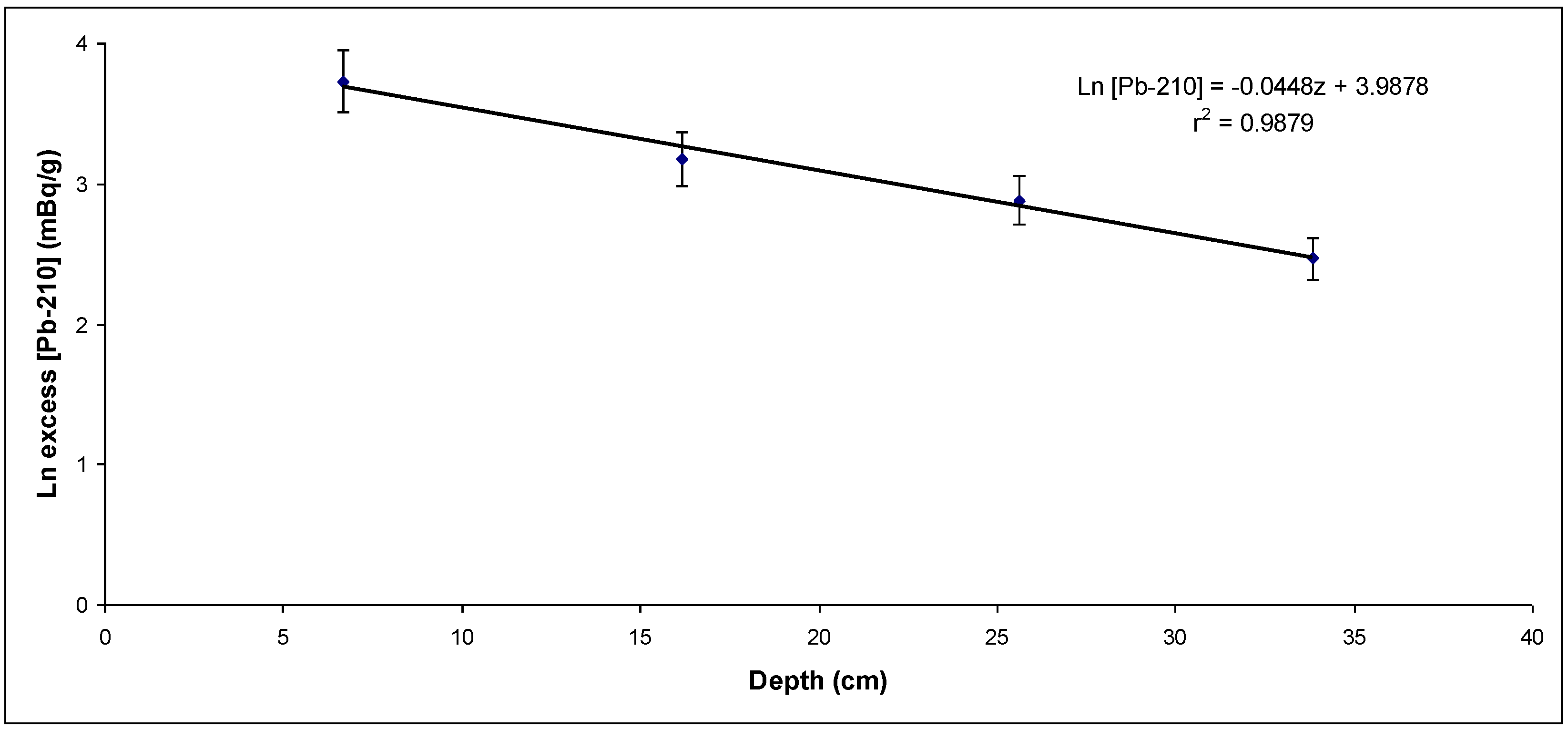
Figure 7.
Unsupported 210Pb activity concentration versus layer depth from the fourth sampling point (sedimentation rate: 0.69 cm/y)
Figure 7.
Unsupported 210Pb activity concentration versus layer depth from the fourth sampling point (sedimentation rate: 0.69 cm/y)
Figure 8.
210Pb and 226Ra concentration from the first sampling point.
Figure 8.
210Pb and 226Ra concentration from the first sampling point.
Figure 9.
210Pb and 226Ra concentration from the second sampling point.
Figure 9.
210Pb and 226Ra concentration from the second sampling point.
In order to calculate the ages of the sediments by the CRS model it is necessary to calculate both the porosity and density for the sediment samples. The porosity and the particle density were calculated according to equations 3 and 4, respectively.
where, mH20 = mass of water present in the sediment (g) (wet weight of sediment (mt)—mass of dry sediment); ms = mass of dry sediment (g) (considered as the specific mass of medium sand = 2.5 g/cm3); ρs = density of dry sediment. The wet density of the sediment can be calculated by the expression:
The density of the particles is important to calculate the corrected thickness (xi) by compaction of the sediment (Equation 5) which in turn will be necessary for calculating the integrated activities through the CRS model, evaluated according to Equation 6.
were, [210Pb] = 210Pb concentration and, [226Ra] = 226Ra concentration.
Table 2,
Table 3,
Table 4,
Table 5 show the results of the ages of the sediments when calculated by both models (CRS and CIC), from the first to the fourth sampling points.
Table 2.
Sediment ages calculated by the Constant Initial Concentration (CIC) model and the CRS model for the first sampling point.
Table 2.
Sediment ages calculated by the Constant Initial Concentration (CIC) model and the CRS model for the first sampling point.
| Depth (theoretical) (cm) | Depth corrected by sediment compaction (cm) | Ages (y) of the sediments (CIC model) | Ages (y) of the sediments (CRS model) | Corresponding year (CRS model) |
|---|
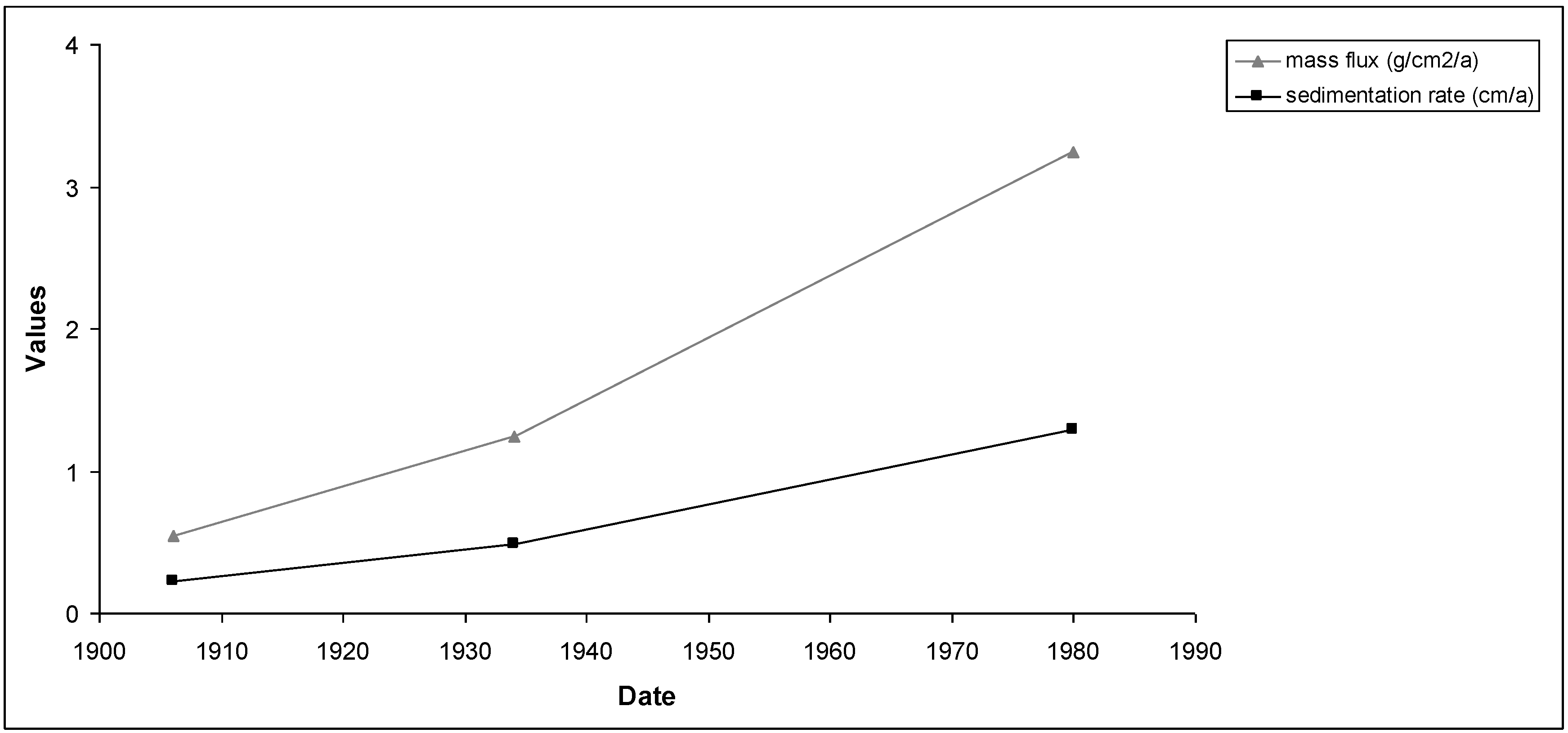
| 3 | 10 | 10 | 29 | 1980 |
| 6 | 20 | 20 | 75 | 1934 |
| 9 | 47 | 40 | 103 | 1906 |
| 12 | 65 | 60 | - | - |
Table 3.
Sediment ages calculated by the CIC model and the CRS models for the second sampling point.
Table 3.
Sediment ages calculated by the CIC model and the CRS models for the second sampling point.
| Depth (theoretical) (cm) | Depth corrected by sediment compaction (cm) | Ages (y) of the sediments (CIC model) | Ages (y) of the sediments (CRS ) | Corresponding year (CRS model) |
|---|
| 3 | 5 | 14 | 27 | 1982 |
| 6 | 15 | 46 | 50 | 1959 |
| 9 | 22 | 65 | 62 | 1947 |
| 12 | 27 | 82 | 73 | 1936 |
| 15 | 34 | 104 | 99 | 1910 |
Table 4.
Sediment ages calculated by the CIC model and the CRS models for the third sampling point.
Table 4.
Sediment ages calculated by the CIC model and the CRS models for the third sampling point.
| Depth (theoretical) (cm) | Depth corrected by sediment compaction (cm) | Ages (y) of the sediments (CIC model) | Ages (y) of the sediments (CRS model) | Corresponding year (CRS model) |
|---|
| 3 | 2.5 | 1 | 12 | 1997 |
| 6 | 12 | 4 | 32 | 1977 |
| 9 | 18 | 6 | 74 | 1935 |
| 12 | 24 | 8 | - | - |
Table 5.
Sediment ages calculated by the CIC model and the CRS models for the fourth sampling point.
Table 5.
Sediment ages calculated by the CIC model and the CRS models for the fourth sampling point.
| Depth (theoretical) (cm) | Depth corrected by sediment compaction (cm) | Ages (y) of the sediments (CIC model) | Ages (y) of the sediments (CRS model) | Corresponding year (CRS model) |
|---|
| 3 | 7 | 10 | 37 | 1972 |
| 6 | 16 | 23 | 48 | 1961 |
| 9 | 26 | 37 | 86 | 1923 |
| 12 | 34 | 52 | - | - |
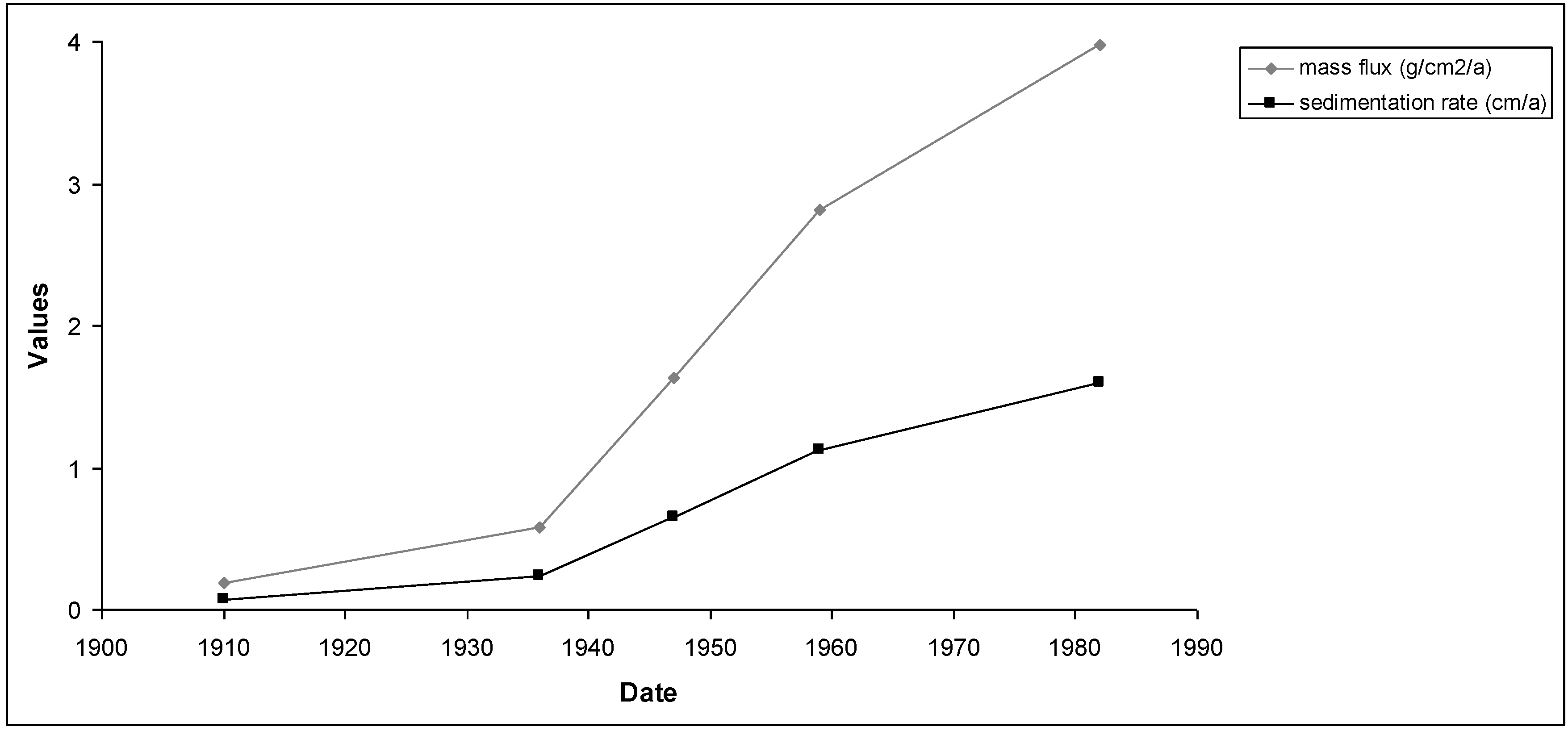
Figure 10 and
Figure 11 show the results of mass fluxes and sedimentation rates for the first and second sampling points.
Figure 10.
Mass fluxes and sedimentation rates calculated by the CRS model for the first sampling point.
Figure 10.
Mass fluxes and sedimentation rates calculated by the CRS model for the first sampling point.
Figure 11.
Mass fluxes and sedimentation rates calculated by the CRS model for the second sampling point.
Figure 11.
Mass fluxes and sedimentation rates calculated by the CRS model for the second sampling point.
This period (1970–1980) corresponds to the most intensive industrial and population growth in the region around the Reservoir and coincide with the history of the area. Sediment ages calculated by the two models showed some discrepancy between the first and third sampling points. This is because the ages obtained from Constant Initial Concentration model (CIC) were not appropriated. Therefore, only for the second sampling point could both models be used without any problem.