Understanding the Future of Change Agency in Sustainability Through Cellular Automata Scenarios: The Role of Timing †
Abstract
: One of the main interdisciplinary challenges today is to understand and change the dominant social perceptions and values that support and perpetuate unsustainable practices. Social computational simulations have been conceived in recent years to understand emergent results from complex systems. These dynamic social models are of interest to sustainability researchers because they provide a means to implement hypotheses and explore scenarios that could help extend our understanding of the future role of change agency in society. Change agents are individuals who directly or indirectly enable sustainable behaviors or inhibit practices that damage the environment and large social groups. Evidence-based strategies, guidelines and methods are necessary in order to manage creative change agency more effectively. This paper presents work with computational simulations, known as cellular automata, in order to explore the role of timing in triggering social change through uncoordinated, autonomous individual action. The paper identifies a number of issues related to creative change agency and proposes associated guidelines for practitioners. As a means of early validation, these findings are portrayed against empirical studies in the literature.1. Computational Social Models to Study Change Agency
Computational simulation has had a significant impact in the social sciences in the last two decades. As processing power became more accessible, it was realized that ‘artificial societies’ could be grown in in silico laboratories to study the emergence of target phenomena [1]. The potential contributions and limitations of computational methods to understand social processes are being increasingly documented, and a large number of approaches, tools and guidelines are emerging [2]. Social theories are predominantly built upon argumentation and equation modeling; computer programming is a third alternative to theorize about complex societal observations.
The main advantages of computational simulations include: the requirement of explicitness, as every modeling detail needs to be defined algorithmically; the exploration of scenarios, as the system can be executed iteratively by traversing every variable range and assessing the output; the replication of studies enabled by its experimental nature; and the possibility of conducting studies on controversial issues, or situations that are impossible to control with human subjects [2,3]. Beyond these methodological aspects, the main modeling advantage is the possibility of capturing the causal link between complex emergent system outcomes and the interaction of simple constituents over time [4,5].
The ability of these computational models to ‘grow’ emergence out of rather simple individual rules makes them of special value in the study of future change agency [6]. Future analysis is a particularly challenging task when the focus is on revealing patterns of extraordinary events, such as the conditions in which intentional change proposals are more likely to happen and the emergence of social and cultural system-wide transformations triggered by such proposals. Computational simulations provide a means to implement hypotheses and explore scenarios about sustainability that help extend our understanding of the role of individuals or minorities in introducing change in society and culture.
In contrast, the main limitations of studying future social scenarios with computer models include: (a) the current computational processing limitations to run models with very large populations (millions) or models with agents representing complex individual reasoning mechanisms; (b) existing display technology limitations of two-dimensional representations in computer screens; (c) data overload; (d) modeling trade-offs between representational simplicity and integration of numerous and complex system constituents and behaviors; (e) of special concern due to the methodological nature of this approach, validation limitations, i.e., in this type of computational model, claims should remain humble and oriented towards the clarifying of complex phenomena, and as a way to build and illustrate different views about future issues. Particularly in this work, the model should not be confused with what is being modeled.
This paper presents insights drawn from extensive experimentation with cellular automata (CA) models of change agency. The aim of the research presented here is to provide concrete evidence from computational simulations for scenario building and argumentation on the role of timing in change agency (to imagine what is possible, rather than to try to explain past events or forecast specific future scenarios). The insights on future change agency presented here are fuzzy by nature, but highly important as they help increase our understanding and formulate research questions for the future.
2. Cellular Automata Models of Social Agreement
Cellular automata (CA) represent a discrete modeling approach used in physics, mathematics, biology, complexity science, and only recently in social science. These models consist of an n-dimensional grid space (usually a two-dimensional toroidal grid of square or hexagonal cells) where each individual cell has a finite number of states and a set of rules that guide its interaction with adjacent neighbors. CA have an initial system state at time t = 0, and every cell updates its individual state at every simulated time step, usually as a function of the state of its neighbors. From such simple modeling conditions, certain CA models generate highly complex system patterns. An early CA is Conway's “Game of Life” [7], which displays interesting patterns from simple life/death or on/off state conditions in a cell's neighborhood. Thomas Schelling's [4] seminal models of social segregation are now paradigmatic in the use of CA to model social processes [8]. Although CA modeling started in the 1960s, it seems to have attracted significant attention recently, according to the number of journal and proceeding entries with the term in the title or abstract: 773 in the 2000–2009 decade against 151 during the 1990s and 129 during the 1980s in the ACM database [9].
Today, cellular automata (CA) models are the most basic form of computational social modeling. These simple rule systems seem largely limited by structure, time sequencing, information processing, initial conditions, and randomness; however, these apparent modeling constraints are disadvantageous only if one claims to be studying the system at certain levels of analysis. In such cases, multi-agent systems would be a better alternative, as they incorporate richer representation tools [10]. However, as a means to understand, illustrate and formulate research questions at a highly abstract level without confusing the model with the modeled, CAs are very helpful because they are extremely easy to model (entirely functional CAs can be done in spreadsheet programs), their behavior is easily tracked visually and in data log files, the description of its structure and algorithms is straightforward, and the results are often quite unexpected [2].
In this section we discuss Robert Axelrod's CA [5] influential model of social interaction, where culture is defined as the set of features shared by a population of individual constituents in a system. This CA was conceived for the study of the dissemination of culture, addressing how a community (i.e., a group of individuals with common values) forms according to the transmission of cultural elements among its individual members. The model describes an individual's culture in terms of a list of features or variables, and for each feature there is a set of possible traits or values. Interaction consists of cells checking for a shared trait with a random adjacent neighbor and picking a different trait, if any, to copy from the neighbor. More formally this simple model of ‘idea contagion’ is described as follows:
Let culture c at a site change as
select a random site s, a random neighbor of that site n, and a random feature f
let G(s, n) be the set of features g such that c(s, g) ≠ c(n, g)
if c(s, f) = c(n, f) and G is not empty, then select a random feature g and set c(s, g) to c(n, g).
The initial system state in this CA is given by the assignment of random cultures (sets of features) to every cell on the grid: at setup, a random trait or value is assigned to every feature or variable within each cell. Cell values can be represented by color schemes for illustration purposes; for instance, Figure 1 shows a CA grid of 250,000 cells after initialization, each is assigned a combination of three values that represent the rgb color palette (red, green, blue) with random integer numbers from 0 to 255. At every simulation step, cells exchange values with adjacent neighbors. Near initial time, cells repeatedly generate new colors due to the combination of values exchanged with neighbors. Due to this effect, all CA models of this type have a ‘diversity hill’ near initial state: a stage where system diversity increases before it gradually drops with the formation of groups or regions of cells with similar color hue. The final state of Axelrod's CA is system equilibrium where either all cells end up displaying the same shared color, or a few individual cells or small cell groups are ‘stuck’ with different colors from the majority. This latter final state occurs when a minority of cells stop all interaction with their neighbors due to incompatibility of values as specified in step #3 above. Final system equilibrium in these CAs is inevitable irrespective of grid size, feature and trait length, random distributions, types of neighborhood, toroidal structure, etc. The only differences in the final states across these parameters involve the time steps required to converge and the size of incompatible same-color minority regions.
These ergodic CA models have been used to formulate claims about the dissemination of culture, in particular the social effects of homophily [5]. In these grids, communication between system constituents is locally-perfect, while distant communication remains unaccounted for. Local interaction occurs at every time step between the same adjacent cells during the entire system history––a limiting assumption that can be challenged. In order to explore other scenarios, mobility is incorporated in these CA models to acknowledge variations in cell contacts. Cell mobility consists of the ability to move around the lattice in discrete steps based on specific neighboring conditions. The behavior remains similar to the model previously described, except that now grids are populated with a low density of active cells (≈70%), which are given the ability to move around the empty areas of the grid as a function of how many neighbors they have. More formally cell mobility is described as follows:
Let culture c at a site change as
select a random site s
if s has less than a number m of neighbors, move one grid step in a random direction
otherwise,
select a random neighbor of that site n, and a random feature f
let G(s, n) be the set of features g such that c(s, g) ≠ c(n, g)
if c(s, f) = c(n, f) and G is not empty, then select a random feature g and set c(s, g) to c(n, g).
The initial system state of this CA is given by the assignment of random cultures (set of features) to every cell, and also a random location on the grid. The main difference at initial time with the previous model is that the grid can be populated with varying density ratios as defined by the experimenter. Figure 2 shows two different CA models at initial time with varying densities. As a result, cells here tend to move across the grid until they gradually start forming stable groups or regions. As group clustering advances, patterns of color exchange can be observed within these groups until each group reaches their own final state of convergence. In rectangular grids with Moore neighborhood (i.e., eight adjacent neighboring cells) the threshold in rule #3 above is ≤3 neighbors; in hexagonal grids the threshold in rule #3 above is ≤2 neighbors. When cells are surrounded by a number of neighboring cells below such threshold, they move randomly across the grid; as neighboring cells stabilize, they anchor the formation of a group around which clustering emerges.
A new rule is further incorporated to extend the notion of cell mobility and intentional group formation: the ability of each cell to move around the empty areas of the grid as a function of their compatibility with their neighbors. To implement this, each cell incorporates a counter that increases one step every time that the condition in rule #4c is unfulfilled, that is, every time that a cell is unable to exchange a value with a neighbor. Then, a threshold t is set after which the cell moves away from its neighbors if no exchange occurs repeatedly. Such ‘mobility upon disagreement’ t value can be equal or similar to the number of features f of a cell, since statistically this is equivalent to registering neighborhood incompatibility.
Under these conditions, initial system state remains unchanged, and the system near initial time follows the same patterns as before. The main difference in this CA is that as proto-groups form, some of them may break apart if their members register incompatibility. In these CA, system equilibrium in convergence is significantly delayed, and occasionally a singular pattern emerges: once that stable groups or regions form, single cells may periodically leave a group and walk across the grid until they join other groups and exchange their values with the outer members of these groups. Such mobility and exchange of values between groups gives way to the emergence of group transformations, partly explained by the introduction of new values and partly explained by the creation of new cultures from the combination of new and old values.
The emerging pattern in such cases, is occasional CA simulations where total equilibrium or convergence fails, especially in very large grids with more than a few hundred thousand cells, each with rich feature sets. Just like certain initial states at Conway's ‘Game of Life’ are able to generate patterns of recursive change, so these mobility CA models are able to grow several groups that continuously affect each other and where new value combinations continuously emerge. Grid density needs not be very low at all: even by setting a few empty spaces in the grid (90% density), the exchange of values slows down significantly causing ‘niches’ where values are protected by groups of adopter cells as seen in Figure 3. The global effect is as if these gaps between cells prevented information from ‘sweeping across’ the grid. In most instances this blockage effect turns out to be beneficial for minority cultures as they don't disappear as easily by the power of the dominant values spreading in all directions and are able to build stronger local momentum.
Also notably, these models are adequate to illustrate a difference akin that between society and culture, which remain conflated in Axelrod's original CA [5]. Here, as stable groups or regions form throughout the grid, they exhibit cycles of convergence and divergence depending on the arrival of new individuals and their gradual assimilation. Thus, a group's color may change periodically, but its overall structure remains constant. Whilst the persistence of stable groups of adjacent cells illustrates social structure, periodical color transformations illustrate cultural evolution, i.e., cyclical value changes within these groups. In this way, these CA models of mobility represent the exchange of ideas between and within stable groups.
The main conclusions from these CA models of social interaction include:
Simple social models of the dissemination of predefined information will always tend to system equilibrium of value convergence (ergodicity). In such process, emergent structures gradually reinforce a dominant universal value, whilst diversity is destroyed.
Distributed, uncoordinated action between individuals who interact locally is sufficient to ‘grow’ emergent system agreement. CAs where individuals have no access to a broad view of the system but only act based on local conditions, illustrate the self-organizing systemic process of creation of coherent agreement structures.
Accounting for mobility is a guaranteed way to ‘grow’ diversity from two main sources: first, the transmission of information between distant groups, and second, the local emergence of new information when existing information from separate sources is combined. This is a way to understand ‘combinatorial innovation’ (intentional agency may be necessary for transformational innovation, see next section).
Even small ‘barriers’ provided by gaps of empty spaces in CA grids cause a significant slow-down in the rate of convergence: by relaxing the assumption of ‘perfect’ communication where all cells influence each other at all time steps, tolerance of diversity is increased through the emergence of niches of diversity.
The size of the system also influences its potential diversity: in larger systems it is harder to achieve equilibrium (at least under these ‘ideal’ distributed conditions). This is consistent with the common-sense notion that large cities are more diverse and tolerant than small towns.
‘Richness’ of information (feature length in this case) equally promotes diversity as a) compatibility is more likely within groups, and b) it is easier to disagree (across more opinion items) -akin the human dimension of interpretation of values and opinion.
Further details, pseudo-code, images and statistical analysis of these CA models are included in [11].
3. Change Agency in Cellular Automata Scenarios
One of the aims in this paper is to present a CA of dissemination of ideas that incorporates the ability to introduce novelty proposals, i.e., a basic model of change agency. Individual constituents of such a system periodically introduce a novel value, disagreeing with the status-quo. At more concrete levels of analysis, it would be necessary to account for differences in abilities amongst individuals, to specify objectives for such intentional creative skills, and to incorporate a representation of problem-solving and associated reasoning mechanisms. At the abstract level of CA, these issues are irrelevant: the modeling aim here is to understand system dynamics where a minority of constituents in a complex system tends to introduce novelty, in order to analyze the conditions under which such dissenting individuals may be able to trigger group changes. Rather than the causation mechanisms at the level of the individual, the focus of this study is on the micro-macro or local-global interactions, such as the effects of various degrees of novelty, the emerging relationships between dissenters, second-order effects of change, the formation of influential minorities, etc.
‘Success’ in this CA context refers to an episode where a change proposed by a single constituent of the system triggers a system-wide change thus causing all or large parts of the system to adopt the said change. ‘Dominance’ is defined as the system state where one single value is pervasive across the population. ‘Dissent’ is used to describe an individual's ability to reject the status-quo and introduce new values.
In this CA model, a minority of individual cells are able to dissent by proposing a new value when they register uniformity within their neighbors. Most of the cells, most of the time, keep disseminating existing values as in the previous model formulation. This is implemented by ascribing all cells with a very low probability (less than 1%) of introducing new values upon detection of a converged state in their neighborhood. This change magnitude is defined based on the rate of mutation in evolutionary systems, including models of cultural evolution [12]. The algorithm can be described as follows: if all adjacent neighbors have the same culture (set of features), try to set a random feature to a random value given a domain probability. More formally, this model of change agency reads:
Let a site s introduce an alternative feature f in culture c as
select all adjacent neighbours nn
let G(s, nn) be the set of features g such that c(s, g) = c(nn, g)
with a probability Pn, select a random feature g and set c(s, g) to c(s, g).
In contrast to the models described previously, in these CA the initial system state is set as total equilibrium or convergence of the population in one dominant value. Therefore, the initial aspect of the grid is the same shared color hue in all cells. As the simulation advances, the system continues to show a uniform color across the grid over long time periods, with the occasional burst of new color emerging from random cells as shown in Figure 4.
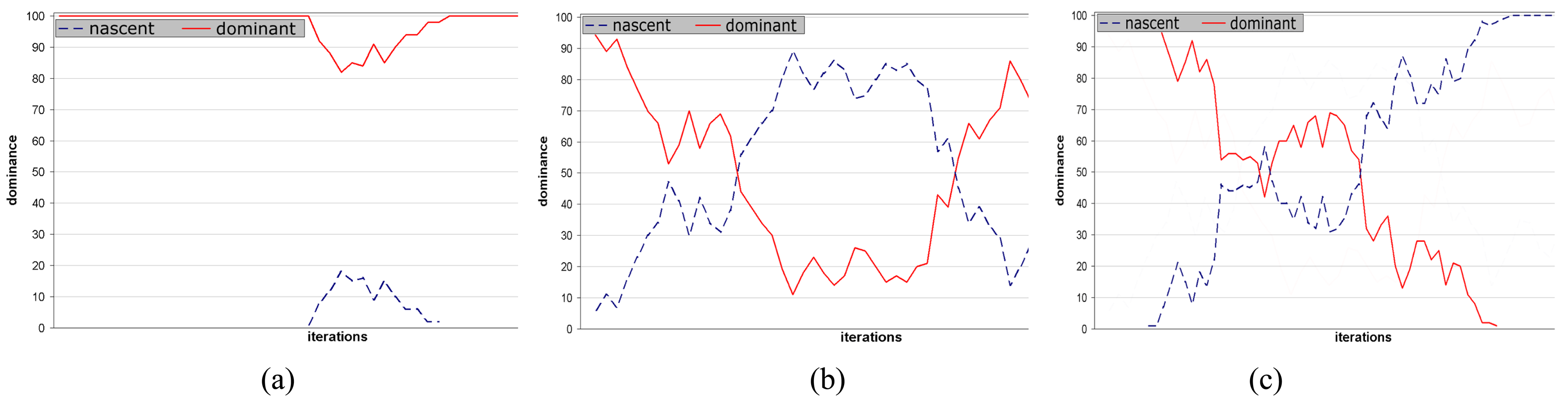
Different change episodes emerge in this CA. Figures 5a, 5b and 5c show three scenarios in time series where the vertical axis represents dominance of values. Figure 5a shows the most common scenario where new proposed values (nascent) disappear rapidly as they are rejected by the vast majority or dominant value. In such cases, the visual representation of the CA shows a constant color occasionally displaying regions bursting with alternative colors, but rapidly returning to total convergence to the same dominant value. Figure 5b illustrates cases where two or more colors compete across the grid, moving rapidly and quickly converging either to the original dominant culture, or as in Figure 5c, to a new culture that gains dominance.
When mechanisms of cell mobility are incorporated into this CA of divergent action (as described in Section 2 above), an extremely low percentage of novelty is sufficient (less than 0.01% are sufficient) to sustain cycles of stable dominance or convergence alternated by quick system transitions to new alternative cultures. As groups form, their members may introduce new values either by generating new proposals or by bringing new cultures from distant groups. In a few instances, these changes may even develop neighboring incompatibility and therefore one or more cells may leave a group and move randomly across the grid until they join or help form other groups.
The main conclusions from these CA models of divergence include:
A single individual has the potential to trigger system-side changes, even at very low probabilities over large periods of time. Whole system transitions seem almost ‘inevitable’ as a consequence of the appropriate uncoordinated sequences of information exchange.
Persistence is a key trait for an individual who aims to trigger intentional change, since system change is possible, but the probabilities of it being introduced by any particular constituent are extremely low and circumstantial.
Change is uncertain and unpredictable: even if an individual proposes a change, this novelty may trigger complex patterns by third-parties beyond the control of the change agent, and thus the system may collectively ‘grow’ a very different outcome.
Local support matters; it is important to have the support of surrounding individuals, and to work on the formation of local groups that can gradually help spread new ideas. Also, local social structures can benefit the rise of a new idea (irrespective of its intrinsic merits) by providing shelter from the status-quo.
The history of a system matters, because a new idea faces specific social and cultural conditions that are constantly changing. New ideas may successfully combine existing features, or they may rely on the long-term structural effects of previous ideas, for example the formation or dispersal of coherent social groups.
The interaction between a dominant majority and dissenting minorities is important because change proposals need to be scarce by definition, otherwise social structures of agreement cannot develop over time. Thus, novelty-seeking and difference-protecting groups are necessary, but equally are imitation groups otherwise no coherence and dominance exists to be replaced. This is a simple, yet powerful insight for innovators, as they must learn to ‘diagnose’ stages of convergence when change is relevant and opportune.
Timing is important (and thus we explore it in the next section): not only as explained above, but also because success depends on so many variables beyond anyone's control. For example, the exact same idea may have entirely different outcomes if it is introduced at different times and within different local conditions.
4. Understanding the Role of Timing in Future Change Agency
Taking the models analyzed above where individuals are able to introduce changes in otherwise stable systems, this section explores CA scenarios where change proposals are systematically introduced throughout a simulation in order to understand local-global interactions through time. Rather than aggregating results from hundreds of different simulation parameters to characterize the average system behavior, these more detailed scenarios are built upon repeatedly intervening one specific CA case where control variables are defined and one single experimental condition is manipulated on every run. One of the advantages of CA modeling is that it is feasible to ensure that all system variables remain constant between simulation runs, including all random processes by controlling the random-generator ‘seeds’ used by the computer to build number sequences. This advantage of replicability enables experimentation with hypotheses on the causes and effects of change.
In this case, a single individual cell is selected at setup, and on every simulation run this cell is enabled to introduce the same new value at an increasing stage of the system run. The same CA model is run one hundred times, each time the same selected cell introducing the same new value at intervals equal to one hundredth of the simulation steps taken by the CA to reach equilibrium given the original conditions of information dissemination as described in Section 2 above. The initial condition of this CA is whole system randomness. At setup, a random trait or value is assigned to every feature or variable within each cell. The final state is invariably-as in Section 2-system equilibrium where either all cells end up displaying the same shared color, or a few individual cells or small cell groups are ‘stuck’ with different colors from the majority.
Near initial time, when the system intrinsically increases its diversity as explained in Section 2, new values that are introduced by the experimental cell fail to affect the final system state: the dominant value remains the same with or without the introduction of this change into the system. Similarly, new values that are introduced near final equilibrium, also fail to affect the final system state as something similar happens as when new value proposals are made in stable populations: it is quickly replaced by the dominant value as shown in Section 3.
However, when new values are introduced in the middle section of the diffusion process, they are more likely to find a ‘region or window of opportunity’ at which they may produce a system-wide transformation. This is shown in Figure 6 where the same CA model (control random-generator seed) is recorded in different timings of novelty: the blue dashed line shows the trend of convergence when no new values are introduced and the resulting dominant value (#2800F3); the red continuous line shows an early introduction of a new value (#FFFFFF) causing a ‘disturbance’ in diversity that is rapidly assimilated by the convergent trend, ending in the same dominant value (#2800F3); the black line shows a ‘timely change’ where the same new value (#FFFFFF) is introduced, this time causing a significant trajectory change in the system that gives rise to a new final dominant value (#28FFF3).
Given the stochastic nature of CA modeling, it is unrealistic to extrapolate results from the different CA model parameters to real documented cases, but notably, this transitional stage closely resembles the ‘mainstream adoption’ stage of the sigmoid (or S-shaped) curve of diffusion in the innovation literature [13]. This key period occurs between the ‘tipping point’ (10% to 25% of adoption) and the ‘inflection point’ (75% to 90% of adoption) [14], which is comparable to the threshold observed in these CA models.
The notion of a ‘sweet spot’ in the time trajectory of these CA models would thus refer to time periods where individual interventions are more likely to trigger system-wide transformations. We may in this way characterize ‘noisy’ states as those where system diversity levels are high and individual change proposals tend to be lost in the chaotic battle between competing values. In contrast, ‘stable’ states are those where system convergence levels are high and individual change proposals are rapidly lost to the few remaining dominant values.
Our findings suggest that periods of opportunity are characterized by a system balance between diversity and convergence. In such transition periods, the local-global relationships in the system seem to facilitate the influence of individuals upon meso-levels of the system (CA neighbors of neighbors); an early influential wave that may grow further to affect the entire system. In a self-organizing diffusion process, these periods seem more likely to occur after an initial stage of agreement-building where local interactions become more coordinated. This corresponds to reaching a ‘tipping point’, a frontier between slow and rapid adoption rates. In these CA models such increase of speed is given by the increase in compatibility of features amongst neighboring and ‘regional’ cells. As regions or ‘neighborhoods of neighborhoods’ become more compatible, the rate of value exchange increases. Later in the process, this period of opportunity gradually ends in the inflection point; adoption slows down again as the differences between local and global states disappear. Particularly in systems of high density or where communication is unobstructed as in these CA, after the inflection point dominant views sweep across the structure and thus prevent any nascent values from building regional momentum.
Within such ‘windows of opportunity’ in these CA models, individual proposals are more likely to become regional forces that ultimately affect the final system state. The size of these key periods and the scope of these regions are likely to vary as a function of the specific parameters and dynamics of each model case, but in general the earlier a change proposal is made within this ‘window of opportunity’, the less predictable that the system state is likely to be: new values introduced are exposed for longer times to combinations with all other existing values. Therefore, one can infer from these CA models that individual change proposals that appear in semi-converged system states are more likely to have a controlled impact in the system state. Notice that this increase in probability is independent of the position of the individual on the CA structure, and independent of the actual value proposal in specific; it is merely a time-based property of the link between individual (micro), regional (meso) and whole system (macro) change.
It would be necessary to engage in further data capturing and analysis of a universe of cases in order to characterize the time dynamics of the likelihood of intentional change depending on a CA's particular history and trajectory, its grid size and structure, its feature length and type of neighborhood, etc. Extensive experimentation would also be necessary with different change proposals introduced by the same cell at different time steps, and with the same change proposal introduced by different cells at the same time steps. This would provide a characterization of specific CA cases and their vulnerability to certain types of changes in certain time periods. Although such detailed work sounds interesting, the outcome would probably not be that useful with this research paradigm, as it would only apply to the peculiarities of each CA case –including the modeling artifacts of its implementation. Arguably, this is precisely what makes this finding interesting: generalizations of creativity and innovation across cases and disciplines are expected at certain levels of analysis, but it would also seem possible that the link between individual and social change includes a fundamental nature of uniqueness in which synchronicity and time are important. Even these simple CA models of convergence and divergence capture the fundamental notion that the same change proposal by the same individual may trigger qualitatively different results depending on its timing in relation to system state.
The main conclusions from these CA scenarios of change proposals throughout time include:
Timing role 01 convergence: system change seems to be favored by early trends of agreement, at earlier periods diversity assimilates and dilutes new proposals and at later periods the status-quo dominates and silences new proposals. As a requisite, the first step in intentional change is therefore to diagnose the situation and act when some degree of early agreement exists.
Timing role 02 compatibility: intentional change strategies may require planning preliminary stages where ideas that are more compatible with current beliefs are accepted at a local or regional level, thus ‘preparing the stage’ for future radical system changes. The result may appear as disruptive outside the local or regional scope of early adoption where the change momentum is built. Conversely, system change may grow out of combinatorial changes which were only possible after the previous introduction of truly new values that are forgotten.
Timing role 03 impact: successful intentional change depends on a number of variables and conditions beyond a single constituent's control. The exact same idea may have entirely different outcomes if it is introduced at different times, not only it may live/die, but also depending on the stage of the whole system, it may combine with other competing ideas, it may remain latent for long periods, or it may burst rapidly without reaching mainstream status. Conversely, the success of dominant ideas cannot be explained by merit alone. In systems where autonomy and interdependence exist, chance is a likely causal factor of innovation.
Timing role 04 opportunistic change: intentional change in complex systems may be easier if emerging trends are identified and built on, in order to stir their trajectories towards a desired state. Innovation may therefore be less about implementation of original ideas and more about improvements of little-known or latent ideas.
Timing role 05 experience: success in triggering system change may fail as a predictor of future change proposals. Every instance of intentional change may require recent measurements and adjustments in order to synchronize personal, local, regional and whole system conditions. If previous success is considered an advantage by itself, experience becomes a handicap for innovation.
Timing role 06 persistence or speed: the speed and scope of system change depend on the complexity of information in the diffusion process. In systems where change proposals require more exchange of opinions or more interactions between system constituents, collective change is more difficult, ideas are more stable, and different versions and combinations of ideas are supported. In systems where change proposals are simple and require low information exchange, adoption may be faster-however, in such systems agreement is shorter in scope and less persistent over time.
Timing 07 situation-making: arguably the most important notion about the role of timing in intentional change here is the confluence between the history/trajectory of the system and the history/trajectory of the individual. Within shared contextual conditions, two or more individuals are likely to identify a common goal for system change. Their proposals are likely to differ, and these proposals are likely to be more or less appropriate as judged by their peers. However, what these CA models illustrate is the power of introducing proposals at appropriate times. Independently of the content of such proposals, when they are introduced matters. Not only the likelihood of acceptance of an idea changes over time, also because an idea may transform the group, it may open and close solution spaces once it is accepted by a majority.
5. Discussion
Discussion of the CA modeling work presented in the previous sections is approached in two parts: first, the roles of timing are compared to findings and insights from published studies in the literature. Then, guidelines for future change agents are drawn.
Timing role 01 convergence: the concept of intentional change being favored in transition stages between chaos and order resonates with the edge effect in ecology. This principle states that the juxtaposition of different ecosystems creates ‘transition areas’ with a tendency for increased diversity of species. In the CA models presented here, a similar transition stage is observed between variety and uniformity. Closer to our domain, Mihaly Csikszentmihalyi concludes that it is misleading to think that creative behavior of the type that achieves social acceptance can ever by widespread due to ‘reality boundaries’ between what is possible (new ideas) and what is useful (new solutions). The system-boundaries of the CA models presented here follow Csikszentmihalyi's tenet: “If all sixth-graders invented wheels, we would be run over. We don't have space for that many wheels” [15].
Timing role 02 compatibility: Rogers [12] identifies compatibility as one of the five main characteristics of innovation and defines it as “the degree to which a product is consistent with existing values and experiences”. Moreover, a major challenge in the study of innovation is that only successful cases are studied, and causal analysis happens after the change gains public attention [12]. This prevents access to the history of a change proposal and how it benefited from, or built on, other short-lived or small-scope changes and their compatibility relationship.
Timing role 03 impact: Dean K. Simonton has developed a model of scientific creativity that acknowledges the importance of luck [16]. According to this model, success is a function of individual output productivity and the expected or average hit rate for specific scientific domains. Such combination of individual and system characteristics (chance, logic, genius and zeitgeist) reinforces the insights gained from the CA models presented here. The concept of ‘hidden costs’ and unexpected consequences also suggest that new ideas can have large, indirect and unforeseeable results which may in turn cause new change proposals in the future.
Timing role 04 opportunistic change: Discoveries and inventions have the fundamental role of creatively destroying paradigms [17,18]. However, social acceptance is more likely when an idea presents subtle improvements that significantly increase its value or meaning [19]. One iconic example is the competition between Edison's phonograph and Berliner's gramophone: whilst the cylinder- based phonograph had clear technological advantages, the more user-centered concept of flat round discs gained industry support and public acceptance and thus transformed the music industry including the contemporary high-definition digital disc formats. The simple CA models presented in this paper illustrate system principles akin those by which Berliner successfully improved Edison's revolutionary platform in order to trigger a whole system and long-term transformation. Another sample case is the patents granted to inventor Andreas Pavel for the “Stereobelt” in 1977 and the ensuing revolution credited to Sony Walkman after 1979 [20].
Timing role 05 experience: Henry Ford's autobiography includes a remarkable insight: “No one ever considers himself expert if he really knows his job. A man who knows a job sees so much more to be done than he has done, that he is always pressing forward and never gives up an instant of thought to how good and how efficient he is. Thinking always ahead, thinking always of trying to do more, brings a state of mind in which nothing is impossible. The moment one gets into the “expert” state of mind a great number of things become impossible” [21].
Timing role 06 persistence or speed: Nelson and Stolterman [22] characterize intentional change in complex systems as the meaning-making process based on judgments on system conditions and individual aims: “Complex organizational systems design needs to be grounded in a tradition that embraces concepts such as judgment, interpretation, meaning making, and composition as elements of the core of organizational design competence” Complexity in our CA models is given by feature length, which provides an organization dimension. These models suggest that in more complex environments, dominant ideas are more persistent and intentional change does require richer processes of interpretation and negotiation. Societal approaches of open collaboration have been identified as the most appropriate innovation strategies for complex situations [23].
Timing 07 situation-making: Gero and Smith [24] define situations as individual “processes that direct how experiences proceed”, and further suggest that situations influence behavior as they “determine what external processes are in the current context”. Although our CA models do not capture such notion of situations as focused worldviews that condition behavior, they do illustrate their potential by showing that an individual process of interpretation is necessary for the synchronization in time and scope of intentional change with the whole system. By showing the timed-based evolution of likelihoods to affect the system, our CA models support the idea that creative situations are built by individuals within which they are able to identify the potential to trigger system change. It follows that a creative situation is not entirely dependent on the individual since exogenous conditions are necessary. Thus, a creative situation can be considered a multi-level concept between system and person, where causality is shared between the change agent's intentions and the aggregate decision of the system to move in certain directions.
The following recommendations stem from the patterns observed in our studies:
Timing role 01 convergence: change agents need to adopt and adapt qualitative research methods of value perception to understand how people perceive the value trajectories of past and present perceptions, and the value potential of future initiatives. Innovative strategies are required to identify ‘transition stages’ or time periods where change is more likely to take off. In principle, this concept would apply at different scales: from the creative process in multidisciplinary teams to the launch and promotion of new policies. According to our work, these transition stages can be diagnosed by increasing degrees of value convergence, i.e., stages in which the diversity of value proposals is decreasing probably after a stage of intense market competition or after a brainstorming session in a creative meeting. Being able to read the right conditions to launch a change proposal will help future change agents to avoid higher risks and frustration. This would also help to avoid misinterpreting the reasons behind the social or group rejection of a new idea.
Timing role 02 compatibility: a range of techniques and toolkits exist to estimate the compatibility of new policies or products, i.e., QFD, Pugh Matrix, Conjoint Analysis, etc. [25]. These or other tools are necessary to analyze and measure future features against current stakeholders' expectations and priorities. New ‘versioning’ strategies are necessary to plan changes in compatibility stages, or to improve the potential of nascent radical ideas by making them more compatible with dominant beliefs, norms and behaviors.
Timing role 03 impact: ethnographic tools and techniques are convenient to carry out pilot studies of new proposals. However, understanding the response of early adopters may cause misleading assumptions about mainstream adopters-the subtle process of interpretation is important, so validating any hypotheses with participatory methods is encouraged. Social and physical simulation methods may be valuable to study the likely effects of a change proposal; for instance, a solution may be ecologically sound at certain scale, but damaging at higher magnitudes. By definition, the innovation process is uncertain; the diffusion of ideas is an emergent process, so foreseeing consequences is a challenge. Learning from the past and building analogies from other domains may provide actionable insights for testing and for embedding anticipatory or adaptive solutions into our future proposals for sustainability.
Timing role 04 opportunistic change: the deliberate planning of second-generation platforms is popular in the design of electronic gadgets. This had turned into an environmental nightmare, but the principle of preparing the stage and learning from early adopters can be applied for more noble purposes, for instance as a way to replace unsustainable habits. Strategic planning can also be used to promote ‘lock-in’ adoption decisions, i.e., acceptance of an idea because a previous idea or product was chosen by the same person, by an influential person, by its social network, or by authorities. Upgrades and accessories can equally be considered to enable opportunistic change. In addition, change agents can take advantage of open technologies or open platforms which stakeholders can constantly modify and use to co-create according to system conditions or changes in their needs and expectations. Since change is likely to evolve beyond the original intent of its author, it is wise to learn when to assign a low priority to authorship and public recognition and focus on the actual impacts of change.
Timing role 05 experience: Bruce Corson's approach to collaborative innovation is based on the term ‘pre-expert’, a way to approach a problematic situation with the minimal preconception about its meaning, structure or dynamics [26]. Collaboration between pre-experts leads to creative solutions because it facilitates the discovery through exploration of novel problem formulations. The challenge is in finding the best balance between the strength of existing knowledge and tools, and the power of asking new questions. Strategies for sustainability are required to manage the interplay between exploration of new solution spaces and exploitation of rich sources and combinations.
Timing role 06 persistence or speed: not all change processes require the same scope and depth; change agents need to define the requirements of the problem at hand in order to decide the best strategies according to the complexity of the problem and the solution. Complex ideas may require simplification to speed up acceptance, or different change proposals may be introduced at stages of increasing complexity. An interesting approach comes from the concept of ‘nudges’ [27]. Strategy for sustainability based on nudges aim for simple and small changes that require minimal effort to be adopted and have the potential to enable significant change, whilst safeguarding the users' right to opt-out. The recent ‘fun theory’ approach to behavioral change is an example of an emotional nudge, although its real impact in long-term complex problems remains to be explored [28].
Timing 07 situation-making: all the previous guidelines conduct to a situational approach to change agency. Perhaps the most important insight for future change agents is to become aware of their situations and to acknowledge the potential to transform their situations. In all, the challenge of triggering successful disruptive changes seems to be less about talented and visionary ‘gurus’ leading hordes of followers, and more about change agents that are able to read their environment, build innovative opportunities, and synthesize or improve change proposals that people value. The causal origins of innovation may be situational combinations of individual and societal conditions.
The CA modeling of social processes presented in this paper is a powerful source of ideas. CA models are valuable as tools for reasoning about complex systems. Although CAs are simple, experimentation is far from exhausted. The models discussed here could evolve in a number of directions: to track individual histories of the change agents, to characterize agent action and system structure, or to embed complexity measures such as system and local entropy. Future work will also require exploring the link between CA modeling and other research paradigms and methods in order to better understand future change agency in complex systems. Lastly, CA models can be developed to gain insights and extract guidelines using specific frameworks, such as Donella Meadow's leverage points [29].





References
- Epstein, J.M.; Axtell, R.L. Growing Artificial Societies: Social Science from the Bottom Up; The MIT Press: Cambridge, MA, USA, 1996. [Google Scholar]
- Gilbert, N. Agent-based Models; Sage Publications: London, UK, 2007. [Google Scholar]
- Subrahmanian, V.S. Cultural modeling in real time. Science 2007, 317, 1509–1510. [Google Scholar]
- Schelling, T.C. Dynamic models of segregation. J. Math. Sociol 1971, 1, 143–186. [Google Scholar]
- Axelrod, R. The Complexity of Cooperation, Agent-based Models of Competition and Collaboration; Princeton University Press: New York, NY, USA, 1997. [Google Scholar]
- Sosa, R.; Gero, J.S.; Jennings, K. Growing and destroying the worth of ideas. Proceedings of the Seventh ACM Conference on Creativity and Cognition, Berkeley, CA, USA, October 2009; pp. 295–304.
- Gardner, M. Mathematical games: The fantastic combinations of John Conway's new solitaire game “Life”. Sci. Am. 1970, 223, 120–123. [Google Scholar]
- Journal of Artificial Societies and Social Simulation Home Page. Available online. http://jasss.soc.surrey.ac.uk/ (accessed on 1 January 2011).
- Association for Computing Machinery Home Page. Available online. http://portal.acm.org (accessed on 1 January 2011).
- Multi-Agent-Based Simulation Home Page. Available online. http://www.cs.vu.nl/MABS10/ (accessed on 1 May 2010).
- Sosa, R.; Gero, J.S. A computational study of creativity in design: The role of society. AI EDAM 2005, 19, 229–244. [Google Scholar]
- Boyd, R.; Richerson, P. Culture and the Evolutionary Process; University of Chicago Press: Chicago, IL, USA, 1985. [Google Scholar]
- Rogers, E.M. Diffusion of Innovations, 4th ed.; Free Press: New York, NY, USA, 1995. [Google Scholar]
- Gladwell, M. The Tipping Point: How Little Things Can Make a Big Difference; Back Bay Books: Boston, MA, USA, 2002. [Google Scholar]
- Epstein, R.; Csikszentmihalyi, M. A creative dialogue. Psych. Today 1999, 32, 58–62. [Google Scholar]
- Simonton, D.K. Creativity in Science: Chance, Logic, Genius, and Zeitgeist; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Schumpeter, J.A. Essays: On Entrepreneurs, Innovations, Business Cycles, and the Evolution of Capitalism; Transaction Publishers: New Brunswick, NJ, USA, 1989. [Google Scholar]
- Kuhn, T.S. The Structure of Scientific Revolutions, 2nd ed.; University of Chicago Press: Chicago, IL, USA, 1970. [Google Scholar]
- Verganti, R. Design Driven Innovation—Changing the Rules of Competition by Radically Innovating what Things Mean; Harvard Business Press: Boston, MA, USA, 2009. [Google Scholar]
- Bowrey, K. Fertile Ground: Law, Innovation and Creative Technologies. In New Directions in Copyright; Macmillan, F., Ed.; Edward Elgar: Northampton, MA, USA, 2007; Volume 5. [Google Scholar]
- Ford, H. My Life and Work; Project Gutenberg. Available online: http://www.gutenberg.org/ebooks/7213 (accessed on 1 January 2011).
- Nelson, H.G.; Stolterman, E. The Design Way: Intentional Change in an Unpredictable World; Educational Technology: Englewood Cliffs, NJ, USA, 2003. [Google Scholar]
- Von Hippel, E. Democratizing Innovation; MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Gero, J.S.; Smith, G.J. Context, situations and design agents. Know-Based Syst. 2009, 22, 600–609. [Google Scholar]
- The Innovator's Toolkit Home Page. Available online http://www.innovatorstoolkit.com/ (accessed on 1 January 2011).
- Corson, B. Sustainable design as a sustained upstream effort. Int. J. Eng. Educ. 2010, 26, 260–264. [Google Scholar]
- Thaler, R.H.; Sunstein, C.R. Nudge: Improving Decisions about Health, Wealth, and Happiness; Yale University Press: New York, NY; USA, 2008. [Google Scholar]
- The Fun Theory Home Page. Available online: http://www.thefuntheory.com/ (accessed on 1 February 2011).
- Meadows, D. Thinking in Systems: A Primer; Earthscan: London, UK, 2008. [Google Scholar]
- †Relevance to Practice: The computational social models discussed in this paper provide actionable insights that could be useful to creative practitioners who aim to trigger change towards sustainability in their professional contexts.
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Sosa, R. Understanding the Future of Change Agency in Sustainability Through Cellular Automata Scenarios: The Role of Timing †. Sustainability 2011, 3, 578-595. https://doi.org/10.3390/su3040578
Sosa R. Understanding the Future of Change Agency in Sustainability Through Cellular Automata Scenarios: The Role of Timing †. Sustainability. 2011; 3(4):578-595. https://doi.org/10.3390/su3040578
Chicago/Turabian StyleSosa, Ricardo. 2011. "Understanding the Future of Change Agency in Sustainability Through Cellular Automata Scenarios: The Role of Timing †" Sustainability 3, no. 4: 578-595. https://doi.org/10.3390/su3040578
APA StyleSosa, R. (2011). Understanding the Future of Change Agency in Sustainability Through Cellular Automata Scenarios: The Role of Timing †. Sustainability, 3(4), 578-595. https://doi.org/10.3390/su3040578



